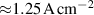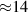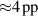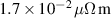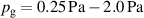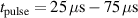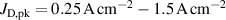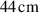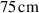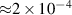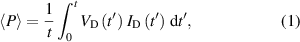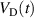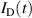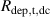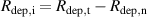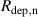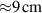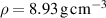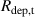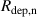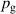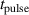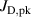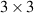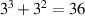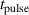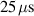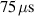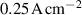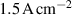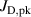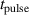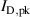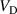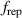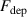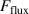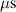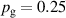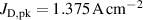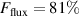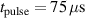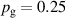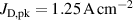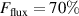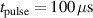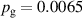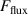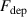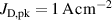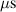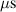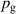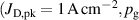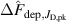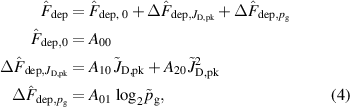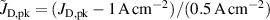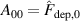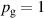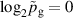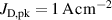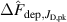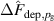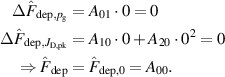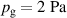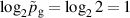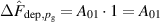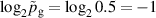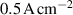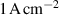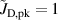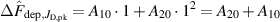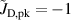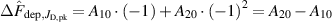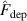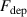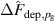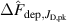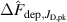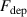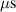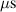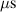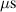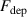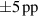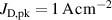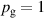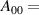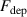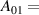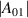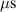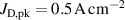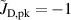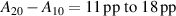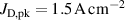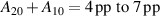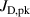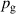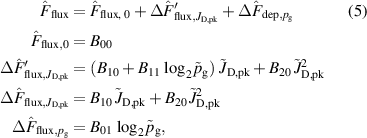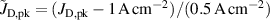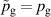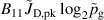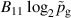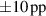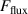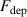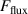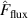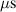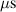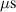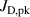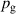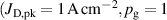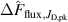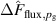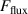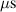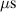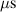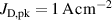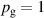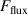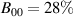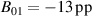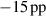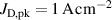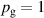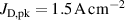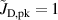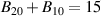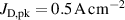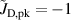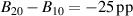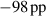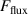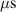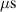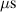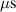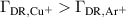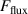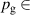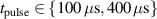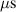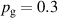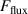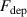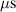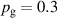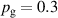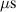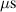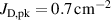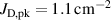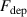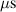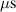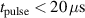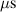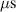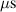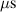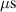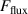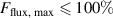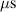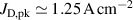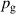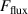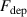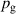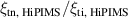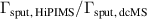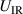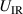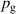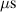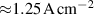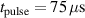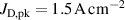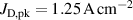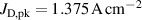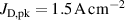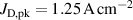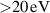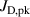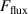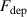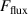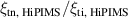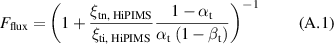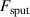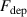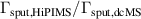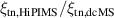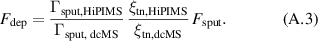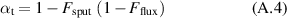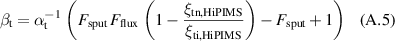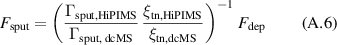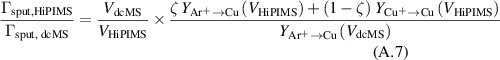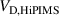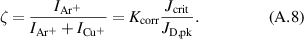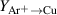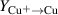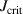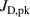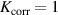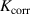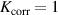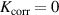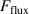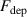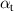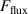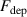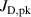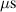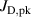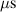Insights into the copper HiPIMS discharge: deposition rate and ionised flux fraction

The measurements were performed in a cylindrical stainless steel deposition chamber, ${44}\,\textrm{cm}$ in diameter and ${75}\,\textrm{cm}$ in height, which was equipped with a 152 mm diameter and 6.4 mm thick Cu target mounted on a standard, unbalanced, planar magnetron assembly. The base pressure was maintained at or below ${\approx}2\times 10^{-4}$ Pa by a Pfeiffer Vacuum (DN250) TMH 1601 P C H turbomolecular pump.

The argon (99.9997% purity) working gas pressure was measured using an MKS 626D Baratron capacitance manometer and calibrated before each discharge by regulating the mass flow in the range of 73 sccm–570 sccm.

The discharges were ignited by an HiPSTER 6 Ionautics HiPIMS pulser unit driven by a Technix SR series 6 kW 1 kV HV dc generator and either triggered internally or externally using an Agilent Technologies 33210A arbitrary wave-form generator. The target voltage and discharge current waveforms were recorded using a PicoScope 4444 20 MHz digital oscilloscope connected to the respective probe outputs of the HiPIMS pulser unit. The average discharge power was calculated by integrating the instantaneous power over a duration of 1 s according to

$$\begin{align} \left\langle P\right\rangle = \frac{1}{t}\int_0^t V_\mathrm{D}\left(t^{\prime}\right)\,I_\mathrm{D}\left(t^{\prime}\right)\,\mathrm{d}t^{\prime}, \end{align} \tag{ 1 }$$

where $V_\textrm{D}(t)$ is the discharge voltage and $I_\textrm{D}(t)$ the discharge current.

In order to maintain a constant average power of 500 W while varying the pulse length, working gas pressure, and peak discharge current density, the pulse repetition frequency was adjusted in the range of 19–1170 Hz. This large range is due to the large variation in average pulse energies (0.42–26 J) from cases at the extreme ends of the explored parameter space. The average power was chosen as low as possible in order to minimise target erosion over the course of the study while still achieving stable discharges for the low repetition rate cases.

The deposition rates were determined as a fraction of the rate measured for a reference direct current magnetron sputtering (dcMS) discharge as explained in section 2.2. When operating in dcMS mode, the dc power supply unit otherwise used to drive the HiPIMS pulser was directly connected to the magnetron assembly instead, and the power was set to 500 W by adjusting the discharge voltage.

The metal ion content in the film-forming flux and the total deposition rate are commonly quantified using the dimensionless ionised flux fraction $F_\mathrm{flux}$ and deposition rate fraction $F_\mathrm{dep}$ defined as

$$\begin{align} F_\mathrm{flux} & = \frac{R_\mathrm{dep,i}}{R_\mathrm{dep,t}} \end{align} \tag{ 2 }$$

and

$$\begin{align} F_\mathrm{dep} & = \frac{R_\mathrm{dep,t}}{R_\mathrm{dep,t,dc}}, \end{align} \tag{ 3 }$$

where $R_\mathrm{dep,t}$ and $R_\mathrm{dep,t,dc}$ are respectively the total deposition rate and the total deposition rate for a reference dcMS discharge operated at the same average power and otherwise identical conditions, and $R_\mathrm{dep,i} = R_\mathrm{dep,t}-R_\mathrm{dep,n}$ and $R_\mathrm{dep,n}$ are the deposition rates due to ions and neutrals only, respectively [31, 34]. As can be seen from the definitions in equations (2) and (3), being ratios, these quantities are independent of the absolute deposition rates and thus average power. This facilitates comparisons and has the advantage of not requiring an absolute rate calibration.

The total as well as neutral deposition rates required for the computation of the ionised flux and deposition rate fractions were measured using a magnetically shielded, charge-selective quartz crystal microbalance (QCM), henceforth referred to as ionmeter, as described by Kubart et al [21]. Such electrostatically [35] or magnetically shielded [36] QCM-based devices have previously been employed to measure the degree of ionisation of the sputtered metal flux in ionised PVD (iPVD). In particular, ionmeters have been used to characterise HiPIMS discharges of, amongst others, Al, Ti and Cu [22, 37, 38], and more recently to experimentally determine the angular dependence of the deposition rates due to ions and neutrals in HiPIMS discharges of Ti [39].

The ionmeter was set up at a typical substrate position, at a distance of ${\approx}{9}\,\textrm{cm}$ from the target surface and directly facing the ionisation region (and target racetrack) as illustrated in figure 1. It was protected by a shutter when not in use and at the beginning as well as the end of a measurement. The bias required for the neutral rate measurements was supplied by an OLTRONIX B60-5 R dc power supply connected over a 500 Ω resistor. The bias voltage, nominally set to $V_\textrm{bias} = +{70}\,\textrm{V}$, and the current drawn by the QCM were monitored using a Tektronix P2220 voltage probe and a Chauvin Arnoux C160 current clamp, both connected to the PicoScope 4444 unit also used to record the discharge current and voltage. Gold-coated AT-cut quartz crystals with a base frequency of 6 MHz were used down to a minimum of 57.5% crystal life, and the film thickness was registered using a Kurt J Lesker FTM-2400 readout unit (film mass density $\rho = {8.93}\,\textrm{g}\,\textrm{cm}^{-3}$, Z-factor Z = 0.44).

Zoom In Zoom Out Reset image size

To make the measurements more robust against eventual noise, all measurements followed the exact same procedure. The recording of the crystal frequency was started with the shutter still closed and the pulser unit turned off. After 10 s, the pulser unit was turned on, and after yet another 10 s, the shutter was opened. After a measurement duration of, depending on the deposition rate, 180–600 s, the shutter was closed, and after yet another 10 s, the discharge was turned off again. Finally, the recording was stopped after at least another 20 s had passed. The rate could then be calculated by comparing the frequency before and after the deposition. An example of such a rate measurement is shown in figure 2. The individual rates have also been normalised with respect to the average power to account for small deviations from the 500 W set point.

Zoom In Zoom Out Reset image size

The bulk of the experiments were performed in three main blocks, starting off with a $3 \times 3$ Box–Behnken-like design (block I) with the variables $p_\textrm{g}$ (working gas pressure), $t_\mathrm{pulse}$ (pulse length) and $J_\mathrm{D,pk}$ (peak discharge current density), which was first extended to a $3 \times 3$ full-factorial-like design (block II), and then again to higher pressures (block III) for a total of $3^3+3^2 = 36$ investigated discharges. The levels for the pulse length $t_\mathrm{pulse}$ were chosen equidistant, ranging from ${25}\,\mu{\textrm{s}}$ to ${75}\,\mu{\textrm{s}}$, while for the working gas pressure $p_\textrm{g}$, a logarithmic scale ranging from 0.25 Pa to 2 Pa was used. Since the maximum reachable peak discharge current density depends on the former two variables, a nominal scale (low, medium, high) ranging from ${0.25}\,\textrm{A}\,\textrm{cm}^{-2}$ to ${1.5}\,\textrm{A}\,\textrm{cm}^{-2}$ was applied for the peak discharge current density $J_\mathrm{D,pk}$ to nevertheless be able to explore high peak discharge current scenarios.

In an attempt to minimise systematic errors that might arise due to, e.g. target erosion [40], crystal usage or chamber and crystal heating over the course of the large number of measurements, the experiments in each block were performed in a randomised order. Additionally, the setup was not modified and vacuum never broken during these three phases. An overview of the complete measurement plan can be found in table 1.

Table 1. The process and flux parameters of the 36 main experiments listed. The experiment numbers reflect the order the experiments have been performed in.

$\#$	$p_{\mathrm{g}}$	$t_{\mathrm{pulse}}$	$I_{\mathrm{D,pk}}$	$V_{\mathrm{D}}$	$f_{\mathrm{rep}}$	$F_{\mathrm{dep}}$	$F_{\mathrm{flux}}$
—	(Pa)	($\mu{\textrm{s}}$)	(A)	(V)	(Hz)	(%)	(%)
7	0.25	25	90	870	580	38	21
6	0.25	50	90	750	360	42	22
1	0.25	50	180	865	145	29	62
4	0.25	75	180	830	94	29	64
10	0.50	25	90	810	605	38	15
3	0.50	25	180	935	250	18	39
8	0.50	50	180	820	130	22	47
11	0.50	75	180	795	77	24	59
9	0.50	75	270	1000	34	20	65
13	1.00	25	180	880	255	16	25
12	1.00	50	180	780	126	17	31
2	1.00	50	270	960	55	8	62
5	1.00	75	225	870	45	15	69
15	0.25	25	45	750	1130	54	11
17	0.25	25	135	940	360	31	48
19	0.25	50	135	800	220	32	39
27	0.25	75	135	745	170	35	38
26	0.25	75	225	930	55	27	81
25	0.50	25	135	875	375	28	31
14	0.50	50	135	750	200	27	26
18	0.50	50	225	905	80	18	68
22	0.50	75	225	905	47	23	73
24	1.00	25	135	820	385	25	22
16	1.00	25	225	950	180	11	33
23	1.00	50	225	860	82	12	56
20	1.00	75	180	760	73	19	48
21	1.00	75	270	960	33	14	66
33	2.00	25	180	838	262	13	17
32	2.00	25	225	900	187	8	18
34	2.00	25	270	970	140	7	32
30	2.00	50	180	740	130	13	21
35	2.00	50	225	816	85	10	49
36	2.00	50	270	892	59	8	77
29	2.00	75	180	725	74	12	22
31	2.00	75	225	810	48	8	46
28	2.00	75	270	900	33	6	46

Additional measurements extending the $p_\textrm{g} = {0.25}$ Pa cases to higher peak discharge current densities and longer pulse lengths, repetitions of previous measurements, and measurements at $J_\mathrm{D,pk} = {1.375}\,\textrm{A}\,\textrm{cm}^{-2}$ were carried out later on to confirm trends seen in the previous measurements. It should however be noted, that by the time these measurements were performed, the setup had undergone some changes and the target had been significantly eroded (erosion depth of 1.8 mm corresponding to a little less than one-third of the target thickness). These measured values are displayed in appendix B together with those of the main measurements, however they are otherwise excluded from the analysis.

The measured deposition rate fraction is visualised by the symbols in figures 4(a)–(c) grouped by pulse length. Fitted surfaces, obtained as described below, are included as an aid for localising the points. There is a clear decreasing trend with both increasing working gas pressure and increasing peak discharge current density. The fitted surfaces should however not be used to extrapolate to values outside the region delimited by the measured points.

Zoom In Zoom Out Reset image size

In order to quantitatively analyse the influence of the process parameters, the variation in the measured deposition rate fraction is formally decomposed into effects due to changes in the working gas pressure $\Delta\hat{F}_{\textrm{dep}, p_\textrm{g}}$ and peak discharge current density $\Delta\hat{F}_{\textrm{dep}, J_\textrm{D,pk}}$ according to

$$\begin{align} \hat{F}_\textrm{dep} & = \hat{F}_\textrm{dep, 0} + \Delta\hat{F}_{\textrm{dep}, J_\textrm{D,pk}}+ \Delta\hat{F}_{\textrm{dep}, p_\textrm{g}}\nonumber\\ \hat{F}_{\textrm{dep}, 0} & = A_{00}\nonumber\\ \Delta\hat{F}_{\textrm{dep}, J_\textrm{D,pk}} & = A_{10}\,\tilde{J}_\textrm{D,pk} + A_{20}\,\tilde{J}_\textrm{D,pk}^2\nonumber\\ \Delta\hat{F}_{\textrm{dep}, p_\textrm{g}} & = A_{01}\,\log_{2}\tilde{p}_\textrm{g}, \end{align} \tag{ 4 }$$

where A₀₀, A₁₀, A₂₀, and A₀₁ are fitting parameters used to estimate and quantify the individual effects and do not have a direct physical meaning. To facilitate the interpretation of the results, the recentred and dimensionless variables $\tilde{J}_\textrm{D,pk} = (J_\textrm{D,pk}-{1}\,\textrm{A}\,\textrm{cm}^{-2})/({0.5}\,\textrm{A}\,\textrm{cm}^{-2})$ and $\tilde{p}_\textrm{g} = p_\textrm{g}$/(1 Pa) have been introduced, where the offsets have been chosen such that $(\tilde{J}_\textrm{D,pk},\log_2\tilde{p}_\textrm{g}) = (0,0)$ corresponds to the chosen reference discharge. Thanks to this change of variables, the fitting parameters have a relatively straightforward meaning. For instance, $A_{00} = \hat{F}_\textrm{dep,0}$ simply corresponds to the estimated value for the chosen reference discharge at $p_\textrm{g} = {1}$ Pa ($\log_2\tilde{p}_\textrm{g} = 0$) and $J_\textrm{D,pk} = {1}\,\textrm{A}\,\textrm{cm}^{-2}$ ($\tilde{J}_\textrm{D,pk} = 0$) since both $\Delta\hat{F}_{\textrm{dep}, J_\textrm{D,pk}}$ and $\Delta\hat{F}_{\textrm{dep}, p_\textrm{g}}$ are trivially equal to zero:

$$\begin{align*} \Delta\hat{F}_{\textrm{dep},p_\textrm{g}}& = A_{01}\cdot 0 = 0\\ \Delta\hat{F}_{\textrm{dep}, J_\textrm{D,pk}}& = A_{10}\cdot0+A_{20}\cdot0^2 = 0\\ \Rightarrow\hat{F}_\textrm{dep}& = \hat{F}_\textrm{dep,0} = A_{00}. \end{align*}$$

Similarly, A₀₁ corresponds to the change associated with changing the working gas pressure by a factor of two, since for example at $p_\textrm{g} = {2} \ \textrm{Pa}$ we have $\log_2\tilde{p}_\textrm{g} = \log_2 2 = 1$ and thus

$$\begin{align*} \Delta\hat{F}_{\textrm{dep},p_\textrm{g}} = A_{01}\cdot 1 = A_{01} \end{align*}$$

or at $p_\textrm{g} = {0.5}\,\textrm{Pa}$ ($\log_2\tilde{p}_\textrm{g} = \log_2 0.5 = -1$)

$$\begin{align*} \Delta\hat{F}_{\textrm{dep},p_\textrm{g}} = A_{01}\cdot\left(-1\right) = -A_{01}. \end{align*}$$

Finally, the change associated with increasing or decreasing the peak discharge current density by ${0.5}\,\textrm{A}\,\textrm{cm}^{-2}$ with respect to the chosen reference peak discharge current density of ${1}\,\textrm{A}\,\textrm{cm}^{-2}$ is given by the sum ($\tilde{J}_\textrm{D,pk} = 1$)

$$\begin{align*} \Delta\hat{F}_{\textrm{dep}, J_\textrm{D,pk}} = A_{10}\cdot1+A_{20}\cdot1^2 = A_{20}+A_{10} \end{align*}$$

respectively the difference ($\tilde{J}_\textrm{D,pk} = -1$)

$$\begin{align*} \Delta\hat{F}_{\textrm{dep}, J_\textrm{D,pk}} = A_{10}\cdot\left(-1\right)+A_{20}\cdot\left(-1\right)^2 = A_{20}-A_{10} \end{align*}$$

of A₂₀ and A₁₀.

Using equation (4) it is now possible to fit response surfaces $\hat{F}_\textrm{dep}$ to the measured $F_\textrm{dep}$ values. The fitted surfaces, obtained using an ordinary least squares regression on the main measurements, are illustrated in figure 4. The individual changes in percentage points (pp) on the deposition rate fraction by changing the working gas pressure $\Delta\hat{F}_{\textrm{dep}, p_\textrm{g}}$ or the discharge current density $\Delta\hat{F}_{\textrm{dep}, J_\textrm{D,pk}}$ are plotted in figures 5(a) and (b), respectively. The corresponding parameter values as well as the root-mean-square error (RMSE) are shown in figure 6.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

As can be seen in figures 5(a) and (b), the fits accurately reproduce the measured deposition rate fraction $F_\textrm{dep}$ to within a margin of $\pm{5}\,\textrm{pp}$ without the need for an interaction term, indicating that the effects of peak discharge current density and working gas pressure are well separable. At the chosen reference point of $J_\textrm{D,pk} = {1}\,\textrm{A}\,\textrm{cm}^{-2}$ and $p_\textrm{g} = {1}$ Pa, the deposition rate fraction is in the range $A_{00} =$ 16%–18% (see figure 6) showing comparatively little variation between the three pulse lengths. Both increasing peak discharge current density and increasing pressure have a negative effect on the deposition rate fraction. Figure 5(a) suggests $F_\textrm{dep}$ decreases linearly with the logarithm of the pressure, a reduction by a factor of two corresponding to, depending on pulse length, an increase of $A_{01} =$ 3 pp–6 pp, and that the pressure effect is stronger for longer pulses, as can also clearly be seen by the increasing value of $\vert A_{01}\vert$ in figure 6. The effect of increasing peak current density, visualised in figure 5(b), is negative and can be well approximated by a second order polynomial. The effect is strongest for the 25 $\mu{\textrm{s}}$ pulses and decreases with increasing pulse length. A decrease of the peak discharge current density by 0.5 A cm⁻² to $J_\textrm{D,pk} = {0.5}\,\textrm{A}\,\textrm{cm}^{-2}$ ($\tilde{J}_\textrm{D,pk} = -1$) leads to an increase in the range of $A_{20}-A_{10} = {11}\,\textrm{pp to 18}\,\textrm{pp}$ and an increase by 0.5 A cm⁻² to $J_\textrm{D,pk} = {1.5}\,\textrm{A}\,\textrm{cm}^{-2}$ ($\tilde{J}_\textrm{D,pk} = 1$) to a decrease in the range of $A_{20}+A_{10} = {4}\,\textrm{pp to 7}\,\textrm{pp}$, highlighting that the deposition rate penality is initially high but diminishes as the peak current density is increased further. This can also be seen when looking at the steepness of the curves in figure 5(b).

The measured ionised flux fraction is shown in figures 7(a)–(c) grouped by pulse length, again together with fitted surfaces to serve as a visual aid. Generally, there is an increasing trend with increasing $J_\textrm{D,pk}$ and a decreasing trend with increasing $p_\textrm{g}$. However, the situation is much less clear than for the deposition rate fraction. Therefore, splitting the change into different effects in a similar fashion to equation (4) proves especially helpful

$$\begin{align} \hat{F}_\textrm{flux} & = \hat{F}_\textrm{flux, 0} + \Delta\hat{F}^\prime_{\textrm{flux}, J_\textrm{D,pk}}+ \Delta\hat{F}_{\textrm{dep}, p_\textrm{g}}\\ \hat{F}_{\textrm{flux}, 0} & = B_{00}\nonumber\\ \Delta\hat{F}^\prime_{\textrm{flux}, J_\textrm{D,pk}} & = \left(B_{10}+B_{11}\,\log_{2}\tilde{p}_\textrm{g}\right)\,\tilde{J}_\textrm{D,pk} + B_{20}\,\tilde{J}_\textrm{D,pk}^2\nonumber\\ \Delta\hat{F}_{\textrm{flux}, J_\textrm{D,pk}} & = B_{10}\,\tilde{J}_\textrm{D,pk} + B_{20}\,\tilde{J}_\textrm{D,pk}^2\nonumber\\ \Delta\hat{F}_{\textrm{flux}, p_\textrm{g}} & = B_{01}\,\log_{2}\tilde{p}_\textrm{g},\nonumber \end{align} \tag{ 5 }$$

where again $\tilde{J}_\textrm{D,pk} = (J_\textrm{D,pk}-{1}\,\textrm{A}\,\textrm{cm}^{-2})/({0.5}\,\textrm{A}\,\textrm{cm}^{-2})$ and $\tilde{p}_\textrm{g} = p_\textrm{g}$/(1 Pa), and where B₀₀, B₁₀, B₂₀, B₀₁, and B₁₁ are fitting parameters. The addition of an interaction term ($B_{11}\,\tilde{J}_\textrm{D,pk}\,\log_{2}\tilde{p}_\textrm{g}$) was necessary to be able to approximate the measurements with reasonable accuracy. In consequence, the interpretation of the parameter values is unfortunately less straightforward. This can be somewhat remedied by considering $B_{11}\,\log_{2}\tilde{p}_\textrm{g}$ to be a correction to B₁₀ as suggested in equation (5). The resulting response surfaces are shown in figures 7(a)–(c). The main effects related to working gas pressure and peak discharge current density are displayed in figures 8(a) and (b), which also show that all measurement points lie within $\pm{10}\,\textrm{pp}$ of the fitted values. Compared to the deposition rate, the deviations are noticeably larger. This is to be expected due to both the larger range of values and inherently larger uncertainty associated with the measurement of $F_\textrm{flux}$ compared to $F_\textrm{dep}$.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The strength of the individual effects are compared in figure 9. At the reference point ($J_\textrm{D,pk} = {1}\,\textrm{A}\,\textrm{cm}^{-2}$, $p_\textrm{g} = {1}$ Pa), the ionised flux fraction $F_\textrm{flux}$ is typically in the range $B_{00} = {28}\%$ to 41% and increases with increased pulse length. The decrease associated with an increase in pressure by a factor two is roughly the same across the different pulse lengths at $B_{01} = {-13}\,\textrm{pp}$ to ${-15}\,\textrm{pp}$. There is a strong increase with increased $J_\textrm{D,pk}$ and the changes are much more pronounced for the 50 $\mu{\textrm{s}}$ and 75 $\mu{\textrm{s}}$ pulses as indicated by the corresponding bars of B₁₀ and B₂₀ in figure 9. Increasing the peak discharge current density from the reference point ($J_\textrm{D,pk} = {1}\,\textrm{A}\,\textrm{cm}^{-2}$, $p_\textrm{g} = {1}$ Pa) by 0.5 A cm⁻² to $J_\textrm{D,pk} = {1.5}\,\textrm{A}\,\textrm{cm}^{-2}$ ($\tilde{J}_\textrm{D,pk} = 1$) leads to an increase of $B_{20}+B_{10} = {15}$ pp to 36 pp while a decrease by the same amount down to $J_\textrm{D,pk} = {0.5}\,\textrm{A}\,\textrm{cm}^{-2}$ ($\tilde{J}_\textrm{D,pk} = -1$) results in a reduction by $B_{20}-B_{10} = {-25}\,\textrm{pp}$ to ${-98}\,\textrm{pp}$. At this point, it should be noted that extrapolation to low peak current densities is problematic and instead a dcMS-like behaviour where generally $F_\textrm{flux}$ is close to zero, as reported elsewhere [23], should be assumed. The negative value of B₂₀ indicates diminishing returns or even slight decreases at the high end, which again is more pronounced for the 50 $\mu{\textrm{s}}$ and 75 $\mu{\textrm{s}}$ pulses. Finally, the values of B₁₁ tell us, that, while for the 25 $\mu{\textrm{s}}$ pulses the effect of changing the peak current density is approximately independent of pressure, the associated variation is larger at higher pressures for the longer pulses.

Zoom In Zoom Out Reset image size

There have been a number of studies of the plasma parameters of a HiPIMS discharge with a copper target, including Langmuir probe studies that report on the electron density and electron energy [41–43], and mass spectrometry studies to determine the ion flux and ion energy [44–46]. In particular, Vlček et al [45] demonstrated that the Cu⁺ ions can dominate the ion flux and reported that Cu⁺ ions constitute up to 92% of the total ion flux onto the substrate. The ionisation region model (IRM) has been applied to model HiPIMS discharges with a copper target [38]. These studies confirmed that the discharges are dominated by self-sputter recycling [47] at high discharge currents, and that the ion flux into the diffusion region is dominated by Cu⁺ ions (i.e. $\Gamma_\mathrm{DR,Cu^+}\gt\Gamma_\mathrm{DR,Ar^+}$). This agrees with the fact that gas-less self-sputtering from a copper target in a HiPIMS discharge has been achieved [48, 49] using a vacuum-arc discharge to ignite the discharge at a background gas pressure of 10⁻³ Pa. These reports indicate that $F_\textrm{flux}$ should be high for at least some HiPIMS discharge conditions, but not how $F_\mathrm{flux}$ and the deposition rate change.

While the authors are not aware of any systematic investigations of how the deposition rate and ionised flux fraction are influenced by the external process parameters in HiPIMS discharges of copper, some work has previously been done for other material systems.

In their investigation of HiPIMS discharges of Al and Ti at different working gas pressures ($p_\textrm{g}\in${0.5 Pa, 2 Pa}), and for different pulse lengths ($t_\textrm{pulse}\in\{{100}\,\mu{\textrm{s}},{400}\,\mu{\textrm{s}}\}$), Lundin et al [22] found ionised flux fractions in the range of 23%–78% and 23%–65%, for Al and Ti, respectively, while varying the average pulse discharge current density in the range of 0.5 A cm⁻² to 2 A cm⁻². For Al, depending on the chosen pressure and pulse length, they reported an increase of 16 pp to 26 pp when going from around 0.5 A cm⁻² to 1 A cm⁻². In the corresponding Ti discharges, the increase was slightly lower or 10 pp to 22 pp, which corresponds to a relative increase of about 35%–80%. The difference between the average pulse discharge current density used in the earlier study by Lundin et al [22] and the peak discharge current density can however be quite large (see e.g. Butler et al [34]), which complicates the comparison somewhat. For reference, while the peak discharge current densities explored in the present study range from 0.25 A cm⁻² to 1.5 A cm⁻², the corresponding average pulse discharge current densities were considerably lower or in the range from 0.1 A cm⁻² to 1.2 A cm⁻².

A more direct comparison can be made with the measurements on Ti HiPIMS discharges by Shimizu et al [37] carried out in the same deposition chamber and using the same magnetron assembly as used for this work. They varied the peak dicharge current density and the pulse length while keeping the average power constant. For pulse lengths between 25 $\mu{\textrm{s}}$ and 75 $\mu{\textrm{s}}$ and at a working gas pressure of $p_\textrm{g} = {0.3}$ Pa, their data shows an increase of the ionised flux fraction in the order of 8 pp–14 pp and a decrease of the deposition rate fraction in the range of −8 pp to −11 pp when increasing the peak discharge current density by 0.5 A cm⁻². Furthermore, the changes of both $F_\textrm{flux}$ and $F_\textrm{dep}$ are larger for shorter pulse lengths. For the 25 $\mu{\textrm{s}}$ pulses, a one-to-one comparison can be made by interpolating the values found for copper to the peak discharge current densities and working gas pressure used in the work by Shimizu et al, as shown in figures 10(a) and (b). At $p_\textrm{g} = {0.3}$ Pa, the corresponding increase in ionised flux fraction is in the range of 27 pp to 35 pp and decrease in deposition rate fraction in the range of −11 pp to −19 pp. As such, the effects are noticeably larger for copper than for Ti.

Zoom In Zoom Out Reset image size

Shimizu et al [37] also noted a decrease in both deposition rate and ionised flux fraction when the pulse length was increased. This is not supported by the presented findings. However, it should be noted that the pulse lengths investigated in the present work are rather short. Conversely, if one were to look only at the Ti discharge with pulse lengths between 25 $\mu{\textrm{s}}$ to 75 $\mu{\textrm{s}}$, no obvious trend would be noticeable either for the cases with $J_\textrm{D,pk} = {0.7}\,\textrm{cm}^{-2}$ and $J_\textrm{D,pk} = {1.1}\,\textrm{cm}^{-2}$. In fact, the range from 25 $\mu{\textrm{s}}$ to 75 $\mu{\textrm{s}}$ has deliberately been chosen for the present work, exactly because it corresponds to the deposition rate maximum for Ti observed by Shimizu et al [37], and because both $F_\textrm{flux}$ and $F_\textrm{dep}$ were expected to decrease when increasing the pulse length—which is confirmed by the additional measurements at 100 $\mu{\textrm{s}}$ and 150 $\mu{\textrm{s}}$ shown in appendix B. The effect of the pulse length on both the deposition rate and the ionised flux fraction in Cu HiPIMS have also been studied by Tiron et al [50]. While they saw a strong increase when going to very short pulses $t_\textrm{pulse}\lt{20}\,\mu{\textrm{s}}$, they also report little to no change between 25 $\mu{\textrm{s}}$ and 50 $\mu{\textrm{s}}$.

While there are no clear direct trends regarding the pulse length in the investigated range, there are notable differences in how the discharges with shorter (25 $\mu{\textrm{s}}$) and the longer (50 $\mu{\textrm{s}}$ and 75 $\mu{\textrm{s}}$) pulses are affected by changes in the other process parameters. Looking at the discharge current waveforms in figure 3, what distinguishes the short pulses is that they are all triangular. For the longer pulses, the shapes vary more and the discharge current waveform can no longer be described simply by the peak discharge current and the pulse width. In consequence, the response surfaces seen in figure 7 are more complex.

The effect of increasing the peak discharge current observed herein is, on the other hand, much clearer and in accordance with expectations. The material pathways model [51, 52], which is briefly described in appendix A, can prove helpful in explaining the observations. As suggested e.g. by Brenning et al [53], an increase in the discharge current density goes hand in hand with an increase in the ionisation probability α_t. This makes intuitive sense, since the discharge current in a HiPIMS discharge is approximately proportional to the plasma density in front of the target [20], and is also supported by estimates of α_t as calculated in appendix A. Assuming a non-zero but constant back-attraction probability β_t , increasing the discharge current density leads on one the hand to an increased ionised flux fraction, since more material is ionised overall, and on the other hand to a decreased deposition rate, as the amount of back-attracted material increases proportionally. As the current is further increased, the additional deposition rate penality becomes smaller due to α_t increasing more slowly as it approaches 100% [20]. Similarly, the additional gain in ionised flux fraction becomes smaller. This is also easily understood. Since the ionised flux fraction has a mathematical upper bound of 100%, assuming a stable HiPIMS discharge, there are two options of what could happen when going to even higher peak discharge current densities: the $F_\textrm{flux}$ approaches some limiting value $F_\textrm{flux, max}\unicode{x2A7D}{100}\%$ or the ionised flux fraction decreases again after reaching a maximum. While the first option would appear more reasonable, the ionised flux fraction for the 75 $\mu{\textrm{s}}$ discharges as shown in figure B.12 in appendix B does show a decrease above $J_\textrm{D,pk}\simeq{1.25}\,\textrm{A}\,\textrm{cm}^{-2}$ suggesting that the second option is also possible. Possible explanations for this unexpected decrease are discussed in section 4.3.

Let us now turn to the effect of the working gas pressure. That lower pressure can be beneficial has previously been suggested by Lundin et al [22], and more recently been supported by measurements of the angular distribution of the neutral and ion fluxes in Ti HiPIMS discharges by Renner et al [39] at different working gas pressures. The present results confirm that reduced pressure increases both the ionised flux fraction and the deposition rate fraction. As seen in section 3, the influence of $p_\textrm{g}$ on both $F_\textrm{flux}$ and $F_\textrm{dep}$ takes in fact a rather simple form, while, however, at the same time eluding a simple explanation in terms of the material pathways model. The estimates in appendix A support the assumption that α_t depends at most weakly on $p_\textrm{g}$. For the deposition rate fraction, which displays very large changes with varying working gas pressure, the dependence can therefore only be in β_t, the ratio of transport parameters $\xi_\textrm{tn, HiPIMS}/\xi_\textrm{ti, HiPIMS}$, and/or the normalised sputter yield $\Gamma_\textrm{sput, HiPIMS}/\Gamma_\textrm{sput, dcMS}$. ⁷ From modelling of Ti/Ar HiPIMS discharges there are indications that a lower pressure is correlated with a lower back-attraction [31], although the physical reasons are not well understood. One possibility deduced from the same modelling work is that a smaller fraction of the applied discharge power goes to Ohmic heating [54] at lower working gas pressure [31]. Ohmic heating is associated with an electric potential difference $U_\textrm{IR}$ across the ionisation region, which means that a lower $U_\textrm{IR}$ at lower $p_\textrm{g}$ might be the reason for a lower β_t. Another possible explanation could be, that at lower pressures the metal species are ionised further away and are therefore less likely to be back-attracted. The ionised flux fraction is even more difficult to reason about, since, depending on the value of the other parameters in the material pathways model, it can be very sensitive to changes in α_t and β_t.

The response surface of the ionised flux fraction for the 75 $\mu{\textrm{s}}$ pulses shown in figure 7(c) suggests a decrease at peak discharge current densities above ${\approx}{1.25}\,\textrm{A}\,\textrm{cm}^{-2}$, which is not seen for the shorter pulse lengths investigated. This is not just an artefact due to fitting with a quadratic function. The ionised flux fraction measured for the $t_\textrm{pulse} = {75}\,\mu{\textrm{s}}$ discharges at $J_\textrm{D,pk} = {1.5}\,\textrm{A}\,\textrm{cm}^{-2}$ are indeed consistently lower than those measured for the $J_\textrm{D,pk} = {1.25}\,\textrm{A}\,\textrm{cm}^{-2}$ at otherwise identical conditions. Later measurements at $J_\textrm{D,pk} = {1.375}\,\textrm{A}\,\textrm{cm}^{-2}$ and again $J_\textrm{D,pk} = {1.5}\,\textrm{A}\,\textrm{cm}^{-2}$, displayed in figure B.12, show with one exception also all lower ionised flux fractions than the $J_\textrm{D,pk} = {1.25}\,\textrm{A}\,\textrm{cm}^{-2}$ discharge at the same pressure. It should be noted, however, that by the time these measurements were performed the target had been significantly eroded and the setup had undergone some changes. A similar unexpected decrease at high peak discharge current densities has already been observed in previous measurements, which were performed to obtain ionised flux fraction for locking the IRM [38] and are included in the supplementary data.

One possible reason for this unexpected trend could be due to limitations of the ionmeter. As illustrated in figure 1, the QCM is biased across a 500 Ω resistor and in consequence a large bias current can introduce a significant voltage drop. During the present measurements, the bias voltage was monitored and was observed to reach values as low as 20 V during the afterglow in some cases. However, under the assumption that the portion of high energy ions (${\gt}{20}\,\textrm{eV}$) in the afterglow is comparatively small, this would still not explain the significant decreases in $F_\textrm{flux}$.

Assuming that this effect is indeed real, another possible explanation can be found in the shape of the discharge current waveform. Lower ionised flux fractions for the 1.5 A cm⁻² than for the 1.25 A cm⁻² discharges have been observed for the 75 $\mu{\textrm{s}}$ pulses at 0.5 Pa, 1.0 Pa, and 1.5 Pa which all have in common that the discharge current maximum occurs much earlier than the end of the pulse (see figure 3). Since during the pulse a lot of ions are recycled and the amount of ions released in the afterglow is mainly determined by the current density at the end of the pulse, this could negatively impact the ionised flux fraction [32].

One of the motivations for this study was the observation of this unexpected decrease in ionised flux fraction at high peak discharge current densities in previous, less systematic, measurements shown in the supplementary data. For this work, the bias voltage applied to the ionmeter has been monitored and overloading of the bias power supply can be excluded as the cause. However, it is still not possible to say with certainty that the observed effect is real. To this end, a follow-up study which, in addition to different direct methods (e.g., retarding field energy analyser (RFEA), gridded QCM), uses an indirect method to qualitatively judge the metal ion content in the film-forming flux, for example by measuring the coverage of vias or trenches in biased substrates, could be used to confirm this effect. Additionally, the deposited films could also be used to link the observed changes in ionised flux fraction and deposition rate to film properties. In particular, it can be expected that there will be an increase in compressive film stress at low pressure, which could introduce further optimisation constraints depending on the application [55].