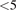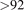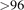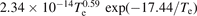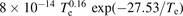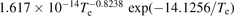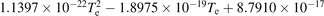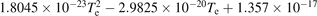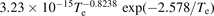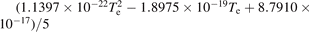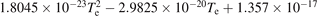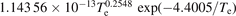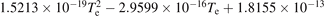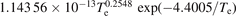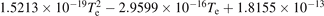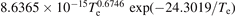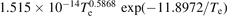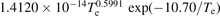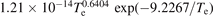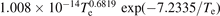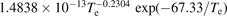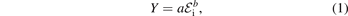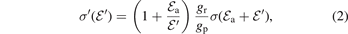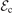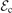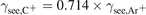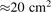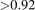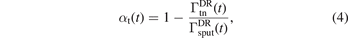Abstract
The ionization region model (IRM) is applied to model a high power impulse magnetron sputtering discharge in argon with a graphite target. Using the IRM, the temporal variation of the various species and the average electron energy, as well as internal parameters such as the ionization probability, back-attraction probability, and the ionized flux fraction of the sputtered species, is determined. It is found that thedischarge develops into working gas recycling and most of the discharge current at the cathode target surface is composed of Ar+ ions, which constitute over 90% of the discharge current, while the contribution of the C+ ions is always small (%), even for peak current densities close to 3 A cm−2. For the target species, the time-averaged ionization probability ⟨αt,pulse⟩ is low, or 13–27%, the ion back-attraction probability during the pulse βt,pulse is high (%), and the ionized flux fraction is about 2%. It is concluded that in the operation range studied here it is a challenge to ionize carbon atoms, that are sputtered off of a graphite target in a magnetron sputtering discharge, when depositing amorphous carbon films.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The magnetron sputtering discharge is a widely used technique to deposit thin films [1]. The magnetron sputtering discharge is based on maintaining a dense plasma in the vicinity of the cathode target by a static magnetic field [2, 3]. This dense plasma that is created near the cathode target, defines the ionization region (IR). When operated as a dc magnetron sputtering (dcMS) discharge the film-forming material consists mainly of neutral atoms. Most of the ions available in the discharge, and the ions that bombard the substrate, are ions of a noble working gas [1].
For many applications it is desired to have a high ionization fraction in the flux of the film-forming material. One such application is the deposition of amorphous carbon films where bombardment by energetic ions is expected to increase the sp3 content in the deposited films. In general, amorphous carbon is a disordered network of carbon atoms and constitutes a mixture of both sp2 and sp3 bonds. Diamond-like carbon (DLC) refers to a metastable form of amorphous carbon that contains a significant fraction of tetrahedrally bonded sp3 [4]. When the C–C sp3 content is larger than 60%, and the film does not contain hydrogen, it is called tetrahedral amorphous carbon (ta-C) [5]. Due to the high sp3 content DLC films are mechanically very hard, are resistant to scratching, have high dielectric constants, high index of refraction and excellent optical transparency. DLC films also exhibit excellent chemical inertness and are resistant to corrosive and/or oxidative attacks in acidic and saline media. Consequently, DLC films are widely used in various industrial applications that require hard and wear resistant films and coatings, including protective coatings on cutting tools, sliding parts within automobile engines, overcoats on hard disc recording heads, and biomedical devices [6–10].
High power impulse magnetron sputtering (HiPIMS) is an approach that normally provides a highly ionized flux of the film-forming material onto the substrate [11]. Pulses, that have a peak power density of up to a few orders of magnitude higher than the power density applied in dcMS, delivered at low repetition frequency and low duty cycle, lead to an electron density that is high enough that the atoms sputtered off the target become mostly ionized as they pass through the dense plasma of the IR [11]. This is indeed the case for metallic targets, and high ionized flux fractions have been demonstrated for HiPIMS discharges operated with various metallic targets [12–14].
However, it has turned out to be a significant challenge to ionize carbon atoms, that are sputtered off of a graphite target in a magnetron sputtering discharge, when depositing carbon films. It has been reported that the measured ionized flux fraction Fflux in an argon-based HiPIMS discharge with a graphite target is low, or below 5% [15]. Similar results based on model calculations, have been reported by Zheng et al [16]. Also, Sarakinos et al [17] have shown that the dominant ionized species in a HiPIMS discharge with argon working gas and a graphite target are Ar+ ions, while C+ ions constitute only about 1% of the total ionic contribution. This is a considerably lower value than commonly observed for metal ions in HiPIMS operation [12, 14, 18–20], which indicates that the HiPIMS discharge is not very efficient in ionizing carbon. This is due to a higher ionization potential and lower electron impact ionization cross section for the carbon atom compared to most metal atoms [21]. For a 16 eV electron the cross section for electron impact ionization of carbon is a factor 10 lower than the electron impact ionization of titanium. Also carbon has higher cohesive energy than many of the metal atoms such as Ti, Cu and Al, which reduces the sputter yield and increases the speed of the sputtered atoms giving them a shorter residence time in the IR. However, for a graphite cathode target HiPIMS gives a higher overall ion flux (mainly consisting of noble working gas ions) with higher average ion energy, observed as broader ion energy distribution compared to the ion energy distribution from a dcMS discharge [17]. Furthermore, using optical emission spectroscopy, DeKoven et al [15] observed more ions (both Ar+ and C+ ions) in HiPIMS operation than when operating as dcMS.
In order to increase the ionized carbon flux fraction it has been suggested to increase the electron temperature in a HiPIMS discharge by using neon as the working gas instead of argon or a mixture of the two [10, 22–24]. The idea is that an energetic electron population is generated and consequently a substantial increase in the C+ ion flux as compared to the conventional argon based HiPIMS process. This strategy has been claimed to facilitate a substantial increase of carbon ionization in HiPIMS discharges. Vitelaru et al [25] indeed report improved DLC film properties by adding neon to the HiPIMS discharge. However, they argue that when the discharge is operated with significant working gas recycling, adding neon to the working gas mixture, does not have much effect on the carbon ionization, as due to the amount of argon in the discharge the effective electron temperature is already high. They also argue that in the cases, for which neon was added to the discharge, and improved DLC film properties were obtained, the discharge was not operated in the working gas recycling regime.
In spite of the limited ionized carbon flux fraction the HiPIMS discharge with a graphite target is being explored extensively for the deposition of DLC films [15, 17, 22, 23, 25–31]. By using HiPIMS to deposit tetrahedral amorphous carbon (ta-C) or DLC thin films the aim is to increase the ionization fraction of the carbon atoms sputtered off the target, as it is known that energetic ion bombardment of the substrate is essential to deposit ta-C or DLC films with high sp3 content. Application of argon based HiPIMS to deposit DLC films has resulted in sp3 fractions up to 45% [15, 17, 32], and up to over 80% by adding an arc at the end of the HiPIMS pulse [28], and by magnetic field-assisted HiPIMS [33], compared to % for films deposited by dcMS [17]. DLC films deposited by filtered cathodic arc can have sp3 fractions above 80% [34–36]. In fact, Akhavan et al [33] have demonstrated that the sp3 fraction in the deposited DLC thin films can be controlled using magnetic field assisted HiPIMS. Increasing the sp3 fractions enhances the properties of the films, including the mass density, hardness, optical gap, carrier properties, etc. It has been observed experimentally that the film mass density varies linearly with the sp3 content [5, 37, 38]. The film mass density has been reported to be in the range 2.2–3.15 g cm−3 for HiPIMS-deposited films [15, 17, 33] compared to roughly 2.0 g cm−3 for dcMS deposited films, 3.1 g cm−3 for rf magnetron sputter deposited films on biased substrate [38], up to 3.2 g cm−3 for films deposited by filtered cathodic arc [34, 39], and up to 3.5 g cm−3 for PLD films [40, 41]. It should be noted that the filtered cathodic arc has very high ionized flux fraction % [42]. It has also been reported that HiPIMS deposited DLC films exhibit much lower surface roughness than dcMS deposited DLC films [15].
In the present work, we try to gain more insight into a HiPIMS discharge with argon as the working gas and graphite as a cathode target, and in particular into the ionization processes, by modeling this discharge using the ionization region model (IRM). The IRM is a time-dependent volume averaged plasma chemical model of the IR in the HiPIMS discharge, that provides the temporal evolution of the densities of ions, neutrals and electrons along with internal discharge parameters, such as the ionization probability αt and the ion back-attraction probability βt for the sputtered species [43, 44]. The IRM is therefore an ideal tool to study the ionization processes and the ionization fraction in a HiPIMS discharge with a graphite target and to explore how to increase the ionization fraction of the sputtered species. In section 2 the IRM is introduced and the addition of carbon atoms and ions to the reaction set, and their interaction with surfaces, is discussed. The experimental discharges that are to be analyzed are discussed in section 3. In section 4, the IRM is applied to three HiPIMS discharges with a graphite target, to determine the temporal evolution of the particle densities, the ionization and back-attraction probabilities of the carbon species, and the ionized flux fraction. The results are discussed with respect to the generalized recycling model in section 5 and the results are summarized in section 6.
2. The ionization region model
The IRM is a global model of the plasma chemistry where the temporal development of the plasma parameters is defined by a set of ordinary differential equations describing the first time derivatives of the cold electron temperature and the particle densities for all the heavy particles. The IRM, therefore, provides the temporal evolution of neutral and charged species and the densities and temperatures of hot and cold electrons in a pulsed magnetron sputtering discharge. The electron density is determined assuming quasi-neutrality of the plasma. The model is limited to the IR, which is defined as an annular cylinder with outer radii rc2, and inner radii rc1 corresponding to the racetrack region on the target surface, and length L = z2 − z1, extending from z1 to z2 axially away from the target. Here, z1 represents the sheath thickness and z2 defines the axial extent of the IR, both measured from the target surface. Geometrical effects are included indirectly as loss and gain rates, across the boundaries of this annular cylinder, to the target and the bulk plasma [43].
The IRM is based on rate coefficients that are calculated using an assumed electron energy distribution function (EEDF) with cold and hot electrons. The cold Maxwellian electron population constitutes the majority of the electrons and therefore dictates the electron density and the effective electron temperature. The IRM uses two sets of rate coefficients, one set for cold electrons, calculated assuming a Maxwellian EEDF and fit in the electron temperature range Te = 1–7 eV, and another for hot electrons and fit in the range 200–1000 eV. We have recently demonstrated by a comparison to the results from a Boltzmann solver that assuming such a bi-Maxwellian EEDF is a good approximation for the HiPIMS discharge [45].
The IRM is a semi-empirical model and experimental data is needed as model inputs [46]. Here, we use the discharge voltage and current waveforms only and determine the minimum in the least square error when the modeled discharge current resembles the experimental waveform the best. The reaction set and the rate coefficients for the argon working gas included in the IRM are mostly the same as used in our earlier work on HiPIMS discharges with a titanium target [47, 48], with modifications concerning the treatment of the afterglow [49] and the rate coefficients involving the metastable argon [45]. The rate coefficients for electron impact de-excitation of the metastable levels are calculated by applying the principle of detailed balancing [50, section 8.5]. Here, we add Ar2+ to the reaction set for argon, which is created by electron impact ionization of Ar and Ar+. All the rate coefficients involving argon that are included in the IRM are listed in table 1. The argon atoms in the ground state can be cold, which refers to argon atoms in the feedstock gas and are at the gas temperature, as well as warm and hot argon atoms. Hot argon atoms refer to argon atoms in the ground state that return from the target immediately after the argon ion impact event, with a typical sputter energy of a few eV, and warm atoms refer to argon atoms in the ground state that are assumed to be implanted in the target at the location of ion impact, and then return to the surface and leave with the target temperature, at most 0.1 eV [51, 52]. We assume that a fraction ξpulse ξH of the recombined Ar+ ions returns as hot neutrals ArH during the pulse, a fraction ξpulse(1 − ξH) returns as warm neutrals ArW during the pulse, and ξpulse is a parameter that is a measure of how much of the trapped Ar returns during the pulse. Here, we assume ξpulse = 1 (i.e. all the Ar atoms return during the pulse). This assumption applies in steady state, even if there is a transitory phase. Indeed, if one imagines this is not the case (meaning ξpulse < 1), then after infinite number of pulses the target will be fully transformed into an Ar/C mixture. But this is not the case. Therefore, the balance between the arrival and the removal of Ar should be, on average, close to 1 per pulse. We also assume that (1 − ξH) = 50% leave as ArW, and that ξH = 50% leave as ArH. However, it is expected that this coefficient depends on the impinging ion energy and target material. The two assumed parameters ξpulse and ξH for the recombined Ar atoms from the target is one of the weak points of the IRM.
Table 1. The reactions and rate coefficients used in the IRM for a discharge with argon as the working gas and graphite cathode target including both hot and cold electrons. For each electron impact reaction a rate coefficient for cold electrons and hot electrons is given. The rate coefficients are calculated assuming a Maxwellian EEDF and fitted in the range Te = 1–7 eV for cold electrons and 200–1000 eV for hot electrons. The rate coefficients for Ar are taken from Rudolph et al [45].
| Reaction | Threshold (eV) | Rate coefficient (m3 s−1) | Reference | |
|---|---|---|---|---|
| (R1) | e + Ar(3p6) → Ar+ + e + e | 15.76 | [73] | |
| (R2) | e + Ar(3p6) → Ar(4s[3/2]2) + e | 11.548 | [74] | |
| (R3) | e + Ar(3p6) → Ar(4s'[1/2]0) + e | 11.723 | [74] | |
| (R4) | e + Ar(4s[3/2]2) → Ar(3p6) + e | Detailed balancing | ||
| (R5) | e + Ar(4s'[1/2]0) → Ar(3p6) + e | Detailed balancing | ||
| (R6) | e + Ar(4s'[1/2]0) → Ar+ + 2e | 4.21 | [75, 76] | |
| (R7) | e + Ar(4s[3/2]2) → Ar+ + 2e | 4.21 | [75, 76] | |
| (R8) | e + Ar+ → Ar2+ + 2e | 27.63 | [77] | |
| 5.22 × 10−14 − 4.943 × 10−17 Te | ||||
| (R9) | e + Ar → Ar2+ + 3e | — | [78] | |
| 6.169 × 10−15 − 1.6316 × 10−17 Te | ||||
| (R10) | e + C(2s22p2 3P) → C(2s22p2 1D) + e | 1.26 | [63, 65] | |
| 3.489 × 10−15 − 2.504 × 10−17 × Te | ||||
| (R11) | e + C(2s22p2 3P) → C(2s22p2 1S) + e | 2.68 | [63, 65] | |
| 3.543 × 10−16 − 2.581 × 10−18 × Te | ||||
| (R12) | e + C(2s22p2 3P) → C(2s2p3 5S°) + e | 4.182 | [63, 65] | |
| 1.701 × 10−15 − 1.2105 × 10−17 × Te | ||||
| (R13) | e + C(2s22p2 1D) → C(2s22p2 3P) + e | Detailed balancing | ||
| 7.1673 × 10−16 − 5.018 × 10−18 × Te | ||||
| (R14) | e + C(2s22p2 1S) → C(2s22p2 3P) + e | Detailed balancing | ||
| 3.7491 × 10−16 − 2.7709 × 10−18 × Te | ||||
| (R15) | e + C(2s2p3 5S°) → C(2s22p2 3P) + e | Detailed balancing | ||
| 3.7181 × 10−16 − 2.7095 × 10−18 × Te | ||||
| (R16) | e + C(2s22p2 1D) → C(2s22p2 1S) + e | 2.922 | [63] | |
| 3.4144 × 10−15 − 1.0218 × 10−17 × Te | ||||
| (R17) | e + C(2s22p2 1S) → C(2s22p2 1D) + e | Detailed balancing | ||
| 1.8364 × 10−14 − 6.0929 × 10−17 × Te | ||||
| (R18) | e + C(2s22p2 3P) → C+ + e | 11.26 | [60] | |
| 1.4348 × 10−13 − 3.3441 × 10−17 Te | ||||
| (R19) | e + C(2s22p2 1D) →C+ + e | 10.0 | Threshold reduction | |
| 1.433 × 10−13 − 3.33 × 10−17 Te | ||||
| (R20) | e + C(2s22p2 1S) →C+ + e | 8.58 | Threshold reduction | |
| 1.433 × 10−13 − 3.33 × 10−17 Te | ||||
| (R21) | e + C(2s2p3 5S°) →C+ + e | 7.08 | Threshold reduction | |
| 1.428 × 10−13 − 3.32 × 10−17 Te | ||||
| (R22) | e + C+→C2+ + 2e | 24.38 | [61, 62] | |
| (R23) | Ar+ + C → Ar + C+ | 6.4 × 10−18 | [70] | |
| (R24) | Ar(3P0) + C(3P, 1D, 1S, 5S°) → Ar + C+ + e | 4.2 × 10−15 | See text | |
| (R25) | Ar(3P2) + C(3P, 1D, 1S, 5S°) → Ar + C+ + e | 4.2 × 10−15 | See text | |
aThis is a fit for Te in the range 200–700 eV. bThis is a fit for Te in the range 100–200 eV. cThis is a fit for Te in the range 50–100 eV.
For a HiPIMS discharge in argon with a Ti target, the internal parameters αt and βt determined by the IRM show excellent agreement when compared to the same internal parameters determined from the measured deposition rate and ionized flux fraction [53].
2.1. The carbon reaction set
The carbon atom enters the discharge as it is sputtered off the graphite target. The sputter yield for bombardment by low energy ions is sometimes approximated by a fit following the general form [54]
where is the energy of the incoming ion and a and b are constants that depend on the ion-target pair. For argon ions bombarding graphite target a = 0.0021 and b = 0.687, and for self-sputter (SS) of a graphite target a = 0.0562 and b = 0.224 [54]. The fit parameters a and b are derived from fits to the sputter yields calculated using the transport of ions in matter (TRIM) code [55]. The sputtered atoms have an energy spectrum that peaks at roughly half the surface binding energy or the cohesive energy and consequently the carbon atoms enter the discharge with a considerable energy (a few eV). The cohesive energy of carbon is 7.37 eV [56, p 50].
When entering the discharge the carbon atom experiences electron impact excitation and ionization, charge transfer, and Penning ionization. Here, a reaction set for the carbon discharge is added to the IRM. Neutral carbon atom (CI) in the ground state is in the 1s22s22p2 configuration along with four excited levels. This includes the metastables 2s22p2 1D and 2s22p2 1S with radiation lifetimes, 3436 s and 1.6 s, respectively [57, 58]. Excitation of a single outer electron leads to the configuration 2s22pnl (n > 2) and excitation of the closed 2s manifold gives 2s2p3 and 2s2p2 nl [57]. This includes the metastable 2s2p3 5S° with radiation lifetime of < 0.1 s [58, 59]. Our model therefore contains the following species: ground state carbon (2s2p2 3P0,1,2, two metastable states (2s22p2 1D, 2s22p2 1S) and 2s2p3 5S°, the singly ionized C+, and the doubly ionized C2+. We assume that the ground state carbon is composed of the three closely spaced levels in the 2s22p2 configuration 3P0, 3P1 and 3P2.
The first ionization energy of carbon is 11.26 eV and the second ionization energy is 24.38 eV. To determine the rate coefficient for electron impact ionization from the ground state carbon atom we use the cross section calculated by Kim and Desclaux [60]. For the ionization rate coefficients from the three lowest excited levels we use the same cross section but apply threshold reduction. The cross sections for electron impact double ionization is a fit to the data collected by Tawara and Kato [61] as discussed by Stevefelt et al [62]. The cross sections for electron impact excitation to the three lowest excited levels (2s22p2 1D, 2s22p2 1S, and 2s2p3 5S°) are taken from the B-spline R-matrix (BSR) with pseudostates calculations of Wang et al [63] and the data was downloaded from the LXCat database [64]. An extensive list of rate coefficients for electron impact ionization and excitation of carbon by the cold electron group is given by Toneli et al [65] and their fits are used for electron impact excitation to the metastable levels. The LXCat data from Wang et al [63] is only available up to 100 eV so for the hot electrons the rate coefficients are fitted in the range 50–100 eV but used over the entire electron temperature range. For each of the electron impact excitation reactions there exists an inverse counterpart in the reaction set. The cross sections for these reactions are obtained by the principle of detailed balancing
where gr and gp are the degeneracies of the reactant and product, respectively, in the forward reaction, and is the threshold energy. To determine the rate coefficient for Penning ionization of carbon through collisions with metastable argon atoms we use published cross sections [66–68] and scale by the square of the atomic radii, the atom mass, and the number of valence electrons [69]. Then we assume the sputtered species to have an average energy of 3 eV. For the charge transfer Ar+ + C → Ar + C+ we use the rate coefficient measured for the charge transfer reaction with O atoms by Gaucherel and Rowe [70]. All the reactions and rate coefficients involving carbon atoms and ions, included in the IRM for this current study are listed in table 1.
To calculate the collisional energy loss per electron–ion pair created , we use the electron impact ionization cross section calculated by Kim and Desclaux [60]. Furthermore, we include the lowest excited levels of the carbon atom listed in table 2. The cross sections for the electron impact excitation and electron elastic scattering off of a carbon atom are taken from the work of Wang et al [63] using the data downloaded from the LXCat database [64]. Figure 1 shows a log–log plot of the collisional energy loss per electron–ion pair created, , as a function of the electron temperature for the ground state carbon atom, calculated assuming a Maxwellian electron energy distribution. The figure shows the collisional energy loss per electron–ion pair created for argon in the ground state used in the IRM, calculated as discussed elsewhere [48], as well.
Table 2. The data used to calculate the collisional energy loss for carbon in the ground state.
| Final state | (eV) | Reference | |
|---|---|---|---|
| (R26) | C+ | 7.864 | [60] |
| (R27) | C(2s22p2 3P0,1,2) | 3(me/MC)Te | [63] |
| (R28) | C(2s22p2 3P1) | 0.002 | [63] |
| (R29) | C(2s22p2 3P2) | 0.006 | [63] |
| (R30) | C(2s22p2 1D2) | 1.26 | [63] |
| (R31) | C(2s22p2 1S0) | 2.68 | [63] |
| (R32) | C(2s22p2 5S°) | 4.182 | [63] |
| (R33) | C(2p3s 3P0) | 7.480 | [63] |
| (R34) | C(2p3s 3P1) | 7.483 | [63] |
| (R35) | C(2p3s 3P2) | 7.488 | [63] |
| (R36) | C(2p3s 1P1) | 7.685 | [63] |
| (R37) | C(2s2p3 3D1) | 7.946 | [63] |
| (R38) | C(2s2p3 3D2) | 7.946 | [63] |
| (R39) | C(2s2p3 3D3) | 7.946 | [63] |
| (R40) | C(2p3p 1P1) | 8.537 | [63] |
| (R41) | C(2p3p 3D1) | 8.640 | [63] |
| (R42) | C(2p3p 3D2) | 8.643 | [63] |
| (R43) | C(2p3p 3D3) | 8.647 | [63] |
| (R44) | C(2p3p 3S1) | 8.771 | [63] |
| (R45) | C(2p3p 3P0) | 8.847 | [63] |
| (R46) | C(2p3p 3P1) | 8.848 | [63] |
| (R47) | C(2p3p 3P2) | 8.851 | [63] |
| (R48) | C(2p3p 1D2) | 9.003 | [63] |
| (R49) | C(2p3p 1S0) | 9.172 | [63] |
Figure 1. A log–log plot showing the collisional energy loss per electron–ion pair created, , as a function of the electron temperature for the ground state carbon atom, calculated assuming a Maxwellian electron energy distribution.
Download figure:
Standard image High-resolution imageFor the secondary electron emission yield due to bombardment by argon ions we use a fit to the secondary electron emission yield for Ar+ ions bombarding Si(111) surface measured by Hagstrum [71] or , where is the ion bombarding energy. Hagstrum [71] find that the secondary electron emission yield from Si and Ge are very similar but differ slightly as the yields from Ge were consistently higher. Si and Ge are semiconductors in column IV just like graphite, which is a semiconductor with small bandgap. Acording to Hagstrum [72] the emitted electrons originate from the valence band of the semiconductor and lower ionization potential leads to higher yield. As there are no available measurements of the secondary electron emission yields due to low ion bombardment of graphite we use the values for Si. For carbon ions bombarding the graphite target we scale by 11.26/15.76 or .
3. Experimental apparatus and method
The discharge voltage and current waveforms were measured for a HiPIMS discharge in argon with a graphite target. The experiments were carried out in a custom-built cylindrical vacuum chamber (height 75 cm and diameter 44 cm) made of stainless steel. The magnetron assembly was mounted on the top circular flange of the chamber, with the cathode target facing downwards. The sputter target was a 2 inch graphite disk mounted on the magnetron assembly. A base pressure of 4 × 10−6 Pa was achieved using a turbomolecular pump backed by a roughing pump. The working gas pressure was kept at 1 Pa by injecting argon gas into the chamber and adjusting a butterfly valve located between the chamber and the turbo molecular pump while the flowrate was maintained at 25.8 sccm. A dc power supply together with a HiPSTER 6 HiPIMS pulsing unit (Ionautics, Sweden) were used to apply voltage pulses to the cathode target. For all cases, an average discharge power ⟨PD⟩ was maintained at 80 W by varying the repetition frequency, and the pulse was kept at constant length of 50 μs. In total, three peak discharge currents were investigated, ID,peak = 20, 40, and 60 A, leading to peak discharge current densities on the two inch cathode target () of about 1, 2, and 3 A cm−2, respectively. To maintain the same average discharge power, the repetition frequency was 520 Hz, 350 Hz, 280 Hz, and the discharge voltage 611 V, 623 V and 634 V, for discharge current densities 1, 2, and 3 A cm−2, respectively. A summary of the experimental discharge parameters is provided in table 3.
Table 3. The experimental parameters for a HiPIMS discharge with graphite target.
| ID,peak (A) | 20 | 40 | 60 |
| VD (V) | 611 | 623 | 634 |
| JD,peak (A cm−2) | 1 | 2 | 3 |
| ⟨PD⟩ (W) | 80 | 80 | 80 |
| f (Hz) | 520 | 350 | 280 |
| pg (Pa) | 1.0 | 1.0 | 1.0 |
| tpulse (μs) | 50 | 50 | 50 |
4. Model results
The measured discharge current waveforms, for the three peak discharge currents explored, are shown in figure 2. In all cases the discharge current waveform appears to be roughly triangular with a sharp peak at the end of the pulse. The IRM is used to analyze the internal properties of these discharges. The volume parameters of the IR are set as follows for the three cases explored: rc1 = 6 mm, rc2 = 19 mm, z1 = 2 mm, z2 = 13 mm. Using the IRM, a best fit to the experimentally determined discharge current waveform for each of the discharge peak currents is determined. The best fit is determined using a fitting map showing the fraction of the discharge voltage that drops across the IR f = VIR/VD versus the back-attraction probability of an ion of the sputtered species during the pulse βt,pulse in figure 3. The root mean square deviation between the modeled and the experimental peak discharge current is color-coded. The blue zones in the fitting map indicate the combinations of f = VIR/VD and βt,pulse where the root mean square deviation of the five highest current values at the pulse end is the smallest, so that the modeled peak discharge current resembles the experimental peak current the best. The blue zones remain somewhat in the same region (combinations of f and βt,pulse) for the three investigated peak discharge currents but shift to higher βt,pulse for increased peak discharge current. The resulting best fits for the discharge currents are also shown in figure 2. The fits are generally very good for most of the pulse on-time. The sputtered ionic species are assumed to have a directional velocity away from the target. Therefore, we assume βt to be close to zero in the afterglow and the back-attraction probability is defined as [49]
During the pulse, the flux towards the diffusion region (DR) is calculated from the flux towards the racetrack [44]. After the pulse is switched off, the ions are estimated to have a similar velocity to that of the sputtered metal species. In all cases the back-attraction probability during the pulse is , and increases with increasing peak discharge current, and for all cases f = VIR/VD ≈ 13%. The average back-attraction probability ⟨βt(t)⟩ is somewhat lower or in the range 83%–88% for the three cases. The ionization flux fraction determined by the IRM is in the range Fflux ≈ 1.3%–2.2%. For comparison DeKoven et al [15] report measured ionization flux fraction of Fflux = 4.5 ± 0.5% for a 6 inch graphite target when the discharge current peaks at 350 A. This corresponds to a peak discharge current density of roughly 2 A cm−2. Therefore, our model results are in good agreement with the measured value. Based on model calculations, Zheng et al [16] report ionized flux fraction of up to 5.5% for a graphite target for a peak power density of 0.5 kW cm−2 and about 1% for lower peak power density, which is also in line with our findings. Some of the key discharge parameters derived from the IRM are listed in table 4.
Figure 2. The temporal evolution of the discharge current and the model fit for peak discharge current of (a) 20 A (1 A cm−2), (b) 40 A (2 A cm−2), and (c) 60 A (3 A cm−2), for a discharge with 2 inch graphite target.
Download figure:
Standard image High-resolution imageFigure 3. The fitting maps showing f = VIR/VD versus the back-attraction probability βt,pulse for peak discharge current of (a) 20 A (1 A cm−2), (b) 40 A (2 A cm−2), and (c) 60 A (3 A cm−2), for a discharge with 2 inch graphite target. The numbered lines show the IRM-calculated ionized flux fractions Fflux. The white circles show where a well fitted current profile is observed.
Download figure:
Standard image High-resolution imageTable 4. Parameters derived from the modeling of a HiPIMS discharge with 2 inch graphite target.
| ID,peak | 20 A | 40 A | 60 A |
| ⟨αt,pulse⟩ | 13% | 21% | 27% |
| βt,pulse | 92% | 99% | 99% |
| ⟨βt(t)⟩ | 83% | 88% | 88% |
| f = VIR/VD | 14% | 13% | 13% |
| Fflux | 1.3% | 1.6% | 2.2% |
| Rarefaction | 66% | 78% | 86% |
Once the best fit of the IRM has been determined, the model results can be analyzed further, including exploring the temporal variation of the discharge composition, and the ionization and back-attraction probabilities of the sputtered species. The temporal evolution of the neutral particle densities is shown in figure 4 for the three different peak discharge currents. The temporal evolution of the neutral particle densities are similar for all the three peak discharge currents. The ground state working gas argon atoms dominate the discharge. The cold (or primary) argon ground state density (denoted ArC(3p6) in figure 4) decreases steadily, with increased discharge current during the pulse, exhibiting a minimum at the end of the pulse. This is an indication of working gas rarefaction. Working gas rarefaction has been observed experimentally in HiPIMS discharges [18, 79] and is known to be rather significant. Before the pulse initiation the density of cold ground state argon atoms at 1 Pa and Tg = 500 K is 1.4 × 1020 m−3, which throughout the pulse was reduced by up to 66%, 78%, and 86% for the 20, 40, and 60 A peak discharge currents, respectively. This can be compared to an observed reduction by up to 50% reported in the IRM work by Huo et al [80] for a 400 μs pulse with an aluminum target at 0.6 A cm−2. So indeed the working gas rarefaction is rather significant for these short pulses of 50 μs. There is a monotonic increase in hot (ArH) and warm (ArW) argon atom densities, while the cold argon ground state density decreases. For the higher peak discharge currents both the ArW and the ArH densities are higher than the cold ground state argon density at the end of the pulse. Note that the total argon ground state density is [Ar(3p6)] = [ArC(3p6)] + [ArW(3p6)] + [ArH(3p6)].
Figure 4. The temporal evolution of the neutral particle densities for a 50 μs pulse with a peak discharge current ID,peak of (a) 20 A (1 A cm−2), (b) 40 A (2 A cm−2), and (c) 60 A (3 A cm−2), with 2 inch graphite target. Note that the total argon ground state density is [Ar(3p6)] = [ArC(3p6)] + [ArW(3p6)] + [ArH(3p6)].
Download figure:
Standard image High-resolution imageAll carbon species densities increase as more and more carbon is sputtered off the target during the pulse (with continuously increasing discharge current). After the end of the pulse the density of the ground state carbon atoms decreases gradually. In comparison, the excited carbon densities are lower but increase along with the ground state densities to a peak and then gradually decrease after the end of the pulse. The excited carbon densities decay much slower than the ground state carbon densities.
The temporal evolution of the charged particle densities is shown in figure 5. The total neutral argon (sum of cold, warm and hot ground state atoms and excited states) and carbon (sum of ground state and excited states) densities are shown as well. The Ar+ ion is the dominating positively charged species in the discharge and its density peaks at the end of the pulse. The density of the C+ ions is more than one order of magnitude smaller, and comparable to the Ar2+ density. The C2+ ion density is more than three orders of magnitude smaller than the Ar+ ion density. Therefore, the C2+ ion is rather insignificant in this discharge.
As discussed in section 1 the main reason for using HiPIMS to deposit amorphous carbon thin films is to achieve an increase in the ionization of the film-forming species and to obtain improved properties of the deposited films. The discharge current composition at the target surface is shown in figures 6(a)–(c) for peak discharge current densities of 1, 2, and 3 A cm−2, respectively. At the target surface, the discharge current is mainly due to Ar+ ions, with a small contribution from Ar2+ and C+ ions, while secondary electrons, and C2+ ions, have a negligible contribution. Less than 5% of the total discharge current, and about 6%–7% of the peak discharge current, at the target surface, is carried by carbon ions as seen in figure 6. This agrees with the observation of Sarakinos et al [17] who demonstrated that Ar+ ions dominate the discharge, while C+ ions constitute only about 1% of the total ionic contribution in the substrate vicinity. In fact Ar2+ ions contribute more to the discharge current at the target surface than the C+ ions. In agreement with previous works, we have seen that the ionized flux fraction of sputtered carbon is low for the operating conditions explored here. The IRM calculates an ionized flux fraction of carbon HiPIMS discharges to be roughly 2% for peak discharge current densities in the range from 1 to 3 A cm−2. This is significantly lower than the ionized flux fraction commonly observed for sputtered metal species in HiPIMS operation [13].
Figure 5. The temporal evolution of the charged particle densities for peak discharge current ID,peak of (a) 20 A (1 A cm−2), (b) 40 A (2 A cm−2), and (c) 60 A (3 A cm−2), for a discharge with 2 inch graphite target and a 50 μs long pulse. The total neutral argon and carbon densities are shown as well.
Download figure:
Standard image High-resolution imageFigure 6. The temporal evolution of the discharge current composition at the target surface for a peak discharge current ID,peak of (a) 20 A (1 A cm−2), (b) 40 A (2 A cm−2), and (c) 60 A (3 A cm−2), for a discharge with 2 inch graphite target and a 50 μs long pulse.
Download figure:
Standard image High-resolution imageOne measure of the ionization of the film-forming material is the ionization probability of the target material αt. The time-dependent ionization probability for the sputtered atoms is defined as
to distinguish it from the usually reported time-averaged ionization probability ⟨αt,pulse⟩ [53]. Here, and are the time-dependent fluxes of particles out of the IR towards the DR and the sputter flux from the target into the IR, respectively. Both are in particles per second, with the dimension of s−1. As the sputter flux drops to zero in the afterglow, it is only defined up to the end of the pulse. The temporal evolution of the ionization probability of carbon αt(t) during the pulse is shown in figure 7. The ionization probability of carbon increases as the pulse progresses. Also, αt(t) shows a clear increasing trend with increasing peak discharge current. The temporal evolution of the electron density is shown in figure 8. The electron density increases with increasing peak discharge current. The increase in αt with increased peak current is expected due to the increased electron density in the discharge as seen in figure 8 and is in good agreement with previous work where titanium shows the same trend [81].
Figure 7. The temporal evolution of the ionization probability of carbon αt for peak discharge current ID,peak of 20 A (1 A cm−2), 40 A (2 A cm−2), and 60 A (3 A cm−2) during the pulse for a discharge with 2 inch graphite target and a 50 μs long pulse.
Download figure:
Standard image High-resolution imageFigure 8. The temporal evolution of the electron density for peak discharge current ID,peak of 20 A (1 A cm−2), 40 A (2 A cm−2), and 60 A (3 A cm−2), for a discharge with 2 inch graphite target and a 50 μs long pulse.
Download figure:
Standard image High-resolution imageThe electron density and the ionization probability are to a large extent determined by the discharge current [81]. The time-averaged ionization probability of carbon during the pulse on ⟨αt,pulse⟩, as calculated by the IRM, is 13%–27% for peak current discharge densities of 1–3 A cm−2, which is significantly lower than for many common metallic targets. In particular, αt for carbon is much lower than it is for titanium. At a peak current density of 1 A cm−2 the time averaged ionization probability for carbon is % compared to a time averaged ionization probability % for titanium [81]. This shows that the primary cause of the low Fflux in carbon HiPIMS discharges is the difficulty of ionizing carbon. The low ionization probability can partially be traced back to the higher ionization potential of carbon (11.26 eV) compared to common metallic targets (6.83 eV for Ti and 5.99 eV for Al). In addition, the high cohesive energy of graphite, gives the carbon atoms a high initial energy after being sputtered: this, in combination with the low mass of carbon atoms results in a high velocity of carbon atoms and consequently a low residence time of carbon within the IR. Also, the back-attraction probability is very high, βt,pulse > 92%, for all investigated pulses which means that more than 9 out of 10 carbon ions (ionized with probability αt) will return to the target. The average back-attraction probability ⟨βt(t)⟩ is in the range 80%–88%. For a discharge with titanium target we found the average back-attraction probability ⟨βt(t)⟩ to be in the range 82%–88% [53]. The electron temperature for the cold electron group for the three cases is shown in figure 9. The electron temperature is high and evolves similarly for all cases during the pulse. For comparison in a HiPIMS discharge with titanium target the cold electron temperature is below 4.9 eV [81]. In this case the presence of metal atoms and ions lowers the electron temperature due to their low ionization potential, which is not the case for graphite target.
Figure 9. The temporal evolution of the electron temperature for the cold electron group for peak discharge current ID,peak of 20 A (1 A cm−2), 40 A (2 A cm−2), and 60 A (3 A cm−2), for a discharge with 2 inch graphite target and a 50 μs long pulse.
Download figure:
Standard image High-resolution image5. Discussion
The discharge current in a HiPIMS discharge is very high, and can be significantly higher than the current that can be maintained by ionizing the atoms and molecules of the working gas. The working gas species, which are ionized for the first time and then go to the target are referred to as primary current Iprim [1, 51, 82]. The discharge current in dcMS discharges is composed only of a primary current, but the maximum steady state supply rate of argon atoms from the surrounding gas reservoir sets a critical upper limit to how large the primary current can become in steady state [44, 51, 52]. This upper limit is Icrit ≈ 7.6 A for the discharges investigated here. Discharge currents ID larger than Icrit are only possible if there is a contribution from recycling of atoms that leave the target, become subsequently ionized and then are drawn back to the target [82]. This can be either atoms of the sputtered material which constitutes a self-sputter (SS) recycling, or neutralized and returning working gas atoms which provides a working gas-recycling current. For all the cases explored here, the discharge current goes well above the critical current during the pulse and the discharges are operated in the working gas recycling regime. The existence of discharges where working gas recycling dominates the discharge current was suggested by Anders et al [51]. Using a discharge with a graphite target, they demonstrated that an argon gas recycling trap can develop if the discharge current is high enough. Later it was argued that working gas recycling occurs in a HiPIMS discharge when the sputter yield is low [48, 82]. In contrast, SS recycling develops in a discharge with a metal target when the SS yield is large and the ionization potential of the metal atom is low [44, 52, 82]. Earlier we combined the processes of SS-recycling and working gas recycling in HiPIMS discharges, and developed a unified treatment, which we refer to as the generalized recycling model [82]. For a HiPIMS discharge with graphite target Vitelaru et al [25] demonstrated two operating regimes: (i) low current mode and (ii) high current mode. In the low current mode the discharge current waveform is relatively flat, while in the high current mode the discharge current waveform develops a triangular shape. Such a triangular waveform has been related to the occurrence of working gas recycling and is observed also for other targets with low sputter yield [48, 83]. The transition between the two discharge current modes occurs at a certain discharge voltage, where a slight increase in the discharge voltage leads to a sharp and significant increase in the discharge current, and that is where the working gas recycling sets in. If the pulse is long enough, and if the power supply can support the required high current, the triangular high current mode (ii) can saturate in a high current plateau mode (iii). Such a case is reported by Anders et al [51] for a 5 cm diameter graphite target a discharge current waveform that is not triangular, but rather exhibits a peak followed by a current plateau. This discharge current waveform appears after a sudden, but reproducible jump, in the plateau current density to JD = 3.2 A cm−2 when increasing the discharge voltage from 1100 to 1150 V.
The main conclusion drawn from this current work is that the modeled HiPIMS discharges with a graphite target in modes (i) and (ii) are mainly governed by the argon working gas. At least for the operation conditions analyzed here these findings agree with the optical emission diagnostics for HiPIMS discharges with a graphite target reported by Anders et al [51]. They found the emitted light from the discharge to be dominated by argon emission and the intensity of the carbon emission lines to be weak. Indeed, they reported a very strong Ar+ emission in the spectrum from the discharge indicating working gas-dominated runaway. Furthermore, we observed earlier a significant working gas recycling when modeling a reactive Ar/O2 HiPIMS discharge with Ti target when the target is poisoned and the discharge current forms a rather distinct triangular waveform [48], somewhat similar with the one measured in the current work. In that case the sputter yield is low and the discharge current at the target surface consists mainly of Ar+ ions, the discharge operates in working-gas recycling mode. The relation between target poisoning and the discharge current waveform in reactive HiPIMS of chromium in an Ar/O2 discharge has been explored experimentally by Layes et al [84]. They relate the triangular waveform to the extreme case of fully poisoned target. This also agrees with the findings of Hála et al [85] who reported a significant rise in Ar+ emission, and substantially diminished emission from Nb atoms and Nb+ ions, when sputtering a poisoned (oxidized) Nb target in HiPIMS, suggesting working gas recycling.
6. Conclusions
We have developed an ionization region model (IRM) of a HiPIMS discharge in argon with a graphite target. The ionized flux fraction for carbon is low or about 2% in the discharge, lower than typically observed for a HiPIMS discharge with a metallic target. The cause of the low ionized flux fraction is the low time-averaged ionization probability ⟨αt,pulse⟩ ≈ 13%–27%, and high back-attraction probability %, both increasing with increased discharge current density. The reason for the low ionization probability αt is the low electron impact ionization cross section of the carbon atom, the high ionization potential, as well as high cohesive energy, which, in combination with the low mass of the carbon atom, causes the sputtered carbon atoms to pass the IR at high velocity, leaving little time for electron impact ionization processes. The contribution of SS compared to working gas sputtering depends heavily on the sputter yields. For high sputter yield materials, such as copper and aluminum, working gas sputtering can be neglected and pure SS is possible. For low sputter yield materials, such as carbon (graphite) or poisoned targets, the discharge is governed by working gas recycling and the Ar+ ion dominates the discharge.
The results presented are, at first glance, not encouraging as to the possibility to produce good quality DLC films by HiPIMS deposition. The calculated data shows only low ionized flux fractions, and thereby only confirm the results from several earlier experiments in HiPIMS discharges [15–17]. The IRM results, however, give some hope in the sense that they show what is needed to improve this figure. Please note that, as discussed in the introduction, there are basically two reasons for low Fflux: a low fraction of ionization of the sputtered target species, and a large back-attraction of these created ions. Our modeling here shows that the first is surmountable. HiPIMS can indeed create a very energetic electron population [45], as compared to the usual 2–5 eV in dcMS [86, 87], and also that the discharge thereby ionizes carbon quite effectively. As can be seen by combining figures 7 and 9, the electron temperature becomes as high as 15 eV at the 60 A current peak, and at this time the momentary ionization probability of sputtered carbon reaches 50%. This means that ionized flux fractions high above a few % are in principle possible, if only a too large ion back-attraction could be avoided. Here it is most fortunate that the discharges, above a current density of about 1 A cm−2, go into a rapidly growing working-gas recycling process. This has the consequence that the discharge current peaks sharply at the pulse end. As a result, a large fraction of the carbon ions are created close to the pulse end, after which there is the possibility of a reduced back-attraction because the applied pulse voltage is switched off [49]. There are several options how to exploit this situation by attempting to reduce the back-attraction of these late-formed ions: using ultra-short and ultra-high current peaks; applying a reversed-polarity peak after these HiPIMS peaks, so called bipolar HiPIMS [88, 89]; and/or tailoring the magnetic geometry (in particular the degree of magnetic unbalance) in order to minimize any back-attracting electric fields between the IR and the substrate during the off-time. An example of utilization of this is demonstrated in the work of Akhavan et al [33] which apply an external magnetic field during the end of the pulse where the ionization probability is the highest, enabling more efficient transport of the carbon ions to the substrate.
Acknowledgments
This work was partially funded by the Free State of Saxony and the European Regional Development Fund (Grant No. 100336119), the Icelandic Research Fund (Grant No. 196141), the Swedish Research Council (Grant No. VR 2018-04139), and the Swedish Government Strategic Research Area in Materials Science on Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009-00971).
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.