Abstract
Amorphous solid water (ASW) is found on icy dust grains in the interstellar medium (ISM), as well as on comets and other icy objects in the outer solar system. The optical properties of ASW are thus relevant for many astrophysical environments, but in the ultraviolet–visible (UV–vis), its refractive index is not well constrained. Here, we introduce a new method based on UV–vis broadband interferometry to measure the wavelength-dependent refractive index n(λ) of amorphous water ice from 10 to 130 K, i.e., for different porosities, in the wavelength range of 210–757 nm. We also present n(λ) for crystalline water ice at 150 K, which allows us to compare our new method with literature data. Based on this, a method to calculate n(λ, ρ) as a function of wavelength and porosity is reported. This new approach carries much potential and is generally applicable to pure and mixed ice, both amorphous and crystalline. The astronomical and physical–chemical relevance and future potential of this work are discussed.
Export citation and abstract BibTeX RIS
1. Introduction
Water ice is ubiquitous both in the solar system and in the interstellar medium. Unless it has been heated above temperatures of roughly 130 K, it resides in the form of amorphous solid water (ASW). In our solar system, water ice has been detected on Kuiper Belt objects (Baragiola 2003; Stern et al. 2015; Raponi et al. 2018), comets (Mumma & Charnley 2011; Raponi et al. 2016), and icy moons such as Europa, Ganymede, and Enceladus (Calvin et al. 1995; Porco et al. 2006; Dalton et al. 2010) as well as in Saturn's rings. The study of water ice on the outer solar system objects is particularly interesting because it provides an understanding of the chemical history of our solar system and holds the potential to explain the origin of water on Earth. Beyond the solar system, observations in the infrared have shown us that ice is residing on cold dust particles throughout the interstellar medium (van Dishoeck et al. 2013; Boogert et al. 2015 and refs. therein). The Infrared Space Observatory (ISO; Gibb et al. 2004), Spitzer telescope, as well as several ground-based observatories revealed that these ices comprise predominantly H2O but also contain other species including CO2, CO, CH4, NH3, and CH3OH (Boogert et al. 2008; Öberg et al. 2011). These ice-covered dust grains provide a surface area for solid-state reactions that result in the formation of larger complex organic molecules (Linnartz et al. 2015; Ligterink et al. 2018 and refs. therein). Many of these are building blocks of matter considered to be important for the origin of life (Ehrenfreund et al. 2002; Herbst & van Dishoeck 2009). Water, as the most abundant component of the ice, largely determines the chemical and physical properties of the ice mantle.
Most of our information of ice beyond the Earth comes from spectroscopic studies of light interacting with the ice. In the solar system, the surface of the icy objects is studied by analyzing reflected sunlight (Calvin et al. 1995; Baragiola 2003; Stern et al. 2015). In the interstellar medium, water ice is mostly observed by infrared absorption features in the light from reddened stars. To interpret and quantify the constituents in the observational spectra of water ices, the optical constants of water ice (ASW or crystalline) are required. One also needs these same numbers to calculate the absorption, transmission, reflection or scattering of light in ice or ice containing clouds in planetary atmospheres. The refractive index of water ice is also used in radiative transfer models of molecular clouds (Pollack et al. 1994), accretion/circumstellar disks (Tilling et al. 2012) and recently to constrain the abundance and grain size of water ice on comet 67P/Churumov–Gerasimenko (Raponi et al. 2016). In these models, the optical constants of water were taken from Warren (1984), who reported the values for fully dense crystalline water in the UV–vis range. However, the water ice in molecular clouds, accretion/circumstellar disks, and on the surface of many outer solar system icy objects is predominantly amorphous and expected to be porous. Using the values for (fully dense) crystalline ice, therefore, is likely to result in less accurate predictions.
The optical properties of pure water ice are described by its refractive index, a complex function consisting of two parameters. The imaginary index, k, describes the attenuation or absorption of the medium and the real refractive index, n, is the ratio of the velocity of light in the medium with respect to the vacuum speed of light. Both k and n are wavelength dependent. In the UV–vis range, wavelength-dependent values of n are only reported for crystalline, and thus fully dense, water ice (Warren 1984; Warren & Brandt 2008), for liquid water, and for steam (Schiebener et al. 1990; Harvey et al. 1998). To the best of our knowledge, no prior laboratory measurements exist of the wavelength-dependent refractive index values for ASW in the UV–vis range.
ASW is a meta-stable form of water ice with no long-range ordering. Most ice under Earth's atmospheric conditions is (hexagonal) crystalline, but in astronomical environments, ASW is most often found (Smith et al. 1989; Boogert et al. 2015), although crystalline ice, thought to be a product of thermal processing of ASW, has been detected as well (Terada & Tokunaga 2012). ASW is formed when water is deposited or chemically formed at temperatures below 130 K (Brown et al. 1996; Baragiola 2003; Dohnálek et al. 2003; Ioppolo et al. 2008; Cuppen et al. 2010; Dulieu et al. 2010; Jing et al. 2011) or when liquid water is rapidly cooled. Amorphous ice can crystallize in an exothermic (energy releasing) and irreversible process (Bossa et al. 2012). Crystallization has a significant barrier and the rate follows a Boltzmann-like dependence on temperature, resulting in very low rates at lower temperatures (see, e.g., Jenniskens & Blake 1996; Maté et al. 2012). The structural organization of water ice can be clearly distinguished when its absorption spectrum is studied in the infrared between 3500 and 3000 cm−1 (2.85 and 3.3 μm). The absorption of ASW shows one broad peak in this range, while crystalline ice appears as a combination of three bands (e.g., Hudgins et al. 1993).
The density of crystalline ice is 0.94 g cm−3, but in ASW, the density is variable. Laboratory studies revealed that vapor-deposited ASW at sample temperatures below ∼130 K is porous with a large specific surface area (Westley et al. 1998; Dohnálek et al. 2003; Clements et al. 2018). The porosity level depends on the growth conditions of the ice, such as the temperature, and in the laboratory deposition angle and deposition rate. A lower deposition temperature, higher deposition angle, and higher deposition rate favor a higher degree of porosity (Dohnálek et al. 2003; Maté et al. 2012). Infrared spectra of porous ASW formed in the laboratory show two weak absorption bands at 3696 and 3720 cm−1 caused by unbound or dangling OH (dOH) bonds. The band strength of the dOH absorption features is positively related to the porosity. Spectroscopic searches for dOH band features in dense clouds did not result in unambiguous identifications (Keane et al. 2001), which has led to the interpretation that ice processing in space ultimately results in compaction (Palumbo 2006; Raut et al. 2007; Accolla et al. 2011; Clements et al. 2018). However, a lack of dOH does not necessarily rule out the presence of partially porous ASW, as Bossa et al. (2015) demonstrated that dOH bonds are not detectable for such ices. The porosities of water ice on ISM dust grains and on many solar system objects are still being debated.
In Section 2, we give an overview about the state-of-the-art of the work focusing on the refractive index of water ice in the UV–vis range. We then explain our new experimental approach and subsequently show the data processing procedures in Section 3. In Section 4, we present the new values for the refractive index of ASW from 210 to 757 nm and for temperatures from 10 to 130 K. Also a measurement for crystalline ice at 150 K is presented. These measurements are combined to derive a function that describes n(λ, ρ) as a function of the wavelength and porosity, using the specific refraction. Finally, in Section 5, we discuss the future potential of the new method introduced here.
2. Materials and Methods
2.1. Refractive Index of Water Ice
The refractive index n can be measured during the deposition of water vapor on a reflective or transparent surface. For volatile species, this is usually done on the tip of a liquid nitrogen or closed cycle helium cryostat placed inside a vacuum chamber (e.g., Goodman 1978; Brown et al. 1996; Dohnálek et al. 2003).
As the thickness increases during the ice growth, periodical fluctuations in the intensity of the transmitted or reflected light appear. These fringes occur due to constructive and destructive interference arising from a difference in the path length of light reflecting internally in the ice and light transmitting directly. The refractive index of the sample is related to the period of the fringes and the thickness d by

where m is the total number of fringes observed at wavelength λ (in nm), n(λ) is the wavelength-dependent refractive index, and θ is the angle of incidence with respect to the surface. Interference is commonly measured in reflection (e.g., Baratta & Palumbo 1998; Fulvio et al. 2009) but can also be observed in transmission. Interference measurements are typically performed using a monochromatic light source, such as a helium–neon laser. The strength of our new approach is that we simultaneously record the interference for all wavelengths covered by a broadband light source. The details are given in Section 2.2.
Warren (1984) and Warren & Brandt (2008) reported n(λ) of crystalline water ice between 200 and 400 nm at a resolution of 50 nm, and between 400 and 800 nm at a resolution of 10 nm. In these cases, discrete wavelengths are measured in separate experiments, placing practical limits on the full wavelength coverage and resolution and ultimately limiting the precision of n to how well the experiments are reproduced. In the case of ASW, n is predominantly measured using helium–neon lasers, and therefore reported at a wavelength of 632.8 nm (Brown et al. 1996; Westley et al. 1998; Dohnálek et al. 2003; Romanescu et al. 2010). Bouilloud et al. (2015) provided an overview of known values of the refractive index for a number of other astrophysically relevant ices, including H2O, CO2, CO, CH4, and NH3.
The refractive index depends on the density (porosity) of the solid. Vacuum deposition of crystalline ice results in a constant density, but for ASW, the porosity increases at lower deposition temperatures (see, e.g., Brown et al. 1996; Westley et al. 1998; Dohnálek et al. 2003). The porosity and the refractive index are related via the Lorentz–Lorenz equation:
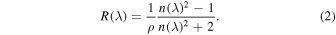
Here, R(λ) is the specific refraction (in units of cm3 g−1) and ρ is the density of the ice. We adopt R(632.8) = 0.2072 cm3 g−1 (Brown et al. 1996) at a density of 0.93 g cm−3 and assume that R is constant at a given wavelength, regardless of the morphology of the ice.3 We will verify the latter assumption. In order to determine the refractive index of porous ASW, one needs to determine or assume the level of porosity. For this study, we rely on the ASW densities reported as function of the deposition temperature by Dohnálek et al. (2003). Using Equation (2) together with the adopted R-value yields the refractive index.
2.2. Experimental Setup
The experiments were done using a recently constructed setup, described in detail in Kofman et al. (2018). We will briefly describe the experimental features that are relevant to this study. The setup is a high vacuum system with a base pressure in the order of 5 × 10−8 mbar. Residual gas in the chamber is dominated by water. At the center of the chamber, a BaF2 sample window is mounted onto the cold-finger of a closed cycle helium cryostat. The temperature of the sample is measured using a chromel-Au/Fe thermocouple and controlled with resistive heating. Temperatures between 10 and 320 K are accessible with an absolute accuracy better than 2 K. For these experiments, water ice is grown using background deposition, the same method as used by Dohnálek et al. (2003). We use a precision dosing valve, which results in a constant deposition rate with less than 3% variation in the pressure over the entire deposition time, and also allows reproducible water partial pressures inside the chamber between different experiments, ensuring that the conditions of separate experiments are comparable.
During water deposition, the chamber pressure is 2.6 × 10−6 mbar, corresponding to a deposition rate of about 0.3 nm s−1 or roughly 1 mono-layer per second. Experiments were performed with sample temperatures of 10, 30, 50, 70, 90, 110, 130, and 150 K. Only in the latter case does this result in the formation of crystalline ice; all other experiments concern ASW.
UV–vis spectra are continuously recorded during the deposition. For the work performed here, the spatially filtered light of a broadband Xe-arc lamp, emitting in the range of 180–1100 nm, is guided through the sample that is positioned perpendicular to the light beam. Light is dispersed by an Andor 303i Shamrock spectrometer equipped with a 10 μm slit and collected on a thermo-electrically cooled CCD (Andor iDus DV420 OE). We record data from 210 to 757 nm at a spectral resolution of 0.56 nm, and at a time resolution of 4.3 s. The broadband spectroscopy applied allows us to measure interference fringes over the full wavelength range during the deposition. From the interference fringes, n can be determined as a function of λ in one experiment, something not possible when only monochromatic light sources are used.
3. Results and Analysis
We demonstrate the data processing procedures on UV–vis signals recorded during the deposition of ASW at 90 K and 10 K in detail. The other experiments are analyzed following the same procedure. The analysis is performed in three steps. First, we determine the refractive index at each wavelength separately. Subsequently, these values are used as starting points to fit a continuous function for n(λ). The data sets are finally combined to derive one equation for the refractive index, n(λ, ρ), as a function of wavelength and porosity using the Lorentz–Lorenz equation.
3.1. Fitting the Period of the Interference
The use of background deposition causes ices to grow on both the front and back side of the window. In the ideal case, the ratio of the deposition rates on each side of the sample would be unity (i.e., 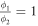 , with ϕi being the deposition rate at the respective side). In practice, this ratio varies between 0.91 and 0.96 in the experiments performed in this study. Measuring the interference pattern monitors the cumulative effect of similar but not fully identical growth processes on both sides of the window. As will be shown below, the effect of asymmetric deposition can be corrected by taking into account the empirically determined
, with ϕi being the deposition rate at the respective side). In practice, this ratio varies between 0.91 and 0.96 in the experiments performed in this study. Measuring the interference pattern monitors the cumulative effect of similar but not fully identical growth processes on both sides of the window. As will be shown below, the effect of asymmetric deposition can be corrected by taking into account the empirically determined  -value. As the light propagates through the growing ice on both sides of the deposition window, the absolute light intensity I at wavelength λ fluctuates as a function of the time t. When the deposition rates at both sides are equal, the signals can be described by a single periodic function:
-value. As the light propagates through the growing ice on both sides of the deposition window, the absolute light intensity I at wavelength λ fluctuates as a function of the time t. When the deposition rates at both sides are equal, the signals can be described by a single periodic function:
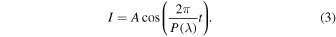
P(λ) is the wavelength-dependent period, and A is the magnitude of the oscillation. Several studies focus on the absolute values of A, and we refer the reader to these reports for a full description of the amplitude of the signal (Goodman 1978; Dohnálek et al. 2003; Romanescu et al. 2010). Note that as in our experiments the light progresses at a normal incidence, the 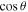 term in Equation (1) equals unity and is left out.
term in Equation (1) equals unity and is left out.
In the case of asymmetric deposition, two cosine terms, one for each side of the window with a corresponding period P(λ) and amplitude A, are required to reproduce the observed interference pattern.
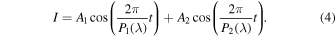
Note that we cannot discriminate which part of this equation describes which side of the window. In order to determine the period from the experimental signals, we take A1 = A2 = 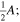 i.e., both sides of the window contribute equally to the amplitude of the signal. This allows us to fit a single value of A, which significantly reduces the complexity of the fitting routine. Similarly, the period is fit with a single value for both signals in the first iteration. Subsequently, we introduce the
i.e., both sides of the window contribute equally to the amplitude of the signal. This allows us to fit a single value of A, which significantly reduces the complexity of the fitting routine. Similarly, the period is fit with a single value for both signals in the first iteration. Subsequently, we introduce the  factor in the second cosine, substituting P2(λ) with
factor in the second cosine, substituting P2(λ) with 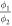 P1(λ). This comes from the fact that the period P(λ) is directly related to the deposition rate ϕ (see Equation (6)). The
P1(λ). This comes from the fact that the period P(λ) is directly related to the deposition rate ϕ (see Equation (6)). The 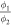 factors are constrained manually for each experiment and are included in the final fits that start from the best-fit solution of the first iteration. Table 1 shows the values of
factors are constrained manually for each experiment and are included in the final fits that start from the best-fit solution of the first iteration. Table 1 shows the values of 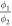 used for the fits of all the experimental temperatures. As the occurrence of the interference minima (see below) is fully determined by
used for the fits of all the experimental temperatures. As the occurrence of the interference minima (see below) is fully determined by  , we can constrain
, we can constrain 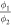 quite accurately. Based on this, we estimate the error on the value for
quite accurately. Based on this, we estimate the error on the value for 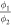 in the order of 1%.
in the order of 1%.
Table 1.
Density of Background-deposited ASW Reported by Dohnálek et al. (2003), the Total Thickness d, 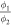 , σfit, Which is the Standard Error on the Refractive Index from the Fit of Equation (7) and Best-fit Values for B1 and B2 from Section 3.3
, σfit, Which is the Standard Error on the Refractive Index from the Fit of Equation (7) and Best-fit Values for B1 and B2 from Section 3.3
| Temperature (K) | ρ | d (nm) |

|
n(632.8) ± σfit | B1 | B2 |
|---|---|---|---|---|---|---|
| 10 | 0.585 ± 0.010 | 1703.6 ± 6.0 | 0.94 ± 0.01 | 1.190 ± 0.004 | 0.309 | 0.098 |
| 30 | 0.636 ± 0.010 | 1659.3 ± 9.7 | 0.94 ± 0.01 | 1.208 ± 0.007 | 0.374 | 0.099 |
| 50 | 0.688 ± 0.010 | 1559.8 ± 4.3 | 0.94 ± 0.01 | 1.226 ± 0.003 | 0.331 | 0.164 |
| 70 | 0.740 ± 0.010 | 1481.7 ± 2.2 | 0.94 ± 0.01 | 1.244 ± 0.002 | 0.377 | 0.164 |
| 90 | 0.791 ± 0.010 | 1436.1 ± 5.9 | 0.95 ± 0.01 | 1.262 ± 0.003 | 0.280 | 0.291 |
| 110 | 0.843 ± 0.010 | 1343.2 ± 3.2 | 0.96 ± 0.01 | 1.280 ± 0.003 | 0.400 | 0.220 |
| 130 | 0.895 ± 0.010 | 1317.6 ± 2.2 | 0.96 ± 0.01 | 1.299 ± 0.002 | 0.417 | 0.258 |
| 150 | 0.925 ± 0.010 | 1177.6 ± 5.7 | 0.92 ± 0.01 | 1.310 ± 0.006 | 0.496 | 0.190 |
Download table as: ASCIITypeset image
The experiments at 90 and 10 K represent two different cases of asymmetric deposition, with 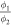 = 0.96 and 0.94, respectively. Figure 1 shows the interference signal measured during the deposition at a few selected wavelengths throughout the recorded range. The seven wavelengths are picked at intervals of 80 nm across the entire measured range. The left panel shows the deposition at 90 K, and the right panel at 10 K. The resulting fits using Equation (4) are also shown. The effect of the asymmetric deposition rates is seen in the decrease in the amplitude of the interference signal after roughly 10 periods in the left panel and after 6 periods in the right panel. Note that this lapse in intensity is persistently seen after the same number of periods at the different wavelengths. Currently, we do not have a full explanation for the difference in the deposition rates at the two sides of the sample, but we intend to make this the subject of an upcoming study. Finally, note that the signal becomes more noisy at wavelengths above 400 nm, an effect of small intensity fluctuations in the spectral energy distribution of the xenon light source.
= 0.96 and 0.94, respectively. Figure 1 shows the interference signal measured during the deposition at a few selected wavelengths throughout the recorded range. The seven wavelengths are picked at intervals of 80 nm across the entire measured range. The left panel shows the deposition at 90 K, and the right panel at 10 K. The resulting fits using Equation (4) are also shown. The effect of the asymmetric deposition rates is seen in the decrease in the amplitude of the interference signal after roughly 10 periods in the left panel and after 6 periods in the right panel. Note that this lapse in intensity is persistently seen after the same number of periods at the different wavelengths. Currently, we do not have a full explanation for the difference in the deposition rates at the two sides of the sample, but we intend to make this the subject of an upcoming study. Finally, note that the signal becomes more noisy at wavelengths above 400 nm, an effect of small intensity fluctuations in the spectral energy distribution of the xenon light source.
Figure 1. The measured light intensity at selected wavelengths during growth of water ice at 90 K (left panel) and 10 K (right panel). The fits of Equation (4) are shown using black dashed lines. Signals are offset for clarity.
Download figure:
Standard image High-resolution image3.2. Deriving the Refractive Index Using the Experimentally Determined P(λ)
In order to calculate the refractive index from the period, we substitute d = ϕmP(λ) in Equation (1). This comes from the fact that the thickness of the ice is equal to the deposition rate ϕ, multiplied by the total deposition time, mP(λ).
This yields:

and after reordering:
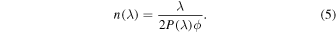
We use this equation to express ne(λ), with the subscript e indicating that these values are obtained from the experiments, as a ratio to n(632.8):
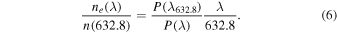
We determine n(632.8) from the Lorentz–Lorenz equation (Equation (2)), and we use the specific refraction R = 0.2072 cm3 g−1 and the density ρ of background-deposited ice from Dohnálek et al. (2003), using their Figure 8 and fitting a linear function for the densities derived between 22 and 140 K. We follow Dohnálek et al. (2003) in their assumption that the level of porosity depends linearly on the deposition temperature (for the range studied). The densities and the resulting refractive indices are shown in Table 1.
Table 2. Selected Specific Refraction (RSM(λ)) and Refractive Index (n(λ)) Values Over the Studied Wavelength Range
| λ (nm) | RSM(λ) | n10(λ) | n30(λ) | n50(λ) | n70(λ) | n90(λ) | n110(λ) | n130(λ) | n150(λ) |
|---|---|---|---|---|---|---|---|---|---|
| 210.8 | 0.2545 ± 0.0061 | 1.2346 | 1.2568 | 1.2793 | 1.3022 | 1.3254 | 1.3489 | 1.3728 | 1.3869 |
| 250.1 | 0.2361 ± 0.0035 | 1.2167 | 1.2371 | 1.2577 | 1.2786 | 1.2998 | 1.3213 | 1.3431 | 1.3559 |
| 300.2 | 0.2248 ± 0.0020 | 1.2057 | 1.2250 | 1.2445 | 1.2643 | 1.2842 | 1.3045 | 1.3250 | 1.3370 |
| 350.2 | 0.2187 ± 0.0012 | 1.1999 | 1.2186 | 1.2375 | 1.2566 | 1.2759 | 1.2955 | 1.3153 | 1.3270 |
| 400.2 | 0.2150 ± 0.0008 | 1.1964 | 1.2147 | 1.2332 | 1.2520 | 1.2709 | 1.2901 | 1.3095 | 1.3209 |
| 450.2 | 0.2126 ± 0.0005 | 1.1940 | 1.2121 | 1.2304 | 1.2489 | 1.2676 | 1.2866 | 1.3057 | 1.3170 |
| 500.2 | 0.2109 ± 0.0003 | 1.1924 | 1.2104 | 1.2285 | 1.2468 | 1.2654 | 1.2841 | 1.3031 | 1.3142 |
| 550.2 | 0.2097 ± 0.0002 | 1.1913 | 1.2091 | 1.2271 | 1.2453 | 1.2637 | 1.2823 | 1.3012 | 1.3122 |
| 600.2 | 0.2088 ± 0.0001 | 1.1904 | 1.2081 | 1.2261 | 1.2442 | 1.2625 | 1.2810 | 1.2997 | 1.3107 |
| 650.2 | 0.2081 ± 0.0000 | 1.1897 | 1.2074 | 1.2252 | 1.2433 | 1.2615 | 1.2800 | 1.2986 | 1.3096 |
| 700.2 | 0.2075 ± 0.0001 | 1.1892 | 1.2068 | 1.2246 | 1.2426 | 1.2608 | 1.2792 | 1.2978 | 1.3087 |
| 750.2 | 0.2071 ± 0.0001 | 1.1888 | 1.2063 | 1.2241 | 1.2420 | 1.2602 | 1.2785 | 1.2971 | 1.3080 |
Note. For brevity, the errors on the values for n(λ) are not shown.
Only a portion of this table is shown here to demonstrate its form and content. A machine-readable version of the full table is available.
Download table as: DataTypeset image
Using Equation (6) and the periods from the fits of the UV–vis signal recorded during the ice deposition, the values of ne(λ) are obtained. The left panel of Figure 2 shows ne(λ) obtained from the signal recorded during the deposition of ASW at 90 K. The figure shows that ne(λ) increases at shorter wavelengths. Between 400 and 760 nm, the refractive index exhibits oscillations of the order of 1% of the n-value, likely due to the lower signal-to-noise ratio at these wavelengths. We can reproduce the fringes and the overall interference pattern seen in the experimental signals when we substitute the period in Equation (4) and calculate the amplitude I on a wavelength-time grid, simulating the UV–vis interference pattern. This gives a qualitative impression of the performance of the fitting routines. In the middle panel of Figure 2, we show the simulated interference pattern, with the right panel showing the recorded UV–vis interference pattern. We see that the fitting routine reproduces the experimental signals well. Figure 3 shows the same panels for the experiment at 10 K. At 10 K, the destructive interference clearly results in a low-amplitude band after six periods, starting at roughly 2000 s at 200 nm, and falling outside of the experimental time range at wavelengths longer than 600 nm. This same pattern can be seen in Figure 1. The experimental signal also shows vertical bands, indicating fluctuations in the total lamp flux, which already were noticed at longer wavelengths in Figure 1.
Figure 2. Left panel: the wavelength-dependent refractive index from fitting the entire interference pattern using Equation (4). Middle panel: simulated two-dimensional interference pattern based on P(λ) and Equation (4). Right panel: experimental data showing the UV–vis signal recorded during the deposition of ASW at 90 K.
Download figure:
Standard image High-resolution imageFigure 3. Left panel: the wavelength-dependent refractive index from fitting the entire interference pattern using Equation (4). Middle panel: simulated two-dimensional interference pattern based on P(λ) and Equation (4). Right panel: Experimental data showing the UV–vis signal recorded during the deposition of ASW at 10 K.
Download figure:
Standard image High-resolution image3.3. Fitting of the Refractive Index Using the Sellmeier Equation
In the previous section, the refractive index derived from the experimental interference patterns showed relatively small and non-physical oscillations above 400 nm. By using a continuous function for n(λ), we can eliminate these artifacts. The wavelength dependency of the refractive index can be approximated by using the Sellmeier dispersion equation (Sellmeier 1871):
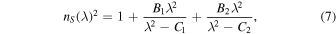
where each term in the summation represents an absorption resonance of strength B at wavelength 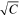 , and nS(λ) is labeled with the subscript S to indicate these values are derived using the Sellmeier equation. We use two sets of parameters to describe nS(λ), corresponding to absorption maxima at 71 and 134 nm (
, and nS(λ) is labeled with the subscript S to indicate these values are derived using the Sellmeier equation. We use two sets of parameters to describe nS(λ), corresponding to absorption maxima at 71 and 134 nm (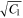 and
and 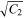 ), the vacuum UV absorption maxima of ASW (Cruz-Diaz et al. 2014). This relates back to the fact that the real and imaginary refractive indices are connected. We assume that the electronic absorption maxima do not change significantly when changing from amorphous to crystalline water ice, an assumption we later verify. B1 and B2 are fit using a least-squares approach with a linear cost function. The best-fit values for B1 and B2 are reported in Table 1. Note that although we adopted the refractive index at 632.8 nm to calculate ne(λ), we do not force the Sellmeier fit through this value.
), the vacuum UV absorption maxima of ASW (Cruz-Diaz et al. 2014). This relates back to the fact that the real and imaginary refractive indices are connected. We assume that the electronic absorption maxima do not change significantly when changing from amorphous to crystalline water ice, an assumption we later verify. B1 and B2 are fit using a least-squares approach with a linear cost function. The best-fit values for B1 and B2 are reported in Table 1. Note that although we adopted the refractive index at 632.8 nm to calculate ne(λ), we do not force the Sellmeier fit through this value.
A conservative estimate of the relative error of the resulting function for nS(λ) can be obtained by calculating the difference between the experimental fit of the period and the Sellmeier fit. The difference between nS(λ) and the experimental ne(λ) provides a measure for the uncertainty at this wavelength. The error, σλ, is calculated by taking the root mean square error of the two values of n at wavelength λ. The average is shown as σfit in Table 1.
In Figure 4, we show the refractive index from the period (from Section 3.1), together with the fit of Equation (7) for all the temperatures, including the 10 and 90 K measurements already shown in Figures 2 and 3. The experimental UV–vis patterns are shown as well. The graphs are shown in pairs of two, where the left panel shows ne(λ) and nS(λ), and the right panel shows the experimental signal. Clearly, the fit based on Equation (7) removes the oscillations still visible when using Equation (4).
Figure 4. The different experiments are presented in pairs of two plots. The left plots show the refractive index of the different experiments as determined by the fitting of the periodic signals (ne(λ), in blue) plot together with the fit to the Sellmeier equation (nS(λ), in orange). The deposition temperatures are indicated in the headers. The right plots show the experimental data recorded at the corresponding temperature.
Download figure:
Standard image High-resolution image3.4. Using the Lorentz–Lorenz Equation to Derive a General Function for the Refractive Index
Although the Sellmeier fits in Figure 4 are generally well constrained, we see disagreements between the experimentally determined values for ne(λ) and nS(λ) in some wavelength domains, particularly in the cases of the 30 and 150 K experiments above 600 nm. Here, the interference patterns are relatively noisy, and as a result, the standard error σfit on the fits is larger for these two experiments. The uncertainty in the resulting nS(λ) values can be further decreased by using the Lorentz–Lorenz equation and producing RT(λ) for each temperature, where the subscript T indicates the deposition temperature, and using the average of the eight measurements to provide one set of values for Ra(λ). This in turn allows us to derive a general function for n(λ, ρ) as a function of wavelength and porosity, which has the advantage that we can calculate the refractive index for any ice porosity. Note that for this, we assume R632.8 = 0.2072 cm3 g−1 and Ra to be independent of temperature, and that the electronic absorption features of ASW and crystalline ice are not significantly different. The respective curves of RT(λ) in Figure 5 for the amorphous and crystalline experiment indicate that this assumption is valid within the uncertainty of the experiments: the largest outlier in this figure is the R90(λ) curve, and the R150(λ) curve agrees closely with those from the other experiments. This indicates that the porosity is the governing factor in the refractive index and that the ordering of the water molecules in the solid phase (i.e., ASW or crystalline ice) is less important. Note that the use of the specific refraction to determine the refractive index of ASW is widely used in the literature (e.g., Brown et al. 1996; Dohnálek et al. 2003, and implicitly in the subsequent work adopting the refractive index from these studies). Here, we provide the proof that this approach is indeed valid.
Figure 5. Derived RT(λ) curves for different deposition temperatures ranging from 10 to 150 K. The black curve shows the fit using Equation (9). The dot at 632.8 nm represents the assumed specific refraction of 0.2072 cm3 g−1.
Download figure:
Standard image High-resolution imageA continuous function for n(λ, ρ), i.e., explicitly using the density ρ and based on the derived Ra(λ) curve, is obtained by rewriting Equation (2) into:
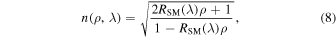
with RSM(λ):

where C1 and C2 are the same absorption maxima as used in the fitting of Equation (7). Equation (9) is fit to the curves in Figure 5, yielding the best-fit parameters D1 = 0.8416 and D2 = 1.0592. We scaled the values of RT(λ) to intersect R(632.8) = 0.2072 cm3 g−1, as any deviation from this value is due to errors in the period determined in Section 3.1. Subsequently, Equation (9) and the Lorentz–Lorenz relation (Equation (2)) were used to calculate the n(λ) for different temperatures and the corresponding densities (as listed in Table 1). The resulting n(λ) curves are shown in Figure 6. These curves all show a similar wavelength behavior, with a nonlinear increase in n for shorter wavelengths. The curves differ with 0.018 for temperature steps of 20 K, resulting from the linear increase in the density as a function of temperature (Dohnálek et al. 2003). Table 2 summarizes a selected set of RSM(λ) and nT(λ) values for the investigated wavelength range. The full list with numbers is available from the supplementary information.
Figure 6. Wavelength-dependent refractive index of water ice grown at 150 K (in gray), compared with literature values from Warren & Brandt (2008), reported as blue crosses. The reference values at 632.8 are shown as solid circles. The other curves represent ASW for which only one reference value at 632.8 nm (indicated by solid circles) exists.
Download figure:
Standard image High-resolution image3.5. Comparison of the n(λ) 150 K Experiment with Literature
Figure 6 shows the refractive index of ASW, with the corresponding densities in the wavelength range between 210 and 757 nm. Also shown is n(λ) of crystalline water ice at 150 K. The values of n(λ) are calculated from RSM(λ) as derived in Section 3.4. A comparison of n(λ) from our crystalline ice deposited at 150 K with literature values of the refractive index as were reported by Warren & Brandt (2008) shows that these reproduce the literature values well. All of the values for n shown in this figure are available in Table 2.
3.6. Imaginary Refractive Index
With the experimental derivation of the real part of the refractive index, it is possible, in principle, to also derive the imaginary part, i.e., the parameter that describes the absorption properties, using the Kramer–Kronig relation. However, as already noted by Warren (1984), in the UV–vis, the imaginary refractive index is several orders of magnitude smaller than n, and as a direct result, in our experiments the accuracy of n is insufficient to constrain relevant imaginary refractive index values.
4. Astrophysical Implications
In the introduction, the relevance of measuring refractive indices for interstellar ices was already mentioned. In most cases, only data for specific wavelengths exist and in the few cases larger wavelength domains have been studied, the resolution is quite low. For this reason, many of the solar system ice and interstellar ice studies rely on refractive index values of crystalline ice reported at moderate resolution. We demonstrated that the refractive index of ASW and crystalline ice shows a similar dependence on the wavelength, but that for the exact values, the porosity is required. In the cases where amorphous, and likely porous, ice is expected to be present, the results from our study improve the fidelity of the simulations, and this should help interpreting astronomical ice studies.
In laboratory studies of astronomical ice analogues, accurate optical constants improve the ability to quantify the solids under investigation. One should consider that all solid-state infrared band strength determinations ultimately rely on quantifying the solid using lasers in the UV–vis. The uncertainty of infrared band strengths is typically of the order of 20% and improvements in the quantification of solids will result in better constrained infrared band strengths. In order to study the refractive index of species for which no specific refraction is available, an alternative approach to determine absolute values of n(λ) can be applied. If one measures the interference at different angles simultaneously (Browell & Anderson 1975; Romanescu et al. 2010), R can be determined by analyzing both signals. We intend to implement an additional helium–neon laser path and use this method, yielding the essential calibration point that will allow us to determine refractive index over the full UV–vis wavelength range. In this way, the n(λ, ρ) values for astronomically relevant ice mixtures, such as H2O:CO2, can be determined.
5. Conclusions
We demonstrate the use of a new method to determine the refractive index of amorphous water ice between 10 and 130 K and crystalline ice at 150 K in the 210–757 nm range, with a wavelength resolution of 0.56 nm, and derive a continuous function to calculate the refractive index based on the porosity and wavelength. The results also indicate that in the UV–vis, crystalline ice, and ASW show the same wavelength dependency, but that the absolute refractive index is a function of the density of the ice. The availability of this data will assist in the interpretation of observations where porous amorphous water ice is involved. With the new method, it is possible to measure the refractive index (and the specific refraction) of any ice or ice mixture using only a single calibration point. In the future, this method may be applied to other ices or ice mixtures, obtaining the refractive index over the full UV–vis range of other astronomically relevant ice constituents. In the astrophysical laboratory, it will help improve quantification of solids and ultimately result in more accurate infrared band strengths. Considering the new range of telescopes that will be available in the coming years (e.g., the James Webb Space Telescope or the ELT in the UV–vis), such information will be very useful.
Financial support is acknowledged through two NWO (Netherlands Organisation for Scientific Research) programs: PEPSci (Planetary and ExoPlanetary Science) and DANII (Dutch Astrochemistry Network). This research has made use of NASA's Astrophysics Data System.
Footnotes
- 3
0.93 g cm−3 is slightly off from the density of crystalline ice (0.94 g cm−3), but as 0.93 g cm−3 is reported with the R-value for the calculations of the refractive index, this value is used.









