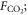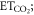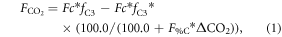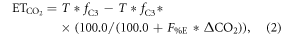Abstract
Rising atmospheric CO2 concentration ([CO2]) enhances photosynthesis and reduces transpiration at the leaf, ecosystem, and global scale via the CO2 fertilization effect. The CO2 fertilization effect is among the most important processes for predicting the terrestrial carbon budget and future climate, yet it has been elusive to quantify. For evaluating the CO2 fertilization effect on land photosynthesis and transpiration, we developed a technique that isolated this effect from other confounding effects, such as changes in climate, using a noisy time series of observed land-atmosphere CO2 and water vapor exchange. Here, we evaluate the magnitude of this effect from 2000 to 2014 globally based on constraint optimization of gross primary productivity (GPP) and evapotranspiration in a canopy photosynthesis model over 104 global eddy-covariance stations. We found a consistent increase of GPP (0.138 ± 0.007% ppm−1; percentile per rising ppm of [CO2]) and a concomitant decrease in transpiration (−0.073% ± 0.006% ppm−1) due to rising [CO2]. Enhanced GPP from CO2 fertilization after the baseline year 2000 is, on average, 1.2% of global GPP, 12.4 g C m−2 yr−1 or 1.8 Pg C yr−1 at the years from 2001 to 2014. Our result demonstrates that the current increase in [CO2] could potentially explain the recent land CO2 sink at the global scale.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Atmospheric CO2 concentrations [CO2] have risen at a rate of 2.16 ± 0.09 ppm yr−1 in recent decades due to human activities (Le Quéré et al 2018) and will continue to increase unless emission reductions occur (Anderson et al 2019). Rising [CO2] has increased photosynthesis at the leaf level (Norby et al 2005, Wenzel et al 2016) and gross primary productivity (GPP) at the ecosystem scale (Wenzel et al 2016). This process, known as the CO2 fertilization effect, arises because the current [CO2] is too low to saturate the carboxylation in the leaf, and thus limits photosynthesis. Therefore, the CO2 fertilization effect is considered a negative feedback process that may reduce [CO2] and mitigate global warming (Booth et al 2012) through the potential enhancement of the land CO2 sink. In addition to the carbon cycle, the hydrological cycle has similarly been impacted by the increase in [CO2] that reduces stomatal conductance (Keenan et al 2013, Frank et al 2015, Cheng et al 2017) and results in a decrease in continental evapotranspiration (ET) and an increase in water runoff (Betts et al 2007).
The magnitude of the CO2 fertilization effect is not well understood because of the difficulty of direct measurements that can disentangle this effect from other processes (Norby et al 2005), limitation in satellite observations (de Kauwe et al 2016b), and the uncertainty in the ecosystem model (Friedlingstein et al 2014, Smith et al 2016). Free-air CO2 enrichment (FACE) experiments can provide a direct estimate of the CO2 fertilization effect by applying a step change in [CO2] (Norby and Zak 2011) to the surrounding environment, but their application is expensive and laborious. Consequently, current experiments are located in easily accessible regions, such as young temperate forests and croplands (Long et al 2004, Körner 2009, Frank et al 2015). Furthermore, while FACE experiments have assessed the CO2 fertilization effect under, for example, a doubling of [CO2], current ecosystems are exposed to a gradually rising [CO2] and their response may differ from that found in the FACE experiments. Although FACE data sets have improved vegetation models representing the ecosystem response to rising [CO2] (Medlyn et al 2015), the mechanisms of the CO2 fertilization effect incorporated into state-of-the-art earth system models has been a major source of uncertainty in climate projections through the internal feedbacks between photosynthesis and other related processes (e.g. respiration, biomass allocation, and mortality) (Booth et al 2012, Wenzel et al 2016, Friedlingstein et al 2014, Churkina et al 2009).
Here, we present a new quantification of the CO2 fertilization effect at the ecosystem scale during the past two decades based on eddy-covariance (EC) flux measurements across arctic, boreal, temperate, and tropical ecosystems at the global scale. Although previously the CO2 fertilization effect was inferentially evaluated for a smaller and shorter data set (Keenan et al 2013), we expanded the analysis by using a 104-flux tower site (770 site years) data set (Ichii et al 2017, Pastorello et al 2017), consisting of forests, grasslands, savanna, shrub, wetlands, tundra, and cropland ecosystem (figure S1 is available online at stacks.iop.org/ERL/15/084009/mmedia, table S1). Our approach used the global network of the direct observations, and quantified the sensitivity of GPP and ET to rising [CO2] with multiple constraints to avoid confounding effects and artifacts. We emphasize that our approach avoids a direct use of decadal trends in the fluxes for estimating the CO2 fertilization effect, which is mostly too small to be detected with common statistical analyses using observational data directly (Baldocchi et al 2018).
2. Method
To isolate the CO2 fertilization effect from other confounding effects, we developed a technique for deriving model parameters that are sensitive to the fertilization effect, using observed diurnal, seasonal, and interannual variations of carbon and water fluxes as well as climate drivers and leaf area index (LAI) (figure S2). The method is similar to the so-called one-point method commonly used in the leaf scale analyses (de Kauwe et al 2016a) that is based on the idea that light-saturated GPP is regulated by CO2 concentration. The responses of water vapor flux and GPP to light, humidity, wind speed, and [CO2] were constrained with direct observations during the past two decades (table S3) based on semi-continuous EC flux measurements across arctic, boreal, temperate, and tropical ecosystems at the global scale. The photosynthetic responses to light and [CO2] were constrained by optimizing the biogeochemical model (A1-1 in supplemental material); stomatal responses to humidity and [CO2] were constrained by the stomatal conductance model (A1-2 in supplemental material); and the responses to wind speed were constrained by the aerodynamic conductance model (A1-4 in supplemental material). The method has been previously applied for leaf-scale (Reed et al 1976), and extended to the canopy scale (Wang et al 2007, Ueyama et al 2016, 2018). After accounting for other confounding effects, such as radiative transfer (A1-3 in supplemental material), boundary layer conductance (A1-4 in supplemental material), and evaporation (A1-6 in supplemental material), we isolated responses of GPP and ET to current gradually rising [CO2] by fitting the fluxes into the CO2 demand and supply functions for photosynthesis in the model after considering other environmental effects (e.g. change in aerodynamic and canopy conductance).
2.1. Data
We used a 104 flux tower sites (770 site years) (Ichii et al 2017, Pastorello et al 2017) covering the period of 1990–2014 across a number of biome types (forests, grasslands, savanna, shrub, wetlands, tundra, and cropland) (figure S1, table S1); 66 sites were forests, whereas 38 sites were non-forested. The data consisted of two data sets, one for Asia, the other covering the rest of the globe. The data set for Asia was an extended version of our previous data set (Ichii et al 2017), which consisted of 60 EC observation sites and these were derived from five databases, namely AsiaFlux (http://asiaflux.net), European Flux Database (http://europe-fluxdata.eu), Forestry and Forest Products Research Institute (FFPRI; http://2.ffpri.affrc.go.jp/labs/flux/), National Institute Agro-Environmental Studies (NIAES), and Arctic Observatory Network (AON; http://aon.iab.uaf.edu/). The data set for the rest of the globe was 44 sites from the FLUXNET2015 (http://fluxnet.fluxdata.org/data/fluxnet2015-dataset/; Pastorello et al 2017), where we selected 39 sites that had more than ten years of data and an additional five sites with less than ten years of data to capture South American and African regions.
We used the original EC measurements of NEE that were not post-processed by principal investigators or their respective Asian databases, and partitioned GPP from FLUXNET2015. We post-processed the Asian data for all sites using a standard protocol for data quality control, and flux partitioning (Ichii et al 2017). Quality control was conducted using a spike detection method (Papale et al 2006) and a filtering with the friction velocity threshold (Reichstein et al 2005). GPP was estimated as the difference between net ecosystem exchange (NEE) and ecosystem respiration (RE). Daytime RE was based on exponential relationships (Lloyd and Taylor 1994), which were determined for each day using nighttime data with a 29-day moving window. GPP and RE were determined as the mean of 100 values obtained from an ordinary bootstrapping procedure. Further details are available in A3 in the supplemental material. For FLUXNET2015 data, we used partitioned GPP based on nighttime data (GPP_NT_VUT_REF) as this approach was similar to the processing for the Asia data set. No gap-filled flux data were used for model optimization in both data sets. The current study focused on C3 photosynthesis, because C4-dominated ecosystems were limited in our data set and a much smaller CO2 fertilization effect is expected in C4 ecosystems than C3-dominated ecosystems (Collatz et al 1992).
2.2. Model and optimization
We used the canopy photosynthesis model (iBLM-EC version 2; further for details can be found in the Supplemental Material) to quantify the CO2 fertilization effect (Ueyama et al 2016, 2018). The model contains coupled effects among the following sub-models: biochemical photosynthesis (Farquhar et al 1980), stomatal conductance (Ball et al 1987), aerodynamic conductance (Lhomme et al 2000), sun/shade radiative transfer including clumping effect (Ryu et al 2011), and vertical nitrogen transfer within the canopy (Lloyd et al 2010). In the biochemical photosynthesis model, photosynthesis is modeled as the minimum rate of Rubisco-limited photosynthesis and RuBP-limited photosynthesis. Rubisco-limited photosynthesis is sensitive to intercellular CO2 concentration, whereas RuBP-limited photosynthesis is sensitive to light. Stomatal conductance is modeled based on a semi-empirical relationship to photosynthetic rate, CO2 concentration at the leaf surface, and humidity (Ball et al 1987). Both photosynthesis and stomatal conductance are further calculated separately for sunlit and shaded leaves, where sunlit and shaded portions are calculated based on a radiative transfer model (Ryu et al 2011) that uses leaf area index (LAI) and clumping index as inputs (He et al 2012, Pisek et al 2015).
Input data for the model include half-hourly or hourly meteorology (wind speed, photosynthetically photon flux density, air temperature, relative humidity, rainfall, atmospheric pressure, net radiation, and ground heat flux), turbulent fluxes (friction velocity, sensible and latent heat fluxes, and GPP), [CO2], LAI, and growth temperature (defined as a mean air temperature over the preceding thirty days). We did not apply the energy imbalance correction for inputs of sensible and latent heat fluxes except for a sensitivity analysis, because uncertainties in this assumption were negligible as shown in Supplemental Material. We rejected data due to wet conditions during rain and within one hour after rain, because uncertainties in this case were larger of the acceptance threshold 10% of estimated CO2 fertilization effect, as shown in supplemental material. Transpiration was partitioned from measured latent heat flux by subtracting evaporation. The evaporation was estimated from potential evaporation at the soil surface for forests (Ryu et al 2011) solving net radiation at forest floor. The evaporation was estimated using LAI by known ratios between ET and transpiration for grassland, tundra, cropland (Wang et al 2014) and rice paddy (Sakuratani and Horie 1985). The direct and diffuse portions of radiation were partitioned based on the method (Weiss and Norman 1985) for solving the sun/shade radiative transfer model. To avoid the effects of inconsistent calibration, arising from inaccuracies in [CO2] measurements at the observation sites, and for consistency among the optimization and CO2 fertilization experiment, [CO2] was derived from CarbonTracker 2015 (CT2015) (Peters et al 2007), with selected pixels centered on each site's geographic position. Since [CO2] by CT2015 was available since 2000, [CO2] prior to 2000 was estimated by subtracting the [CO2] difference between values from 2000 and values from a target year at the Mauna Loa observatory from the CT2015 data for 2000. LAI in each site was from field observations if available (table S1). If time-variant LAI was not available, LAI was derived from MODIS MOD15A2H after smoothing the signal using TIMESAT (Eklundh and Jönsson 2015) and adjusting the mean annual maximum using site observations from literature (table S1).
We derived the parameters of the sun/shade canopy photosynthesis model from the constraint optimization (table S3) using the observed data to ensure that model accurately predicted the responses of EC-derived GPP, canopy-integrated gs, and thus transpiration to rising [CO2]. Parameters that are sensitive to CO2 fertilization, i.e. Vcmax25 and Jmax25 in the biochemical photosynthesis model (Farquhar et al 1980) as well as mbb and bbb in the stomatal conductance model (Ball et al 1987), were determined using EC-based GPP and transpiration data. The parameters were determined based on a global optimization method (SCE-UA; Duan et al 1992) for each day and each site with an eight-day moving window (figure S3). We only used successfully converged parameters for estimating the CO2 fertilization effect. We calculated mean and standard deviations of the parameters based on ten optimization runs from randomly generated initial values. We rejected the data when standard deviation of determined parameters was greater 10% of their absolute value for minimizing equifinality in parameterization (Medlyn et al 2005). Thus, uncertainties of the parameters associated with the optimization were less than 10% of the value. For quantifying the range of uncertainties from the biochemical photosynthesis model and parameterizations that were not directly constrained using observations, we quantified the CO2 fertilization effect using six different submodels (Collatz et al 1991, de Pury and Farquhar 1997, Bernacchi et al 2001, 2003, Kosugi et al 2003, Kattge and Knorr 2007, von Caemmerer et al 2009). We used the ensemble mean and standard deviations of the estimated six CO2 fertilization effects, which yielded a coefficient of variation of 10.3% across the six different parameterizations of the biochemical model (figure S4). Root mean square errors in half-hourly GPP and latent heat flux were 2.60 μmol m−2 s−1 and 34.6 W m−2, respectively; slopes and R2 between observations and the parameterized model also supported the validity of the optimization (figure S5).
Since the actual parameters for CO2 fertilization processes (CO2 demand and supply functions for photosynthesis; von Caemmerer et al 2009) were constrained each day through the optimization, the parameterized model can predict a theoretical sensitivity to rising atmospheric [CO2] for a given day. The CO2 fertilization effect was calculated at the half-hourly or hourly time step, and then averaged on an annual basis using daytime data when photosynthetically photon flux density (PPFD) was greater than 500 μmol m−2 s−1. The quantified CO2 fertilization effect represents the changes in GPP and gs by changes in [CO2] whilst allowing environmental conditions (e.g. climate and LAI) to change over time (Ueyama et al 2016). Here, we used [CO2] in the year 2000 as a baseline (369.55 ppm of the annual CO2 concentration at Mauna Loa) (Le Quéré et al 2018) and evaluate the effects of changing [CO2] before and after 2000.
We separated two processes related to the changes in GPP and gs, namely the passive response by a hyperbolic response of photosynthesis to [CO2] and the ecophysiological acclimation, known as down regulation. We defined the ecophysiological acclimation as the interannual/decadal variations in the ecophysiological parameters throughout observation periods. Based on this definition, we estimated the contributions of the ecophysiological acclimation to changes in GPP and gs by isolating the components associated with changes in interannual/decadal variations in the ecophysiological parameters (Vcmax25, Jmax25, mbb and bbb). To examine the possible change associated with the ecophysiological acclimation, another experiment was conducted for sites having more than four years of data, where the CO2 fertilization experiment was conducted using median seasonality in the parameters instead of daily parameters in each year. CO2 fertilization effects between the two experiments would be different, if interannual variations or a directional shift in the parameters played an important role in determining the magnitude of the fertilization effect. The comparison was done for the years after 2000 when accurate ancillary inputs, such as LAI and [CO2], were available.
We tested how the EC data constrained the CO2 fertilization effect using data from 14 sites selected from the FLUXNET2015 data set (table S2). As a non-constrained experiment, we input biased parameters (Vcmax25, Jmax25, and mbb) into the model. We added or subtracted one standard deviation of the parameter distribution within a plant functional type to the determined parameters, and then estimated the range of uncertainties for the non-constrained simulation. In the non-constrained simulation, relative uncertainties of the CO2 fertilization for GPP, gs, and iWUE were 23% ± 11%, 60% ± 58%, and 4% ± 5%, respectively. This indicates that the EC data effectively reduced the uncertainties in the CO2 fertilization for GPP and gs.
2.3. Upscaling
For evaluating the CO2 fertilization effect at the global scale, the effect examined at the site level was upscaled using a random forest regression, which is a machine-learning based regression. Changes in fluxes per change in [CO2] (unit of % per ppm) were estimated for each site that contained more than four years of data (66 sites; table S1). The changes in fluxes were then modeled using a random forest regression by growing season and annual mean air temperatures, annual sum of precipitation, seasonal maximum of LAI, land cover (the alternative of forest or non-forest), and growing season length defined as number of days when mean air temperature was greater than 5 °C. We applied a 5 × 2 nested cross-validation with random search to tune generalized hyper parameters of the random forest regression; the nested cross validation effectively splits train, validation, and test sets for generalization. We measured the generalization error using the nested cross validation rather than using hold-out data due to the limited available data. For estimating possible uncertainties in the model tuning, we constructed 20 random forest regressions which had different hyper parameters using the 5 × 2 cross-validation scheme from 20 different initial parameters. The estimated R2 score was 0.61 ± 0.05 for the effects for GPP and 0.78 ± 0.05 for gs.
The CO2 fertilization effect was upscaled to the globe using the random forest regressions and gridded climate and satellite remote sensing data. For the global analyses, we calculated the CO2 fertilization effect at an annual timescale for each grid that had a 0.25° × 0.25° spatial resolution. The change in GPP and ET associated with rising [CO2] was estimated for the globe from 2000 to 2014 at the annual timescale. The mean climatology of annual mean air temperature and annual sum of precipitation from 2000 to 2014 was created based on Ichii et al (2013) by merging CRU-TS climate data and National Centers for Environmental Prediction (NCEP)/the National Center for Atmospheric Research (NCAR) reanalysis (NCEP/NCAR reanalysis) data with the quarter-degree spatial resolution (Ichii et al 2013). The maximum LAI was derived from MODIS standard product (MOD15A2H; collection 6) at the quarter-degree spatial resolution. Spatial averaging and quality assurance for the satellite data were the same as those in our previous study (Kondo et al 2015, Ichii et al 2017). A global map of forest classes for 2000 (Schulze et al 2019) was used for classifying forest/non-forest ecosystems. Rising [CO2] compared with the level at year 2000 was determined based on a one-degree spatial resolution, where mean annual [CO2] was calculated from CT2015. Assuming that fluxes based on the upscaling of the eddy covariance observations (Kondo et al 2015) already includes the CO2 fertilization effect, finally, the CO2 fertilization effect in the fluxes ( g C m−2 yr−1, mm yr−1) can be defined as follows:
where Fc and T are annual GPP (g C m−2 yr−1) and transpiration (mm yr−1), respectively, in each year derived from empirical data-driven upscaling EC fluxes using the support vector regression (SVR) (Kondo et al 2015). The upscaled global fluxes based on SVR were reprocessed using latest MODIS data (collection 6). The first term of the right side is fluxes of C3 vegetation that includes the CO2 fertilization effect, and the second term is fluxes of C3 vegetation that does not include the CO2 fertilization effect. The denominator of the second term increases with increasing [CO2] since 2000, and the effect of the CO2 fertilization is subtracted from the second term according to the change of flux with respect to the increasing [CO2] in each grid. Transpiration was partitioned from the upscaled ET based on an empirical method (Wei et al 2017). Satellite-derived LAI and land cover data (MOD12Q1) were used for calculating the fraction of transpiration from ET at an eight-day interval. fC3 was the fraction of C3 vegetation within a grid based on the global map for C4 vegetation percentage (Still et al 2009). For multiplying C3 fraction, our estimates of the global CO2 fertilization effect only consider the C3 vegetation. F%C and F%E were changes in Fc and T, respectively, per change in [CO2] (% ppm−1) derived from the random forest regressions tuned for the site-scale analysis (shown in above paragraph), and ΔCO2 was the change in [CO2] in each year since 2000 (ppm yr−1). An ensemble mean of the 20 different random forest regressions was used to estimate the CO2 fertilization effect and its standard deviation was used for the interval. The declining response of the CO2 fertilization effect (figures 1(c), (f)) was considered in the upscaling, using a regression shown in figures 1(c), (f).
Figure 1. Inferred fractional changes in gross primary productivity (GPP) (a), canopy-integrated stomatal conductance (gs) (b), and intrinsic water use efficiency (iWUE; GPP/gs) (c) associated with rising atmospheric CO2 concentration ([CO2]). The CO2 fertilization effect was quantified with changes in [CO2] since the year 2000, which was taken as baseline (ΔCO2). The fractional changes were shown as the ratio of GPP, gs, or iWUE calculated with and without the CO2 fertilization effect. Analysis was performed based on the coupled photosynthesis and stomatal conductance model, with optimized parameters for each day and each site. Dots and bars represent the mean and range of uncertainties with different formulations in the photosynthesis models, respectively. Relationship between fractional change in GPP (d), gs (e), and iWUE (f) associated with rising [CO2] and change in annual mean [CO2]. Relationship between fractional change in GPP (g), gs (h), and iWUE (i) per unit of [CO2] change and change in annual mean [CO2]. Square dots in (g)–(i) represent averaged values for ΔCO2 bins of two ppm. The statistically significant regressions (p ≤ 0.01) are shown in (d)–(g), (i).
Download figure:
Standard image High-resolution imageFor estimating potential uncertainties in the upscaled CO2 fertilization effect associated with the input data, we compared the upscaled results by replacing the input data. First, we replaced the input global climate data from the CRU/NCEP data to ERA5 reanalysis data (DOI:10.24381/cds.68d2bb30). Second, we replaced the input MODIS-based LAI data to the Global Inventory Modeling and Mapping Studies (GIMMS) LAI3g product (Zhu et al 2013), which was based on the advanced very high resolution radiometer (AVHRR). The CRU data are based on station observations, which is less uncertain than the reanalysis data. The MODIS-based LAI is generally more accurate than LAI by the AVHRR. Since the upscaled CO2 fertilization effects did not differ in terms of the different input data (table S4), we showed the upscaled results based on the combination of the CRU/NCEP and MODIS LAI data as our best guess. The small sensitivity to the input data could be because the current upscaling only used the annual aggregated variables (figure S6); thus, biases at the short timescales in the input data did not significantly propagated to the upscaled estimates.
3. Results and discussion
On average across all biomes, GPP increased concurrently with rising [CO2] at the rate of 0.273% ± 0.014% yr−1 (figure 1(a)) or 0.138% ± 0.007% ppm−1 (figures 1(d), (g)) from 1990 to 2014; plus-minus sign denotes 95% confidence interval. The change was greater for non-forest than forest sites (p < 0.01; figures 1(a), (b)), consistent with FACE experiments which showed a higher increase in GPP at ecosystems with lower leaf area (Norby and Zak 2011). This was probably because light more regulated photosynthesis of forests that had greater leaf area than non-forests, and thus greater contributions of shade-leaves weakened the sensitivity to [CO2] in forests than non-forests. Stomatal conductance decreased at a rate of −0.143% ± 0.012% yr−1 (figure 1(b)) or −0.073% ± 0.006% ppm−1 (figure 1(e)) over the same time period. The decrease in gs was significantly greater in forests than non-forests (p < 0.01; figures 1(d), (e)), because greater increase in GPP by rising [CO2] mitigated decrease in gs in non-forests. Given the increase in GPP and the decrease in gs, intrinsic water use efficiency (iWUE; defined as GPP/gs) increased at the rate of 0.400% ± 0.011% yr−1 (figure 1(c)) or 0.202% ± 0.006% ppm−1 (figure 1(f)). The magnitude of the CO2 fertilization effect (figures 1(d)–(f)) was roughly comparable to the values observed from previous FACE assessments in a temperate zone (0.13% ppm−1 for net ecosystem productivity (NEP); Norby et al 2005), and 0.2%–0.3% ppm−1 for iWUE; Frank et al 2015) and global-scale modeling that was constrained with [CO2] growth rate for high-latitudes (0.13% ± 0.03% ppm−1 for NEP) and the extratropics (0.11% ± 0.03% ppm−1 for NEP) (Wenzel et al 2016).
Importantly, the CO2 fertilization effect for GPP and iWUE slightly declined with rising [CO2] (p ≤ 0.01) (figures 1(g), (i)). This decline of the CO2 fertilization effect could be caused by two different processes: the passive response by a hyperbolic response of photosynthesis to [CO2] and/or ecophysiological acclimation, known as down regulation. To isolate the two processes, we quantified the ecophysiological acclimation, assuming that the ecophysiological acclimation occurred with interannual/decadal changes in the ecophysiological parameters (Vcmax25, Jmax25, mbb, and bbb; shown in method). The simulations suggested that the down regulation mechanism played a marginal role on the estimated magnitudes in the CO2 fertilization effect. This in turn indicates that the canopy-integrated parameters did not change significantly during the study period. The magnitude of the change from ecophysiological acclimation was one order of magnitude smaller (figure 2) than the passive response to rising [CO2] (Katul et al 2000) with unchanged parameters (figures 1(g)–(i)). Nevertheless, the ecophysiological acclimation rather amplified the CO2 fertilization effect in GPP at 54% of the ecosystems that we examined, and dampened the decrease in gs at 63% of the ecosystems (figure 2). This is possibly because a decrease in photosynthetic capacity of leaves was compensated by increasing LAI. Long-term field studies for partitioning change in leaf-scale parameters and LAI need to disentangle the compensation.
Figure 2. Probability density distributions of the difference between the CO2 fertilization effects in GPP (a), canopy-integrated stomatal conductance (gs) (b), and intrinsic water use efficiency (iWUE) (c), estimated using daily optimized parameters and using median seasonal variation of the parameters. The analysis was done for 31 eddy covariance sites having more than four years of data. Estimates using the median seasonality remove year-to-year and decadal shift in physiological adjustment; thus, the difference represents change in CO2 fertilization effect associated with the physiological adjustment. A positive value represents an increase in GPP and iWUE or dampened decrease in gs associated with physiological adjustment.
Download figure:
Standard image High-resolution imageThe spatial variability of the isolated CO2 fertilization effect on GPP and gs was explained environmental drivers, such as mean annual air temperature, growing season length and temperature, and land cover type (figure S6; R2 = 0.59 ± 0.05 for GPP and R2 = 0.72 ± 0.11 for gs). The increase in GPP due to rising [CO2] was greater in warmer regions than in colder regions (R2 = 0.29, p < 0.01; figure S7). This was likely because rising [CO2] could have effectively mitigated photorespiration under higher temperatures (Cernusak et al 2013). The fractional decrease in gs tended to be greater in ecosystems in colder rather than warmer climates (R2 = 0.14; p < 0.01), probably because gs is related to GPP (Ball et al 1987), and thus the greater fertilization effect on GPP alleviated the decrease in gs in warmer ecosystems.
The upscaled CO2 fertilization effect of the global C3 vegetation accounted for a substantial impact on the current increasing trend in global GPP (figure 3(a)). Based on the upscaled CO2 fertilization effect using random forest regression (figure S6) and a data-driven global GPP estimation (Kondo et al 2015), we found that rising [CO2] (29.0 ppm between 2000 and 2014; Peters et al 2007) enhanced GPP at a rate of 0.08% ppm−1 at the global scale, which was equivalent to an increase of 0.16% yr−1, or 0.23 Pg C yr−2. This enhancement is approximately 60% of the current increasing trend in global GPP (Kondo et al 2015) (0.38 Pg C yr−2; red line in figure 3(a)) and other studies (0.59 ± 0.12 Pg C yr−2; Cheng et al 2017), indicating that the CO2 fertilization is the most important process driving the current increase in the global GPP. Enhanced GPP from CO2 fertilization after the baseline year 2000 is, on average, 1.2% of global GPP (152.8 Pg C yr−1), 12.4 g C m−2 yr−1 or 1.8 Pg C yr−1 at the years from 2001 to 2014. This increase was surprisingly large, because the current global land sink was estimated to be 3.5 ± 1.0 Pg C yr−1 during 2008–2017 (Le Quéré et al 2018). The tropical forests benefited substantially from the CO2 fertilization effect (figure 3(e)), due to greater effects per rising [CO2] (figure 3(c)) and greater GPP in tropical forests. During the study period, the global GPP increased (p < 0.01), but diminished the trend if the CO2 fertilization effect estimated in this study was excluded (figure 3(a)). Note that our estimates of the global CO2 fertilization effect were only quantified for C3 vegetation, neglecting contributions by C4 vegetation, and thus the estimated magnitude was likely underestimated.
Figure 3. Global mean GPP and evapotranspiration (ET) based on upscaling of eddy covariance fluxes and change in the fluxes associated with rising atmospheric CO2 concentration (a), (b). Fluxes subtracting the CO2 fertilization effect are also shown with blue lines in (a), (b). Linear regressions in (a), (b) were tested based on Mann–Kendall trend test. Shadows in (a), (b) represent the standard deviation of the upscaling based on bootstrapping. Spatial distributions of changes in GPP and ET associated with rising atmospheric CO2 concentration in 2014 (c)–(f). The distributions for relative changes to fluxes (unit of % ppm−1) are shown in (c) for GPP and (d) for ET, whereas those for absolute change (unit for g C m−2 yr−1 for GPP and mm yr−1 for ET) are shown in (e) for GPP and (f) for ET. The CO2 fertilization effect was quantified, with the atmospheric CO2 concentration in 2000 as a baseline. Note that upscaled ET was the sum of evaporation and transpiration, whereas the CO2 fertilization effect occurs only transpiration; the magnitude of the change in ET (b), (d), (f) was estimated after partitioning transpiration from ET. The shadows represent the range of uncertainties associated with different model parameterization, energy imbalance, intercepted evaporation, and upscaling.
Download figure:
Standard image High-resolution imageOur analysis showed that rising [CO2] dampened an increase in the global ET (figure 3(b)). The global ET was estimated to increase at a rate of 1.04 mm yr−2. This increase resulted from a positive balance between the negative effect of decreased gs due to rising [CO2] and the positive effect of the enhanced atmospheric evaporative demand induced by global warming (Katul and Novick 2009, Cheng et al 2017). In practice, we inferred that without rising [CO2], the global ET would have increased at a rate of 1.24 mm yr−2 because the regulation of gs by rising [CO2] dampened global transpiration (Wullschleger et al 2002), resulting in the reduction of ET by a rate of 0.20 mm yr−2 (figure 3(b)).
Growing number and further long-term monitoring of eddy covariance observations will further reduce the uncertainties in the CO2 fertilization effect. Limited data in the current analysis is available for data whose temporal extent longer than nine years and for tropics where the CO2 fertilization effect estimated to be large, resulting in biased estimates in the global upscaling. This is the major shortcoming in our estimates, but will be minimized with future FLUXNET activities by further covering wide range of [CO2], climate, and ecosystem types.
4. Conclusion
The CO2 fertilization effect, the increase in GPP and decrease in gs, should be occurring in global ecosystems at present, ranging from the tropics to the arctic. The quantified effect was comparable to results from previous field experiments in temperate regions (Norby et al 2005, Frank et al 2015), reinforcing the validity of our approach. Our study enabled spatial upscaling from available flux tower data to provide a global understanding of tropical, boreal, and arctic regions, where direct measurements are scarce or simply not available, and gives insight into the possible mechanisms of the current land CO2 sink and decadal trends in ET. By constraining a simple model with observed big data, the direct CO2 fertilization effect was estimated globally in this study, but other indirect effects, such as, changes in LAI and extra-growth by relaxed drought owing to the CO2 fertilization effect (Long et al 2004, Norby and Zak 2011), should be evaluated in future studies. It is unclear whether current estimates of GPP and ET based on empirical upscaling (e.g. Kondo et al 2015, Ichii et al 2017) and semi-empirical models (e.g. Heinsch et al 2006) can take account the CO2 fertilization effect. Careful investigations are necessary on how the CO2 fertilization effect is linked to input variables, such as satellite-derived spectral indices and environmental variables, for accurately estimating global GPP and ET.
Acknowledgments
This study was supported by the JSPS KAKENHI, Grant Number 16K12588. Databases of eddy covariance measurements (AsiaFlux, KoFlux, European Fluxes Database Cluster, FFPRI, NIAES, and the NSF Arctic Observatory Network) facilitated this study. This work used eddy covariance data, FLUXNET2015, acquired and shared by the FLUXNET community, including those networks: AmeriFlux, AsiaFlux, NECC, OzFlux TERN, TCOS-Siberia, and USCCC. The ERA-Interim reanalysis data provided by ECMWF and processed by LSCE. The FLUXNET eddy covariance data processing and harmonization was carried out by the European Fluxes Database Cluster, AmeriFlux Management Project, and Fluxdata project of FLUXNET, with the support of CDIAC and ICOS Ecosystem Thematic Center, and the OzFlux, ChinaFlux and AsiaFlux offices. LBM acknowledges the support of the 'RUDN University program 5–100'. The GIMMS LAI3g product was provided by Professor R B Myneni.
Data availability
All flux data are available from respective databases or by authors upon request. (https://doi.org/10.25412/iop.11559480.v1) The program codes of the iBLM-EC are available from the author's web-site (http://atmenv.envi.osakafu-u.ac.jp/staff/ueyama/softwares/) or a supplemental material from the IOP Publishing Figshare repository. The inferred daily ecophysiological parameters, annual CO2 fertilization effects, and the gridded data for the global CO2 fertilization effects are available through a supplemental material from the IOP Publishing Figshare repository.