Nonlinear Fourier transform assisted high-order soliton characterization

The term of soliton was coined in 1965 to reflect the particle-like nature of solitary waves that remained intact even after mutual collisions [1]. Since then, soliton has been discovered and studied in many branches of physics including optics [2, 3]. Generally, a soliton refers to the localized solution of integral nonlinear systems [1], for instance, the nonlinear Schrodinger equation (NLSE). As a balanced product of nonlinearity and dispersion, the fundamental (first-order) soliton can propagate without distortion over the lossless optical fiber. Due to the natural information coding for binary communication, ultrashort pulse duration and distortion-free transmission, the fundamental soliton is regarded as a perfect candidate for high-speed fiber optical transmission [4]. Over the past decade, ultrafast fiber lasers have risen as an attractive platform for investigating the physics underpinning generation of various solitons. In contrast to a light pulse propagation over a fiber—where the system is conservative with the assumption of lossless propagation, a fiber laser is a paradigm of dissipative systems, where gain and loss affect the pulse generation, while simultaneously it is a periodic boundary system. To identify a pulse, complete measurements include the use of an oscilloscope to measure pulse information in time domain and a spectrometer to obtain the pulse property in the frequency domain. Obtaining meaningful insight into the nonlinear dynamics of solitons has prompted development of several advanced characterization methodologies, providing new ultrafast measurement tools to reveal transient phenomena arising in nonlinear laser dynamics. For instance, the dispersive Fourier transform (DFT) method has been successfully applied for investigating soliton explosions [5], bound solitons [6, 7], transition dynamics from Q-switching to mode locking [8] and buildup dynamics of harmonic mode locking [9]. Furthermore, the methodology of space-time duality has been successfully exploited to realize time lenses for direct observation of rogue waves [10] and unknown soliton dynamics [11]. In addition, the continuum generation has been shown great potential in obtaining soliton number for a given optical pulse [12]. Although the DFT and time lens methods have successfully realized soliton characterization in the Fourier frequency domain and time domain, respectively, a new method that can identify more soliton pulse characterizations covering broader aspects is always welcomed.

The nonlinear Fourier transform (NFT), also known as the inverse scattering transform in the mathematical literature [13], is a powerful method that has been invented and extensively used for the description of solutions to the so-called integrable nonlinear partial differential equations, for example the NLSE, that governs at leading order the propagation of the optical and hydrodynamic waves. Originally, the IST method was a result of extensive efforts in theoretical physics and applied mathematics in 1960s and later, closely associated with the notion of solitons in integrable models [14, 15]. As a powerful mathematical tool, IST has shown great potential in identifying coherent wave packets in the ocean [16–18] and optical fibers [19–21]. With the approach of NFT, signal can be decomposed into a continuous spectrum (non-soliton components) and a discrete spectrum (soliton components) to obtain the corresponding nonlinear spectrum [22, 23]. By converting the nonlinear transmission impairments arising in the standard single mode fiber (SSMF) to a phase shift in nonlinear spectrum, NFT has shown great potential in nonlinear transmission impairments compensation [24–26]. Meanwhile, as a method to obtain analytic solutions to the nonlinear Schrödinger equation (NLSE), the NFT can be used to analyze signals in optical fibers, such as rogue waves [27] and Kerr optical frequency combs [28]. Generally, NFT is associated with the integrable conservative Hamiltonian models. However, recent research has shown that NFT has the capability to characterize the soliton pulses from dissipative systems, especially soliton pulses generated from fiber lasers [29–33]. In our previous work, we have proposed a method of soliton distillation to distinguish solitons from the resonant continuous wave (CW) background according to their different eigenvalue distributions based on the NFT [32]. Furthermore, by using the approach of soliton distillation, we recover the pure solitons dynamic of pulses from fiber laser, including the state of single pulse, the state of single pulse in period doubling, and the states of double pulses and triple pulses [33]. With the help of NFT, the signal can be described by the combination of discrete spectrum and continuous spectrum. Eigenvalues are distributed in the discrete spectrum only. We have demonstrated that the pure fundamental soliton distributed energy in the discrete spectrum only if the appropriate normalization factor is taken during the NFT [32, 33]. Based on our previous success, we believe that the NFT method is able to comprehensively characterize solitons especially high-order soliton propagation over the SSMF.

In the following sections, we focus on eigenvalue analysis of high-order solitons. With the approach of NFT, the nonlinear spectrum of high-order solitons can be investigated. When propagating along SSMF, phase rotation of the nonlinear spectrum caused by fiber nonlinearity can be observed. Furthermore, soliton pulse can be reconstructed with only the discrete spectrum, confirming the eigenvalues can characterize soliton pulse with good accuracy. In comparison with the DFT and time lens methods, such NFT methodology provides a new viewpoint on the physics of soliton pulses, which is a significant supplement to the existing means of characterizing soliton pulses.

When propagating over the SSMF, the time and space dependence of the slowly varying envelope of the signal is determined by the NLSE [34],

$$\begin{equation}\mathrm{i}\frac{\partial E(t,z)}{\partial z}+\mathrm{i}\frac{\alpha (z)}{2}E(t,z)-\frac{{\beta }_{2}}{2}\frac{{\partial }^{2}E(t,z)}{\partial {t}^{2}}+\gamma \vert E(t,z){\vert }^{2}E(t,z)=0,\end{equation} \tag{ 1 }$$

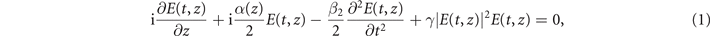
where E(t, z) is the slowly varying envelope of the optical signal, z is the space coordinate along the direction of propagation, γ is the nonlinear parameter, β₂ is the second-order dispersion parameter, and α(z) is the attenuation coefficient. For its practical interest, here we neglect higher order dispersion and consider only the anomalous dispersion (β₂ < 0). In the particular case where the loss can be either neglected or mitigated through the use of distributed amplification, the NLSE is usually written into the normalized form as:

$$\begin{equation}\mathrm{i}\frac{\partial q(\tau ,l)}{\partial l}+\frac{1}{2}\frac{{\partial }^{2}q(\tau ,l)}{\partial {\tau }^{2}}+\vert q(\tau ,l){\vert }^{2}q(\tau ,l)=0,\end{equation} \tag{ 2 }$$

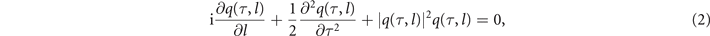
where τ, l, and q(τ, l) are the normalized time, distance, and amplitude. As the NLSE with zero right-hand side is integrable, the explicit procedures for NFT and inverse NFT (INFT) are known [22–24]. The decomposition of the signal into spectral data is achieved by solving the Zakharov–Shabat problem (ZSP) equations for auxiliary functions v₁, v₂ [34]

$$\begin{equation}\begin{gathered}\frac{\mathrm{d}{\mathit{v}}_{1}(\tau ,\lambda )}{\mathrm{d}\tau }=q(\tau ){\mathit{v}}_{2}(\tau ,\lambda )-\mathrm{i}\lambda {\mathit{v}}_{1}(\tau ,\lambda ),\\ \frac{\mathrm{d}{\mathit{v}}_{2}(\tau ,\lambda )}{\mathrm{d}\tau }=-{q}^{\ast }(\tau ){\mathit{v}}_{1}(\tau ,\lambda )+\mathrm{i}\lambda {\mathit{v}}_{2}(\tau ,\lambda ),\end{gathered}\end{equation} \tag{ 3 }$$

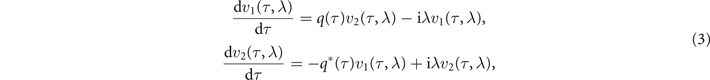
where λ is the spectral parameter, which plays a role of a nonlinear analog of frequency. The scattering data a(λ) and b(λ) serve as the basis on which the nonlinear spectrum is defined. Due to the boundary condition, they can be calculated

$$\begin{equation}\begin{gathered}a(\lambda )=\underset{\tau \to \infty }{\mathrm{lim}}\,{\mathit{v}}_{1}(\tau ,\lambda ){\mathrm{e}}^{j\lambda \tau },\\ b(\lambda )=\underset{\tau \to \infty }{\mathrm{lim}}\,{\mathit{v}}_{2}(\tau ,\lambda ){\mathrm{e}}^{-j\lambda \tau }.\end{gathered}\end{equation} \tag{ 4 }$$

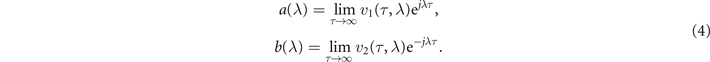
Then, the nonlinear spectrum can be defined as

$$\begin{equation}\begin{gathered}{Q}_{\mathrm{c}}(\lambda )=b(\lambda )/a(\lambda ),\quad \lambda \in R,\\ {Q}_{\mathrm{d}}({\lambda }_{n})=b({\lambda }_{n})/{a}^{\prime }({\lambda }_{n}),\quad \lambda \in {C}^{+},\end{gathered}\end{equation} \tag{ 5 }$$

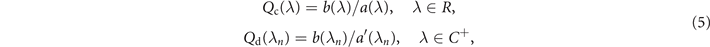
where Q_c(λ) and Q_d(λ_n ) are continuous spectrum and discrete spectrum, respectively. Eigenvalue λ_n is the root of a(λ) and a'(λ) is the derivative of a(λ). After propagating distance z governed by the NLSE, the variation in the corresponding spectrum values satisfy the following rules:

$$\begin{equation}\begin{gathered}{Q}_{\mathrm{c}}(\lambda ,z)={Q}_{\mathrm{c}}(\lambda ,0)\cdot {\mathrm{e}}^{-2j{\lambda }^{2}z},\\ {Q}_{\mathrm{d}}({\lambda }_{n},z)={Q}_{\mathrm{d}}({\lambda }_{n},0)\cdot {\mathrm{e}}^{-2j{{\lambda }_{n}}^{2}z}.\end{gathered}\end{equation} \tag{ 6 }$$

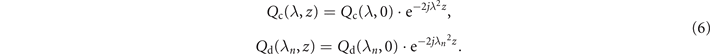
In the nonlinear frequency domain, the SSMF channel evolves into a linear channel, whose transfer function is 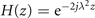$H(z)={\mathrm{e}}^{-2j{\lambda }^{2}z}$. In another word, the amplitude of nonlinear spectrum remains constant, while its phase varies linearly with the transmission distance. For the NLSE, the field energy can be presented as a sum of continuous spectrum and discrete spectrum:

$$\begin{equation}{\int }_{-\infty }^{\infty }\vert q(t,z){\vert }^{2}\mathrm{d}t=\frac{1}{\pi }{\int }_{-\infty }^{\infty }\mathrm{log}(1+\vert {Q}_{\mathrm{c}}(\lambda ){\vert }^{2})\mathrm{d}\lambda +4\sum\limits _{n=1}^{N}\mathrm{Im}({\lambda }_{n}),\end{equation} \tag{ 7 }$$

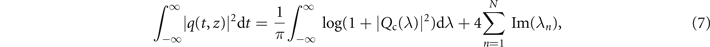
where the left side of equation corresponds to the energy calculated in the temporal domain E_t(z), while the right side consists of a contribution of the continuous spectrum energy E_c(z) and the discrete spectrum E_d(z), so E_t(z) = E_c(z) + E_d(z).

As the fundamental solution of NLSE, the nonlinear spectrum of fundamental soliton only contains discrete spectrum with single eigenvalue and its temporal waveform is [35]

$$\begin{equation}q(t)=-2j{\lambda }_{\mathrm{I}}\,{\mathrm{e}}^{-j\angle {Q}_{\mathrm{d}}({\lambda }_{n})}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{h}(2{\lambda }_{\mathrm{I}}(t-{t}_{0})){\mathrm{e}}^{-2j{\lambda }_{\mathrm{R}}t},\end{equation} \tag{ 8 }$$

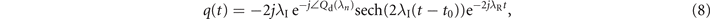
where λ_R and λ_I are the real and imaginary parts of eigenvalue λ_n , ∠Q_d(λ_n ) is the spectrum phase, and t₀ is the time center associated with λ_I and spectrum amplitude. As shown in equation (8), the eigenvalue λ_n specifies the soliton parameters with an amplitude of 2λ_I and a frequency of 2λ_R. For a high-order soliton, its nonlinear spectrum contains more eigenvalues and the nonlinear spectrum evolution also satisfies phase rotation, as equation (6) shows.

Different from conventional Fourier transform, NFT is sensitive to signal energy. With the signal amplitude increasing, its nonlinear spectrum does not increase linearly. Consequently, the amplitude of a soliton pulse can influence its eigenvalue distribution. Here, we consider soliton described as q(t) = A ⋅ sech(t), where A is the amplitude of the soliton pulse. Figure 1 shows the evolution of eigenvalues versus amplitude in the three dimensions (3D), where the x axis is real part, y axis is the amplitude, and z axis is the imaginary part. It is obvious that the number of eigenvalues increases with the growing amplitude, due to the enhanced soliton power. Meanwhile, for soliton with amplitude A (when A is an integer), its nonlinear spectrum contains A eigenvalues, which are {0.5i, 1.5i, ..., (A − 0.5)i}, respectively.

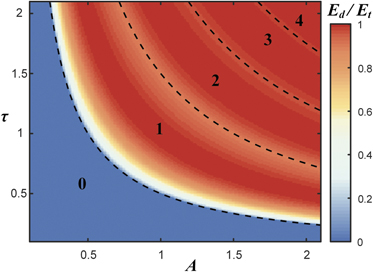
Zoom In Zoom Out Reset image size

Alternately, the temporal waveform of the soliton pulse with sech-type shape can be simply expressed as q(t) = A ⋅ sech(t/τ). Besides the amplitude A, the pulse-width τ is also an important parameter, which can directly affect the distribution of nonlinear spectral energy and eigenvalue distribution. Figure 2 shows the number of discrete eigenvalues N with respect to two soliton parameters including the amplitude A and the pulse-width τ. The numbers on the plot denote areas with different numbers of discrete eigenvalues. A direct numerical solution of the ZSP problem is compared with the analytical solution of Aτ = N − 1/2, indicating of excellent agreement. The set of eigenvalue λ_n is defined as λ_n = i(Aτ + 1/2 − n), where n are positive integers satisfying condition Aτ + 1/2 − n > 0, providing for Im(λ_n ) > 0. Black dashed lines in figure 2 defined by the analytical expression Aτ + 1/2 = n separate areas with different numbers of discrete eigenvalues. The colors in figure 2 display a fraction of the energy E_d, corresponding to the discrete spectrum, to the total energy E_t. We derive the analytical expression for the fraction of energy containing in the spectrum

$$\begin{equation}\frac{{E}_{\mathrm{d}}}{{E}_{\mathrm{t}}}=\frac{{A}^{2}{\tau }^{2}-{(\rho -1/2)}^{2}}{{A}^{2}{\tau }^{2}},\end{equation} \tag{ 9 }$$

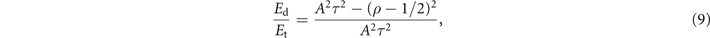
where ρ = frac(Aτ + 1/2) is a fractional part of Aτ + 1/2. One can see that once Aτ > 0, the proportion of the energy contained in the discrete spectrum to the total energy is always quite high—more than 80%. Here, continuous spectrum contains extremely lower energy. In consideration of both discrete spectrum and continuous spectrum, soliton pulse can be reconstructed with the approach of INFT. In particular, when Aτ is an integer, there are Aτ eigenvalues and the energy ratio can exceed 99.99%. This indicates that the dynamics is dominated by the soliton structures and NFT could be a much simpler way to describe the system with Aτ identified (discrete eigenvalues). Consequently, we choose τ = 1 and consider initial condition of N-soliton as q(t) = N ⋅ sech(t), where N is the soliton order.

Zoom In Zoom Out Reset image size

Firstly, we consider fundamental soliton q(t) = sech(t) and its temporal waveform, eigenvalue distribution and continuous spectrum are shown in figure 3. In nonlinear spectrum, there is a single eigenvalue λ = 0.5i, as shown in figure 3(b). The real part and imaginary part of eigenvalue are referred to the frequency and amplitude of a fundamental soliton, respectively, which satisfies the equation (8). In this case, the ratio of the energy E_d, corresponding to the discrete spectrum, to the total energy E_t is 99.99%, which means the energy is almost entirely concentrated in the discrete spectrum. By filtering out the continuous spectrum and reserving discrete spectrum, the soliton can be reconstructed by INFT, as shown in figure 3(c).

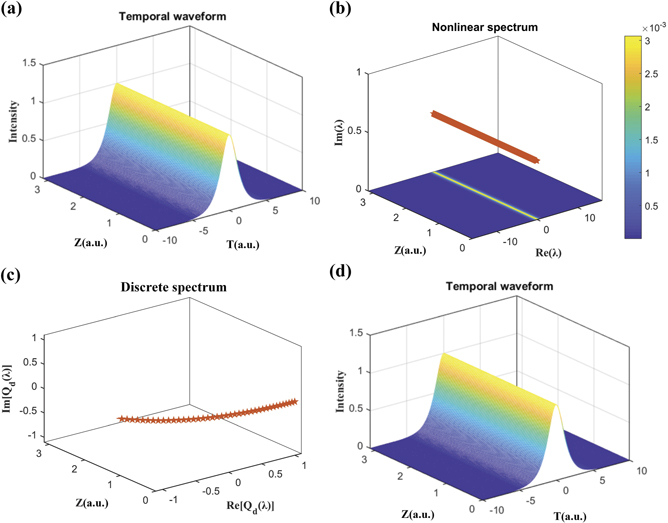
Zoom In Zoom Out Reset image size

Then, we examine application of the NFT for analysis of dynamics of solitons generated from equation (2). A numerical modeling is performed using the standard split-step Fourier method. We consider the initial condition of fundamental soliton as q(t, z = 0) = sech(t). Figure 4 shows the temporal waveform and nonlinear spectrum of fundamental soliton. As the localized solution of NLSE, the fundamental soliton can propagate without the distortion along the SSMF, as shown in figure 4(a). In nonlinear frequency domain, there exists a single eigenvalue λ = 0.5i and it remains constant during the SSMF propagation, as shown in figure 4(b). While, the continuous spectrum has an amplitude of ∼10⁻³. Figure 4(c) shows the 3D evolution of the discrete spectrum Q_d(λ, z) with distance z in the complex plane. Clearly, we can see that, the phase of discrete spectrum changes with the transmission distance, induced by fiber nonlinearity. This phase change satisfies equation (6). Notably, the discrete spectrum occupies nearly 99.99% of the energy, while the continuous spectrum has almost zero energy distribution. The single eigenvalue characterizes the formed fundamental soliton with good accuracy. This is illustrated by the reconstruction of the soliton 3D evolution from just the eigenvalue and its corresponding discrete spectrum as shown in figure 4(d) (here we neglect the continuous spectrum).

Zoom In Zoom Out Reset image size

Furthermore, we consider the initial condition of second-order soliton as q(t, z = 0) = 2 ⋅ sech(t). Figure 5 shows the temporal waveform and nonlinear spectrum of second-order soliton. During propagation, the temporal waveform oscillates periodically with the transmission distance and the period z₀ is π/2. Figure 5(b) shows the 3D evolution of the nonlinear spectrum with z in the complex plane, including both the eigenvalue and continuous spectrum during the propagation of second-order soliton. The second-order soliton has two eigenvalues {0.5i, 1.5i} and they are fixed during the SSMF propagation. While, the continuous spectrum oscillates in the same period as the temporal waveform but with an amplitude of ∼10⁻⁴. Figure 5(c) shows the 3D evolution of the discrete spectrum Q_d(λ, z) with distance z in the complex plane. Clearly, we can see that, the phase of discrete spectrum changes during pulse propagation, induced by fiber nonlinearity. Two discrete spectra of two eigenvalues have different transform speed and this phase transformation satisfies the equation (6). Figure 5(d) shows the reconstruction of the soliton 3D evolution from just the two eigenvalues and their corresponding discrete spectrum, revealing these two eigenvalues can characterize the formed second-order soliton with good accuracy.

Zoom In Zoom Out Reset image size

Generally, the higher is the order of a soliton, the more eigenvalues it has, as shown in figure 1. Moreover, the temporal waveform of high-order soliton also oscillates periodically during the SSMF propagation. Setting initial condition q(t, z = 0) = 3 ⋅ sech(t), a third-order soliton can also be obtained. Figure 6 shows the temporal waveform and nonlinear spectrum of third-order soliton. In nonlinear frequency domain, third-order soliton has three eigenvalues {0.5i, 1.5i, 2.5i} and they keep constant along the SSMF, as shown in figure 6(b). At the same time, the continuous spectrum oscillates periodically with nearly an amplitude of 10⁻³. As equation (6) shows, the rotational velocity of the nonlinear spectrum is determined by the square of the imaginary part of the eigenvalue. Consequently, three discrete spectra of third-order soliton, corresponding to three eigenvalues, rotate at different angular velocities, as shown in figure 6(c). Similarly, we reconstruct soliton by INFT on discrete spectrum only and plot 3D evolution of reconstructed soliton in figure 6(d).

Zoom In Zoom Out Reset image size

An intrinsic property of the high-order soliton is that its temporal waveform is periodic during the SSMF propagation with a soliton period of z₀ = π/2. In nonlinear frequency domain, it is fingerprinted by the periodic phase rotation of discrete spectrum determined by equation (6). Animations provided in supplementary materials (https://stacks.iop.org/NJP/24/033039/mmedia) show the temporal waveform and nonlinear spectrum evolution dynamics of a fundamental soliton (movie S1), a second-order soliton (movie S2) and a third-order soliton (movie S3), respectively. Clearly, we can see the phase of discrete spectrum rotates with the SSMF propagation. For fundamental soliton, there is a single eigenvalue λ = 0.5i and its discrete spectrum evolution satisfies 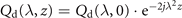${Q}_{\mathrm{d}}(\lambda ,z)={Q}_{\mathrm{d}}(\lambda ,0)\cdot {\mathrm{e}}^{-2j{\lambda }^{2}z}$. As for second-order soliton, there are two eigenvalues (λ₁ = 0.5i and λ₂ = 1.5i). Their discrete spectra (Q_d(λ₁) and Q_d(λ₂)) have different transform speed and the ratio of their phase transformation is 1:9, satisfying the equation (6). Similarly, the phase evolution speed ratio of third-order soliton discrete spectra is 1:9:25. Then, figure 7 shows discrete spectrum phase evolution of a fundamental soliton, a second-order soliton and a third-order soliton, respectively. Notably, the phase difference between discrete spectrum of high-order soliton (second-order and third-order) also periodically oscillates. This period of oscillation is π/2, in consistent with temporal period. It illustrated that the periodic temporal oscillation can also be characterized by phase rotation of discrete spectrum in nonlinear frequency domain, verifying that NFT is a perfect optical processing method in soliton study.

Zoom In Zoom Out Reset image size

Theoretically, NFT should be rigorously bound with the property of the NLSE, which describes the classical integrable nonlinear systems as it was first shown in the seminal work by Zakharov and Shabat [34]. Please note that we do not aim to solve underlying equations, but rather to use NFT for signal processing and to describe signal with less variables, for example here the discrete eigenvalues only, simplifying the description compared to conventional presentation. For higher-order soliton, there are more eigenvalues in nonlinear frequency domain. It is distinguishable to use eigenvalue number to identify the order number of high-order soliton. While propagating along the SSMF, the fiber nonlinearity converts to a phase rotation of discrete spectrum. As for more complex and fundamental higher-order NLSE solutions on a condensate, in its core there is still an integrable NLSE. Therefore, NLSE-based techniques can be inherently useful for analysis of the solutions, such as a higher-order Akhmediev-, Kusnetsov–Ma, and Peregrine-type solutions [36–40], which will be our work in future. Therefore, NFT provide an alternative way to describe solitons in general, which compliments temporal and spectral measurement. In practice, deviations, induced by noise or higher-order effects, will introduce a penalty to the characterization results. On such occasion, reconstruction of pure soliton pulse with a nonlinear spectrum containing discrete eigenvalues might technically be challenging. Recently, the choice of windowing [41] and normalization [30] have been fully discussed, which greatly promoted analysis of the experimental data with NFT. We anticipate that new effective algorithms will be available for future NFT software toolboxes, in order to make it a routine technique for analysis of experimental data.

We have investigated the nonlinear spectrum of high-order soliton. The high-order soliton has an enhanced number of eigenvalues depending on the soliton order. During the SSMF propagation, their eigenvalues remain constant, while the corresponding discrete spectrum rotates along with the SSMF. The periodic temporal oscillation of high-order soliton can be characterized by a phase rotation of discrete spectrum in nonlinear frequency domain. After INFT on discrete spectrum, soliton can be reconstructed and the reconstructed soliton is almost the same as the high-order soliton, which means that the eigenvalues can characterize the generated high-order soliton with good accuracy. The characterization methodology based on NFT is expected to be the third basic optical measuring solution besides an oscilloscope (measuring pulse time domain information) and a spectrometer (measuring pulse frequency domain information).

This work was supported by National Key R&D Program of China (2018YFB1801001), Fundamental Research Funds for the Central Universities (HUST 2020kfyXJJS007), National Natural Science Foundation of China (61875061), the Protocol of the 9th Session of China-Croatia Scientific and Technological Cooperation Committee (Grant No. 9-28), the Protocol of the 38th Session of China-Poland Scientific and Technological Cooperation Committee (Grant No. 6), National Agency for Academic Exchange in Poland PPN/BCN/2019/1/00068.

The data generated and/or analysed during the current study are not publicly available for legal/ethical reasons but are available from the corresponding author on reasonable request.