Abstract
Divergence gating, a novel method to generate far-field isolated attosecond pulses (IAPs) through controlling divergences of different pulses, is proposed and realized by relativistic chirped laser–plasma interactions. Utilizing various wavefronts for different cycles of incident chirped lasers, reflected harmonics with minimum divergences are obtained only at the peak cycle when plasma targets are adjusted to proper distances from foci of lasers. Therefore, the corresponding attosecond pulse is isolated in far field due to much slower decay during propagation than others. Confirmed by three-dimensional numerical simulations, millijoule-level sub-50 as IAPs with intensity approaching 1016 W cm−2 (1017–1018 W sr−1) are obtained by our scheme, where low-order harmonics can be preserved.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Isolated attosecond pulses (IAPs) have attracted broad interests during decades [1–3] for their rich applications among the resolution and control of ultrafast electron movement in atoms [4], molecules [5], materials [6, 7], and high-energy-density plasma [8, 9]. Getting rid of intensity limitations from the ionization threshold, relativistic high-order harmonic generation (RHHG) [10–15] has been regarded as the most promising way towards ultraintense attosecond pulses (APs) for attosecond-pump-attosecond-probe experiments [16], which are challenging for those produced from gaseous high-order harmonic generation [17] due to low photon flux as well as pulse energy in the magnitude of 10−9 J [16]. However, such APs are obtained generally in form of trains as the harmonic emission is driven by periodical interactions between lasers and overdense plasmas [13].
Series of methods [18–28] have been proposed to generate IAPs through RHHG, which can be classified as 'temporal gating' and 'spatial gating'. Different from temporal gating where APs can only be generated efficiently once because of few-cycle incident lasers [18], well-controlled laser polarization [19–21] or specially designed targets [22] as well as their transparency [23, 24], spatial gating separates APs in space through different reflected directions of them due to attosecond lighthouses [25–27] or tightly focused lasers [28]. For temporal gating, not only do some of methods require ultrathin targets [22–24], but also most of them have to filter out low-order harmonics (photon energy Eph ≲ 30 eV typically) which are usually produced efficiently for several optical cycles. While attosecond lighthouse effects used in spatial gating can relax the requirement of filters to Eph ≳ 20 eV, experimentally challenging preplasma scales L ≲ 10−2 λ0 is required [25], which greatly limits the generation efficiency at the same time [29, 30]. Here, λ0 represents the central wavelength of incident lasers. The introduction of high-pass spectral filters greatly suppresses the intensity of IAPs due to fast decay of harmonic intensities [13]. What's more, the removed spectra ranging from near ultraviolet (NUV) to vacuum ultraviolet (VUV) are critical for attosecond science in valence-shell phenomena [31, 32], molecule excitation [33] and nonlinear cluster dynamics [9, 34].
To generate IAPs with spectra and energy preserved as much as possible, the idea of divergence gating is proposed in this paper. Divergence gating separates APs through the modulation of divergences, where APs emitted in the peak optical cycles of incident lasers have minimum divergences and experience much lower energy density decay during propagation than other pulses. As all harmonics including fundamental frequency waves are influenced, divergence gating has the potential to generate near-axis IAPs in the far field with lower requirements of filters, even preserving all harmonics. Recently, the optically-curved plasma surfaces due to laser–plasma interactions have been proved to act like plasma mirrors (PMs) [35] which significantly affect the divergences of harmonics from RHHG and can be controlled by the convex wavefronts of defocused quasi-monochromatic incident lasers [27]. However, as the wavefronts are identical for different cycles, divergences of generated harmonics almost keep the same during interactions [36], forbidding the realization of divergence gating. Fortunately, defocused chirped lasers provide different wavefronts for each cycle due to the variational wavelength, i.e., variational Rayleigh length. To the best of our knowledge, chirped lasers, which are becoming accessible with relative bandwidth as high as 60% [37] and power approaching 100 TW [38] and even PW [39] in the future, are never used to generate IAPs based on RHHG although they have been investigated widely in particle acceleration [40, 41], pair production [42], and even gaseous high-order harmonic generation [43, 44].
In this paper, divergence gating as a method to generate isolated far-field APs is realized through relativistic chirped laser–plasma interactions, verified by theoretical analysis and three-dimensional (3D) numerical simulations. It is proposed that as the divergent incident wavefronts of chirped lasers change for different optical cycles due to varying wavelengths, the focusing effect of concave PMs can only be offset exactly in the peak incident cycle when overdense plasma targets are placed an optimal distance behind the focal planes. Therefore, the minimum divergence is achieved only for harmonics emitted from the peak cycle, which is critical for divergence gating. Based on this, the minimum energy threshold of filters 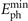 is provided in theory, consistent with 3D numerical simulations where intense far-field IAPs containing millijoule (mJ) energy are obtained with broad bandwidth including low-order harmonics preserved (≳10 eV). Such brilliant sub-50 as IAPs significantly benefit attosecond-pump-attosecond-probe experiments, especially those requiring NUV or VUV photons.
is provided in theory, consistent with 3D numerical simulations where intense far-field IAPs containing millijoule (mJ) energy are obtained with broad bandwidth including low-order harmonics preserved (≳10 eV). Such brilliant sub-50 as IAPs significantly benefit attosecond-pump-attosecond-probe experiments, especially those requiring NUV or VUV photons.
2. Theoretical analysis
The scheme of divergence gating is illustrated in figure 1(a). A chirped Gaussian incident laser (orange hollow column), which is linear-polarized in the y direction, propagates along X-axis and irradiates on the overdense plasma target (grey block) obliquely with angle α and central wavelength λ0, where exponential preplasma density profile with scale L is assumed. Keeping a distance xf between the plasma bulk and focal plane of incident laser, the transverse incident electric field E acting on the target is given as [41, 45, 46]:

where 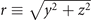 and ξ ≡ t − xf/c. Here,
and ξ ≡ t − xf/c. Here, 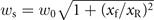 ,
, 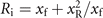 ,
, 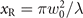 , k = 2π/λ, λ = λ0/(1 + sξ), ω0 = 2πc/λ0 and
, k = 2π/λ, λ = λ0/(1 + sξ), ω0 = 2πc/λ0 and 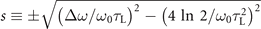 [41] represent the beam radius at which the field amplitude is 1/e times of the axial value, radius of curvature, Rayleigh length, wave number, wavelength, central angular frequency and chirp parameter (
[41] represent the beam radius at which the field amplitude is 1/e times of the axial value, radius of curvature, Rayleigh length, wave number, wavelength, central angular frequency and chirp parameter ( for positive chirp and
for positive chirp and  for negative chirp) of the incident laser on plasma surface, respectively. Besides,
for negative chirp) of the incident laser on plasma surface, respectively. Besides, 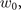 Δω, τL, c, y and z represent the beam waist, band width, pulse duration (full-width at half-maximum), speed of light in vacuum and the positions in two orthogonal transverse directions, respectively. The phase ϕ0 ≡ ϕC + ϕG includes the contribution of carrier envelope phase ϕC (CEP) and Gouy phase
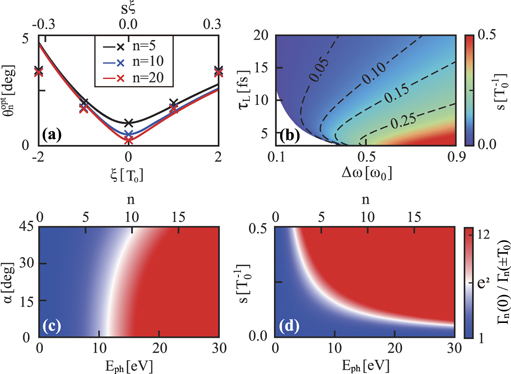
Δω, τL, c, y and z represent the beam waist, band width, pulse duration (full-width at half-maximum), speed of light in vacuum and the positions in two orthogonal transverse directions, respectively. The phase ϕ0 ≡ ϕC + ϕG includes the contribution of carrier envelope phase ϕC (CEP) and Gouy phase 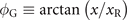 . We note that ξ = 0 when the temporal envelope of the laser field achieves its maximum. Besides, as illustrated in figure 2(b), values of s increase quickly with the increase of Δω or decrease of τL for most of situations (
. We note that ξ = 0 when the temporal envelope of the laser field achieves its maximum. Besides, as illustrated in figure 2(b), values of s increase quickly with the increase of Δω or decrease of τL for most of situations (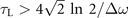 in specifically), while the minimum of the second one is limited by the first due to the transform limit (white area). The relationship between s and τL for a given Δω is non-monotonical as both the Gaussian envelope and frequency chirping contribute to the bandwidth. Therefore, for fixed Δω, the chirp parameter s, which characterizes the changing rate of frequency, changes nonlinearly with different τL which determines the bandwidth of Gaussian envelope by 0.44/τL [46] and equals 0 for transform-limited (TL) and infinite-duration beams.
in specifically), while the minimum of the second one is limited by the first due to the transform limit (white area). The relationship between s and τL for a given Δω is non-monotonical as both the Gaussian envelope and frequency chirping contribute to the bandwidth. Therefore, for fixed Δω, the chirp parameter s, which characterizes the changing rate of frequency, changes nonlinearly with different τL which determines the bandwidth of Gaussian envelope by 0.44/τL [46] and equals 0 for transform-limited (TL) and infinite-duration beams.
Figure 1. 3D PIC simulations and far-field results. (a) 3D schematic for the generation of far-field IAPs through divergence gating, where a y-polarized Gaussian chirped laser (orange hollow column) obliquely irradiates an overdense target (grey block) along X-axis with an incident angle α = 15° and distance xf from its focal plane to the target. Reflected by the optically-curved PM, the reflected laser (purple hollow column) propagates along X'-axis with IAPs (red solid) obtained in the far field after passing through a proper filter (brown cylinder, 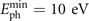 ). Spatial–temporal near-field distributions of the incident (orange shadow) and reflected laser (purple shadow) intensities on tz-plane (y = 0) as well as their on-axis waveforms (colorful and purple solid) are obtained from 3D PIC simulations where defocused distance xf = b0
xR0 ≈ 23.31λ0 and plasma scale length L = 0.1λ0. The specific definition of the ratio b0 is provided in the text. The wavefronts of reflected laser are represented by green solid lines. Besides, the red dashed line illustrates the 1/e2 of the maximum intensity of IAP. (b) Theoretical results of wavefronts of incident chirped lasers (dashed) and optically-curved profiles of parabolic PMs (solid) for different ξ. (c) Comparison between curvatures
). Spatial–temporal near-field distributions of the incident (orange shadow) and reflected laser (purple shadow) intensities on tz-plane (y = 0) as well as their on-axis waveforms (colorful and purple solid) are obtained from 3D PIC simulations where defocused distance xf = b0
xR0 ≈ 23.31λ0 and plasma scale length L = 0.1λ0. The specific definition of the ratio b0 is provided in the text. The wavefronts of reflected laser are represented by green solid lines. Besides, the red dashed line illustrates the 1/e2 of the maximum intensity of IAP. (b) Theoretical results of wavefronts of incident chirped lasers (dashed) and optically-curved profiles of parabolic PMs (solid) for different ξ. (c) Comparison between curvatures 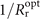 calculated from equation (7) (black solid) and near-field wavefronts of reflected laser (red circles) illustrated in (a). (d) On-axis temporal intensity distribution (purple solid) of near-field AP train obtained from reflected laser in (a) with the same filter used.
calculated from equation (7) (black solid) and near-field wavefronts of reflected laser (red circles) illustrated in (a). (d) On-axis temporal intensity distribution (purple solid) of near-field AP train obtained from reflected laser in (a) with the same filter used.
Download figure:
Standard image High-resolution imageFigure 2. (a) Relations between ξ and 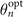 calculated from equation (8) for n = 5 (black solid), 10 (blue solid) and 15 (red solid) with crosses representing corresponding approximate values
calculated from equation (8) for n = 5 (black solid), 10 (blue solid) and 15 (red solid) with crosses representing corresponding approximate values ![${\theta }_{0}\sqrt{[{n}^{-2}{\beta }_{n}^{-2}(\xi )+4{\beta }_{n}^{2}(\xi ){b}_{0}^{2}{s}^{2}{\xi }^{2}]/(1+{b}_{0}^{2})}$](https://content.cld.iop.org/journals/1367-2630/24/3/033038/revision2/njpac59ecieqn15.gif) , where α = 15°, βn
= 0.9,
, where α = 15°, βn
= 0.9, 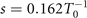 and L = 0.1λ0. (b) The value of chirped parameter s determined by Δω and τL. (c) The dependence of Γn
(0)/Γn
(±T0) on α and Eph. (d) The dependence of Γn
(0)/Γn
(±T0) on s and Eph. Extra parameters in (c) and (d) are the same as (a).
and L = 0.1λ0. (b) The value of chirped parameter s determined by Δω and τL. (c) The dependence of Γn
(0)/Γn
(±T0) on α and Eph. (d) The dependence of Γn
(0)/Γn
(±T0) on s and Eph. Extra parameters in (c) and (d) are the same as (a).
Download figure:
Standard image High-resolution imageReflected along X'-axis, the reflected laser (purple hollow column) is focused by the optically-curved dense electron layer, which is compressed by the driving laser and acts like a PM. Due to the spatial distribution of the light pressure ∝E2, the displacement of surface electrons varies in transverse directions, resulting in parabolic PMs formed naturally [35], whose focal length 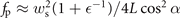 and profile illustrated in figure 1(b) (solid). Here,
and profile illustrated in figure 1(b) (solid). Here,  ≡ aL
λ0(1 − sin α)/πL accounts for the electron dynamics of plasma [35]. Its reciprocal
≡ aL
λ0(1 − sin α)/πL accounts for the electron dynamics of plasma [35]. Its reciprocal  −1 describes the influence of laser intensity on the optical properties of curved PMs, which is negligible when aL ≫ 1 as
−1 describes the influence of laser intensity on the optical properties of curved PMs, which is negligible when aL ≫ 1 as  −1 ∼ 0. The dimensionless parameter aL ≡ eE/me
cω0 is the normalized amplitude of electric field strength with me and e representing the mass and absolute charge of electrons respectively. Assuming the reflected harmonics have Gaussian spatial distributions either, their radii of curvature Rr on PMs satisfy 1/Ri − 1/Rr = 1/fp cos α on the meridional plane [47] and are given as
−1 ∼ 0. The dimensionless parameter aL ≡ eE/me
cω0 is the normalized amplitude of electric field strength with me and e representing the mass and absolute charge of electrons respectively. Assuming the reflected harmonics have Gaussian spatial distributions either, their radii of curvature Rr on PMs satisfy 1/Ri − 1/Rr = 1/fp cos α on the meridional plane [47] and are given as
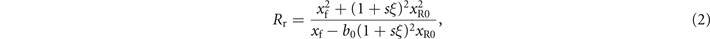
where b0 ≡ 4πL cos α/λ0(1 +  −1) is actually the ratio of the optimal xf to xR0 to realize divergence gating as discussed later and
−1) is actually the ratio of the optimal xf to xR0 to realize divergence gating as discussed later and 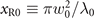 is the Rayleigh length of incident lasers for the central wavelength. It is clear that the curvature
is the Rayleigh length of incident lasers for the central wavelength. It is clear that the curvature 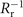 is independent on frequencies of harmonics, which is rational as all harmonics are generated in a region with thickness about the skin depth (sub-10 nm) causing similar shape of spatial distributions. The dependence of
is independent on frequencies of harmonics, which is rational as all harmonics are generated in a region with thickness about the skin depth (sub-10 nm) causing similar shape of spatial distributions. The dependence of 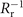 on ξ is introduced by various wavefronts of chirped lasers (dashed) and profiles of parabolic PMs (solid) as shown in figure 1(b). Then, the propagation of reflected harmonics is considered with their radii on PMs wsn
= βn
ws (βn
⩽ 1) assumed, where the intensity is 1/e2 times of the axial value. In this paper, symbols with subscript n represent the corresponding physical quantities for harmonics whose photon energy Eph = nɛ0 and ɛ0 is the energy of single photon at central wavelength λ0. Utilizing the well-known q-parameters of Gaussian beams [46], we have
on ξ is introduced by various wavefronts of chirped lasers (dashed) and profiles of parabolic PMs (solid) as shown in figure 1(b). Then, the propagation of reflected harmonics is considered with their radii on PMs wsn
= βn
ws (βn
⩽ 1) assumed, where the intensity is 1/e2 times of the axial value. In this paper, symbols with subscript n represent the corresponding physical quantities for harmonics whose photon energy Eph = nɛ0 and ɛ0 is the energy of single photon at central wavelength λ0. Utilizing the well-known q-parameters of Gaussian beams [46], we have 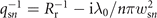 and
and 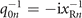 for harmonics on the PM and at their focal planes respectively, where xRn
represents the Rayleigh length of the corresponding harmonic. Considering an equivalent definition of q-parameter as q ≡ x + ixR [46], qsn
and q0n
satisfy
for harmonics on the PM and at their focal planes respectively, where xRn
represents the Rayleigh length of the corresponding harmonic. Considering an equivalent definition of q-parameter as q ≡ x + ixR [46], qsn
and q0n
satisfy 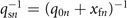 for the free propagation distance xfn
in vacuum between the two positions. After derivation, the expressions of xfn
and xRn
are given as
for the free propagation distance xfn
in vacuum between the two positions. After derivation, the expressions of xfn
and xRn
are given as

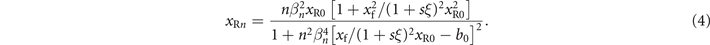
According to equation (4) and the definition of divergences 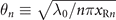 , we get the divergences of harmonics, which vary for different ξ, as
, we get the divergences of harmonics, which vary for different ξ, as
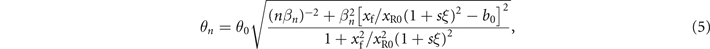
where 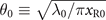 is the divergence of incident laser for central wavelength.
is the divergence of incident laser for central wavelength.
Further, as refocused harmonics propagate a distance xfar (much larger than xRn
and xfn
) from PMs to far-field observation points on the X'-axis, the far-field harmonic intensity ![${I}_{n}^{\text{far}}\approx {I}_{n}^{\text{focus}}/[1+{({x}_{\text{far}}/{x}_{\text{R}n})}^{2}]$](https://content.cld.iop.org/journals/1367-2630/24/3/033038/revision2/njpac59ecieqn26.gif) where
where 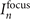 represents the intensity of the reflected harmonic at its focus. Similarly, the near-field harmonic intensity on PMs
represents the intensity of the reflected harmonic at its focus. Similarly, the near-field harmonic intensity on PMs ![${I}_{n}^{\text{near}}={I}_{n}^{\text{focus}}/\left[1+{\left({x}_{\mathrm{f}n}/{x}_{\mathrm{R}n}\right)}^{2}\right]$](https://content.cld.iop.org/journals/1367-2630/24/3/033038/revision2/njpac59ecieqn28.gif) . Therefore,
. Therefore, ![${I}_{n}^{\text{far}}\approx {I}_{n}^{\text{near}}[1+{({x}_{\mathrm{f}n}/{x}_{\mathrm{R}n})}^{2}]/[1+{({x}_{\text{far}}/{x}_{\mathrm{R}n})}^{2}]$](https://content.cld.iop.org/journals/1367-2630/24/3/033038/revision2/njpac59ecieqn29.gif) . Assuming
. Assuming 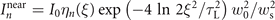 and considering equations (3)–(5) as well as the far field condition xfar ≫ xRn
, we obtain
and considering equations (3)–(5) as well as the far field condition xfar ≫ xRn
, we obtain
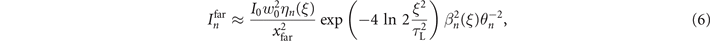
where I0 and ηn
(ξ) represent the focal intensity of incident lasers and generation efficiency of harmonics, respectively. As 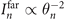 , the minimum θn
should be achieved exactly at the peak laser cycle (ξ = 0) to take full advantage of divergence gating. Specifically, for optimal xf = b0
xR0, we get
, the minimum θn
should be achieved exactly at the peak laser cycle (ξ = 0) to take full advantage of divergence gating. Specifically, for optimal xf = b0
xR0, we get 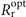 and
and 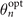 as
as
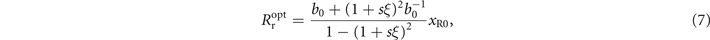
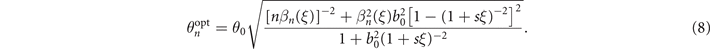
In this situation, foci of harmonics generated at the peak laser cycle (ξ = 0) are on the PMs as xfn = 0 according to equation (3), indicating that the convex wavefront of the incident laser exactly offset the focusing effect of concave PMs within the central optical period.
As shown in equation (7), the flat near-field wavefronts 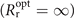 of reflected pulses are realized when ξ = 0, which indicates the minimum divergence and lowest decay during propagation comparing to harmonics generated at other cycles with either concave
of reflected pulses are realized when ξ = 0, which indicates the minimum divergence and lowest decay during propagation comparing to harmonics generated at other cycles with either concave 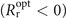 or convex
or convex 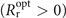 wavefronts on PMs. Considering APs are generated efficiently once a cycle
wavefronts on PMs. Considering APs are generated efficiently once a cycle  for oblique incidence, we have
for oblique incidence, we have ![${\theta }_{n}^{\text{opt}}(\pm {T}_{0})\sim {\theta }_{0}\sqrt{[{n}^{-2}{\beta }_{n}^{-2}(\pm {T}_{0})+4{\beta }_{n}^{2}(\pm {T}_{0}){b}_{0}^{2}{s}^{2}{T}_{0}^{2}]/(1+{b}_{0}^{2})}$](https://content.cld.iop.org/journals/1367-2630/24/3/033038/revision2/njpac59ecieqn38.gif) for small sT0 ≪ 1, which is much bigger than the divergence of harmonics at the peak cycle
for small sT0 ≪ 1, which is much bigger than the divergence of harmonics at the peak cycle 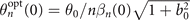 . Defining
. Defining 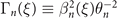 , we get the effect of divergence gating as
, we get the effect of divergence gating as
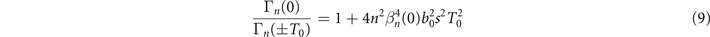
which is independent on τL for a fixed chirp parameter.
Finally, as the satellite harmonics can be ignored compared with the one generated at the peak laser cycle when 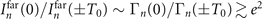 , we get the critical photon energy of filters
, we get the critical photon energy of filters  to produce far-field IAPs through divergence gating. Here, e is the base of the natural logarithm. Considering that influences of temporal envelope
to produce far-field IAPs through divergence gating. Here, e is the base of the natural logarithm. Considering that influences of temporal envelope 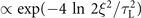 and generation efficiency ηn
(ξ) on
and generation efficiency ηn
(ξ) on  have been neglected during theoretical analysis for simplicity, the requirements of
have been neglected during theoretical analysis for simplicity, the requirements of 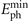 can be further relaxed as shown in simulations. We note that there is astigmatism for reflected pulses from parabolic PMs when α ≠ 0 as harmonics satisfy 1/Ri − 1/Rr = cos α/fp on the sagittal plane [48]. As a result, the corresponding optimal defocused distance xf = b0
xR0 cos2
α, whose relative error comparing to the one on the meridional plane is smaller than 0.1 when α < 18° and can be neglected. Besides, the chirp induced by plasma surface deformation hardly affects our scheme as it does not influence the focusing properties of PMs.
can be further relaxed as shown in simulations. We note that there is astigmatism for reflected pulses from parabolic PMs when α ≠ 0 as harmonics satisfy 1/Ri − 1/Rr = cos α/fp on the sagittal plane [48]. As a result, the corresponding optimal defocused distance xf = b0
xR0 cos2
α, whose relative error comparing to the one on the meridional plane is smaller than 0.1 when α < 18° and can be neglected. Besides, the chirp induced by plasma surface deformation hardly affects our scheme as it does not influence the focusing properties of PMs.
3. Simulation results
3D numerical simulations are carried out with time-domain near-to-far-field transformation (TDNFFT) method [49, 50] to verify our theory where particle-in-cell (PIC) code 'EPOCH' [51] is used to provide near-field data for it. In simulations, except noted in text, the Gaussian-like linear-polarized chirped laser (orange hollow column) with λ0 = 800 nm (ɛ0 ≈ 1.55 eV), w0 = 2 μm, τL = 8 fs ∼ 3T0, Δω = 0.5ω0
 , ϕ0 = 0 and peak intensity I0 ≈ 1.92 × 1021 W cm−2 (aL = 30) at focus is incident along X-axis from the right boundary as shown in figure 1(a). The quadratic polynomial phase factor about ξ in equation (1) is introduced to PIC simulations to initialize the chirp. According to reference [45], the influence of temporal envelope on the formula of incident beams considered in simulations can be neglected.
, ϕ0 = 0 and peak intensity I0 ≈ 1.92 × 1021 W cm−2 (aL = 30) at focus is incident along X-axis from the right boundary as shown in figure 1(a). The quadratic polynomial phase factor about ξ in equation (1) is introduced to PIC simulations to initialize the chirp. According to reference [45], the influence of temporal envelope on the formula of incident beams considered in simulations can be neglected.
Irradiated by lasers with incident angle α = 15° and defocused distance xf, the bulk density n0 and thickness d of the thin foil (grey block) are 100nc
 and 0.5λ0 respectively. Clearly, for the peak cycle (ξ = 0), the laser intensity acting on plasma surfaces
and 0.5λ0 respectively. Clearly, for the peak cycle (ξ = 0), the laser intensity acting on plasma surfaces 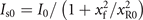 . Before the bulk, the preplasma with exponential density scale L = 0.1λ0 is set. As the interaction between the beam and preplasma is dominant and the width of interaction region is about the skin depth, the small thickness of plasma bulk is chosen to save computational resources whose rationality has been verified [52]. In addition to computationally expensive 3D PIC simulations which are performed with limited numerical resolution (illustrated in figure 1 with simulation time step Δt ≈ T0/300), high-precision two-dimensional (2D) PIC simulations are also carried out (Δt ≈ T0/2263) for figures 3–5, where the 3D far-field results are calculated through TDNFFT method based on axisymmetric approximations. We note that all far-field results are calculated in 3D geometries except for figure 3(f) where the result in 2D situation is shown for the comparison. The size of 3D (2D) PIC simulation box x × y × z (x × y) is 8.5λ0 × 25λ0 × 20λ0 (10λ0 × 35.5λ0), containing 850 × 2500 × 2000 (8000 × 28 400) cells with 2 (16) and 1 (8) superparticles per cell for electrons and immobile ions, respectively. The hole-boring effect is negligible in our scheme. All of far-field results are calculated after reflected pulses propagating a distance xfar = 105
λ0.
. Before the bulk, the preplasma with exponential density scale L = 0.1λ0 is set. As the interaction between the beam and preplasma is dominant and the width of interaction region is about the skin depth, the small thickness of plasma bulk is chosen to save computational resources whose rationality has been verified [52]. In addition to computationally expensive 3D PIC simulations which are performed with limited numerical resolution (illustrated in figure 1 with simulation time step Δt ≈ T0/300), high-precision two-dimensional (2D) PIC simulations are also carried out (Δt ≈ T0/2263) for figures 3–5, where the 3D far-field results are calculated through TDNFFT method based on axisymmetric approximations. We note that all far-field results are calculated in 3D geometries except for figure 3(f) where the result in 2D situation is shown for the comparison. The size of 3D (2D) PIC simulation box x × y × z (x × y) is 8.5λ0 × 25λ0 × 20λ0 (10λ0 × 35.5λ0), containing 850 × 2500 × 2000 (8000 × 28 400) cells with 2 (16) and 1 (8) superparticles per cell for electrons and immobile ions, respectively. The hole-boring effect is negligible in our scheme. All of far-field results are calculated after reflected pulses propagating a distance xfar = 105
λ0.
Figure 3. Far-field results in 3D geometries when xfar = 105
λ0 with 2D PIC simulations carried out. (a) and (d) are the far-field temporal intensity distribution and time-frequency analysis of reflected on-axis APs (Eph ⩾ 10 eV) obtained from normally incident (α = 0°) chirped (the top half,  ) and non-chirped (the bottom half) driving lasers respectively, where dashed lines represent the values of
) and non-chirped (the bottom half) driving lasers respectively, where dashed lines represent the values of  . (b) and (e) are similar to (a) and (d) respectively, but for α = 15°. (c) is the spatial–temporal distribution of far-field APs on the z-t plane (y = 0, x = xfar = 105
λ0) for the same case illustrated in the top half of (b). (f) The far-field temporal intensity distribution of reflected on-axis APs calculated from 2D TDNFFT method, as a comparison to the 3D result shown in the top half of (b).
. (b) and (e) are similar to (a) and (d) respectively, but for α = 15°. (c) is the spatial–temporal distribution of far-field APs on the z-t plane (y = 0, x = xfar = 105
λ0) for the same case illustrated in the top half of (b). (f) The far-field temporal intensity distribution of reflected on-axis APs calculated from 2D TDNFFT method, as a comparison to the 3D result shown in the top half of (b).
Download figure:
Standard image High-resolution imageIn figure 1(a) where xf = b0
xR0 ∼ 23.31λ0, Is0 ≈ 7.97 × 1020 W cm−2, curvatures of chirped incident laser change for different optical cycles due to the time-varying wavelengths (colorful solid), which is indicated by its spatial–temporal distribution of intensities (orange shadow). Such various spatial distributions cause variation in the focal length fp of the optically-curved PM, resulting in wavefronts (green solid) of near-field reflected laser change significantly for different optical cycles. As shown in the intensity distribution (purple shadow), the flat reflected wavefront is obtained only at the peak cycle ξ = 0, which meets our expectation and indicates the realization of divergence gating. Clearly, the IAP (red solid) is obtained in the far field after passing through a proper filter (brown cylinder, 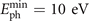 ) while the attosecond pulse train (APT, purple solid in figure 1(d)) is obtained in near field with the same filter used for the near-field reflected pulses (purple solid in figure 1(a)). Quantitatively, as illustrated in figure 1(c), the numerical results (red cycles) of curvature
) while the attosecond pulse train (APT, purple solid in figure 1(d)) is obtained in near field with the same filter used for the near-field reflected pulses (purple solid in figure 1(a)). Quantitatively, as illustrated in figure 1(c), the numerical results (red cycles) of curvature 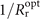 are consistent with the theoretical predictions (black solid) for different cycles, calculated from wavefronts (green solid) in figure 1(a) and equation (7) respectively. We note the varying distances between circles are introduced by the chirp.
are consistent with the theoretical predictions (black solid) for different cycles, calculated from wavefronts (green solid) in figure 1(a) and equation (7) respectively. We note the varying distances between circles are introduced by the chirp.
Figure 2(a) illustrates the theoretical θn
for the same case as figure 1(a), where βn
is assumed to be 0.9 for n = 5, 10 and 20 (black, blue and red). Because the approximate values of ![${\theta }_{n}^{\text{opt}}(\xi )\sim {\theta }_{0}\sqrt{[{n}^{-2}{\beta }_{n}^{-2}(\xi )+4{\beta }_{n}^{2}(\xi ){b}_{0}^{2}{s}^{2}{\xi }^{2}]/(1+{b}_{0}^{2})}$](https://content.cld.iop.org/journals/1367-2630/24/3/033038/revision2/njpac59ecieqn53.gif) represented by crosses are close to the corresponding precise theoretical values calculated from equation (8) (solids) when |ξ| ⩽ T0, equation (9) is valid and capable to evaluate
represented by crosses are close to the corresponding precise theoretical values calculated from equation (8) (solids) when |ξ| ⩽ T0, equation (9) is valid and capable to evaluate  required by divergence gating. Besides, the lines and crosses confirm that the minimum divergences are obtained at the peak cycle (ξ = 0) as expected. Here, the chirped parameter
required by divergence gating. Besides, the lines and crosses confirm that the minimum divergences are obtained at the peak cycle (ξ = 0) as expected. Here, the chirped parameter 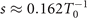 is determined by Δω and τL as shown in figure 2(b). The influence of incident angle α on divergence gating is considered in figure 2(c). To obtain far-field IAPs, the requirement of
is determined by Δω and τL as shown in figure 2(b). The influence of incident angle α on divergence gating is considered in figure 2(c). To obtain far-field IAPs, the requirement of 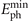 is increased for bigger α which means more narrow spectra as well as less energy are preserved. Therefore, although the most efficient RHHG is achieved when α ∼ 55° [53], α = 15° is chosen to balance the generation efficiency and isolation of APs with astigmatism considered at the same time. Further, figure 2(d) illustrates the dependence of Γn
(0)/Γn
(±T0) on Eph and s for α = 15°. Clearly, IAPs are predicted to be produced when
is increased for bigger α which means more narrow spectra as well as less energy are preserved. Therefore, although the most efficient RHHG is achieved when α ∼ 55° [53], α = 15° is chosen to balance the generation efficiency and isolation of APs with astigmatism considered at the same time. Further, figure 2(d) illustrates the dependence of Γn
(0)/Γn
(±T0) on Eph and s for α = 15°. Clearly, IAPs are predicted to be produced when 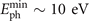 for
for 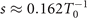 and βn
= 0.9. The same βn
is set for all harmonics to show the effects of divergence gating briefly in theory and the value 0.9 is chosen based on the simulation result of harmonics contained in the peak AP.
and βn
= 0.9. The same βn
is set for all harmonics to show the effects of divergence gating briefly in theory and the value 0.9 is chosen based on the simulation result of harmonics contained in the peak AP.
As illustrated in figures 3(a) and (b) where α = 0° (Is0 ≈ 7.60 × 1020 W cm−2) and 15° (Is0 ≈ 7.97 × 1020 W cm−2) respectively, the unchirped incident laser with the same intensity as the chirped one can only generate ATPs (blue solids) on the axis when harmonics whose Eph < 10 eV are filtered out. Corresponding to our theoretical predictions, once divergence gating is realized by chirped lasers, the intensity distributions of reflected APs (red solids, 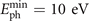 ) show that satellite pulses can be ignored if their emission intervals with the peak AP approach one cycle as their intensities are lower than
) show that satellite pulses can be ignored if their emission intervals with the peak AP approach one cycle as their intensities are lower than 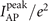 (red dashed). Here,
(red dashed). Here, 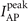 represents intensity of the peak AP and all far-field results are obtained when xfar = 105
λ0. However, as APs are generated each half cycle for normal incidence, intense far-field IAP is only obtained for α = 15° with intensity and duration about 1016 W cm−2 and 40 as respectively, as shown in figure 3(b). The little higher
represents intensity of the peak AP and all far-field results are obtained when xfar = 105
λ0. However, as APs are generated each half cycle for normal incidence, intense far-field IAP is only obtained for α = 15° with intensity and duration about 1016 W cm−2 and 40 as respectively, as shown in figure 3(b). The little higher 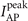 for cases using chirped lasers is caused by slightly smaller divergences. Comparisons with cases using TL pulses with the same bandwidth Δω = 0.5ω0 are discussed in the appendix. Besides, for the case shown in the top half of figure 3(b), its spatial–temporal distribution on z–t plane (y = 0) in the far field is illustrated in figure 3(c), where near-axis IAP is obtained with total angular spread reaching 12 mrad (|z| ≲ 600λ0 when xfar = 105
λ0). Therefore, the energy of it is about 1.5 mJ and its peak intensity can be boosted to 1020–1021W cm−2 after refocused to micrometer scales. Besides, the curved wavefronts of APs indicate their arriving time varies with transverse positions of the observation plane, caused by the natural spherical far-field wavefront of the Gaussian beam whose radius approximates to xfar.
for cases using chirped lasers is caused by slightly smaller divergences. Comparisons with cases using TL pulses with the same bandwidth Δω = 0.5ω0 are discussed in the appendix. Besides, for the case shown in the top half of figure 3(b), its spatial–temporal distribution on z–t plane (y = 0) in the far field is illustrated in figure 3(c), where near-axis IAP is obtained with total angular spread reaching 12 mrad (|z| ≲ 600λ0 when xfar = 105
λ0). Therefore, the energy of it is about 1.5 mJ and its peak intensity can be boosted to 1020–1021W cm−2 after refocused to micrometer scales. Besides, the curved wavefronts of APs indicate their arriving time varies with transverse positions of the observation plane, caused by the natural spherical far-field wavefront of the Gaussian beam whose radius approximates to xfar.
The time-frequency analysis of APs obtained from chirped (the top half) and non-chirped driving lasers (the bottom half) are presented in figures 3(d) and (e), which verify that divergence gating greatly suppresses intensities of satellite APs while hardly affect the peak one as expected. What's more, to compare with 3D far-field results shown in figure 3(b), the 2D result (red solid) for chirped laser–plasma interactions (same parameters as the case represented by the red solid in figure 3(b)) is illustrated in figure 3(f). As expected, a weaker effect of divergence gating is observed in the 2D situation where the APT instead of IAP is obtained while intensities of satellite pulses are also suppressed comparing to the 3D results for unchirped driving pulses (blue solid in figure 3(b)).
Our scheme works for a broad range of parameters as illustrated in figures 4(a)–(c) where filters with 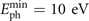 are used. Figure 4(a) shows that with the increase of band width Δω, the intensity rate between the strongest and second strong APs Irate (red circle) improves while the duration τAP of peak APs (blue triangle) keeps constant
are used. Figure 4(a) shows that with the increase of band width Δω, the intensity rate between the strongest and second strong APs Irate (red circle) improves while the duration τAP of peak APs (blue triangle) keeps constant  , consistent with our theoretical predictions shown in figure 2(d). Besides, the smallest bandwidth ∼0.35ω0 is required to obtain IAP in the far field. Figure 4(b) shows the relations of L with Irate and IAPs can be obtained for 0.075 ≲ L/λ0 ≲ 0.125 which is feasible in experiments nowadays [54]. We note that the decline of the performance of divergence gating for L > 0.1λ0 stems from the decreased harmonic generation efficiency as well as worse optical properties of PMs because of instability [55]. Furthermore, there is about 50% probability to generate IAPs for random ϕ0, i.e. random CEP, as illustrated in figure 4(c), which is capable to perform pump-probe experiments requiring IAPs without the stabilization of CEP with the help of CE tagging technology [18, 56, 57]. We note that such result is three times of those obtained from reference [18] where unchirped three-cycle lasers and filters with
, consistent with our theoretical predictions shown in figure 2(d). Besides, the smallest bandwidth ∼0.35ω0 is required to obtain IAP in the far field. Figure 4(b) shows the relations of L with Irate and IAPs can be obtained for 0.075 ≲ L/λ0 ≲ 0.125 which is feasible in experiments nowadays [54]. We note that the decline of the performance of divergence gating for L > 0.1λ0 stems from the decreased harmonic generation efficiency as well as worse optical properties of PMs because of instability [55]. Furthermore, there is about 50% probability to generate IAPs for random ϕ0, i.e. random CEP, as illustrated in figure 4(c), which is capable to perform pump-probe experiments requiring IAPs without the stabilization of CEP with the help of CE tagging technology [18, 56, 57]. We note that such result is three times of those obtained from reference [18] where unchirped three-cycle lasers and filters with 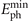 as high as 35 eV are used.
as high as 35 eV are used.
More interesting, the far-field IAP (blue solid) is obtained without filters when ϕ0 = −0.1π, τL = 8 fs and Δω = 0.5ω0
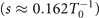 as shown in figure 4(d). Due to all harmonics are preserved, the intensity and energy of the IAP (τAP = 49 as) reach 1.8 × 1016 W cm−2 (1.1 × 1018 W sr−1) and mJ, respectively. Finally, in the bottom half of the same figure, we present that the divergence gating is valid for lasers with long pulse duration as τL ≈ 16 fs whose bandwidth Δω = 0.5ω0
as shown in figure 4(d). Due to all harmonics are preserved, the intensity and energy of the IAP (τAP = 49 as) reach 1.8 × 1016 W cm−2 (1.1 × 1018 W sr−1) and mJ, respectively. Finally, in the bottom half of the same figure, we present that the divergence gating is valid for lasers with long pulse duration as τL ≈ 16 fs whose bandwidth Δω = 0.5ω0
 . Through increasing the
. Through increasing the 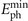 to 20 eV based on the prediction in figure 2(d), the far-field IAP (red solid, ∼4 × 1014 W cm−2 or 2.5 × 1016 W sr−1) is generated with little longer τAP ≈ 72 as. Here, intensities of incident beams are the same as the one used in figure 1 and ϕ0 = 0. Further simulations (not shown) confirm that the divergence gating also works for incident laser intensities in 1020 W cm−2 which is achievable for 100 TW class facilities. What's more, according to the theoretical prediction of equation (9) and the estimation based on high-precision 1D simulations, IAPs in the water-window regime (282–533 eV) can be obtained through divergence gating with such laser intensities irradiated on the PM.
to 20 eV based on the prediction in figure 2(d), the far-field IAP (red solid, ∼4 × 1014 W cm−2 or 2.5 × 1016 W sr−1) is generated with little longer τAP ≈ 72 as. Here, intensities of incident beams are the same as the one used in figure 1 and ϕ0 = 0. Further simulations (not shown) confirm that the divergence gating also works for incident laser intensities in 1020 W cm−2 which is achievable for 100 TW class facilities. What's more, according to the theoretical prediction of equation (9) and the estimation based on high-precision 1D simulations, IAPs in the water-window regime (282–533 eV) can be obtained through divergence gating with such laser intensities irradiated on the PM.
Figure 4. Far-field results in 3D geometries with 2D PIC simulations carried out. The dependence of Irate (red circles) and τAP (blue triangles) on (a) Δω, (b) L or (c) ϕ0 when Eph ⩾ 10 eV. (d) The on-axis far-field intensity temporal distribution of reflected APs when chirped incident lasers are used (Δω = 0.5ω0) for ϕ0 = −0.1π without filters (blue solid) or τL ≈ 16fs with Eph ⩾ 20 eV (red solid). More parameters are provided in the text.
Download figure:
Standard image High-resolution image4. Conclusions
In summary, we have proposed a scheme called divergence gating realized by defocused chirped lasers to obtain IAPs in far field. Theoretical analysis and numerical simulations show that the divergence of the reflected peak AP is much smaller than others when solid targets are placed at a position behind the focal plane of the incident laser with distance xf = [4πL cos α/λ0(1 +  −1)]xR0. As the much lower decrease of on-axis intensity, far-field IAPs can be obtained after propagation, if filters satisfy
−1)]xR0. As the much lower decrease of on-axis intensity, far-field IAPs can be obtained after propagation, if filters satisfy 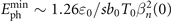 . 3D simulation results show that our scheme is robust and bright sub-50 as mJ-level IAPs are obtained in the far field without the requirement of stable CEP by chirped lasers with intensities of 1.92 × 1021 W cm−2. Besides, our scheme can produce intense IAPs even without filters, whose intensities reach 1.8 × 1016 W cm−2 (1.1 × 1018 W sr−1). Through divergence gating, generated mJ-level IAPs with broad spectrum and intense photon flux benefit the metrology and utilization of IAPs [58] greatly, especially for attosecond-pump-attosecond-probe experiments.
. 3D simulation results show that our scheme is robust and bright sub-50 as mJ-level IAPs are obtained in the far field without the requirement of stable CEP by chirped lasers with intensities of 1.92 × 1021 W cm−2. Besides, our scheme can produce intense IAPs even without filters, whose intensities reach 1.8 × 1016 W cm−2 (1.1 × 1018 W sr−1). Through divergence gating, generated mJ-level IAPs with broad spectrum and intense photon flux benefit the metrology and utilization of IAPs [58] greatly, especially for attosecond-pump-attosecond-probe experiments.
Acknowledgments
Y Zhang thanks L Li for the helpful discussion. This work is supported by the Science Challenge Project, No. TZ2018005; the National Natural Science Foundation of China, Grant Nos. 12135001, 11921006 and 11825502; the Strategic Priority Research Program of the Chinese Academy of Sciences, Grant No. XDA25050900. B Qiao acknowledges support from the National Natural Science Funds for Distinguished Young Scholars, Grant No. 11825502. Y Zhang acknowledges support from the China Scholarship Council for Visiting PhD Students, File No. 202106010198. The simulations are carried out on the Tianhe-2 supercomputer at the National Supercomputer Center in Guangzhou.
Data availability statement
The data generated and/or analysed during the current study are not publicly available for legal/ethical reasons but are available from the corresponding author on reasonable request.
Appendix.: Comparison with cases using transform-limited driving lasers
For the typical chirped incident laser used in this paper (I0 ≈ 1.92 × 1021 W cm−2, τL = 8 fs, Δω = 0.5ω0), its intensity can be increased to 6.53 × 1021 W cm−2 with duration decreased to 2.3 fs after compressed to the TL beam [46]. Utilizing such TL pluses, 2D PIC simulations are carried out with far-field results calculated in 3D geometries. The far-field on-axis intensity distributions of cases where TL pulses interact with targets away from their focal planes (xf = b0 xR0 ≈ 23.68λ0, Is0 ≈ 2.66 × 1021 W cm−2) or at foci are illustrated in figures 5(a) and (b), respectively. Other simulation parameters are the same as those used in the case illustrated by the red line of figure 3(b).
Figure 5. The far-field temporal intensity distributions of the reflected on-axis APs (after transformed to 3D geometry) obtained from 2D PIC simulations for cases where TL pulses with bandwidth Δω = 0.5ω0 are used. (a) and (b) are the results when xf = b0
xR0 ≈ 23.68λ0 and xf = 0 are respectively taken. The other parameters are α = 15°, τL = 2.3 fs, I0 = 6.53 × 1021 W cm−2 (Is0 ≈ 2.66 × 1021 W cm−2 for the defocused case) and ϕ0 = 0. Note that the dashed line represents the value of 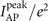 .
.
Download figure:
Standard image High-resolution imageClearly, because of larger divergences caused by optically-curved PMs, the case using the focused TL pulse (figure 5(b)) generates much weaker far-field APs than those using proper defocused pulses no matter they are TL beams (figure 5(a)) or not (figure 3(b)) [36]. Besides, for defocused situations, although the IAP generated by the TL beam (figure 5(a)) is intenser due to higher incident intensity, its isolation property (Irate ≈ 12) is worse than the one obtained through the divergence gating, illustrated by red solids (Irate ≈ 16) in figure 3(b) and it is very challenging to compress such incident lasers to the TL situation (as short as 2.3 fs) in experiments.