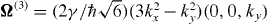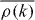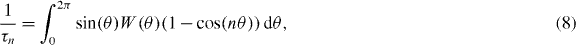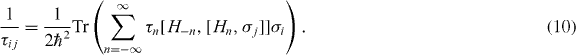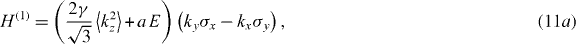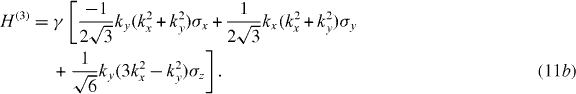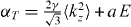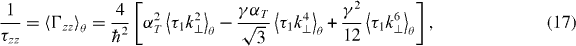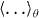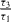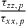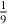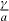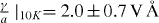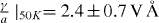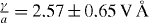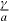Abstract
Time-resolved optical spectroscopy experiments in (111)-oriented GaAs/AlGaAs quantum wells (QWs) show a strong electric field dependence of the conduction electron spin relaxation anisotropy. This results from the interplay between the Dresselhaus and Rashba spin splitting in this system with C3v symmetry. By varying the electric field applied perpendicular to the QW plane from 20 to 50 kV cm−1 the anisotropy of the spin relaxation time parallel (τs∥) and perpendicular (τs⊥) to the growth axis can be first canceled and eventually inversed with respect to the one usually observed in III–V zinc-blende QW (τs⊥ = 2τs∥). This dependence stems from the nonlinear contributions of the k-dependent conduction band spin splitting terms which begin to play the dominant spin relaxing role while the linear Dresselhaus terms are compensated by the Rashba ones through the applied bias. A spin density matrix model for the conduction band spin splitting including both linear and cubic terms of the Dresselhaus Hamiltonian is used which allows a quantitative description of the measured electric field dependence of the spin relaxation anisotropy. The existence of an isotropic point where the spin relaxation tensor reduces to a scalar is predicted and confirmed experimentally. The spin splitting compensation electric field and collision processes type in the QW can be likewise directly extracted from the model without complementary measurements.

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
GENERAL SCIENTIFIC SUMMARY Introduction and background. The control of the electron spin in semiconductors for potential use in transport devices or quantum information applications is an important issue in the field of spintronics. In semiconductors, the main challenge is to find materials or systems where the electron spin relaxation time can be tailored on demand and made long enough to process information based on the spin states. Usually the spin relaxation time of electrons in AlGaAs/GaAs-type quantum well devices is short and anisotropic, i.e. it depends on the orientation of the electron wavevector. Both phenomena, the spin relaxation and its anisotropy, are a consequence of the spin–orbit interaction present in semiconductor structures.
Main results. We show here that by a proper design of a AlGaAs/GaAs quantum well device, the spin–orbit interaction can be fully controlled by a simple external electrical field. This results from the electric field dependent interplay between the two mechanisms (Rashba and Dresselhaus contributions) at the origin of the spin–orbit-induced spin relaxation of conduction band electrons in semiconductor devices. As a consequence, the electron spin relaxation time, whatever the spin direction is, can be controlled and increased drastically. The particular dependence of the spin relaxation of conduction band electron on the applied electric field also leads to the possibility of controlling the spin relaxation anisotropy. This can be cancelled and eventually inversed with respect to that usually observed in other zinc-blende semiconductor structures.
Wider implications. Since the principle exploited here relies only on symmetry considerations, it can in principle be applied to other zinc-blende or wurtzite heterostructures, greatly expanding the possibility of designing devices for spin control and manipulations in semiconductors.
 Figure. Schematic representation of the spin relaxation time parallel (τzs) and perpendicular (τ⊥s) to the quantum well plane as a function of the applied electric field which controls the ratio of the spin-orbit induced spin relaxation mechanisms.
Figure. Schematic representation of the spin relaxation time parallel (τzs) and perpendicular (τ⊥s) to the quantum well plane as a function of the applied electric field which controls the ratio of the spin-orbit induced spin relaxation mechanisms.
1. Introduction
The study of spin relaxation processes in two-dimensional (2D) systems is crucial to the understanding of the operation of spintronics devices. The dominant process governing the spin relaxation in III–V zinc-blende semiconductor quantum wells (QWs) finds its origin in the spin splitting of the conduction band (CB) at k ≠ 0 and can be thoroughly interpreted on the basis of the Dyakonov–Perel (DP) model [1–5]. According to this model, the spin relaxation process originates from the k-dependent Larmor precession, in the intervals between collisions, of the electron spin in the effective magnetic field which represents the CB spin splitting. The spin relaxation time τsi of a CB electron spin oriented along a direction i can thus be simply written in the collision dominated regime as 1/τsi = 〈Ω2⊥〉τp, where 〈Ω2⊥〉 is the mean square of the precession vector in the plane perpendicular to the spin direction i and τp the electron momentum scattering time4.
In QWs of the GaAs/AlGaAs type, both the bulk inversion asymmetry [6] (BIA or Dresselhaus term) and the structure inversion asymmetry [7] (SIA or Rashba term) contribute to the direction and magnitude of the total precession vector Ω = ΩBIA + ΩSIA. In particular, the orientation of the BIA term, originating from the combined effect of spin–orbit interaction and the lack of crystal inversion symmetry, depends on the actual structure growth direction. Conversely, the SIA contribution, occurring if the structure lacks symmetry along the growth direction, can be for instance induced by the presence of an external or internal electric field [8–11]. For fields directed along the growth axis z, ΩSIA lies in the QW plane and it is proportional to . By appropriate choices of the structure growth direction and induced strength of the Rashba term, the CB spin splitting can be externally manipulated for some orientations and eventually made negligibly small.
A most compelling situation occurs in the particular case of (111)-oriented heterostructures. When an external electric field E is applied perpendicular to the QW plane, using the natural orientation for the x,y and z coordinates along the and [111] directions, respectively, the total effective precession vector field writes [12–14]
where γ and a are, respectively, the Dresselhaus and Rashba coefficients, the wavevector perpendicular to the growth direction and 〈k2z〉 the averaged squared wavevector along the growth direction5. This relation shows that in first approximation the CB spin splitting can be electrically canceled whenever the cubic Dresselhaus terms are negligible compared to the linear ones. This opens up the possibility of drastically decreasing the efficiency of the DP spin relaxation mechanism to first order in k for all the three spin components by electrically adjusting the SIA term to compensate the BIA one. A new class of spin-based devices relying on this electrical cancelation of the CB spin splitting have been demonstrated: the simultaneous control of the the spin relaxation time in the three spin directions has been recently reported in biased structures up to 250 K [15–18]. The role of the non-equivalent 〈111〉 substrate orientations has also been determined [19]. More recently, the gate-control of the electron spin diffusion length has also been reported [20].
Nevertheless, strict spin splitting cancelation cannot occur due to the presence of higher order terms in k due to the Dresselhaus contribution. Despite being negligible near the CB edge and at low temperature, the nonlinear terms progressively play the dominant role as the linear ones are electrically compensated by the Rashba ones. This contributes to the limitation imposed to the spin lifetimes but also of new interesting possibilities such as the control of the spin relaxation anisotropy whose description is the aim of this work.
In this paper we report on the experimental evidence of the control of the electron spin relaxation anisotropy in (111)-oriented GaAs/AlGaAs QWs. We show that by adjusting the external bias applied to a p–i–n structure, the spin relaxation anisotropy can be either canceled or inversed with respects to the unbiased case. We demonstrate that the observed electric field dependent anisotropy can be efficiently described in the framework of a spin density matrix formalism model [21] including both the linear and cubic terms of the effective DP spin precession vector Ω in the non-degenerate regime and explicitly taking into account the electron scattering processes. The model correctly predicts the existence of the observed isotropic point for the spin relaxation tensor and quantitatively describes the experimental results allowing the simultaneous direct determination of the Dresselhaus to Rashba contribution ratio γ/a, the dominant collision process and, lastly, the momentum scattering time τp without the need of mobility measurements.
2. Sample details
The investigated sample consists of a non-intentionally doped GaAs/Al0.3Ga0.7As 20 multiple QW (MQW) structure with 15 nm well width grown by molecular beam epitaxy on a n-doped (111)B GaAs substrate mis-oriented 3° toward x. The MQW is embedded between a 500 nm GaAs/500 nm p-doped (p = 1.2 × 1018 cm−3) GaAs constituting the bottom buffer/p-contact layers and a 10 nm n-doped (n = 2.8 × 1018 cm−3) GaAs as the top n-contact. The reverse bias voltage is applied between the unetched top n-contact and the chemically etched p-contact. The built-in junction electric field E is about 20 kV cm−1. The application of a bias in these samples allows us to tune the sign and amplitude of the Rashba contribution to the spin splitting.
The sample is optically excited by circularly polarized (σ+) 1.5 ps light pulses generated by a mode-locked Ti–Sa laser propagating along the growth axis z∥[111] with a repetition frequency of 80 MHz (average power Pexc = 10 mW, 50 μm diameter spot). The laser excitation energy is set to 1.56 eV, i.e. above the electron–light hole ground state of the QW transition. The dynamics of the photoluminescence (PL) emitted by the electron–heavy hole ground state transition is then recorded using a S1 photocathode streak camera with an overall time resolution of 8 ps. The electron spin relaxation time parallel to the growth direction τs∥ is then extracted from the dynamics of the degree of circular polarization according to Pc = (I+ − I−)/(I+ + I−), where I+ and I− represent, respectively, the intensities of the PL co- and counter-polarized with the excitation laser. Since the spin relaxation time of the photogenerated holes is of the order of 1 ps [4], the circular polarization degree of the detected luminescence associated to the fundamental QW transition corresponds directly to the electron spin polarization degree. The value of the spin relaxation time τs⊥ perpendicular to the growth direction, i.e. lying in the QW plane, is obtained from the measurement of the conduction electron spin Larmor precession by placing the sample in an external magnetic field provided by permanent magnets and applied perpendicularly to the growth axis (Voigt geometry). The electron spin experiences now both an in-plane and out-of-plane relaxation and τs⊥ can be calculated from the decay time τsenv of the Pc beats envelope according to 1/τsenv = 1/2(1/τs∥ + 1/τs⊥), provided that [(τs⊥)−1 − (τs∥)−1]/2ωL < 1 [22], ωL being the angular frequency of the Larmor precession.
3. Experimental results
Figures 1(a)–(c), black lines, report the comparison between the measured circular polarization dynamics Pc recorded for different electric field values in the absence of any external magnetic field (B = 0). The average spin direction is here along z. We observed a hundredfold increase of the spin relaxation time τs∥ as the external bias is changed from V =0 to −5.5 V [15]. This is what expected from the electric field induced Rashba contribution when it progressively compensates the Dresselhaus terms. The red curves present the corresponding dynamics of the Pc degree in the presence of a magnetic field applied perpendicular to the growth direction (B ≠ 0, Voigt configuration). We find a likewise electric field induced increase of the spin relaxation time perpendicular to the growth direction τs⊥. However, the actual electric field dependence of τs⊥ is rather different compared to τs∥. At V =0 V (i.e. when the Rashba term is solely due to the junction built-in electric field), the magnetic field induced oscillations of the Pc dynamics are systematically above the corresponding values for B = 0 yielding τs∥ < τs⊥. This is consistent with the usual spin relaxation anisotropy predicted by Dyakonov and Perel [2] for zinc-blende QWs. By increasing the external bias, we observe that the anisotropy of the spin relaxation times can be first canceled, τs∥ = τs⊥, figure 1(b) and eventually inversed: τs∥ > τs⊥, figure 1(c). As it will be explained in the model presented below, this is a consequence of the presence of cubic Dresselhaus terms in equation (1) showing that for a given k, compensation of the Rashba and Dresselhaus terms can only occur for the QW in-plane components whereas the z component is unaffected by the electric field. As the in-plane precession vector is progressively brought to compensation, electron spins oriented along the z-axis will experience longer spin relaxation times compared to the ones oriented in the plane since the latter will precess around a nonzero vector orthogonal to the QW plane. This is schematically reported in figure 1(d): the black and red curves reproduce the spin relaxation times as a function of the relative weight of the Rashba to Dresselhaus linear contributions to the spin–orbit Hamiltonian αSIA and αBIA, respectively. The three different regimes to which the spin relaxation anisotropy has been adjusted in the experimental data presented in figure 1 are here shaded. For αSIA ≪ αBIA or αSIA ≫ αBIA the precession vector is dominated by the linear terms lying in the QW plane—see the arrow in the inset of figure 1(d). The situation is inversed upon compensation of the in-plane precession vector: now αSIA ≈ αBIA and Ω ≈ Ω(3), being the cubic Dresselhaus term. Ω(3) is essentially oriented along the growth direction and characterized by terms cubic in k unaffected by the electric field.
Figure 1. Comparison between the longitudinal and transverse spin relaxation times τs∥, τs⊥ measured through the PL circular polarization dynamics Pc with and without an external magnetic field. (a) τs∥ < τs⊥, (b) τs∥ ≈ τs⊥ and (c) τs∥ > τs⊥. The insets in (a) and (b) report the Pc dynamics measured for a different value of the magnetic field at T = 10 K for V =0 and −2.5 V, respectively. (d) The schematic dependence of τs∥ and τs⊥ as a function of the ratio between the Rashba (αSIA) and Dresselhaus (αBIA) linear contributions to the CB splitting. The inset presents a representation of the effective magnetic field precession vector Ω in the two opposite situations achievable with the application of the external bias: αSIA ≪ or ≫ αBIA and αSIA ≈ −αBIA.
Download figure:
Standard image High-resolution imageThe weight of the Dresselhaus cubic terms is exalted when the temperature increases: a larger range of electron states with different wavectors are populated. Equation (1) shows that for a fixed external electric field the compensation cannot occur simultaneously for a range of wavevectors: at higher temperatures or higher carrier densities, the compensation effect progressively lessens. This temperature dependence is observable in figure 2 where the ensemble of the spin relaxation times measured for T = 10 and 50 K is presented. The impact of the temperature on the electrical control of the spin relaxation is revealed in a modified electric field dependence of the spin relaxation time and anisotropy whose description is the subject of the rest of the paper.
Figure 2. Comparison between experimental and simulated electric field dependence of the spin relaxation time. (a), (b) Circles: spin relaxation time parallel to the growth direction τs∥ as a function of the electric field measured at T = 10 and 50 K, respectively. The solid and dashed lines are fits to the data according to the models presented in the text. (c), (d) Squares: the measured spin relaxation time ratio τs∥/τs⊥ as a function of the electric field for the same temperatures. The solid and dashed black lines are the calculated ratios according to the models. The gray dotted curve show the calculated ratio multiplied by a global factor C = 1.66 (see text). The horizontal line is a guide to the eye to highlight the isotropic spin relaxation points.
Download figure:
Standard image High-resolution image4. Model
In order to quantitatively delineate the electric field and temperature dependence on the spin relaxation anisotropy, we briefly describe the model used here following the approach initially developed by Averkiev and Golub for 〈001〉-oriented QWs [21, 23]. The model presents the DP mechanism using the spin density matrix formalism explicitly taking into account the collision processes. Although it can be applied at any carrier concentration, we present here only the case of a non-degenerate electron gas, which corresponds to our experimental situation. In what follows, we consider that only the first confined level in the QW is populated, that the energy dispersion is isotropic and that all particles are in the elastic scattering regime.
4.1. Calculation of electron spin relaxation in (111)-oriented QWs
Under these assumptions, the dynamics of the spin-density matrix ρ for the spin–orbit Hamiltonian HSO = HD + HR is written as
where is the collision integral and Wk,k' the electron scattering probability from wavevector state k to k'.
Considering HSO as a small perturbation, it results that the spin relaxation times are much longer than the time needed for the momentum distribution to become isotropic: it is convenient thus to decompose the spin matrix density in the form [21]
where is the quasi-equilibrium component presenting uniform spin polarization (isotropic part of spin density matrix) and ρ'(k) is the non-equilibrium component (i.e. the anisotropic part of spin density matrix which satisfies ). The bar means here the averaging over the direction of k. Taking the k-average of equation (2) we obtain
Under the quasi-static limit (∂ρ'(k)/∂t) = 0, the anisotropic part of the density matrix should return to isotropy on a typical time corresponding to the momentum scattering time [24]. Keeping the first order of spin–orbit coupling term in the previous equation, we have
The solution in the 2D case is found by expanding HSO in terms of its Fourier components
where Hn(k) is the coefficient defined as
k is the in-plane wavevector considering the motion in the x–y plane, φ is the polar angle of the k vector with respect to the x-axis. The scattering time τn is then given as
in which θ = φ − φ' is the angle between k and k'. Now the angular average is obtained as
Then the components of the relaxation tensor Γ are found as
Recalling the Dresselhaus and Rashba contributions to the Hamiltonian of an electron in the CB of a 〈111〉-QW, the first and third order of Hamiltonians are written as:
in which the spin relaxation rates Γxx,Γyy,Γzz are given by
denoting k⊥ = (kx,ky,0) according to the natural axis orientations for 〈111〉 structures defined above and . Finally, the spin lifetimes for electrons in the non-degenerate regime are determined by performing the thermal average of the corresponding scattering rates [23]
in which the symbol means the thermal average. Cartoixà et al [13] have shown that
for a non-degenerate electron gas where τp is the transport mobility scattering time, ν is the energy dependent coefficient which depends on the scattering process when we assume an energy dependent scattering time τ∝Eν. The thermal wavevector is defined as where m*c is the electron effective mass, kB is the Boltzmann constant and T is the temperature.
Finally, the spin relaxation rates parallel and perpendicular to the growth direction are obtained as
with
It should be noted that τs∥ and τs⊥ are symmetric functions of the electric field centered nearby the compensation field Ep defined by αtot(Ep) = 0. In order to grasp the essential features of the model, it is convenient to recast the spin relaxation times in the more familiar Lorentzian form:
with
in which the subscript p denotes the peak value. The values of ν,τ1 and τ3 for different scattering mechanisms according to Kainz et al [25] are listed in the table 1.
Table 1. Characteristic exponent ν in the scattering time for different scattering mechanisms in a 2D electron gas [25].
| Scattering mechanism | ν | ||
|---|---|---|---|
| Type I: acoustic phonons (deformation potential), | |||
| optical phonons (deformation potential), | |||
| ionized impurities (screened), | |||
| neutral impurities, | |||
| alloy scattering, | |||
| interface roughness | 0 | 1 | |
| Type II: acoustic phonon (polar, piezoelectric), | |||
| optical phonon (polar) | 1 | ||
| Type III : ionized impurities, | |||
| (weakly screened) | 2 |
Several interesting features can be extracted from the modeled spin relaxation times. Firstly, for a given QW at a given temperature, the fitting parameters are the momentum scattering time τp, the collision coefficient ν with the respective scattering times τ1 and τ3 and finally the Dresselhaus (γ) and Rashba (a) coefficients. Equation (25) shows that the spin relaxation anisotropy at compensation can be used to determine the dominant scattering type in the structure. The exponent ν, characteristic of a class of scattering processes, being set, the compensation electric field Ep and the half width of the spin relaxation curves are solely function of γ/a for a given temperature. If an independent measurement of the Rashba term a is available, the momentum scattering time τp is fully determined without any mobility measurements.
4.2. Simulations
According to the fitting strategy detailed above, we first determine the dominant collision type in our structure. Figures 2(a) and (b), circles, present the measured spin relaxation time τs∥ along the z-axis at two different temperatures. Figures 2(c) and (d), squares, report the measured ratio τs∥/τs⊥. This value increases up to a maximum at compensation, determined by the cubic Dresselhaus terms and at both temperatures reaches values greater than 11/6. This suggests that the dominant scattering mechanism in our sample is of type I, allowing us to set ν = 0 6 and τ3/τ1 = 1, thus reducing the number of fitting parameters. By setting 〈k2z〉 = 2.5 × 1016 m−2 obtained in the framework of a finite QW barrier calculation [26]7, and taking a = 7e Å2 from [20], using τp and as only fitting parameters, we obtain: and . The corresponding values obtained for the momentum scattering times are τ10Kp = 6 ps and τ50Kp = 195 fs. This calculated are consistent with the values measured recently [20] by transient spin grating technique at T = 50 K in the same sample: . The simulations are in reasonably good agreement with the experimental results. We have also performed a second fitting procedure by fixing the Dresselhaus to Rashba coefficients ratio as measured in [20]. According to equation (24d), this fixes as well the compensation electric field value. However, a direct use of Ep has not allowed us to obtain a good fit to the data. These discrepancy is ascribed to the errors in the evaluation of the applied electric fields through the bias8. In order to decouple the evaluation of from possible electric fields errors, we have performed the second fitting procedure allowing the compensation field as fitting parameter. The results are reported in figures 2(a) and (b) as dashed lines and the corresponding values are: E10Kp = −57 kV cm−1, E50Kp = −60 kV cm−1, τ10Kp = 6 ps and τ50Kp = 163 fs.
The solid and dashed black lines in figures 2(c) and (d) report the calculated ratios τs⊥/τs∥ for both temperatures, respectively, for the two fitting procedures. The proposed models produce a reasonable agreement with the experimental data. Nevertheless, it is clear that the spin relaxation time ratio is greater than the maximum possible predicted by this model. This discrepancy is stronger at the higher temperature and the trend continues at T = 100 K (not shown). This indicates that different processes not considered in this model gain importance as the temperature increases producing a corresponding deviation from the model modifying the anisotropy ratio. The gray dotted line in figures 2(c) and (d) finally reproduces the calculated spin relaxation ratio τs∥/τs⊥ for both temperatures multiplied by a global constant factor C = 1.66. Interestingly, this simple phenomenological modification better reproduces the anisotropies and the electric field value at the isotropic point. We ascribe the observed discrepancies to the limitation of the model in which only a simple scattering model is taken into account and other spin relaxation processes are not considered such as the QW width and electric field fluctuations which could induce, respectively, spin relaxation through the spatial variation of the confinement energy [27] and produce an inhomogeneous Rashba contribution [28, 29]. Moreover, we have neglected the small piezoelectric field present at V = 0 due to the slight lattice mismatch between GaAs and Al0.3Ga0.7As.
Finally, we briefly discuss the model-predicted temperature and momentum scattering time dependence of the compensation and isotropic electric fields. Figure 3(a) reproduces the calculated temperature dependences of the spin relaxation times. Consistently with the increasing weight of the Dresselhaus cubic terms, a progressive decrease of the largest spin relaxation time is observed together with a decrease of the value of the compensation field and isotropic points. Despite the overall decrease of the maximum spin relaxation time attainable, the compensation field is however achieved at lower electric field values.
Figure 3. (a) Calculated temperature dependence of the spin relaxation times. Solid and dashed lines represent τs∥ and τs⊥, respectively. The parameters are taken from the fit at T = 10 K and extrapolated for higher temperatures according to the model. Momentum scattering times are, respectively, τp = 6, 0.2 and 0.2 ps. (b) Temperature dependence of the compensation (Ep) and isotropic (Ei) fields according to equation (26) for ν = 0. (c) The motional narrowing effect calculated for T = 10 K.
Download figure:
Standard image High-resolution imageAccording to the model described above, the isotropic electric field dependence on the temperature follows:
and the temperature dependence of Ei and Ep are reported in figure 3(b). A stronger temperature dependence is expected for Ei compared to Ep. No dependence on the momentum scattering time is however expected for both fields as represented in figure 3(c), where the increase of the spin relaxation time can be solely ascribed to the motional narrowing effect characteristic of the DP mechanism.
5. Conclusions
In conclusion, we have shown that the spin relaxation time anisotropy of the CB electron in (111)-oriented GaAs/AlGaAs QWs can be electrically controlled thanks to the interplay between the Dresselhaus and Rashba spin splitting. By varying the external bias, the anisotropy can be either canceled or inversed with respect to the unbiased case. We have shown that the particular electric field dependence is due to the cubic terms of the Dresselhaus contribution to the spin–orbit Hamiltonian which play an increasing important role either as the linear terms are compensated by the field induced Rashba one or as the temperature is increased. The control of the spin anisotropy at room temperature should be possible in narrower QW structures where the Dresselhaus linear terms remain dominant at higher temperatures.
Acknowledgments
We gratefully thank C Fontaine and A Arnoult for sample growth and technical support. We also acknowledge S Tarasenko and E Sherman for fruitful discussions. This work was supported by the France–China NSFC-ANR research project SPINMAN (grant number 10911130356), CAS grant number 2011T1J37, National Basic Research Program of China (2009CB930500) and National Science Foundation of China (grant numbers 10774183 and 10874212).
Footnotes
- 4
Strictly speaking this formula is valid only when τ1 = τ3 defined in equation (8), i.e. when the dominant scattering process is characterized by ν = 0. This turns out to be the case in this work: see full model later in the text.
- 5
- 6
We have checked that acoustic phonon, and still more optical phonon, scattering processes are not relevant for temperatures below 100 K since they lead to a at least one order of magnitude larger momentum scattering time τp. Being the QWs non-intentionally doped and relatively wide, we as well discard impurity and alloy scattering processes. As a consequence, the most likely scattering process is due to interface roughness.
- 7
For simplicity we have not taken into account possible variations of 〈k2z〉 with electric field.
- 8
The electric field value has been evaluated by the measurement of the quantum confined Stark effect.





![$[11\bar {2}],[\bar {1}10]$](https://content.cld.iop.org/journals/1367-2630/15/9/095016/revision1/nj476103ieqn2.gif)
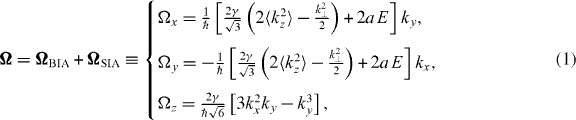
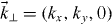
![$\boldsymbol {\Omega }\approx \boldsymbol {\Omega }^{(1)}=1/\hbar [ (2\gamma /\sqrt {3} )2\langle k_z^2\rangle +2aE ] (k_y,-k_x,0 )$](https://content.cld.iop.org/journals/1367-2630/15/9/095016/revision1/nj476103ieqn4.gif)