Abstract
TOI-216 is a pair of close-in planets with orbits deep in the 2:1 mean motion resonance. The inner Neptune-class planet (TOI-216b) is near 0.12 au (orbital period Pb ≃ 17 days) and has a substantial orbital eccentricity (eb ≃ 0.16) and large libration amplitude (Aψ ≃ 60°) in the resonance. The outer planet (TOI-216c) is a gas giant on a nearly circular orbit. We carry out N-body simulations of planet migration in a protoplanetary gas disk to explain the orbital configuration of TOI-216 planets. We find that TOI-216b's migration must have been halted near its current orbital radius to allow for a convergent migration of the two planets into the resonance. For the inferred damping-to-migration timescale ratio τe/τa ≃ 0.02, overstable librations in the resonance lead to a limit cycle with Aψ ≃ 80° and eb < 0.1. The system could have remained in this configuration for the greater part of the protoplanetary disk lifetime. If the gas disk was removed from inside out, this would have reduced the libration amplitude to Aψ ≃ 60° and boosted eb via the resonant interaction with TOI-216c. Our results suggest a relatively fast inner-disk removal (∼105 yr). Another means of explaining the large libration amplitude is stochastic stirring from a (turbulent) gas disk. For that to work, overstable librations would need to be suppressed, τe/τa ≃ 0.05, and very strong turbulent stirring (or some other source of large stochastic forcing) would need to overcome the damping effects of gas. Hydrodynamical simulations can be performed to test these models.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
TOI-216 hosts a pair of close-in exoplanets discovered by the Transiting Exoplanet Survey Satellite (TESS; Kipping et al.2019; Dawson et al. 2019, 2021; Table 1). The initial analysis confirmed two planets—an inner Neptune with a significant orbital eccentricity and an outer half-Jupiter—with orbits near 2:1 resonance. The physical characterization of the system was refined from stellar modeling, new transit observations, and radial velocity (RV) and transit timing variation (TTV) analysis. TOI-216 is a main-sequence K dwarf with mass M* = 0.77 M⊙ and a slightly substellar metallicity. The key characteristics of the planetary system are (i) mb = 0.059 MJup and mc = 0.56 MJup (<5% 1σ uncertainties), (ii) practically coplanar orbits, (iii) eb = 0.16 and ec < 0.01, and (iv) Pb = 17.097 days and Pc = 34.552 days. The two planets are firmly in 2:1 resonance, exhibiting resonant librations with the amplitude Aψ = 60° ± 2° (only 3% uncertainty, Figure 1; Dawson et al. 2021). The large resonant amplitude of the two planets in the resonance is therefore very well established.
Figure 1. (A) The resonant librations of TOI-216 (green; the red star marks the current orbits) with the resonance portrait in the background (Nesvorný & Vokrouhlický, 2016). (B) The resonant and near-resonant domains. TOI-216b and c are deep in 2:1 resonance (the posteriori sample from Dawson et al. 2021 is shown as red dots). Exoplanet orbits are more commonly found just wide of resonances (e.g., KOI-142 and TOI-2202). The orbital domain where the two orbits are just wide (or narrow) of the 2:1 resonance is indicated by (or ). See Section 2 and Nesvorný & Vokrouhlický (2016) for a definition of the resonant action Ψ, resonant angle ψ, and displacement from the resonance δ.
Download figure:
Standard image High-resolution imageTable 1. Parameters of the TOI-216 System from Dawson et al. (2021)
| Parameter | Value | Uncertainty |
|---|---|---|
| TOI-216 | ||
| M* (M⊙) | 0.77 | 0.03 |
| R* (R⊙) | 0.748 | 0.015 |
| Planet b | ||
| Mb (MJup) | 0.059 | 0.002 |
| Pb (day) | 17.0968 | 0.0007 |
| eb | 0.160 | 0.003 |
| ϖb (°) | 291.8 | 1.0 |
| λb (°) | 82.5 | 0.3 |
| Planet c | ||
| Mc (MJup) | 0.56 | 0.02 |
| Pc (day) | 34.5516 | 0.0003 |
| ec | 0.005 | 0.003 |
| ϖc (°) | 190 | 50 |
| λc (°) | 27.8 | 1.7 |
| 2:1 Resonance | ||
| Aψ (°) | 60 | 2 |
| Pψ (yr) | 4 | — |
| PΔϖ (yr) | 23 | — |
Note.
Osculating orbital elements are given at epoch BJD 2458325.3279. The three rows at the bottom are the resonant amplitude (Aψ ), period of resonant librations (Pψ ), and the circulation period of Δϖ = ϖb − ϖc (PΔϖ ). The periods were determined here from a numerical integration of the nominal solution (Figure 2)Download table as: ASCIITypeset image
Having such an accurate characterization of a fully resonant system of two exoplanets is rare. The classic GJ 876 RV system consists of four known planets, three of which are in a chaotic Laplace resonance (1:2:4; Marcy et al. 2001; Laughlin et al. 2005; Rivera et al. 2005, 2010; Nelson et al. 2016; Millholland et al. 2018). The Laplace resonance in GJ 876 was assembled by planetary migration in a protoplanetary gas disk (Snellgrove et al. 2001; Lee & Peale 2002; Crida et al. 2008; Delisle et al. 2012; Martí et al. 2013; Batygin et al. 2015; Dempsey & Nelson 2018). Definitive inferences about the disk properties, however, are difficult to obtain in this case (Cimerman et al. 2018). Most Kepler planets have nonresonant orbits. Kepler-9 is an iconic discovery of the Kepler mission (Holman et al. 2010). Here, the two planets—now thoroughly characterized from TTVs (Freudenthal et al. 2018)—are awkwardly placed near (but not in) the 2:1 resonance, in a domain where resonant librations exist (δ = 3.1 and Ψ = 5.7 in Figure 1(B), but outside the plotted range), a configuration that suggests additional perturbations (e.g., scattering).
Dawson et al. (2021) reported a preliminary dynamical analysis of TOI-216. They integrated a sample of best-fit solutions for 1 Myr and found them to be dynamically stable. Resonant capture was illustrated in two examples. In either of them, TOI-216c migrated inward using the user-defined force in the mercury6 integrator (Chambers et al. 1999). The radial migration of TOI-216b and eccentricity damping from disk torques were ignored. In the first example, TOI-216b was placed on an eccentric orbit before capture (eb = 0.08; roughly half of the present value), as needed for the planet to be captured with Aψ ∼ 60°. The resonant interaction with TOI-216c increased the orbital eccentricity of TOI-216b after capture. The migration torques on TOI-216c were then switched off, some ∼25,000 yr after the start of the integration, to obtain the final eccentricity eb ≃ 0.16. The second example in Dawson et al. (2021) invoked perturbations from an additional planet (approximated by an instantaneous change of TOI-216b's eccentricity vector). Dawson et al. (2021) also suggested that the small mutual inclination of TOI-216b's and c's orbits (iM ≃ 2°) could have been excited by the inclination 4:2 resonance.
Here we develop a new dynamical model to explain the main characteristics of the TOI-216 system (Section 2). Our model does not require special timing of the gas disk removal and/or additional planets. We suggest that TOI-216b was trapped near the transition to the inner, magnetorotational instability (MRI)-active zone of the protoplanetary disk (Flock et al. 2019) and waited for TOI-216c to migrate inward (Section 3). The 2:1 resonance between the two planets could have been established relatively early during the disk lifetime (Section 4). Our model includes eccentricity damping (Section 5) and provides constraints on the migration-to-damping timescale ratio (Section 6). We invoke overstable librations to generate the large libration amplitude in the resonance (Section 7). A relatively fast inside-out disk removal is proposed to boost TOI-216b's eccentricity to the observed value (Section 8). This represents an interesting constraint on the physical mechanism of the inner-disk dispersal. The influence of additional planets and turbulent stirring is discussed in Sections 9 and 10, respectively.
2. Resonant Dynamics and TTVs
To highlight the orbital resonance in the TOI-216 system, it is useful to project the planetary orbits onto the representative plane defined by parameters δ and (e.g., Nesvorný & Vokrouhlický 2016 Figure 1). The parameter δ, defined in Equation (23) in Nesvorný & Vokrouhlický (2016) as a function of orbital elements of two planets, is approximately preserved by resonant dynamics. It can roughly be thought of as the distance from the resonance. Away from the resonance, and if the orbital eccentricities are small, δ is related to the super-frequency (the inverse of the usual super-period): it increases, in the absolute value, as the system moves away from the resonance. Negative values of δ imply that the planetary orbits are spaced more widely than the actual resonance (P2/P1 > k/(k − 1), where P1 and P2 are the orbital periods of the inner and outer planets, and k = 2 for the 2:1 resonance). Large positive values of δ mean that the orbits are packed more tightly (P2/P1 < k/(k − 1)). 4
Resonant librations exist only for δ ≥ δ* = (27/32)1/3 ≃0.945 (Figure 1(B)). Inside the libration island, δ is a measure of planet eccentricities at the equilibrium point around which the system librates. Action Ψ and angle ψ are resonant variables. Angle ψ is a combination of the usual resonant angles σ1 = 2λ2 − λ1 − ϖ1 and σ2 = 2λ2 − λ1 − ϖ2, where λj and ϖj are the mean and periapse longitudes of the two planets. Whereas the libration (circulation) of σ1 and/or σ2 is in general a good indicator of the resonant (nonresonant) configuration of orbits, exceptions are known to exist (e.g., Petit et al. 2020). It is therefore more definitive to verify the behavior of ψ.
The representative plane is the same for any first-order resonance k:(k − 1) with k ≥ 2; only the mapping from the orbital elements to δ, Ψ, and ψ depends on k. All planet pairs in and/or near the first-order resonances can therefore be placed on it. This makes the representative plane particularly useful for a comparative analysis of resonant and near-resonant systems.
The present orbits of TOI-216 planets have δ = 2.1, Ψ = 2.8, and ψ = 220°, and this places them firmly in the 2:1 resonant island where ψ librates around 180° (Figure 1). We performed a short integration of TOI-216 orbits with swift_mvs (Levison & Duncan 1994) starting from the best-fit parameters reported in Dawson et al. (2021). The resonant amplitude of ψ is found to be Aψ ≃ 60°. The period of resonant librations is Pψ ≃ 4 yr. TOI-216b eccentricity shows resonant oscillations between 0.124 and 0.166. The periapse longitude difference, Δϖ = ϖb − ϖc, circulates in a retrograde sense with the period of Pϖ ≃ 23 yr (Figure 2).
Figure 2. The orbits of TOI-216 planets corresponding to the best-fit solution from Dawson et al. (2021). The resonant librations are highlighted in panel C. In panel D, we show Δϖ = ϖb − ϖc.
Download figure:
Standard image High-resolution imageThe resonant dynamics of the TOI-216 planets explains the measured TTVs (Dawson et al. 2021). According to Equation (2) in Nesvorný & Vokrouhlický (2016), the main TTV period should be equal to the libration period in the 2:1 resonance. From their Equation (38), for m1 ≪ m2, we have
where P1 = 17.1 days, Pτ ≃ 3.3 (Figure 8 in Nesvorný & Vokrouhlický 2016), m2/M* = 6.9 × 10−4, f = 1.19 (f is one of the two standard resonant coefficients in the disturbing function expansion, here for 2:1), and the resonant ratio of semimajor axes . This gives PTTV ≃3.3 yr, slightly shorter than the libration period measured from numerical integrations. The difference is caused by an approximation in Nesvorný & Vokrouhlický (2016), where only terms up to the first order in eccentricities are retained in the disturbing function. The actual TTV measurements reported in Dawson et al. (2021) covered just under 900 days, some 60% of the full TTV/libration period.
Similarly, for m1 ≪ m2, the TTV amplitudes of the two planets are
where AΨ is the amplitude of the resonant oscillations of action Ψ (zero for an exact resonance; Equation (6) in Nesvorný & Vokrouhlický 2016). For AΨ ∼ 0.7 (Figure 1(A)), this evaluates to A1 ∼ 2.0 days and A2 ∼ 0.35 days, or ∼6000 minutes and ∼1000 minutes for the full TTV range over the whole libration cycle. For comparison, the observed TTVs—measured from the incomplete libration cycle—are 4000 minutes and 700 minutes, respectively (Dawson et al. 2021).
3. Convergent Migration
The main goal of this work is to explain the orbital configuration of TOI-216 planets and to obtain useful constraints on the timescale of planet migration/damping and disk properties. Several conditions must be satisfied. First of all, the TOI-216 system almost certainly requires a convergent approach of planets into the 2:1 resonance. How the orbits converged is uncertain. The massive outer planet TOI-216c should have opened a deep gap in the gas disk (e.g., Crida et al.2006) and slowly migrated inward by type II migration (e.g., Kanagawa et al. 2018). The inner planet TOI-216b should have opened a shallower gap and migrated faster. In fact, the mass ratio of the two planets places them firmly in the regime of divergent migration (Kanagawa & Szuszkiewicz 2020). From this, we deduce that the TOI-216b migration must have been stalled near its current a1 ≃ 0.12 au to allow TOI-216c to catch up.
There are several possibilities. TOI-216b could have stopped near the truncation of the protoplanetary disk by its host star magnetosphere (e.g., Frank 1992). Strong positive corotation torques are expected at the magnetospheric cavity radius (Masset et al. 2006; Romanova et al. 2019; Ataiee & Kley 2021). The magnetospheric cavity radius is estimated to be at rc ∼ 0.05 au for M* = 1 M⊙, R* = 2 R⊙, B* = 1 kG, and yr−1, where B* is the stellar magnetic field strength and is the mass accretion rate (Bouvier et al. 2014, pp. 433–450). The cavity is expected to expand as the mass accretion rate decreases (e.g., Liu et al. 2017). Alternatively, as we argue in this study, TOI-216b could have stopped at the transition radius from the outer dead zone (DZ) to the inner MRI-active zone (e.g., Kretke & Lin 2012). We adopt a detailed model of the inner disk from Flock et al. (2019). The model matches interferometric observations of the inner edges of the disks around Herbig Ae/Be stars (Flock et al. 2016). In the nominal disk model for a solar-type star (Flock et al. 2019), the zero-torque radius—which acts as a barrier for migrating planets—is located at ≃0.12 au.
The disk model was constructed in Flock et al. (2019) by solving for a hydrostatic equilibrium of a passively irradiated disk around an early solar-type star. The turbulent gas viscosity ν was given by the usual α prescription: (Shakura & Sunyaev 1973), where cs is the sound speed and Ω is the orbital frequency. The internal energy and radiation field were obtained as a steady-state solution of the equations describing the heating, cooling, and flux-limited diffusion of the disk's thermal radiation. The gas opacity was derived from Malygin et al. (2014). The dust opacities were computed for a mixture of astrophysical silicate and graphite from Wolf & Voshchinnikov (2004). The model accounts for the sublimation of refractory grains close to the central star (Isella & Natta 2005) and computes the dust-to-gas ratio as a function of temperature and radially integrated optical depth. When the temperature exceeds TMRI ≃ 900 K, the disk is assumed to be ionized and MRI active (Desch & Turner 2015), with a boost to α (= αMRI). The outer dead zone with T < TMRI is characterized by a relatively low value of α (= αDZ).
Specifically, as a fiducial case for this study, we adopt the MREF disk from Flock et al. (2019). The MREF model uses the stellar temperature T* = 4300 K, radius R* = 2.6 R⊙ (as appropriate for a young solar-type star) and mass M* = 1.0 M⊙ to determine the stellar luminosity. The accretion-stress-to-pressure ratios, αMRI = 0.01 and αDZ = 0.001, are taken to model the disk in the inner MRI-active region and outer dead zone, respectively. The uniform mass accretion rate is set to yr−1. The most important feature of the MREF disk for this study is the surface density bump related to the change of α at the ionization transition (TMRI). The surface density bump produces a region of outward migration with a zero-torque radius on its outer edge. The zero-torque radius position mainly depends on the stellar luminosity.
We first consider the radial migration of TOI-216c. According to Kanagawa et al. (2015; also see Duffell & MacFadyen 2013; Fung et al. 2014), a massive planet opens a gap with the contrast of perturbed and unperturbed gas densities:
and
Here, Σgap is the surface density at the gap's bottom, Σ is the unperturbed background surface density (i.e., before the planet is introduced), q = mp/M* is the planet-to-star mass ratio, and h = H/r is the gas disk height over radius ratio. Numerically, for TOI-216c and Flock's MREF disk, we have qc = 6.9 ×10−4, h = 0.02 (appropriate for the current orbital radius of TOI-216c, r ≃ 0.19 au), and α = 10−3. This gives K = 1.5 × 105 and Σgap/Σ = 1.7 × 10−4. Clearly, TOI-216c is expected to open a deep gap in the gas disk and migrate inward in the type II regime.
Our understanding of type II migration is incomplete (e.g., Robert et al. 2018; Chrenko & Nesvorný 2020), but here we use equations from Kanagawa et al. (2018) to get a rough sense of TOI-216c's migration timescale. The point is not to rigidly tie our expectations to these results—and to the MREF disk from Flock et al. (2019)—but to establish a theoretical reference in one specific case. In the linear theory, the disk torque exerted on a planet is given as a sum of Lindblad and corotation torques (e.g., Paardekooper et al. 2010). To a factor of the order of unity, the migration timescale of a deep-gap-opening planet can be approximated as
Note that τa is defined such that τa > 0 (τa < 0) for inward (outward) migration. For TOI-216c, we have α = 10−3, h = 0.02, Σ = 3000 g cm−2 for r = 0.19 au from MREF, mc ≃ 0.56 MJup, P ≃ 35 days, and thus τa,2 ∼ 0.8 Myr (we fixed c = 2 in Equation (19) in Kanagawa et al. 2018). This shows that TOI-216c is expected to migrate on a megayear-long timescale when it reaches r = 0.19 au (the migration timescale would have been shorter at r ≫ 0.19 au as τa ∝ mp/Σr2). The MREF disk with yr−1 has a surface density at 1 au that is a factor of ∼2.5 below the minimum mass solar nebula (MMSN; Hayashi 1981). If TOI-216c formed early and migrated in a more massive disk than MREF, its initial migration could have been faster. These initial stages are not, however, of immediate concern here.
We now turn our attention to TOI-216b and first discuss its migration in the MREF disk's dead zone (r > 0.15 au). Adopting qb = 7.3 × 10−5, h = 0.02, and α = 10−3, we find K ∼ 1.7 × 10−3, suggesting that TOI-216b should have also opened a relatively deep gap (Σgap/Σ ∼ 0.014). Because, according to Equation (5), τa ∝ Mp in this regime, we find τa,1 ∼ 0.08 Myr. The migration timescale of TOI-216b is therefore an order of magnitude shorter than that of TOI-216c: the convergent migration cannot happen in this case. The same result is obtained for a wide range of smooth disk models. For example, for higher viscosities and/or larger scale heights, TOI-216b would not be capable of opening a gap in the gas disk. It would therefore migrate even faster by full type I torques. We conclude that the convergent migration of TOI-216b and c, which is needed for their capture into the 2:1 resonance, is difficult to obtain in a smooth disk.
Given the results discussed above, we find it likely that TOI-216b had arrived near its current orbital radius—either formed there or migrated from larger orbital radii—before the two planets were captured into the resonance. The radial migration of TOI-216b must have stopped near r = 0.12 au to allow for TOI-216c to catch up. The transition between the outer dead and inner MRI-active zones in disks from Flock et al. (2019) offers a plausible mechanism for achieving this. Here the steep rise of the surface density with the orbital radius produces a planet trap (Masset et al. 2006), where planets can be held in place by very strong positive torques (exceeding, by at least an order of magnitude, the negative torques in the outer smooth disk; Flock et al. 2019; see Schobert et al. 2019 for massive, viscously heated disk models). TOI-216b could have been trapped relatively early during the disk lifetime and waited for TOI-216c to move in.
In summary, the planet trap at the transition to the inner MRI-active disk region can generate favorable conditions for the convergent migration of TOI-216b and c and their subsequent capture in the resonance.
4. Resonant Capture
Once TOI-216b's migration stops (or at least considerably slows down), the two planets can be captured in 2:1 resonance. The capture is guaranteed if (i) the evolution into the resonance is sufficiently slow (adiabatic) and (ii) the orbital eccentricities are small. Mathematically, condition (i) requires that the time of resonance width crossing during migration, Δt, is longer than the libration period, Plib. Batygin (2015) computes
where τ1 and τ2 are the migration timescales of the two planets discussed in Section 3. For Plib/Δt < 1, we therefore have that (here we assumed that (τ1 − τ2)/τ1 τ2 ∼ 1/τ2; i.e., TOI-216b is trapped and nonmigrating), or τ2 ≳ 100 yr. This condition is easily satisfied for TOI-216c (we found τ2 ∼ 0.8 Myr in Section 3). We tested it numerically and found that the capture is guaranteed if τ2 ≥ 100 yr, but can often happen even if τ2 = 30–100 yr when the precapture inner planet's eccentricity is very low (e1 ∼ 0.001). If e1 ∼ 0.05, τ2 = 50 yr does not produce capture (even if the condition (ii) is satisfied).
As for (ii), as the parameter δ crosses δ* during migration (see Section 2), the area enclosed by the orbits in phase space of Ψ and ψ (adiabatic invariant) must be smaller than the area enclosed by the separatrix (which forms at δ = δ*; Henrard & Lemaitre 1983). For m1 ≪ m2 and e1 ≫ e2, this leads to a simple condition:
for q2 = qc (Goldreich & Schlichting 2014; Batygin 2015). This condition should be easily satisfied for TOI-216b if its orbital eccentricity is damped by gas. The stochastic forcing from turbulence in a gas disk is expected to excite e1 ∼ 0.01 (e.g., Nelson 2005). Once the resonant lock is established, it cannot be disrupted by turbulence (e.g., Adams et al. 2008; Rein 2012; Paardekooper et al. 2013; Batygin & Adams 2017).
We verified by numerical integrations that, indeed, the capture is guaranteed if e1 < 0.14. In fact, the above criterion is quite conservative, and there is a good chance of capture even if the eccentricity is above the critical limit. If e1 ∼ 0.1 before capture, the capture into resonance leads to a large, but not too large, libration amplitude that would be compatible with measured Aψ ≃ 60° (Dawson et al. 2021). With migration and without the eccentricity damping, which is the setup of the numerical simulations performed here, the resonant coupling to TOI-216c would lead to a very high eccentricity of TOI-216b and escape from the resonance. Some eccentricity damping is therefore needed to stabilize the orbits in the resonance (Sections 5 and 6). When the eccentricity damping is included, however, it is difficult to explain why the inner planet's eccentricity could have been so large before capture (Figure 3). Thus, invoking a large precapture eccentricity does not seem a particularly attractive means of explaining the TOI-216 system.
Figure 3. Capture in the 2:1 resonance with a large precapture eccentricity of TOI-216b. Here we set e1 = 0.16 at t = 0 (panel B; similar to the present eccentricity of TOI-216b), τa,2 = 105 yr, τe,1 = 5 × 103 yr, and p = 0 (Section 5), and let the two planets migrate into the resonance. For numerical convenience, the timescales used here are shorter, by a factor of ∼8, than the ones expected for the MREF disk (Section 3). The time of capture is fine-tuned such that TOI-216b's eccentricity is not damped too much before the capture happens. This generates an initial libration amplitude similar to that of the real system (panel C). The simulation is stopped when a1 ≃ 0.12 au and before the libration amplitude diminishes from damping effects. The special timing of capture—just after e1 is boosted by some process and before the disk is removed—is difficult to avoid in this case.
Download figure:
Standard image High-resolution imageWe notice that—if TOI-216c is placed beyond 0.25 au and migrated inward—TOI-216b is very often captured in 3:1 resonance. The capture is nearly certain for τa,2 ≳ 105 yr and eb = 0.001–0.1. Moreover, if a sufficiently strong eccentricity damping is included, eb reaches the equilibrium eccentricity (Section 6), and the TOI-216 planets end up surviving in the 3:1 resonance. Low eccentricities and short migration timescales could resolve this problem (e.g., e1 = 0.001 and τa,2 ≲ 5 × 104 yr), but we argued for τa,2 > 105 yr in Section 3. TOI-216c could have formed on a close-in orbit below the 3:1 resonance with TOI-216b, but this seems unlikely. Possibly the best solution to this problem hinges on the parameterization of the migration/damping torques. We numerically find that permanent 3:1 resonance capture only happens if the eccentricity damping is decoupled from the migration torques (the case with p = 0—see the next section). Resonant capture can be avoided if the eccentricity damping happens at a constant angular momentum (p = 1 in the next section). In that case, TOI-216b either avoids capture in 3:1 resonance or is released from the resonance shortly after capture via a dynamical process related to overstable librations (Section 7).
5. Parameterization of Disk Torques
The disk torques are usually implemented by adding the acceleration term
where r and v are the position and velocity vectors, vz is the z component of velocity, k is a unit vector along the z direction, and τi is the inclination damping timescale (not considered here). Using Lagrange equations, this can be written as
with p = 1. Subscripts 1 and 2 can be added here to indicate the inner and outer planets, respectively. The second term in Equation (9) appears because the radial force applied in the second term of Equation (8) conserves the angular momentum, , where G is the gravitational constant, M = M* + mp, and μ = M* mp/M. Thus, as the eccentricity is damped, the semimajor axis must decrease for L = const.
If p = 0 instead, which is the case considered in the previous section, the semimajor axis migration would be independent of eccentricity damping. It is not clear which of the functional forms best expresses the actual disk torques—this is something that needs to be addressed by hydrodynamical simulations. Here we investigate cases with 0 ≤ p ≤ 1. For p < 1, we simply compute the orbital elements of each planet at each time step, apply Equations (9) and (10), and return to the position and velocity vectors.
6. Equilibrium Eccentricity
In the 2:1 resonance, eb is expected to grow toward the equilibrium eccentricity, eeq, that depends on the differential migration rate of the two planets, 1/τa = 1/τa,2 − 1/τa,1, and the eccentricity-damping rate, 1/τe = 1/τe,1 + (m1/m2)/τe,2, where τe,j = −ej /(dej /dt) (e.g., Lee & Peale 2002; Goldreich & Schlichting 2014; Deck & Batygin 2015; Delisle et al. 2015; Terquem & Papaloizou 2019; τe,j > 0 corresponds to eccentricity damping). The second term in the expression for 1/τe can be ignored for TOI-216 as m1/m2 ≪ 1.
By balancing the disk and resonant torques, and assuming m1 ≪ m2, we find that the inner planet, if captured in the 2:1 resonance, should approach the equilibrium eccentricity of
(e.g., Goldreich & Schlichting 2014; τa > 0 and τe > 0 assumed here; i.e., convergent migration with damping). The equilibrium eccentricity thus mainly depends on
but there is also a dependence on p (Figure 4). For reference, to have eeq ≃ eb = 0.16, we would need τe /τa ≃ 0.05 for p = 0 or τe /τa ≃ 0.1 for p = 1 (i.e., the migration timescale would need to exceed the damping timescale by a factor ∼10–20).
Figure 4. The equilibrium eccentricities of TOI-216b inside the 2:1 resonance. Here we show the results for p = 0 and τa /τe = 10, 20, 40, 80, and 160 (black lines from top to bottom). In all cases we set m1 = 0 to be able to accurately compare the results with Equation (11), plotted as dashed lines here. The green line is an example with the real mass of TOI-216b and τa /τe = 20. The red line shows the result for p = 1, τa /τe = 160, and m1 = 0. The equilibrium eccentricity is a factor of smaller than for p = 0. This holds for any τa /τe . Thus, for example, the case with τa /τe = 40 and p = 0 is identical to the case with τa /τe = 20 and p = 1.
Download figure:
Standard image High-resolution image7. Overstable Librations
Ideally, we would like to invoke a situation with eeq ≃ eb =0.16. Unfortunately, for p = 1, the resonant librations with such a large eccentricity are unstable. The libration amplitude would increase beyond limits and the planets escape from the resonance (the so-called overstable librations; e.g., Goldreich & Schlichting 2014; Deck & Batygin 2015; Delisle et al. 2015). Our N-body integrations indicate that the escape timescale is extremely short once the overstable librations set in (<104 yr; Figure 5). One would therefore have to opportunistically remove the gas disk just at the right moment to end up with Aψ ≃ 60°. If p = 0 instead, and assuming eb ∼ 0 before capture, the libration amplitude is not excited (Figure 6)—the equilibrium point is stable in this case (Deck & Batygin 2015).
Figure 5. Capture in the 2:1 resonance with a small precapture eccentricity of TOI-216b, and p = 1. Here we set e1 = 0.01 at t = 0, τa,2 = 105 yr, τa,1 = −104 yr for a < 0.15 au, τe,1 = 103 yr, and let the two planets migrate into the resonance. This leads to e1 ≃ 0.16 shortly after capture, but the libration amplitude rapidly increases, and the orbits escape from the 2:1 resonance at t ≃ 16,500 yr. ACR in panel D stands for apsidal corotation resonance (Beaugé & Ferraz-Mello 1993). For numerical convenience, here we use shorter migration/damping timescales than the ones expected for the MREF disk (Section 3).
Download figure:
Standard image High-resolution imageFigure 6. Capture in the 2:1 resonance with a small precapture eccentricity of TOI-216b, and p = 0. Here we set e1 = 0.01 at t = 0, τa,2 = 105 yr, τa,1 = −104 yr for a < 0.15 au, τe,1 = 500 yr, and let the two planets migrate into the resonance. This eventually leads to e1 ≃ 0.16 and a very small libration amplitude. The periapse longitudes end up in the apsidal corotation resonance with Δϖ ≃ 0 (panel D; Beaugé & Ferraz-Mello 1993). Short migration/damping timescales are used here for numerical convenience.
Download figure:
Standard image High-resolution imageOverstable librations are a dynamical effect that have been first noted in studies of dust particle dynamics in exterior resonances with terrestrial planets (Beaugé & Ferraz-Mello 1994; Šidlichovský & Nesvorný 1994) and the tidal evolution of Saturn's satellites (Meyer & Wisdom 2008). When the Poynting–Robertson drag, tidal drag, or other generic drag/torque (Gomes 1995) is included in the equations of motion describing the resonant dynamics, the equilibrium point may become unstable. Whether the resonant equilibrium becomes unstable, and what the eventual fate of a resonant system is, depends on a number of parameters.
Goldreich & Schlichting (2014) examined this problem for a pair of resonant planets with m1 ≪ m2 and disk torques with p ≠ 0. They found that the 2:1 resonant equilibrium is stable if
where eeq is related to the migration and damping timescales via Equation (11) (coefficient f = 1.19 for 2:1; Nesvorný & Vokrouhlický 2016). For q2 = qb = 6.7 × 10−4 and p = 1, this gives the condition eeq ≲ e* = 0.06. If e* < eeq < 2e* instead, the resonant equilibrium is unstable, the libration amplitude increases, and the system eventually evolves onto a limit cycle with a fixed value of Aψ . Finally, for eeq > 2e* ≃ 0.12, the resonant amplitude should increase beyond limits and planets escape from the resonance (Goldreich & Schlichting 2014).
The analytic thresholds are only approximate because mb ≠ 0 (see Deck & Batygin 2015 for a generalization of these formulas to massive inner planets). For TOI-216 and p = 1, we numerically find that eeq > 0.09 leads to escape from the resonance; this value is smaller than the analytic limit, 2e* ≃ 0.12. In addition, whereas the analytic estimate suggests that the limit cycles should exist for e* < eeq < 2e* and any p > 0, it is difficult to numerically find them when p → 0. For example, p < 0.05 would be needed for e* ∼ eb = 0.16, but with p values this small, the transition from the stability to out-of-bounds growth of Aψ is razor sharp.
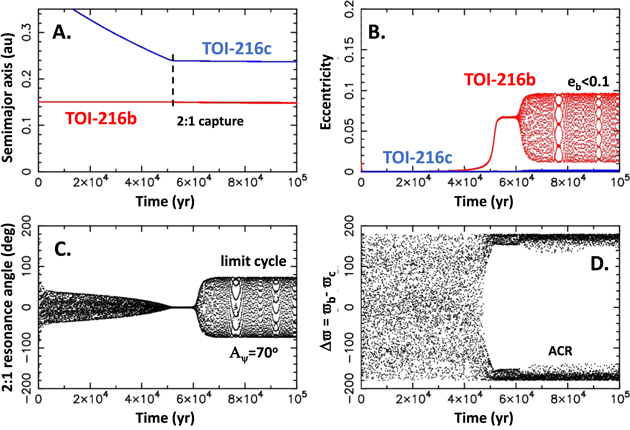
Figure 7 shows an interesting case where the two TOI-216 planets are captured into the resonance with Aψ ∼ 0 but then the overstable librations set in and lead to a limit cycle with Aψ ∼ 70°. The two planets could stay in this configuration almost indefinitely (as long as the disk conditions do not change). This is because TOI-216b is pushed in past the zero-torque radius where the strong positive torques on TOI-216b balance TOI-216c's migration torques (as long as the two planets are coupled via 2:1 resonance). For that to happen, from the angular momentum conservation, we have that
(weak eccentricity dependence ignored here). This gives τa,1/τa,2 ≃ −0.084. We therefore set τa,1/τa,2 = −0.084 in Figure 7. In reality, the system should have evolved to this equilibrium as the negative torque on TOI-216b increased when the planet was pushed farther past the zero-torque radius (Flock et al. 2019). We assume that the negative torques are strong enough such that TOI-216b cannot be pushed all the way into the inner cavity.
Figure 7. Capture into the 2:1 resonance with a small precapture eccentricity of TOI-216b, and p = 1. Here we set e1 = 0.01 at t = 0, τa,2 = 105 yr, τa,1 = −8,500 yr for a < 0.15 au, τe,1 = 150 yr. This leads to overstable librations and a limit cycle with e1 < 0.1 (panel B) and Aψ ≃ 70° (panel C). ACR in panel D stands for apsidal corotation resonance (Beaugé & Ferraz-Mello 1993). Short migration/damping timescales are used here for numerical convenience.
Download figure:
Standard image High-resolution imageWhereas the model shown in Figure 7 could provide an explanation for the observed resonant amplitude of the TOI-216 planets, it falls short in matching TOI-216b's large eccentricity (eb ≃ 0.16). This leads to the question of whether TOI-216b's eccentricity could have been excited when the gas disk was removed. Many additional simulations were performed here to investigate this problem. We tested the exponential disk dispersal at all radii, inside-out removal by the magnetospheric cavity expansion (Liu et al. 2017), and outside-in removal by photoevaporation (Alexander et al. 2014, pp. 475–496, as parameterized, e.g., in Ali-Dib & Petrovich 2020). These simulations show that only the inside-out removal provides the desired effect: as the disk torques on TOI-216b cease but TOI-216c continues to migrate inward, eb increases via resonant interaction with TOI-216c. This is the base of the dynamical model described in the next section.
8. Putting Things Together
The proposed orbital history of TOI-216b and c is shown in Figure 8. There are several stages. In stage A (time t < 1.27 Myr), TOI-216b moves to the zero-torque radius where it is held in place. In the model shown in Figure 8 we placed TOI-216b on an initial orbit with a1 = 0.15 au and e1 = 0.01 and let it migrate in to a1 = 0.13 au (this initial stage is difficult to see in Figure 8 because TOI-216b's migration is relatively fast), but the details of this do not matter. TOI-216b could have formed much farther out and reached 0.13 au after a long-range migration, or it could have formed at the pressure bump near the transition from the dead to MRI-active zones (Flock et al. 2019), where accumulating pebbles may trigger the streaming instability (Youdin & Goodman 2005). TOI-216b's migration would have been short range in the latter case because the pressure bump and zero-torque radii are close to each other in the MREF disk (Flock et al. 2019). TOI-216c was placed at 1 au and migrated inward with τa,2 = 0.8 Myr (Section 3) and τe,2 = τa,2/50 = 0.016 Myr (the results are not sensitive to τe,2).
Figure 8. The dynamical model for TOI-216 proposed in this work. The four stages, A–D, are described in the main text. Initially, TOI-216b (red line in panel A) was placed at 0.15 au and migrated to the zero-torque radius at 0.13 au (t < 0.05 Myr), while TOI-216c continued migrating inward (blue line; stage A). The two planets become locked in 2:1 resonance at time t ≃ 1.25 Myr after the start of the simulation, and overstable librations lead to a limit cycle with e1 < 0.1 (stage B). As the gas disk is removed from inside out just after t = 3 Myr, damping of TOI-216b's eccentricity ceases, but TOI-216c continues to migrate in (stage C). The resonant coupling lifts b's e to the observed value. The orbits of TOI-216b and c after the gas disk dispersal (stage D) are a good match to observations (cf. Figure 2).
Download figure:
Standard image High-resolution imageAs for the torques applied to TOI-216b, the zero-torque radius is placed at 0.13 au. For a1 < 0.13 au, we linearly ramp up the positive torque such that τa,1/τa,2 = −0.084 at r = 0.12 au. This is the expected orbital radius where the disk torques on TOI-216b and c should balance each other (Equation (14)). For ab > 0.13 au, we linearly increase the negative migration torque on TOI-216b until it reaches τa,1 = 0.08 Myr, roughly at 0.15 au, which is the migration timescale inferred for TOI-216b in a smooth disk (Section 3). The eccentricity-damping timescale is set to τe,1 = 0.02∣τa,1∣ (i.e., the damping timescale scales linearly with the amplitude of τa,1). The disk torques are parameterized by p = 1 (Section 5) such that the overstable librations can arise.
As TOI-216c migrates past a ≃ 0.27 au at t ≃ 1.07 Myr, the two planets are briefly captured in 3:1 resonance. Overstable librations set in and the orbits are almost immediately released. That is one of the reasons why we prefer p ≠ 0 (permanent capture in 3:1 resonance would happen for p = 0). The two planets become locked in 2:1 resonance at the beginning of stage B (t ≃ 1.27 Myr). As TOI-216c continues migrating inward, it pushes TOI-216b past the zero-torque radius into the region with strong positive migration torques. This leads to a1 ≃ 0.12 au, as anticipated from the design described above. Overstable librations set in immediately after capture and lead to a limit cycle with a large libration amplitude (Aψ ≃ 80°) and eb ≲ 0.1. This stage could last indefinitely as long as the disk conditions do not change; hence, no special timing needed. Here we assume that stage B lasts until t = 3 Myr, a time interval comparable to the typical disk lifetimes (2–5 Myr; Williams & Cieza 2011).
Then, during stage C, the gas disk is removed from the inside out (e.g., when the magnetospheric cavity expands; Liu et al. 2017 rebound not included). The principal disk torques on TOI-216b cease when the cavity moves past ≃0.12 au, but TOI-216c continues migrating in. This boosts eb during stage C. The initial (eI; at the beginning of stage C) and final (eF; at the end of stage C) eccentricities of TOI-216b are related by
where Δt is the duration of stage C (i.e., the time between disk removal at 0.12 au and 0.19 au; e.g., Malhotra 1995). With eI = 0.05, eF = 0.16, τa,2 = 0.8 Myr, we solve for Δt to estimate Δt ≃ 25,000 yr, which is the duration of stage C used in Figure 8.
Both TOI-216b and c migrate inward during stage C, but given its short duration, these changes are difficult to resolve on the scale of Figure 8 (TOI-216b moves from a1 ≃ 0.12 au to a1 ≃ 0.118 au). The libration amplitude slightly decreases (as the adiabatic invariant is conserved; Henrard & Lemaitre 1983). Finally, in stage D (t > 3.025 Myr), the disk cavity moves beyond 0.2 au, and the orbital configuration freezes in place. The semimajor axes of the two planets are a1 ≃ 0.118 au a2 ≃0.188 au, the libration amplitude is Aψ ≃ 60°, and the orbital eccentricity of TOI-216b oscillates between 0.14 and 0.19. The final orbits are an excellent match to observations (Dawson et al. 2021).
9. Were There More Inner Planets?
The model presented here has several advantages. It does not require additional planets. TTV and RV measurements do not reveal additional massive planets in the TOI-216 system, but the present limits are not too strong (Dawson et al. 2021). Hypothetical additional planets could have also been eliminated. Here we look into this possibility by investigating Kepler-class systems of super-Earths with np = 2, 3, and 4 inner planets. For simplicity, the inner planets are given masses mp = mb/np; that is, mp ≃ 9.4, 6.3, 4.7 MEarth for np = 2, 3, and 4, respectively. They are initially placed on nearly circular and nearly coplanar orbits between 0.15 and 0.5 au and migrate inward to produce resonant chains. The migration and damping torques are defined following the method described in the previous section. All collisions are assumed to be accretional. TOI-216c is placed on an outer orbit and migrated inward with τa,2 = 0.8 Myr.
Figure 9 shows a typical case for the system starting with three inner planets. After a series of resonant captures and instabilities, the three inner planets merge into a final planet with the mass identical to that of TOI-216b. TOI-216b and TOI-216c are then captured in 2:1 resonance where overstable librations set in and increase the resonant amplitude to ≃80°. TOI-216b's eccentricity shows oscillations reaching up to e ∼ 0.1 during this stage. The disk is removed after t = 3 Myr with Δt = 25,000 yr (the same as in the previous section), producing an eccentricity surge very similar to that shown in Figure 8. The final architecture of the model system is again a good match to TOI-216.
Figure 9. A dynamical model with three inner super-Earths. Three planets, each with mp = mb/3 ≃ 6.3 MEarth, were initially placed at 0.15, 0.3, and 0.4 au and migrated inward. This initial stage is difficult to see in the figure because the migration is relatively fast. By t = 50,000 yr after the start of the simulation the three planets settle in a stable resonant chain. The chain is destabilized as TOI-216c migrates in. First, the two middle planets collide near t = 0.87 Myr. Then, shortly after t = 1 Myr, TOI-216c is captured into 3:1 resonance with the middle planet. The resonance is short lived as overstable librations set in. The two inner planets are subsequently extracted from the resonance and merge, producing a final planet with the mass equal to that of TOI-216b. The following evolution is similar to that shown in Figure 8. The bottom panels show angular variables for the innermost planet and TOI-216c.
Download figure:
Standard image High-resolution imageThe cases with np = 2 and np = 4 produce the same dynamics with the inner planets merging and eventually forming a single, more massive inner planet, which is then captured into 2:1 resonance with TOI-216c. The final configuration of orbits is practically the same, independently of whether we start with one (previous section) or np = 2–4 inner planets. This demonstrates that TOI-216 may have initially hosted a Kepler-like system of super-Earth/mini-Neptunes. The system would have been destabilized when TOI-216c moved in, and the inner planets would have merged into what is now TOI-216b. The initial number of planets, their masses, and orbits are unknown, and our only constraint is that the total mass of the inner system was ∼18.8 MEarth, slightly exceeding that of Neptune. The TOI-216 system would be special because the massive TOI-216c formed and migrated all the way from its birth location to a < 0.2 au, whereas no such massive close-in planets affected the Kepler systems in general.
10. Stochastic Forcing
Here we investigate additional means of explaining the orbital configuration of TOI-216 planets. The turbulent stirring has been previously suggested to interfere with the capability of mean motion resonances to capture and retain Kepler-class planets in the resonant chains (e.g., Adams et al. 2008; Rein & Papaloizou 2009; Rein 2012; Paardekooper et al. 2013; Batygin & Adams 2017). The turbulent stirring arises when fluctuations within a turbulent disk produce a random gravitational field, which then affects the embedded planets (e.g., Laughlin et al. 2004; Nelson 2005). Here we adopt the analytic formulation from Okuzumi & Ormel (2013). In the limit of ideal MRI turbulence, the diffusion coefficients for a and e are estimated as
For our fiducial MREF disk, this evaluates to Da ≃ 3.5 ×10−13 au2 yr−1 and De ≃ 1.3 × 10−11 yr−1 for TOI-216b and Da ≃ 2.9 × 10−13 au2 yr−1 and De ≃ 4.0 × 10−12 yr−1 for TOI-216c. We adopted Σ = 3000 g cm−2, α = 0.01 for TOI-216b and α = 0.001 for TOI-216c. This choice is somewhat arbitrary because the α parameter changes with radial distance in our fiducial disk, and it is therefore not clear what effective α value should be used in Equations (16) and (17).
The stochastic forcing was implemented in the N-body integrator. We apply stochastic kicks in a and e once every Δt, where Δt < P1, P2, and adjust the amplitude of these changes such that the random walk in a and e—without damping/migration and mutual interaction between planets—reproduces the expected characteristics of diffusion (with Da and De given above). This should at least qualitatively replicate the diffusive evolution expected from the turbulent stirring. To separate the effects of turbulent stirring from those of overstability, all integrations reported here use p = 0 (Section 5). In this case, the resonance equilibrium is stable and the resonant amplitude, if excited by turbulence or other means, is expected to be reduced by the damping effects of gas. This means that the resonant amplitude can become large only if the turbulent stirring is strong enough to overcome the amplitude damping. We set τe /τa = 0.05 to generate e1 ≃ 0.16 via resonant interaction.
With the nominal diffusion coefficients reported above, the orbital evolution of the two planets is very similar to that without any stirring (e.g., Figure 6). If TOI-216c starts beyond 3:1 resonance with TOI-216b, the two planets become captured in 3:1 resonance with Aψ ≃ 0 and remain in resonance. If TOI-216c starts closer-in and does not cross the 3:1 resonance during migration, the two planets are captured in 2:1 resonance with Aψ ≃ 0. The nominal turbulent stirring is clearly not strong enough to produce any significant libration amplitude. We therefore test models in which the magnitude of stochastic forcing is increased. We believe that this is reasonable because the existing models of stochastic forcing in a protoplanetary disk are approximate. Hydrodynamical instabilities can generate large-scale motions of gas, which cannot be accurately represented with the Shakura–Sunyaev α prescription (e.g., Flock et al. 2017). For example, the Rossby instability at the inner edge of the dead zone can generate a vortex that would interact with TOI-216b.
Any detailed modeling of these effects is left for future work. Here we just ask, and answer, the question of how much stochastic forcing is needed to produce Aψ ∼ 60°. We use the numerical scheme described above and increase the diffusion coefficients by a constant factor, f > 1. Figure 10 shows the result for f = 400. In this case, the two planets are captured in 3:1 resonance for only a brief interval of time (near t = 1.05 Myr). The subsequent capture in 2:1 resonance is permanent. The libration immediately reaches Aψ > 40° due to the stochastic forcing and remains large during the whole disk lifetime. The disk is instantaneously removed at t = 3 Myr after the start of the simulation; the timescale or means of disk removal do not matter in this case. The final orbits of TOI-216b and c are a good match to observations, featuring e1 ≃ 0.16 and Aψ ≃ 60°. By testing different values of f we find that f > 100 is needed to avoid permanent capture in the 3:1 resonance and have a reasonable chance of ending up with Aψ ≃ 60° in 2:1 resonance.
Figure 10. A dynamical model with strong turbulent stirring. TOI-216b (red line in panel A) is held at the zero-torque radius and TOI-216c migrates in (blue line). The two planets become locked in 2:1 resonance at time t ≃ 1.25 Myr after the start of the simulation. The resonant amplitude increases to >40° due to the strong turbulent stirring applied to both planets (Section 10). The gas disk is instantaneously removed at t = 3 Myr; a more gradual disk removal would not change things as long as the stirring-to-damping strength remains the same (see discussion in the main text). The orbits of TOI-216b and c after the gas disk dispersal (t > 3 Myr) are a good match to observations.
Download figure:
Standard image High-resolution imageIt is not clear whether such a large boost to the nominal stochastic forcing can be justified. The effects of turbulence, as described in Okuzumi & Ormel (2013), are relatively weak in the MREF disk. To obtain f > 100, α would have to be increased by a factor of >100 or Σ would have to be increased by a factor of >10 (Equations (16) and (17)). None of these parameter choices is reasonable. If anything, the nonideal MRI effects and/or gap opening would reduce—not increase—the strength of turbulent stirring experienced by the two planets. TOI-216b's interaction with an inner vortex could be more promising (e.g., Faure & Nelson 2016). By switching different components of stochastic forcing on and off, we find that the diffusion in the semimajor axis of TOI-216b is mainly responsible for generating the large libration amplitude. Thus, the constraint obtained here can be formulated as Da > 3.5 × 10−11 au2 yr−1 for TOI-216b. Hydrodynamical simulation can be used to test whether such a large stochastic forcing is possible. 5
11. Discussion
We find that τe /τa ≃ 0.02 for p = 1 (Section 8) or τe /τa ≃ 0.05 for p = 0 (Section 10). From Equations (12) and (14), and ignoring factors ∼1, it can shown that this is equivalent to τe,1/τa,1 ≃ 0.02 or 0.05 in a smooth disk. In other words, the damping-to-migration timescale ratio is of the order of, or larger than, the disk aspect ratio (h = 0.02) in the reference protoplanetary disk used here (Flock et al. 2019). This constraint is obtained from analyzing the TOI-216 system in a regime where e > h. In the low-eccentricity regime with e < h, it is found from theory and hydrodynamical simulations that τe /τa ∼ h2 (Papaloizou & Larwood 2000; Cresswell et al. 2007). If this is applied to the TOI-216 system, it would be difficult to understand how the very strong eccentricity damping was overcome to generate e > h.
Some eccentricities could have been excited by the gravitational interaction between inner planets (Section 9 and Figure 9), but this would require that the eccentricity of TOI-216b was excited shortly before capture of TOI-216b and c into 2:1 resonance; it would otherwise be damped to very low values (see Figure 9). The τe /τa ∼ h2 scaling strictly applies only to small planets that do not open gaps in the gas disk, but TOI-216b is expected to open a gap (Section 3). The timescale of eccentricity damping for the gap-opening planets is not well understood. It is possible that damping is not as strong as in the type I migration regime. Once e > h, the eccentricity damping is expected to weaken as τe ∝ e2 (Papaloizou & Larwood 2000; Cresswell et al. 2007), which may be consistent with the constraint obtained here.
So far we discussed the cases with p = 0 and p = 1, with the former value being favored in the model with strong stochastic forcing (Section 10) and the latter value in the model with overstable librations (Sections 8 and 9). By testing 0 < p < 1, we found that a wide range of p-values works to generate the type of evolution shown in Figures 8 and 9, given that the τe /τa ratio is slightly adjusted in each case. But there are limits to that. For example, we find that p ≲ 0.05 is needed for stable librations with eeq ≃ 0.16, which would indicate a very weak coupling between e and a (Section 5). Although analytic limits from Goldreich & Schlichting (2014) suggest that the limit cycles with Aψ ≃ 60° should exist for these low values of p (Section 7), we do not find them numerically: the libration amplitude stays zero for p < 0.05 and grows beyond limits for p > 0.05. Also, given the problems with the permanent capture of TOI-216b and c in 3:1 resonance, we find that these very small values of p probably do not apply (except, perhaps, in the case with a very strong stochastic forcing; Section 10). For comparison, Tanaka & Ward (2004) found p ≃ 0.4 from their 3D disk model (e < h and no gap opening). If these results are applicable to TOI-216, this would favor the model with overstable librations and the fast inner-disk removal (Sections 8 and 9).
We adopted a number of simplifications in this work. The migration and damping torques, and their dependence on radius, as described in Section 8, were kept fixed for the whole integration interval (except for the final stages when the torques were removed). In reality, the torques should have been modified as the disk's surface density, scale height, and viscosity changed. This should not be a problem, however, as long as the TOI-216b and c evolved onto a limit cycle with Aψ ≃ 80° during the late stages. For example, if τe and τa were shorter initially, the two planets would have more rapidly moved into resonance, and if τe /τa ≃ 0.02, they would have more rapidly reached the limit cycle. The τe /τa ratio should have changed as well. The cases with two planets in 2:1 resonance, τe /τa > 0.02, and p = 1 would not work, because the resonance would be short lived (Section 7). The cases with τe /τa < 0.02 would work as long as τe /τa → 0.02 toward the end of the disk lifetime. If so, TOI-216b's eccentricity and the libration amplitude would more gradually increase during the disk lifetime. Similar considerations apply to the stochastic stirring model as well.
We adopted the MREF disk from Flock et al. (2019) and assumed that the zero-torque radius was at ≃0.13 au during the whole disk lifetime. This is unlikely to be realistic because the zero-torque radius is expected to move as the disk parameters change (Flock et al. 2016, 2019; Ueda et al. 2017). During the early disk stages, when the accretion rate and surface density were high, the MRI/DZ transition was likely located at larger orbital radii (due to the viscous heating; Schobert et al. 2019). If TOI-216b and c formed and migrated early, they could have been captured in 2:1 resonance early as well with the two planets way out beyond their present orbital radii. They would migrate in, as the disk cools down, with TOI-216b following the zero-torque radius. The effects of viscous heating decrease in importance for M⊙ yr−1 (Schobert et al. 2019) and can be ignored for M⊙ yr−1 (Flock et al. 2019). Thus, the situation should gradually approach the conditions investigated here (as decreased). Additional complications could arise from planetary mass loss/gain (Matsumoto & Ogihara 2020), tides (e.g., Lithwick & Wu 2012; Batygin & Morbidelli 2013), etc., but these effects do not seem important a priori for TOI-216.
There is a number of potentially complex hydrodynamical effects that we did not take into account in this work. If TOI-216b opened a gap in the gas disk near the zero-torque radius, this would influence the surface density profile in the region where Σ(r) rapidly changes with radius, and would feedback on torques experienced by TOI-216b. Would the planet trap at the MRI/DZ transition be strong enough to hold TOI-216b in place (Ataiee & Kley 2021)? When TOI-216b evolved onto a large-eccentricity orbit near the inner disk's edge, it would move—when following the orbit between the pericenter and apocenter—in a radial interval where the disk properties abruptly change. How would the migration/damping work in this situation (e.g., Ogihara et al. 2010)? Moreover, TOI-216c could have opened a very wide gap, which, at least in some situations, could have reached all the way down to TOI-216b (once the two planets moved onto the close-in orbits in 2:1 resonance). Would this create favorable conditions for the formation of the present orbital architecture of the TOI-216 planets, or could these cases be ruled out? Hydrodynamical studies will be needed to answer these questions, and this is left for future work (Figure 11).
Figure 11. (A) The vertical structure of the inner protoplanetary disk obtained with Fargo3D (Benítez-Llambay & Masset 2016). In this preliminary simulation, we reproduce the MREF disk structure from Flock et al. (2019). To this end, we modified Fargo3D to solve the hydrostatic radiation-hydrodynamics (RHD) equations in the radial and vertical directions (no azimuthal cells, no viscous heating). The disk viscosity was given by the usual α prescription (Shakura & Sunyaev 1973) with αMRI = 0.01 in the inner MRI-active zone and αDZ = 0.001 in the outer dead zone. The α transition was set at TMRI = 900 K (Desch & Turner 2015), with the temperature being self-consistently computed in the code. The disk structure features a hot dust halo inside of the inner rim at 0.06 au, a curved dust rim between 0.06 and 0.1 au, a small shadowed region at 0.1–0.2 au, and a flared disk beyond 0.2 au. The white and blue lines in (A) are the silicate sublimation front and optical depth τ = 2/3 for the starlight irradiation. (B) TOI-216b and c open gaps and migrate—here in a locally isothermal 2D disk, α = 0.01 for r < 0.1 au and α = 0.001 for r > 0.1 au. The simulation with hydrodynamic Fargo3D was run over 105 periods of the inner planet.
Download figure:
Standard image High-resolution imageWe also need to clarify a few things about the constraint on the inner-disk removal timescale, Δt ∼ 25,000 yr, in the model with overstable librations. Strictly speaking, this constraint is tied to the migration timescale of TOI-216c at the time of the gas disk dispersal, which depends on α, h, and Σ via Equation (5). Here we opted for α = 10−3, h = 0.02, and Σ, as appropriate for the MREF disk model from Flock et al. (2019) ( M⊙ yr−1), which gives τa,2 ≃ 0.8 Myr (Section 3). The TOI-216 constraint therefore implies Δt/τa,2 ∼ 0.03. So, for example, if the accretion rate (and surface density) was 10 times lower at the time of the inner-disk removal, which is a factor of ∼25 lower than the MMSN (at 1 au), with everything else being the same, this would imply Δt ∼ 250,000 yr. We quote an intermediate value, Δt ∼ 105 yr, in the abstract. It is also possible that α in the dead zone was significantly lower than the one adopted here. This may formally not have a large effect on τa,2, as 1/τa,2 ∝ αΣ (Equation (5)) and Σ ∝ 1/α; the α dependence thus cancels out for fixed . For fixed Σ (e.g., the disk wind model; Suzuki et al. 2010; Bai & Stone 2013; Simon et al. 2013), τa,2 ∝ 1/α instead. The migration of gap-opening planets in very low-viscosity disks (α ≲ 10−5) is complex and poorly understood (e.g., Lega et al. 2021).
In the model described in Sections 8 and 9, the disk needs to be removed from inside out such as the migration/damping torques are first removed from TOI-216b and then, after Δt, from TOI-216c. The magnetospheric cavity expansion during the late stages of the disk evolution (e.g., Liu et al. 2017) could be responsible for this. Alternatively, TOI-216c could have carved a deep gap in the disk and cut the supply of gas from >0.2 to <0.2 au. The inner disk would then be removed on the viscous timescale (Crida & Morbidelli 2007):
For a = 0.12 au, α = 0.001, and h = H/a = 0.02, we obtain τα ∼ 40,000 yr. This means that the inner disk could be removed very quickly. In summary, the reduction of the inflowing gas material from the outer disk regions by TOI-216c should lead to a relatively fast inner-disk depletion (e.g., Tanigawa & Tanaka 2016). For things to work, however, the migration of TOI-216c would have to stop as well, and it is not clear whether this is the case because TOI-216c would still feel torques from the outer disk.
It has been established that the TOI-216 planets are not in the apsidal corotation resonance (Figure 2; ACR, see Beaugé & Ferraz-Mello 1993 and Hadden & Payne 2020 for context). Instead, the periapse longitude difference, Δϖ = ϖb − ϖc, circulates with the period of PΔϖ ≃ 23 yr. This may seem surprising because simple capture in the resonance should lead to ACR locking. The examples of our model with overstable librations shown in Figures 8 and 9 do not end up in ACR, but we were unable to tune things up well enough to replicate the observed behavior of Δϖ. This happens because the eccentricity of TOI-216c ends up too low and ϖ2 has a fast and nonuniform precession. There is no source of excitation of ec in this model other than the resonant interaction with TOI-216b. Here we ignored the apsidal precession of the two planets from the gas disk (e.g., Ali-Dib & Petrovich 2020). We tested the influence of the disk potential using the scheme described in Vokrouhlický & Nesvorný (2019) and found that it does not change things, because the inner disk in the MREF model has a relatively low mass. The eccentricity of TOI-216c is excited in the model with the strong stochastic forcing (Figure 10). The final precession of ϖ1 − ϖ2 in this model is a good match to observations.
12. Conclusions
The main results obtained in this work are as follows.
- 1.TOI-216 is a system of two planets: the inner Neptune-class planet with the orbital period P ≃ 17 days and outer half-Jupiter on a nearly circular orbit (Dawson et al. 2021). The observed TTVs are caused by the dynamical interaction of the two planets in 2:1 resonance. The full TTV amplitudes, once the observations will cover the whole libration cycle, are expected to be ∼6000 minutes for TOI-216b (4.2 days or 24% of the orbital period!) and ∼1000 minutes for TOI-216c.
- 2.We developed a dynamical model for the capture of TOI-216 planets in 2:1 resonance. To reach resonance, TOI-216b must have waited near the inner edge of the disk—possibly near the zero-torque radius at the transition from the outer dead to inner MRI-active zones (Flock et al. 2019). Alternatively, it could have been held in place by the one-sided torques at the magnetospheric cavity radius (e.g., Romanova et al. 2019).
- 3.Once TOI-216b's migration was stalled, the two planets could have been captured into 2:1 resonance. For the disk parameters adopted here, the capture is certain. With the two planets in resonance, the main challenge is to explain the large eccentricity of TOI-216b (eb = 0.16) and large libration amplitude (Aψ ≃ 60°), without invoking special circumstances.
- 4.In resonance, the migrating TOI-216c pushed TOI-216b inside the zero-torque radius where the strong positive torques on TOI-216b compensated for TOI-216c's migration and held the two planets in place. For τe /τa ≃ 0.02, the resonant interaction of planets would lead to a limit cycle with e1 < 0.1 and Aψ ≃ 80° (for the nominal parameterization of torques with p = 1; Section 5). The system could have remained in this configuration for the greater part of the protoplanetary disk lifetime.
- 5.Then, if the inner disk was removed from inside out on a timescale Δt ∼ 0.03τa,2 ( ∼105 yr for the migration timescales of TOI-216c considered here), TOI-216b's eccentricity was boosted to the observed value and Aψ slightly decreased (due to the adiabatic invariant conservation). The final configuration obtained in the model matches the observed orbital properties of the TOI-216 system.
- 6.If there was a Kepler-like system of inner super-Earths/mini-Neptunes around TOI-216, it would have been destroyed by the migrating TOI-216c. The inner planets would have merged into a single planet—TOI-216b. The subsequent evolution of TOI-216b and c in 2:1 resonance would be similar to that discussed for a pair of planets above.
- 7.The model with strong stochastic stirring is an interesting alternative to overstable librations. In this model, the overstable librations would need to be suppressed (p ≃ 0), and τe /τa ≃ 0.05. To obtain Aψ ≃ 60°, however, the stochastic diffusion would have to exceed, by at least two orders of magnitude, the one expected from the nominal turbulent stirring (Okuzumi & Ormel 2013). This could be potentially accomplished if TOI-216b interacted with an inner vortex (e.g., Faure & Nelson 2016),
- 8.Hydrodynamical simulations can be performed to test these models. The first question to ask is whether p ≃ 0 (i.e., the semimajor axis migration and eccentricity damping are independent of each other; Equations (9) and (10)), which would favor the stochastic stirring model, or p > 0.05, which would favor the model with overstable librations (for p = 1, the eccentricity damping would happen at constant angular momentum; Section 5).
While interesting in its own right, the TOI-216 system may play an important role as a means of placing much-needed constraints on the nature of protoplanetary disks and their interaction with planets. Other resonant and near-resonant exoplanet pairs of interest include KOI-1599 (Panichi et al. 2019), Kepler-88 (Nesvorný et al. 2013; Barros et al. 2014), K2-19 (Petigura et al. 2020; Petit et al. 2020), K2-146 (Hamann et al. 2019), TOI-2202 (Trifonov et al. 2021), and HD 45364 (Hadden & Payne 2020). The results obtained here can also be placed in the context of resonant and near-resonant planet chains, including Kepler-11 (Lissauer et al. 2011, 2013), Kepler-60 (Goździewski et al. 2016), Kepler-80 (MacDonald et al. 2016), Kepler-223 (Mills et al. 2016), Kepler-444 (Campante et al. 2015; Papaloizou 2016; Mills & Fabrycky 2017), K2-32 (Heller et al. 2019), K2-138 (Christiansen et al. 2018; Lopez et al. 2019), TOI-178 (Leleu et al. 2021), and TRAPPIST-1 (Gillon et al. 2017; Luger et al. 2017; Ormel et al. 2017; Delrez et al. 2018; Grimm et al. 2018; Agol et al. 2021), and close-in systems of Kepler planets in general (Fabrycky et al. 2014; Winn & Fabrycky 2015; Zhu & Dong 2021).
This work was supported by NASA's XRP program. The work of O.C. was supported by the Czech Science Foundation (grant No. 21-23067M), the Charles University Research program (grant No. UNCE/SCI/023), and the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID:90140). M.F. acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (grant agreement No. 757957). We thank Bekki Dawson for discussions.
Footnotes
- 4
Indices 1 and 2 are used to indicate parameters of the inner and outer planets, respectively. They are interchangeable with indices b and c wherever the text is specific to the TOI-216 system.
- 5
Alternatively, one could consider a case with very weak amplitude damping (i.e., large τe ), but that would probably imply, with τe /τa = 0.05, unrealistically long migration timescales.