Abstract
We study the Lagrange stability in the spatial elliptic restricted three-body problem. In this study, we essentially use the boundedness of the motion of a small particle with respect to planar coordinates and show that this plays a key role in ensuring the boundedness of the motion in the spatial case. As a result, we obtain the Lagrange stability theorem for an infinitely small particle in the spatial elliptic restricted three-body problem. The proposed approach can then be extended to the case of the general three-body problem.
Export citation and abstract BibTeX RIS
1. Introduction
The restricted three-body problem (for mass points), being simple in its formulation under the assumption that the mass of one of these points is negligibly small with respect to the masses of the other two points (Szebehely 1967; Roy 1978), remains to be relevant until now because it is used in solving many practical problems of celestial mechanics (Szebehely 1967; Makó & Szenkovits 2004; Makó 2005; Georgakarakos 2008; Voyatzis et al. 2012; Makó 2014; Gong & Li 2015). In particular, in the framework of the space exploration program, such systems as Earth–Moon–spacecraft, Sun–Earth–Moon, Sun–Jupiter–asteroid, etc., are usually considered as cases of the restricted three-body problem. This approach gives the possibility of obtaining quantitative results more simply with the use computer modeling and, as it is proved by longtime experience, representing quite accurately the key qualitative features of the movement of bodies.
As it is known, in the case where the restricted problem is circular and, as a consequence, it has the first integral (the Jacobi integral), Hill (1878) succeeded to prove the existence of bounded motions of a small particle provided that the level constant h of the Jacobi integral is negative and 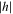 exceeds a certain critical value
exceeds a certain critical value  . In particular, the region of possible motions of an infinitesimally small particle in this case can be represented as the union of a region
. In particular, the region of possible motions of an infinitesimally small particle in this case can be represented as the union of a region  of motions bounded in coordinates (Hill domain) and a region
of motions bounded in coordinates (Hill domain) and a region 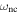 of motions bounded in velocities, i.e.,
of motions bounded in velocities, i.e., 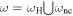 and, additionally,
and, additionally,  .
.
As it was shown recently by Sosnitskii (2018), in the case of the spatially restricted circular problem, if h is negative and the absolute value of h is sufficiently large and 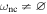 , the motions of a small particle in the region ωnc are Lagrange stable. In this paper, we prove the Lagrange stability in the case of the spatial elliptic restricted problem under the condition that the motion is distal, i.e., the distances from the small particle to massive bodies are bounded from below.
, the motions of a small particle in the region ωnc are Lagrange stable. In this paper, we prove the Lagrange stability in the case of the spatial elliptic restricted problem under the condition that the motion is distal, i.e., the distances from the small particle to massive bodies are bounded from below.
2. Equations of the Motion in the Elliptic Restricted Three-body Problem
Thus, we consider the case of the restricted three-body problem where vectors 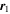 and
and  , being solutions of the two-body problem, correspond to elliptical orbits of points with masses m1 and m2. Passing further to the relative lengths of the vectors and considering equations of the restricted problem as a special case of equations for the general three-body problem (Sosnitskii 2008), we obtain
, being solutions of the two-body problem, correspond to elliptical orbits of points with masses m1 and m2. Passing further to the relative lengths of the vectors and considering equations of the restricted problem as a special case of equations for the general three-body problem (Sosnitskii 2008), we obtain
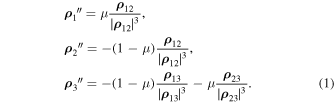
Here, 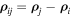

 , where r0 is a constant parameter having the dimension of a unit of length; the prime sign means differentiation with respect to the dimensionless time
, where r0 is a constant parameter having the dimension of a unit of length; the prime sign means differentiation with respect to the dimensionless time
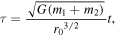
where 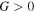 is the gravitational constant, and
is the gravitational constant, and
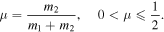
System (1) can be also represented in the form
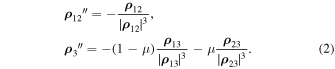
The systems of Equations (1) and (2) are referred to the inertial reference system with the origin at the center of mass of two massive bodies. In particular, if 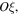
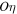 , and
, and  are axes of this coordinate system, then we assume that
are axes of this coordinate system, then we assume that 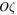 is perpendicular to the plane of rotation of two massive bodies.
is perpendicular to the plane of rotation of two massive bodies.
In the reference frame under consideration, let 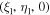 and
and 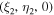 be coordinates of bodies with masses
be coordinates of bodies with masses  and μ, respectively, and let
and μ, respectively, and let  be coordinates of a small particle. Then the third vector equation of system (1) can be rewritten in the form
be coordinates of a small particle. Then the third vector equation of system (1) can be rewritten in the form

where
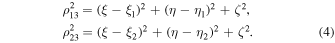
In addition to the inertial coordinate system, we introduce an auxiliary moving coordinate system with its origin located at the center of mass of the pair  and its two axes
and its two axes  oriented along the directions of the vectors
oriented along the directions of the vectors  and
and 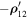 belonging to the plane of rotation of massive bodies. The third axis Oz is chosen to be perpendicular to this plane, and, therefore, the axes
belonging to the plane of rotation of massive bodies. The third axis Oz is chosen to be perpendicular to this plane, and, therefore, the axes 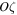 and Oz coincide.
and Oz coincide.
Let us consider
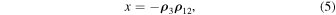
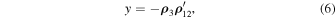
where 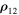 and
and 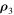 are solutions of system (2), and
are solutions of system (2), and  and
and 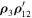 are dot products. As it was shown in Sosnitskii (2017), the quantities x and y can be treated, from a generalized viewpoint, as projections of the vector
are dot products. As it was shown in Sosnitskii (2017), the quantities x and y can be treated, from a generalized viewpoint, as projections of the vector 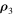 onto Ox- and Oy-axes, respectively, in the chosen moving reference frame that belong to the plane of rotation of the pair of massive bodies.
onto Ox- and Oy-axes, respectively, in the chosen moving reference frame that belong to the plane of rotation of the pair of massive bodies.
Differentiating equalities in Equations (5) and (6), we obtain the following pair of equations:
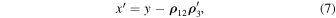
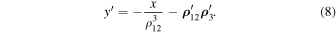
Further, differentiating Equation (7), we obtain
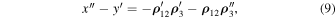
whence, taking into account Equation (8), we have
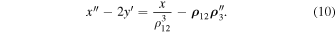
Equations (8) and (10) will be used in our study in what follows.
Let us establish a number of useful relations implied by equalities (5) and (6). In particular, in view of equality (6), we have

Similarly,
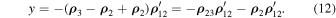
Observing that
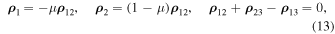
instead of Equations (11) and (12) we obtain
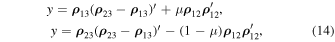
whence
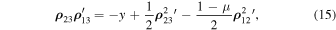
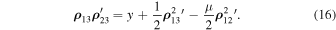
In accordance with Sosnitskii (2017), we have the relation

Also, a similar equality is true for the generalized velocities:
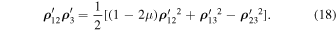
Further, due to equality (5), we can represent equality (17) in the form
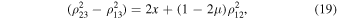
where 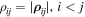 (
( ). Having obtained Equations (15), (16), and (19), we also have
). Having obtained Equations (15), (16), and (19), we also have
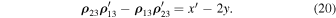
It is worth noting that we have arrived at a similar equality in a more complicated way in the case of the circular restricted problem.
Let us derive additionally a number of important equalities that will be similar to those already known for the circular restricted three-body problem.
On the base of the equality
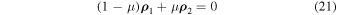
we obtain
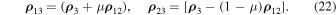
Similarly,
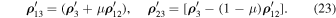
Due to Equation (22) we yield
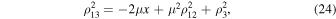
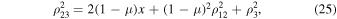
and this implies
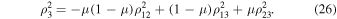
Setting  in Equations (24) and (25), we arrive at equalities valid in the circular restricted problem.
in Equations (24) and (25), we arrive at equalities valid in the circular restricted problem.
In view of Equation (23), we have the following analogues of equalities (24) and (25), which are related to the generalized velocities 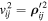 and
and 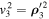 :
:
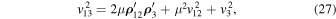
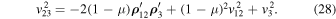
This implies
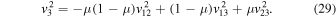
Taking into account the obtained equalities, the distance equations for the elliptic restricted problem, which were previously used by Sosnitskii (2017), can be represented in the form

where
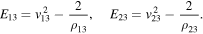
3. Theorem on the Lagrange Stability of the Motion
Lemma. If in the spatial elliptic restricted three-body problem a motion of the system determined by Equation (1) satisfies the distal condition
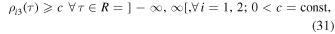
then the motion is bounded in coordinates x and y determined by equalities (5) and (6).
The proof is the same as in the case of Theorems 1 and 2 in Sosnitskii (2017) and follows immediately from the definition of projection of a vector onto a direction.
As a consequence of the lemma, we obtain the boundedness of the motion of a small particle along the coordinates ξ and η in the inertial reference frame.
Theorem 1. If in the spatial restricted elliptic three-body problem the motion of an infinitesimal particle determined by Equation (1) satisfies the distality condition in Equation (31) and 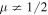 , then the motion is Lagrange stable, i.e.,
, then the motion is Lagrange stable, i.e.,
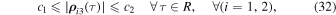
where c1 and c2 are positive constants.
Proof. Using equalities (22), (24) and (25), we rewrite the second equation of system (2) in the form
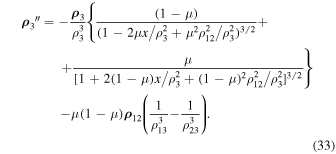
Suppose now that under the conditions of the theorem the considered motion is not bounded. Then there is a sequence 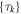 ,
,  , such that
, such that
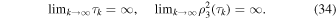
Passing over to the limit, in view of Equation (33) and the lemma, we arrive at the two-body problem where the motion of an infinitesimal particle corresponds to a hyperbolic or parabolic orbit.
In accordance with the lemma, the motion of a small particle is bounded in coordinates x and y. Therefore, in the inertial reference frame, this motion occurs within a certain cylindrical surface with a bounded directrix located in the plane of rotation of two massive bodies and a generatrix parallel to the 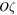 -axis. Each of the orbits, both hyperbolic and parabolic, are not bounded in two-dimensions (coordinates). Consequently, none of these orbits can be immersed in the mentioned cylindrical surface, except for the cases where they degenerate, respectively, into a rectilinear hyperbola and a rectilinear parabola, which are parallel to the
-axis. Each of the orbits, both hyperbolic and parabolic, are not bounded in two-dimensions (coordinates). Consequently, none of these orbits can be immersed in the mentioned cylindrical surface, except for the cases where they degenerate, respectively, into a rectilinear hyperbola and a rectilinear parabola, which are parallel to the 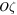 -axis. However, it is easy to show that this is impossible in the case where
-axis. However, it is easy to show that this is impossible in the case where 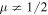 .
.
If the orbit of a small particle is rectilinear and parallel to the 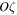 -axis, then the following equalities hold:
-axis, then the following equalities hold: 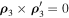 and
and  . Due to the latter, we obtain
. Due to the latter, we obtain
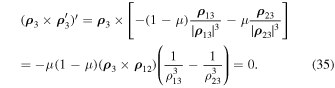
In accordance with Equation (35), we have satisfied at least one of the equalities
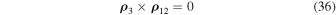
and
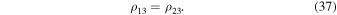
If equality (36) holds, then the small particle belongs to the straight line formed by the pair 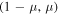 . Therefore, in this case, since the directrix of the cylindrical surface is bounded, the modulus of the radius vector
. Therefore, in this case, since the directrix of the cylindrical surface is bounded, the modulus of the radius vector 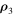 of the small particle is also bounded.
of the small particle is also bounded.
Now, let 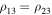 . We are going to show that the motion of system (1) is bounded in this case. To this end, we consider Equation (10) and rewrite it in the form
. We are going to show that the motion of system (1) is bounded in this case. To this end, we consider Equation (10) and rewrite it in the form
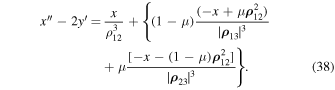
In accordance with Equation (19), we have
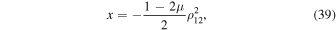
and this implies
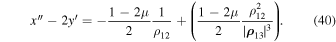
Suppose on the contrary that the considered motion for 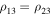 is not bounded. Then there exists a sequence
is not bounded. Then there exists a sequence  ,
,  , for which Equation (34) holds and, therefore, in accordance with Equation (40) (due to
, for which Equation (34) holds and, therefore, in accordance with Equation (40) (due to  ), one can find a sufficiently large number s for
), one can find a sufficiently large number s for 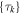 such that the following inequality holds for
such that the following inequality holds for  :
:

According to the conditions of Theorem 1, the considered motion is distal, and, therefore, the velocities in system (1) are bounded. It is the boundedness of the velocities that allows us to pass over from inequality in Equation (41), which is valid for a sequence of points, to the inequality
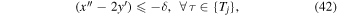
where  denotes a sequence of time intervals of the form
denotes a sequence of time intervals of the form
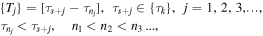
that grow in length. Following the scheme of the proof of Lemma 2 from Sosnitskii (2018), we arrive at the conclusion that the motion is bounded. Thus, Theorem 1 is proved. 
As we can see, key points in the proof of Theorem 1 are the boundedness of the motion of a small particle relative to a pair of plane coordinates, and the fact that the unboundedness is possibly determined only by the spatial coordinate ζ. Thus, if we have a possibility for the unboundedness of the motion in the case under consideration, then it is one-dimensional. On the other hand, assuming that the motion is unbounded, we arrive at two-dimensional unboundedness. It is the difference in dimensions of these unboundedness that allowed us to conclude that Theorem 1 is valid.
When proving the boundedness of motions in the framework of Theorem 1, in contrast to the works of other authors who investigated the boundedness using analytical methods (see, for example, Makó & Szenkovits 2004; Makó 2005; Gong & Li 2015), we do not use the Jacobi function (time-dependent Jacobi integral) or an invariant relation in the terminology by Szebehely (1967), but we find a new source in the depths of the elliptic restricted problem, which is more suitable for solving the problem under consideration. This is what makes our approach special.
If we take into account the work of Sosnitskii (2019), then it is quite obvious that the proposed approach is applicable to the general case of the three-body problem, which is considered in the next section.
4. General Three-body Problem
In the general three-body problem, we represent the equations of motion in the following form (Sosnitskii 2019):
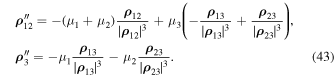
As we see, these equations are very close in form to the equations of the restricted problem. Considering equalities (Sosnitskii 2019)
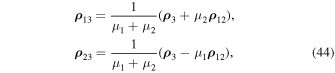
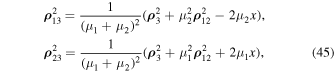
where, in accordance with Lemma represented in Sosnitskii (2019), the variable x is a bounded quantity, we rewrite the second equation of system (43) in the following form:
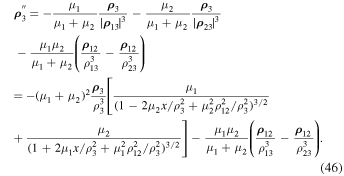
We see that it coincides with Equation (33) for 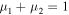 , and, in many respects, the situation in the general three-body problem is similar to that considered above, and this provides all the prerequisites for a successful application of the scheme presented in the proof of Theorem 1.
, and, in many respects, the situation in the general three-body problem is similar to that considered above, and this provides all the prerequisites for a successful application of the scheme presented in the proof of Theorem 1.
Definition. In accordance with Golubev & Grebenikov (1985), we say that a fixed pair of mass points 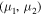 of system (43) is Hill stable if the following inequality is satisfied:
of system (43) is Hill stable if the following inequality is satisfied:
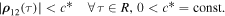
Theorem 2. Let a motion 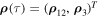 of system (43) be distal and belong to the set
of system (43) be distal and belong to the set
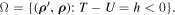
Then, if the pair of mass points 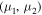 accompanying this motion is Hill stable and
accompanying this motion is Hill stable and 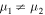 , then the motion is Lagrange stable, i.e.,
, then the motion is Lagrange stable, i.e.,
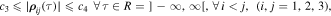
where c3 and c4 are positive constants.
Proof. Under the conditions of Theorem 2, in accordance with Lemma and the theorem from Sosnitskii (2019), the motion of the third body is bounded with respect to the pair of planar coordinates 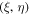 in the inertial reference frame with the origin at the center of mass of system (43) and with axes
in the inertial reference frame with the origin at the center of mass of system (43) and with axes 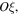
 , and
, and 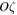 . We assume that the
. We assume that the 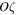 -axis is perpendicular to the
-axis is perpendicular to the 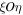 -plane.
-plane.
The boundedness of the motion of the third body relative to the planar coordinates 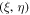 implies that this motion occurs within a cylindrical surface with a bounded directrix located in the
implies that this motion occurs within a cylindrical surface with a bounded directrix located in the 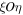 -plane and a generatrix parallel to the
-plane and a generatrix parallel to the 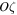 -axis. If we assume that the motion of system (43) is not bounded, then, using Equation (46) and passing over to the limit as in the case of the restricted problem, we arrive at the two-body problem with hyperbolic or parabolic orbits of the third body, respectively. Therefore, in what follows, we can use the scheme of the proof of Theorem 1.
-axis. If we assume that the motion of system (43) is not bounded, then, using Equation (46) and passing over to the limit as in the case of the restricted problem, we arrive at the two-body problem with hyperbolic or parabolic orbits of the third body, respectively. Therefore, in what follows, we can use the scheme of the proof of Theorem 1.
In particular, if the orbit of the third body is rectilinear and parallel to the 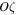 -axis, then the following equalities are still valid:
-axis, then the following equalities are still valid:  and
and 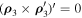 . This implies
. This implies
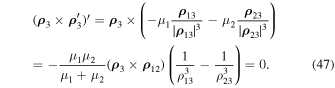
Due to Equation (47) we can conclude that at least one of the following equalities holds:
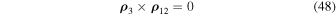
and
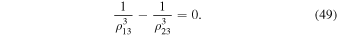
Let us show first that if equality (48) holds, then the motion of system (43) is bounded. Noticing that in this case we have

and we represent equality (48) in the form
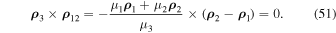
This allows us to conclude that if Equation (48) is satisfied, then all three bodies are located on one straight line.
Consider now equality (4) from Sosnitskii (2019):

As mentioned above, the x variable is bounded. Therefore, the difference
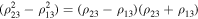
is bounded too. Since, in accordance with the conditions of the theorem, the motion is distal and all three bodies are on one straight line, we have
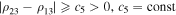
and, therefore, the sum 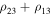 is bounded. In view of Equation (44) we conclude that
is bounded. In view of Equation (44) we conclude that 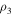 is bounded.
is bounded.
Now let Equation (49) hold, i.e., 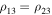 . We are going to show that in this case the motion of system (43) is bounded.
. We are going to show that in this case the motion of system (43) is bounded.
We use the following couple of equations from Sosnitskii (2019):

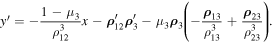
Under the condition  , from this we obtain
, from this we obtain
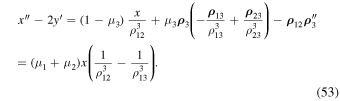
Further, based on equality (52), Equation (53) can be represented in the form
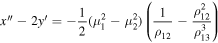
and following the scheme of the proof of Theorem 1 we complete the proof of Theorem 2. 
Although Theorem 2 confirms the result already obtained in the work of Sosnitskii (2013), nevertheless, in our opinion, it is interesting from a theoretical point of view, since the new ideas presented in the proof here are important in the framework of investigation of both the elliptic restricted problem and the general three-body problem.
5. Conclusion
We succeeded to suggest an approach in which both the elliptic restricted problem and the general three-body problem are considered from a unified point of view and thus highlight the key conditions that are common to these problems and ensuring the Lagrange stability. These conditions are the presence of a Hill-stable pair of mass points and the distality of the motion. In a certain sense, Theorem 1 obtained above can be regarded as the result of the author's investigations related to the restricted problem. Starting from the planar circular restricted problem (Sosnitskii 2017), we gradually moved (Sosnitskii 2018) toward the spatial elliptic restricted problem. In this case, as is known, the Jacobi integral does not exist and it would seem difficult to expect for obtaining any general statements related to the motion of a small particle. Nevertheless, we managed to find a base point for proving Theorem 1 and building a bridge from the restricted problem to the general three-body problem. Since the qualitative conclusions about the nature of the motion of the third body in accordance with Theorems 1 and 2 coincide, there is every reason to conclude that model of the elliptic restricted problem is correct. The fact that Theorem 1 was fairly easily extended to the general case of the three-body problem indicates how important the concept of Hill-stable pairs of mass points is both in the restricted and in the general case of the three-body problem. It should be noted here that the existence of a Hill-stable pair in the restricted problem is a consequence of the statement of the restricted problem itself.
As for the condition of distality of the motion in the elliptic restricted problem and in the general case of the three-body problem, things are much more complicated here. The problem of the choice of the initial conditions and parameters of the system, which would ensure the distality of the motion and, as a consequence, the absence of pairwise collisions, unfortunately remains open. In this case, following Weierstrass (Mittag-Leffler 1912), we can only assert that a typical situation corresponds to the movement without collisions.
In this connection, it is interesting to note that the case of the distality of motions looks completely different in a circular restricted problem. It is distinguished by the fact that in this case there is a region ωnc of distal motions, and thus there are no pairwise collisions in ωnc. The existence of such a region is ensured by the Jacobi integral. Using it, we proved the boundedness of motions in the region ωnc in the spatial case (Sosnitskii 2018), which enabled us to supplement Hill's approach to studying the motion of an infinitesimal particle. However, in this connection it should be noted that in the case of the general three-body problem, the problem of structure for the set of pairwise collisions (in particular, whether it is dense everywhere in the space of states) remains open. Consequently, the problematic issue is the correspondence of the circular restricted problem to the case of the general three-body problem, when the latter admits collisions.



