Abstract
Controlling sound fields is a key technology for noise removal, acoustic lenses, energy harvesting, etc. This study investigated the control of sound field by a periodic layered structure. At first, we formulated the wave propagation in a periodic layered structure and proved that the wave fields constructed by the periodic boundary conditions are limited to plane wave modes with discretely different propagation directions. Numerical calculations clarified that the desired plane wave mode can be obtained in the transmitted wave through an intermediate thin-plate stacked region in a periodic layered structure, in which Lamb waves travel in each plate at different phase velocities and create phase difference at the exit of the intermediate thin-plate region. Further numerical investigations revealed that tuning frequency and the length of the thin-plate region provides wave field more dominantly with a single wanted plane wave mode.
Export citation and abstract BibTeX RIS
1. Introduction
Controlling wave propagation is widely studied in the field of light and electromagnetic waves as a part of intensive research on photonic crystals and metamaterials. A photonic crystal is a structure whose refractive index changes periodically in the propagation direction and enables the design of a structure that intentionally controls the propagation of light and electromagnetic waves. 1–8) For example, it is possible to control the color scattered from a substance by calculating the passband and the band gap in which electromagnetic waves can propagate and cannot propagate in the structure, respectively. Optical waveguides can be designed by combining these photonic crystals, and light can also be intentionally confined by means of structural defects, which realizes an ultra-compact high-power laser. 3–5) In the studies of metamaterials, moreover, Pendry et al. 9) and Shelby et al. 10) experimentally confirmed the existence of substances with a negative refraction angle in the 2000s, which proved that ultra-high resolution microscopes that exceeded the diffraction limit and optical camouflage materials, called transparent cloak, have become feasible.
Following the studies on photonic crystals and metamaterials for electromagnetic waves, sound wave control has also been studied. For example, a periodic structure scattering sound wave called a phononic crystal also has a characteristic with passbands and band gaps that can be designed like a photonic crystal of electromagnetic waves. 11–16) In addition, unprecedented characteristics of ultrasonic wave and their applications are studied such as acoustic diodes that transmit sound waves in one direction, 17–20) acoustic cloaking devices that allow sound waves to bypass without being reflected, 21–24) and efficient sound wave absorbers. 25–28)
These studies analyze wave propagation based on Bloch's theorem, which can be used for structures whose physical properties change periodically in the propagation direction. Their theoretical systems have been established in the fields of electromagnetic waves and sound waves, which has already been applied to various devices as written above. On the other hand, we considered a periodic layered structure that does not change in geometries and properties in the propagation direction. 29) This study analyzes wave propagation in such a periodic layered structure by means of wave theory and numerical experiments using the finite element method. In the next section, the theory of the wave field transmitting through a periodically repeating layered structure is developed. Furthermore, assuming a structure having a plate stacked intermediate region between homogeneous isotropic elastic media, Sect. 3 describes the analysis of transmitted acoustic field using numerical calculations, and examine the design of a stacked plate region that can transmit a plane wave propagating in the specific direction.
2. Formulation of wave propagation in a periodic layered structure
2.1. Wave propagation under periodic boundary condition
When a periodic external vibration load is applied to a periodic structure in which the same layered structures are stacked as shown in Fig. 1, the wave field in the structure must become a periodic motion due to the periodic boundary condition. This section describes formulation of the wave propagation governed by the periodic boundary condition and wave equation for isotropic media.
Fig. 1. (Color online) Periodic layered structure and periodic external loading considered in this study. A region between dashed lines denotes a fundamental layer.
Download figure:
Standard image High-resolution imageConsider periodic external forces and a periodic layered structure with fundamental layers of thickness l that consist of isotropic homogeneous regions and intermediate scatterer as shown in Fig. 1. It is assumed that the cross-sectional structure in the x–y plane is periodic at the distance of l in the y direction, and the external vibration distribution also maintains the periodicity of the distance l. Now, the external force and the structure are uniform in the z direction, which is perpendicular to the x–y plane, and plane strain is assumed. Then vibration on the x–y plane is considered. At this time, using the scalar potential  and the z component of the vector potential
and the z component of the vector potential  the wave equations for longitudinal and transverse waves in the isotropic homogeneous regions can be written as
30)
the wave equations for longitudinal and transverse waves in the isotropic homogeneous regions can be written as
30)
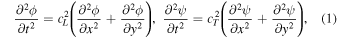
where t is time, and  and
and 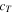 are the longitudinal wave velocity and transverse wave velocity in the isotropic homogeneous regions, respectively. Assuming a harmonic vibration field with an angular frequency ω propagating with the wave number
are the longitudinal wave velocity and transverse wave velocity in the isotropic homogeneous regions, respectively. Assuming a harmonic vibration field with an angular frequency ω propagating with the wave number  of the longitudinal wave component and the wave number
of the longitudinal wave component and the wave number 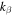 of the transverse wave component in the x direction, the solution of Eq. (1) can be written as
of the transverse wave component in the x direction, the solution of Eq. (1) can be written as
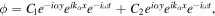
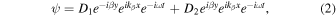
where  and
and  are arbitrary constants, and i is an imaginary unit. The first term of the first equation in Eq. (2) represents a plane wave having a wavenumber component
are arbitrary constants, and i is an imaginary unit. The first term of the first equation in Eq. (2) represents a plane wave having a wavenumber component 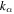 and
and  in the x and y directions, respectively, and the second term represents a plane wave having a wavenumber component
in the x and y directions, respectively, and the second term represents a plane wave having a wavenumber component  and
and  in the x and y directions. Because the phases must match at every y position in a distance of l in the periodic structure as shown in Fig. 1 even in the intermediate scatterer region, the following equations hold
in the x and y directions. Because the phases must match at every y position in a distance of l in the periodic structure as shown in Fig. 1 even in the intermediate scatterer region, the following equations hold
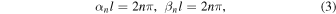
where  is an arbitrary integer,
is an arbitrary integer, 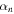 and
and 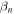 are the y component of wave number for the order of n. The wavenumber component in the x-direction with respect to the order n is also written as,
are the y component of wave number for the order of n. The wavenumber component in the x-direction with respect to the order n is also written as,
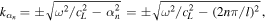

That is, due to the above constraints under the periodic boundary condition as shown in Fig. 1, the general solution of Eq. (1) can be expressed by the sum with respect to n as follows
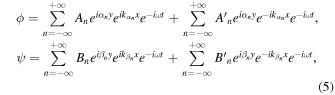
where 
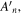
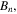 and
and  are arbitrary constants.
are arbitrary constants.
2.2. Characteristics of plane wave modes in an isotropic periodic structure
For an isotropic periodic layered structure, the scalar potential  and vector potential
and vector potential 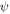 can be expressed as the summation of plane wave modes with different propagation directions. Because the expressions of
can be expressed as the summation of plane wave modes with different propagation directions. Because the expressions of 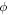 and
and 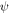 are only different in the velocities
are only different in the velocities 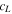 and
and 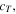 now we consider only the transverse wave-derived
now we consider only the transverse wave-derived 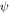 that is mainly discussed in the later numerical analyses. When considering only the wave in the +x direction, the first term remains in Eq. (5) as follows
that is mainly discussed in the later numerical analyses. When considering only the wave in the +x direction, the first term remains in Eq. (5) as follows
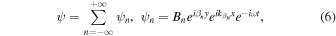
where the wave number 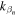 in the x direction takes a real number or a pure imaginary number depending on the sign of radicand of Eq. (4). Figure 2 is a dispersion relation of the second equation in Eq. (4) showing with the vertical axis representing the normalized frequency
in the x direction takes a real number or a pure imaginary number depending on the sign of radicand of Eq. (4). Figure 2 is a dispersion relation of the second equation in Eq. (4) showing with the vertical axis representing the normalized frequency  and the horizontal axis representing the real and imaginary parts of the normalized wavenumber
and the horizontal axis representing the real and imaginary parts of the normalized wavenumber  where
where  is the frequency and
is the frequency and  If the frequency satisfies
If the frequency satisfies  the wave number in the x direction
the wave number in the x direction 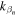 becomes a real number, forming a wave front towards the x direction. Then the angle of wave direction with respect to the x axis is expressed as,
becomes a real number, forming a wave front towards the x direction. Then the angle of wave direction with respect to the x axis is expressed as,
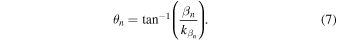
The right sketches of Fig. 2 show the wave front for 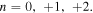 All of these plane wave modes propagate at the transverse wave speed of
All of these plane wave modes propagate at the transverse wave speed of 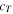 (wavelength
(wavelength 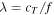 ). On the other hand, when
). On the other hand, when 
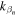 is a pure imaginary number and the wave field becomes attenuated as x increases. For example, if square or elliptical periodic obstacles are located as shown in Fig. 1, such non-propagation modes are indispensable for representing the wave field scattered from the obstacles. Strictly speaking, a large number of modes of the longitudinal wave component
is a pure imaginary number and the wave field becomes attenuated as x increases. For example, if square or elliptical periodic obstacles are located as shown in Fig. 1, such non-propagation modes are indispensable for representing the wave field scattered from the obstacles. Strictly speaking, a large number of modes of the longitudinal wave component  are also superposed in the scattering wave field as well as the propagating and non-propagating modes of transverse waves.
are also superposed in the scattering wave field as well as the propagating and non-propagating modes of transverse waves.
Fig. 2. Dispersion curves for the periodical structure. The solid and dashed lines denote real part and imaginary part of the normalized wavenumbers. n indicates the periodic index shown in Eq. (3).
Download figure:
Standard image High-resolution image2.3. Energy flux of plane wave modes in a periodic structure
Considering the wave field propagating the periodic structure as a superposition of modes propagating (or attenuating) in the x direction as represented by Eq. (5), all modes are orthogonal. Therefore, the mode conversion characteristics of the waves transmitted through the scattering region can be evaluated by using the energy flux of each mode propagating through the cross section in the y direction.
The energy flux that passes through one layer of the periodic structure in the +x direction can be expressed as
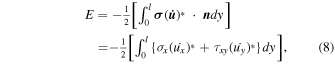
where  is the stress tensor,
is the stress tensor,  is the first derivative of the displacement vector
is the first derivative of the displacement vector  with respect to time,
with respect to time, 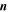 is the unit vector in the +x direction, and * is the complex conjugate.
is the unit vector in the +x direction, and * is the complex conjugate.  and
and  are normal stress and shear stress in the x direction, and
are normal stress and shear stress in the x direction, and  and
and 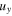 are displacements in the x and y directions. Using the first term in the +x direction of Eq. (5), each of these components required for the calculation of the energy flux can be written as
are displacements in the x and y directions. Using the first term in the +x direction of Eq. (5), each of these components required for the calculation of the energy flux can be written as
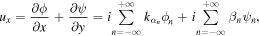
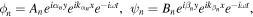
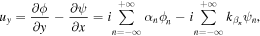

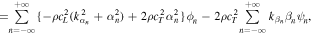

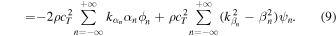
Substituting Eq. (9) into (8), it can be written as
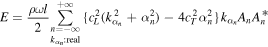
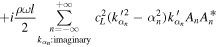

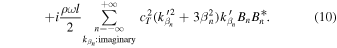
The energy flux can be written separately as the sum of the modes with real wave numbers  and
and 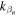 (propagating mode) and the sum of the modes with pure imaginary wave numbers
(propagating mode) and the sum of the modes with pure imaginary wave numbers  and
and  (evanescent mode). Now, because
(evanescent mode). Now, because 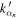 and
and  are real numbers represented by
are real numbers represented by  and
and 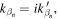 the four summation terms are real, respectively. Since the time average of the energy flux passing through the cross section
the four summation terms are real, respectively. Since the time average of the energy flux passing through the cross section 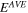 is the real part of Eq. (10), it is represented by the sum of only the propagation modes as,
is the real part of Eq. (10), it is represented by the sum of only the propagation modes as,
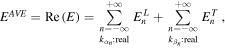
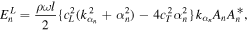
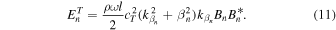
Here, since 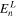 and
and  depend only on the amplitudes
depend only on the amplitudes 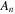 and
and  of the nth mode, respectively, and are not affected by the other modes, they represent the time average of the energy flux of the nth mode derived from longitudinal and transverse waves, respectively.
of the nth mode, respectively, and are not affected by the other modes, they represent the time average of the energy flux of the nth mode derived from longitudinal and transverse waves, respectively.
The squares of the amplitudes of each mode,  and
and  can be extracted from the displacement distribution in the y direction as follows by using the orthogonality of the modes. Let the integral of the product of the displacement
can be extracted from the displacement distribution in the y direction as follows by using the orthogonality of the modes. Let the integral of the product of the displacement  and
and 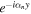 be
be 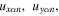 respectively, as
respectively, as
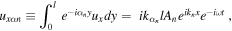
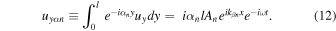
The squares of the complex values are
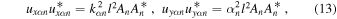
then, the squares of the amplitudes can be obtained as,
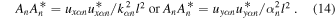
Similarly,  can be obtained as,
can be obtained as,

Inserting these values into the second and third equations of Eq. (11), the time average of the energy flux of the nth mode can be calculated.
3. Numerical experiment of waveform control by a periodic plate structure
3.1. Delay control using velocity dispersion of Lamb wave
As described above, all modes propagating in the 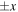 directions in a periodic layered structure satisfy the condition of Eq. (4). In the vicinity of the scattering obstacles, the wave field is expressed as a superposition of propagation modes and an infinite number of evanescent modes as shown in Eq. (5). On the other hand, in the regions apart from the scattering obstacles, the wave field can be expressed as the sum of a finite number of propagating modes. Therefore, if the scattering region is designed so that a certain propagation mode becomes dominant, direction-controlled transmitted waves and reflected waves can be obtained. This section describes the direction control of ultrasonic wave in a periodic structure that consists of homogeneous elastic regions and an intermediate plate stacked region.
directions in a periodic layered structure satisfy the condition of Eq. (4). In the vicinity of the scattering obstacles, the wave field is expressed as a superposition of propagation modes and an infinite number of evanescent modes as shown in Eq. (5). On the other hand, in the regions apart from the scattering obstacles, the wave field can be expressed as the sum of a finite number of propagating modes. Therefore, if the scattering region is designed so that a certain propagation mode becomes dominant, direction-controlled transmitted waves and reflected waves can be obtained. This section describes the direction control of ultrasonic wave in a periodic structure that consists of homogeneous elastic regions and an intermediate plate stacked region.
Lamb waves propagating in the longitudinal direction in a thin plate have dispersion characteristics in which the phase velocity and group velocity differ depending on the thickness and frequency. Figure 3(a) is the phase velocity dispersion curve of A0 mode for an aluminum alloy plate with longitudinal and transverse wave velocities of 6400 m s−1 and 3170 m s−1, respectively. The lower horizontal axis is the product of frequency  and plate thickness
and plate thickness  divided by the transverse wave velocity
divided by the transverse wave velocity  and the left vertical axis is the normalized phase velocity
and the left vertical axis is the normalized phase velocity 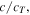 where the phase velocity of A0 mode of Lamb wave
where the phase velocity of A0 mode of Lamb wave  is divided by the transverse wave velocity
is divided by the transverse wave velocity 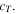 As seen in the figure, in the low
As seen in the figure, in the low  region
region 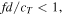 the phase velocity changes significantly with respect to the frequency and plate thickness. Considering this property and setting the structure in which flat plates with different thicknesses are stacked as shown in Fig. 3 in the middle, this section discusses control of the direction of transmitted waves by adjusting the thickness.
the phase velocity changes significantly with respect to the frequency and plate thickness. Considering this property and setting the structure in which flat plates with different thicknesses are stacked as shown in Fig. 3 in the middle, this section discusses control of the direction of transmitted waves by adjusting the thickness.
Fig. 3. (Color online) Phase control using a stacked plate structure.
Download figure:
Standard image High-resolution imageIntensive analyses of Lamb waves in Ref. 31 showed that reflection and scattering are relatively small at the entrance of a plate stacked region when a transverse plane wave is incident from the left region. Therefore, each plate vibrates in the vertical direction as an A0 mode of Lamb wave. Because the A0 modes have different phase velocities in the plates with different thickness, the phase shifts at the exit, the right edge of the thin plate stacked region as shown in Fig. 3(b). Since this phase shift can be predicted from the dispersion curve, the phase shift at the exit can be controlled by adjusting the plate thickness 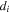 and the length of stacked plate region L for the frequency
and the length of stacked plate region L for the frequency  (or angular frequency
(or angular frequency 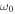 ) used. For example, by adjusting the phase at the exit to be
) used. For example, by adjusting the phase at the exit to be  (
( is an arbitrary constant), the vibration distribution in the y direction becomes
is an arbitrary constant), the vibration distribution in the y direction becomes  and then the nth-order plane wave mode can dominantly form in the right transmission region.
and then the nth-order plane wave mode can dominantly form in the right transmission region.
Table I shows the combination of plates in which the thickness and length of each stacked plate are set, considering that the transverse wave mode with 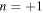 dominantly forms in the transmitted region at the frequency of 4.5 MHz. It was assumed that there are four plates per periodic layer. Figure 3(c) shows the phase difference between the entrance and exit of the stacked plate region represented by the following equation.
dominantly forms in the transmitted region at the frequency of 4.5 MHz. It was assumed that there are four plates per periodic layer. Figure 3(c) shows the phase difference between the entrance and exit of the stacked plate region represented by the following equation.
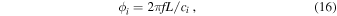
where  (
(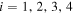 ) is the phase velocity of the Lamb wave A0 mode propagating in the ith plate as shown in Figs. 3(a) and 3(b) that depends on the plate thickness
) is the phase velocity of the Lamb wave A0 mode propagating in the ith plate as shown in Figs. 3(a) and 3(b) that depends on the plate thickness 
 is the length of the stacked plate region, 3.5 mm, and f is the frequency of 4.5 MHz.
is the length of the stacked plate region, 3.5 mm, and f is the frequency of 4.5 MHz.
Table I. Parameters for the thin plate stacked structure.
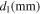
|
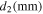
|
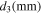
|

|
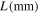
|
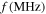
|
|---|---|---|---|---|---|
| 0.32 | 0.28 | 0.22 | 0.18 | 3.5 | 4.5 |
The circles in Fig. 3(c) plots the phase 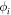 against the center positions of the four plates. As shown in Fig. 3(b),
against the center positions of the four plates. As shown in Fig. 3(b), 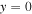 and
and 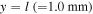 are set on the periodic boundary, and flat plates with thicknesses
are set on the periodic boundary, and flat plates with thicknesses  and
and 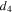 are stacked in ascending order of y position. Since the Lamb wave of A0 mode vibrates in approximately uniform distribution in the plate thickness direction, it can be considered that the A0 mode has the phase shown in the bar graph in Fig. 3(c) at the exit of the stacked plate region. In Fig. 3(c), a straight line with a slope of
are stacked in ascending order of y position. Since the Lamb wave of A0 mode vibrates in approximately uniform distribution in the plate thickness direction, it can be considered that the A0 mode has the phase shown in the bar graph in Fig. 3(c) at the exit of the stacked plate region. In Fig. 3(c), a straight line with a slope of  (l = 1 mm, n = +1) is added. This line means the ideal distribution for the formation of the transverse wave mode with
(l = 1 mm, n = +1) is added. This line means the ideal distribution for the formation of the transverse wave mode with  Therefore, the single plane wave mode is expected to appear largely when the bar chart becomes closer to the line.
Therefore, the single plane wave mode is expected to appear largely when the bar chart becomes closer to the line.
3.2. Numerical experiments using finite element analysis
In order to verify the above-mentioned transverse wave propagation control, we calculated the wave propagation for such a periodic structure using the finite element software COMSOL Multiphysics. Figure 4 is a schematic figure of the calculation region. The upper and lower boundaries are periodic boundaries, and the left and right ends are absorbing regions so that reflected waves from the both ends can be sufficiently suppressed. The upper and lower boundaries of each plate in the intermediate scattering region where four plates are stacked are set as traction free boundaries force. The displacement vibrates in the cross section, and a plane strain state is assumed, which is the same assumptions as in Sect. 2. In addition, the calculation was performed in the frequency domain, and a steady-state solution for a certain frequency f was obtained. The calculation area is one cycle of the periodic structure (length l = 1.0 mm in the y direction) whose dimensions are as shown in Fig. 4. The absorbing region is divided into 148 912 on each side by a triangular element with a maximum side length of 0.01 mm, and the remaining area is divided into 1050 in the x direction and 100 in the y direction by a square element with a side length of 0.01 mm. The incident wave was a transverse plane wave towards the stacked plate region from the left by applying a body force in the y direction to an element located 1.0 mm away from the left end, "entrance" of the intermediate stacked region. Assuming that the material is an aluminum alloy, the longitudinal wave velocity and transverse wave velocity are the same as above, 6400 and 3170 m s−1, and the density is 2700 kg m−3. The generated transverse wave passes through the entrance of the stacked region, propagates in the four plates as A0 mode of Lamb wave, and arrives at the exit (right end of the intermediate stacked region). These Lamb waves have different phases at the exit as described above.
Fig. 4. Calculation geometry in this study. A fundamental layer of a periodic structure.
Download figure:
Standard image High-resolution image3.3. Calculation results and energy analysis of transmission modes
Figure 5 shows the wave propagation at 4.5 MHz under the above calculation conditions. The color is the vertical component of the rotation of the displacement vector ![${\left[\text{rot}\,{\boldsymbol{u}}\right]}_{z},$](https://content.cld.iop.org/journals/1347-4065/61/SG/SG1048/revision2/jjapac48ccieqn100.gif) which represents the transverse wave component in the wave field. Four periodic calculation regions are displayed, stacking vertically in the y direction so that the wave propagation can be clearly seen. The vibration was attenuated in the absorbing regions at the left and right ends, and the reflected waves from the both ends was sufficiently suppressed. In addition, the wave propagation seems to be continuous at the periodic boundaries, showing the calculation with the periodic boundary conditions was correctly executed.
which represents the transverse wave component in the wave field. Four periodic calculation regions are displayed, stacking vertically in the y direction so that the wave propagation can be clearly seen. The vibration was attenuated in the absorbing regions at the left and right ends, and the reflected waves from the both ends was sufficiently suppressed. In addition, the wave propagation seems to be continuous at the periodic boundaries, showing the calculation with the periodic boundary conditions was correctly executed.
Fig. 5. (Color online) Wave motion through the stacked plate region as shown in Table I.
Download figure:
Standard image High-resolution imageIn the right region where the transmitted wave is shown, the plane wave seems to propagate in the upper right direction. However, because modes other than  are also included, the broken striped pattern appeared in whole area. To analyze the transmitted waves quantitatively, the energy ratio of each mode in the transmitted wave to the total energy of the transmitted wave was calculated.
are also included, the broken striped pattern appeared in whole area. To analyze the transmitted waves quantitatively, the energy ratio of each mode in the transmitted wave to the total energy of the transmitted wave was calculated.
The energy of the transmitted wave 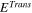 can be calculated as the time average of the vibrating energy flux transmitted through the cross section by taking the real part of Eq. (8) in the transmission region. The time average of the energy flux in each mode can also be calculated according to the second and third equations of Eq. (11). In the frequencies and a structure used in this calculation, four propagation modes exist in the periodic structure: longitudinal wave with
can be calculated as the time average of the vibrating energy flux transmitted through the cross section by taking the real part of Eq. (8) in the transmission region. The time average of the energy flux in each mode can also be calculated according to the second and third equations of Eq. (11). In the frequencies and a structure used in this calculation, four propagation modes exist in the periodic structure: longitudinal wave with  and transverse wave with
and transverse wave with  The time averaged energy fluxes
The time averaged energy fluxes  and
and 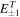 were calculated using the displacement and stress in the transmission region.
were calculated using the displacement and stress in the transmission region.
Table II shows the energy of each mode as a ratio to the energy of the entire transmitted wave.  and
and  match with an error of 1% or less, showing that the energy calculation method for each mode in the previous section is correct. In addition,
match with an error of 1% or less, showing that the energy calculation method for each mode in the previous section is correct. In addition, 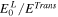 is very small, which means that the longitudinal wave component hardly appears due to the mode conversion when a transverse plane wave is incident. The transverse wave with
is very small, which means that the longitudinal wave component hardly appears due to the mode conversion when a transverse plane wave is incident. The transverse wave with  appears largely in the transmission region, and
appears largely in the transmission region, and  exceeds 70%. On the other hand, since the energy ratio
exceeds 70%. On the other hand, since the energy ratio  of the desired transverse wave with
of the desired transverse wave with 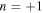 is about 30%, the conversion to the mode with
is about 30%, the conversion to the mode with 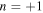 was not well performed in this stacked plate region. In the transmission region of Fig. 5, the transmitted wave appears to propagate diagonally upward (large arrow in the Fig. 5). However, the white lines connecting the same phase points differ from the wave front of the large arrow. In other words, as a result of the mixture of the mode with
was not well performed in this stacked plate region. In the transmission region of Fig. 5, the transmitted wave appears to propagate diagonally upward (large arrow in the Fig. 5). However, the white lines connecting the same phase points differ from the wave front of the large arrow. In other words, as a result of the mixture of the mode with  that propagates in the horizontal direction of the solid arrow and the mode with
that propagates in the horizontal direction of the solid arrow and the mode with  that propagates in the diagonal direction, it propagates in the direction of the thick arrow. This is supported by the fact, shown in Table II, that the mode with
that propagates in the diagonal direction, it propagates in the direction of the thick arrow. This is supported by the fact, shown in Table II, that the mode with  and the mode with
and the mode with 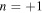 are relatively large in the energy, and the mode with
are relatively large in the energy, and the mode with  is almost nonexistent.
is almost nonexistent.
Table II. Transmission energy rate for all propagating modes (%).
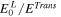
|

|

|

|
|---|---|---|---|
| 0.08 | 71.22 | 28.59 | 0.11 |
3.4. Redesign the stacked region with frequency and length
Although the thickness and length of each plate were determined so as to match the transverse wave mode with  by calculating the phase shift from the dispersion curve, the transmitted wave could not be made into a wave field dominated by the mode with
by calculating the phase shift from the dispersion curve, the transmitted wave could not be made into a wave field dominated by the mode with 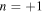 as described above. Therefore, in this section, the energy of each mode in the transmitted wave is calculated for the stacked plate region determined in the previous section when the frequency and a stacked plate length are changed.
as described above. Therefore, in this section, the energy of each mode in the transmitted wave is calculated for the stacked plate region determined in the previous section when the frequency and a stacked plate length are changed.
Figure 6 shows the energy flux rate of each mode propagating in the transmission region when the frequency is changed in 0.01 MHz increments from 4 to 5 MHz. 4.50 MHz is the frequency used in the previous section. The ratio of each mode in the transmission region changes significantly due to subtle changes in frequency. At all frequencies, the longitudinal wave mode is close to 0, which indicates that the ratio of mode conversion to longitudinal waves by the stacked plate region is very small when a transverse plane wave is incident. Moreover, although the mode with 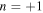 is larger than the
is larger than the  mode over the frequency range, the mode with
mode over the frequency range, the mode with  is the largest in some frequency ranges, which denotes that frequency tuning is necessary for forming the transmitted wave of a single
is the largest in some frequency ranges, which denotes that frequency tuning is necessary for forming the transmitted wave of a single 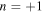 mode. For example, the wave motion shown in Table II and Fig. 5 is given at the frequency where the transverse wave mode with
mode. For example, the wave motion shown in Table II and Fig. 5 is given at the frequency where the transverse wave mode with  is dominant.
is dominant.
Fig. 6. (Color online) Energy flux rate in a transmission region.
Download figure:
Standard image High-resolution imageFigures 7(a) and 7(b) show the wave propagation at 4.20 MHz and 4.63 MHz, respectively, where the energy rate of the transverse wave mode with 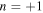 is the largest and the second largest. As Fig. 5, the vertical component of the rotation of the displacement vector
is the largest and the second largest. As Fig. 5, the vertical component of the rotation of the displacement vector ![${\left[\text{rot}\,{\boldsymbol{u}}\right]}_{z}$](https://content.cld.iop.org/journals/1347-4065/61/SG/SG1048/revision2/jjapac48ccieqn132.gif) is shown in color. Unlike in Fig. 5, the transverse wave mode with
is shown in color. Unlike in Fig. 5, the transverse wave mode with  becomes smaller, and the mode with
becomes smaller, and the mode with  exceeds 70%, then the transmitted wave with the dominant mode of
exceeds 70%, then the transmitted wave with the dominant mode of 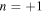 can be observed. However, because small amount of the
can be observed. However, because small amount of the 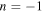 mode is superposed, the plane wave propagation towards the right lower direction can also be seen.
mode is superposed, the plane wave propagation towards the right lower direction can also be seen.
Fig. 7. (Color online) Wave motion in the periodic layered structure at the frequencies where the transverse plane wave of the order of 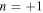 is dominant.
is dominant.
Download figure:
Standard image High-resolution imageNext, the energy of the transmitted mode was calculated for different lengths of the intermediate plate region. Figure 8 shows the energy flux rate of all propagating modes in the transmitted wave at the frequency of 4.5 MHz for different lengths of the stacked plate region in 0.1 mm increments from L = 3.0 mm to 4.0 mm. Since the mode with  is generally larger than the
is generally larger than the 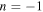 mode in this length range, the wave propagating to the lower right is small.
mode in this length range, the wave propagating to the lower right is small.
Fig. 8. (Color online) Energy flux rate for different lengths of the stacked plate region.
Download figure:
Standard image High-resolution imageFigures 9(a) and 9(b) show the wave motion for L = 3.8 and 3.4 mm, where the ratio of the mode with  is the largest and the second largest in the length range of Fig. 8. The color represents
is the largest and the second largest in the length range of Fig. 8. The color represents ![${\left[\text{rot}\,{\boldsymbol{u}}\right]}_{z}$](https://content.cld.iop.org/journals/1347-4065/61/SG/SG1048/revision2/jjapac48ccieqn141.gif) as in Figs. 5 and 7. Since both the
as in Figs. 5 and 7. Since both the  mode and the
mode and the  mode are small, a clear plane wave front propagating to the upper right is formed as a result of the fact that the
mode are small, a clear plane wave front propagating to the upper right is formed as a result of the fact that the  mode is dominant.
mode is dominant.
Fig. 9. (Color online) Wave motion in the periodical stacked region with the length where the transverse plane wave of the order of 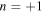 is dominant.
is dominant.
Download figure:
Standard image High-resolution imageThe results shown above indicates that it is possible to realize a transmitted wave with the dominant mode of 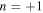 by adjusting frequency and length of a stacked plate region from the stacked plate intermediate region originally designed with dispersion curves.
by adjusting frequency and length of a stacked plate region from the stacked plate intermediate region originally designed with dispersion curves.
In this way, when a periodic external load is applied to a periodic layered structure, the transmitted wave field is limited to the propagation modes in which the wave number in the propagation direction expressed by Eq. (4) is a real value, and each mode propagates in its own angular direction. Therefore, each single mode can be measured by installing a receiving transducer that matches the unique direction.
4. Conclusions
This study examined the possibility of controlling the direction of wave propagation for a periodic layered structure. First, we formulated the wave propagation in the periodic structure, showing that only plane waves with discrete propagation angles can exist because they must satisfy the phase matching condition at the periodic boundaries, and that the plane wave modes can be evaluated by the time averaged energy flux. Furthermore, using the numerical calculation of wave propagation in the frequency domain, we tried to control the phase at the exit of an intermediate region where plates with different thickness are stacked. The results showed that the transverse wave mode with  propagating in the diagonal direction can be predominantly transmitted when a transverse wave is incident on the intermediate stacked thin plate structure.
propagating in the diagonal direction can be predominantly transmitted when a transverse wave is incident on the intermediate stacked thin plate structure.
Since the formulation shown in Sect. 2 can be applied in any structures with periodicity even if the intermediate region is not a stacked plate, we will try to control the direction of wave propagation in various intermediate regions in the next step.
Acknowledgments
This work was supported by Japan Society for the Promotion of Science KAKENHI [grant number 21H01573].










