Abstract
We present and validate a mathematical model for multicomponent thermodynamic activity in phase-separated cation-exchange membranes (e.g., perfluorinated sulfonic-acid ionomers). The model consists of an expression for the free energy of the membrane and of the surrounding electrolyte solution. A modified Stokes-Robinson ionic solvation framework treats the solution-like non-idealities resulting from hydration, electrostatics, ion association, and physical interactions in bulk solution and in ionomer hydrophilic domains. Inside the membrane, a mechanics-based composite approach accounts for the swelling of the hydrophobic matrix. Treating the membrane microstructure as a disordered system of domains calculates steric exclusion of ions. Electroneutrality guarantees that the charge of mobile ions in the membrane is equal to the charge on polymer groups. Osmotic coefficients for electrolytes from literature parameterize solution-like interactions while mechanical and X-ray scattering characterization gives most membrane-specific parameters. Model predictions compare favorably to measured membrane thermodynamics (i.e., water and ion uptake) in dilute and concentrated binary and ternary salt electrolytes and in water vapor. Interactions between ions in the membrane are similar to those present in bulk electrolytes. Our results reveal that water and ion uptake is dictated by a balance between solution-like energetics and membrane swelling.
Export citation and abstract BibTeX RIS
List of symbols
| Roman | |

|
Partial molar volume of species  m3 mol−1 m3 mol−1
|

|
Modulus of the polymer backbone, Pa |

|
Equivalent weight of polymer, gpolymer 
|

|
Equilibrium constant to form associated species 
|

|
Molar mass of species  g mol−1 g mol−1
|

|
Avogadro's constant, 6.0221 × 1023 mol−1 |

|
Total solvation number of ion 
|

|
Domain radius, nm |

|
Diameter limiting electrostatic interactions of species  nm nm
|

|
Molar concentration of species  mol dm−3 mol dm−3
|

|
Dissociation fraction of species  into species into species 
|

|
Water binding constant to species 
|

|
Molality of species  mol kg−1solvent mol kg−1solvent
|

|
Moles of species  mol mol
|

|
Elastic pressure, Pa |

|
Mole fraction of species 
|

|
Charge number of species 
|

|
Debye–Hückel limiting slope in water, 1.1777 m3/2 mol-1/2 |

|
Debye–Hückel parameter in water, 3.291 m3/2 mol−1/2 nm−1 |

|
Faraday's constant, 96,487 C mol−1 |

|
Free energy, J |

|
Ionic strength, mol m−3 |

|
universal gas constant, 8.3145 J mol-1 K−1 |

|
Temperature, 298 K |

|
Volume, m3 |

|
Distance of closest approach between ions, nm |
| Spacing between charged groups of the polymer, nm | |

|
Spacing between hydrophilic domains, nm |

|
Scaling constant |

|
Pressure, Pa |

|
Stoichiometric coefficient of species 
|
| Greek | |

|
Ratio of free species  before and after solvation before and after solvation
|

|
Specific interaction parameter between  and and  , kg mol-1 , kg mol-1
|

|
Volume fraction of species 
|

|
Absorption non-ideality parameter |

|
Quasi-electrostatic potential, V |

|
Membrane water content, molwater 
|

|
Chemical potential, J mol−1 |

|
Density, kg m−3 |

|
Debye–Hückel function 2 |

|
Debye–Hückel function 1 |
| Subscript | |

|
Solvent (i.e., water) |

|
Hydrophilic domain |

|
Membrane |

|
Species 
|
| Superscript | |

|
Infinite dilution |

|
Molecular Construct |

|
Experimental Construct |

|
Reference |

|
Electrostatic contribution |

|
Swelling contribution |

|
Excess contribution |

|
Ideal mixing contribution |

|
Physical, non-electrostatic contribution |

|
Solvation contribution |

|
Steric contribution |

|
Solution phase |

|
Membrane phase |

|
Phase |

|
Dry membrane |
Aqueous cation-exchange polymers are an important class of membrane-electrolytes because the imbibed solvent imbues the material with high conductivity while maintaining mechanical stability.1–3 Both of these attributes are essential for membrane electrolytes in numerous energy-storage and conversion devices.1–8 However, the favorable ion-transport properties of these membranes pose a challenge when multiple ions are present.4,8,9 Specifically, there is tradeoff between increasing the absorption and transport of certain species that are desirable, such as current-carrying ions, while limiting movement of contaminants, additives, or redox-active species that decrease device performance.4,10
Electrolyte membranes and hydrogels in energy-storage and conversion devices typically contain fixed ionic groups that are charge balanced by mobile cations to realize high ionic conductivity.2 The prototypical ion-conducting membranes are perfluorinated sulfonic-acid (PFSA) ionomers, which contain negatively charge sulfonate groups and protons or other cationic counter ions.2 These membranes absorb water and ions from the surrounding solution.2 Intense research efforts have yielded compelling approaches for modeling transport and thermodynamics in these membranes,5,11–21 yet these systems are still poorly understood due to their chemical complexity and corresponding nanostructural heterogeneity.22
One source of complexity is the extensive thermodynamic coupling between species.12,13,16,23 Specifically, the presence, concentration, and properties of one species affect the behavior of all other components.23,24 The specific and electrostatic interactions of ions with the membrane, solvent, and other ions cause preferential partitioning of some species from the solution over others.25–29 Furthermore, electroneutrality dictates that charge density everywhere is zero, creating a Donnan potential that induces uptake of ions of opposite charge to the fixed groups on the polymer.3,27–30 Further complicating matters, the presence and concentration of species change speciation via shifting acid and ion-pairing equilibria of active species.7
Consequently, concentration and speciation of components inside the membrane differ drastically from that in the external solution.23,25 Because ion and solvent uptake and species identity impact transport properties, permeability and conductivity depend on the concentration of species in the external solution.5,24,31,32 Accordingly, experimental characterization of the mobility of species inside separators requires both transport and thermodynamic measurements.32,33 Moreover, ion partitioning, water uptake, conductivity, and other transport properties in the membrane vary drastically when measured in different liquid electrolytes or after different membrane pretreatments.9,34 Membrane properties that are measured in one electrolyte environment do not set the behavior in another.34,35 However, mathematical models of molecular thermodynamics can address this challenge by predicting chemical activity across a range of conditions.36
The influence of species partitioning on transport properties suggests that tuning thermodynamic properties may improve device performance.4,10,17 Numerous membrane characteristics, including chemical structure, water content, and pretreatments, alter membrane performance.9,37–39 Microscopic thermodynamic theories provide insights into how characteristics of the membrane influence its properties and inform strategies for improving device performance.
This paper is the first of a three-part series that uses mathematical modeling to understand phase-separated cation exchange membranes that contain absorbed solvent and multiple ions. Here in Part I, we develop and validate a semi-empirical microscopic thermodynamic description of the system. Part II40 develops and validates a microscale concentrated-solution description of multi-ion and solvent transport in these membranes. As a case study, Part III41 simulates transport in an all-vanadium redox flow-battery separator and elucidates the underlying structure/property/function relationship for membranes in these systems and proposes improved design targets.
The outline of the papers is as follows. The theory section presents a molecular thermodynamic model that calculates ion and water uptake as a function of external solution concentration and separator structure. The model relies on semi-empirical parameters that are mostly available from measurements of bulk solution aqueous electrolytes. We discuss parameter choice and summarize numerical implementation of the model. In the results and discussion section, the model is validated against literature data. The theory reveals how the uptake of species is coupled and quantifies the relative importance of the involved molecular interactions.
Theory
Although numerous water-filled ion-conducting membrane architectures exist,4,17 here we focus on the perfluorinated sulfonic-acid (PFSA) chemistry because of its extensive characterization and widespread use.2 PFSA ionomers nanophase separate into hydrophilic, water-filled, ion-conducting domains and hydrophobic, structural domains.2 This section first defines the equilibrium conditions dictating ion and solvent uptake in the membrane. A semi-empirical microscopic model of the system provides a free-energy expression and accompanying electrochemical potentials for each species. We also address how to account for species association.
Equilibrium between phases
Chemical equilibrium dictates ion and solvent partitioning between the external solution phase  and the membrane phase
and the membrane phase  follows42
follows42
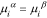
where  is the (electro)chemical potential of species
is the (electro)chemical potential of species  in phase
in phase  (
( or
or  ); water is defined as species
); water is defined as species  . The chemical potential of neutral species
. The chemical potential of neutral species  is defined as the derivative of the free energy of
is defined as the derivative of the free energy of  with respect to
with respect to  , the moles of species
, the moles of species  43,
43,
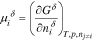
where  and
and  are the temperature and pressure, respectively. We use Eq. 2 to calculate the chemical potentials of charged species. The resulting chemical potentials always appear in neutral pairings to ensure that they are independent of the electrical state of the phase43 (see Species Chemical Potential). Chemical potential, and subsequent predictions of species partitioning, require a well-defined free-energy expression.
are the temperature and pressure, respectively. We use Eq. 2 to calculate the chemical potentials of charged species. The resulting chemical potentials always appear in neutral pairings to ensure that they are independent of the electrical state of the phase43 (see Species Chemical Potential). Chemical potential, and subsequent predictions of species partitioning, require a well-defined free-energy expression.
Free energy
We define a hypothetical reference state (denoted with superscript  ) as the pure liquid solvent, hypothetical ionic species that do not interact with each other (i.e. ideal solution at unit mole fraction) and fully dissociated, and the unswollen polymer membrane (
) as the pure liquid solvent, hypothetical ionic species that do not interact with each other (i.e. ideal solution at unit mole fraction) and fully dissociated, and the unswollen polymer membrane ( ). The change in free energy from the reference,
). The change in free energy from the reference,  , consists of ideal mixing between ions and solvent,
, consists of ideal mixing between ions and solvent,  , ion solvation,
, ion solvation,  , electrostatic interactions between ions,
, electrostatic interactions between ions,  , short-range and non-electrostatic specific physical interaction between ions,
, short-range and non-electrostatic specific physical interaction between ions,  , swelling of the polymer,
, swelling of the polymer,  , and steric interactions between the ions and polymer,
, and steric interactions between the ions and polymer,  . With the usual assumption of superposition of free energy processes,36 the free energy of the membrane phase is
. With the usual assumption of superposition of free energy processes,36 the free energy of the membrane phase is
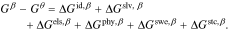
For the external solution, the final two terms are excluded since the polymer is absent
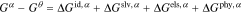
where the two superscripts denote contribution and phase.
The first change from the reference state free energy comes from ideal mixing of the ions and solvent36,43
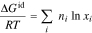
where  is the gas constant and
is the gas constant and  is the mole fraction of species
is the mole fraction of species  (
( ). The tethered polymer charged groups are in the hydrophilic domain and partially mix with the absorbed electrolyte solution.44 We idealize the polymer ionic groups with moles
). The tethered polymer charged groups are in the hydrophilic domain and partially mix with the absorbed electrolyte solution.44 We idealize the polymer ionic groups with moles  as free ions in the hydrophilic domains that contribute to the free energy accordingly.
as free ions in the hydrophilic domains that contribute to the free energy accordingly.  is equal to the mass of the polymer divided by its equivalent weight (EW, equal to g-polymer per mole of ionic group).2 Unlike many models for polymer membranes (i.e. Flory-Huggins theory45), the model neglects mixing between the uncharged volume fraction of the membrane
is equal to the mass of the polymer divided by its equivalent weight (EW, equal to g-polymer per mole of ionic group).2 Unlike many models for polymer membranes (i.e. Flory-Huggins theory45), the model neglects mixing between the uncharged volume fraction of the membrane  and the solution in the hydrophilic domains because the strong segregation of phases means they are not freely interspersed.2
and the solution in the hydrophilic domains because the strong segregation of phases means they are not freely interspersed.2
The terms on the right of Eqs. 3 and 4 except  are the "excess" free energy,
are the "excess" free energy,  .36 For any species
.36 For any species  the excess chemical potential,
the excess chemical potential,  , is normalized to approach zero (
, is normalized to approach zero ( ) as the moles of all species
) as the moles of all species  except the solvent (i.e.
except the solvent (i.e.  ) approaches zero (i.e.
) approaches zero (i.e.  ) and the membrane is fully relaxed. The excess free energy in most bulk aqueous electrolyte solutions is known.46 Literature provides numerous theories for these terms in
) and the membrane is fully relaxed. The excess free energy in most bulk aqueous electrolyte solutions is known.46 Literature provides numerous theories for these terms in  36 and a few expressions for membrane specific terms,
36 and a few expressions for membrane specific terms,  and
and  .2,28,30,47 Despite over 100 years of intense research effort, all accurate and tractable thermodynamic theories for concentrated electrolytes (>1 mol l−1) require semi-empirical adjustable parameters.48
.2,28,30,47 Despite over 100 years of intense research effort, all accurate and tractable thermodynamic theories for concentrated electrolytes (>1 mol l−1) require semi-empirical adjustable parameters.48
Here, we choose expressions for the excess free energy that are consistent with the physical description of the membrane, are relatively simple to implement numerically, require few membrane-specific adjustable parameters, and are predictive for bulk single and mixed-salt electrolyte solution thermodynamics or mechanical measurements of the membrane. Because the ion molality inside the membrane can exceed 20 mol kg−1,2 these expressions must also be valid at extremely high electrolyte concentrations. The parameters, while semi-empirical, are physically grounded. By modeling the thermodynamic nonidealities in the membrane hydrophilic domains with expressions for solution-like excess energies, we assume that molecular interactions in the pores are not drastically altered in the confined environment. This assumption is justified by the relatively short range of solvation, specific, and electrostatic interactions, at the high ionic strengths found in the hydrophilic domains of the membrane (i.e. the range of molecular interactions is less than the size of the hydrophilic domains).49
Solvation energy accounts for the entropy decrease due to free solvent molecules binding to unsolvated ions and limiting the configurations that can be accessed50,51
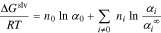
where  and
and  are the ratios of free solvent and unbound ions, respectively, after solvation to before solvation.
are the ratios of free solvent and unbound ions, respectively, after solvation to before solvation.  is the fraction of unsolvated ions
is the fraction of unsolvated ions  at infinite dilution; the form of the last term in Eq. 6 ensures that excess chemical potential is normalized so that
at infinite dilution; the form of the last term in Eq. 6 ensures that excess chemical potential is normalized so that  as
as  . Supplemental Material (SM) discusses expressions for these variables as derived by Stokes and Robinson,51 Schonert,52,53 and Zerres and Prausnitz50 in terms of the solvent/ion
. Supplemental Material (SM) discusses expressions for these variables as derived by Stokes and Robinson,51 Schonert,52,53 and Zerres and Prausnitz50 in terms of the solvent/ion  binding constant
binding constant  and the total number of solvent molecules in ion
and the total number of solvent molecules in ion  's solvation shell,
's solvation shell,  .
.
Upon charging, the ions interact through long-range electrostatic forces. Debye–Hückel theory characterizes these interactions.43,53,54 Accordingly, a solution with ionic strength,  (
( ), where the sum is over all mobile ions and excludes the fixed-charged groups of the membrane), has an electrostatic free energy
), where the sum is over all mobile ions and excludes the fixed-charged groups of the membrane), has an electrostatic free energy
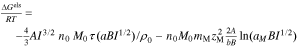
where  is the Debye-Huckel limiting slope (=1.177 m3/2 mol−1/2 for water at 298 K),
is the Debye-Huckel limiting slope (=1.177 m3/2 mol−1/2 for water at 298 K),  is the Debye-Huckel solvent parameter (= 3.291 m3/2 mol−1/2 nm−1 for water at 298 K),
is the Debye-Huckel solvent parameter (= 3.291 m3/2 mol−1/2 nm−1 for water at 298 K),  is the molecular weight of the solvent (=18 g mol−1),
is the molecular weight of the solvent (=18 g mol−1),  is the density of the solvent (=0.997 g cm−3),
is the density of the solvent (=0.997 g cm−3),  is a function (
is a function ( ),
),  is the distance of closest approach between ions (i.e. average diameter),
is the distance of closest approach between ions (i.e. average diameter),  is the spacing between charged groups in the membrane, and
is the spacing between charged groups in the membrane, and  is the charge number of species
is the charge number of species  . The first term accounts for electrostatic interactions between mobile ions and the second term accounts electrostatic interactions between mobile ions and the ions of the membrane.43,54 The second term is zero in the external solution phase. This expression follows from a statistical-mechanical derivation given in Refs 54,55 that we modify by accounting for the radius of the ions.43
. The first term accounts for electrostatic interactions between mobile ions and the second term accounts electrostatic interactions between mobile ions and the ions of the membrane.43,54 The second term is zero in the external solution phase. This expression follows from a statistical-mechanical derivation given in Refs 54,55 that we modify by accounting for the radius of the ions.43
Equations 6 and 7 are parameterized based only on the properties of the individual ions in the electrolyte (i.e.  and
and  ) and are independent of which pairs of cations and anions are present. At higher electrolyte concentrations, specific interactions between cation and anion pairs lead to additional short-range interactions (following50, we describe this as a physical contribution). Zerres and Prausnitz50 combined Eqs. 6 and 7 with a semi-empirical term for the specific physical interactions outlined by Scatchard56 where the interactions are proportional to the concentrations of the ions43
) and are independent of which pairs of cations and anions are present. At higher electrolyte concentrations, specific interactions between cation and anion pairs lead to additional short-range interactions (following50, we describe this as a physical contribution). Zerres and Prausnitz50 combined Eqs. 6 and 7 with a semi-empirical term for the specific physical interactions outlined by Scatchard56 where the interactions are proportional to the concentrations of the ions43
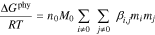
where  is the specific interaction parameter between
is the specific interaction parameter between  and
and  and is symmetric (i.e.
and is symmetric (i.e.  ). Because of the rarity of interactions between like-charged ions,
). Because of the rarity of interactions between like-charged ions,  for
for  .43 For favorable short-range interactions between species,
.43 For favorable short-range interactions between species,  . whereas unfavorable interactions give
. whereas unfavorable interactions give  .
.
Hydrophilic domains must swell to make space for the ions and solvent to enter the membrane.45 Numerous research gives expressions for the excess Helmholtz free energy of an elastically swelling polymer membrane in terms of the integral of the microscopic swelling pressure,  , generally given in the form45,57–59
, generally given in the form45,57–59
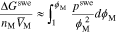
where we approximate the excess Helmholtz energy (on the right side) as equal to the excess Gibbs energy (on the left side) due system incompressibility. The free energy  on the left side is normalized by the dry polymer volume,
on the left side is normalized by the dry polymer volume,  , where
, where  is the partial molar volume of polymer per ionic group (=
is the partial molar volume of polymer per ionic group (=  ),
),  is the volume fraction of the polymer membrane, and
is the volume fraction of the polymer membrane, and  is the density of the dry membrane (= 2.1 g cm−3). Because there is much less volume of ions than membrane or solvent, we neglect the ion volume fraction for calculations of
is the density of the dry membrane (= 2.1 g cm−3). Because there is much less volume of ions than membrane or solvent, we neglect the ion volume fraction for calculations of  (
( ) and set the partial molar volume to the pure species molar volume.
) and set the partial molar volume to the pure species molar volume.  arises from the microscopic deformation of the polymer membrane due to solvent absorption and is unrelated to the thermodynamic pressure
arises from the microscopic deformation of the polymer membrane due to solvent absorption and is unrelated to the thermodynamic pressure  Specific to phase-separated polymers, we use the expression from Kusoglu et al.57 for the elastic swelling pressure generated due to deformation of the hydrophobic polymer matrix when solvent enters the hydrophilic domains
Specific to phase-separated polymers, we use the expression from Kusoglu et al.57 for the elastic swelling pressure generated due to deformation of the hydrophobic polymer matrix when solvent enters the hydrophilic domains
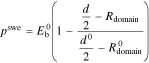
where  is Young's modulus of the dry polymer,
is Young's modulus of the dry polymer,  is the size of hydrophilic domains and
is the size of hydrophilic domains and  is the spacing between hydrophilic domains and superscript
is the spacing between hydrophilic domains and superscript  denotes the dry membrane property.
denotes the dry membrane property.  is the size of the domains in the dry state that includes the volume of charged polymer groups and counter ions. Supplemental Material (SM) discusses the specific expressions for the domain size and spacing dependence on membrane volume fraction, i.e.
is the size of the domains in the dry state that includes the volume of charged polymer groups and counter ions. Supplemental Material (SM) discusses the specific expressions for the domain size and spacing dependence on membrane volume fraction, i.e.  and
and  .
.
The size of the hydrophilic domains also dictates the steric confinement of the ions inside them (e.g. excluded volume that is inaccessible to the ions). The free energy of these steric interactions for an ion  of diameter
of diameter  due to confinement induced entropy loss in the membrane is idealized as a system of randomly oriented walls with an average spacing of
due to confinement induced entropy loss in the membrane is idealized as a system of randomly oriented walls with an average spacing of  47
47
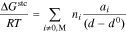
where  the same as in Eq. 10.
the same as in Eq. 10.
Species chemical potential
Equation 2 defines the chemical potentials of all species. Because the Gibbs energies given in Eqs. 3 and 4 are expressed as the sum of different contributions, chemical potential contributions similarly superimpose
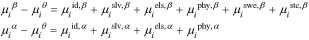
where the chemical potential of component  satisfies Eq. 2 and the superscripts correspond to the respective free-energy terms and phase. Table I gives expressions for each term. We neglect changes in partial molar volume, which are small.60
satisfies Eq. 2 and the superscripts correspond to the respective free-energy terms and phase. Table I gives expressions for each term. We neglect changes in partial molar volume, which are small.60
Table I. Summary of equations for the chemical potential terms.
| Contribution | Term | Expression |
|---|---|---|
| Ideal mixing |

|

|
| Solvation |

|

|

|

|
|
| Charging |

|
![$-ART{z}_{i}^{2}\left[\frac{{I}^{1/2}}{1+Ba{I}^{1/2}}+\frac{{m}_{{\rm{M}}}{z}_{{\rm{M}}}^{2}}{2bBI}\right]$](https://content.cld.iop.org/journals/1945-7111/167/1/013547/revision1/jesab6723ieqn184.gif)
|

|

|
|
| Physical |

|

|

|

|
|
| Swelling |

|

|

|
![${\bar{V}}_{0}{E}_{{\rm{b}}}^{0}\left[1-\tfrac{\tfrac{d\left({\phi }_{{\rm{M}}}\right)}{2}-{R}_{{\rm{domain}}}\left({\phi }_{{\rm{M}}}\right)}{\tfrac{{d}^{0}}{2}-{R}_{{\rm{domain}}}^{0}}\right]$](https://content.cld.iop.org/journals/1945-7111/167/1/013547/revision1/jesab6723ieqn194.gif)
|
|
| Steric |

|

|

|

|
|
| where | ||

|
||
Although not explicitly shown, the electrochemical potential of charged species depends on the chemical contributions outlined in Eq. 12 as well as on the electrical state of the phase. To incorporate this latter dependence while ensuring that the chemical contributions to electrochemical potential are thermodynamically accessible,43 Smyrl and Newman use a reference ion to define a so-called quasi-electrostatic potential,  (see,43 pg. 95).61 A useful reference for PFSAs with water is the proton because it exists in both the external solution and inside the membrane. Accordingly,
(see,43 pg. 95).61 A useful reference for PFSAs with water is the proton because it exists in both the external solution and inside the membrane. Accordingly,  is defined as
is defined as
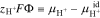
where  is Faraday's constant,
is Faraday's constant,  is the charge number of
is the charge number of  . and the subscript
. and the subscript  denotes protons. We define the electrochemical potential of other species such that the reference and excess chemical potentials (i.e. all the terms on the right sides of Eq. 12 except
denotes protons. We define the electrochemical potential of other species such that the reference and excess chemical potentials (i.e. all the terms on the right sides of Eq. 12 except  ) are well-defined and independent of electrical state,
) are well-defined and independent of electrical state,
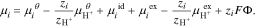
At equilibrium,  is referenced to the electrostatic potential in the solution (i.e.
is referenced to the electrostatic potential in the solution (i.e.  ). We can now use Eq. 2 to calculate the excess chemical potential of charged species because the excess chemical potential terms in Eq. 14 appear only in neutral combinations of species guaranteeing that they are independent of electrical state.43 Electroneutrality in each phase
). We can now use Eq. 2 to calculate the excess chemical potential of charged species because the excess chemical potential terms in Eq. 14 appear only in neutral combinations of species guaranteeing that they are independent of electrical state.43 Electroneutrality in each phase  is a constraint on (i.e. specifies) the quasi-electrostatic potential,
is a constraint on (i.e. specifies) the quasi-electrostatic potential,
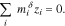
Electroneutrality in cation-exchange membranes requires absorption of fewer anions than cations. Many researchers describe this phenomenon as the result of an electrostatic potential difference between the solution and the membrane (i.e. Donnan potential).62 As an alternative to using a quasi-electrostatic potential to quantify the electric state of the material, one may instead define the potential as proportional to the electrochemical potential of one of the species (e.g. set it to the potential of a hydrogen reference electrode).43 The choice between these two definitions does not affect the calculated ion and water uptake.43
Substituting Eq. 14 for an electroneutral sum of two species (i.e.  ) into Eq. 1 characterizes the tendency of
) into Eq. 1 characterizes the tendency of  and
and  to sorb into the membrane, which the factor
to sorb into the membrane, which the factor  quantifies18–21
quantifies18–21
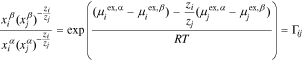
where  is independent of the electrostatic potential for
is independent of the electrostatic potential for  . For a neutral species
. For a neutral species  ,
,  is zero and we drop the second subscript
is zero and we drop the second subscript  for convenience. Because
for convenience. Because  is the sum of different free-energy contributions,
is the sum of different free-energy contributions,  is the product of these contributions,
is the product of these contributions,  . If
. If  and
and  are two oppositely charged ions (such as the anion and cation of a salt) and
are two oppositely charged ions (such as the anion and cation of a salt) and  , the oppositely charged pairs
, the oppositely charged pairs  and
and  partition into the membrane according to ideal Donnan equilibrium.
partition into the membrane according to ideal Donnan equilibrium.  indicates that
indicates that  and
and  favorably partition into the membrane while if partitioning is unfavorable,
favorably partition into the membrane while if partitioning is unfavorable,  .
.
Speciation
The microscale description of the system's free energy, Eqs. 5 to 11, are based on the physical properties of all distinct species present, which include solvent, free ions, ion pairs, or undissociated acids. Therefore, the model requires specification of component speciation (we will call this the "Molecular Construct")—for example, treating sulfuric acid as protons, sulfates, and bisulfates (see,43 pg. 119). Conversely, experiments typically report concentrations of fully dissociated species (we will call this the "Experimental Construct")—for example, treating sulfuric acid as only protons and sulfate ions. Both treatments are thermodynamically consistent.43 The Molecular Construct introduces an additional variable,  : the moles of species
: the moles of species  in the Experimental Construct,
in the Experimental Construct,  , that partially associates into
, that partially associates into  moles of species
moles of species  in the Model Construct
in the Model Construct
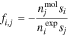
where superscript  and
and  denote the construct and
denote the construct and  and
and  are the stoichiometric coefficients of the association reaction of species
are the stoichiometric coefficients of the association reaction of species  in species
in species  respectively. Note that
respectively. Note that  . Chemical equilibrium of these reactions specified
. Chemical equilibrium of these reactions specified  42
42
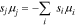
where the sum is over species  that associate to form
that associate to form  . The superscript is not applied to the electrochemical potential because it is independent of the chosen construct. For the case
. The superscript is not applied to the electrochemical potential because it is independent of the chosen construct. For the case  ,
,  and
and  . The thermodynamic equilibrium constant for the association reaction to form
. The thermodynamic equilibrium constant for the association reaction to form  is
is  . This speciation equilibrium constant is defined in terms of the species chemical potential at the hypothetical reference state of unit mole fraction and ideal solution (i.e.
. This speciation equilibrium constant is defined in terms of the species chemical potential at the hypothetical reference state of unit mole fraction and ideal solution (i.e.  and
and  ) and is dimensionless; the more-commonly reported equilibrium constant,
) and is dimensionless; the more-commonly reported equilibrium constant,  , is defined in terms of species chemical potential at the reference state of an ideal solution at unit molarity (i.e.
, is defined in terms of species chemical potential at the reference state of an ideal solution at unit molarity (i.e.  and
and  ). These two constants are related by
). These two constants are related by  where
where  is the solvent concentration for an electrolyte with an infinitely dilute salt concentration.36,43 At infinite salt dilution,
is the solvent concentration for an electrolyte with an infinitely dilute salt concentration.36,43 At infinite salt dilution,  for
for  and
and  .43
.43
To calculate the contributions to the chemical potential throughout this paper (such as in Table I), we use composition variables in the Molecular Construct,  ,
,  , and
, and  ; the superscript
; the superscript  is not explicitly written throughout for simplicity. If one chooses to write the ideal chemical potential in the Experimental Construct (i.e.
is not explicitly written throughout for simplicity. If one chooses to write the ideal chemical potential in the Experimental Construct (i.e.  , as we do in Part III of this series41) rather than the Molecular Construct (i.e.
, as we do in Part III of this series41) rather than the Molecular Construct (i.e.  ), the term
), the term  is added to
is added to  . The calculated chemical potential
. The calculated chemical potential  is independent of the chosen construct. When presenting results, we convert concentrations to the Experimental Construct for consistency with measurements unless otherwise stated.
is independent of the chosen construct. When presenting results, we convert concentrations to the Experimental Construct for consistency with measurements unless otherwise stated.
Numerical implementation
Equations 1 and 18 with those in Table I are a nonlinear, coupled algebraic system. At a given solution species composition in the Experimental Construct, we calculate the solvent and solute uptake in the membrane as follows:
We determine the chemical potential of species in the external solution using Eq. 12 with expressions from Table I. Equations 13 and 14 specify the electrochemical potential of each species in solution. A modified Levenberg-Marquardt63 algorithm finds  in Eq. 17 for all species in the external solution that satisfies the root of the equilibrium speciation equations (Eq. 18 for each speciation reaction). To determine the excess chemical potential of solvation, a modified Powell hybrid algorithm64 concurrently solves for
in Eq. 17 for all species in the external solution that satisfies the root of the equilibrium speciation equations (Eq. 18 for each speciation reaction). To determine the excess chemical potential of solvation, a modified Powell hybrid algorithm64 concurrently solves for  that is the root to Equations in A1 in SM for the solvation expression. The initial guess is a negligible fraction of free solvent.
that is the root to Equations in A1 in SM for the solvation expression. The initial guess is a negligible fraction of free solvent.
A modified Levenberg-Marquardt63 algorithm finds the polymer volume fraction,  , solute molality,
, solute molality,  , and quasi-electrostatic potential,
, and quasi-electrostatic potential,  , inside the membrane that satisfies electroneutrality (Eq. 15) and equality of the electrochemical potential of unassociated species between phases (Eq. 1). Alternatively, Eqs. 15 and 16 also specify partitioning, but without requiring calculation of
, inside the membrane that satisfies electroneutrality (Eq. 15) and equality of the electrochemical potential of unassociated species between phases (Eq. 1). Alternatively, Eqs. 15 and 16 also specify partitioning, but without requiring calculation of  . Because Eq. 18 makes electrochemical potential of associating ions and their products dependent, using Eq. 1 on ion-pairs is redundant. Equations 12 and 14 determine the electrochemical potential of species inside the membrane. All root-finding algorithms are implemented in SciPy 0.18.1 package Python 3.6 with a relative tolerance of 1.49 × 10–8. The NumPy packaged performed array operations.
. Because Eq. 18 makes electrochemical potential of associating ions and their products dependent, using Eq. 1 on ion-pairs is redundant. Equations 12 and 14 determine the electrochemical potential of species inside the membrane. All root-finding algorithms are implemented in SciPy 0.18.1 package Python 3.6 with a relative tolerance of 1.49 × 10–8. The NumPy packaged performed array operations.
Parameters
Operating parameters for this study are ambient temperature (298 K) and pressure (101 kPa). All the electrolytes in this study are aqueous (i.e. water is the solvent). We study the Nafion PFSA chemistry because data are widely available.2,23,32,33,37,65,66 We use data from Nafion N117, N115, N212, and N211 where the N11x sequence is extruded and the series N21x is cast from a dispersion. Designation x denotes thickness in units of mils. All membranes have an equivalent chemical formula.2 In addition to different processing methods, the membranes undergo various pretreatments (e.g. boiling) that can alter their properties, such as membrane modulus.59,67 Variations in water and ion uptake between membranes may be predicted if mechanical properties of the membrane are available. Lacking this information and to ensure that the results are representative of Nafion across treatment history, we use datasets from multiple studies and for membranes from different series at the same environmental conditions. We also note the range of experimental values found in literature whenever possible.
Table II lists the physical properties of the individual ions, the ion pairs, and the membrane that parameterize the model. These parameters have varying levels of empiricism. Certain properties are not fit (of the vapor-equilibrated membrane 
 and
and  ) because they are specified by independent measurements or theories that contain no adjustable properties. Based on molecular dynamics simulations and small-angle X-ray measurements,
) because they are specified by independent measurements or theories that contain no adjustable properties. Based on molecular dynamics simulations and small-angle X-ray measurements,  is 0.47 nm.2,68 Due to structural rearrangements of PFSAs,
is 0.47 nm.2,68 Due to structural rearrangements of PFSAs,  for membranes equilibrated in a solution is lower than membranes in vapor (so-called Schröder's paradox).58,59,69,70 SM details compilation of the values of these parameters from literature.
for membranes equilibrated in a solution is lower than membranes in vapor (so-called Schröder's paradox).58,59,69,70 SM details compilation of the values of these parameters from literature.
Table II. The value and approach to model parameters.
| Parameters | Value | Notes | |
|---|---|---|---|
| Individual Ions | |||
| cations | anions | ||
ion diameter, 
|
 [nm] [nm] |
0.3 [nm] | physical arguments |
ion/solvent biding 
|
various, see SM | 0.0 | fit to bulk-solution data |
ion solvation number 
|
5 
|
0.0 | physical arguments |
| Ion Pairs | |||
equilibrium constant 
|
various, see SM | from literature, various methods | |
cation/anion interaction parameter 
|
various, see SM | fit to bulk-solution data | |
cation/membrane interaction parameter 
|
various, see Table II | fit to membrane uptake data | |
| Membrane | |||
dry membrane modulus 
|
136 (liquid)/320 (vapor) [MPa], see SM | fit to membrane uptake data/mechanical measurement | |
radius of hydrophilic domain 
|
see SM | geometric arguments | |
spacing between domains 
|
see SM | small-angle X-ray scattering measurements | |
spacing between charged groups, 
|
0.47 nm | molecular dynamics simulations and small-angle X-ray scattering measurements | |
Other properties are adjusted to fit measured bulk aqueous electrolyte water activity ( ,
,  ,
,  ,
,  , the anion/cation interaction parameter). Because there are many parameters to fit uniquely, physical arguments and previous research suggest simplifications. For instance, the weak solvation of anions supports that their
, the anion/cation interaction parameter). Because there are many parameters to fit uniquely, physical arguments and previous research suggest simplifications. For instance, the weak solvation of anions supports that their  's and
's and  's are zero.50 Further, we follow previous electrolyte models by setting
's are zero.50 Further, we follow previous electrolyte models by setting  to a fixed value for all ions.43 Ample research demonstrates that these simplifications, although somewhat ad hoc, provide accurate predictions of thermodynamic activity of binary and mixed electrolytes.43,50,53 As SM details, the remaining
to a fixed value for all ions.43 Ample research demonstrates that these simplifications, although somewhat ad hoc, provide accurate predictions of thermodynamic activity of binary and mixed electrolytes.43,50,53 As SM details, the remaining  's and
's and  's are fit to the measured osmotic coefficients of 28 salts consisting of pairings of 10 cations and 5 anions across a large range of concentrations (e.g. up to 15 mol kg−1 for LiBr).46,71
's are fit to the measured osmotic coefficients of 28 salts consisting of pairings of 10 cations and 5 anions across a large range of concentrations (e.g. up to 15 mol kg−1 for LiBr).46,71
The only parameters adjusted to fit membrane specific data are  , the modulus of the polymer backbone in liquid water, and
, the modulus of the polymer backbone in liquid water, and  , the cation/membrane interaction parameter. The modulus of the membrane in liquid water is challenging to measure due to a highly non-linear shear response.72 The backbone modulus it is estimated to be between 131 to 181 MPa.72 By fitting water and ion uptake measurements in liquid water, we set
, the cation/membrane interaction parameter. The modulus of the membrane in liquid water is challenging to measure due to a highly non-linear shear response.72 The backbone modulus it is estimated to be between 131 to 181 MPa.72 By fitting water and ion uptake measurements in liquid water, we set  to136 MPa, which is within the measured range.. Table III gives values for
to136 MPa, which is within the measured range.. Table III gives values for  that were also fit to water and ion membrane uptake measurements, which are presented in the Results and Discussion section. The physical interactions between H+, Li+, Na+, or K+ and the membrane have a similar value as these cations have with trifluoromethanesulfonic anions, CF3SO3− (TFMS−), which is a simple fluorosulfonate anion structurally similar to the sulfonate group in PFSAs.71 We did not find thermodynamic activity of other TFMS salt solutions in the literature.
that were also fit to water and ion membrane uptake measurements, which are presented in the Results and Discussion section. The physical interactions between H+, Li+, Na+, or K+ and the membrane have a similar value as these cations have with trifluoromethanesulfonic anions, CF3SO3− (TFMS−), which is a simple fluorosulfonate anion structurally similar to the sulfonate group in PFSAs.71 We did not find thermodynamic activity of other TFMS salt solutions in the literature.
Table III. Values of membrane-cation specific fitting parameters in the model.
| Cation |
 [kg mol−1] [kg mol−1] |
 [kg mol−1] [kg mol−1] |
|---|---|---|
| H+-M− | 0.133 | 0.148 |
| Li+-M− | 0.141 | 0.128 |
| Na+-M− | 0.085 | 0.0576 |
| K+-M− | 0.000 | −0.0293 |
| Cs+-M− | −0.08 | |
| Cu2+-M− | 0.55 | |
| Ca2+-M− | 0.28 | |
| Ni2+-M− | 0.4 | |
| Fe3+-M− | 0.85 | |
| VO2+-M− | 0.08 | |
| VO2+-M− | 0.25 |
Vanadium ions are relevant in flow-battery applications, which is the focus of Part III,41 but measurements for thermodynamic activity of vanadium electrolyte solutions are scarce.73 Consequently, values of  and
and  for vanadium ions in their various oxidation states are set equal to cations that have the same charge (see SM).
for vanadium ions in their various oxidation states are set equal to cations that have the same charge (see SM).
Results and Discussion
Ion- and water-uptake isotherms in a single electrolyte and water vapor
Figure 1 shows measured (symbols) and calculated membrane water (a) and anion (c) uptake at as a function of external sulfuric acid concentration37,66 (circles) for various Nafion types (N117, N212, and N211) and hydrobromic acid (diamonds74 and triangles75). For both water and ion uptake, agreement between the model and experiment is good up to ∼8 molal in the external electrolyte. Note the overlap of HBr and H2SO4 data points at low concentrations. Despite the very different nature of the HBr (a 1-1 salt) and H2SO4 (a 2-1 salt if fully dissociated), water and ion uptake are similar at the same electrolyte concentration This similarity is in part due to the high concentration of H+ in the membrane that ensures that the sulfate in the membrane is almost entirely in the bisulfate (HSO4−) form. Consequently, the HBr and H2SO4 both behave as univalent acids.
Figure 1. Membrane water (a) and anion (c) uptake calculated (solid lines) and measured (symbols) at varying external H2SO4 concentration measured by Tang et al.37,66 (circles) for various Nafion types (N117, N212, N211) and HBr concentration measured by Bai74 (diamonds) and Yeo75 (triangles), and calculated. (b) shows contributions to the total water  in the HBr system from solution-like
in the HBr system from solution-like  steric
steric  and swelling
and swelling  nonidealities. (d) shows contributions to the total hydrobromic acid
nonidealities. (d) shows contributions to the total hydrobromic acid  from solution-like
from solution-like  and steric
and steric  nonidealities.
nonidealities.
Download figure:
Standard image High-resolution imageAs the external acid concentration increases, the membrane water content decreases because the difference between solution osmotic pressure ( ) and the membrane osmotic pressure
) and the membrane osmotic pressure  decreases. This leads to water content decreasing as the balance between osmotic, which keeps water in the membrane, and swelling pressures (
decreases. This leads to water content decreasing as the balance between osmotic, which keeps water in the membrane, and swelling pressures ( ), which pushes water out of the membrane, shifts in favor of the latter. Using the HBr solution as an example, Fig. 1b shows that the effect of thermodynamic non-idealities on solvent uptake are small but unfavorable. Solution-like interactions (
), which pushes water out of the membrane, shifts in favor of the latter. Using the HBr solution as an example, Fig. 1b shows that the effect of thermodynamic non-idealities on solvent uptake are small but unfavorable. Solution-like interactions ( ) of the highly concentrated solution in the membrane are favorable for water uptake, but . membrane swelling (
) of the highly concentrated solution in the membrane are favorable for water uptake, but . membrane swelling ( ) is always unfavorable for water uptake. These effects partially balance over a range of concentrations.
) is always unfavorable for water uptake. These effects partially balance over a range of concentrations.
Increasing the external acid concentration drives acid into the membrane as the external concentration is greater than that in the membrane. Figure 1d shows the nonidealities associated with hydrobromic acid uptake,  , and the contributions from solution-like interactions,
, and the contributions from solution-like interactions,  , and steric effects,
, and steric effects,  . There is no swelling contribution to ion chemical potential. Acid partitioning into the membrane is greater than expected for an ideal solution at low external acid concentrations. The enhanced uptake is due to favorable electrostatic interactions (i.e. negative excess free energy) that increase with ion concentration (see Eq. 7). Holding all else constant, ions move to a phase with more electrostatic interactions (i.e. to higher ionic strength). Since the membrane has a higher ionic strength than the external solution, the favorable electrostatic interactions (
. There is no swelling contribution to ion chemical potential. Acid partitioning into the membrane is greater than expected for an ideal solution at low external acid concentrations. The enhanced uptake is due to favorable electrostatic interactions (i.e. negative excess free energy) that increase with ion concentration (see Eq. 7). Holding all else constant, ions move to a phase with more electrostatic interactions (i.e. to higher ionic strength). Since the membrane has a higher ionic strength than the external solution, the favorable electrostatic interactions ( = 3.0) compensate for the unfavorable effects of solvation (
= 3.0) compensate for the unfavorable effects of solvation ( = −0.5) and specific interactions (
= −0.5) and specific interactions ( = −1.6) in the concentrated electrolyte solution of the membrane.
= −1.6) in the concentrated electrolyte solution of the membrane.
At higher external acid concentrations, electrostatic interactions in the membrane are similar to those in the external solution, and the energetic benefit of acid partitioning into the membrane is smaller. Moreover, as water dehydrates the membrane, the pores shrink, as Fig. S1 shows (see SM) (available online at stacks.iop.org/JES/167/013547/mmedia), and the ions are more sterically hindered. Thus, at high external electrolyte concentrations, anions are excluded more from the membrane than predicted for an ideal solution. However, in the dehydrated membrane, the average hydrophilic domain remains larger than the diameter of the ions and steric hindrance does not fully exclude co-ions.
Figure 1 shows that electrolytes with the same cation but different anions partition into PFSA membranes similarly. To explore how the cation impacts electrolyte partitioning, Fig. 2 shows measured (symbols) and calculated (solid lines) membrane water (a) and anion (b) uptake as a function of external concentration of NaCl76 (squares) and HBr (diamonds74 and triangles75). The scales in Figs. 1 and 2 are not the same. At low salt concentrations, fractionally changing electrolyte concentrations does not change water content in the membrane. For concentrations above ∼1 molal, the water content decreases with increasing electrolyte concentration in both NaCl and HBr solutions as the membrane absorbs ions and dehydrates due to the high osmotic pressure of the surrounding solution.
Figure 2. Measured (symbols) and calculated (solid lines) membrane water (a) and anion (b) uptake in varying external solution concentrations of NaCl measured by Nare¸bska et al.76 (squares) and HBr measured by Bai74 (diamonds) and Yeo75 (triangles). Shaded region denotes the range of values from literature of N117 solvent uptake in liquid water in H- (purple) and Na-form (yellow) membranes.2
Download figure:
Standard image High-resolution imageAt low electrolyte concentrations, membranes in NaCl solutions have a lower water content and higher anion uptake than in HBr at the same electrolyte concentration. In the limit of a membrane in pure water, the H-form of the membrane has higher water uptake than the Na-form in pure water; Fig. 1 shows with the shaded purple and yellow regions, respectively, that provide the range of literature-reported water uptake in these membranes.2 Compared to Na+, H+ has stronger solvation ( provided in SM) and unfavorable physical interaction with the sulfonate group on the membrane (
provided in SM) and unfavorable physical interaction with the sulfonate group on the membrane ( , as Table III shows). Consequently, water uptake and dilution of the H+−SO3− pairs is more favorable than dilution of Na+−SO3− pairs. Similarly, uptake of Na+ is slightly more favorable than of H+.
, as Table III shows). Consequently, water uptake and dilution of the H+−SO3− pairs is more favorable than dilution of Na+−SO3− pairs. Similarly, uptake of Na+ is slightly more favorable than of H+.
At high concentrations, this effect is eliminated with equal or higher water uptake in NaCl than in HBr solutions. Compared to Na+, the unfavorable interactions between H+ and its co-ion ( , as SM shows) shifts the osmotic pressure balance in favor of the external electrolyte and drives water from the membrane into the solution to dilute H+-Br− pairs.
, as SM shows) shifts the osmotic pressure balance in favor of the external electrolyte and drives water from the membrane into the solution to dilute H+-Br− pairs.
The data shown in Figs. 1 and 2 are used to determine the parameters  and
and  , respectively, and
, respectively, and  . These values are the best-eye fit to the data. The fitted values of the specific interactions between cations and the membrane,
. These values are the best-eye fit to the data. The fitted values of the specific interactions between cations and the membrane,  , are very similar to the fitted interactions between alkali cations and CF3SO3− in solution,
, are very similar to the fitted interactions between alkali cations and CF3SO3− in solution,  . The similarity of
. The similarity of  and
and  suggests that short-range specific interactions between cations and the membrane sulfonate groups are comparable to the interactions between cations and simple sulfonate anions in solution. Consequently, this approach explains the observed water and ions uptake behavior over a range of concentrations by accounting for solution-like interactions in the membrane. Confined pore geometry or long-range electrostatic ion condensation, as other researchers have proposed, can potentially predict
suggests that short-range specific interactions between cations and the membrane sulfonate groups are comparable to the interactions between cations and simple sulfonate anions in solution. Consequently, this approach explains the observed water and ions uptake behavior over a range of concentrations by accounting for solution-like interactions in the membrane. Confined pore geometry or long-range electrostatic ion condensation, as other researchers have proposed, can potentially predict  without fitting to experiments. 18,19,77–79
without fitting to experiments. 18,19,77–79
Figure 3 shows that the model effectively calculates (lines) measured (symbols) water uptake of N212 membranes in proton- (diamonds) and sodium-form (squares) in water vapor. Membrane water uptake at 100% relative humidity and salt-free liquid water is different despite a water activity of unity in both systems. This difference is termed Schröder's paradox and has been extensively studied.2,80–82 Here, we attribute the decreased water uptake in water vapor to structural rearrangement of the hydrophilic domains upon exposure to water vapor leading to different backbone polymer moduli  , (see SM for details).72 No additional fitting parameters are used to calculate membrane water uptake in water vapor; agreement between theory and experiment is good. The model's successful thermodynamic predictions of membranes vapor and liquid environments further supports the proposed form of the Gibbs energy in Eqs. 3 and 4.
, (see SM for details).72 No additional fitting parameters are used to calculate membrane water uptake in water vapor; agreement between theory and experiment is good. The model's successful thermodynamic predictions of membranes vapor and liquid environments further supports the proposed form of the Gibbs energy in Eqs. 3 and 4.
Figure 3. Measured (symbols) and calculated (solid lines) N212 membrane water uptake in water vapor as a function of relative humidity for membranes in proton-form (diamonds) and sodium-form (squares) measured by Shi et al.83
Download figure:
Standard image High-resolution imageIon partitioning in dilute, mixed electrolytes
We explore ion specificity of the model through partitioning of cations from dilute mixed electrolytes. Focusing on membranes in dilute electrolyte makes anion uptake negligible because of Donnan exclusion. Okada et al. measured water content and cation partitioning in varying compositions of mixed electrolytes of  and HCl (or LiCl) where
and HCl (or LiCl) where  is Li+, Na+, K+, Cs+, Ni2+, Cu2+, and Fe3+.32,33,65,84 The external solutions were at 0.06 mol kg−1 total ion (chloride, proton, and cation
is Li+, Na+, K+, Cs+, Ni2+, Cu2+, and Fe3+.32,33,65,84 The external solutions were at 0.06 mol kg−1 total ion (chloride, proton, and cation  ) concentration.65 The fraction of protons (or lithium ions) in the solution is quantified as the fraction of chloride anions in the solution charge balanced by protons
) concentration.65 The fraction of protons (or lithium ions) in the solution is quantified as the fraction of chloride anions in the solution charge balanced by protons  and in the membrane as the fraction of sulfonate groups balanced by protons
and in the membrane as the fraction of sulfonate groups balanced by protons  (where the subscript
(where the subscript  is replaced by
is replaced by  for membranes exchanged from lithium-form).
for membranes exchanged from lithium-form).
Figure 4 shows that as the measured32 (symbols) and predicted (lines) proton fraction in the membrane,  , as a function of the proton fraction of the surrounding mixed proton-alkali electrolyte,
, as a function of the proton fraction of the surrounding mixed proton-alkali electrolyte,  (a) and water content,
(a) and water content,  as a function of
as a function of  (c). The values of
(c). The values of  ,
,  ,
,  are best-eye fit to the water uptake and ion partitioning in Fig. 4; we use the values of
are best-eye fit to the water uptake and ion partitioning in Fig. 4; we use the values of  and
and  obtained from ion and water uptake isotherms (Figs. 1 and 2) without additional fitting. Agreement is good particularly considering the experimental scatter reported in literature, which Fig. 4 notes for completely exchanged alkali-form membranes with a shaded region.2 Figure S2 shows that the model is externally valid by predicting water and ion uptake of membranes in mixed lithium-alkali electrolytes at the same conditions (see SM).
obtained from ion and water uptake isotherms (Figs. 1 and 2) without additional fitting. Agreement is good particularly considering the experimental scatter reported in literature, which Fig. 4 notes for completely exchanged alkali-form membranes with a shaded region.2 Figure S2 shows that the model is externally valid by predicting water and ion uptake of membranes in mixed lithium-alkali electrolytes at the same conditions (see SM).
Figure 4. Measured32 (symbols) and calculated (solid lines) membrane proton fraction in the membrane  as a function of external solution proton fraction
as a function of external solution proton fraction  (a) and water content in the membrane,
(a) and water content in the membrane,  as a function of proton fraction in the membrane
as a function of proton fraction in the membrane  (c) in a mixed aqueous electrolyte of hydrochloric acid and lithium (up triangles), sodium (squares), potassium (pentagons), and cesium (diamonds) chloride. The external solutions were at 0.06 mol kg−1 total ion concentration.32 Shaded regions denote the range of published water uptakes of membranes in liquid water of fully ion-exchanged membranes Ref. 2. (b) shows contributions to the total the ratio
(c) in a mixed aqueous electrolyte of hydrochloric acid and lithium (up triangles), sodium (squares), potassium (pentagons), and cesium (diamonds) chloride. The external solutions were at 0.06 mol kg−1 total ion concentration.32 Shaded regions denote the range of published water uptakes of membranes in liquid water of fully ion-exchanged membranes Ref. 2. (b) shows contributions to the total the ratio  from solvation
from solvation  and physical
and physical  nonidealities. (d) shows contributions to the total water
nonidealities. (d) shows contributions to the total water  from solvation
from solvation  , physical
, physical  , and swelling
, and swelling  nonidealities.
nonidealities.
Download figure:
Standard image High-resolution imageAs the alkali cation fraction in solution increases, the fraction of alkali cations in the membrane increases. If alkali cation  and protons equally partition into the membrane (
and protons equally partition into the membrane ( ), then
), then  is a straight line between 0 and 1 for
is a straight line between 0 and 1 for  and
and  . Ideal partitioning nearly occurs for Na+-H+ exchange. For
. Ideal partitioning nearly occurs for Na+-H+ exchange. For  , the alkali cations prefer to be in the solution more than do protons; ion exchange shows positive deviation from equal partitioning (i.e. curved upward in Fig. 4a, as is the case for Li+-H+ exchange) whereas for
, the alkali cations prefer to be in the solution more than do protons; ion exchange shows positive deviation from equal partitioning (i.e. curved upward in Fig. 4a, as is the case for Li+-H+ exchange) whereas for  , the alkali cations prefer to be in the membrane more than protons, and ion-exchange curve shows negative deviation (i.e. curved downwards in Fig. 4a, as is the case for K+-H+ and Cs+-H+ exchange). Figure 4a shows that
, the alkali cations prefer to be in the membrane more than protons, and ion-exchange curve shows negative deviation (i.e. curved downwards in Fig. 4a, as is the case for K+-H+ and Cs+-H+ exchange). Figure 4a shows that  . This trend follows a Hofmeister series.85
. This trend follows a Hofmeister series.85
To understand why univalent cations follow this trend, we study K+-uptake more closely as an example; Fig. 4b plots  with the contributions of nonideality from solvation,
with the contributions of nonideality from solvation,  , and from physical interactions between the membrane and alkali cations and protons,
, and from physical interactions between the membrane and alkali cations and protons,  , as a function of
, as a function of  .
.  is less than unity because K+ is less solvated than H+ and can therefore exist in the concentrated solution of the membrane without requiring a full solvation shell (i.e.
is less than unity because K+ is less solvated than H+ and can therefore exist in the concentrated solution of the membrane without requiring a full solvation shell (i.e.  ). K+ has more favorable physical interactions with the sulfonate group (i.e.
). K+ has more favorable physical interactions with the sulfonate group (i.e.  so that
so that  ). Because we use the same cation radii for all univalent ions, steric and electrostatic interactions are essentially identical for H+ and K+ (i.e.
). Because we use the same cation radii for all univalent ions, steric and electrostatic interactions are essentially identical for H+ and K+ (i.e.  ). Consequently, specific, physical interactions between the cations and sulfate groups primarily dictate uptake preference of ion exchange.
). Consequently, specific, physical interactions between the cations and sulfate groups primarily dictate uptake preference of ion exchange.
Figure 4c shows that the trend of membrane ion-exchange preference is also exhibited in water uptake. The water content of membranes exchanged with cations follow the order Li+ > H+  Na+ > K+ > Cs+. Using H+-K+ exchange as an example, Fig. 4b plots
Na+ > K+ > Cs+. Using H+-K+ exchange as an example, Fig. 4b plots  and the contribution to water uptake from solvation
and the contribution to water uptake from solvation  , cation-sulfonate physical interactions
, cation-sulfonate physical interactions  , and swelling
, and swelling  . The decrease in water content as the membrane exchanges from H-form to K-form is due to the more favorable interactions of K+ with the sulfonate compared to H+. The more favorable interactions of K+ with the sulfonate groups means that there is a smaller driving force for water to dilute the K+-SO3+ pairs.
. The decrease in water content as the membrane exchanges from H-form to K-form is due to the more favorable interactions of K+ with the sulfonate compared to H+. The more favorable interactions of K+ with the sulfonate groups means that there is a smaller driving force for water to dilute the K+-SO3+ pairs.  and
and  change slightly with ion exchange from H-form to K-form. But these changes are not directly due to ion exchange, but indirectly related to higher cation concentration and decreased swelling of the membrane because of lower water content in K-form membranes. Based on this analysis, stronger favorable interactions between cations and sulfonate groups reduce water uptake.
change slightly with ion exchange from H-form to K-form. But these changes are not directly due to ion exchange, but indirectly related to higher cation concentration and decreased swelling of the membrane because of lower water content in K-form membranes. Based on this analysis, stronger favorable interactions between cations and sulfonate groups reduce water uptake.
Figure 5 shows calculated (lines) and measured65 (symbols) proton fraction in the membrane,  , as a function of the proton fraction of the surrounding mixed electrolyte,
, as a function of the proton fraction of the surrounding mixed electrolyte,  (a) and water content,
(a) and water content,  as a function of
as a function of  (c), for mixed chloride electrolytes with protons and multivalent cation Ni2+, Ca2+, Cu2+, and Fe3+. We fit
(c), for mixed chloride electrolytes with protons and multivalent cation Ni2+, Ca2+, Cu2+, and Fe3+. We fit  ,
,  ,
,  , and
, and  to the measured water uptake and ion partitioning in Fig. 5 by eye.
to the measured water uptake and ion partitioning in Fig. 5 by eye.
Figure 5. Measured (symbols)65 and calculated (solid lines) membrane proton fraction in the membrane  as a function of external solution proton fraction
as a function of external solution proton fraction  (a) and water content in the membrane,
(a) and water content in the membrane,  as a function of proton fraction in the membrane
as a function of proton fraction in the membrane  (c) in a mixed aqueous electrolyte of hydrochloric acid and calcium (right triangles), nickel (down triangle), copper (left triangle), and iron (crosses) chloride. The external solutions were at 0.06 mol kg−1 total ion concentration.65,84
(c) in a mixed aqueous electrolyte of hydrochloric acid and calcium (right triangles), nickel (down triangle), copper (left triangle), and iron (crosses) chloride. The external solutions were at 0.06 mol kg−1 total ion concentration.65,84
Download figure:
Standard image High-resolution imageAs the proton content of the external solution decreases, the proton content in the membrane sharply decreases. This is consistent with ideal-solution Donnan theory that shows that multivalent ions  preferentially partition into the membrane over univalent ions
preferentially partition into the membrane over univalent ions  according to Eq. 16 with
according to Eq. 16 with  .19 Figure 5a shows that despite very different bulk solution properties, multivalent ions display nearly identical thermodynamic behavior in the membrane.
.19 Figure 5a shows that despite very different bulk solution properties, multivalent ions display nearly identical thermodynamic behavior in the membrane.
The model slightly over predicts exchange into the membrane of divalent ions and has larger errors for trivalent ions. If experimental artifacts from incomplete exchange are negligible, then these results demonstrate that upon accounting for solution-like interactions, the membrane does not uptake trivalent ions as much as expected. In addition to ideal-solution Donnan theory, the principle cause of the preferential partitioning of multivalent cations into the membrane is the strong electrostatic interactions between the cations and multiple sulfonate groups. However, the extent of these electrostatic interactions in the membrane is overestimated by the model since sulfonate groups are treated as a line-charge rather than as imbeded at the interface of a phase-seperated structure that cannot freely interact with the trivalent iron cation. This omission may explain the relatively high values of  for multivalent ion
for multivalent ion  given in Table III.
given in Table III.
Figure 5b shows that the model very accurately predicts water uptake in these membranes as a function of fractional proton exchange  . Consequently, this approach of incorporating solution-like interactions of multivalent electrolyte solutions in the membrane is sufficient to calculate water uptake into the membranes at dilute conditions. As with monovalent cations, the
. Consequently, this approach of incorporating solution-like interactions of multivalent electrolyte solutions in the membrane is sufficient to calculate water uptake into the membranes at dilute conditions. As with monovalent cations, the  and
and  values determine the water uptake in the membranes.
values determine the water uptake in the membranes.
Ion- and water-uptake isotherms in mixed electrolytes
We now consider ion uptake from ternary electrolytes that are relevant in vanadium redox-flow-batteries. Figure 6 shows vanadium ion partitioning in a mixed sulfuric-acid electrolyte by plotting measured23 (symbols) and predicted (lines) uptake of vanadium IV ( ) and V (
) and V ( ) (a) and total sulfate (dashed lines, right axis) and water uptake (solid lines, left axis) (b) as a function of total external vanadium concentration. The total sulfate molarity is 5 mol L−1, which we convert to molality using a density of sulfuric acid solution of 1.3 g cm−3 given by34. We fit
) (a) and total sulfate (dashed lines, right axis) and water uptake (solid lines, left axis) (b) as a function of total external vanadium concentration. The total sulfate molarity is 5 mol L−1, which we convert to molality using a density of sulfuric acid solution of 1.3 g cm−3 given by34. We fit  and
and  to reduce error between the measured and calculated vanadium ion uptake in Fig. 6a (see Table III). As the vanadium concentration in the external solution increases, the membrane absorbs more vanadium. V(V) absorbs less into the membrane because of its lower charge. The water content of the membrane remains constant as the vanadium concentration increases whereas the total sulfate concentration decreases slightly. The model simultaneously calculates these three properties accurately.
to reduce error between the measured and calculated vanadium ion uptake in Fig. 6a (see Table III). As the vanadium concentration in the external solution increases, the membrane absorbs more vanadium. V(V) absorbs less into the membrane because of its lower charge. The water content of the membrane remains constant as the vanadium concentration increases whereas the total sulfate concentration decreases slightly. The model simultaneously calculates these three properties accurately.
Figure 6. Measured23 (symbols) and calculated (solid lines) membrane vanadium content  of V(IV) (octagons) and V(V) (diamonds) (a), water content λ (b, left axis) and total sulfate content
of V(IV) (octagons) and V(V) (diamonds) (a), water content λ (b, left axis) and total sulfate content  (b, right axis) as a function external vanadium concentration in sulfuric acid with a total sulfate concentration of 5 mol L−1. Dotted line in (a) is the content of V(IV)-bisulfate ion pairs
(b, right axis) as a function external vanadium concentration in sulfuric acid with a total sulfate concentration of 5 mol L−1. Dotted line in (a) is the content of V(IV)-bisulfate ion pairs 
Download figure:
Standard image High-resolution imageIn concentrated electrolytes, ion association is an important phenomenon. First, protons and sulfate associate to form bisulfate, as previously discussed. The dotted line in Fig. 6a shows that  further associates with
further associates with  leading to
leading to  ion pairs.86 Changing concentrations of various species shifts this equilibrium and couples the thermodynamic behaviors of the different species.
ion pairs.86 Changing concentrations of various species shifts this equilibrium and couples the thermodynamic behaviors of the different species.
Conclusions
This work develops a mathematical model for multicomponent thermodynamic activity of both water and ions in phase-separated cation-exchange membranes. Microscale theory predicts how the free energy of the system changes with electrolyte concentration and membrane water content. The free energy accounts for the thermodynamic behavior of water and ions as they exhibit in bulk electrolyte solutions. We include swelling and steric interactions with the polymer into these expressions to account for the membrane.
The proposed model shows that a balance between solution-like interactions and polymer swelling dictates water uptake of membranes in concentrated electrolytes. The molecular properties of the aqueous cation are particularly important to describe water and ion uptake. More favorable interactions between cations and polymer sulfonate group increase their uptake and reduce water uptake.
The molecular-thermodynamic attributes of the ions in bulk electrolyte solution describe their thermodynamic properties in membranes. The model relies on one membrane-specific adjustable parameter and one membrane-cation specific adjustable parameter. The model quantitatively agrees with experiments over a wide range of electrolyte concentrations and compositions.
Acknowledgments
The work presented here was funded, in part, by the Advanced Research Projects Agency–Energy (ARPA-E), US Department of Energy (DOE) under Award Numbers DEAR0000149 (UTRC) and DEAC0205CH11231 (LBNL with cost share from UTRC). (The information, data, or work presented herein was funded in part by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof). Andrew Crothers and Adam Weber also acknowledge that this material is based upon work supported in part by the Army Research Office under contract AWD00004008. Work by Robert Darling was supported as part of the Joint Center for Energy Storage Research, an Energy Innovation Hub funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under contract DE-AC02-06CH11357. Work by Clayton Radke was also partially supported by the Fuel Cell Performance and Durability Consortium (FC-PAD), by the Fuel Cell Technologies Office (FCTO), Office of Energy Efficiency and Renewable Energy (EERE), of the U.S. Department of Energy under contract number DEAC0205CH11231. The authors acknowledge fruitful discussions with Meron Tesfaye, Douglas Kushner, Peter Dudenas, and Michael Gerhardt.








