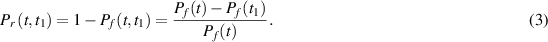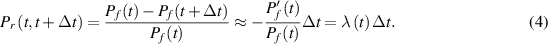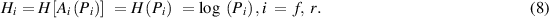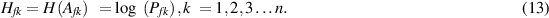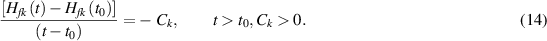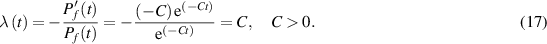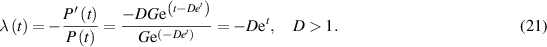Reliability science is like an edifice to be built up with solid bricks

The steam engine was the first machine to provide large amounts of energy without space and time restrictions. It ushered the Industrial Revolution, a movement that affected every country in the world and gave rise to the mass production of goods for civilian and military use. The new economy, which gradually took shape beginning in the early 1800s, led customers and manufacturers to be more sensitive about the performances of equipment and the quality of products. This focus became even more pronounced with the Second World War, which saw the most powerful production organization that had ever been set up to that time. The increasing reliance on technology has enhanced the need for more precise evaluation of machines and tools. There was an effort to sharpen the notions of risk and reliability and quantify them. In the sixties of the past century, capitalist and communist economies began to support reliability studies with vigor.

Theoretical and empirical research projects confronted a vast assortment of issues since the early stages (Saleh and Marais 2006, Rueda and Pawlak 2004). Scholars drew attention from tiny components to complex machinery, from material products to processes and organizations, from equipment to living beings. Phenomena such as wear and tears, aging, redundancy and risks have been extensively explored. Many measures have been devised to achieve the desired quality of products through prevention, maintenance, optimization and safety techniques (Nowakowski 2015). Testing and control methods have been improved. Broad movements and global events have also attracted the attention of researchers. For instance, climate changes harm installations around the world; and cybersecurity has become an hot topic in the last few years (Alazab and Alazab 2024). Actually, the studies about reliability and risk have penetrated numerous fields from engineering to medicine, from software systems to telecommunications, from economics to social systems, and more (Juran 1995, Meeker 2009).

The abundant and multifaceted works give the impression of a rather wild territory. Karl Popper long argued about science and pseudo-science, nowadays the debate seems revolving about science and chaos. In fact, some wonder whether reliability constitutes an original body of knowledge or is nothing more than adds-on of traditional disciplines (Anderson-Cook 2019); others believe that reliability regards psychology and social science (Thompson 2003); others confine reliability to the engineering domain (Elsayed 1996). Aven (2021) develops an accurate analysis and asks whether reliability is a part of statistical inference.

Researchers who are more sensitive to fundamental themes are inclined to write reviewing papers and debating philosophical themes inspired by reliability (Alston 1995). They seem to ignore that a scientific discipline looks like a building which must be constructed brick by brick, that is to say, scientists have to discover general properties, formalize them and control the exceptions (Reznikov 2020). Such a constructive approach was applied by the Soviet school, who from the very beginning offered a contribution to the reliability field in mathematical terms and also in terms of direction. Researchers did not confine themselves to generic discourses but investigated general aspects of systems and laid the foundations of the new science. They put up the first 'bricks' and began to construct the formal-mathematical 'building' (Ushakov 2000). Not in vain do we read significant re-published volumes whose first editions are dated by 1960–1970-s. A good example is the book (Bazovsky 2004) re-printed 40 years after the first edition.

This article aims to continue the work of the pioneers and propose an answer to the debate whether the bathtub curve is a suggestive metaphor or a trustworthy scientific law.

Let us begin with the first stone laid by Boris Gnedenko et al (2015) who delivered the following theoretical results which are now lying at the heart of the reliability theory.

Suppose the system S functions without failure during the event K which occurs in the interval (0, t), and during L in (t, t₁). The system does not have any failure, so the probability of steady work between t and t₁ is given by:

$$\begin{equation}{P_f}\left(t,{t_1}\right) = P\left(K/L\right) = \frac{{P\left(KL\right)}}{{P\left(K\right)}}.\end{equation} \tag{ 1 }$$

The event KL makes steady work in (0, t₁), and (1) becomes:

$$\begin{equation}{P_f}\left(t,{t_1}\right) = \frac{{{P_f}\left({t_1}\right)}}{{{P_f}\left(t\right)}}.\end{equation} \tag{ 2 }$$

Let failure be the complement of good functioning:

$$\begin{equation}{P_r}\left(t,{t_1}\right) = 1 - {P_f}\left(t,{t_1}\right) = \frac{{{P_f}\left(t\right) - {P_f}\left({t_1}\right)}}{{{P_f}\left(t\right)}}.\end{equation} \tag{ 3 }$$

Assuming t₁ = (t + Δt), we get:

$$\begin{equation}{P_r}\left(t,t + \Delta t\right) = \frac{{{P_f}\left(t\right) - {P_f}\left(t + \Delta t\right)}}{{{P_f}\left(t\right)}} \approx - \frac{{P_f^{\prime}\left(t\right)}}{{{P_f}\left(t\right)}}\Delta t = \lambda \left(t\right)\Delta t.\end{equation} \tag{ 4 }$$

And we get:

$$\begin{equation}{P_f}\left(t\right) = {\text{e}}{\,^{ - \int\limits_0^t \lambda \left(t\right){\text{d}}t}}\end{equation} \tag{ 5 }$$

where the hazard rate λ(t), also called failure or mortality rate, is the instantaneous interruption rate and measures the propensity of S to fail depending on the age it has reached:

$$\begin{equation}\lambda \left(t\right) = - \frac{{P_f^{\prime}\left(t\right)}}{{{P_f}\left(t\right)}}.\end{equation} \tag{ 6 }$$

The probability of good functioning (5) establishes the concept of reliability in mathematical terms, but it is much more than just a definitional formula. Let us point out that logical demonstration, strong and simple, proves function (5), Moreover the events K and L make a Markovian chain, so the function (5) proves to be typical of the stochastic systems in point of logic. This means that:

• S degenerates even if it was designed and constructed without mistakes, if it is effectively managed, if it is maintained and there are not external risks. The exponential trend comes directly from the very structure of S without excluding other factors.
• The decrease of P_f (t) regards any system, no matter if it is artificial or natural.
• It is impossible to avoid the dwindle of P_f (t), practitioners can only slow down its speed.
• This goal is not so handy since the exponential function describes 'the most rapid' evolution.

Equation (5) has broad coverage, being an optimal combination of simplicity and strength, so it turns out to be a law underpinning the reliability science which involves engineering (mechanical, electrical, chemical etc) and biological sciences (medicine, physiology, microbiology etc).

A scientific law describes significant and undisputable facts. Gnedenko and his colleagues gave the rigorous justification of a phenomenology that had long been sensed and perceived in an approximate way. They did not waste time in ethereal considerations and factually laid the foundation stone of the new discipline proving how it is ruled by a unifying principle.

Currently, the hazard function is viewed as the most informative descriptor of the system behavior and capacity. A large number of textbooks and technical manuals present the bathtub curve as a well-established law which agrees with common experience and intuition (Rausand and Hoyland 2004, Nachlas 2017). However, critical voices have long been raised about this curve. Multiple evidence in technology (Martin 2006, Gaonkar et al 2021) and biology (Jones et al 2014) disprove the bathtub curve as standard reference. Among theorists Asher (1984) is one of the pioneers in this field of research, more recent works can be mentioned (Moubray 1997, Klutke et al 2003, Cheng 2006) which demonstrate significant exceptions to the theoretical forecast.

In reality, Gnedenko et al (2015) holds the bathtub curve is derived from 'many empirical results' and the rigorous demonstration is still lacking; so, we point out:

• 1.  
  Equation (5) plots the increasing degradation of the system, which, however, has not yet been formalized.
• 2.  
  The bathtub curve has to be formally justified.
• 3.  
  Over the years, experiments have shown numerous exceptions to the bathtub curve.

We reasonably conclude that after the first brilliant mathematical results (5) and (6), we should find a precise time function which:

• (a)  
  Describes the degradation of S growing over time (issue 1).
• (b)  
  Demonstrate the bathtub trend of λ(t) (issue 2).
• (c)  
  Explains the exceptions of the bathtub trends (issue 3).

I worked on this project for many years, and the partial results have been published (Rocchi 2000, 2002, 2017a) and collected in the book (Rocchi 2017b). This paper aims to discuss the strengths and weaknesses of the results obtained. The following pages illustrate how objectives (a), (b) and (c) have been achieved.

Let the system S has either the functioning state A_f or the failure state A_r , when:

$$\begin{equation}{P_f}\left( t \right)\end{equation} \tag{ 7a }$$

$$\begin{equation}{P_r}\left( t \right){\text{ }} = {\text{ }}\left[ {1{\text{ }}-{P_f}\left( t \right)} \right].\end{equation} \tag{ 7b }$$

Universal experience shows how systems relentlessly degrade and become unable to achieve the goals for which they were built. Repairs and maintenance slow the descent of P_f (t) but anyway S reaches its final end; devices are dumped and living beings die. This means that the failure state A_r , once entered, cannot be left.

The literature presents two main models to address such situations: the absorbing Markovian state and the irreversible thermodynamic state. I found the second formal model more fruitful and imported the Boltzmann entropy into the reliability field. The idea is that A_f and A_r can be reached without restriction and then they take on two alternative behaviors. If the state is easily abandoned, then it is reversible; if the state cannot be abandoned then it is irreversible. The properties of reversibility and irreversibility are similar to the faces of the same coin, that is why they can be formalized jointly by Boltzmann-like entropy which tells something more than the bare probabilities of the state A_f and A_r . This function is formally based on the axioms of continuity, monotonic increment and additivity. The proof can be found in (Rocchi 2017b) and yields the following result:

$$\begin{equation}{H_i}_{} = H\left[ {{A_i}\left( {{P_i}} \right)} \right]{\text{ }} = H\left( {{P_i}} \right){\text{ }} = {\text{log}}{\text{ }}\left( {{P_i}} \right),i{\text{ }} = {\text{ }}f,{\text{ }}r.\end{equation} \tag{ 8 }$$

The domain of (8) is the variation range of probability and the codomain is (−∞, 0) (figure 1).

Zoom In Zoom Out Reset image size

Why use entropy H(P_i )? How does it produce new results beyond the probability description?

The system degenerates in various ways during infancy, maturity and ageing, and H(P_i ) allows us to describe the various forms of degradation in simple and elegant manners. As an example, the reader reads 'the principle of degradation' in this section, more results in the next pages.

What is the physical meaning of H(P_i )? And its properties?

The Boltzmann-like entropy applies to both the states of S, more specifically the reliability entropy H_f expresses the aptitude of S to work and the recovery entropy H_r illustrates the disposition of S to be repaired. Four extreme situations, coupled two by two and deriving from (7a ) and (7b ), should explain more clearly the properties of H_f and H_r .

• [a1]  
  When H_f is 'high', it means that the functioning state is rather stable, and the system works steadily. In particular, the more H_f is high, the more A_f is irreversible.
• [a2]  
  At the same time H_r is 'low', S leaves A_r quickly and one says that S is easily restored or maintained.
• [b1]  
  On the other hand, when H_f is 'low', S often abandons A_f since it is ineffective and incapable of working.
• [b2]  
  At the same time H_r is 'high', the workers operate on S with effort. In particular, the more H_r is 'high', the more the failure state becomes irreversible, S is hard to repair and/or maintain.

Situation, which [b1] and [b2] point out by words, is formalized as follows:

$$\begin{equation}\mathop {\lim }\limits_{{P_f} \to 0} H\left({P_f}\right) = - \infty \end{equation} \tag{ 9a }$$

$$\begin{equation}\mathop {\lim }\limits_{{P_r} \to 1} H\left({P_r}\right) = 0.\end{equation} \tag{ 9b }$$

Limits (9a ) and (9b ) describe the irreversible final condition of S. They apply to the irreparable system which runs until the first failure and the reparable system whose restorations do not modify the final destine when S goes to the scrap if it is a device, and to the death if living being.

The derivative of H_i is always positive:

$$\begin{equation}H^{\prime}\left({P_i}\right) = \frac{1}{{{P_i}\log \left(e\right)}},\,i = f\,{\text{or}}\,r.\end{equation} \tag{ 10 }$$

So H(P_i ) varies monotonically with P_i and in turn probability implies its time dependency:

$$\begin{equation}{H_i} = {\text{ }}H\left( {{P_i}} \right) = {\text{ }}H\left[ {{P_i}\left( t \right)} \right] = {\text{ }}{H_i}\left( t \right),\,\,i{\text{ }} = {\text{ }}f\,{\text{or}}\,r.\end{equation} \tag{ 11 }$$

Result (5) shows how probabilities (7a ) and (7b ) approach the limit values (8a ) and (8b ) by time passing, so we can fix the following tenet.

Principle of degradation: let t₀ and t are two times belonging to the system lifespan. If S is not restored, we have:

$$\begin{equation}{H_f}\left( t \right){\text{ }} \lt {H_f}\left( {{t_0}} \right),\quad t \gt {t_0}\end{equation} \tag{ 12a }$$

$$\begin{equation}{H_r}\left( t \right){\text{ }} \gt {H_r}\left( {{t_0}} \right),\quad \gt {t_0}.\end{equation} \tag{ 12b }$$

In summary, the running system S passes from situation [a1] and [a2] to limit situation (9a ) and (9b ) due to ineluctable and irreversible principle of degradation (12a ) and (12b ).

A number of processes go regularly in only one direction and do not revert, such as the quantum wave which collapses and becomes a particle, but a particle never collapses; puffs of smoke expand in the air but not shrink; and heat goes from a warmer body to a colder one. These and other one-way processes are named 'arrows of time', so the univocal evolution (12a ) and (12b ) can be classified as 'the deterioration arrow of time'; it holds how machines, plants and animals become older and never younger; systems go toward death and not toward youth.

All these phenomena make evident the irreversible progress of time whose nature is still under discussion. Scholar debates whether the arrows of time are parts of time's intrinsic structure, or instead they are due to the property of physical processes that evolve one way over time. In a manner, results (12a ) and (12b ) give a contribution to the debate.

In conclusion, Boltzmann-like entropy conforms to objective (a) of section 3 and shows how system degradation involving the states A_f and A_r in parallel never spontaneously reverses.

Suppose the functioning state A_f includes n sub-states that, in practice, are the operations or the functions of S. In accordance with (8), we define the reliability entropy H_fk of the generic substate A_fk :

$$\begin{equation}{H_{fk}} = H\left( {{A_{fk}}} \right){\text{ }} = {\text{log}}{\text{ }}\left( {{P_{fk}}} \right),k{\text{ }} = 1,2,3 \ldots n.\end{equation} \tag{ 13 }$$

Let us analyze the behavior of S in four steps.

5.1. Constant λ

The substate A_fk is subjected to the principle (12a ) which is driven by various intrinsic and extrinsic factors. Let us consider the most regular situation; H_fk decreases at constant rate over time, and we formalize the principle of degradation this way:

$$\begin{equation}\frac{{\left[ {{H_{fk}}\left(t\right) - {H_{fk}}\left({t_0}\right)} \right]}}{{\left(t - {t_0}\right)}} = - \;{C_k},\quad \quad t > {t_0},{C_k} > 0.\end{equation} \tag{ 14 }$$

For the sake of simplicity let H_fk (t₀) = 0 and t₀ = 0, we get:

$$\begin{equation}{H_{fk}}\left(t\right) = - \,{C_k}t.\end{equation} \tag{ 15 }$$

Suppose (15) true for every substate A_{f 1}, A_{f 2}, A_{f 3},.... A_fn , then it can be proved that the probability of good functioning until the first failure follows the exponential law with constant hazard rate:

$$\begin{equation}{P_f} = {P_f}\left( t \right){\text{ }} = {\text{ }}{e^{-Ct}},\,\,\,C > {\text{ }}0\end{equation} \tag{ 16 }$$

$$\begin{equation}\lambda \left(t\right) = - \frac{{P_f^{\prime}\left(t\right)}}{{{P_f}\left(t\right)}} = - \frac{{\left( - C\right){{\text{e}}^{\left( - Ct\right)}}}}{{{{\text{e}}^{\left( - Ct\right)}}}} = C,\quad C > 0.\end{equation} \tag{ 17 }$$

5.2. Linear effect

Universal experience makes us aware that senility aggravates the degradation process. More precisely each component A_fk adversely affects neighboring parts, hence we examine separately the structure of S making a chain or otherwise a web.

If the system is linear, then A_fk can damage only a close component. The probability of good operation for a system damaged by the linear cascade effect conforms to the law of exponential power, and the hazard rate is a power of time:

$$\begin{equation}{P_f} = {P_f}\left(t\right) = B{{\text{e}}^{\left( - A{t^n}\right)}},\quad A,B,n > 1\end{equation} \tag{ 18 }$$

$$\begin{equation}\lambda \left(t\right) = - \frac{{P^{\prime}\left(t\right)}}{{P\left(t\right)}} = \frac{{\left( - AB{t^{n - 1}}\right){{\text{e}}^{\left( - A{t^n}\right)}}}}{{B{{\text{e}}^{\left( - A{t^n}\right)}}}} = A{t^{n - 1}},\quad A,B,n > 1.\end{equation} \tag{ 19 }$$

5.3. Compound effect

If the system is complex, the generic A_fk harms all the substates around it. The probability of good functioning under the compound cascade effect is the exponential-exponential function, and the hazard rate is exponential of time:

$$\begin{equation}{P_f} = {P_f}\left(t\right) = G{{\text{e}}^{\left( - D{e^t}\right)}},\quad G,D > 1\end{equation} \tag{ 20 }$$

$$\begin{equation}\lambda \left(t\right) = - \frac{{P^{\prime}\left(t\right)}}{{P\left(t\right)}} = \frac{{ - DG{{\text{e}}^{\left(t - D{e^t}\right)}}}}{{G{{\text{e}}^{\left( - D{e^t}\right)}}}} = - D{{\text{e}}^t},\quad D > 1.\end{equation} \tag{ 21 }$$

5.4. Decreasing λ

Let us go through the initial period of the system lifespan.

In the case S has been set up with a number of defects, λ(t) starts somewhat high. Manufacturers commit to correcting errors and improving the quality of S, so initial hazard rate rapidly slows down. For the sake of simplicity, a straight line formalized the decreasing hazard rate:

$$\begin{equation}\lambda \left( t \right){\text{ }} = {\text{ }} - mt{\text{ }} + {\text{ }}c,{\text{ }}m,c > {\text{ }}0.\end{equation} \tag{ 22 }$$

5.5. Overall curve

The assumptions of subsections 5.1–5.4 do not apply to all systems running in the world. Experimentalists have found several exceptions. Figure 2 shows how only 4% of aircraft components comply with the ideal scheme. Sometimes, empirical data make so irregular trends as the hazard rate seems like a roller-coaster curve', this occurs especially for electronic equipment (Wong 1981).

Zoom In Zoom Out Reset image size

6.1. Variety of situations

6.2. Strong and weak sides

Is reliability a scientific discipline?

This problem sounds outdated since the first stones have been laid and are broadly shared. The problem we are facing today is how to continue the research and extend the foundations of this discipline. The goal cannot be reached through philosophical ruminations, but by means of precise mathematical results that are consistent with one another. Our work follows this direction.

The Boltzmann-like entropy is introduced to make explicit the progressive degradation of systems and how the internal structure of S determines the decay of S without excluding external failure factors.

The function H(P_i ) shows how the standard λ(t) describes an ideal situation. It derives from precise assumptions, which may be partially true or even completely false in physical reality, depending on a number of factors. Therefore, empirical evidence that seems to contradict the bathtub-like trend of the hazard rate does not actually refute the curve but rather refutes the assumptions that are typical for each period of the system's life.

When the ideal assumptions are not verified, the entropy function continues to provide valuable support because it provides information about the condition of S or its context; and, in this way, reliability and risk analysis finds significant help. This is just to emphasize how the present theoretical work does not provide ethereal support but offers efficient tools for practitioners.