Abstract
Coulomb coupled quantum dot arrays with staircase ground state configuration have been proposed in literature for enhancing heat-harvesting and refrigeration performance (Erdman et al 2018 Phys. Rev. B 98, 045433; Walldorf et al 2017 Phys. Rev. B 96, 115415; Daré 2019 Phys. Rev. B 100 195427; Zhang and Chen 2019 Physica E 114, 113635; Daré and Lombardo 2017 Phys. Rev. B 96, 115414; Zhang et al 2016 Energy 95, 593; Sánchez and Büttiker 2011 Phys. Rev. B 83 085428; Singha 2018 Phys. Lett. A 382, 3026). Due to their mutual Coulomb interaction, a performance analysis of such systems remains complicated and necessitates consideration of microscopic physics using density matrix formulation. However the path of transport analysis starting from the system Hamiltonian to density matrix formulation is complicated and lacks the simplicity and intuitive aspect of sequential electron transport conveyed by the quantum master equation (QME) approach. In this paper, starting from the system Hamiltonian and employing the density matrix formulation, I derive the QME of a system of three quantum dots, two of which are electro-statically coupled. The framework elaborated in this paper can be further extended to derive QME of systems with higher number of Coulomb coupled quantum dots. Hence, the formulation developed in this paper can pave the way towards an intuitive analysis of transport physics for an array of Coulomb coupled quantum dots in the sequential tunneling regime.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Recently with the progress of fabrication technology, a lot of effort has been geared towards nanoscale solid state quantum dot devices which, due to their discrete energy spectrum, form ideal beds of quantum computation, heat harvesting and refrigeration, etc. Due to their small size, quantum dots that are separated in space often exhibit capacitive charge coupling which offers another degree of freedom to manipulate charge, energy and spin. This phenomenon of electrostatic or charge-based coupling between spatially separated quantum dots is known as Coulomb coupling, which gives rise to a well known phenomena known as Coulomb blockade. Quantum dots that are spatially separated, may be bridged to obtain strong electrostatic coupling between them [1, 2]. In addition, the bridge may be fabricated between two desired dots to radically increase their mutual electrostatic coupling, without affecting the other dots [1–3]. The effect of Coulomb coupling on the current spectra as well as methods to enhance Coulomb coupling between quantum dots has been well explored via experiments [1–3]. However, a theoretical analysis of such Coulomb coupled dots is complicated and requires a full analysis of the microscopic physics starting from the system Hamiltonian. This is particularly true when a few or all of the dots in the system are Coulomb coupled to one or more adjacent dots. In addition, the analysis approach of such set-ups, starting from the system Hamiltonian, often masks the intuitive aspect of sequential transport physics, which is generally beneficial to the experimental community to further refine device characteristics.
In this paper, starting from the microscopic physics, I methodically derive the quantum master equations (QME) of Coulomb-coupled dot arrays in the sequential tunneling limit. In addition to being a simpler framework, the QME approach [4–9] bears the intuitive aspect of sequential electron transport and have been extensively used in literature to analyze the properties of single electron transistors and quantum dots in the Coulomb blockade regime. However, to the best of my knowledge, such approach has not yet been used to analyze arrays of quantum dots in which one or more dots may be Coulomb coupled with some others. Here, starting from the system Hamiltonian and the density matrix formulation, I derive the quantum master equations of the Coulomb coupled system demonstrated in figure 1. Such type of Coulomb coupled systems have already been proposed for the optimal non-local refrigeration [10]. The system consists of three dots S1, S2, and G1 which are electrically coupled to the reservoirs L, R and G respectively. S1 and S2 are tunnel coupled to each other, while G1 is capacitively coupled to S1. The ground states of S1 and S2 form a stair-case configuration with 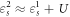 .
.
Figure 1. Schematic of a system of coupled quantum dots S1, S2 and G1. The dot S1 and S2 are electrically connected to the reservoirs L and R respectively, while G1 is electrically connected to the reservoir G. S1 and S2 are tunnel coupled while G1 and S1 are capacitively coupled with a mutual charging energy U.
Download figure:
Standard image High-resolution imageTo derive the quantum master equations of the system, I start from the device Hamiltonian. The increase in total total electrostatic energy EC of the system consisting of three dots, due to fluctuations from the reservoirs, can be given by:
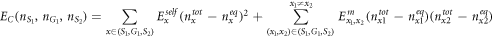
where 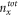 is the total electron number, and
is the total electron number, and 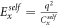 is the electrostatic energy due to self-capacitance
is the electrostatic energy due to self-capacitance 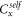 of quantum dot 'x' with its surrounding terminals.
of quantum dot 'x' with its surrounding terminals.  is the electrostatic energy arising out of interdot Coulomb interaction between two different quantum dots that are separated in space.
is the electrostatic energy arising out of interdot Coulomb interaction between two different quantum dots that are separated in space. 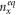 is the electron number at system equilibrium at 0 K and is to be determined by the minimum possible electrostatic energy of the system.
is the electron number at system equilibrium at 0 K and is to be determined by the minimum possible electrostatic energy of the system. 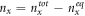 is the number of electrons in the ground state of the dot x. The electron number in the ground state of the quantum dots may fluctuate at finite temperature due to fluctuations from the reservoirs. Here, a minimal physics based model is used to derive the rate equations. I assume that the electrostatic energy due self-capacitance is much greater than than the average thermal voltage kT/q or the applied bias voltage V, that is
is the number of electrons in the ground state of the dot x. The electron number in the ground state of the quantum dots may fluctuate at finite temperature due to fluctuations from the reservoirs. Here, a minimal physics based model is used to derive the rate equations. I assume that the electrostatic energy due self-capacitance is much greater than than the average thermal voltage kT/q or the applied bias voltage V, that is 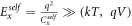 , such that electron occupation probability or transfer rate via the Coulomb blocked energy level, due to self-capacitance, is negligibly small. The analysis of the entire system of dots may hence be approximated by limiting the maximum number of electrons in each dot to one. Thus the analysis of the entire system may be limited to eight multi-electron levels, which I denote by the electron occupation number in the ground state of each quantum dot. Hence, a possible state of interest in the system may be denoted as
, such that electron occupation probability or transfer rate via the Coulomb blocked energy level, due to self-capacitance, is negligibly small. The analysis of the entire system of dots may hence be approximated by limiting the maximum number of electrons in each dot to one. Thus the analysis of the entire system may be limited to eight multi-electron levels, which I denote by the electron occupation number in the ground state of each quantum dot. Hence, a possible state of interest in the system may be denoted as  , where
, where  . To proceed further from here, with a slight abuse of notation, I simply denote the eight multi-electron states as
. To proceed further from here, with a slight abuse of notation, I simply denote the eight multi-electron states as 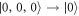 ,
, 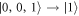 ,
, 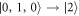 ,
, 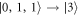 ,
, 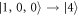 ,
, 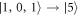 ,
, 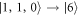 , and
, and 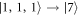 .
.
The Hamiltonian of the system consisting of these three quantum dots without any reservoir coupling may be written as:
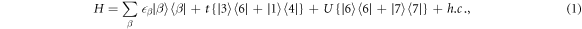
where 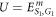 is the Coulomb coupling energy between the dots S1 and G1 in figure 1 and t is the electron hopping amplitude between the adjacent dots S1 and S2. Under the assumption of weak reservoir to system coupling and small hopping amplitude t, the temporal dynamics of the system density matrix can be evaluated by the partial trace over the density matrix of the entire set-up of the reservoirs and the dots [4–9]. Taking the partial trace of the combined density matrix over the reservoir states, the diagonal and the non-diagonal elements of the density matrix ρ of the system of quantum dots may be given as a set of modified Liouville euqations [4–9]:
is the Coulomb coupling energy between the dots S1 and G1 in figure 1 and t is the electron hopping amplitude between the adjacent dots S1 and S2. Under the assumption of weak reservoir to system coupling and small hopping amplitude t, the temporal dynamics of the system density matrix can be evaluated by the partial trace over the density matrix of the entire set-up of the reservoirs and the dots [4–9]. Taking the partial trace of the combined density matrix over the reservoir states, the diagonal and the non-diagonal elements of the density matrix ρ of the system of quantum dots may be given as a set of modified Liouville euqations [4–9]:
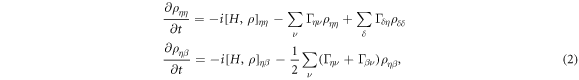
where [A, B] denotes the commutator of A and B and  . The elements
. The elements  and
and  in the above equation denote any diagonal and non-diagonal element of the system density matrix respectively. The parameters Γij take into account the transition between system states due to electronic tunneling between the system and the reservoirs and are only non-zero when the system can transit from state
in the above equation denote any diagonal and non-diagonal element of the system density matrix respectively. The parameters Γij take into account the transition between system states due to electronic tunneling between the system and the reservoirs and are only non-zero when the system can transit from state  to
to  (or vice-versa) due to tunneling of electrons in and out of the system from the reservoir. In our derivation, assuming a statistical quasi-equilibrium distribution of electrons inside the reservoirs, we can express
(or vice-versa) due to tunneling of electrons in and out of the system from the reservoir. In our derivation, assuming a statistical quasi-equilibrium distribution of electrons inside the reservoirs, we can express 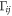 as:
as:
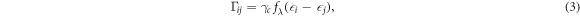
fλ( ) being occupancy probability of the corresponding reservoir λ at energy
) being occupancy probability of the corresponding reservoir λ at energy  and
and 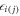 is the total electronic energy of the system in the state i (j). ᵞl=ᵞr=ᵞg=ᵞc denotes the reservoir to system coupling strength..
is the total electronic energy of the system in the state i (j). ᵞl=ᵞr=ᵞg=ᵞc denotes the reservoir to system coupling strength..
To derive the quantum master equations for the entire system, it is essential to derive the inter-dot tunneling rates. For the particular system schematic demonstrated in figure 1, interdot tunneling changes the system states as:  and
and  . Taking the time derivative of the density matrix to be zero in steady state, I use the second equation of (2), to get,
. Taking the time derivative of the density matrix to be zero in steady state, I use the second equation of (2), to get,
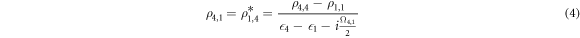
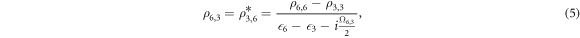
where Ωi, j is the combination of all the reservoir-to-system tunneling events (or vice-versa) leading to the decay of the states i and j. For the system under consideration, Ω4,1 and Ω6,3 can be given by:
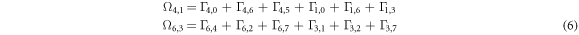
The time derivative of diagonal density matrix elements ρ6,6 and ρ3,3 can be written as (using the first equation of 2):
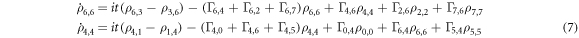
I next substitute, in equation (7), the expressions for ρ6,3, ρ3,6, ρ4,1 and ρ1,4 from equation (4), to get the time evolution of the density matrix elements of ρ6,6 and ρ4,4 as:
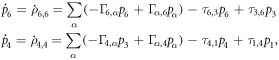
where 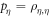 and
and
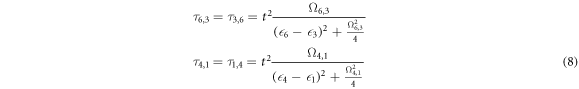
In the set of equations (8), τ4,1 and 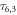 correspond to the interdot tunneling rates when the number of electrons in dot G1 is 0 and 1 respectively. When
correspond to the interdot tunneling rates when the number of electrons in dot G1 is 0 and 1 respectively. When 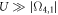 , by an appropriate choice of
, by an appropriate choice of  and
and 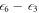 , such that,
, such that,  , that is by making
, that is by making  , we may arrive at a condition where
, we may arrive at a condition where  . Such a condition implies that the tunneling probability between the dots is negligible in the absence of an electron in G1, which is the combined impact of the capacitive coupling between
. Such a condition implies that the tunneling probability between the dots is negligible in the absence of an electron in G1, which is the combined impact of the capacitive coupling between  and staircase ground-state configuration of
and staircase ground-state configuration of  .
.
Next, I proceed towards deriving the QME of the system demonstrated in figure 1. Since, the electronic transport and ground states in S1 and G1 are mutually coupled, I treat the pair of dots S1 and G1 as a sub-system (ς1), S2 being the complementary sub-system (ς2) of the entire system consisting of three dots. I assume that 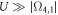 and
and 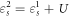 , such that
, such that 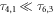 . For all practical phenomena relating to electron transport, it can hence be assumed that
. For all practical phenomena relating to electron transport, it can hence be assumed that  . The state probability ς1 is denoted by
. The state probability ς1 is denoted by 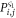 , i and j being the number of electrons in the dot S1 and G1 respectively.
, i and j being the number of electrons in the dot S1 and G1 respectively. 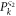 , on the other hand, denotes the probability of occupancy of the dot S2 in the sub-system ς2. Note that breaking down the entire system into two sub-system in this way is possible only in the limit of weak tunnel and Coulomb coupling between the two sub-systems, as such the state of one sub-system remains unaffected by a change in state of the other sub-system. In such a limit, the diagonal elements of the density matrix can be written as:
, on the other hand, denotes the probability of occupancy of the dot S2 in the sub-system ς2. Note that breaking down the entire system into two sub-system in this way is possible only in the limit of weak tunnel and Coulomb coupling between the two sub-systems, as such the state of one sub-system remains unaffected by a change in state of the other sub-system. In such a limit, the diagonal elements of the density matrix can be written as: 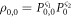 ,
,  ,
,  ,
,  ,
,  The QME for the sub-system ς1 and ς2 can, hence, be derived by expressing the sub-system state probabilities as the sum of two or more diagonal elements of the density matrix:
The QME for the sub-system ς1 and ς2 can, hence, be derived by expressing the sub-system state probabilities as the sum of two or more diagonal elements of the density matrix:
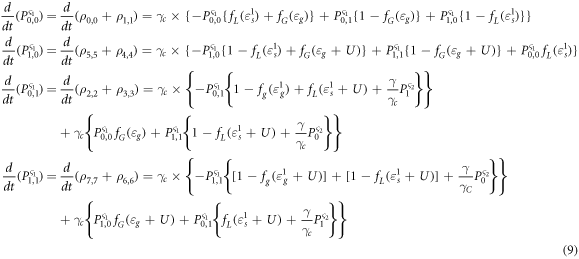
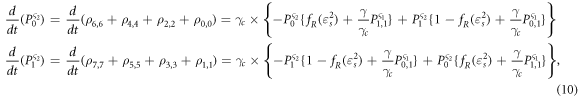
where  and
and 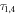 are assumed to be zero and
are assumed to be zero and  . An intuitive approach to derive the QME for an arbitrary array with higher number of Coulomb coupled quantum dots is detailed in the Supplementary section. The sets of equations (9) and (10) coupled to each other. To calculate the values of the state probabilities, these sets of equations may be solved numerically using any iterative method. On solution of the state probabilities given by equations (9) and (10), the charge current
. An intuitive approach to derive the QME for an arbitrary array with higher number of Coulomb coupled quantum dots is detailed in the Supplementary section. The sets of equations (9) and (10) coupled to each other. To calculate the values of the state probabilities, these sets of equations may be solved numerically using any iterative method. On solution of the state probabilities given by equations (9) and (10), the charge current  through the system can be calculated using the equations:
through the system can be calculated using the equations:

Next, I use the set of equations (9)–(11), to characterize the set-up demonstrated in figure 1. Without loss of generality, I assume that  and
and 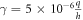 . In particular, I show the characteristics of the set-up, as captured by the proposed QME for three different cases: (i) fixed voltage bias, (ii) fixed temperature bias and (iii) varying voltage bias and capacitive coupling energy. Figure 2(a) demonstrates the regime of current flow through the system at
. In particular, I show the characteristics of the set-up, as captured by the proposed QME for three different cases: (i) fixed voltage bias, (ii) fixed temperature bias and (iii) varying voltage bias and capacitive coupling energy. Figure 2(a) demonstrates the regime of current flow through the system at 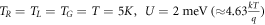 , and a voltage bias
, and a voltage bias 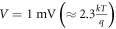 for a range of positions of εg and
for a range of positions of εg and  . We note that the maximum current flow occurs when εg goes a few kT below the equilibrium Fermi energy μ0, that is when the level εg is always occupied with an electron, as expected. Similarly, the current flow occurs when
. We note that the maximum current flow occurs when εg goes a few kT below the equilibrium Fermi energy μ0, that is when the level εg is always occupied with an electron, as expected. Similarly, the current flow occurs when  lies in the bias window, that is from
lies in the bias window, that is from  . Figure 2(b) demonstrates the regime of short-circuited thermoelectric current flow through the system for a temperature bias given by
. Figure 2(b) demonstrates the regime of short-circuited thermoelectric current flow through the system for a temperature bias given by  and
and 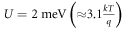 for a range of position of εg and
for a range of position of εg and 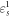 . This short-circuited current flows by absorbing heat energy from the reservoir G and constitutes the non-local thermoelectric action proposed in the [11–17]. Figure 2(c) shows the regime of current flow (absolute value) with variation of the Coulomb coupling energy U and the voltage bias V at
. This short-circuited current flows by absorbing heat energy from the reservoir G and constitutes the non-local thermoelectric action proposed in the [11–17]. Figure 2(c) shows the regime of current flow (absolute value) with variation of the Coulomb coupling energy U and the voltage bias V at 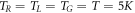 ,
,  and
and  . As expected, the current magnitude increases to saturation with increase in magnitude of the applied bias V and decreases with the increase in U (since the electron occupancy in probability in εg decreases with increase in U. In addition the energy level
. As expected, the current magnitude increases to saturation with increase in magnitude of the applied bias V and decreases with the increase in U (since the electron occupancy in probability in εg decreases with increase in U. In addition the energy level  moves outside the bias window with an increase in U).
moves outside the bias window with an increase in U).
Figure 2. The characteristics of the set-up as predicted by the proposed QME. Colour plot for (a) current for a given voltage bias.  a voltage bias
a voltage bias 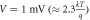 (b) Short-circuited current for a given temperature bias.
(b) Short-circuited current for a given temperature bias.  and
and 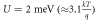 (c) variation in current magnitude with applied voltage V and Coulomb coupling energy U.
(c) variation in current magnitude with applied voltage V and Coulomb coupling energy U. 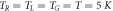 and
and  and
and 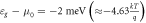 . μ0 is the equilibrium Fermi energy of the entire system and
. μ0 is the equilibrium Fermi energy of the entire system and  is the average temperature of the reservoirs L(R) and G.
is the average temperature of the reservoirs L(R) and G.
Download figure:
Standard image High-resolution imageTo conclude, in this paper, I have methodically derived the QME for a Coulomb coupled system with three quantum dots. The proposed QME has been derived from the system Hamiltonian using density matrix formulation and captures the intuitive aspects of the sequential electron transport and current flow. The framework elaborated in this paper can be further extended to derive QME of systems with higher number of Coulomb coupled quantum dots. Hence, the formulation developed in this paper can pave the way towards an intuitive analysis of transport physics for an array of Coulomb coupled quantum dots in the sequential tunneling regime.
Acknowledgments
The author would like to thank Sponsored Research and Industrial Consultancy (IIT Kharagpur) for their financial support via grant no. IIT/SRIC/EC/MWT/2019-20/162.



