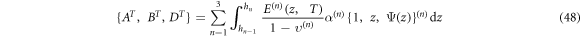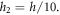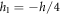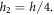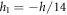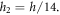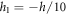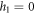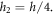Abstract
A higher-order shear deformation plate theory (HSDT) is applied in this work to study the thermomechanical bending behavior of sandwich plates composed of functionally graded (FG) face sheets and fully ceramic core. Material properties of the FG sandwich plate are dependent on temperature and supposed to be graded continuously across the sandwich plate thickness direction. Power-law model is adopted to describe continuous variation of material properties of FG sandwich plate. Temperature variation along the thickness direction is obtained by solving the one-dimensional heat conduction equation. An accurate solution of temperature variation along the thickness direction is employed by taking into account the thermal conductivity, the inhomogeneity parameter and the sandwich schemes. The governing equations of simply-supported FG sandwich plates are derived by means of the Hamilton's variational principle combined with the Navier's solutions. Numerical results indicate the impact of volume fraction index, temperature difference and side-to-thickness ratio on the deflections and stresses are carried out. The accuracy of the proposed five-order shear deformation theory is validated by comparing it with some available solutions in the literature. The present model is simple and can theoretically cover the existing polynomial models.
Export citation and abstract BibTeX RIS
Corrections were made to this article on 21 January 2020. Surname of third author corrected.
1. Introduction
Among microstructures, Functionally Graded Materials (FGM) have increased the interest of the scientific community, owing to their high thermal and mechanical properties. These Materials have been adopted as an important component in various industries such as aircraft, automobile, aerospace, and shipbuilding due to their high durability and strength.
In the past few years, thermomechanical deformation behavior of FG plates has attracted the attention of several research in various engineering industries like aerospace structures, nuclear power plants and heat engine components etc. Reddy and Chin (1998) examined dynamic behavior of FG cylinders and plates by including thermomechanical coupling by utilizing the finite element method (FEM). On the basis of the third-order shear deformation theory (TSDT), Reddy (2000) developed a theorical formulation to analyze stresses and deflections of FG plates using the finite element method. The thermomechanical coupling and time dependency are taken into account. Using the asymptotic method, three-dimensional (3D) deflections of FG plates with simply supported boundary conditions are examined by Reddy and Cheng (2001). Using the TSDT, the effect of uniform temperature rise combined with uniform lateral pressure on the nonlinear bending of FG plates for different boundary conditions is discussed by Yang and Shen (2003). Senthil and Batra (2003) reported an analytical solution to study the bending of FG plates under time-dependent thermomechanical loads. Aliaga and Reddy (2004) employed the TSDT and the von Karman geometric nonlinearity for linear and nonlinear thermomechanical deflection of FG plates under dynamic and static loads. The transient thermoelastic deformations and stresses of simply supported and clamped FG plates are carried out by Qian and Batra (2004) by employing the meshless local Petrov–Galerkin method in conjunction with the HSDT. Based on the element-free Galerkin method, Dai et al (2005) applied a meshfree model to examine the thermomechanical static deflections and dynamic behavior of FG plates containing piezoelectric sensors and actuators using the first order shear deformation plates theory (FSDT). Navazi and Haddadpour (2007) employed the Galerkin's method to examine the aero-thermoelastic stability of FG panels. Brischetto et al (2008) utilized Carrera's unified formulation to investigate the effect thermomechanical loadings on the deformations of FG plates. Ying et al (2009) employed the 3D thermoelasticity solution, the differential quadrature technique and the state space method to analyze the thermomechanical behavior of FG thick plates. Using the FSDT and the element-free kp-Ritz method, the deflections and stresses of FG plate under effect of thermomechanical loadings was examined by Lee et al (2009). Alibeigloo (2010) performed an analytical solution to analyze the thermoelastic behavior of FG plates based on the state-space method and Fourier series expansion. Zenkour and Alghamdi (2010a) investigated the static of ceramic/metal FG sandwich plates subjected to thermomechanical loads using different HSDTs and the classical plate theory (CPT). They have also used the same displacement theories and solution procedure to analyze the response of FG sandwich plates tacking into account the thickness stretching effect (Zenkour and Alghamdi 2010b). Zenkour (2010) utilized the sinusoidal shear deformations plate theory (SSDT) to analyze the response of FG plates under hygro-thermo-mechanical loads and subjected to elastic foundations. Based on the Lord–Shulman theory, Zhou et al (2011) employed the generalized coupled thermoelasticity to examine the transient response of three-dimensional FG plate under effect of time-dependent thermal loads. Houari et al (2013) modeled a new HSDT to simulate the thermoelastic response of FG sandwich plates. A refined four variables shear deformations plate theory is developed by Tounsi et al (2013) to stydy the thermoelastic bending response of FG sandwich plates. Taibi et al (2015) performed four variables shear deformations theory to investigate thermomechanical deformations of FG plate due to Pasternak foundation. Also, Zidi et al (2014) discussed the influences of hygro-thermo-mechanical loading on the deflections and stresses of FG plates. Another four variable refined plates theory are employed by Tlidji et al (2014) and Li et al (2016). Sobhy (2015) investigated the temperature-dependent thermomechanical bending of FG plates subjected to Winkler/Pasternak elastic foundation under different boundary conditions. Sharma et al (2016) utilized the finite element method for transient thermoelastic of FG plates with varying grading parameter. Li et al (2017) investigated the stresses and deflections of novel model of FG sandwich plate with both FG core and FG face layers. Using mesh-free method based on the FSDT, Momeni-Khabisi (2017) analyzed the static and free vibrations behaviors of orthotropic FG plates under different boundary conditions. Sator et al (2019) developed 2D formulation to analyze static of FG plates under effect of stationary thermal load. Babak Safaei et al (2019) investigated the thermal and mechanical loadings effect on bending of sandwich plates with one porous polymeric core and two carbon nanotube/polymer nanocomposite outer layers.
In this article, we present an exact analytical solution of temperature change through the FG sandwich plate thickness for bending behavior of ceramic/metal FG sandwich plates. Two types of thermal conditions are employed, thermal condition I to confirm the validity the proposed theory, and thermal condition II to perform the novel study. The thermal condition II is obtained by solving one-dimensional heat conduction equation. This solution takes into consideration the thermal conductivity, the volume fraction index and the sandwich scheme. The variation of material properties through-the-thickness are temperature dependent and vary according to a power-law function. Governing equations are derived by employing Hamilton's variational principle combined with Navier's solutions for simply supported FG sandwich plates.
2. FG sandwich plates
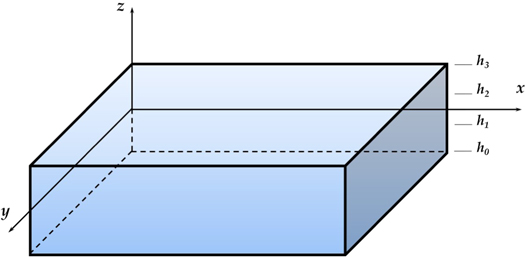
In this paper, we considered a rectangular sandwich plate with thickness 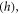 length
length 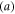 and width
and width  composed of three sheets (two FG face sheets and fully ceramic core). The vertical positions of the bottom face and the top face of the sandwich are
composed of three sheets (two FG face sheets and fully ceramic core). The vertical positions of the bottom face and the top face of the sandwich are 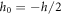 and
and 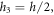 respectively. while the two interfaces are at
respectively. while the two interfaces are at  and
and  (figure 1). The variation of volume fraction through-the-thickness of the FG sandwich plate varies as follow:
(figure 1). The variation of volume fraction through-the-thickness of the FG sandwich plate varies as follow:
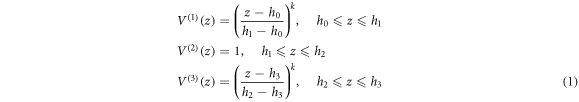
where  is the power-law index.
is the power-law index. 
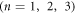 denote the effective material properties of
denote the effective material properties of 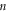 layer of FG sandwich plate and can be written as
layer of FG sandwich plate and can be written as
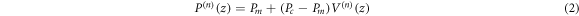
where  and
and  presents material properties of ceramic and metal constituents, respectively.
presents material properties of ceramic and metal constituents, respectively.
Figure 1. Coordinate system and geometry of the FG sandwich plate.
Download figure:
Standard image High-resolution image3. Basic equations
From the HSDT, the displacement field for the considered FG sandwich plate is expressed as
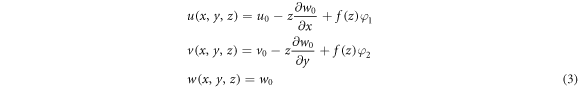
where 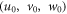 and
and 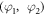 are respectively, the displacements and rotations of transverse normal on the plane
are respectively, the displacements and rotations of transverse normal on the plane 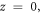 and
and 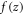 denotes the function in a way that determines the distribution of the transverse shear strains and stresses across the thickness of the plate. For example, Reddy (1990) obtained the displacement of field by setting
denotes the function in a way that determines the distribution of the transverse shear strains and stresses across the thickness of the plate. For example, Reddy (1990) obtained the displacement of field by setting  and Touratier (1991) proposed the SSDT by setting
and Touratier (1991) proposed the SSDT by setting 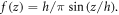 The displacement field for the CPT is obtained by setting
The displacement field for the CPT is obtained by setting 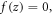 and
and 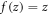 for the FSDT.
for the FSDT.
The present HSDT is given by sitting 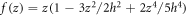
(Daikh and Zenkour, 2019)
The strains-displacements relations are defined as
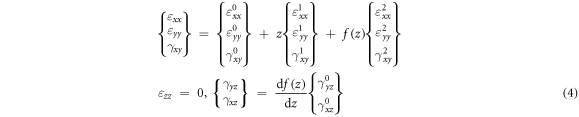
where

The stress-strain relationships contain the thermal effects can be written as
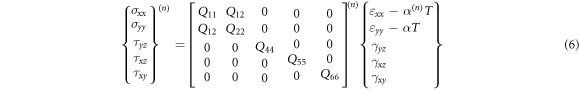
where
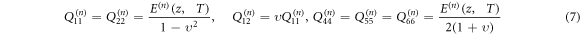
4. Governing equations
Employing the virtual work principle, the equations of equilibrium associated with the HSDT can be expressed as (Zenkour and Alghamdi 2010a)
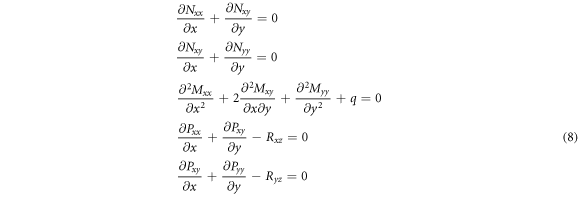
where q is the applied mechanical load. The components of stress resultants (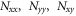 ), moment resultants (
), moment resultants (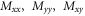 ), additional stress couples (
), additional stress couples (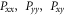 ) related with the transverse shear effect, and the transverse shear stress resultants (
) related with the transverse shear effect, and the transverse shear stress resultants ( ) are defined as
) are defined as
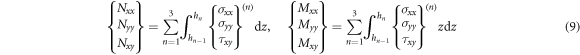
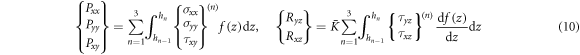
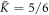 is the shear correction factor of the FSDT. The stress resultants can be expressed as
is the shear correction factor of the FSDT. The stress resultants can be expressed as
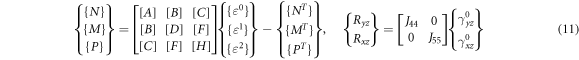
Where
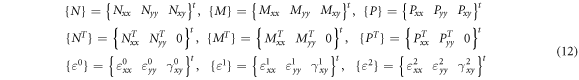
The coefficients 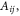
 ...,
...,  are the plate stiffness, defined by
are the plate stiffness, defined by

 denote the temperature distribution along the plate thickness direction. The stress resultants
denote the temperature distribution along the plate thickness direction. The stress resultants  the moment resultants
the moment resultants 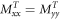 and the additional stress couples
and the additional stress couples  due to thermal loading are defined by
due to thermal loading are defined by
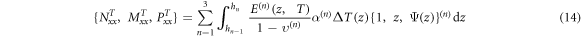
5. Thermal loads type distributions
5.1. Thermal condition I
In general, FGMs were designed as thermal barrier materials. The use of FGM structures in high-temperature environment leads to considerable changes in material properties. The material properties are changed along the thickness direction as (Kim 2005)
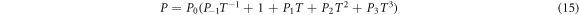
where
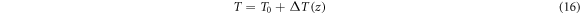
where 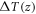 is the temperature change and
is the temperature change and 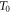 is the ambient temperature.
is the ambient temperature. 

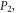 and
and  are temperature coefficients (table 1).
are temperature coefficients (table 1).
Table 1. Temperature-dependent coefficients of elastic modulus E (Pa), coefficient of thermal expansion α(K−1), mass density ρ (Kg m−3) and thermal conductivity k (W mK−1).
| P0 | P−1 | P1 | P2 | P3 | |
|---|---|---|---|---|---|
| ZrO2 (Ceramic) | |||||
| E | 244.27 e + 9 | 0 | –1,371 e–03 | 1,214 e–06 | –3,681e–10 |
| α | 12.766 e–06 | 0 | –1,491 e–03 | 1,006 e–05 | –6,778e–11 |
| ρ | 3000 | 0 | 1,133 e–04 | 0 | 0 |
| k | 1.8 | 0 | 0 | 0 | 0 |
| Ti-4V-6Al (Metal) | |||||
| E | 122.56e+9 | 0 | 4.586e–4 | 0 | 0 |
| α | 7.5788e–6 | 0 | 6.638e–4 | –3.147e–6 | 0 |
| ρ | 4429 | 0 | 0 | 0 | 0 |
| k | 7.82 | 0 | 0 | 0 | 0 |
The temperature field 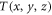 can be written as the form
can be written as the form

where  is the temperature distribution along the surface domain Ω. Most of researchers used nonlinear form of temperature profile
is the temperature distribution along the surface domain Ω. Most of researchers used nonlinear form of temperature profile  according to the displacement field as (Zenkour 2010)
according to the displacement field as (Zenkour 2010)
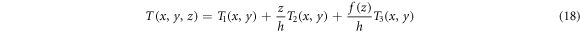
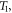
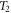 and
and 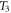 are thermal loadings. The temperature distribution is constant in the thickness direction for the CPT, linear for FSDT and nonlinear for the HSDT. The transverse thermal loads are given as
are thermal loadings. The temperature distribution is constant in the thickness direction for the CPT, linear for FSDT and nonlinear for the HSDT. The transverse thermal loads are given as
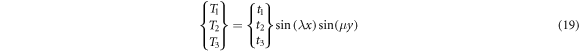
where 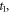
 and
and 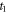 are constant temperatures and
are constant temperatures and 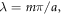

5.2. Thermal condition II
Another nonlinear temperature change along the thickness of the sandwich is proposed in this work by taking into account the effect of thermal conductivity, volume fraction index and the type of FG sandwiches. This solution is derived by solving one-dimension heat transfer equation (Kim 2005)
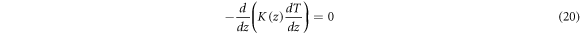
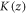 is the thermal conductivity variation along z direction. Employing the boundary conditions
is the thermal conductivity variation along z direction. Employing the boundary conditions  at
at 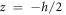 and
and 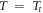 at
at 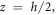 the temperature variation is obtained as (Daikh and Megueni 2018)
the temperature variation is obtained as (Daikh and Megueni 2018)
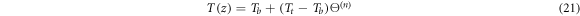
where
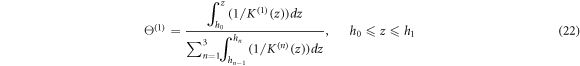
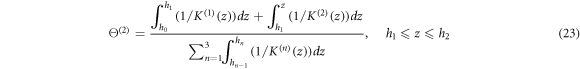
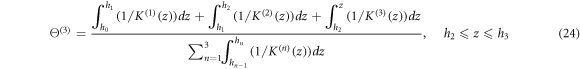
The solution of the previous equation can be written in the form of polynomial series as (Daikh et al 2019, Daikh 2019)
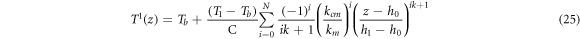
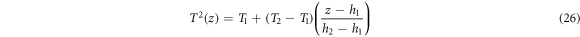
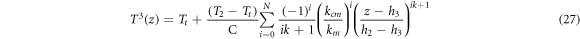
where
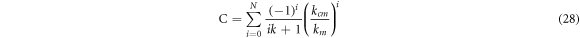
and
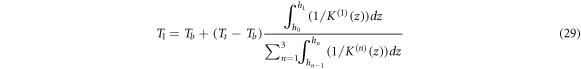
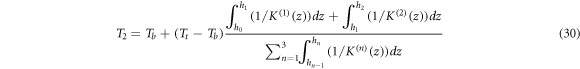
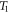 and
and  are the temperature values at the interface positions
are the temperature values at the interface positions  and
and  respectively. The temperature field
respectively. The temperature field  are sinusoidally distributed over the reference surface domain Ω as follow
are sinusoidally distributed over the reference surface domain Ω as follow
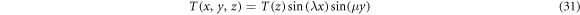
6. Solution procedure
The solution of the equilibrium equations is explored for simply supported plate subjected to thermomechanical loadings with sinusoidally distribution. The boundary conditions are
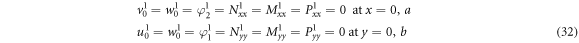
The displacement that satisfy the previous boundary conditions according to the solution procedure of Navier can be written as
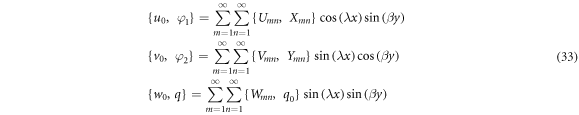
where 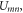


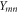 and
and  are arbitrary parameters.
are arbitrary parameters. 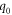 represents the intensity of the applied loading at the center of the plate.
represents the intensity of the applied loading at the center of the plate.
Inserting equation (33) into equation (8), one obtains the operator equation
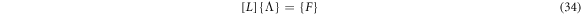
where  The elements
The elements 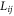 of the symmetric matrix (L) are given in appendix.
of the symmetric matrix (L) are given in appendix.
The stress components can be expressed as follows
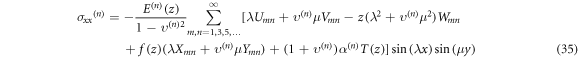
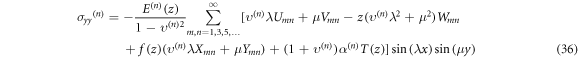
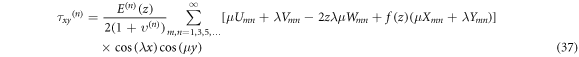
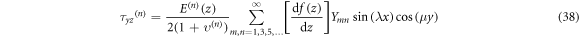
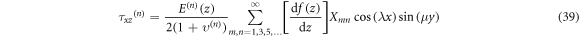
7. Numerical results
This work presents bending analysis of a rectangular simply-supported sandwich plate with FG face layers and ceramic core under impact of thermal and mechanical loads. Materials chosen in this analysis are Zirconia (ZrO2) and Titanium alloy (Ti-6Al-4V). The face sheets are graded from metal to ceramic. Numerical results are presented including dimensionless stresses and deflections. Several types of FG sandwich plates are proposed.
- 1-0-1 FG sandwich plate with

- 1-1-1 FG sandwich plate with
 and
and 
- 2-1-2 FG sandwich plate with
 and
and 
- 1-2-1 FG sandwich plate with
 and
and 
- 3-1-3 FG sandwich plate with
 and
and 
- 2-2-1 FG sandwich plate with
 and
and 
- 2-1-1 FG sandwich plate with
 and
and 
7.1. Validation of results (thermal condition I)
In the following part, using the thermal condition I, the proposed theory will be validated by comparing the present results with the reported outcomes in the literature. The materials chosen in this section are Titanium ( and
and 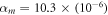 ) and Zirconia (
) and Zirconia (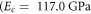 and
and  ). Poisson's ratio is chosen as constant
). Poisson's ratio is chosen as constant 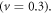 The dimensionless parameters are stated as
The dimensionless parameters are stated as
Dimensionless center deflection
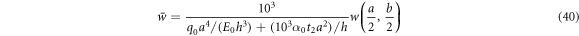
Dimensionless axial stress

Dimensionless shear stress
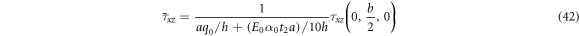
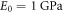 and
and  are reference values. Also, it is proposed that
are reference values. Also, it is proposed that 
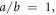
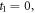 and
and 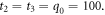
Tables 2–4 summarizes the results in terms of dimensionless deflections 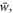 axial stresses
axial stresses 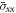 and shear stresses
and shear stresses  of FG sandwich plates, as computed by the present theory, against predictions by Li et al (2016) based on a higher-order refined plates theory RPT, and those ones by Zenkour and Alghamdi (2010b) according to the TSDT, SSDT, FSDT and CPT.
of FG sandwich plates, as computed by the present theory, against predictions by Li et al (2016) based on a higher-order refined plates theory RPT, and those ones by Zenkour and Alghamdi (2010b) according to the TSDT, SSDT, FSDT and CPT.
Table 2.
Dimensionless center deflections 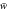 of the different FGM sandwich plates (Thermal condition I).
of the different FGM sandwich plates (Thermal condition I).
| k | Theory | 1-0-1 | 3-1-3 | 2-1-2 | 1-1-1 |
|---|---|---|---|---|---|
| 0 | Present | 0.801 904 | 0.801 904 | 0.801 904 | 0.801 904 |
| RPTa | 0.864 140 | 0.864 140 | 0.864 140 | 0.864 140 | |
| SSDTb | 0.796 783 | 0.796 783 | 0.796 783 | 0.796 783 | |
| TSDTb | 0.808 168 | 0.808 168 | 0.808 168 | 0.808 168 | |
| FSDTb | 0.895 735 | 0.895 735 | 0.895 735 | 0.895 735 | |
| CPTb | 0.457 873 | 0.457 873 | 0.457 873 | 0.457 873 | |
| 1 | Present | 1.069 523 | 1.051 591 | 1.042 720 | 1.017 611 |
| RPTa | 1.149 038 | 1.130 125 | 1.120 741 | 1.094 113 | |
| SSDTb | 1.062 840 | 1.045 026 | 1.036 213 | 1.011 263 | |
| TSDTb | 1.077 690 | 1.059 613 | 1.050 672 | 1.025 367 | |
| FSDTb | 1.190 728 | 1.170 533 | 1.160 568 | 1.132 449 | |
| CPTb | 0.610 331 | 0.599 853 | 0.594 688 | 0.580 125 | |
| 2 | Present | 1.128 667 | 1.112 108 | 1.102 961 | 1.074 761 |
| RPTa | 1.210 756 | 1.193 444 | 1.183 826 | 1.154 061 | |
| SSDTb | 1.121 608 | 1.105 175 | 1.096 094 | 1.068 091 | |
| TSDTb | 1.137 297 | 1.120 582 | 1.111 353 | 1.082 911 | |
| FSDTb | 1.257 304 | 1.238 234 | 1.227 765 | 1.195 703 | |
| CPTb | 0.645 223 | 0.635 301 | 0.629 860 | 1.613 208 | |
| 3 | Present | 1.148 870 | 1.135 178 | 1.126 824 | 1.099 136 |
| RPTa | 1.231 675 | 1.217 447 | 1.208 690 | 1.179 518 | |
| SSDTb | 1.141 655 | 1.128 080 | 1.119 793 | 1.092 312 | |
| TSDTb | 1.157 693 | 1.143 856 | 1.135 420 | 1.107 475 | |
| FSDTb | 1.280 741 | 1.264 724 | 1.255 041 | 1.223 232 | |
| CPTb | 0.657 539 | 0.649 211 | 0.644 176 | 0.627 647 | |
| 4 | Present | 1.157 485 | 1.146 114 | 1.138 551 | 1.111 954 |
| RPTa | 1.240 542 | 1.228 791 | 1.220 879 | 1.192 880 | |
| SSDTb | 1.150 192 | 1.138 926 | 1.131 428 | 1.105 041 | |
| TSDTb | 1.166 403 | 1.154 902 | 1.147 260 | 1.120 403 | |
| FSDTb | 1.290 961 | 1.277 527 | 1.268 689 | 1.237 931 | |
| CPTb | 0.662 909 | 0.655 937 | 0.651 345 | 0.635 363 | |
| 5 | Present | 1.161 748 | 1.152 092 | 1.145 172 | 1.119 631 |
| RPTa | 1.244 905 | 1.234 980 | 1.227 750 | 1.200 876 | |
| SSDTb | 1.154 412 | 1.144 851 | 1.137 993 | 1.112 660 | |
| TSDTb | 1.170 720 | 1.160 948 | 1.153 952 | 1.128 152 | |
| FSDTb | 1.296 101 | 1.284 626 | 1.276 497 | 1.246 833 | |
| CPTb | 0.665 606 | 0.659 666 | 0.655 446 | 0.640 037 |
aResults obtained by Li et al (2016). bResults obtained by Zenkour and Alghamdi (2010a).
Table 3.
Dimensionless axial stresses  of the different FGM sandwich plates (Thermal condition I).
of the different FGM sandwich plates (Thermal condition I).
| k | Theory | 1-0-1 | 3-1-3 | 2-1-2 | 1-1-1 |
|---|---|---|---|---|---|
| 0 | Present | –2.420 650 | –2.420 650 | –2.420 650 | –2.420 650 |
| RPTa | –2.911 440 | –2.911 440 | –2.911 440 | –2.911 440 | |
| SSDTb | –2.388 909 | –2.388 909 | –2.388 909 | –2.388 909 | |
| TSDTb | –2.461 177 | –2.461 177 | –2.461 177 | –2.461 177 | |
| FSDTb | –3.597 007 | –3.597 007 | –3.597 007 | –3.597 007 | |
| CPTb | –1.706 393 | –1.706 393 | –1.706 393 | –1.706 393 | |
| 1 | Present | –2.436 340 | –2.524 235 | –2.567 749 | –2.690 964 |
| RPTa | –2.892 290 | –2.985 255 | –3.031 378 | –3.162 208 | |
| SSDTb | –2.406 797 | –2.494 126 | –2.537 365 | –2.659 816 | |
| TSDTb | –2.473 903 | –2.562 491 | –2.606 343 | –2.730 494 | |
| FSDTb | –3.471 099 | –3.569 762 | –3.618 476 | –3.756 017 | |
| CPTb | –1.658 265 | –1.709 610 | –1.734 921 | –1.806 283 | |
| 2 | Present | –2.146 448 | –2.227 557 | –2.272 443 | –2.410 920 |
| RPTa | –2.589 234 | –2.674 492 | –2.721 838 | –2.868 271 | |
| SSDTb | –2.118 721 | –2.199 231 | –2.243 800 | –2.381 343 | |
| TSDTb | –2.181 780 | –2.263 627 | –2.308 903 | –2.448 528 | |
| FSDTb | –3.145 662 | –3.238 636 | –3.289 757 | –3.446 485 | |
| CPTb | –1.487 285 | –1.535 904 | –1.562 571 | –1.644 167 | |
| 3 | Present | –2.047 401 | –2.114 354 | –2.155 339 | –2.291 347 |
| RPTa | –2.486 287 | –2.556 476 | –2.599 635 | –2.743 281 | |
| SSDTb | –2.020 416 | –2.086 818 | –2.127 487 | –2.262 512 | |
| TSDTb | –2.081 815 | –2.149 449 | –2.190 823 | –2.328 042 | |
| FSDTb | –3.031 284 | –3.109 180 | –3.156 414 | –3.311 823 | |
| CPTb | –1.426 935 | –1.467 745 | –1.492 417 | –1.573 414 | |
| 4 | Present | –2.005 212 | –2.060 678 | –2.097 767 | –2.228 427 |
| RPTa | –2.442 566 | –2.500 626 | –2.539 661 | –2.677 611 | |
| SSDTb | –1.978 593 | –2.033 567 | –2.070 352 | –2.200 020 | |
| TSDTb | –2.039 172 | –2.095 247 | –2.132 710 | –2.264 592 | |
| FSDTb | –2.981 507 | –3.046 666 | –3.089 733 | –3.239 941 | |
| CPTb | –1.400 620 | –1.434 783 | –1.457 288 | –1.535 602 | |
| 5 | Present | –1.984 375 | –2.031 338 | –2.065 254 | –2.190 727 |
| RPTa | –2.421 017 | –2.470 126 | –2.688 425 | –2.638 288 | |
| SSDTb | –1.957 959 | –2.004 482 | –2.038 109 | –2.162 596 | |
| TSDTb | –2.018 086 | –2.065 589 | –2.099 863 | –2.226 550 | |
| FSDTb | –2.956 534 | –3.012 040 | –2.505 817 | –3.196 423 | |
| CPTb | –1.387 402 | –1.416 513 | –1.437 193 | –1.512 698 |
aResults obtained by Li et al (2016). bResults obtained by Zenkour and Alghamdi (2010a).
Table 4.
Dimensionless shear stresses 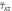 of the different FGM sandwich plates (Thermal condition I).
of the different FGM sandwich plates (Thermal condition I).
| k | Theory | 1-0-1 | 3-1-3 | 2-1-2 | 1-1-1 |
|---|---|---|---|---|---|
| 0 | Present | 0.173 023 | 0.173 023 | 0.173 023 | 0.173 023 |
| SSDTa | 0.171 603 | 0.171 603 | 0.171 603 | 0.171 603 | |
| TSDTa | 0.174 481 | 0.174 481 | 0.174 481 | 0.174 481 | |
| FSDTa | 0.173 624 | 0.173 624 | 0.173 624 | 0.173 624 | |
| 1 | Present | 0.275 035 | 0.275 935 | 0.277 957 | 0.285 381 |
| SSDTa | 0.277 018 | 0.278 534 | 0.280 890 | 0.289 195 | |
| TSDTa | 0.272 347 | 0.272 511 | 0.274 133 | 0.280 495 | |
| FSDTa | 0.221 768 | 0.213 318 | 0.210 115 | 0.203 004 | |
| 2 | Present | 0.271 970 | 0.270 370 | 0.273 112 | 0.285 641 |
| SSDTa | 0.272 583 | 0.271 861 | 0.275 130 | 0.289 157 | |
| TSDTa | 0.270 952 | 0.268 314 | 0.270 427 | 0.281 157 | |
| FSDTa | 0.244 354 | 0.230 915 | 0.225 945 | 0.215 140 | |
| 3 | Present | 0.269 963 | 0.263 726 | 0.265 935 | 0.280 009 |
| SSDTa | 0.269 608 | 0.264 263 | 0.267 073 | 0.282 953 | |
| TSDTa | 0.270 110 | 0.262 832 | 0.264 327 | 0.276 238 | |
| FSDTa | 0.257 465 | 0.240 850 | 0.234 789 | 0.221 768 | |
| 4 | Present | 0.270 936 | 0.259 929 | 0.261 216 | 0.275 291 |
| SSDTa | 0.270 016 | 0.259 822 | 0.261 729 | 0.277 764 | |
| TSDTa | 0.271 755 | 0.259 812 | 0.260 366 | 0.272 098 | |
| FSDTa | 0.266 029 | 0.247 232 | 0.240 436 | 0.225 945 | |
| 5 | Present | 0.273 314 | 0.258 036 | 0.258 355 | 0.271 833 |
| SSDTa | 0.272 070 | 0.257 496 | 0.258 433 | 0.273 950 | |
| TSDTa | 0.274 512 | 0.258 437 | 0.258 029 | 0.269 077 | |
| FSDTa | 0.272 062 | 0.251 677 | 0.244 354 | 0.228 818 |
aResults obtained by Zenkour and Alghamdi (2010a).
Dimensionless center deflection of FG sandwich plate for different values of  and sandwich schemes is presented in table 2. We can see that the decrease of core thickness, increases the dimensionless deflection. Also, with increasing of power law index
and sandwich schemes is presented in table 2. We can see that the decrease of core thickness, increases the dimensionless deflection. Also, with increasing of power law index 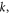 the dimensionless deflection increases. Maximum and minimum value occurs for the FG plate without ceramic core 1-0-1 and 1-1-1, respectively. The value of
the dimensionless deflection increases. Maximum and minimum value occurs for the FG plate without ceramic core 1-0-1 and 1-1-1, respectively. The value of 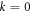 presents a pure ceramic plate wherever the plate scheme is, this can justify the same results. It can be seen that the ceramic plates have the lowest values of deflections, because it is stiffer than the FGM ones. Tables 3 and 4 illustrates the stress
presents a pure ceramic plate wherever the plate scheme is, this can justify the same results. It can be seen that the ceramic plates have the lowest values of deflections, because it is stiffer than the FGM ones. Tables 3 and 4 illustrates the stress  and stress
and stress  respectively, for several values of inhomogeneity index
respectively, for several values of inhomogeneity index 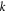 and different FG sandwich schemes. The highest axial stress
and different FG sandwich schemes. The highest axial stress 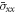 and shear stress
and shear stress 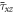 occurs for the 1-1-1 FG plate. As clearly visible in these tables, our results are in good agreement with the other HSDTs and particularly the third-order shear deformation theory. The used theory is simple and can theoretically cover the existing polynomial models (Nguyen et al 2016).
occurs for the 1-1-1 FG plate. As clearly visible in these tables, our results are in good agreement with the other HSDTs and particularly the third-order shear deformation theory. The used theory is simple and can theoretically cover the existing polynomial models (Nguyen et al 2016).
7.2. Parametric study and discussion (thermal condition II)
In the following section, a new analysis of FG sandwich plates is performed using an exact solution of temperature distribution across the sandwich thickness direction. Thermal analysis is performed by solving the equation of heat transfer (Thermal condition II). Material properties are dependent on temperature (see table 1).
The dimensionless parameters are defined as:
Dimensionless center deflection
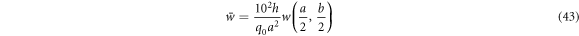
Dimensionless axial stress
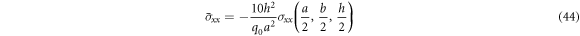
Dimensionless shear stress
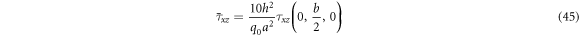
As mentioned before, in this study we analyze the effect of the high temperature (thermal condition II) on the bending of FG sandwich plates. Thus, tables 5–7 illustrates the influence of the inhomogeneity parameter and the sandwich schemes on the response of FG plates under various values of temperature difference 
 Here, the temperature of the bottom surface is fixed at
Here, the temperature of the bottom surface is fixed at 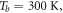 while the temperature of the bottom surface
while the temperature of the bottom surface  is varied.
is varied.
Table 5.
Dimensionless center deflections  of the different FGM sandwich plates (Thermal condition II).
of the different FGM sandwich plates (Thermal condition II).
| ΔT | k | Theory | 1-0-1 | 1-1-1 | 2-1-2 | 1-2-1 | 2-2-1 | 2-1-1 |
|---|---|---|---|---|---|---|---|---|
| ΔT = 0 | 0 | Present | 1.761 533 | 1.761 533 | 1.761 533 | 1.761 533 | 1.761 533 | 1.761 533 |
| TSDT | 1.761 583 | 1.761 583 | 1.761 583 | 1.761 583 | 1.761 583 | 1.761 583 | ||
| FSDT | 1.761 646 | 1.761 646 | 1.761 646 | 1.761 646 | 1.761 646 | 1.761 646 | ||
| 1 | Present | 2.419 007 | 2.277 076 | 2.342 669 | 2.176 021 | 2.221 960 | 2.296 258 | |
| TSDT | 2.419 2979 | 2.277 252 | 2.342 922 | 2.176 220 | 2.222 284 | 2.296 681 | ||
| FSDT | 2.426 157 | 2.283 329 | 2.349 738 | 2.180 727 | 2.227 269 | 2.302 297 | ||
| 2 | Present | 2.619 482 | 2.456 830 | 2.536 347 | 2.325 327 | 2.381 039 | 2.472 284 | |
| TSDT | 2.619 946 | 2.457 148 | 2.536 782 | 2.325 657 | 2.381 550 | 2.472 932 | ||
| FSDT | 2.628 756 | 2.465 880 | 2.546 342 | 2.332 207 | 2.388 596 | 2.480 598 | ||
| 5 | Present | 2.751 343 | 2.609 637 | 2.686 114 | 2.463 975 | 2.517 865 | 2.609 872 | |
| TSDT | 2.751 904 | 2.610 170 | 2.686 782 | 2.464 561 | 2.518 650 | 2.610 760 | ||
| FSDT | 2.760 030 | 2.621 528 | 2.698 398 | 2.473 445 | 2.527 630 | 2.619 702 | ||
| ΔT = 100 K | 0 | Present | 2.021 572 | 2.021 572 | 2.021 572 | 2.021 572 | 2.021 572 | 2.021 572 |
| TSDT | 2.021 623 | 2.021 623 | 2.021 623 | 2.021 623 | 2.021 623 | 2.021 623 | ||
| FSDT | 2.021 646 | 2.021 646 | 2.021 646 | 2.021 646 | 2.021 646 | 2.021 646 | ||
| 1 | Present | 2.596 138 | 2.485 675 | 2.538 547 | 2.400 244 | 2.456 083 | 2.517 666 | |
| TSDT | 2.596 445 | 2.485 873 | 2.538 817 | 2.400 494 | 2.456 486 | 2.518 178 | ||
| FSDT | 2.603 473 | 2.492 278 | 2.545 914 | 2.405 341 | 2.462 076 | 2.524 413 | ||
| 2 | Present | 2.766 355 | 2.641 850 | 2.704 960 | 2.532 141 | 2.600 422 | 2.673 591 | |
| TSDT | 2.766 828 | 2.642 195 | 2.705 418 | 2.532 531 | 2.601 036 | 2.674 348 | ||
| FSDT | 2.775 670 | 2.651 239 | 2.715 183 | 2.539 465 | 2.608 795 | 2.682 692 | ||
| 5 | Present | 2.876 267 | 2.771 654 | 2.830 538 | 2.652 576 | 2.720 391 | 2.789 698 | |
| TSDT | 2.876 824 | 2.772 210 | 2.831 217 | 2.653 226 | 2.721 295 | 2.790 700 | ||
| FSDT | 2.884 806 | 2.783 777 | 2.842 872 | 2.662 482 | 2.731 007 | 2.800 245 | ||
| ΔT = 300 K | 0 | Present | 2.916 896 | 2.916 896 | 2.916 896 | 2.916 896 | 2.916 896 | 2.916 896 |
| TSDT | 2.916 942 | 2.916 942 | 2.916 942 | 2.916 942 | 2.916 942 | 2.916 942 | ||
| FSDT | 2.916 604 | 2.916 604 | 2.916 604 | 2.916 604 | 2.916 604 | 2.916 604 | ||
| 1 | Present | 3.036 615 | 3.075 594 | 3.065 727 | 3.071 653 | 3.163 736 | 3.161 031 | |
| TSDT | 3.036 987 | 3.075 924 | 3.066 095 | 3.072 100 | 3.164 365 | 3.161 794 | ||
| FSDT | 3.044 956 | 3.083 798 | 3.074 514 | 3.078 487 | 3.171 854 | 3.169 997 | ||
| 2 | Present | 3.068 368 | 3.114 566 | 3.100 614 | 3.113 022 | 3.229 434 | 3.216 435 | |
| TSDT | 3.068 889 | 3.115 017 | 3.101 149 | 3.113 648 | 3.230 335 | 3.217 499 | ||
| FSDT | 3.078 325 | 3.125 626 | 3.112 134 | 3.122 376 | 3.240 406 | 3.228 104 | ||
| 5 | Present | 3.086 384 | 3.135 936 | 3.115 393 | 3.143 806 | 3.268 176 | 3.234 141 | |
| TSDT | 3.086 954 | 3.136 591 | 3.116 135 | 3.144 710 | 3.269 413 | 3.235 472 | ||
| FSDT | 3.094 964 | 3.149 453 | 3.128 512 | 3.155 792 | 3.281 603 | 3.247 222 |
Table 6.
Dimensionless axial stresses  of the different FGM sandwich plates (Thermal condition II).
of the different FGM sandwich plates (Thermal condition II).
| ΔT | k | Theory | 1-0-1 | 1-1-1 | 2-1-2 | 1-2-1 | 2-2-1 | 2-1-1 |
|---|---|---|---|---|---|---|---|---|
| ΔT = 0 | 0 | Present | –1,994 987 | –1,994 987 | –1,994 987 | –1,994 987 | –1,994 987 | –1,994 987 |
| TSDT | –1,994 322 | –1,994 322 | –1,994 322 | –1,994 322 | –1,994 322 | –1,994 322 | ||
| FSDT | –1,975 763 | –1,975 763 | –1,975 763 | –1,975 763 | –1,975 763 | –1,975 763 | ||
| 1 | Present | –1,736 482 | –1,635 395 | –1,682 763 | –1,561 991 | –1,555 678 | –1,604 998 | |
| TSDT | –1,735 992 | –1,634 913 | –1,682 284 | –1,561 005 | –1,554 693 | –1,603 993 | ||
| FSDT | –1,721 788 | –1,621 434 | –1,668 594 | –1,547 706 | –1,541 170 | –1,590 105 | ||
| 2 | Present | –1,881 125 | –1,767 796 | –1,824 585 | –1,672 489 | –1,658 308 | –1,719 367 | |
| TSDT | –1,880 630 | –1,767 317 | –1,824 113 | –1,671 484 | –1,657 301 | –1,718 331 | ||
| FSDT | –1,865 683 | –1,753 512 | –1,810 016 | –1,657 855 | –1,643 303 | –1,703 806 | ||
| 5 | Present | –1,971 740 | –1,879 559 | –1,932 499 | –1,774 929 | –1,746 524 | –1,810 198 | |
| TSDT | –1,971 224 | –1,879 102 | –1,932 047 | –1,773 940 | –1,745 512 | –1,809 130 | ||
| FSDT | –1,955 163 | –1,865 133 | –1,917 576 | –1,760 172 | –1,731 106 | –1,793 920 | ||
| ΔT = 100 K | 0 | Present | –1,716 123 | –1,716 123 | –1,716 123 | –1,716 123 | –1,716 123 | –1,716 123 |
| TSDT | –1,715 490 | –1,715 490 | –1,715 490 | –1,715 490 | –1,715 490 | –1,715 490 | ||
| FSDT | –1,697 825 | –1,697 825 | –1,697 825 | –1,697 825 | –1,697 825 | –1,697 825 | ||
| 1 | Present | –1,773 999 | –1,716 293 | –1,746 262 | –1,664 472 | –1,658 359 | –1,690 228 | |
| TSDT | –1,773 519 | –1,715 823 | –1,745 794 | –1,663 510 | –1,657 404 | –1,689 256 | ||
| FSDT | –1,759 551 | –1,702 560 | –1,732 328 | –1,650 414 | –1,644 138 | –1,675 652 | ||
| 2 | Present | –1,875 271 | –1,816 786 | –1,850 812 | –1,751 117 | –1,738 906 | –1,776 103 | |
| TSDT | –1,874 786 | –1,816 319 | –1,850 351 | –1,750 140 | –1,737 935 | –1,775 106 | ||
| FSDT | –1,860 109 | –1,802 757 | –1,836 502 | –1,736 747 | –1,724 247 | –1,760 922 | ||
| 5 | Present | –1,930 888 | –1,897 816 | –1,925 058 | –1,829 367 | –1,804 572 | –1,838 827 | |
| TSDT | –1,930 380 | –1,897 370 | –1,924 614 | –1,828 407 | –1,803 601 | –1,837 800 | ||
| FSDT | –1,914 640 | –1,883 644 | –1,910 394 | –1,814 888 | –1,789 539 | –1,822 970 | ||
| ΔT = 300 K | 0 | Present | –0,678 101 | –0,678 101 | –0,678 101 | –0,678 101 | –0,678 101 | –0,678 101 |
| TSDT | –0,677 509 | –0,677 509 | –0,677 509 | –0,677 509 | –0,677 509 | –0,677 509 | ||
| FSDT | –0,660 984 | –0,660 984 | –0,660 984 | –0,660 984 | –0,660 984 | –0,660 984 | ||
| 1 | Present | –2,062 944 | –2,168 077 | –2,131 324 | –2,201 175 | –2,196 487 | –2,161 012 | |
| TSDT | –2,062 496 | –2,167 646 | –2,130 892 | –2,200 293 | –2,195 618 | –2,160 132 | ||
| FSDT | –2,049 268 | –2,155 133 | –2,118 173 | –2,187 934 | –2,183 176 | –2,147 393 | ||
| 2 | Present | –2,010 678 | –2,149 028 | –2,098 758 | –2,196 274 | –2,193 298 | –2,141 449 | |
| TSDT | –2,010 221 | –2,148 601 | –2,098 331 | –2,195 385 | –2,192 427 | –2,140 555 | ||
| FSDT | –1,996 315 | –2,135 820 | –2,085 249 | –2,182 783 | –2,179 651 | –2,127 330 | ||
| 5 | Present | –1,948 787 | –2,118 063 | –2,052 407 | –2,184 390 | –2,176 733 | –2,103 674 | |
| TSDT | –1,948 303 | –2,117 651 | –2,051 991 | –2,183 518 | –2,175 867 | –2,102 757 | ||
| FSDT | –1,933 388 | –2,104 689 | –2,038 519 | –2,170 799 | –2,162 773 | –2,088 947 |
Table 7.
Dimensionless shear stresses 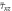 of the different FGM sandwich plates (Thermal condition II).
of the different FGM sandwich plates (Thermal condition II).
| ΔT | k | Theory | 1-0-1 | 1-1-1 | 2-1-2 | 1-2-1 | 2-2-1 | 2-1-1 |
|---|---|---|---|---|---|---|---|---|
| ΔT = 0 | 0 | Present | 0.242 783 | 0.242 783 | 0.242 783 | 0.242 783 | 0.242 783 | 0.242 783 |
| TSDT | 0.238 572 | 0.238 572 | 0.238 572 | 0.238 572 | 0.238 572 | 0.238 572 | ||
| FSDT | 0.190 986 | 0.190 986 | 0.190 986 | 0.190 986 | 0.190 986 | 0.190 986 | ||
| 1 | Present | 0.276 813 | 0.257 226 | 0.263 553 | 0.251 794 | 0.256 355 | 0.263 662 | |
| TSDT | 0.272 785 | 0.253 303 | 0.259 689 | 0.247 680 | 0.252 291 | 0.259 580 | ||
| FSDT | 0.276 484 | 0.217 944 | 0.224 276 | 0.210 515 | 0.214 911 | 0.221 859 | ||
| 2 | Present | 0.296 685 | 0.263 689 | 0.274 015 | 0.255 208 | 0.262 449 | 0.274 236 | |
| TSDT | 0.292 706 | 0.260 026 | 0.270 418 | 0.251 249 | 0.258 539 | 0.270 256 | ||
| FSDT | 0.253 764 | 0.228 705 | 0.238 110 | 0.217 944 | 0.224 276 | 0.234 494 | ||
| 5 | Present | 0.328 717 | 0.272 491 | 0.289 462 | 0.259 231 | 0.270 644 | 0.289 504 | |
| TSDT | 0.324 322 | 0.269 174 | 0.286 105 | 0.255 531 | 0.266 910 | 0.285 510 | ||
| FSDT | 0.276 484 | 0.240 584 | 0.253 764 | 0.225 916 | 0.234 494 | 0.248 655 | ||
| ΔT = 100 K | 0 | Present | 0.242 658 | 0.242 658 | 0.242 658 | 0.242 658 | 0.242 658 | 0.242 658 |
| TSDT | 0.238 446 | 0.238 446 | 0.238 446 | 0.238 446 | 0.238 446 | 0.238 446 | ||
| FSDT | 0.190 784 | 0.190 784 | 0.190 784 | 0.190 784 | 0.190 784 | 0.190 784 | ||
| 1 | Present | 0.274 450 | 0.255 539 | 0.261 651 | 0.250 342 | 0.255 650 | 0.263 560 | |
| TSDT | 0.270 453 | 0.251 666 | 0.257 829 | 0.246 287 | 0.251 668 | 0.259 558 | ||
| FSDT | 0.232 091 | 0.216 453 | 0.222 447 | 0.209 404 | 0.215 034 | 0.222 487 | ||
| 2 | Present | 0.293 370 | 0.261 675 | 0.271 650 | 0.253 494 | 0.261 751 | 0.274 465 | |
| TSDT | 0.289 403 | 0.258 053 | 0.268 076 | 0.249 597 | 0.257 939 | 0.270 572 | ||
| FSDT | 0.250 148 | 0.226 634 | 0.235 489 | 0.216 463 | 0.224 451 | 0.235 386 | ||
| 5 | Present | 0.323 584 | 0.270 173 | 0.286 479 | 0.257 331 | 0.270 088 | 0.290 273 | |
| TSDT | 0.319 194 | 0.266 869 | 0.283 110 | 0.253 684 | 0.266 456 | 0.286 358 | ||
| FSDT | 0.271 223 | 0.237 819 | 0.250 148 | 0.224 014 | 0.234 698 | 0.249 822 | ||
| ΔT = 300 K | 0 | Present | 0.241 746 | 0.241 746 | 0.241 746 | 0.241 746 | 0.241 746 | 0.241 746 |
| TSDT | 0.237 518 | 0.237 518 | 0.237 518 | 0.237 518 | 0.237 518 | 0.237 518 | ||
| FSDT | 0.189 276 | 0.189 276 | 0.189 276 | 0.189 276 | 0.189 276 | 0.189 276 | ||
| 1 | Present | 0.268 767 | 0.249 693 | 0.255 862 | 0.244 671 | 0.251 153 | 0.260 044 | |
| TSDT | 0.264 931 | 0.246 072 | 0.252 258 | 0.240 880 | 0.247 449 | 0.256 328 | ||
| FSDT | 0.227 908 | 0.213 262 | 0.218 873 | 0.206 672 | 0.214 056 | 0.222 444 | ||
| 2 | Present | 0.287 098 | 0.255 480 | 0.265 608 | 0.247 231 | 0.256 889 | 0.271 284 | |
| TSDT | 0.283 233 | 0.252 106 | 0.262 216 | 0.243 631 | 0.253 412 | 0.267 721 | ||
| FSDT | 0.244 582 | 0.222 816 | 0.231 039 | 0.213 342 | 0.223 697 | 0.236 019 | ||
| 5 | Present | 0.315 793 | 0.264 165 | 0.280 493 | 0.250 954 | 0.265 333 | 0.288 144 | |
| TSDT | 0.311 444 | 0.261 045 | 0.277 212 | 0.247 598 | 0.262 067 | 0.284 559 | ||
| FSDT | 0.263 652 | 0.233 253 | 0.244 575 | 0.220 466 | 0.234 175 | 0.251 237 |
It is clear that temperature has a considerable influence on the dimensionless deflection, where the increase of temperature increases the deflection of the plate. For more details, the impact of temperature, power law index  the sandwich scheme and the geometrical parameter
the sandwich scheme and the geometrical parameter  on the bending response of FG sandwich plates is presented in the following figures.
on the bending response of FG sandwich plates is presented in the following figures.
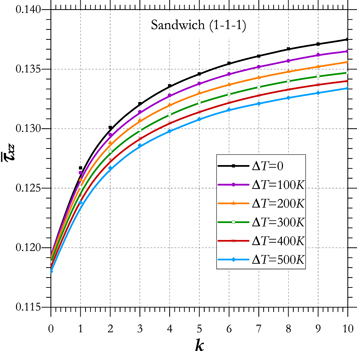
Figure 2 describe the influence of the side-to-thickness ratio 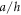 on the center deflections of sandwich plates 1–1–1 for temperature difference
on the center deflections of sandwich plates 1–1–1 for temperature difference 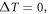



 and
and 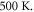 It is clear that the deflection
It is clear that the deflection 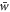 increase by increasing of the parameter
increase by increasing of the parameter 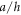 and the difference between the results under various temperature deference
and the difference between the results under various temperature deference  increases as the parameter
increases as the parameter 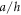 increase.
increase.
Figure 2. Effect of the temperature difference 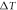 on the deflections
on the deflections 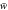 against the side–to–thickness ratio
against the side–to–thickness ratio 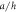
Download figure:
Standard image High-resolution imageFigure 3 shows the effect of parameter 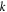 and the temperature difference on the dimensionless deflections
and the temperature difference on the dimensionless deflections  of FG sandwich plates. It can be noticed from this figure that deflections
of FG sandwich plates. It can be noticed from this figure that deflections  increase as the parameter
increase as the parameter 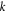 increase. The existence of high temperature demotes the stiffness of the sandwich plate. Therefore, from the figures 2 and 3, the increasing the temperature lead to an increment in the dimensionless center deflections.
increase. The existence of high temperature demotes the stiffness of the sandwich plate. Therefore, from the figures 2 and 3, the increasing the temperature lead to an increment in the dimensionless center deflections.
Figure 3. Effect of the temperature difference 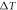 on the deflections
on the deflections 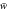 against the power law index
against the power law index 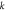
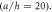
Download figure:
Standard image High-resolution imageThe dimensionless axial stress 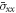 of FG sandwich plate under different of temperatures difference
of FG sandwich plate under different of temperatures difference  as a function of power law index
as a function of power law index  is depicted in figure 4. As visible in this figure, in the case of
is depicted in figure 4. As visible in this figure, in the case of 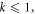 the increase of
the increase of  increases the stress
increases the stress 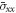 rapidly. then,
rapidly. then,  decrease gradually for
decrease gradually for 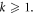
Figure 4. Effect of the temperature difference 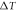 on the stress
on the stress 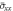 against the power law index
against the power law index 

Download figure:
Standard image High-resolution imageThe variation of dimensionless shear stress 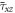 under effect of power law index
under effect of power law index  is displayed in figure 5. The stress
is displayed in figure 5. The stress  increase by increasing of index
increase by increasing of index  As clearly visible, the increase of temperature difference
As clearly visible, the increase of temperature difference 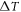 decrease the shear stress
decrease the shear stress 
Figure 5. Effect of the temperature difference 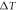 on the stress
on the stress 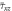 against the power law index
against the power law index 

Download figure:
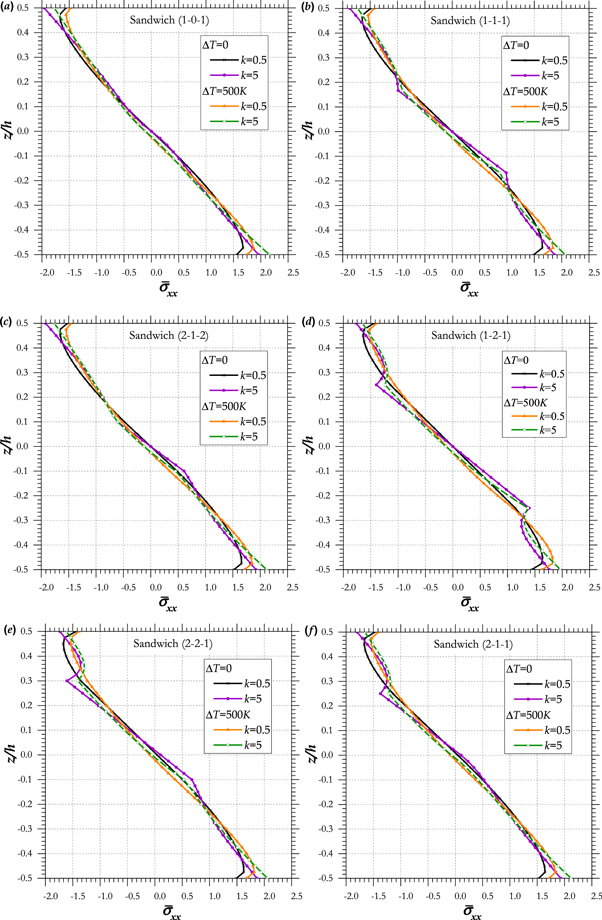
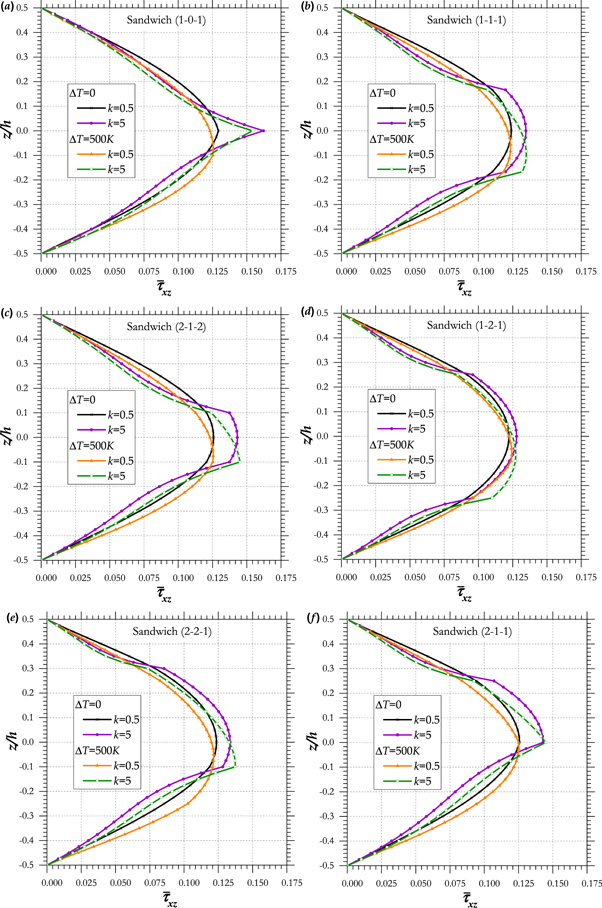
Standard image High-resolution imageThe transverse shear and axial stresses for various schemes of functionally graded sandwich plates are depicts in figures 6 and 7 respectively. The temperature difference is taken as 
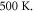
Figure 6. Dimensionless axial stresses 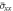 for different values of power law index
for different values of power law index 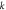
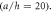
Download figure:
Standard image High-resolution imageFigure 7. Dimensionless shear stresses  for different values of power law index
for different values of power law index 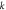
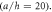
Download figure:
Standard image High-resolution imageFigure 6 illustrates the dimensionless axial stresses  through-the-thickness of the plate with inhomogeneity parameter
through-the-thickness of the plate with inhomogeneity parameter 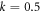 and
and  The dimensionless stresses are compressive above the mid–plane and tensile below the mid–plane.
The dimensionless stresses are compressive above the mid–plane and tensile below the mid–plane.
It can be observed that the FG sandwich plate with index  yields the maximum tensile stresses at the bottom surface for
yields the maximum tensile stresses at the bottom surface for  and the maximum compressive stresses at the top surfaces for
and the maximum compressive stresses at the top surfaces for 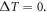 Also, dimensionless axial stresses
Also, dimensionless axial stresses  are continuous and smooth along the thickness of sandwich plates with power law index
are continuous and smooth along the thickness of sandwich plates with power law index  wherever the temperature difference is.
wherever the temperature difference is.
Figure 7 presents the shear stresses distribution through–the–thickness for 
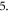 The maximum values of stress
The maximum values of stress 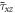 occurs at a point of the core layer of the sandwich plate. The largest magnitude is obtained for the plates under temperature difference
occurs at a point of the core layer of the sandwich plate. The largest magnitude is obtained for the plates under temperature difference  with index
with index 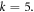
8. Conclusion
In this study, the thermomechanical bending of FG sandwich plates is investigated. Material properties of the FG layers are temperature dependent and assumed to vary continuously in the thickness direction of the plate based on the power-law function. Hamilton's principle in conjunction with the Navier's solution were applied to calculate the bending behavior of FG sandwich plates based on a new higher order shear deformation plates theory. An exact solution for the nonlinear temperature distribution variation along the thickness direction of the FG sandwich plate is proposed in this paper taking into account the influence of thermal conductivity, the power law index and the scheme of the sandwich. A large numerical investigation examined the effect of various parameters such as the high temperature, the power law index, the side to thickness ration and the different sandwich schemes on the deflections and stresses of FG plates. Based on the numerical results, it was found that the dimensionless center deflection increases by increasing of side-to-thickness ratio 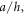 the power law index
the power law index  and the high temperature. A considerable effect of the temperature on the dimensionless axial and shear stresses. A good agreement is achieved between the present results and those given from the literature.
and the high temperature. A considerable effect of the temperature on the dimensionless axial and shear stresses. A good agreement is achieved between the present results and those given from the literature.
Appendix
The elements 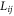 of the symmetric matrix (L) are
of the symmetric matrix (L) are
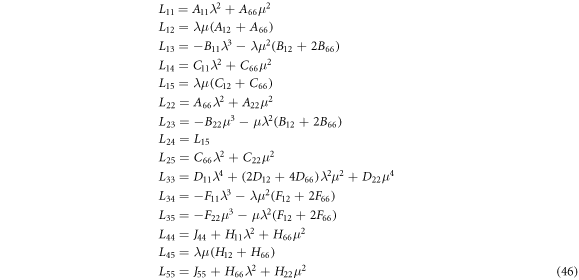
The components of the generalized force vector  are obtained as
are obtained as
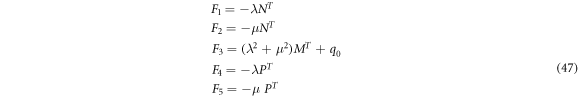
where