Abstract
Multiferroic materials with strong coupling between different degrees of freedom are prone to exhibit giant multicaloric effects resulting from the application or removal of diverse external fields. These materials exhibit a synergic response to the combined action of two fields when the monocaloric effects are both conventional (or both inverse), while a non-synergic response occurs when one of the monocaloric effects is conventional and the other is inverse. In all cases, the multicaloric properties (isothermal entropy and adiabatic temperature changes) do not result from the simple addition of the corresponding monocaloric quantities because there is a contribution from the interplay between degrees of freedom (cross-coupling term). In this paper, we analyse in detail the contribution of the cross-coupling term to the multicaloric entropy values obtained for both synergic and non-synergic multicaloric materials. We first introduce basic thermodynamic concepts accounting for the multicaloric effects, and next the contribution from the cross-coupling term is illustrated via several model examples. We finally analyse the realistic situation for two prototype materials with synergic and non-synergic multicaloric effects.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Multicaloric materials have been defined as those materials that can support more than one caloric effect [1]. Thus, multicaloric effects arise in a given material when more than one type of caloric effect can be driven by simultaneous or sequential application/removal of two or more external fields. Multicaloric effects are particularly interesting in systems with strong interplay between two or more properties since the caloric response to one of the fields is expected to be affected by secondary fields. Therefore, in this class of materials multicaloric effects differ from the simple addition of the corresponding monocaloric effects, which are those resulting from the application or removal of a single external field (in the absence of any other applied field).
The study of multicaloric effects has emerged in recent years as an alternative to monocaloric effects with the aim to take advantage of the coupling between different degrees of freedom that are known to occur in many giant caloric materials [2–4]. This is, for instance, the case of many giant magnetocaloric materials where the existence of a first-order magnetic transition, that is at the origin of the large magnetic field-induced caloric response, is a consequence of the strong coupling between magnetism and structure. Therefore, the interplay of different properties suggests that a caloric response might be improved by application of the external fields thermodynamically conjugated to these quantities. Hence, the study of cross-coupling effects in this class of materials is essential to reach a deep understanding of their multicaloric behaviour, which is a crucial step for the design and development of new materials with improved caloric properties.
Many different classes of materials may, in principle, show multicaloric effects. Among them, multiferroic materials appear as one of the best candidates since they are characterised by a strong intrinsic coupling between ferroic properties, thus suggesting that these materials might support more than one caloric effect occurring in a not independent way. In general, multiferroic materials are classed into three main categories: magnetostructural, electrostructural and magnetoelectric multiferroics [5]. These three classes are characterised, respectively, by a strong coupling between lattice and magnetic, lattice and electric, and magnetic and electric degrees of freedom. At present, however, multicaloric effects have only been studied in detail in the first class of multiferroic materials [6, 7] and to a less extent in the second one. To the best of our knowledge, no multicaloric behaviour has been reported in single-phase materials with intrinsic magnetoelectric coupling.
With regards to multicaloric effects driven by two fields, two main classes of materials can be considered depending on whether the corresponding monocaloric effects are both conventional or one is conventional while the other is inverse [8]. In the first case, caloric effects are synergic in the sense that under application or removal of both fields the corresponding effects add to each other. By contrast, in the non-synergic case the two effects tend to cancel each other. While at first glance the former case appears to be more interesting for the development of materials with improved caloric properties, the possibility of controlling hysteresis by means of two applied fields in the second class of materials suggests that both synergic and non-synergic materials deserve to be studied in detail. Furthermore, it is possible to obtain a synergic response for the latter case by the combined application of one field and removal of the second field.
In the present paper, we will discuss the specific features of the coupling in multicaloric materials by particularly addressing under which circumstances it is possible to: (i) enhance the caloric response by applying multiple fields, (ii) tune and broaden the operation range using a secondary field and (iii) tune hysteresis and improve the cycling reproducibility by using two fields.
2. Thermodynamics essentials
In this section we start with a brief discussion of the thermodynamics of multicaloric effects. For the sake of simplicity, we will consider a material that shows cross-response to fields
y
1 and
y
2 (for instance, magnetic field and stress), with the corresponding thermodynamically conjugated property being
X
1 and
X
2, respectively. The key point is to take advantage of the fact that entropy is an extensive state function, which imposes that simultaneous application of the two fields must lead to the same change of entropy as first applying
y
1 while keeping 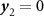 , and next applying
y
2 while keeping
y
1 constant. Following the general thermodynamic development given in [9], the multicaloric entropy change can then be computed as,
, and next applying
y
2 while keeping
y
1 constant. Following the general thermodynamic development given in [9], the multicaloric entropy change can then be computed as,
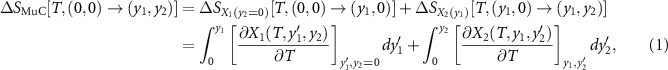
where the fields have been assumed to be applied in specific directions and X1 and X2 are the corresponding projections of
X
1 and
X
2 along these directions. The first integral in the right-hand side is simply the monocaloric effect associated with the property
X
1, which has been obtained using the Maxwell relation, 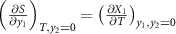 .
.
The second integral can be decomposed as follows,
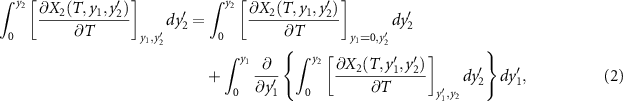
The first term on the right-hand side is the monocaloric effect associated with the property
X
2, taking into account the Maxwell relation  . The second term can be expressed as,
. The second term can be expressed as,
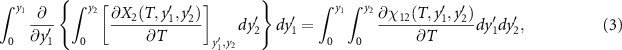
where χ12 is the cross-susceptibility defined as,

This last term associated with the temperature change of the cross-susceptibility is the coupling term, 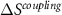 , that measures the cross-response contribution to the multicaloric effect. Therefore, the multicaloric entropy change is given by the sum of the corresponding monocaloric effects and the cross-response or coupling term. It is interesting to note that,
, that measures the cross-response contribution to the multicaloric effect. Therefore, the multicaloric entropy change is given by the sum of the corresponding monocaloric effects and the cross-response or coupling term. It is interesting to note that,

which shows that the coupling term is related to the curvature of the entropy surface in a T-y1-y2 space.
In what follows, we will consider given cases with synergic and non-synergic responses, and we will analyse the coupling term obtained as: 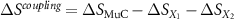 .
.
In figures 1 and 2, we present schemes that illustrate the entropy's temperature dependence in the absence of applied field and under applied (constant) external field(s). We also show how the monocaloric and multicaloric entropy changes can be derived from these curves. It is evidenced that the multicaloric effect does not correspond to the simple addition of the monocaloric effects and includes a contribution from the cross-coupling response of the material. For the sake of simplicity, we have considered an ideal first-order phase transition (occurring at a fixed temperature for each applied field) and field-independent specific heat for the high and low-temperature phases. Furthermore, we have also considered a temperature and field-independent transition entropy change, ( ). Usually, in giant caloric materials the phase transition does not occur at a fixed temperature but it spreads over a certain temperature range. Hence, a more realistic case, with the phase transition spreading over a specific temperature interval, is shown in figure 3.
). Usually, in giant caloric materials the phase transition does not occur at a fixed temperature but it spreads over a certain temperature range. Hence, a more realistic case, with the phase transition spreading over a specific temperature interval, is shown in figure 3.
Figure 1. Schematics of the multicaloric effect for synergic (conventional) monocaloric effects. Top panels illustrate the entropy as a function of temperature in the absence of applied external field (black curves) and under applied field(s) (coloured curves). For conventional monocaloric effects, the transition is shifted to higher temperatures [ and
and  ] when external field(s) are applied. For the multicaloric effect, the application of both fields results in a shift of the transition temperature to higher values [
] when external field(s) are applied. For the multicaloric effect, the application of both fields results in a shift of the transition temperature to higher values [ >
>  >
>  ]. The entropy change resulting from the application of field(s) at a given temperature is indicated by the orange arrow. Bottom panels illustrate the entropy change resulting from the application of field(s) as a function of temperature. It is shown that the entropy change corresponding to the combined application of two fields (y1 and y2) results from the sum of the monocaloric effects arising from the application of one field, plus the contribution from the cross-coupling term (
]. The entropy change resulting from the application of field(s) at a given temperature is indicated by the orange arrow. Bottom panels illustrate the entropy change resulting from the application of field(s) as a function of temperature. It is shown that the entropy change corresponding to the combined application of two fields (y1 and y2) results from the sum of the monocaloric effects arising from the application of one field, plus the contribution from the cross-coupling term (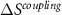 ).
).
Download figure:
Standard image High-resolution imageFigure 2. Schematics of the multicaloric effect for non-synergic conventional (CE1) and inverse (CE2) monocaloric effects. Top panels illustrate the entropy as a function of temperature in the absence of applied external field (black curves) and under applied field(s) (coloured curves). For the conventional monocaloric effect (CE1), the transition is shifted to higher temperatures [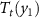 ] when the external field is applied. For the inverse monocaloric effect (CE2), the transition is shifted to lower temperatures [
] when the external field is applied. For the inverse monocaloric effect (CE2), the transition is shifted to lower temperatures [ ] when the external field is applied. In this example, the combined action of the two fields shifts the transition to higher temperatures [
] when the external field is applied. In this example, the combined action of the two fields shifts the transition to higher temperatures [ <
<  <
<  ] resulting in a total conventional multicaloric effect. The entropy change resulting from the application of field(s) at a given temperature is indicated by the orange arrow. Bottom panels illustrate the entropy change resulting from the application of field(s) as a function of temperature. It is shown that the entropy change corresponding to the combined application of two fields (y1 and y2) is obtained as the sum of the monocaloric effects arising from the application of one field, plus the contribution from the cross-coupling term (
] resulting in a total conventional multicaloric effect. The entropy change resulting from the application of field(s) at a given temperature is indicated by the orange arrow. Bottom panels illustrate the entropy change resulting from the application of field(s) as a function of temperature. It is shown that the entropy change corresponding to the combined application of two fields (y1 and y2) is obtained as the sum of the monocaloric effects arising from the application of one field, plus the contribution from the cross-coupling term ( ).
).
Download figure:
Standard image High-resolution imageFigure 3. Schematics of the multicaloric effect for synergic monocaloric effects for a non-ideal first-order phase transition. Top panels illustrate the entropy as a function of temperature in the absence of applied external field (black curves) and under applied field(s) (coloured curves). For conventional monocaloric effects, the transition is shifted to higher temperatures [ and
and  ] when the external field(s) are applied. For the multicaloric effect, the application of both fields shifts the transition temperature to higher values [
] when the external field(s) are applied. For the multicaloric effect, the application of both fields shifts the transition temperature to higher values [ >
>  >
>  ]. The entropy change resulting from the application of field(s) at a given temperature is indicated by the orange arrow. Bottom panels illustrate the entropy change resulting from the application of field(s) as a function of temperature. It is shown that the entropy change corresponding to the combined application of two fields (y1 and y2), results from the sum of the monocaloric effects arising from the application of one field, plus the contribution from the cross-coupling term (
]. The entropy change resulting from the application of field(s) at a given temperature is indicated by the orange arrow. Bottom panels illustrate the entropy change resulting from the application of field(s) as a function of temperature. It is shown that the entropy change corresponding to the combined application of two fields (y1 and y2), results from the sum of the monocaloric effects arising from the application of one field, plus the contribution from the cross-coupling term ( ).
).
Download figure:
Standard image High-resolution imageFigure 1 corresponds to the synergic case. For the monocaloric effect CE1, application of a field y1 shifts the transition to a temperature  higher than the zero field transition temperature
higher than the zero field transition temperature  . The resulting entropy change in that case (indicated by the orange arrow) corresponds to a conventional caloric effect in which application of a field reduces the entropy of the material. A similar behaviour is observed for caloric effect CE2. In that case, the transition shifts to the temperature
. The resulting entropy change in that case (indicated by the orange arrow) corresponds to a conventional caloric effect in which application of a field reduces the entropy of the material. A similar behaviour is observed for caloric effect CE2. In that case, the transition shifts to the temperature  and the field-induced entropy change is also negative. For the multicaloric effect (MuCE), the application of the two fields (y1 and y2) shifts the transition temperature to a value higher than for each monocaloric effect:
and the field-induced entropy change is also negative. For the multicaloric effect (MuCE), the application of the two fields (y1 and y2) shifts the transition temperature to a value higher than for each monocaloric effect: 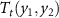 >
> 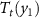 >
> 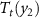 . The corresponding isothermal entropy changes for each monocaloric and multicaloric effects are illustrated in the bottom panels. It is shown that application of two fields results in a broader temperature window where giant caloric effects can be obtained. In this simplified example, there is no gain in the
. The corresponding isothermal entropy changes for each monocaloric and multicaloric effects are illustrated in the bottom panels. It is shown that application of two fields results in a broader temperature window where giant caloric effects can be obtained. In this simplified example, there is no gain in the  value when the two fields are applied. Finally, the scheme clearly illustrates that the multicaloric entropy change (green area) is not the direct sum of the two individual caloric effects (red and blue areas), but there is also a contribution from the cross-coupling term (
value when the two fields are applied. Finally, the scheme clearly illustrates that the multicaloric entropy change (green area) is not the direct sum of the two individual caloric effects (red and blue areas), but there is also a contribution from the cross-coupling term (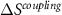 , orange areas) which is positive from
, orange areas) which is positive from 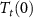 to
to 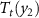 and negative from
and negative from  to
to  . The positive
. The positive  values compensate the negative
values compensate the negative  values arising from CE2, and the physical significance of that compensation is the fact that once the transition has already been induced (by application of field y1), application of a secondary field (y2) does not further modify the entropy of the sample. On the other hand, the negative
values arising from CE2, and the physical significance of that compensation is the fact that once the transition has already been induced (by application of field y1), application of a secondary field (y2) does not further modify the entropy of the sample. On the other hand, the negative  values from
values from  to
to  are responsible for the enlargement of the temperature window where giant caloric effects can be obtained.
are responsible for the enlargement of the temperature window where giant caloric effects can be obtained.
Figure 2 illustrates the non-synergic case. Here CE1 corresponds to a conventional monocaloric effect where application of a field y1 shifts the transition to a higher temperature  >
>  . By contrast, CE2 corresponds to an inverse monocaloric effect where application of the field y2 shifts the transition to a lower temperature
. By contrast, CE2 corresponds to an inverse monocaloric effect where application of the field y2 shifts the transition to a lower temperature  <
<  . Hence, application of the two fields can shift the transition to temperatures higher or lower than
. Hence, application of the two fields can shift the transition to temperatures higher or lower than  , depending on the sensitivity of the transition temperature to the field (
, depending on the sensitivity of the transition temperature to the field ( and
and  ) and also on the actual strength of the fields y1 and y2. In the particular example shown in figure 2, combined application of the two fields shifts the transition to higher temperatures and the resulting multicaloric effect is conventional. The corresponding isothermal entropy changes for each monocaloric and multicaloric effects are illustrated in the bottom panels, which are positive for the inverse caloric effect CE2, and negative for the conventional caloric effect CE1 and for the multicaloric effect MuCE. It is shown that application of two fields results in a narrower temperature window (compared to monocaloric effect CE1). It is worth stressing that by conveniently tuning the y1 and y2 values it is possible to change the sign of the multicaloric
) and also on the actual strength of the fields y1 and y2. In the particular example shown in figure 2, combined application of the two fields shifts the transition to higher temperatures and the resulting multicaloric effect is conventional. The corresponding isothermal entropy changes for each monocaloric and multicaloric effects are illustrated in the bottom panels, which are positive for the inverse caloric effect CE2, and negative for the conventional caloric effect CE1 and for the multicaloric effect MuCE. It is shown that application of two fields results in a narrower temperature window (compared to monocaloric effect CE1). It is worth stressing that by conveniently tuning the y1 and y2 values it is possible to change the sign of the multicaloric  values from negative to positive, and for a particular combination of these fields
values from negative to positive, and for a particular combination of these fields  vanishes [it corresponds to the case where the positive shift of the transition induced by y1 exactly matches the negative shift of the transition induced by y2:
vanishes [it corresponds to the case where the positive shift of the transition induced by y1 exactly matches the negative shift of the transition induced by y2:  ]. The multicaloric entropy change is not the sum of the monocaloric values, but it also has a contribution from the coupling term, which reverses its sign depending on the temperature range. The negative
]. The multicaloric entropy change is not the sum of the monocaloric values, but it also has a contribution from the coupling term, which reverses its sign depending on the temperature range. The negative  values from
values from  to
to  compensate for the positive values that should arise from the inverse caloric effect CE2. On the other hand, the positive
compensate for the positive values that should arise from the inverse caloric effect CE2. On the other hand, the positive  values from
values from  to
to  give rise to a narrower temperature window (compared to that of the monocaloric effect CE1).
give rise to a narrower temperature window (compared to that of the monocaloric effect CE1).
Finally, figure 3 illustrates the multicaloric effect for synergic monocaloric effects for a non-ideal first-order phase transition spreading over a specific temperature interval. While the essential features described in the ideal case (expanded temperature window and existence of a coupling contribution with alternating sign) are also found in this case, the synergic effect is more clearly visible in figure 3 since the multicaloric  values are larger than those corresponding to each monocaloric effect. As shown in the figure, the values for the applied fields y1 (for CE1) and y2 (for CE2) are not large enough to induce the transformation of the full sample; therefore the resulting isothermal entropy changes are lower than the transition entropy change. By contrast, for the multicaloric effect, the combined action of the two fields gives rise to the full transformation of the sample, resulting in a multicaloric entropy change value matching the transition entropy change.
values are larger than those corresponding to each monocaloric effect. As shown in the figure, the values for the applied fields y1 (for CE1) and y2 (for CE2) are not large enough to induce the transformation of the full sample; therefore the resulting isothermal entropy changes are lower than the transition entropy change. By contrast, for the multicaloric effect, the combined action of the two fields gives rise to the full transformation of the sample, resulting in a multicaloric entropy change value matching the transition entropy change.
3. Data treatment and analysis
As detailed in the previous sections, the multicaloric response of a given material cannot be derived from the knowledge of its monocaloric behaviour, and it is therefore necessary to conduct experiments in which the sample is subjected to more than one external stimulus (stress and magnetic field for the case of materials undergoing magnetostructural transitions). Because experimental systems capable of applying both magnetic field and stress are scarce, there are few experimental studies on multicaloric effects and materials. In relation to magnetic field and hydrostatic pressure, the existence of commercial magnetometers which are equipped with a CuBe piston clamp pressure cell enables measuring the temperature dependence of the magnetization in samples subjected simultaneously to magnetic field and hydrostatic pressure. From these data it is possible to compute the multicaloric response of the sample by the indirect method, using the Maxwell relations [10]. However, to the best of our knowledge, there is no commercial device which enables the simultaneous application of magnetic field and uniaxial stress (or other stress modes), and therefore bespoke experimental devices need to be designed in order to experimentally determine the multicaloric response of samples subjected to uniaxial stress and magnetic field [11].
Recently we have designed and built a differential scanning calorimeter (DSC) which enables simultaneous application of compressive uniaxial stress and magnetic field [12]. From the thermal curves recorded at selected (constant) values of magnetic field and stress, it is possible to build the temperature dependence of the entropy (referenced to a given value) at selected values of field and stress, from which the multicaloric response of the material can be computed as described in the following subsection, via the quasi-direct method.
3.1. Building entropy curves from calorimetric data
For first-order magnetostructural transitions, the combination of DSC measurements in samples subjected to mechanical and magnetic fields, with specific heat data enables computation of the entropy (referenced to a reference value) as a function of temperature, magnetic field and stress [ ] [13]. In general, for metals and alloys the specific heat is not significantly affected by stress; therefore it can be assumed to be stress-independent to a good approximation. However, for magnetic materials in the vicinity of a magnetic phase transition, the specific heat may depend on magnetic field. Therefore heat capacity measurements as a function of temperature and magnetic field are needed in order to obtain reliable
] [13]. In general, for metals and alloys the specific heat is not significantly affected by stress; therefore it can be assumed to be stress-independent to a good approximation. However, for magnetic materials in the vicinity of a magnetic phase transition, the specific heat may depend on magnetic field. Therefore heat capacity measurements as a function of temperature and magnetic field are needed in order to obtain reliable  functions.
functions.
It is to be noted that, within the temperature range where the first-order transition occurs, the measurement of specific heat is affected by the latent heat of the transition. Therefore reliable C data are only available for the pure phases above and below the first-order transition. In that temperature interval, the specific heat of the sample can be obtained as a weighted average of the specific heats of the high (CH
) and low (CL
) temperature phases:  , where x is the fraction of the sample in the high-temperature phase.
, where x is the fraction of the sample in the high-temperature phase.
The temperature dependence of the entropy at selected values of stress and magnetic field can then be computed referenced to the value of the entropy (S0) at a reference state 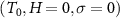 :
:
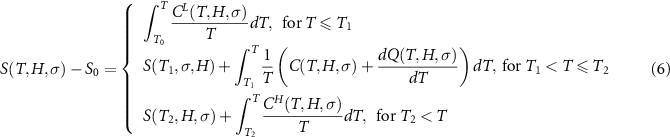
T1 and T2 denote the start and finish transition temperatures, respectively, and 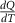 is the baseline corrected DSC calorimetric signal. The reference state S0 is chosen at a temperature T0 well above (or below) the transition region, where the specific heat is independent of stress and magnetic field. This requirement is fulfilled for the paramagnetic phase, which corresponds to the high-temperature phase for samples with a conventional magnetocaloric effect and to the low-temperature phase for samples with an inverse magnetocaloric effect.
is the baseline corrected DSC calorimetric signal. The reference state S0 is chosen at a temperature T0 well above (or below) the transition region, where the specific heat is independent of stress and magnetic field. This requirement is fulfilled for the paramagnetic phase, which corresponds to the high-temperature phase for samples with a conventional magnetocaloric effect and to the low-temperature phase for samples with an inverse magnetocaloric effect.
The above procedure provides entropy curves only for the specific stress and magnetic field values used in the experiments. In order to obtain  over the entire coordinate phase-space, it is necessary to fit an appropriate function that reproduces the experimental data at the specific σ and H values. Examples are shown in supplementary material, and typically they encompass one or two sigmoid functions which capture the large entropy variation at the first-order phase transition [6, 7]. As an example, figure 4 shows selected isothermal entropy surfaces for non-synergic Ni-Mn-In. Data correspond to the application of magnetic field and removal of uniaxial stress, as indicated by the arrows along the axis. A detailed analysis of the multicaloric response of this alloy can be found in [6]. It is to be noted that the curvature of the isothermal
over the entire coordinate phase-space, it is necessary to fit an appropriate function that reproduces the experimental data at the specific σ and H values. Examples are shown in supplementary material, and typically they encompass one or two sigmoid functions which capture the large entropy variation at the first-order phase transition [6, 7]. As an example, figure 4 shows selected isothermal entropy surfaces for non-synergic Ni-Mn-In. Data correspond to the application of magnetic field and removal of uniaxial stress, as indicated by the arrows along the axis. A detailed analysis of the multicaloric response of this alloy can be found in [6]. It is to be noted that the curvature of the isothermal  is indicative of a non-vanishing contribution from the cross-coupling term in this material.
is indicative of a non-vanishing contribution from the cross-coupling term in this material.
Figure 4. Entropy surfaces. Examples of isothermal entropy surfaces for selected values of temperature for a Ni-Mn-In alloy. The entropy values are referenced to the entropy at a temperature T0 = 256 K, in the absence of magnetic field and at atmospheric pressure, and they correspond to the application of a magnetic field and the removal of a uniaxial stress, as indicated by the arrows (see [6] for more details).
Download figure:
Standard image High-resolution imageThe knowledge of  over the whole phase-space enables a straightforward computation of the isothermal entropy change arising from an arbitrary increase of stress and magnetic field, as follows:
over the whole phase-space enables a straightforward computation of the isothermal entropy change arising from an arbitrary increase of stress and magnetic field, as follows:
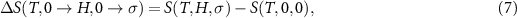
and by inversion of the  curves, the adiabatic temperature change is obtained as:
curves, the adiabatic temperature change is obtained as:
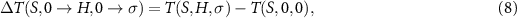
where results are commonly plotted as a function of the initial temperature prior to application of the fields. Equivalent expressions hold for the removal of stress and magnetic field.
4. Hysteresis
For the sake of clarity, in the previous sections we have implicitly assumed that the phase transitions occurred in thermodynamic equilibrium. However, for most giant caloric materials, the magnetostructural transition is first-order and accompanied by hysteresis in temperature and field(s). A detailed study of the effect of hysteresis on the thermal response of monocaloric materials has already been reported [14] and will not be further discussed in this paper.
Here, we address how hysteresis affects the multicaloric response of a material, as schematised in figures 1–3. For simplicity, we have assumed thermal hysteresis to be field(s) independent. For synergic (conventional) effects [figure 5 upper panels (a)–(d)], application of each field stabilises the low-temperature phase, promoting the transition from the high-temperature to the low-temperatures phase, which corresponds to the cooling branch in the thermal hysteresis loops for a thermally induced transition. In that case, the resulting isothermal entropy changes resulting from the application of one or two fields are not affected by hysteresis (see figure 5(d)), provided that the field(s) are applied either in the high-temperature phase or at a temperature on the cooling branch of the loop. In other words, the schematics illustrated in figures 1 and 3 are still valid, with the only peculiarity that the indicated transition temperatures do not correspond to the equilibrium transition but rather to values located in the cooling branch of the thermal hysteresis loop.
Figure 5. Effect of hysteresis on the multicaloric response. Entropy as a function of temperature in the absence of applied external field (black curves) and under applied fields (coloured curves). Solid lines correspond to heating runs and dashed lines, to cooling runs. Top panels illustrate the case of two conventional monocaloric effects, and the corresponding multicaloric effect. In all cases application of field(s) shifts the transition to higher temperatures and promotes the transition from the high to the low-temperature phases. Bottom panels illustrate the case of a conventional (CE1) and an inverse (CE2) monocaloric effects. For the conventional monocaloric effect (CE1), application of a field (y1) shifts the transition to higher temperatures and promotes the transition from the high to the low-temperature phases, and for an inverse monocaloric effect (CE2), application of the field (y2) shifts the transition to lower temperatures thus promoting the transition from the low to the high-temperature phases. For the multicaloric effect (MuCE), application of the two fields does not promote the phase transition because the transition temperature is only slightly shifted to higher temperatures and the state of the sample lies within the hysteresis loop.
Download figure:
Standard image High-resolution imageThe situation is more complex for non-synergic multicaloric materials [figure 5 lower panels (e)–(h)]. For the conventional monocaloric effect (CE1, figure 5(f)), application of the field stabilises the low-temperature phase, thus promoting the transition from the high to the low-temperature phase, which corresponds to the cooling branch in the thermal hysteresis loop. By contrast, for the inverse monocaloric effect (CE2, figure 5(g)), the field stabilises the high-temperature phase, promoting the transition from the low-temperature to the high temperature phase, which corresponds to the heating branch of the thermal hysteresis loop. Therefore, application of the two fields can bring the material to a state within the hysteresis loop. In that circumstance, the state of the material depends on the minor hysteresis loops [15], which are usually not known, and the caloric response is significantly reduced (or even suppressed). However, a significant multicaloric effect for the non-synergic case can still be obtained, provided that the applied fields are strong enough so that the thermal hysteresis loop under applied field(s) does not overlap the loop in the absence of fields.
In non-synergic multicaloric materials, independently modifying two (or more) external fields enables an advantageous manipulation of hysteresis. On the one hand, it has been shown [3, 10] that it is possible to reduce (or even suppress) the hysteresis in magnetic field by a convenient cycle in which magnetic field is applied at ambient pressure, while it is removed under an applied hydrostatic pressure. It is worth recalling that hysteresis is not suppressed for such a multi-stimuli cycle, but rather the hysteresis in one field (magnetic field) is transferred to the second field (pressure) [1]. The energy losses in the multicaloric cycle are similar to those corresponding to the single magnetic field cycle. However, in practical applications for refrigerating purposes, the multicaloric cycle can be advantageous because it enhances the reversibility of the process by transferring the hysteresis from the primary to the secondary fields.
A second feature multicaloric cycles offer is the possibility of taking advantage of hysteresis in the so-called positive-hysteresis cycles [16]. In that cycle, hysteresis locks the material in the magnetised state when magnetic field is removed. Applying mechanical stress unlocks the phase transition and brings the material back to its original state. This method of operation provides several advantages compared to monocaloric cycles because application/removal of the field(s) is decoupled from the heat transfer step (for monocaloric cooling, the external fields need to be maintained during heat exchange). Such a decoupling enables the utilisation of more focused magnetic fields, with the consequent reduction of the permanent magnet volume and increased field strength.
5. Illustrative cases
To illustrate the ideas described in the previous sections, we have selected two prototype multicaloric materials (Fe-Rh and Ni-Mn-Ga) undergoing magnetostructural phase transitions. For compositions close to the stoichiometry, Fe-Rh is ferromagnetic above room temperature, with a cubic CsCl structure ( space group). Upon cooling, it undergoes a magnetostructural transition from a ferromagnetic to an antiferromagnetic phase which does not break the crystal symmetry but involves a ∼1% unit cell volume increase. Associated with this phase transition, Fe-Rh exhibits giant inverse magnetocaloric and conventional barocaloric effects [17], and hence this material is a good example for the non-synergic multicaloric case.
space group). Upon cooling, it undergoes a magnetostructural transition from a ferromagnetic to an antiferromagnetic phase which does not break the crystal symmetry but involves a ∼1% unit cell volume increase. Associated with this phase transition, Fe-Rh exhibits giant inverse magnetocaloric and conventional barocaloric effects [17], and hence this material is a good example for the non-synergic multicaloric case.
Ni2MnGa is a prototype magnetic shape memory alloy. At room temperature, it exhibits a Heusler structure ( ) and is ferromagnetic with a Curie temperature slightly above ambient. Upon cooling it undergoes a martensitic transition towards a lower crystal symmetry phase which is also ferromagnetic [18]. It has been shown that by appropriate doping with Cu it is possible to shift both the martensitic transition and Curie temperatures in such a way that the two phase transitions (magnetic and martensitic) merge, thus giving rise to a single magnetostructural transition [19]. Associated with this transition, giant conventional magnetocaloric and elastocaloric effects have been reported for Ni50Mn18.5Ga25Cu6.5 [7], and this alloy is a good candidate to illustrate the synergic multicaloric case.
) and is ferromagnetic with a Curie temperature slightly above ambient. Upon cooling it undergoes a martensitic transition towards a lower crystal symmetry phase which is also ferromagnetic [18]. It has been shown that by appropriate doping with Cu it is possible to shift both the martensitic transition and Curie temperatures in such a way that the two phase transitions (magnetic and martensitic) merge, thus giving rise to a single magnetostructural transition [19]. Associated with this transition, giant conventional magnetocaloric and elastocaloric effects have been reported for Ni50Mn18.5Ga25Cu6.5 [7], and this alloy is a good candidate to illustrate the synergic multicaloric case.
Figure 6 shows the entropy curves ((a)–(c), top panels) and the corresponding isothermal entropy changes ((d)–(f), lower panels) along with the contribution from the cross-coupling term (g) for the non-synergic Fe49Rh51 (raw data are from [10]). The entropy change of the magnetostructural transition ( ) in this material has been found to be independent of both magnetic field and pressure, within experimental errors. The entropy curves derived from calorimetric data can be well fitted by a simple function such as:
) in this material has been found to be independent of both magnetic field and pressure, within experimental errors. The entropy curves derived from calorimetric data can be well fitted by a simple function such as:
Figure 6. Multicaloric effect in non-synergic Fe49Rh51. Top panels (a)–(c): entropy curves in the absence of applied fields (black curves), for a 5 kbar applied hydrostatic pressure (blue curves), for a 5 T applied magnetic field (red curves), and for the combined application of 5 T and 5 kbar (green curves). Darker lines correspond to cooling runs and lighter lines correspond to heating runs. Bottom panels (d)–(f) show the corresponding isothermal entropy changes for the multicaloric (d), barocaloric (e) and magnetocaloric (f) effects. Panel (g) shows the isothermal entropy change arising from the cross-coupling term.
Download figure:
Standard image High-resolution image
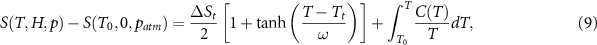
where Tt represents the transition temperature, ω is a parameter which accounts for the spread in temperature of the phase transition, and C is the specific heat [20]. Examples for this fit are given in the supplementary material.
Because the magnetostructural transition in Fe49Rh51 is very sharp and is strongly sensitive to the external fields, the transition shift with the applied fields (5 T and 5 kbar) considered here is large enough to overcome the effect of thermal hysteresis. Therefore the experimental data reproduce very well the ideal non-synergic case illustrated in figure 2. As shown in figure 6, application of a magnetic field shifts the transition to lower temperatures, resulting in a positive magnetocaloric  associated with an inverse magnetocaloric effect. On the other hand, applying hydrostatic pressure shifts the transition towards higher temperatures giving rise to a negative
associated with an inverse magnetocaloric effect. On the other hand, applying hydrostatic pressure shifts the transition towards higher temperatures giving rise to a negative  associated with a conventional barocaloric effect. In both cases, the saturation
associated with a conventional barocaloric effect. In both cases, the saturation  values match the transition entropy change (
values match the transition entropy change ( ). For the particular combination of magnetic field (
). For the particular combination of magnetic field ( = 5 T) and pressure (p = 5 kbar) values, the phase transition shifts to lower temperatures giving rise to an inverse multicaloric effect spreading over a temperature window narrower than that corresponding to the monocaloric effects. The contribution from the cross-coupling term is shown in figure 6(g). In the high-temperature region, the increase in entropy associated with the cross-coupling term compensates for the decrease in entropy from the barocaloric effect. In contrast, in the low-temperature region, it partially compensates for the inverse magnetocaloric effect, resulting in a narrower temperature window. It is worth noting, however, that a non-synergic multicaloric effect can be turned into synergic by applying one field and removing the second field [6, 10, 21].
= 5 T) and pressure (p = 5 kbar) values, the phase transition shifts to lower temperatures giving rise to an inverse multicaloric effect spreading over a temperature window narrower than that corresponding to the monocaloric effects. The contribution from the cross-coupling term is shown in figure 6(g). In the high-temperature region, the increase in entropy associated with the cross-coupling term compensates for the decrease in entropy from the barocaloric effect. In contrast, in the low-temperature region, it partially compensates for the inverse magnetocaloric effect, resulting in a narrower temperature window. It is worth noting, however, that a non-synergic multicaloric effect can be turned into synergic by applying one field and removing the second field [6, 10, 21].
The multicaloric synergic effect in Ni50Mn18.5Ga25Cu6.5 is presented in figure 7.Top panels (a–c) show the entropy curves computed from calorimetric cooling runs (raw data are from [7]). The resulting entropy changes are shown in bottom panels (d–f). The contribution from the cross-coupling term is shown in panel (g). For Ni50Mn18.5Ga25Cu6.5, the transition entropy change  has been found to decrease with increasing magnetic field and increasing stress [7], and such dependence is responsible for the crossover observed in the entropy curves at low temperatures in figures 7(a)–(c). In addition, such a
has been found to decrease with increasing magnetic field and increasing stress [7], and such dependence is responsible for the crossover observed in the entropy curves at low temperatures in figures 7(a)–(c). In addition, such a 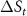 dependence in H and σ imposes the use of fitting functions with more free parameters than the one given by equation (9). Examples are given in the Supplementary Material. As shown in figure 7, application of magnetic field and/or uniaxial stress shifts the transition to higher temperatures, resulting in conventional magnetocaloric and elastocaloric effects. Applying both fields shifts the transition to temperatures higher than for the application of a single field, which gives rise to a broader temperature window where giant caloric effects occur. For the particular magnetic field shown (
dependence in H and σ imposes the use of fitting functions with more free parameters than the one given by equation (9). Examples are given in the Supplementary Material. As shown in figure 7, application of magnetic field and/or uniaxial stress shifts the transition to higher temperatures, resulting in conventional magnetocaloric and elastocaloric effects. Applying both fields shifts the transition to temperatures higher than for the application of a single field, which gives rise to a broader temperature window where giant caloric effects occur. For the particular magnetic field shown ( = 5 T), the shift in the transition temperature is large enough to promote the transformation of the full sample, and the maximum magnetocaloric entropy change matches the transition entropy change [
= 5 T), the shift in the transition temperature is large enough to promote the transformation of the full sample, and the maximum magnetocaloric entropy change matches the transition entropy change [ ]. On the other hand, the shift in the transition due to a 20 MPa uniaxial stress is not large enough and the sample is only partially transformed, resulting in an elastocaloric
]. On the other hand, the shift in the transition due to a 20 MPa uniaxial stress is not large enough and the sample is only partially transformed, resulting in an elastocaloric  lower than the transition entropy change [
lower than the transition entropy change [ ]. The combined action of 5 T and 20 MPa induces the transformation of the full sample, with a corresponding isothermal entropy change that matches the transition entropy change [
]. The combined action of 5 T and 20 MPa induces the transformation of the full sample, with a corresponding isothermal entropy change that matches the transition entropy change [ ]. However, multicaloric
]. However, multicaloric  values are lower than magnetocaloric ones due to the decrease in transition entropy with increasing magnetic field and stress, which imposes
values are lower than magnetocaloric ones due to the decrease in transition entropy with increasing magnetic field and stress, which imposes  <
<  . The cross-coupling contribution is responsible for the enlargement of the temperature window to higher temperatures. Furthermore, at high temperatures it compensates for the
. The cross-coupling contribution is responsible for the enlargement of the temperature window to higher temperatures. Furthermore, at high temperatures it compensates for the  values associated with the elastocaloric effect. Interestingly, the cross-coupling contribution enhances the multicaloric response of the material at low or moderate applied fields.
values associated with the elastocaloric effect. Interestingly, the cross-coupling contribution enhances the multicaloric response of the material at low or moderate applied fields.
Figure 7. Multicaloric effect in synergic Ni50Mn18.5Ga25Cu6.5. Top panels (a)–(c): entropy curves corresponding to cooling runs, in absence of applied fields (black curves), for a 20 MPa applied uniaxial stress (blue curve), for a 5 T applied magnetic field (red curve), and for the combined application of 5 T and 20 MPa (green curve). Bottom panels (d)–(f) show the corresponding isothermal entropy changes for the multicaloric (d), elastocaloric (e) and magnetocaloric (f) effects. Panel (g) shows the isothermal entropy change corresponding to the cross-coupling.
Download figure:
Standard image High-resolution image6. Summary and outlook
We have studied the multicaloric response of materials with synergic and non-synergic monocaloric effects, subjected to the combined action of two external fields. It is shown that the multicaloric entropy change is the sum of the corresponding monocaloric values plus a contribution arising from the interplay between the physical properties thermodynamically conjugated to the applied fields (cross-response contribution). We have also proposed a methodology to systematically quantify the contribution from the cross-response to the total multicaloric entropy change, which has been applied to prototype synergic (Ni-Mn-Ga-Cu) and non-synergic (Fe-Rh) multicaloric materials.
For the synergic case, the cross-coupling contribution is responsible for enlarging the temperature window where giant caloric effects are observed, while for the non-synergic case, the cross-coupling contribution reduces the temperature window.
The first-order magnetostructural transition occurring in most giant caloric materials spreads over a specific range of temperature and field(s), and typically large values of the applied fields are required to induce the transformation of the whole sample. In this case, the cross-coupling contribution becomes particularly relevant for synergic materials since it enhances the caloric response at lower values of the applied fields. Avoiding large fields is very advantageous in the design of practical refrigeration and heat pumping devices.
Although at first glance non-synergic materials appear less appealing, it is worth noting that synergic effects can be obtained by applying one field and removing the second. Furthermore, on the one hand, these materials enable fine-tuning of hysteresis with two applied fields. On the other hand, they are best suited for hysteresis-positive refrigerating cycles.
Acknowledgments
Financial support from MCIN/AEI/10.13039/501100011033 (Spain) under Grant Nos. PID2020-113549RB-I00/AEI and IJC2020-043957-I, and from AGAUR (Catalonia) under Project SGR00328 is acknowledged. A.G acknowledges financial support from Universitat de Barcelona under a Margarita Salas fellowship, supported by the Spanish Ministry of Universities with funding from the European Union under the NextGenerationEU program.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Supplementary data (0.2 MB PDF)








