Abstract
The C20 molecule exists as three low-energy isomers: the monocyclic ring, a corannulene-like bowl structure, and the cage-the smallest possible fullerene. The curious structures of these isomers, along with the valuable properties and possible applications of fullerenes more generally, mean that C20 has attracted interest both experimentally and computationally. Unfortunately, previous theoretical studies have found these C20 isomers present a significant computational challenge, and widely used methods such as Density Functional Theory with different functionals have been unable to agree on even the relative ordering of the isomer energies. Even accurate high-level methods such as coupled-cluster with singles, doubles, and perturbative triples (CCSD(T)) and Diffusion Monte Carlo (DMC) have previously disagreed on the energetic ordering of these isomers. Here we re-examine the ring, bowl, and cage isomers of C20 using a more accurate DMC technique. We employ a novel method to go beyond the single-determinant DMC approaches previously used, and instead use more accurate multi-determinant trial wavefunctions. Our results show that the fullerene cage exhibits different electron correlation effects than the ring and bowl, which when taken into account leads to a reordering of their relative energies. This finally establishes agreement between DMC and relatively recent complete-basis CCSD(T) results, thereby resolving a long-standing disparity between these two high-level descriptions of the C20 isomers. The approach we use is generalisable, and could be used to provide insight into even larger systems in future.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Since their discovery in 1985 [1, 2], fullerenes have attracted considerable attention within the fields of materials science and nanotechnology, for their distinct electronic and structural properties and wide range of potential applications [3–5]. A member of the highly applicable and useful set of allotropes of carbon, together with diamond, graphite, graphene, and carbon nanotubes, fullerenes consist of carbon rings of five to seven atoms, which are fused to form a closed or partially closed cage.
These unique fullerene structures result in a number of valuable properties. For instance, the most widely studied C60 'buckminsterfullerene' sphere forms superconducting crystals when doped with alkali metals [6–9]. It is also an exceptional radical scavenger, is highly robust, and can be easily modified, allowing for the formation of derivatives with varying physical characteristics [10]. These properties make the fullerenes valuable for biological applications, and they have indeed demonstrated antioxidant, antiviral, and anticancerous activity [4, 11–14]. Fullerenes also behave as strong electron-acceptors within energy conversion systems, and thus C60 derivatives have been studied extensively as components of organic solar cells [15].
Research into systems such as fullerenes, which have curious and exciting structures and properties, serves not only to contribute to the development, refinement, and industrial realisation of these potential applications, but also to improve our understanding of the unique chemistry and physics that governs their behaviour. An improved depth of understanding is crucial for the continued development of novel materials for advanced technology applications.
One particular fullerene that has captured the interest of both experimentalists and theoreticians is the smallest member of the fullerene family - the C20 cage [16–33]. Along with the fullerene cage, C20 exists as two other low-energy isomers; the monocyclic ring, and corannulene-like bowl structure, which aligns with a section of C60 [34]. These three structures are depicted in figure 1.
Figure 1. The three low-energy isomers of C20. (From the left) The monocyclic ring, corannulene-like bowl structure, and the fullerene cage.
Download figure:
Standard image High-resolution imageAll three of the low-lying C20 isomers have been experimentally observed. Based on these studies, the ring is experimentally considered to be the lowest energy structure [35, 36], with the higher energy bowl and cage isomers identified relatively recently through spectroscopic evidence [31]. However, despite the numerous theoretical studies that have been conducted, computational methods have been unable to find the same agreement amongst the calculated relative energies of these three C20 isomers. The contradicting theoretical results published in previous studies have been summarised in multiple sources including References [21] and [32].
The computational challenge of these systems stems from the very different structures present in the ring, bowl, and cage isomers, which result in very different electronic structure effects. For one computational method to accurately describe all three systems, the method must be able to represent the diverse electronic properties present across the three different structures with consistent accuracy. It must be able to treat the somewhat long-range electron correlation of the wide two-dimensional ring as accurately as the high curvature of the compact three-dimensional cage, for instance. The ring, bowl, and cage C20 isomers have thus become known as stringent test systems, used to assess the accuracy and consistency of the various computational methods available. Therefore application of theoretical techniques to the C20 isomers not only advances the understanding of these unique structures, but provides insight into the most trustworthy computational methods for modelling analogous systems going forward.
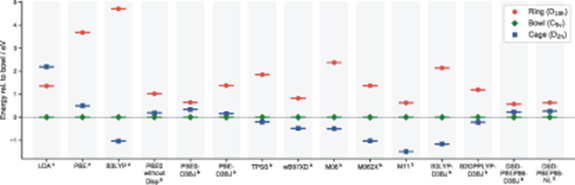
Density Functional Theory (DFT) is often the computational method of choice for these kind of molecular systems, however application of DFT to the challenging C20 isomers provides a clear demonstration of contradicting theoretical results, and why care should be taken around the application and interpretation of DFT. Figure 2 depicts the energies of the ring and cage structures, relative to the bowl, as predicted by DFT using a range of different functionals. The data in this plot was provided by Reference [18], as well as calculations performed during this study, with details described in section 3. From figure 2, it is clear that different DFT functionals predict very different relative energies for the C20 isomers. In fact, many functionals fail to even agree on the lowest energy structure. This problem is not unique to the C20 isomers [39].
Figure 2. The relative energies of the ring, bowl, and cage C20 isomers, as predicted by DFT using a range of different functionals. Energies are presented in eV relative to the bowl isomer. a Energies were calculated during this study, using Gaussian16 [37] and the BFD-VTZ basis set and corresponding pseudopotentials [38] (further details in section 3). b Relative energies were reproduced from Reference [18].
Download figure:
Standard image High-resolution imageThe variation in these DFT results demonstrates that for systems as sensitive as these C20 isomers, a higher level theory is required to more accurately represent these molecules, or at the very least, benchmark the DFT results to allow the most accurate and trustworthy functional to be identified.
Coupled-cluster with singles, doubles, and perturbative triples (CCSD(T)) has become known as the 'gold standard' of quantum chemistry, and has a well demonstrated ability to describe a range of molecular systems with consistent accuracy [40, 41]. Unfortunately, the N7 scaling of CCSD(T) computational cost means this method quickly becomes prohibitively computationally demanding as the system size increases, though localised variations such as DLPNO-CCSD(T) have recently demonstrated substantially improved computational efficiency, while maintaining the accuracy of CCSD(T) [42, 43].
Alternatively, Quantum Monte Carlo (QMC) methods, in particular the accurate real space Diffusion Monte Carlo (DMC) approach, scales as N3 (albiet with a large prefactor), and has also been shown to describe molecular systems very accurately. Accurate high-levels methods such as DMC and CCSD(T) are generally expected to provide similar results, once relatively small errors such as multi-reference effects and basis set incompleteness have been accounted for. However, the results from previous DMC studies of C20 have been compared to early CCSD(T) calculations, and found to disagree. The DMC results predicted the bowl to be the lowest energy structure, with either the cage and ring degenerate, or the ring at slightly lower energy than the cage [23, 44, 45]. Whereas early small-basis CCSD(T) results agreed with the bowl as the lowest energy structure, but had the ring as the highest energy, and the cage ranging from degenerate with the bowl to just below the ring, depending on the method used to optimise the structures [46, 47].
The computational resources available today have recently allowed CCSD(T) to be reapplied to the three C20 isomers, using substantial basis sets as well as explicitly correlated methods [18, 19]. Similarly, our implementation of DMC within the CMQMC code [48] has reached a stage where previous DMC studies may be improved upon by extending the DMC trial-wavefunction from a single Slater determinant, to a more accurate multi-determinant expansion. Furthermore, here we generate the trial-wavefunction multi-determinant expansion without the need for the costly Configuration Interaction (CI) calculations often employed.
In this study, we therefore present these multi-determinant DMC calculations for the ring, bowl, and cage C20 isomers, in order to provide the most accurate DMC results available for these systems. These C20 isomers are amongst the largest systems to be described using multi-determinant DMC [49, 50]. Through comparison to recent CCSD(T) results, we are thus able to resolve a long standing conundrum as to why previous CCSD(T) and DMC C20 results were not in agreement.
2. Multi-determinant DMC trial-wavefunction
The QMC calculations presented in this study have been performed using both single-determinant and multi-determinant trial-wavefunctions. We start here by describing our motivation for this approach, along with our novel method for generating the multi-determinant trial-wavefunctions. This method identifies important determinants to be included in the trial-wavefunction using an efficient and parallelisable Variational Monte Carlo (VMC) approach with the potential to scale to large systems.
Most common real space QMC methods, such as VMC and DMC require as an input, a trial-wavefunction (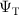 ) to be used for the fixed node approximation [51]. This trial-wavefunction acts as a constraint which enforces the sign structure of the wavefunction, as required for fermionic electronic structure calculations.
) to be used for the fixed node approximation [51]. This trial-wavefunction acts as a constraint which enforces the sign structure of the wavefunction, as required for fermionic electronic structure calculations.
The accuracy of DMC calculations is actually dependent on how well this trial-wavefunction represents the sign structure of the exact ground state. Errors in calculated DMC energies resulting from the use of an approximate trial-wavefunction are referred to as fixed node errors. Fortunately, these errors are generally small, and DMC accurately describes a range of systems. Furthermore, DMC energies are variational, so they can be systematically improved by increasing the accuracy of the trial-wavefunction.
While various forms of the trial-wavefunction have been employed [52, 53], here we take the most common approach by constructing 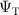 from a combination of Slater determinants, D (or Configuration State Functions, CSFs), and a Jastrow factor (J), which is a compact and efficient way of including explicit dynamical electron correlation effects:
from a combination of Slater determinants, D (or Configuration State Functions, CSFs), and a Jastrow factor (J), which is a compact and efficient way of including explicit dynamical electron correlation effects:

The standard procedure is to optimise the parameters of the Jastrow factor and CSF coefficients ci (if required) through VMC (details in section 3). The resulting 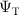 is then used for the more accurate DMC calculation.
is then used for the more accurate DMC calculation.
For many problems, a trial-wavefunction constructed from only a single Slater determinant plus Jastrow factor is sufficient to provide very accurate DMC results [54–56]. In this case, the sum in equation (1) disappears, and the single-determinant trial-wavefunction becomes 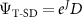 . The determinant (D) is often simply constructed from Hartree–Fock (HF) or Kohn-Sham (KS) orbitals.
. The determinant (D) is often simply constructed from Hartree–Fock (HF) or Kohn-Sham (KS) orbitals.
For tricky systems, a more accurate multi-determinant form of the trial-wavefunction may be required, and the sum in equation (1) runs over a chosen space of 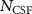 CSFs. Efficient methods have been developed to work with large multi-determinant expansions in QMC calculations [49], and the remaining challenge is to identify the set of CSFs that most effectively improves the nodal surface of the trial-wavefunction. In many cases, Configuration Interaction (CI) calculations are performed to generate a suitable set of CSFs. This CSF space is typically reduced using selected-CI [57] or truncation approaches, which estimate the contribution of each CSF to the QMC energy [58]. Unfortunately, the CI calculations can become prohibitively expensive as the size of the system increases, and can thus be a bottleneck for multi-determinant QMC calculations.
CSFs. Efficient methods have been developed to work with large multi-determinant expansions in QMC calculations [49], and the remaining challenge is to identify the set of CSFs that most effectively improves the nodal surface of the trial-wavefunction. In many cases, Configuration Interaction (CI) calculations are performed to generate a suitable set of CSFs. This CSF space is typically reduced using selected-CI [57] or truncation approaches, which estimate the contribution of each CSF to the QMC energy [58]. Unfortunately, the CI calculations can become prohibitively expensive as the size of the system increases, and can thus be a bottleneck for multi-determinant QMC calculations.
Here, we have taken a different approach which is designed for computational efficiency, allowing multi-determinant DMC calculations to be performed for large systems. We start by generating all single and double excitations from the reference determinant within a defined active space. Next, rather than performing a CI calculation to determine the important CSFs, we use a VMC approach to estimate the coefficient of each CSF, in the presence of the Jastrow factor, using an expression based on perturbation theory. The details of this expression are outlined within the Theoretical Methods of section 6.
While this estimation is of course approximate, tests have found the estimated coefficients to closely resemble those obtained from a full VMC optimisation of all CSF coefficients in the presence of the Jastrow factor (figure 5 in section 6). Most importantly, this method only needs to be accurate enough to identify the CSFs with significant coefficients. It is these which are included, in order to efficiently improve upon the single-determinant wavefunction. Furthermore, by removing the need for costly CI calculations, and estimating the CSF coefficients using a parallelisable and efficient VMC calculation, this approach allows a sensible multi-determinant space to be generated for the relatively large C20 isomers considered here, and would continue to scale to even larger systems.
3. Computational details
The geometries of each isomer were optimised with either HF, or DFT and the B3LYP functional using Gaussian16 [37]. Identification of a minimum was confirmed by checking for imaginary frequencies. The symmetries of each isomer were chosen to be  (ring), C5v (bowl), and
(ring), C5v (bowl), and 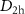 (cage), based on the data available in previous studies [16, 18].
(cage), based on the data available in previous studies [16, 18].
The CSFs and determinants used for each trial-wavefunction were generated using GAMESS 2012 [59]. Each active space for each system is defined here as (N, M), for N electrons in M spatial orbitals. To generate the multi-determinant parts of each trial-wavefunction, all single and double excitations within the chosen active space were generated from HF orbitals. The coefficients of the CSFs were then estimated using the procedure described in section 2, and each multi-determinant space selected by including CSFs with largest estimated coefficients first. The multi-determinant calculations were performed using the structures optimised with HF [37], and the single and double excitations were generated using HF orbitals. DMC energy improvements due to the multi-determinant trial-wavefunction are thus measured relative to the single-determinant DMC with a HF trial-wavefunction.
All calculations performed here used the energy-consistent pseudopotentials of Burkatzki et al [38] and their corresponding valence-triple-zeta basis sets (BFD-VTZ). Convergence of our QMC results with the triple-zeta basis set was confirmed by performing test calculations with the larger quadruple-zeta basis.
Jastrow factors for the QMC trial-wavefunctions were constructed using explicit electron-electron, electron-nucleus, and electron-electron-nucleus correlation terms. For each isomer and trial-wavefunction, the Jastrow parameters and CSF coefficients were optimised by minimising the variational energy of the wavefunction, using an approach based on the linear method [60].
DMC calculations were performed with a variant of the UNR algorithm [61] that uses electron-by-electron moves. Size-consistent T-moves [62] and efficient small quadrature grids [54] were used to handle the non-local components of the pseudopotentials. The imaginary-time step size was chosen to be 0.002 a.u. Each calculation was run until the statistical uncertainty in the total energy, corrected for serial correlation, was below 0.001 Hartree (0.027 eV). The CMQMC software package was used for all QMC calculations [48].
4. Results and discussion
4.1. Single-determinant DMC
We start our discussion here by presenting the relative energies of the C20 isomers, calculated using DMC with only a single-determinant trial-wavefunction. These are presented in table 1. The DMC(SD-HF) results refer to DMC relative energies calculated using a single-determinant trial-wavefunction constructed from HF orbitals, whereas DMC(SD-B3LYP) indicates the single-determinant part of the trial-wavefunction used DFT orbitals with the B3LYP functional. In each case the geometries of the structures were optimised using the same level of theory from which the trial-wavefunction was constructed.
Table 1. The relative energies of the three low-lying C20 isomers, calculated using DMC with single-determinant trial-wavefunctions. The DMC(SD-HF) results were calculated using a single-determinant trial-wavefunction constructed from HF orbitals, whereas the DMC(SD-B3LYP) values used DFT with the B3LYP functional to calculate the single-determinant trial-wavefunction orbitals. In each case the geometries of the structures were optimised using the same level of theory from which the trial-wavefunction was constructed. Further computational details can be found in section 3. The energies are presented relative to the lowest energy bowl isomer, in eV. Statistical errors on the last digit are shown in parentheses.
| Bowl (C5v) | 0.00 (3) | 0.00 (3) |
Ring ( ) ) |
0.76 (3) | 0.89 (3) |
Cage ( ) ) |
0.98 (3) | 0.91 (2) |
For both sets of results calculated with CMQMC, the bowl is predicted to be the lowest energy isomer. However, while DMC(SD-B3LYP) results predict the cage and the ring to be degenerate within statistical errorbars, the use of HF geometries and HF orbitals splits this degeneracy and predicts the ring to be the lower energy structure. The use of DFT orbitals for single-determinant DMC trial-wavefunctions has previously been found to provide more accurate energies than HF [63, 64], and DFT with the B3LYP functional is generally considered to provide accurate optimised geometries [65]. The results calculated here are consistent with this, as the DMC(SD-B3LYP) total energies were variationally lower than the DMC(SD-HF) values, across all three isomers. The DMC(SD-B3LYP) results are thus taken as the more trustworthy of the single-determinant DMC results.
These DMC(SD-B3LYP) results are in approximate agreement with the early DMC results published by Hsing et al [23], in which the ring( ) and cage(C3v) structures were calculated to be 0.55 (5) and 0.69 (5) eV higher energy than the lowest energy bowl, using a plane-wave basis and LDA orbitals. Raghavachari et al [44] and Anderson et al [45] additionally presented some early DMC results where the energy of the cage isomer was found to be higher than the ring, using HF geometries and trial-wavefunctions with a relatively small 6-311G* basis set. The source of the discrepancy between these published DMC results has never been clearly established, but becomes evident through comparison to the CMQMC data in table 1. By using HF geometries and trial-wavefunctions, Raghavachari et al [44] and Anderson et al [45] observed the same increased energy of the cage, relative to the ring, as seen in the DMC(SD-HF) values of table 1. Whereas, by using a DFT LDA trial-wavefunction, Needs et al [23] observe the same approximate degeneracy of the ring and cage given by the DMC(SD-B3LYP) values presented here.
) and cage(C3v) structures were calculated to be 0.55 (5) and 0.69 (5) eV higher energy than the lowest energy bowl, using a plane-wave basis and LDA orbitals. Raghavachari et al [44] and Anderson et al [45] additionally presented some early DMC results where the energy of the cage isomer was found to be higher than the ring, using HF geometries and trial-wavefunctions with a relatively small 6-311G* basis set. The source of the discrepancy between these published DMC results has never been clearly established, but becomes evident through comparison to the CMQMC data in table 1. By using HF geometries and trial-wavefunctions, Raghavachari et al [44] and Anderson et al [45] observed the same increased energy of the cage, relative to the ring, as seen in the DMC(SD-HF) values of table 1. Whereas, by using a DFT LDA trial-wavefunction, Needs et al [23] observe the same approximate degeneracy of the ring and cage given by the DMC(SD-B3LYP) values presented here.
4.2. Multi-determinant DMC
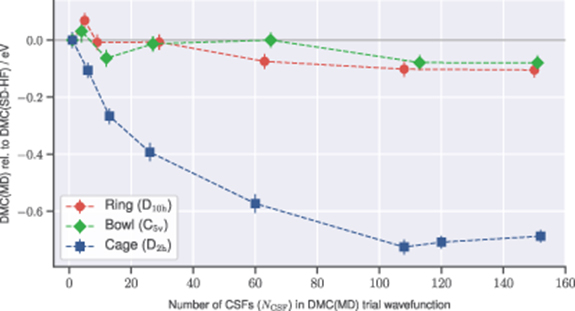
Beyond these single-determinant DMC results, we have investigated the effect of including an increasing number of carefully selected single and double excitations into the multi-determinant DMC trial-wavefunction. Figure 3 presents the reduction in the DMC(MD) energy of the ring, bowl, and cage C20 isomers as the number of CSFs in the trial-wavefunction is increased. The DMC(MD) energies in figure 3 are therefore shown relative to DMC(SD-HF) results for each isomer.
Figure 3. The reduction in the DMC energies of the ring, bowl, and cage C20 isomers, as the number of CSFs in each multi-determinant DMC trial-wavefunction (NCSF) is increased. The multi-determinant DMC(MD) energies are presented relative to the DMC energies calculated using a single-determinant HF trial-wavefunction (DMC(SD-HF)). A change in the DMC(MD) energies indicates the inclusion of increasingly large multi-determinant expansions in the DMC trial-wavefunction is improving upon the fixed node error of the single-determinant DMC results.
Download figure:
Standard image High-resolution imageEach multi-determinant expansion was generated from single and double excitations from a HF determinant reference, within a chosen active space. For each isomers, the (N,M) active space used was ring: (12,12), bowl: (8,15), cage: (12,16). These were chosen by considering the structure and degeneracies within the HF molecular orbitals. CSFs from the single and double excitation space were then sequentially included based on those with largest coefficients, as estimated using the method described in section 2. Larger active spaces such as (22,34) for the bowl isomer were additionally investigated, but were found to have little effect on the CSFs included in the truncated multi-determinant expansions and resulting DMC(MD) energies.
Figure 3 presents the reduction in the fixed node DMC error achieved by improving the trial-wavefunction using multi-determinant expansions. The results are of particular interest because of the different ways the DMC(MD) energies of each isomer react to the inclusion of additional determinants. The ring and bowl isomers are both relatively unaffected. This suggests that for these systems, a single-determinant trial-wavefunction is actually capturing most of the electron correlation effects required to accurately represent the wavefunction nodal surface.
The cage, however, behaves quite differently. For instance, including only six CSFs in the trial-wavefunction already has a marked effect on the DMC(MD) energy. With a multi-determinant expansion of only 13 CSFs, the DMC(MD) energy is reduced by 0.27 eV. This energy improvement continues up to the 108 CSFs considered, at which point the DMC(MD) energy has been lowered by 0.73 eV. Increasing the number of CSFs to approximately 150 confirms this multi-determinant DMC energy has converged within statistical errorbars. These results indicate that unlike the ring and bowl structures, significant fixed node errors exist for the cage using a single-determinant trial-wavefunction. In other words, for the cage isomer, a single HF determinant is unable to accurately represent the DMC nodal surface, and a linear combination of determinants is required to more accurately describe this system.
An analogy can be made between this behaviour of the cage and systems with significant static correlation, for which an accurate quantum chemical description requires multi-reference effects. These are systems where the HF determinant is insufficient to provide an accurate reference for the calculation, and instead a multi-determinant reference is required. Common examples often mentioned include the bond breaking process, cis-trans rotations, as well as equilibrium molecular examples such as ozone. The presence of strong correlation and the need for a multi-determinant description of the C20 fullerene cage has previously been discussed in the literature [16, 24]. However the direct relationship between the multi-reference requirements in traditional quantum chemical calculations and the impact on nodal surface errors within DMC is non-trivial, and unfortunately, the presence of correlation effects not captured by a single-determinant DMC trial wavefunction cannot currently be predicted a priori.
It should be noted that the multi-determinant expansions used for the DMC(MD) calculations in figure 3 only include up to double excitations within a restricted set of active space orbitals, and this space was further truncated based on CSF coefficient estimates. It is possible that including higher excitations, additional occupied or virtual orbitals, or CSFs with smaller coefficients, could have an effect on the DMC(MD) energies of the ring or bowl isomers, or further reduce the fixed node error and continue to lower the DMC(MD) energy of the cage. For systems with particularly challenging electronic structure, a well-known example of which is the chromium dimer [66], these higher order effects may become important. However, for many cases, including these C20 isomers, the use of low-lying single and double excitations is expected to be sufficient to capture most of the important electronic structure effects.
The multi-determinant trial-wavefunctions that have been employed here, using relatively low computational overhead and methods predicted to scale efficiently, has allowed us to identify variations in the behaviour of the different isomers, and significantly improve the DMC description of the C20 fullerene cage. This represents significant progress, particularly for these C20 isomers, which have previously been considered large for the level of accuracy achieved here.
4.3. Comparison to CCSD(T)
Finally, here we consider the relative energies of the C20 isomers, as calculated using our largest multi-determinant DMC trial-wavefunction, compared to both the single-determinant DMC results from section 4.1, and recent published CCSD(T) calculations. This comparison is presented in figure 4. From the comparison of the DMC results calculated in this study, it is clear the multi-determinant trial-wavefunctions have broken the ring-cage degeneracy given by the DMC(SD-B3LYP) results and lowered the cage to only 0.34 (3) eV above the lowest energy bowl isomer.
Figure 4. The relative energies of the ring, bowl, and cage C20 isomers-a comparison of the DMC results calculated during this study, to published CCSD(T) data. The DMC(SD-HF) and DMC(SD-B3LYP) values are the single-determinant DMC results presented in table 1. The DMC(MD) results were taken from the DMC energies using the most accurate multi-determinant trial-wavefunction; those with multi-determinant expansions of approximately 100 CSFs. a Reference [19]: CCSD(T) with a cc-pVTZ basis set, using geometries optimised at the CCSD/cc-pVDZ level. b Reference [18]: Geometries were optimised using DFT with the PBE0 functional and cc-pVTZ basis set. The CCSD(T)/V{T,Q}Z results have been extrapolated from cc-pVTZ and cc-pVQZ CCSD(T) data to the basis set limit. The MP2-F12/VTZ-F12+HLC/VTZ values combine MP2 at the basis set limit with differences between MP2 and CCSD(T) results, and are described as the most accurate explicitly correlated results of the Reference [18] study.
Download figure:
Standard image High-resolution imageThe CCSD(T) results presented in figure 4 are those calculated by Bartlett et al [19] with a cc-pVTZ basis set, using geometries optimised at the CCSD/cc-pVDZ level (labelled CCSD(T)/cc-pVTZ). Also shown are results taken from a study by Martin et al [18], which have been calculated using geometries optimised with the PBE0 DFT functional and a cc-pVTZ basis set. The CCSD(T)/V{T,Q}Z results have been extrapolated from cc-pVTZ and cc-pVQZ CCSD(T) data to the basis set limit. The MP2-F12/VTZ-F12+HLC/VTZ values are described as the most accurate results of the Martin et al study. These combine MP2 at the basis set limit with differences between MP2 and CCSD(T) results [18].
By directly comparing this literature CCSD(T) data to the DMC(MD) results calculated here, figure 4 shows that while DMC with a single-determinant trial-wavefunction was unable to agree with the relative energies predicted by CCSD(T), the more accurate multi-determinant DMC values are now in good agreement. In all cases, the bowl is predicted to be the lowest energy C20 isomer. The most accurate DMC(MD) results and all CCSD(T) methods then predict the cage to be approximately 0.35 eV higher in energy, and the ring higher energy above that.
These results also suggest that DMC with a multi-determinant trial-wavefunction is a reliable and accurate computational method, for increasingly large systems, for which the scaling of CCSD(T) will make it computationally infeasible. Furthermore, from comparison to the relative energies predicted by various DFT functionals (Reference [18] and figure 2), the most accurate DMC(MD) results presented here suggest the best DFT representation of the C20 isomers is provided by PBE0-D3BJ or the double hybrid DSD-PBEP86-NL.
5. Conclusion
In this paper, we have examined the computationally challenging problem of predicting the relative energies of the ring, bowl, and cage C20 isomers. For a theoretical method to describe these three very different structures correctly, it must be able to treat the different electron correlation effects present in each system with equivalent accuracy. Previous studies have shown that common computational methods are unable to achieve this balanced treatment, and thus disagree on the relative energies of these C20 isomers. Surprisingly, even the accurate high-level CCSD(T) and DMC methods have disagreed in the past. The sources of this discrepancy had been postulated to be either basis set errors in the early CCSD(T) results, beyond-CCSD(T) multi-reference effects, or fixed-node errors in previous DMC calculations.
Here we have identified the primary reason for the disagreement as being due to the fixed-node errors in DMC. By developing a novel approach that enables the construction of multi-determinant trial wavefunctions for DMC calculations of large systems, we have been able to provide a more consistently accurate description of the three C20 isomers than previous single-determinant DMC studies.
Our calculations showed that while the ring and bowl are well-described using a single-determinant DMC approach, the energy of the cage is improved substantially by using a multi-determinant trial wavefunction. The nature of electron correlation is thus significantly different in the fullerene cage than in the other isomers, and the multi-determinant wavefunction is necessary to adequately capture these effects in fixed-node DMC. The more accurate treatment of the fullerene cage enabled by our approach leads to a general agreement between CCSD(T) and DMC results, with the bowl predicted to be the lowest energy structure, the cage approximately 0.35 eV higher in energy, and the ring isomer higher in energy again.
This study has demonstrated the continued need for accurate high-level treatments of electron correlation effects, to provide a depth of understanding that is important for the development of new materials. The scalable multi-determinant DMC approach applied here has been shown to provide insight and improved accuracy, with regards to the C20 isomers. The general applicability of this method is currently being investigated through application to a range of different problems, including larger systems for which multi-determinant DMC was previously out of reach. Our results have helped shine light on the challenging problem of describing the C20 isomers by resolving the previous disagreement between two accurate high-level computational techniques.
6. Theoretical methods
6.1. Perturbation theory coefficient estimate
We begin by writing our complete wavefunction in terms of a reference state  and a linear combination of basis states:
and a linear combination of basis states:

In contrast to what would be done in a traditional CI calculation, our basis states are products of a Jastrow factor and a configuration state function (CSF), D:

and our reference state is a single-determinant Slater-Jastrow wavefunction:

(although note that in principle the reference state could be a multi-Slater-Jastrow expansion too).
Our goal is to find the coefficients ci that have appreciable weight. To do this we construct a bi-orthonormal perturbation theory, in much the same way as was done by Toulouse and Umrigar [60]. The basic result of this approach is that our ci coefficients can be approximated (to first order) using the expression:
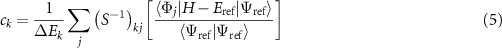
where  is the variational energy of the reference state
is the variational energy of the reference state 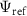 , S is the overlap matrix between basis states that have been projected to be orthogonal to the reference, i.e.:
, S is the overlap matrix between basis states that have been projected to be orthogonal to the reference, i.e.:
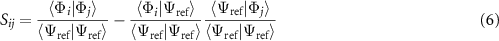
and we are free to choose the energy denominators ΔEk. We further simplify this result by making the approximation  , which would be true if the basis states were orthogonal. This removes the need to build the inverse of the overlap matrix, which would be a bottleneck for large active spaces. Our perturbative expression for the CSF coefficients is then:
, which would be true if the basis states were orthogonal. This removes the need to build the inverse of the overlap matrix, which would be a bottleneck for large active spaces. Our perturbative expression for the CSF coefficients is then:

which is evaluated using Variational Monte Carlo. We define the energy denominators in the same way as standard Møller-Plesset theory, using sums and differences of the Hartree–Fock orbital eigenvalues.
6.2. Comparison of PT estimate to full wavefunction optimisation
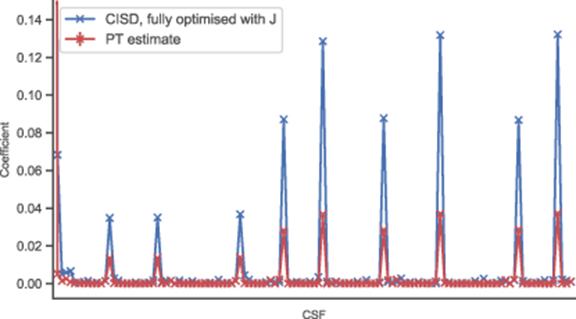
The coefficients predicted by the perturbation theory (PT) estimation method described above are shown for the Beryllium atom in figure 5, labelled 'PT estimate'. These are compared to the coefficients obtained by generating all configuration interaction single and double (CISD) CSFs, and then optimising all coefficients and Jastrow parameters by minimising the variational energy of the wavefunction ('CISD, fully optimised with J'). The coefficients from the PT estimate match the trend from the complete optimisation. These results suggest that using the PT estimate to identify important CSFs, with significant coefficients, would lead to selection of the same space as full optimisation of the coefficients in the presence of the Jastrow factor.
Figure 5. A comparison of the coefficients predicted by the PT estimate in section 6.1 ('PT estimate') to those obtained from a full variational energy optimisation of all CSF coefficients and Jastrow factor parameters ('CISD, fully optimised with J'). The system shown is the Beryllium atom, calculated using a SV (Dunning-Hay) basis set. The coefficients were generated from all single and double excitations from the Hartree–Fock reference.
Download figure:
Standard image High-resolution imageAcknowledgments
Computational resources were supplied by the Australian National Computational Infrastructure (NCI) national facility under the Partner Allocation Scheme Grant dr4.