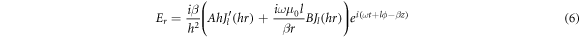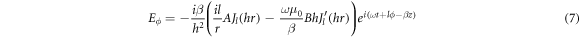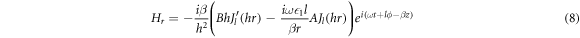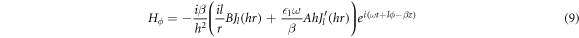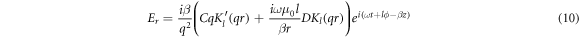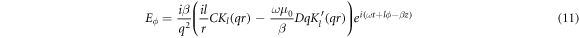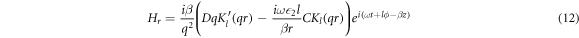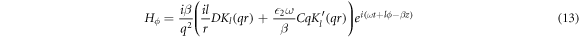Abstract
This paper aims to calculate the photonic band structure in a distributed Bragg reflector pillar. The one-dimensional periodic photonic pillar consists of alternating layers of GaAs and air. We consider the dependence of the GaAs dielectric constant on the hydrostatic pressure at a fixed temperature value. The guided-mode expansion method is employed in the case of the photonic pillar; on expanding the magnetic field of the pillar into the basis of guided modes of a homogeneous waveguide, a linear eigenvalue problem is obtained. It is observed that the photonic band structure consists of true-guided modes outside the light dispersion in the effective core, and the radiative modes are located above the light dispersion. When the pressure is increased at a given temperature, the dielectric band exhibits a shift to higher frequencies, while the air band exhibits a slight shift to lower frequencies, resulting in a decrease in the width of the photonic band gap. The calculation of the photonic pillar fundamental mode did not yield a cutoff frequency.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
One of the main aims of the scientific community is the manufacture of materials of increasingly smaller dimensions, so that more compact devices, which consume less power and operate at higher speeds, can be produced. This trend towards miniaturization, based on the ability to observe and manipulate matter on a small scale, aims at providing novel and/or improved functionalities in diverse fields such as electronics, photonics, medicine, textiles, and sustainable energy. Photonics tries to understand the behavior of light in materials with the objective of designing and implementing devices for the service of the community. Among the artificial materials with innovative applications used to control the propagation of light, are photonic crystals (PCs), which are characterized by the spatial periodicity of the dielectric constant [1, 2]. The idea that leads to the concept of PC can be understood by using an analogy between the photons in a periodic dielectric potential and the electrons in an atomic crystal. The periodicity of the electronic potential is the reason for the existence of a permitted and prohibited band structure in atomic crystals [3]. In photonic crystals, a periodic dielectric function is responsible for the existence of photonic bands and gaps (PBG) [4]. Initially, studies were conducted only in three-dimensional (3D) PCs, which are characterized by having a complete PBG where the propagation of light is inhibited for all polarization states [5, 6]. Subsequently, the one-dimensional (1D) and two-dimensional (2D) classification of PCs has emerged. The PBG has important applications in optical nanoswitches [7, 8], optical transistors [9, 10], photonic crystal fibers [11, 12], optical cloaking [13, 14], superprisms and superlenses [15, 16], among others.
In 2D-PCs, the periodicity varies in two dimensions and extends to infinity in a direction orthogonal to the plane of periodicity. This does not resemble real structures, since the manufacture implies thicknesses of finite dimensions, which causes the confinement of the light to not occur in the non-periodic direction. The most straightforward design in the pursuit of confining light with the desired properties of 3D-PCs is to fabricate finite height 2D-PCs. These structures, commonly known as PC slabs, consist of a 2D-PC embedded in a plane dielectric waveguide [17, 18]. The confinement of light is achieved through total internal reflection, which results due to the dielectric discontinuity between the waveguide in the vertical direction and the periodic pattern of the 2D-PC that controls the in-plane propagation of light [19, 20]. In most of the photonic structures mentioned above, the possibility of any alteration in the PBG after their manufacture is practically non-existent, which can severely limit their practical use. Several approaches have been proposed to tune or adjust both the band structure and the photonic gap, thus opening a new perspective in scientific research. From a theoretical point of view, temperature is a mechanism for tuning the photonic gap and transmission spectra. J. Manzanares et al [21] considered a 2D-PC composed by air rods with a circular cross-section embedded in InSb. The authors reported that the concentration of intrinsic semiconductor carriers depends on temperature. The simultaneous effects of thermal and thermo-optical expansion in 2D-PC composed by Si rods embedded in air are researched by H. Elsayed et al [22], concluding that the increase of temperature over room temperature increases the width of the PBG. The shift towards higher energies of the photonic band structure in a 2D lattice honeycomb is investigated in [23], where the dependence of the optical properties of GaAs on pressure and temperature is considered. In the case of 2D-PCs where the GaAs scatterers are arranged in square lattice, a slight shift towards higher energies of the band structure is observed with an increase in temperature [24]. The use of superconducting materials as components in PCs for the adjustment of the PBG and the transmittance spectrum has also attracted attention. Recently, A. Aly investigated the response of the transmittance spectrum as a function of the applied pressure in a 1D-PC composed of a superconductor (Ti2Ba2Ca2Cu3O10) and a semiconductor (GaAs) material [25]. The results obtained in this study show that the cutoff frequency can be tuned to higher values with the increase in the applied pressure. Previously, Segovia et al [26, 27] reported the effects of temperature and pressure on the photonic band structure in 2D-PCs and PC slabs, composed of rods with circular cross-section arranged in a hexagonal lattice. The authors also reported a marked shift to higher frequencies of the photonic band structure with an increase in hydrostatic pressure. However, Tefelska et al [28] experimentally researched the effects of hydrostatic pressure on polarization and the properties of propagation in liquid crystal photonic fibers. They concluded that the increase in pressure reduces the width of the PBG, along with changes in the state of polarization. Similar results are reported by Wolinski et al [29] when experimentally considering the influence of temperature, external electric field, and hydrostatic pressure on the propagation properties of liquid crystal fibers. They observe a displacement of the PBG in the transmittance spectrum when the temperature changes. This displacement determines the thermal characteristics of the ordinary refractive index of the liquid crystal. By increasing the pressure between 0 and 73.2 MPa, the position of the PBG depends not only on the refractive index of the material but also on the geometry of the fiber. Wu et al [30] built a Fabry–Perot interferometer, measuring reflectance by gradually increasing pressure from 0 to 40 MPa. They found that the reflectance moves toward shorter wavelengths with increasing pressure. In the work of Olyaee and Dehghani [31], they introduced a pressure sensor which consisted of a PC waveguide coupled to a nanocavity. The waveguide is configured by removing a row of cylindrical Si rods and the nanocavity by inserting a point defect in the 2D-PC periodicity. The sensor designed has a quality factor of 1470, and it is calibrated to measure applied pressure at a wide range of linearity between 0 and 10 GPa. The previous theoretical and experimental research studies are currently finding important applications in medicine [32], oil prospecting [33], and in images sensitive to pressure and time, as it is the case in obtaining high quality fingerprints [34].
The primary aim of our study is to theoretically calculate the photonic band structure by considering the effects of hydrostatic pressure in a distributed Bragg reflector (DBR) pillar. The guided-mode expansion method is employed to perform the calculations. We have organized this paper as follows. In section 2, we present the theoretical model along with the main equations of the guided-mode expansion (GME) method. Sections 3 and 4 present the results and conclusions, respectively.
2. Theoretical framework
In this study, we used the GME theory, which is based on the GME theoretical model proposed by D. Gerace for photonic crystal slabs [35], to calculate the photonic band structure of a 1D cylindrical photonic pillar. The photonic heterostructures of interest can be viewed as a multilayer waveguide, i.e., a waveguide, the dielectric constant of which varies from layer to layer along the axis of symmetry. In this section, the theoretical basis and the procedure for the calculation of the photonic band structure are established in the following order. First, the guided modes in an infinite waveguide using Maxwell's electromagnetic theory are obtained, and then the 1D photonic pillar is constructed and the Bloch-Floquet theorem is used to calculate the dispersion relation.
2.1. Modal equation of the homogeneous cylindrical waveguide
Figure 1 shows a homogeneous waveguide of circular cross-section with a core of dielectric constant  1 and radius R. The dielectric constant of the cladding is
1 and radius R. The dielectric constant of the cladding is  2. Here, we are interested in the modes that propagate along the z-axis. The generalized expressions of the electromagnetic field with frequency ω are given by:
2. Here, we are interested in the modes that propagate along the z-axis. The generalized expressions of the electromagnetic field with frequency ω are given by:
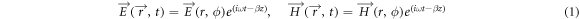
where 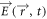 ,
, 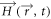 , and β represent the electric and magnetic fields, and the propagation constant, respectively. In cylindrical coordinates, the wave equation can be expressed as:
, and β represent the electric and magnetic fields, and the propagation constant, respectively. In cylindrical coordinates, the wave equation can be expressed as:
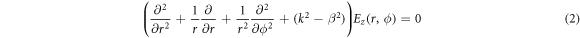
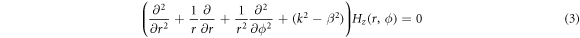
To obtain the solution of equations (2) and (3) we consider the modes that are guided in the structure and evanesce to r ⟶ ∞ . The solutions in the core (r ≤ R) and cladding (r > R) are:
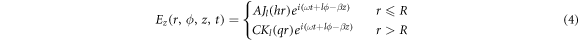
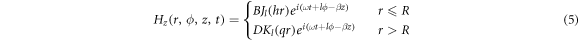
where A, B, C, and D are complex constants [36]. Jl
and Kl
are the l-th order Bessel function and the l-th order modified Bessel function of the second kind, respectively. Here, l is the quantum number, which has values l = 0, 1, 2 and so on. The wave vectors along the internal and external radial directions with k0 = ω/c are represented by 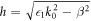 and
and  , respectively.
, respectively.
Figure 1. Schematic of the homogeneous circular waveguide.
Download figure:
Standard image High-resolution imageThe other components of the electromagnetic field are given by:
- For the core (r ≤ R)




- For the cladding (r > R)




where  and
and  . By imposing the boundary conditions, which ensure the continuity of the tangential components of the electromagnetic fields at the interface (r = R), the modal equation [37] is obtained, through which the following dispersion relation for the homogeneous waveguide can be obtained:
. By imposing the boundary conditions, which ensure the continuity of the tangential components of the electromagnetic fields at the interface (r = R), the modal equation [37] is obtained, through which the following dispersion relation for the homogeneous waveguide can be obtained:
where  . The modal equation (equation (14)) provides the mode basis of the infinite circular waveguide, in which the hybrid modes represented by HElm
and EHlm
are known to exist; moreover, for the principal angular number l and order of the mode (m), β yields a discrete and finite set of energies.
. The modal equation (equation (14)) provides the mode basis of the infinite circular waveguide, in which the hybrid modes represented by HElm
and EHlm
are known to exist; moreover, for the principal angular number l and order of the mode (m), β yields a discrete and finite set of energies.
2.2. Description of the GME method in distributed Bragg reflector pillar
In this section, the basis of the guided modes obtained by solving equation (12), will be employed for the calculation of the photonic band structure of an infinite DBR pillar of radius R, surrounded by air, and composed of alternating layers of the dielectric materials with dielectric constants  1 and
1 and  2, as shown in figure 2(a). The main idea of the GME is to carry out the expansion of the PC modes on the basis of the guided modes of the effective waveguide with wave vector
2, as shown in figure 2(a). The main idea of the GME is to carry out the expansion of the PC modes on the basis of the guided modes of the effective waveguide with wave vector  in the z-direction. 1D periodicity of the dielectric constant is introduced into the waveguide core as follows:
in the z-direction. 1D periodicity of the dielectric constant is introduced into the waveguide core as follows:
Figure 2. (a) Schematic of the DBR pillar consisting of alternating layers of dielectric media with dielectric constants  1 and
1 and  2, and thicknesses d1 and d2 respectively. The pillar radius is R. (b) Unit cell of the DBR pillar with lattice constant a.
2, and thicknesses d1 and d2 respectively. The pillar radius is R. (b) Unit cell of the DBR pillar with lattice constant a.
Download figure:
Standard image High-resolution imageConsidering that the media constituting the PC is linear, isotropic, lossless, nondispersive, and non-magnetic, the wave equation that governs the propagation of light within the PC is given by:
where c is the speed of light. 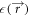 is the dielectric constant that fully defines the system, and satisfies the relation
is the dielectric constant that fully defines the system, and satisfies the relation 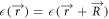 , with
, with 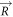 being the lattice vector [2]. The
being the lattice vector [2]. The 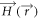 field is expanded on the basis of the guided modes of the homogeneous waveguide as follows:
field is expanded on the basis of the guided modes of the homogeneous waveguide as follows:
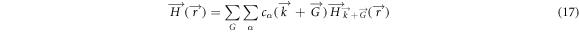
where 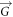 is the reciprocal lattice vector, the Bloch vector
is the reciprocal lattice vector, the Bloch vector 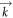 is restricted to the first Brillouin zone, and α represents the guided modes [35]. Substitution of equation (17) in equation (16) results in a linear eigenvalue problem,
is restricted to the first Brillouin zone, and α represents the guided modes [35]. Substitution of equation (17) in equation (16) results in a linear eigenvalue problem,
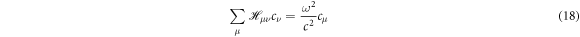
where the matrix elements 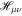 are represented by
are represented by
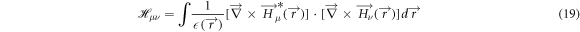
For calculating  for the DBR pillar, the expressions of the magnetic field corresponding to the core (equations (8) and (9) and the cladding (equations (12) and (13) are substituted in equation (19), to obtain:
for the DBR pillar, the expressions of the magnetic field corresponding to the core (equations (8) and (9) and the cladding (equations (12) and (13) are substituted in equation (19), to obtain:
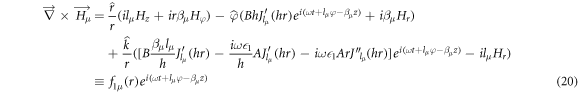

where the dependent functions of the profiles of the electromagnetic fields in the core and the cladding are designated as f1μ,ν (r) and f2μ,ν (r), respectively. Equations (20) and (21)are substituted in equation (19), considering that the integration domain corresponds to both the interior and exterior of the DBR pillar, as follows:
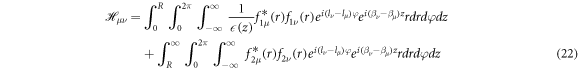
Using, 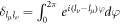 and
and  , in equation (22), we obtain
, in equation (22), we obtain
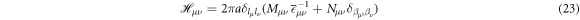
where a is the lattice constant and 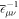 is the inverse of the dielectric constant, and is given by
is the inverse of the dielectric constant, and is given by
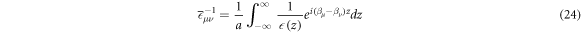
In equation (25), Mμ ν (pillar interior) and Nμ ν (pillar exterior) are given by
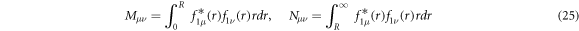
Once the matrix elements  have been calculated, the optical response of the DBR pillar can be evaluated by solving the eigenvalue problem in equation (18) to obtain the photonic band structure.
have been calculated, the optical response of the DBR pillar can be evaluated by solving the eigenvalue problem in equation (18) to obtain the photonic band structure.
3. Results and discussions
GME was applied to the 1D DBR pillar case, where the pillar consists of alternating layers of the semiconductor GaAs ( 1) and air (
1) and air ( 2). We have considered that the dielectric constant of GaAs depends on the hydrostatic pressure (P) and temperature (T) applied, as
2). We have considered that the dielectric constant of GaAs depends on the hydrostatic pressure (P) and temperature (T) applied, as
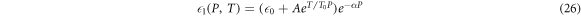
where  0 = 12.446, A = 0.21125, T0 = 240.7 K, and α = 0.00173 kbar−1 [37]. In the calculation of
0 = 12.446, A = 0.21125, T0 = 240.7 K, and α = 0.00173 kbar−1 [37]. In the calculation of  , the integration is carried out within the unit cell shown in figure 2(b), thus we obtain
, the integration is carried out within the unit cell shown in figure 2(b), thus we obtain
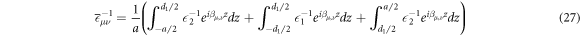
where βμ,ν = βμ − βν . By solving the integrals in equation (27), we obtain

It is important to note that the optical response of the DBR pillar can be understood from the 1D photonic band structure. Segovia et al, [26, 27] reported that the predominant effect on the optical response of 2D photonic crystal slabs at a given temperature is due to the hydrostatic pressure. As a result, in our numerical calculations, we kept the temperature constant at 4 K. Each of the layers is a quarter of wavelength (λ/4), thick, i.e.,  and
and 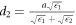 with a = d1 + d2. For l = 0 and m = 1, the photonic modes are classified into HE01 and EH01, which correspond to the transverse electric (TE) and transverse magnetic (TM) modes, respectively. In figure 3(a), which shows the plot of the dimensionless frequency ω
a/2π
c = a/λ vs wave vector in first Brillouin zone, one can observe the formation of photonic band structure both inside and outside the light for modes HE01 and EH01. The values chosen for the radius of the photonic pillar and the hydrostatic pressure are R = 5a and P = 0 kbar, respectively. It can be observed that the PBG between the first and the second band lies between 0.086 ≤ ω
a/2π
c ≤ 0.191 (HE01 mode) and 0.094 ≤ ω
a/2π
c ≤ 0.189 (EH01 mode). The 1D photonic band structure consists of true-guided modes outside the light line, which represents the light dispersion in the effective core, while the radiative modes are located above the light line. The cutoff frequency for the modes HE01 and EH01 is ω
a/2π
c = a/λ = 0.021 and 0.032, respectively. The 1D photonic band structure of the HE01 mode, for pressures of 30 and 70 kbar, is shown in figure 3(b). The PBG is in the frequency intervals of 0.088 ≤ ω
a/2π
c ≤ 0.191 (for 30 kbar) and 0.09 ≤ ω
a/2π
c ≤ 0.19 (for 70 kbar). With an increase in the pressure, the dielectric band shifts towards the higher frequencies (see lower inset), while the air band shows a slight shift towards the lower frequencies (see upper inset) resulting in a decrease in the width of the PBG. The cutoff frequency remains approximately constant with the increase in pressure.
with a = d1 + d2. For l = 0 and m = 1, the photonic modes are classified into HE01 and EH01, which correspond to the transverse electric (TE) and transverse magnetic (TM) modes, respectively. In figure 3(a), which shows the plot of the dimensionless frequency ω
a/2π
c = a/λ vs wave vector in first Brillouin zone, one can observe the formation of photonic band structure both inside and outside the light for modes HE01 and EH01. The values chosen for the radius of the photonic pillar and the hydrostatic pressure are R = 5a and P = 0 kbar, respectively. It can be observed that the PBG between the first and the second band lies between 0.086 ≤ ω
a/2π
c ≤ 0.191 (HE01 mode) and 0.094 ≤ ω
a/2π
c ≤ 0.189 (EH01 mode). The 1D photonic band structure consists of true-guided modes outside the light line, which represents the light dispersion in the effective core, while the radiative modes are located above the light line. The cutoff frequency for the modes HE01 and EH01 is ω
a/2π
c = a/λ = 0.021 and 0.032, respectively. The 1D photonic band structure of the HE01 mode, for pressures of 30 and 70 kbar, is shown in figure 3(b). The PBG is in the frequency intervals of 0.088 ≤ ω
a/2π
c ≤ 0.191 (for 30 kbar) and 0.09 ≤ ω
a/2π
c ≤ 0.19 (for 70 kbar). With an increase in the pressure, the dielectric band shifts towards the higher frequencies (see lower inset), while the air band shows a slight shift towards the lower frequencies (see upper inset) resulting in a decrease in the width of the PBG. The cutoff frequency remains approximately constant with the increase in pressure.
Figure 3. 1D photonic band structure of the DBR pillar. (a) HE01 (black line) and EH01 (red line) modes. (b) HE01 mode for pressures of P = 0 kbar (black line), P = 30 kbar (blue line) and P = 70 kbar (orange line). The DBR pillar has the following parameters R = 5a and T = 4 K. Solid line is the light line.
Download figure:
Standard image High-resolution imageThe 1D photonic band structure for photonic modes of order m = 1 and principal angular quantum number l = 0 and 1, are presented in figure 4(a). The effective homogeneous structure supports a set of guided bands, as well as a continuum of modes that are radiative. The modes are identified by the standard name of the guided modes of a circular dielectric waveguide. The radius of the DBR pillar and the pressure were considered to be R = 5a and P = 0 kbar, respectively. Our results indicate that the highest-energy mode is EH11 with a cutoff frequency of 0.0385, while the fundamental mode of the pillar with the lowest energy is the HE11 mode. There is no cutoff frequency in the fundamental mode, instead, there is an overlap of the photonic band (green line) with the light line (as shown in figure 4). When the hydrostatic pressure is increased, the photonic band structure of the HE11 mode exhibits a behavior similar to the HE01 mode in figure 3(b). The region of forbidden frequencies, for P = 0 kbar, lies in 0.088 ≤ ω a/2π c ≤ 0.188; however, when the pressure is increased to 70 kbar, the PBG shifts to 0.091 ≤ ω a/2π c ≤ 0.187. The insets of figure 4(b) show the shift to higher and lower frequencies of the dielectric and air bands, respectively.
Figure 4. 1D photonic band structure of the DBR pillar. (a) The photonic band modes are classified according to angular momentum l. (b) HE11 mode for pressures P = 0 kbar (green line) and P = 70 kbar (orange line).
Download figure:
Standard image High-resolution image4. Conclusions
The GME method has been used to calculate the photonic band structure of a DBR pillar. The optical response of the structure is determined by considering the dependence of the dielectric constant of GaAs on the applied hydrostatic pressure. A decrease in the width of the photonic band gap is observed with an increase in the hydrostatic pressure due to the shift towards higher and lower frequencies of the dielectric and air bands, respectively. Further, our calculations based on GME did not indicate the presence of a cutoff frequency for the DBR pillar fundamental mode.