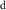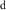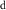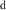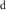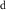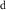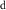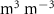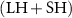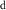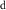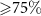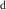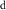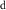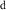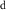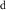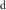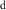CO₂-plant effects do not account for the gap between dryness indices and projected dryness impacts in CMIP6 or CMIP5

Drought is a surface water shortage, usually driven by below-normal precipitation (P), that negatively impacts water resource production (i.e. stream runoff and groundwater recharge) and/or photosynthesis, with societal consequences (e.g. Wilhite and Glantz 1985, AMS Council 2013). Aridity is a permanent, climatological lack of enough P to support plentiful regional water resources or vegetation (Budyko and Miller 1974, Middleton and Thomas 1997), which plays a key role in human settlement patterns (e.g. Seager et al 2018).

However, because water resource production and photosynthesis are strongly constrained by the evaporative environment as well as P, the most effective methods for quantifying aridity and drought from climate data require both P and potential evaporation E₀. E₀ integrates radiation, temperature, humidity, and wind speed to quantify the rate at which the atmosphere is capable of evaporating surface water (e.g. Hartmann 2016). The aridity index or AI (Transeau 1905, Middleton and Thomas 1997) is the ratio P/E₀ of annual climatological means. The Standardized Precipitation-Evapotranspiration Index or SPEI (Vicente-Serrano et al 2010) is the difference P − E₀ smoothed to a user-defined timescale and transformed to a normal distribution. The Palmer Drought Severity Index or PDSI (Palmer 1965) is a bucket model of soil moisture forced by monthly P and E₀. Lower AI and more negative PDSI and SPEI values indicate drier conditions, with reduced water resources and vegetation. These indices are widely used and understood.

According to the standard Penman–Monteith equation (Monteith 1981, Allen et al 1998), E₀ substantially increases with future greenhouse warming, mainly due to its dependence on temperature (Scheff and Frierson 2014). Since projected changes in land P with warming are much less robust (e.g. IPCC 2013, Greve and Seneviratne 2015), global-scale climate model studies of AI (Feng and Fu 2013, Fu and Feng 2014, Scheff and Frierson 2015, Huang et al 2015, Fu et al 2016, Zarch et al 2017, Park et al 2018, Wang et al 2021), PDSI (Dai 2013, Cook et al 2014, Zhao and Dai 2015, Zhao and Dai 2016, Lehner et al 2017), and SPEI (Cook et al 2014, Touma et al 2015, Naumann et al 2018) almost always obtain widespread drying in future high-emission scenarios. The same models also project widespread future declines in near-surface soil moisture SM$_{\textrm{s}}$ (Dai 2013, IPCC 2013, Berg et al 2017) and relative humidity RH (IPCC 2013, Byrne and O'Gorman 2016), which are used to argue for the physical relevance of the AI- or PDSI-based drying projections (e.g. Sherwood and Fu 2014, Dai et al 2018).

Yet, as argued above, the core purpose of AI, PDSI, and SPEI, and the main use of SM$_{\textrm{s}}$, is to indicate negative impacts to water-resource production and/or photosynthesis (Roderick et al 2015, Greve et al 2017, Scheff et al 2017, Scheff 2018). And, the same models that project widespread global declines in AI, PDSI, SPEI, SM$_{\textrm{s}}$, and RH with strong future warming project much more equivocal, two-sided changes in water-resource generation (IPCC 2013, Roderick et al 2015, Zhao and Dai 2015, Zhao and Dai 2016, Swann et al 2016, Milly and Dunne 2016, Milly and Dunne 2017, Greve et al 2017, Scheff et al 2017) and deep-layer soil moisture SM$_{\textrm{d}}$ (Berg et al 2017, Berg and Sheffield 2018, Greve et al 2019). Furthermore, these models project ubiquitous future increases in photosynthesis (Greve et al 2017, Greve et al 2019, Scheff et al 2017, Mankin et al 2018) and leaf coverage (Mankin et al 2019), a.k.a. 'greening.' Thus, it is not clear if the AI, PDSI, and SPEI projections are actually relevant for warming impacts on water availability, nor (likewise) if the models' prognostic runoff, SM$_{\textrm{d}}$, and/or vegetation projections are reliable. Scheff (2018) and Scheff et al (2017) show that this 'index-impact gap' is also clear in global observations during CO₂-driven climate changes (both recent and geologic), lending it additional credence. However, it is much less pronounced in certain regions, such as the American Southwest (Cook et al 2015, Ault et al 2016), particularly for SM$_{\textrm{d}}$.

What is the reason for this discrepancy? Most of the above studies argue that projected future AI, PDSI and SPEI do not resemble projected climate change impacts in many places mainly because they do not account for the beneficial effect of elevated CO₂ on plant water requirements, which tends to reduce evapotranspiration (ET) and increase photosynthesis (Roderick et al 2015, Swann et al 2016, Greve et al 2017, Greve et al 2019, Milly and Dunne 2017, Scheff et al 2017). Yang et al (2019) and Yang et al (2020) modify the standard Penman–Monteith equation to include this stomatal effect and find that the resulting AI and PDSI come much closer to the models' hydrologic projections, and Lemordant et al (2018) show that CO₂-plant effects dramatically alter key model hydrologic outputs. Certainly, the bulk of projected future greening would not occur without these simulated CO₂ effects (Arora et al 2013, Shao et al 2013).

However, many other proposed causes of the index-impact gap in models, especially with regard to hydrologic impacts (i.e. water resources and SM$_{\textrm{d}}$), are unrelated to CO₂-plant effects. Zhao and Dai (2015), Dai et al (2018) and Mankin et al (2018) argue that the gap occurs partly because the increase in instantaneous P rate in a warming world drives greater runoff production for the same long-term total P. Observed and projected shifts in P towards the hydrological wet season (e.g. Chou et al 2013, Allen and Anderson 2018) would have the same effect, and Berg et al (2017) argue that the gap between SM$_{\textrm{d}}$ and SM$_{\textrm{s}}$ also stems from rectification of the seasonal cycle. Massmann et al (2019) show that warming itself may reduce ET by closing stomata (Novick et al 2016), apart from CO₂. Further, Mankin et al (2019) find that in much of the mid-latitudes, the projected increase in growing-season length due to CO₂ and warming cancels any plant water savings from CO₂-induced stomatal closure, so that the net hydrologic impact of plant responses to CO₂ and warming is often negative, not positive. Lehner et al (2019) argue that models' prognostic runoff responses to climate change are biased positive, because flaws in the land hydrologic parameterizations cause modeled runoff to be too sensitive to P, and not sensitive enough to warming. Finally, Milly and Dunne (2016) and Vicente-Serrano et al (2020) argue that Penman–Monteith E₀ (and thus AI, PDSI and SPEI) is not always relevant to real watersheds under climate change, regardless of CO₂ effects.

On the vegetation side, CMIP-type models generally do not include any representation of drought-driven mortality (Anderegg et al 2015, Allen et al 2015), and often only minimal representations of vegetation heat stress (Peñuelas et al 2017, Brodribb et al 2020) and nutrient constraints (e.g. Wieder et al 2015). Thus, their strong greening projections under high CO₂ are likely overestimates. Mankin et al (2018) and Mankin et al (2019) argue that a substantial part of the projected greening (and resulting ET increase) is due to warming rather than CO₂ effects, especially in the extratropics where temperature may be a more important limiting factor than moisture. More generally, not all vegetation is vulnerable to water shortage, so even at constant CO₂, vegetation changes would not always be expected given dryness-index changes. Furthermore, with some exceptions (Donohue et al 2013, Zhu et al 2016), most studies of observed vegetation greening to date (e.g. Fensholt et al 2012, Mishra et al 2015, Ju and Masek 2016) invoke CO₂ changes minimally, or not at all. Instead, they attribute most greening to factors such as temperature and precipitation changes, topographic effects, fire suppression and other disturbance regime changes, land use change, and woody plant encroachment on grasslands.

Thus, it is not at all clear that CO₂-plant effects are the main reason why simulated and observed mean eco-hydrologic impacts of climate change are not as negative as AI, PDSI, or SPEI in many regions. Indeed, Milly and Dunne (2016) found that in one model, the gap between AI and runoff responses persisted even when those effects were switched off, at least in the global average. Here, we extend that comparison to many more models, variables, and regions, showing that even when CO₂-plant effects are suppressed, mean AI, PDSI, and SPEI (index) projections under strong warming scenarios are much more widely negative than mean runoff, SM$_{\textrm{d}}$, or vegetation (impact) projections under the same scenarios.

We examine monthly output equatorward of 55^∘ from 11 climate models in the Coupled Model Intercomparison Project phase 6 (CMIP6; Eyring et al 2016), listed in table S1 in supplementary material (available online at stacks.iop.org/ERL/16/034018/mmedia). We compare the results of two idealized modeling experiments that each start from a constant-forcing control run and then strongly warm the planet by increasing CO₂ 1% per year for 140 years, i.e. from 280 ppm in year 1 of the experiment to ≈1130 ppm in year 140 of the experiment, analogous to high-emission future warming scenarios like RCP8.5. In experiment '1pctCO2', both the vegetation and radiation schemes 'see' this large CO₂ increase, as in the experiments discussed in section 1. Experiment '1pctCO2-rad' (Jones et al 2016) is identical to 1pctCO2 except that the vegetation schemes instead 'see' a constant 280 ppm of CO₂, so any index-impact gap in 1pctCO2-rad must occur for a reason other than simulated CO₂-plant effects. These experiments are solely designed to test the CMIP models' response to high CO₂; they have no forcings other than this idealized 1%-per-year CO₂ increase and they do not directly correspond to any particular real years, though CO₂ levels in the later years of the simulations are comparable to high-emission future scenarios.

For each model, the climatological annual-mean responses of P, E₀, AI, PDSI, SPEI, RH, SM$_{\textrm{s}}$, SM$_{\textrm{d}}$, water resource generation (i.e. total runoff Q), runoff ratio Q/P, photosynthesis, leaf area index LAI, and evaporative fraction EF are quantified using the difference between years 111–140 (mean CO₂ ≈970 ppm) and years 1–30 (mean CO₂ ≈325 ppm) of the 'r1i1p1' run, except where noted in table S1. (Other runs would be expected to behave similarly; 'r1i1p1' is specified just for reproducibility.) Monthly E₀ is computed using the standard Penman–Monteith equation (Allen et al 1998) and AI for each 30-year period is the ratio of 30-year-mean P to 30-year-mean E₀, all as in Scheff et al (2017). PDSI and 12-month SPEI are computed from monthly P and E₀ as in Cook et al (2014) using years 1–30 as the reference period; SPEI is set to −2.33 (100-year drought) when P − E₀ is less than the origin of the reference distribution (S Vicente-Serrano, pers. comm.). As in Scheff et al (2017), monthly RH is defined as monthly-mean vapor pressure divided by saturation vapor pressure at monthly-mean temperature, for consistency with the E₀ calculation.

SM$_{\textrm{s}}$ uses the 'mrsos' output (mm of water in the top 10 cm of the soil), and SM$_{\textrm{d}}$ is derived by summing the 'mrsol' output (mm of water in each soil layer) to a depth of 2 m, using a fraction of the bottom layer if necessary. They are each converted to volumetric water content ($\mathrm{m}^3\ \mathrm{m}^{-3}$), by dividing by 100 and 2000 mm respectively. Q is calculated as P minus ET rather than using model runoff output, to emphasize total water-resource generation and avoid inconsistencies in how models defined runoff. Q/P, which AI predicts in the present climate (Gentine et al 2012), is the ratio of 30-year means. Photosynthesis is quantified using gross primary productivity (GPP; 'gpp' output), which is the flux of carbon through the stomata (Bonan 2015) and thus the most water-linked metric. EF, a close cousin of the Bowen ratio, is the fraction of the 30-year-mean total turbulent heat flux $(\mathrm{LH}+\mathrm{SH})$ made up by the latent heat flux LH; decreases in EF represent drought impacts to the atmosphere.

For each variable, the responses are nearest-neighbor interpolated to a common 3^∘ grid, and multi-model statistics are taken. For SM$_{\textrm{d}}$, only nine models are available (table S1); restricting the remainder of the study to only those models does not substantially change the results below. We also conduct a similar analysis on the CMIP5 (Taylor et al 2012) 1pctCO2 vs. 'esmFdbk1' experiments, with details and results in supplementary material.

Figure 1 maps the median responses to the 'standard' 1pctCO2 experiment, in which both climate and vegetation respond to the large CO₂ increase. The index-impact gap common to coupled-model high-emission experiments is apparent: RH, AI, SPEI, PDSI, and SM$_{\textrm{s}}$ (figures 1(a)–(e)) robustly and widely decline, but EF, SM$_{\textrm{d}}$, Q/P, and Q respond much more heterogeneously (i.e. more like P; figures 1(f)–(j), and LAI and GPP robustly and near-ubiquitously increase (figures 1(k)–(l)). However, EF still resembles PDSI in some places, facially suggesting that PDSI could be relevant for atmospheric impacts (Dai et al 2018) despite its dissimilarity to water-resource and ecological impacts. Figure S1 in supplementary material reproduces figure 1 but using standardized changes; results are similar, except that Q and Q/P responses become much weaker than the other metrics, reinforcing the sense of a gap.

Zoom In Zoom Out Reset image size

Figure 2 maps the responses to the 1pctCO2-rad experiment, in which climate responds to the large CO₂ increase, but vegetation does not. Despite the lack of any CO₂-plant effects, the index-impact gap is still wide, especially for hydrologic impacts: RH, AI, SPEI, PDSI, and SM$_{\textrm{s}}$ (figures 2(a)–(e)) again show widespread robust declines, but the responses of Q/P (figure 2(h)) and especially Q (figure 2(j)) are again much more two-sided. In particular, the Americas are dominated by AI, SPEI, and PDSI 'drying', yet have less consistent decreases in Q/P, and regional decreases and increases in Q. In Africa and Australia, Q and Q/P increases are actually more extensive than decreases, despite strongly drying AI, PDSI and SPEI. However, in general, the gap is not quite as large as in figure 1, both because RH, AI, SPEI, and PDSI dry slightly less, and because Q and Q/P dry slightly more, consistent with Swann et al (2016). Thus, CO₂ effects still appear to cause some of the gap, by reducing ET and thus increasing both E₀ and Q in figure 1 relative to figure 2 (Brutsaert and Parlange 1998, Berg et al 2016).

Zoom In Zoom Out Reset image size

SM$_{\textrm{d}}$ (figure 2(g)) declines more robustly than Q, but not always as robustly as AI or SPEI, especially in Eurasia, North America and Australia. The declines are still weaker and less consistent than those in SM$_{\textrm{s}}$ (figure 2(e)). Interestingly, EF (figure 2(f)) responds much more like P (figure 2(i)) than like the indices, SM$_{\textrm{s}}$, or even SM$_{\textrm{d}}$, implying that the relative consistency of EF with PDSI in figure 1 may just be a fortuitous effect of CO₂ reducing ET. Finally, as expected, LAI and GPP (figures 2(k)–(l)) lose their large, near-ubiquitous increases (which are likely overestimates as discussed in section 1) and resemble the indices much more closely, particularly in the tropics and subtropics. This implies that CO₂ effects can explain much of the simulated low-latitude gap between index and vegetation responses in high-emission scenarios. Yet, LAI and GPP still change little (or even increase) in many regions where AI, SPEI and PDSI strongly decline, particularly in the mid-latitudes and Australia. Figure S2 reproduces figure 2 using standardized changes; again the main difference is relative weakening of the Q and Q/P responses.

Figure 3 distills figures 1 and 2 by plotting each panel as a single point in area-with-robust-drying vs. area-with-robust-wetting space, color-coded by type of metric (where 'robust' means stippled on figures 1 or 2; that is, ${\geqslant}75\%$ intermodel agreement). It is immediately apparent that while the gap between the index (AI, PDSI, SPEI) and hydrologic impact (Q, Q/P) projections under a high-emission scenario is larger with CO₂-plant effects on (left), it is still large even with CO₂-plant effects turned off (right). In the latter case, for PDSI, more than four times as much land area has robust drying as robust wetting, yet the areas of robust Q increase and robust Q decrease are equal (figure 3, right), complicating the interpretation of PDSI as a water-resource proxy under climate change (e.g. Cook et al 2009). For AI, more than 10 times as much land area has robust drying as robust wetting, yet the area of robust Q/P decrease is only twice the area of robust Q/P increase, despite the theoretical basis for AI as the primary driver of Q/P variation in the present climate (Budyko and Miller 1974).

Zoom In Zoom Out Reset image size

For SM$_{\textrm{d}}$ and (especially) GPP and LAI, the gap from AI, PDSI, and SPEI responses without CO₂-plant effects (right) is much smaller than with CO₂-plant effects (left), mainly because the massive GPP and LAI increases are much reduced. However, the gap is still noticeable: similar to Q/P, robust GPP and SM$_{\textrm{d}}$ decreases are only about 2–3 times more widespread than respective increases, even though robust PDSI, AI and SPEI decreases are over 4, 10, and 20 times more widespread than respective increases. LAI more strongly tends to decrease, similar to PDSI, but still not as much as AI, SM$_{\textrm{s}}$ or SPEI. Thus, the indices still do not seem to be particularly reliable proxies for projected future vegetation-related impacts, even in a world where CO₂ does not affect vegetation. As discussed above in the context of figure 2, this is particularly so in parts of the midlatitudes, where growing-season lengthening is an important driver of vegetation increases (e.g. Mankin et al 2018, Mankin et al 2019). Also, EF is even farther from the indices when CO₂-plant effects are off (right) than on (left), confirming that any apparent relevance of the indices for EF in figure 1 is just a fortuitous consequence of CO₂ effects on transpiration.

We quantify several of the index-impact gaps in greater detail by mapping disagreement between the impact variables (Q, Q/P, SM$_{\textrm{d}}$, GPP) and the indices and similar variables (AI, PDSI, SPEI, SM$_{\textrm{s}}$) across the multi-model ensemble (figure 4). Specifically, we map the percentage of models that obtain increases in impact variables despite decreases in index-type variables (minus the percentage that do the opposite, which is much smaller). With CO₂-plant effects on (left column), a large proportion of the models simulate hydrologic and vegetation increases despite declining indices, as expected (though there are also regional exceptions). With CO₂-plant effects turned off (right column), this proportion persists, albeit slightly diminished. Again, the gaps between Q and Q/P and the indices (figures 4(a)–(f)) and between SM$_{\textrm{d}}$ and SM$_{\textrm{s}}$ (figures 4(g)–(h)) are particularly persistent. (Some very dry regions do have the opposite sign gap, but Q ≈ 0 in such places.)

Zoom In Zoom Out Reset image size

In contrast, the prevalence of SM$_{\textrm{d}}$ increases despite PDSI declines (figure 4(i)) is more noticeably reduced once CO₂ effects are turned off (figure 4(j)), while regions with the opposite sign gap are expanded. This relative agreement makes sense, since PDSI is a fundamentally a model of SM$_{\textrm{d}}$. Finally, the very large proportion of models that increase GPP despite index declines (e.g. figure 4(k)) largely vanishes or reverses in the tropics when CO₂ effects are turned off, but still noticeably persists in the mid-latitudes (figure 4(l)); results are similar for LAI. This again suggests that growing-season lengthening, in addition to CO₂, is a key driver of the gap between index and vegetation responses in the midlatitudes.

Figures S3–S6 reproduce figures 1–4 but using nine CMIP5 models, for cleaner comparison with the literature cited in section 1. The results are very similar, though the index-impact gaps (both with and without CO₂) tend to be even wider in CMIP5 than in CMIP6. Whether this is due to model improvement going from CMIP5 to CMIP6, or just different model selection (tables S1 vs. S2), is unknown. The lack of index-impact gaps in CMIP5 in parts of the American Southwest (Cook et al 2015, Ault et al 2016) is also apparent in figure S6.

In short, figures 1–4 and S3–S6 show that while some simulated index-impact gaps under high-emission scenarios are in fact driven by CO₂-plant effects (e.g. low-latitude greening despite index declines, or PDSI declining more than SM$_{\textrm{d}}$), most of the others (e.g. Q, Q/P and mid-latitude vegetation increasing despite index declines, and SM$_{\textrm{d}}$ declining less than SM$_{\textrm{s}}$) persist without any CO₂-plant effects. Thus, contrary to studies like Swann et al (2016), Milly and Dunne (2017), Scheff et al (2017), and Greve et al (2017), but in agreement with Mankin et al (2019) and Greve et al (2019), we find that CO₂-plant effects are not the sole or dominant reason that prognostic impact outputs disagree with PDSI, SPEI, and AI under future global warming scenarios. Instead, other mechanisms must be in play to explain most of these gaps.

What could those other, non-CO₂ factors be? The easiest explanations are that the indices are just simple formulas, and should not be expected to reflect complex climate change impacts in the first place (e.g. Milly and Dunne 2016, Greve et al 2019)—and/or that mean changes in runoff and vegetation production are not actually what the indices are built to measure. However, the indices all have long histories of successful use in the present climate as hydrological and ecological impact proxies, continue to be frequently used to quantify future climate change's broad dryness effects (e.g. Lehner et al 2017, Naumann et al 2018, Wang et al 2021), rest on solid theoretical foundations (Penman–Monteith E₀, the Budyko curve, soil moisture modeling, the complementary principle), and do in fact agree with the impact projections in some places (figures 4 and S6; Cook et al 2015, Ault et al 2016). Where there are disagreements, they are mostly in one direction (indices drier than simulated impacts; figure 4) even with CO₂ effects turned off. Thus, it is important to understand where the differences come from, so as to better assess the relevance and applicability of both types of future projections.

For water-resource (Q and Q/P) responses, there is no shortage of potential non-CO₂ mechanisms by which they could skew more positive than index responses, as detailed in section 1. Again, these include direct closure of leaf stomata by high temperatures and vapor-pressure deficits (Novick et al 2016, Massmann et al 2019), concentration of P into fewer, heavier events (e.g. Mankin et al 2018, Dai et al 2018), and concentration of P into the hydrological wet season (e.g. Chou et al 2013), all of which are accounted for in the models but not in the indices. Biases in model Q and Q/P sensitivity to P and temperature (Lehner et al 2019) could also be important. More broadly, some of the gap between Q and PDSI responses could also simply be that PDSI is a soil-moisture model, despite its frequent tacit use to indicate runoff scarcity. However, there is no similar 'apples and oranges' argument for the large gap between Q/P and AI responses, since Q/P is the quantity that AI classically predicts (Budyko and Miller 1974, Gentine et al 2012). Planned offline land-modeling work will test many of the above mechanisms.

For vegetation-related impacts (GPP and LAI), CO₂ clearly causes the simulated departure from the indices in the tropics and subtropics (compare figures 1(d), (l) and 2(d), (l)). However, there is still a large non-CO₂-related gap in parts of the midlatitudes, most easily explained by the lengthening of temperate growing seasons with simulated global warming (e.g. Mankin et al 2019), as stated in section 3. Whether a longer growing season could overcome increased future drought stress to cause greening in the real-world midlatitudes absent CO₂ effects is far from certain. However, observations to date (Zhu et al 2016) show that greening has been much more prevalent than de-greening at all latitudes, including the mid-latitudes. (As discussed in section 1, many studies also invoke disturbance, mortality, and land-use change processes to explain the observed greening, but those are largely absent from the CMIP warming simulations, so could not be the main causes of the future simulated greening.)

Likewise, the almost total persistence of the gap between SM$_{\textrm{d}}$ and SM$_{\textrm{s}}$ responses when CO₂ effects are turned off strongly suggests that its main cause is the seasonal mechanism proposed by Berg et al (2017), rather than plant savings of SM$_{\textrm{d}}$ due to elevated CO₂. Similarly, the gap between EF and index responses is even stronger when CO₂ effects are off, so it must have a non-CO₂ cause, likely the basic thermodynamic EF increase with warming and/or the strong constraint of EF by radiation and P (Scheff 2018).

As a final caveat, these simulations only examine transient climate responses, rather than fully equilibrated climate responses. Thus, it is not clear from this study whether the index-impact gaps, and their attribution to CO₂-plant effects vs. warming, would persist over very long time scales on which vegetation (and thus hydrology) could further evolve. However, since the century-scale transient climate response is most relevant to climate change on human time scales, and since most future simulations are also transient, the simulations examined here are still of immediate relevance.

A number of studies find that simple climatic dryness and drought indices, such as the Aridity Index (AI), Palmer Drought Severity Index (PDSI), and Standardized Precipitation-Evapotranspiration Index (SPEI), indicate much more widespread drying under strong future global warming scenarios than implied by high-complexity models of hydrology and vegetation. Many of these studies ascribe these simulated 'index-impact gaps' to the direct effects of very high CO₂ on plant physiology. To the contrary, here we show that for hydrology and for mid-latitude vegetation, these gaps strongly persist even in specialized simulations (CMIP6 1pctCO2-rad; CMIP5 esmFdbk1) in which direct CO₂-plant effects are completely turned off. This strongly suggests key non-CO₂ cause(s) for the modeled index-impact gaps for hydrology and for mid-latitude vegetation. Future work will test several candidate causes for the hydrologic index-impact gap from the literature using land-modeling experiments, and will also analyze the index-impact gaps in observations.

No new data were created or analyzed in this study.

We acknowledge the World Climate Research Programme, which, through its Working Group on Coupled Modelling, coordinated and promoted CMIP6 and CMIP5. We thank the climate modeling groups for producing and making available their model output, the Earth System Grid Federation (ESGF) for archiving the data and providing access, and the multiple funding agencies who support CMIP and ESGF. All data is freely available at https://esgf-node.llnl.gov/search/cmip6/ and https://esgf-node.llnl.gov/search/cmip5/. J S was supported by a UNC Charlotte Faculty Research Grant and J S M was supported by NOAA MAPP Award NA20OAR4310414 and the Dartmouth Burke Research Initiation Award.