Change points of global temperature

The idea of a recent 'hiatus', 'pause' or 'slowdown' of global temperature rise has received considerable public and scientific attention in recent years (Mooney 2013, Hawkins et al 2014). The time interval to which people refer differs but is usually taken as starting either in 1998 or 2001. Global temperature trends starting from these particularly warm years until the present are smaller than the long-term trend since 1970 of 0.16 ± 0.02 °C per decade, though still positive.

While close to 50 papers have already been published on the 'hiatus' or 'pause' (Lewandowsky et al, in press), the important question of whether there has been a detectable change in the warming trend (rather than just variability in short-term trends due to stochastic temperature variations) has received little attention. An appropriate statistical tool to answer this question is change point (CP) analysis (e.g. Carlin et al 1992). CP analysis allows us to determine the magnitude of changes in rates of temperature increase/decrease and estimate the timings at which these changes occur.

We present an approach to CP analysis known as CP linear regression (e.g. Carlin et al 1992). This approach models a time series as piecewise linear sections and objectively estimates where/when changes in data trends occur. The model forces each line segment to connect, avoiding discontinuities. Isolated pieces of trend line with sudden temperature changes between them (i.e. a 'stairway model') would not provide a physically plausible model for global temperature given the thermal inertia of the system. A change in climate forcing can instantly change the rate of warming, but cannot instantly change global temperature.

To specify the model, consider a sample size of n, with response data ${y}_{1},\ldots ,{y}_{n}$ observed at continuous times ${x}_{1},\ldots ,{x}_{n}$ with ${x}_{1}\lt {x}_{2}\lt \ldots \lt {x}_{n}$. In the simplest regression case of a single CP we have:

$$\begin{eqnarray*}{y}_{i}=\left\{\begin{array}{ll}\alpha +{\beta }_{1}({x}_{i}-\gamma )+{\epsilon }_{i} & {\rm{when}}\;{\rm{}}{x}_{i}\lt \gamma ,\\ \alpha +{\beta }_{2}({x}_{i}-\gamma )+{\epsilon }_{i} & {\rm{otherwise}}.\end{array}\right.\end{eqnarray*}$$

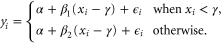
Here α is the expected value of y at the CP, ${\epsilon }_{i}\sim N(0,{\sigma }^{2})$ and ${\sigma }^{2}$ is the residual variance. Most importantly γ is the time value where a change in rate occurs, and ${\beta }_{1}$ and ${\beta }_{2}$ are the slopes before and after the trend change.

The CP model can be extended to deal with m CPs, ${\gamma }_{l}$ where l = 1,...,m. It is convenient to fit these models in a Bayesian framework (e.g. Gelman et al 2003) so that we can include external prior information where necessary, and have full access to all the uncertainties on the parameters. Of most interest are the priors for the CP parameters ${\gamma }_{l}$ (the timings of the rate changes). These parameters are given uniform prior distributions over the entire range of the data, with the condition that they are ordered chronologically. Using Bayes' theorem allows the data to inform the model and update prior information to give posterior estimates for ${\gamma }_{l}$ and any other parameters of interest. We defer discussion of the technical details involved in this model to appendix A.

The model as described takes the number of CPs m as a fixed parameter. To determine the most appropriate value of m, and thus the number of CPs, we use the deviance information criterion (DIC; Spiegelhalter et al 2002). The DIC works by penalising the deviance (a measure of the quality of the model's fit to data) by its complexity, determined by the effective number of parameters. In general as model complexity increases, the deviance will decrease, so adding this penalty will select parsimonious models that fit the data well but are not too complex. The DIC is negatively orientated (i.e. a smaller value indicates a better model). When running the models, we choose a range of values for m, e.g. from 0 to 5. Parameter convergence is monitored, models that do not show convergence are rejected and from the remainder DIC is used to decide on the most appropriate model for the data.

The models were fitted in JAGS (just another Gibbs sampler; Plummer 2003). JAGS is a tool for analysis of Bayesian hierarchical models using Markov Chain Monte Carlo (MCMC) simulation. MCMC is a technique to approximate Bayesian posterior distributions for unknown parameters. The method simulates a Markov process (a type of random walk) where the distribution of the values it will take after a very large number of iterations is the required posterior distribution (see appendix B for more details on MCMC). JAGS offers cross platform support, and provides a direct interface to R using the package rjags (Plummer 2014). Bayesian models fitted using MCMC provide samples from the posterior distribution of the parameters. From these samples we can compute any summary statistics we require (e.g. means and standard deviations). When JAGS models are run, a number of samples are usually discarded as the algorithm converges to the true posterior, and a further number are thinned out to avoid autocorrelation in successive samples. We check convergence using standard methods in the R package coda (Plummer et al 2006). The R code required to run the CP models is provided in the supplementary material.

In figure 1 we present a CP analysis applied to four global annual temperature data series (HadCRUT4, 2015, GISTEMP 2015, NOAA 2015, Cowtan and Way 2015). In all cases, by monitoring convergence and using DIC, we find that the best fit is obtained with three CPs situated in about 1912, 1940 and 1970. The linear sections correspond to well-known stages of global temperature evolution, where the plateau from 1940 to 1970 is related to a near-balance of positive (greenhouse gas) and negative (aerosol) anthropogenic forcings, while the ∼0.6 °C warming since 1970 has been attributed almost entirely to human activity (IPCC 2014). The three CP fit is similar to a smooth nonlinear trend line obtained by singular spectrum analysis (Rahmstorf and Coumou 2011).

Zoom In Zoom Out Reset image size

Our approach aims to identify trend changes in the data series. A side effect of the CP model choice is that the first derivative of temperature (i.e. the rate of change) over time is discontinuous; at a CP the rate of temperature increase/decrease switches from one value to another. Physically this is not implausible. A sudden change in the rate of temperature change is far less unphysical than a sudden change in temperature. The former could be caused by a change in the rate of forcing. An alternative approach would be to use a spline model and this would be particularly useful if our interests lay specifically in observing continuous rates of temperature change. Cubic splines are a popular choice (Eilers and Marx 1996), as these have two continuous derivatives. However, the choice of continuous derivatives is entirely arbitrary; curves with two continuous derivatives are appealing as they appear smooth to the human eye. Neither approach is inappropriate, indeed, we could think of our CP analysis as a version of a spline model where the knots (places where to splines intersect) are the CPs. When comparing a cubic spline fit with our three CP model fit we found the results to be very similar, so the additional degrees of freedom offered by the cubic spline appear unnecessary. We therefore simply apply the model that gives us direct access to the quantity of interest, namely detectable changes in linear rates of global temperature rise and their corresponding timings.

Residual analysis demonstrates that our three CP model suitably captures the signal similarly to that of a cubic spline model, i.e. the residual data after subtracting the model fit indicated that most of the climate signal is fully accounted for. Using fewer than three CPs leaves one with highly auto-correlated residuals, i.e. a remnant climate signal. Attempts to find a fourth CP fail with poor parameter convergence.

Comparison of the three CP model with a piecewise linear regression model that forces a trend change in 1998 and 2001 gives further validation to our results. For each record the comparison indicates only minor differences between the two models (figures 2 and 3). Further, the 95% confidence intervals for the fitted values (not shown) show strong overlap indicating no notable difference in both cases. Based on these results it is unsurprising that we did not find a fourth trend change in these data. The smallest difference between the trends with and without a forced CP in 1998 or 2001 is found in the (Cowtan and Way 2015) series, which arguably gives the best global coverage due to their sophisticated method of filling gaps in surface observations with the help of satellite data (Cowtan and Way 2014). The CP analysis thus provides strong evidence that there has been no detectable trend change in any of the global temperature records either in 1998 or 2001, or indeed any time since 1980. Note that performing the CP analysis on the global temperature records excluding the 2013 and 2014 observations does not alter this conclusion.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Finally to conclusively answer the question of whether there has been a 'pause' or 'hiatus' we need to ask: If there really was zero-trend since 1998, would the short length of the series since this time be sufficient to detect a CP? To answer this, we took the GISTEMP global record and assumed a hypothetical climate in which temperatures have zero trend since 1998. The estimated trend line value for 1998 is 0.43 °C (obtained by running the CP analysis on the original data up to and including 1998). Using this, we simulated 100 de-trended realizations for the period 1998–2014 that were centered around 0.43 °C. We augmented the GISTEMP data with each hypothetical climate realization and ran the four CP model on the augmented data sets. This allowed us to observe how often a fourth CP could be detected if the underlying trend for this period was in fact zero. Results showed that 92% of the time the four CP model converged to indicate CPs in approximately 1912, 1940, 1970 and a fourth CP after 1998. Thus, we can be confident that if a significant 'pause' or 'hiatus' in global temperature did exist, our models would have picked up the trend change with a high probability of 0.92.

CP regression analysis does not detect a significant change or'pause' in global warming trends since ∼1970. Consistent with this, recent intervals of rapid warming like 1990–2006 have not been interpreted as significant acceleration (Rahmstorf et al 2007). Recent variations in short-term trends are fully consistent with an ongoing steady global warming trend superimposed by short-term stochastic variations. This conclusion is consistent with modelling (Kosaka and Xie 2014, Risbey et al 2014) and statistical analysis (Foster and Rahmstorf 2011) suggesting that ENSO variability is the main physical reason for the observed variation in warming trends.

Analysis of the extremes is also consistent with an ongoing warming trend. The hottest years on record were 2014, 2010 and 2005 (except in Cowtan and Way where 2014 ranks second); for a steady warming trend of 0.16 °C per decade and the observed variance of the residual, a new record is expected on average every four years (Rahmstorf and Coumou 2011). While it has been shown that global temperature over the 21st century will potentially demonstrate periods of no trend or even slight cooling in the presence of longer-term warming (Easterling and Wehner 2009), since 1976 not even a ten-year cold record has been set. We conclude that, based on the available data, the use of the terms 'hiatus' or 'pause' in global warming is inaccurate.

We are grateful to the two anonymous reviewers for their comments that improved the early version of the paper. This research is supported by the Programme for Research in Third Level Institutions (PRTLI) Cycle 5 and co-funded by the European Regional Development Fund, and the Science Foundation Ireland Research Frontiers Programme (2007/RFP/MATF281).

In the multiple CP case we have ${\gamma }_{l}$, where $l=1,\ldots ,m$, assuming ${x}_{1}\lt {\gamma }_{1}\lt {\gamma }_{2}\lt \ldots \lt {\gamma }_{m}\lt {x}_{n}$. We now have $m+1$ independent data segments and y_i is drawn from the probability density function of the jth segment for $j=1,...,m+1$. Therefore we can write the model when i is in the jth segment as:

$$\begin{eqnarray*}&&{y}_{i}\sim \\ &&\left\{\begin{array}{l}N({\alpha }_{1}+{\beta }_{j}({x}_{i}-{\gamma }_{1}),{\sigma }^{2}),\;{\rm{when}}\;{\rm{}}j=1,2,\\ N({\alpha }_{j-1}+{\beta }_{j}({x}_{i}-{\gamma }_{j-1}),{\sigma }^{2}),\\ \qquad {\rm{when}}\;{\rm{}}j=3,\ldots ,m+1.\end{array}\right.\end{eqnarray*}$$

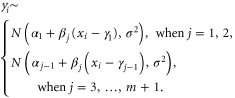
Setting this model in a Bayesian framework, we write the parameters as $\theta =\{\alpha ,\beta ,\gamma ,{\sigma }^{2}\}$ where for example $\alpha =\{{\alpha }_{j}\;:j=1,\ldots ,m+1\}$. We can then use Bayes' theorem to find the posterior distribution of the parameters given the data:

$$\begin{eqnarray}&&p(\theta | y,x)\propto \displaystyle \prod _{j=1}^{m+1}\left(\displaystyle \prod _{i\in J}p({y}_{i}| {x}_{i},\theta )\right)p(\theta ).\end{eqnarray} \tag{ 1 }$$

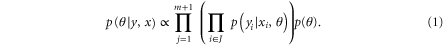
For all models demonstrated in this paper, we use only vague N(0,1e + 6) prior distributions for the α parameters. Prior distributions are not necessary for ${\beta }_{j}$ where j = 2,...,m as these can be deterministically evaluated since neighbouring segments must join together. We use:

$$\begin{eqnarray}&&{\beta }_{j}=\displaystyle \frac{{\alpha }_{j}-{\alpha }_{j-1}}{{\gamma }_{j}-{\gamma }_{j-1}},j=2,\ldots ,m.\end{eqnarray} \tag{ 2 }$$

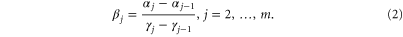
The only free slope parameters ${\beta }_{1}$ and ${\beta }_{m+1}$ are given vague N(0,1e + 6) prior distributions. The CP ${\gamma }_{l}$ parameters are given uniform prior distributions over the entire time range of the data, ${\gamma }_{l}\sim U({x}_{1},{x}_{n})$, l = 1,...,m. When $l\gt 1$ we set the condition that ${\gamma }_{l}$ are ordered, so that ${\gamma }_{1}\lt {\gamma }_{2}\lt \ldots \lt {\gamma }_{m}$.

We provide a summary of the use of MCMC methods in Bayesian analysis. For those interested in the more technical details involved in MCMC we recommend the introduction chapter in the Handbook of Markov Chain Monte Carlo (Brooks et al 2011).

MCMC is a technique used to solve the problem of sampling from complicated distributions. It is particularly useful for the evaluation of posterior distributions in Bayesian models. From Bayes' theorem we have:

$$\begin{eqnarray*}&&\underset{\mathrm{Posterior}}{\underbrace{P(\theta | X)}}\propto \underset{\mathrm{Likelihood}}{\underbrace{P(X| \theta )}}\underset{\mathrm{Prior}}{\underbrace{P(\theta )}},\end{eqnarray*}$$

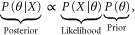
where X is our data and θ is an unknown parameter or vector of parameters. MCMC algorithms work by drawing values for θ from the posterior distribution (the probability distribution for θ given some observed data). The Markov chain component of the MCMC algorithm implies that a future value of our parameter(s) ${\theta }_{t+1}$ only depends on the current value ${\theta }_{t}$ and does not depend on any of the previous values ${\theta }_{t-1},{\theta }_{t-2},\ldots {\theta }_{0}$. In some MCMC algorithms the parameter value will either be accepted or rejected. This acceptance/rejection step is governed by a specified probability rule. We always accept values that are 'good' (i.e. that are supported by the data). However, occasionally we accept values that are 'worse' than the current value (although still supported by the data). It is this strategy that allows us to sample a probability distribution for our parameter(s) rather than only finding a point estimate. The algorithm converges when the sampled parameter values stabilize and if the algorithm is efficient then it will converge towards the parameter's posterior probability distribution. Often, during the warm-up phase of the algorithm, samples are discarded. This is known as the burn in period. Only samples beyond the burn in period are used as samples from the posterior distribution. The Monte Carlo step implies that by sampling enough times from the posterior distribution we can get a good estimate for our parameter(s) by taking an average of all the samples.

Two popular MCMC algorithms are Metropolis–Hastings (M–H) and the Gibbs sampler. In the M–H algorithm, samples are selected from an arbitrary 'proposal' distribution and are retained or not according to an acceptance rule. The Gibbs sampler is a special case in which the distributions are conditional (or 'proposed' conditional) distributions of single components of a parameter vector. JAGS (Plummer 2003) is a program that was developed to perform these MCMC methods on Bayesian statistical models. An appropriate likelihood for the data and priors for the unknown parameter(s) are specified in a model file and JAGS generates MCMC samples from this model using Gibbs sampling. JAGS therefore produces sample values for our unknown parameter(s) and once we are happy that the algorithm has converged these samples can be used to obtain point estimates (means, medians) and uncertainties³ .