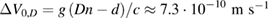Abstract
A recent paper (Ashby 2018 Metrologia 55 1) provides a rigorous relativistic treatment of the laser interferometer with a free-falling cube retroreflector. When considering the phase shift due to the light propagation within the glass cube, the associated effect was found to be 6.8 µGal. The constant phase shift was misinterpreted in the data analysis, producing a pseudo effect. We show that the time-dependent phase shift within the glass cube causes a negligible bias of the computed gravity acceleration and analyze the misconceptions that afforded a different conclusion.
Export citation and abstract BibTeX RIS
1. Introduction
The paper [1] develops a comprehensive relativistic theory of the laser interferometer with a falling retroreflector. The most important topic of [1] is the phase shift within the falling glass cube. The shift-associated corrections to the estimated parameters of initial displacement Z0, velocity V0 and gravity acceleration g were found to be (equation (47) [1]):
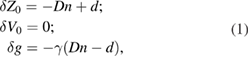
where δZ0, δV0, and δg are the corrections to be added to the respective parameter estimates, D = 0.0175 m is the cube depth, d = D/4, n = 1.52 is the refractive index of glass, and γ ≈ 3.072 · 10−6 s−2 is the vertical gravity gradient. Here the gravity correction δg is significant and amounts to −6.8 µGal1. The sign of that correction is unclear: the abstract and equation (45) both indicate a negative effect, but equations (47) and (48) provide negative corrections, while the comparison of the experimental results of D ≠ 0 with D = 0.0175 m above equation (45) is confusing. In this comment we discuss the speed-of-light corrections derivable from equation (33), including the light propagation within the cube.
2. Finite speed of light, glass cube and measured gravity (relativistic derivation)
The full relativistic treatment of the test beam phase at the point of interference is given in equation (33) [1]. To get the displacement model from the phase difference signal, as needed in this regression task, we follow the author of [1] and add the phase of the reference beam ΩT to (33) (Ω is the angular frequency of the reference signal), substitute 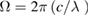 (c is the speed of light and λ is the laser wavelength), multiply it by
(c is the speed of light and λ is the laser wavelength), multiply it by  and re-arrange the components. The displacement is then given by
and re-arrange the components. The displacement is then given by
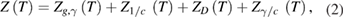
where


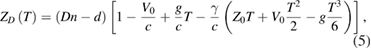
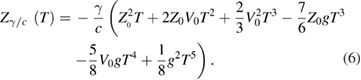
Owing to validity of the superposition principle in this linear regression task, four additive displacement components (3) to (6) can be analyzed separately, so that their separate contributions to the measurement result can be later combined. The first component  delivers the unbiased estimate of g. The second component
delivers the unbiased estimate of g. The second component  is the perturbation due to the finite speed of light, which allows us to derive the speed-of-light effect and correction. The component
is the perturbation due to the finite speed of light, which allows us to derive the speed-of-light effect and correction. The component  assembles perturbation terms associated with light propagation within the cube: it is responsible for the possible bias in the g estimate. The last component
assembles perturbation terms associated with light propagation within the cube: it is responsible for the possible bias in the g estimate. The last component  with the factor
with the factor  contains the remaining negligible terms.
contains the remaining negligible terms.
The speed-of-light perturbation component (4) agrees with that shown in [2], in equation (13)2. Taking the second derivative of (4), the perturbing acceleration yields
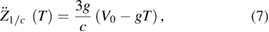
which agrees with the results of [2–4]3. Then the correction for the case considered in [1] (the beamsplitter is below the falling cube) is obtained from (7) as
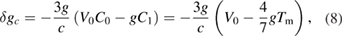
where the averaging coefficients C0 and C1 are defined in [4], and Tm is the total measurement time interval. Alternatively, the speed-of-light effect can be compensated by transforming the time variable [6]:

As in (7), the perturbing acceleration due to the light propagation within the cube is derived from (5) as
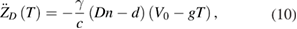
and the associated correction4 is

which for the given parameters of D, n, d and V0 = 0.4 m s−1, Tm = 0.2 s does not exceed 1 · 10−7 µGal. This negligible value supports the conclusions of the comment in [3].
Therefore, the relativistic time-dependent dynamical effect due to the light propagation within the glass cube (equation (10)) is negligible. This fact is also confirmed by the experiment in [1]: the author says after expression (45) that 'the same number (of −6.8 µGal) arises if all terms of order c−2 in equation (33) are neglected'.
3. Glass cube and measured gravity (non-relativistic derivation)
Here we again follow the author's approach in Appendix B of [1]. Re-arranging the terms in expression (B.7)5 or omitting all terms of order c−2 in equation (33) [1], the phase difference reads
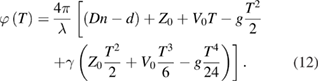
The author of [1] considers the displacement observed in (12) as
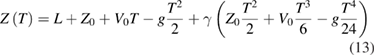
with the constant term L = (Dn − d), and fits the free-fall motion model (equation (5) in [1]):
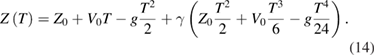
Least-squares adjustment of the model (14) to the displacement (13) without L returns unbiased estimates6:

When fitting the model (14) to the constant position L (velocity and acceleration equal to zero), it is reduced to
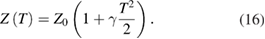
Least-squares adjustment of the model (16) to the constant L = (Dn − d) returns the biases
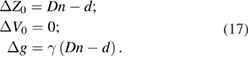
Summing up the biases (15) and (17) yields the above result (equation (1)), which now means that the measured gravity relates rather to Z = (Dn − d) than to Z = 0. This is a natural consequence of the modeled non-homogeneity of the gravity field (equation (4) in [1]), which we write here as

If for some reason the bias ΔZ0 ≠ 0 appears in the fitted parameters of the model (14), the measurement result g is corrected at the post-fit step using (18) as

However, the author of [1] applies such a correction in another way: he modifies the fitted model (14) with an attempt to compensate the theoretical bias ΔZ0 with the correction δZ0 = − ΔZ0. At the end of appendix B he says: 'this correction (i.e. δZ0 = −(Dn − d)) inserted into the T2 term in equation (B.7) then leads to the last line of equation (47) (i.e. δg = −γ(Dn − d))'. Then his actual fitted model equals to:
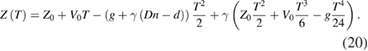
The difference between gravity estimates from the models (14) and (20) is the constant Δg = γ(Dn − d) = 6.8 µGal; hence the issue of light propagation within the cube in both relativistic and non-relativistic treatments is reduced to analyzing the evident zero response of the absolute gravimeter to the constant phase shift  in equation (12). Clearly, instead of correcting the computed measurement result by (19), the author corrects the theoretical model (20), assuming that the estimate of the initial position Z0 (and thus of the cube's release position) is biased. This step is caused by misinterpretation of the constant phase shift in equation (12) and by a vague definition of the regression model (equation (14) above or equation (5) in [1]).
in equation (12). Clearly, instead of correcting the computed measurement result by (19), the author corrects the theoretical model (20), assuming that the estimate of the initial position Z0 (and thus of the cube's release position) is biased. This step is caused by misinterpretation of the constant phase shift in equation (12) and by a vague definition of the regression model (equation (14) above or equation (5) in [1]).
4. Free-fall trajectory and regression model
An important feature of absolute gravity measurements in the non-homogeneous gravity field is the necessity to refer the derived gravity estimate to a certain height above the site mark, usually to the mechanically fixed resting position of the cube's optical center. In section 3 of [1], the origin of the laboratory frame (Z = 0) is placed on the point on the beamsplitter where the beams recombine. Then the author treats the parameters of model (5) in [1] as 'corresponding to release from position Z0'. Here the author confuses the fitted regression parameter Z0 with a known external quantity, the distance from the beamsplitter to the resting position of the cube.
The distance from the beamsplitter to the resting position of the cube (or more often, the distance between the site reference mark and the cube's optical center in the resting position) is needed for the height reductions outside the regression problem. It is measured independently for every set-up of an individual absolute gravimeter, either with a glass prism or with a hollow retroreflector.
The interferometer used measures the relative displacement of the cube during its free fall between two positions connected by a continuous interference signal, but not the absolute distance from a reference plane to the cube ([7], part II, chapter 4). The first position Z1 = 0 (start of fringe counting from the level Z = 0) exists below the release position when the cube's velocity is essentially non-zero, and the last one emerges before the cube is caught, far above the beamsplitter. Therefore, it is impossible to interferometrically measure the absolute distance from the beamsplitter to the resting position of the cube and to associate it with the regression parameter Z0. Also, the level Z = 0 where Z1 = 0, coincides neither with the beamsplitter nor with the release position of the cube's optical center. Besides, any constant phase shifts, including that from the glass cube, disappear in the measured optical path difference, as mentioned in the comment in [8]7. Without loss of generality, the interference signal in the laser displacement interferometer with an arbitrary displacement Z(t), as seen by the photodetector and used for counting fringes, is given by
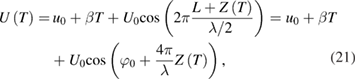
where u0 and β are the dc offset and the linear drift factor, respectively, U0 is the amplitude of the fringe signal, L is an arbitrary distance offset and Z(T) is the observed relative displacement, which is modeled by equation (14). Here the initial phase φ0 is

hence, the initial distance from the arbitrary reference plane is wrapped into the distance interval of L ⩽ λ/2 = 316.5 nm in equation (21). However, the author includes the compensating offset of L = (Dn − d) = 22.2 mm in the fitted model (20). If the reference plane or the beamsplitter (with the whole interferometer) is shifted up or down, the shift could not alter the cube's resting position, its initial velocity at Z1 = 0, the total measured displacement interval and hence the measured gravity acceleration. Equation (22) means that the absolute distance from the beamsplitter to the falling cube is 'invisible' in the interference signal (21), because the initial phase φ0 does not contain full information about the initial position and/or about the constant phase shift. Therefore, a constant shift L = ΔZ0 = (Dn − d) cannot appear in the free-fall trajectory constructed from (21), and thus the regression model (20) is incorrect.
5. On the meaning of the parameter Z0 in regression models of absolute gravimeters
Since the parameter of initial position in the correct regression model (14) is now irrelevant to the cube's resting position, the meaning of Z0 has to be explained. The fringe-counting interferometer used provides time stamps Ti at the scaled zero-crossings in the interference signal (21), which are used to construct the experimental free-fall trajectory Zi(Ti). The adjustable parameter Z0 in the model (14) is needed not for estimating the cube's resting position or the distance from the beamsplitter, but for absorption of random displacement noise in the trajectory Zi(Ti) when fitting a parabola. If we set8 T1 = 0 and Z1 = 0, then this trajectory and the obtained gravity estimate can be connected to the cube's resting position through the distance interval  , computed at the post-fit step9 (see figure 15 in [9] for more details). When fitting a model (14) to the trajectory data Zi(Ti) in this coordinate system, the theoretical trajectory comes close to point (0,0), only missing it due to data noise. The estimated value of Z0 in these coordinates becomes close to zero with no interpretable significance. In fact, some earlier free-fall motion models of absolute gravimeters completely ignored this parameter [10]. Nowadays the parameter Z0 is always included to improve the immunity of gravity estimates to displacement noise (see table 2 in [11]).
, computed at the post-fit step9 (see figure 15 in [9] for more details). When fitting a model (14) to the trajectory data Zi(Ti) in this coordinate system, the theoretical trajectory comes close to point (0,0), only missing it due to data noise. The estimated value of Z0 in these coordinates becomes close to zero with no interpretable significance. In fact, some earlier free-fall motion models of absolute gravimeters completely ignored this parameter [10]. Nowadays the parameter Z0 is always included to improve the immunity of gravity estimates to displacement noise (see table 2 in [11]).
One could use another coordinate origin and place Z = 0 in the cube's resting position. In this case it is necessary to specify in advance the position h0 of the first trajectory's coordinate Z1 = h0 relative to Z = 0 [12]. For example, one can trigger the start of data acquisition at a pre-defined fringe frequency f0, so that each drop corresponds to the same starting position 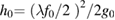 [9]. A constant offset h0 can be added to the constructed free-fall trajectory as an external known quantity, but the adjustable parameter Z0 still should be included in the regression model (14). It is needed for a tiny adjustment of the first point of the fitted parabola to the level Z = −h0. The gravity estimate g from the model (14) is then shifted to Z = 0 outside the regression procedure as gtop = g + γZ0. Omitting the parameter Z0 under the gravity gradient terms in the model (14) [12] automatically reduces the gravity estimate to the level Z = 0.
[9]. A constant offset h0 can be added to the constructed free-fall trajectory as an external known quantity, but the adjustable parameter Z0 still should be included in the regression model (14). It is needed for a tiny adjustment of the first point of the fitted parabola to the level Z = −h0. The gravity estimate g from the model (14) is then shifted to Z = 0 outside the regression procedure as gtop = g + γZ0. Omitting the parameter Z0 under the gravity gradient terms in the model (14) [12] automatically reduces the gravity estimate to the level Z = 0.
Equivalently, in the gravimeter used the time origin (T = 0) is shifted backward by -T0 from the time stamp of the first counted fringe to the instant of the test mass release for a free-fall motion, and the parameter Z0 is omitted under the gravity gradient terms in the model (14) [12]. Then the parameter Z0 adjusts the first point of the fitted parabola to the level h0 = -V0T0 + g(T0)2/2, and the gravity estimate is automatically reduced to the cube's resting position. The interval h0 connects two positions of the cube's optical center, first one at its resting position and second one at the height level of the first counted fringe, and does not require any additional consideration of properties of the cube. It is important to underline, that the role of hight transfer here is given to the known quantity of T0, but not to the estimate of Z0.
6. Conclusions
The phase shift due to light propagation within a falling glass cube was misinterpreted in the experimental data analysis in [1], which led to the reporting of a pseudo effect of 6.8 µGal. The author's misconception is that he stops at the theoretical phase of the test beam (33) [1], while physical observation of the interference pattern (equation (21)) should be considered. Then his regression model with or without relativistic components is reducible to equation (20), which corresponds to releasing the cube from the level of −22.2 mm relative to the cube's true resting position. A relativistic time-dependent dynamical effect on the phase, as mentioned in [5], exists, but is negligible (equation (11)). There is no need to account for the light propagation within the falling glass cube or modify currently used methods to address the finite speed-of-light effect in absolute gravimeters.
Acknowledgments
The above analysis was made within the author's collaboration with Project A01 of DFG Sonderforschungsbereich 1128, Relativistic geodesy and gravimetry with quantum sensors (geo-Q), funded by Deutsche Forschungsgemeinschaft (Germany).
Footnotes
- 1
1 µGal = 10−8 m s−2.
- 2
The signs of some terms differ because the Z-axis in [2] is positive downwards.
- 3
- 4
- 5
In the original text, (B.7) is given with a misprint: a factor 2 is missed at T2.
- 6
We denote 'bias' or 'effect' with the symbol 'Δ', which has an opposite sign to 'correction', denoted with 'δ'.
- 7
The irrelevance of the derived speed-of-light correction to the constant phase shifts is also mentioned in [2].
- 8
The author of [1] agrees that the coordinates' origin in this regression task can be arbitrarily shifted along either the time or the distance axis.
- 9
In this case, gravity at the resting position is
 . Bias in the estimated initial velocity due to light propagation within the cube, derived from equation (5), amounts to
. Bias in the estimated initial velocity due to light propagation within the cube, derived from equation (5), amounts to  and is negligible in this application.
and is negligible in this application.