Abstract
In the subject paper Ashby (2018 Metrologia 55 1–10) of the comment Svitlov (2018 Metrologia 55 609–13), light propagation through an absolute gravimeter was analyzed, including the propagation delay through the falling retroreflector and through the vacuum. The resulting expression for the interference signal applies without any subsequent 'speed of light' correction. Other corrections appeared for the three fitting parameters 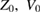 and g, which are, respectively, the initial position and velocity, and the acceleration of gravity at the reference point. The comment assumes the value of Z0 is known a priori; this case was not addressed in Ashby (2018 Metrologia 55 1–10). Also, the comment misunderstands statements made in Ashby (2018 Metrologia 55 1–10) regarding the derivation of the relativistic/non-relativistic parts of the corrections (equation (47) of Ashby (2018 Metrologia 55 1–10)), and mistakenly claims they apply to the undifferenced interference signal. In this reply we show why, because of inapplicable assumptions, approximations and misunderstandings, the comment does not apply to the results of Ashby (2018 Metrologia 55 1–10).
and g, which are, respectively, the initial position and velocity, and the acceleration of gravity at the reference point. The comment assumes the value of Z0 is known a priori; this case was not addressed in Ashby (2018 Metrologia 55 1–10). Also, the comment misunderstands statements made in Ashby (2018 Metrologia 55 1–10) regarding the derivation of the relativistic/non-relativistic parts of the corrections (equation (47) of Ashby (2018 Metrologia 55 1–10)), and mistakenly claims they apply to the undifferenced interference signal. In this reply we show why, because of inapplicable assumptions, approximations and misunderstandings, the comment does not apply to the results of Ashby (2018 Metrologia 55 1–10).
Export citation and abstract BibTeX RIS
The purpose of [1] was to provide a relativistic analysis of the propagation of light through a falling retroreflector gravimeter, including propagation through the retroreflector. The result was an expression for the interference signal at the recombination point (equation (33) of [1] with the reference beam phase removed). Accounting for propagation delay in the solid retroreflector results in several contributions to the final interference signal involving properties of the retroreflector: the corner-to-face distance D, center of mass (CM)-to-face distance d, and refractive index n. The interference signal is a fifth degree polynomial in the time T. The advantage of the relativistic expression is that no 'speed of light' correction is needed, as all propagation delays are accounted for.
In [1], data from 5000 drops were first fitted with the fully relativistic expression, then fitted using the relativistic expression with D and d set to zero. Differences in the resulting values of g (the acceleration of gravity at the reference point) and the other fitting parameters (Z0 and 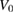 , the initial position and velocity, respectively) were reported, which turned out to be the same in every drop. A theoretical explanation for these differences was obtained by taking the corresponding differences for the theoretical interference signal; agreement between the numerical differences and the theoretical differences was excellent. The comment [2] contradicts the conclusions reported in [1], primarily because the comment assumes that the initial retroreflector position parameter Z0 is known a priori, but also because statements made in [1] have been misinterpreted. Fitting a model to data is independent of the derivation of the model; choosing which parameters to include in the fit to the model may or may not lead to a good fit. In fact, in the data processed and reported on in [1] no a priori value for Z0 was available; the fit value for g would depend critically on the value of Z0 inserted into the model.
, the initial position and velocity, respectively) were reported, which turned out to be the same in every drop. A theoretical explanation for these differences was obtained by taking the corresponding differences for the theoretical interference signal; agreement between the numerical differences and the theoretical differences was excellent. The comment [2] contradicts the conclusions reported in [1], primarily because the comment assumes that the initial retroreflector position parameter Z0 is known a priori, but also because statements made in [1] have been misinterpreted. Fitting a model to data is independent of the derivation of the model; choosing which parameters to include in the fit to the model may or may not lead to a good fit. In fact, in the data processed and reported on in [1] no a priori value for Z0 was available; the fit value for g would depend critically on the value of Z0 inserted into the model.
It is worthwhile to summarize the theory leading to the differences derived in [1]. A polynomial model of degree N with time T as independent variable, which is fitted to a given data set, will return specific numerical values of the polynomial coefficients. If there are two different models of the same degree for the data, the coefficients may have different interpretations but will be numerically equal. The numbers then have to be interpreted in terms of the models. In the present case we are comparing two models of the same degree based on the interference signal derived in [1]. To compress the algebra, we work with the interference signal multiplied by  where c is the speed of light and Ω is the angular frequency of the reference beam light. We write this function as
where c is the speed of light and Ω is the angular frequency of the reference beam light. We write this function as
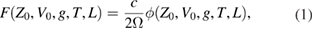
where 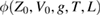 is the interference signal and L = Dn − d. In the model adopted in [1] the CM motion as a function of time T is
is the interference signal and L = Dn − d. In the model adopted in [1] the CM motion as a function of time T is
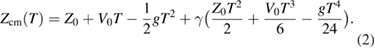
It was shown in [3] that 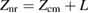 represents a fictitious point above the corner from which the actual interference signal can be inferred by considering the time required for the signal from the fictitious point to pass through a vacuum with speed c to the point of recombination. The quantity
represents a fictitious point above the corner from which the actual interference signal can be inferred by considering the time required for the signal from the fictitious point to pass through a vacuum with speed c to the point of recombination. The quantity 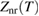 simply contains all the 'non-relativistic' contributions that were derived in appendix B of [1]. After computing Znr at the retarded time, expanding in powers of c−1 while keeping the first term in c−1, the interference signal at the recombination point can be compactly expressed in terms of F with
simply contains all the 'non-relativistic' contributions that were derived in appendix B of [1]. After computing Znr at the retarded time, expanding in powers of c−1 while keeping the first term in c−1, the interference signal at the recombination point can be compactly expressed in terms of F with
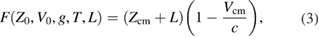
where Vcm is the CM velocity obtained by differentiating equation (2). Terms of degree higher than unity in the gravity gradient (γ) are neglected. The 'relativistic' part of the signal can be identified from equation (3) as the part containing c−1.
For brevity we define a difference operator Δ acting on a polynomial by

The two models compared are: the first term, which includes optical properties of the prism; and the second term, which omits them. In neither case is any additional 'speed of light' correction relevant. Both models are derived from, but are not equivalent to, the assumed CM motion of the prism, equation (2). The quantities  represent small differences for the three free parameters of interest. If they are sufficiently small that equation (4) can be linearized, this becomes
represent small differences for the three free parameters of interest. If they are sufficiently small that equation (4) can be linearized, this becomes
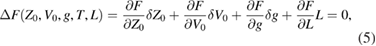
the last term arising because the signal is linear in L. The difference is zero numerically from fitting to the same data so the net coefficient of each power of T in equation (5) must vanish or be negligible. Because both models are polynomials of degree five in T, six conditions on the corrections are obtained. These six equations for coefficients of the successive powers of T, in order corresponding to T0 to T5, can be written in matrix form:
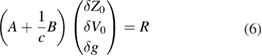
where R is a column matrix representing the last term in equation (5), A is a 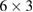 matrix of non-relativistic coefficients, and B represents relativistic contributions that have the factor c−1. R has both non-relativistic and relativistic contributions. The algebra is tedious and is not given here1. The rank of the matrix A + B/c is 3 (as are the ranks of A and B separately), so three independent equations can be selected, say, the first three, corresponding to powers of
matrix of non-relativistic coefficients, and B represents relativistic contributions that have the factor c−1. R has both non-relativistic and relativistic contributions. The algebra is tedious and is not given here1. The rank of the matrix A + B/c is 3 (as are the ranks of A and B separately), so three independent equations can be selected, say, the first three, corresponding to powers of 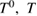 and T2. The solutions that result are
and T2. The solutions that result are
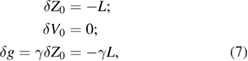
and these are the differences to which the fitting routines converge. Substituting these solutions into the remaining three equations, corresponding to powers  and T5, gives the respective residuals proportional to the small quantity
and T5, gives the respective residuals proportional to the small quantity  :
:
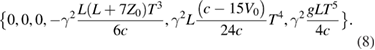
Such higher degree terms in γ have been neglected throughout [1]; numerical values of the phase residuals for  s are less than 10−8 radians and are negligible. The derived differences, equations (7), agree with differences obtained from numerical fits, showing in two ways that the optical properties of the retroreflector are significant, not negligible as claimed in the comment [2]. No substantive critique of the interference phase signal derivation, or of the steps described above that lead to the differences, equations (7), have been encountered yet. We now discuss a selected set of issues we have with the comment [2].
s are less than 10−8 radians and are negligible. The derived differences, equations (7), agree with differences obtained from numerical fits, showing in two ways that the optical properties of the retroreflector are significant, not negligible as claimed in the comment [2]. No substantive critique of the interference phase signal derivation, or of the steps described above that lead to the differences, equations (7), have been encountered yet. We now discuss a selected set of issues we have with the comment [2].
The comment assumes Z0 is known a priori, or 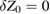 . It is then logically inconsistent to apply the result for
. It is then logically inconsistent to apply the result for  from equations (7), as in equation (20) of [2], because the results in equations (7) are related to each other by the linearization process described above. A different analysis is required, which was not given in [1].
from equations (7), as in equation (20) of [2], because the results in equations (7) are related to each other by the linearization process described above. A different analysis is required, which was not given in [1].
Terms in equation (6) of the comment [2] that are proportional to 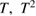 and T3 were neglected there. But they are important for reducing residuals to negligible levels, equation (8). They are not negligible.
and T3 were neglected there. But they are important for reducing residuals to negligible levels, equation (8). They are not negligible.
Two facts were discovered while seeking an explanation for the numerical value of 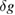 . First, keeping only the relativistic terms in equation (6)—those having the factor c−1—the same solutions equations (7) result. Second, if all relativistic effects are omitted by letting
. First, keeping only the relativistic terms in equation (6)—those having the factor c−1—the same solutions equations (7) result. Second, if all relativistic effects are omitted by letting  , the difference operation equations (5) or (6) leads again to equations (7). The comment [2] misunderstands these results, asserting that it confirms 'the relativistic time-dependent dynamical effect due to the light propagation within the cube is negligible'. The misunderstanding mistakenly elevates the vanishing of a difference between relativistic terms to the vanishing of all the relativistic terms in the interference signal. In reporting numerical differences in [1], relativistic terms were not neglected.
, the difference operation equations (5) or (6) leads again to equations (7). The comment [2] misunderstands these results, asserting that it confirms 'the relativistic time-dependent dynamical effect due to the light propagation within the cube is negligible'. The misunderstanding mistakenly elevates the vanishing of a difference between relativistic terms to the vanishing of all the relativistic terms in the interference signal. In reporting numerical differences in [1], relativistic terms were not neglected.
In equations (2)–(6) of [2] the so-called 'displacement' (the signal, equation (3), is not a displacement) is divided into the sum of four contributions. Such divisions are arbitrary since any function of the time could be added to one of the contributions as long as it is subtracted from another. For example, it is of particular interest to write all of the non-relativistic contributions (which were derived separately in appendix B of [1]) in one component of the model, such as
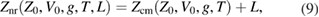
instead of grouping the term L elsewhere and using only  as in the comment. For example, equation (9) by itself when linearized with the difference operator
as in the comment. For example, equation (9) by itself when linearized with the difference operator 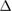 gives:
gives:
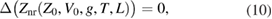
and leads to the solutions in equations (7). However the model displacement of the CM motion used in [1] was actually  , not
, not  as claimed in [2].
as claimed in [2].
The first 'displacement' component considered by [2] (equation (2) of [2]), is just the CM position, 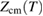 , of the falling prism. The comment asserts that this expression 'delivers the unbiased estimate of g'. But the comment assumes the value of Z0 is known a priori, (see section 4 in [2], first paragraph) 'being measured for every setup of an individual absolute gravimeter, either with the glass prism or with a hollow retroreflector'. The constraint
, of the falling prism. The comment asserts that this expression 'delivers the unbiased estimate of g'. But the comment assumes the value of Z0 is known a priori, (see section 4 in [2], first paragraph) 'being measured for every setup of an individual absolute gravimeter, either with the glass prism or with a hollow retroreflector'. The constraint  was not considered in [1]; it creates a separate problem deviating in many ways from [1]. If Z0 were known a priori to within a few microns the fitting routines would be different and it is not clear that linearization is appropriate. Results from two such different situations lead to errors if combined as in equation (20) of [2], which contradicts equation (10) above. On the other hand, user manuals for such gravimeters give the equivalent of the CM position
was not considered in [1]; it creates a separate problem deviating in many ways from [1]. If Z0 were known a priori to within a few microns the fitting routines would be different and it is not clear that linearization is appropriate. Results from two such different situations lead to errors if combined as in equation (20) of [2], which contradicts equation (10) above. On the other hand, user manuals for such gravimeters give the equivalent of the CM position 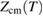 for the model of free fall [4], the constants being 'free parameters providing the best estimates for initial position, velocity and gravity'. In many references, Z0 is regarded as an adjustable parameter [5–7]. Measurements can provide a good estimate for Z0 but allowance is usually made for variations in the conditions of each individual drop. In [1], fitting determined Z0 with uncertainties of a few microns. It seems unlikely that a priori measurements could attain such accuracy; the CM is inside the glass.
for the model of free fall [4], the constants being 'free parameters providing the best estimates for initial position, velocity and gravity'. In many references, Z0 is regarded as an adjustable parameter [5–7]. Measurements can provide a good estimate for Z0 but allowance is usually made for variations in the conditions of each individual drop. In [1], fitting determined Z0 with uncertainties of a few microns. It seems unlikely that a priori measurements could attain such accuracy; the CM is inside the glass.
The coefficient of T2 in equation (9) is proportional to  ; this is the prism acceleration at T = 0. If there is no correction to the unbiased value of Z0 in the fits there will be no correction to g. The comment claims that the measured value of g relates to Z = L rather than to Z = 0. This is incorrect as the computation consistently fits the model to the given data, with g denoting its value at the reference position Z = 0. The quantity
; this is the prism acceleration at T = 0. If there is no correction to the unbiased value of Z0 in the fits there will be no correction to g. The comment claims that the measured value of g relates to Z = L rather than to Z = 0. This is incorrect as the computation consistently fits the model to the given data, with g denoting its value at the reference position Z = 0. The quantity 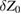 refers to a correction for the initial position at T = 0.
refers to a correction for the initial position at T = 0.
In equation (20) of the comment, an expression is given claiming to represent the actual fitted model for the 5000 drops reported in [1]. The expression is incorrect in more than one way. The data were fitted to a model based on Zcm, but given in equation (3) above or equation (33) of [1], including relativistic effects. In equation (20) of [2] the value of g has been adjusted but it was assumed that 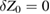 , so results reported in [1] cannot be reliably used in that equation.
, so results reported in [1] cannot be reliably used in that equation.
At the end of section 2 of [2] it is claimed that the time-dependent dynamical effect due to the light propagation within the cube is negligible, confirmed by the fact that the 'same number (−6.8 μGal) arises if all terms of order c−2 are neglected'. Such terms were actually not neglected in the fits; the quote from [1] only describes results of taking differences of the non-relativistic part of the signal. As shown above, it is possible to separate the expression into relativistic and non-relativistic parts and discuss individual parts, but the full expression (with and without L) was actually used for fitting. It is a misunderstanding of the attempt to understand differences, equation (6), by looking at parts of the difference separately. Considering them together is sufficient.
An interference phase with all relativistic terms omitted is the subject of section 3 of the comment. This section is based on a misunderstanding of the statement quoted in the preceding paragraph, which was intended to express the fact (derived and discussed above), that if all 'relativistic' terms in equation (6) were omitted, the difference solutions equations (7) would still result. The use of an interference phase as in equation (12) of the comment is not relevant, as such a phase was not used in the fitting reported in [1].
In equation (21) of the comment an expression for the interference signal 'as it is seen by the photodetector and is used for counting fringes' is provided in which the argument of the trigonometric functions neglects all relativistic effects. The phase used in [1] had higher degree polynomial terms, up to T5 (up to T3 multiplying L), so conclusions following from equation (21) of the comment do not apply to results reported in [1].
In summary, [1] accounts for light propagation in the falling retroreflector and predicts small differences for the fitted values for g and Z0 when properties of the prism are included or omitted respectively, but with no 'speed of light' correction in either case. The interference signal derived in [1] can support various observables. For example, a frequency observable could be obtained by differentiating the signal with respect to time. Observables could be constructed from first or second differences in the time, or for three-level schema, etc. No additional 'speed of light' correction is needed. The comment [2] accepts the interference signal derived in [1], then rearranges terms, makes certain assumptions and approximations, and revives the unnecessary 'speed of light' correction. Misunderstandings of [1] are a serious problem within [2]. Because the comment assumes Z0 is known a priori and misunderstands statements about differences resulting from comparison with and without the optical quantity Dn − d, the comment does not provide a valid critique of [1].
Footnotes
- *
Work of the U.S. government, not subject to copyright.
- 1
An expanded version of this reply is posted on https://doi.org/10.1088/1681-7575/aaac42

