Abstract
Einstein–Podolsky–Rosen (EPR) steering is different from quantum entanglement because of its unique asymmetry. Multipartite asymmetric EPR steering can break through one-to-one monogamy steering and achieve one to many one-way steering. That is to say, the state of one part can steer the other rest parts simultaneously, while the other parts cannot steer this part. Here, a scheme is proposed to generate one to many one-way steering by optical parametric amplification cascaded with a sum-frequency generation process. One to many non-monogamy EPR steering, such as one to two and one to three one-way steering are demonstrated based on the criterion for asymmetric EPR steering. It is also find that different kinds of asymmetric EPR steering can be obtained by choosing different nonlinear parameters. This non-monogamous one to many quantum control has potential application in constructing quantum networks and realizing one-way quantum computing.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Quantum steering was first proposed by Schrödinger [1] in response to the Einstein–Podolsky–Rosen (EPR) paradox [2]. It describes two spatially separated systems sharing entangled states, in which the local measurement of one system can nonlocally manipulate the state of the other system [3]. In 2007, based on the violation of the local hidden state model, Wiseman et al [4, 5] strictly defined the EPR steering and proved that the steering is a strict subset of entanglement. The quantum correlation property of EPR steering is between quantum entangled state [2] and Bell nonlocality [6]. EPR steering has unique asymmetry, which is different from quantum entangled states and Bell nonlocality. The case where Alice can control Bob's state but Bob cannot control Alice's state leads to one-way steering [4, 7]. Due to the asymmetric nature of EPR steering, some quantum information work that depends on entanglement can be done, such as quantum secret sharing [8] and quantum key distribution [9, 10], one-way quantum computing [11–14], etc.
However, how to generate quantum steering is a prerequisite for carrying out these quantum information works. Therefore, it has attracted widespread attention from researchers. Reid et al [15] analyzed the relation between entanglement and Bell's theorem and discussed the continuous variable EPR paradox in laser experiments. Händchen et al [16] observed the generation of one-way EPR steering in experiment. Wollmann et al [17] demonstrated the one-way steering property. Sun et al [18] experimentally demonstrated asymmetric EPR steering for a class of two-qubit states. Xiao et al [19] experimentally demonstrated one-way EPR steering in a two-qubit state using multiple measurement setups. Cavaillès et al [20] demonstrated EPR steering by using continuous-variable and discrete-variable entangled optical qubits. Tischler et al [21] experimentally proved the conclusion of one-way EPR steering. He and Reid [22] investigated the possibility of EPR paradox between two entangled oscillators. Schneeloch et al [23] tested the possibility of exclusive one-way steering in a two-qubit state. Olsen [24] demonstrated asymmetric Gaussian harmonic steering in the process of second harmonic generation. Qin et al [25] investigated an asymmetric EPR steering between two multiple entangled state subsystems. Zheng et al [26] proposed a phase control method to generate direction steering between two completely symmetric modes. Chen et al [27] proposed a hybrid cavity magneto-mechanical system to produce relatively obvious asymmetric EPR steering. Liang et al [28] gave a scheme to produce asymmetric EPR steering by spontaneous parametric down-conversion cascaded with double sum-frequency generation. Chen et al investigated the asymmetric EPR steering [29] and tripartite EPR steering [30] in the processes of three-photon parametric down-conversion. Shen et al [31] proposed a scheme to produce quadripartite EPR steering in an optical superlattice. Olsen [32] proposed to control asymmetric EPR steering in nondegenerate optical parametric oscillator with an injected signal. Zhai et al [33] proposed a scheme to generate quadripartite EPR steering by three different energy-level cascaded four-wave mixing. Liang et al [34] proposed to generate quadripartite EPR steering by optical parametric oscillation cascaded with a sum-frequency process. Liu et al [35] proposed a scheme to generate tripartite EPR steering by spontaneous parametric down-conversion cascaded with a sum-frequency generation. Recently, Hao et al [36] observed for the first time the non-monogamous sharing relationship of tripartite EPR steering. This is actually a two to one asymmetric EPR steering. However, there are few reports on non-monogamous 'one to many' asymmetric EPR steering.
In this paper, we propose a scheme to generate non-monogamous one to many asymmetric EPR steering produced by optical parametric oscillation cascaded with a sum-frequency generation. This cascaded nonlinear process can be achieved in an optical superlattice by quasi-phase-matching technique [37]. Based on the criterion of asymmetric EPR steering [38], we theoretically proved that asymmetric EPR steering one to one, even one to two and one to three asymmetric EPR steering, can be obtained in this cascaded nonlinear process which is different from two to one asymmetric EPR steering in [36]. Because in our solution, non-monogamous one to many manipulation can be achieved. It is also found that the nonlinear parameters have important influences on the asymmetric EPR steering. The damping rates γ is related to the reflection transmission coefficient of the optical cavity for 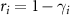 and
and 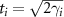 [39] and the value can be changed by changing the transmission and reflection system of the coupling cavity mirror. The nonlinear coupling parameter κ in our scheme can be changed by designing the parameters of optical superlattice [37, 40], which is the advantage of our scheme over the previous atomic system scheme. Therefore, different kinds of asymmetric EPR steering can be obtained by choosing different nonlinear parameters. Optical parametric down-conversion cascaded with a sum-frequency generation without [40] and with [41] optical cavity both have been realized in previous experiments. Multiple beam resonances of different frequencies have also been experimentally achieved [42]. So we think the cascaded nonlinear processes of optical parametric oscillation cascaded with a sum-frequency generation in our scheme is feasible in the experiment. The results obtained in this paper will help people to better understand multipartite asymmetric EPR steering and have potential applications in building quantum networks [43, 44] and one-way quantum computing [11–14]. For example, in quantum networks and quantum computing, if we want to achieve that A can simultaneously manipulate B, C, and D, but B, C, and D cannot affect A in reverse, we can use the non-monogamous quantum steering state we have prepared that can be one-to-three. Or in quantum communication, A can send information to B, C, and D, but B, C, and D do not know where the information actually comes from. So this one to many non-monogamous quantum steering state can have special applications.
[39] and the value can be changed by changing the transmission and reflection system of the coupling cavity mirror. The nonlinear coupling parameter κ in our scheme can be changed by designing the parameters of optical superlattice [37, 40], which is the advantage of our scheme over the previous atomic system scheme. Therefore, different kinds of asymmetric EPR steering can be obtained by choosing different nonlinear parameters. Optical parametric down-conversion cascaded with a sum-frequency generation without [40] and with [41] optical cavity both have been realized in previous experiments. Multiple beam resonances of different frequencies have also been experimentally achieved [42]. So we think the cascaded nonlinear processes of optical parametric oscillation cascaded with a sum-frequency generation in our scheme is feasible in the experiment. The results obtained in this paper will help people to better understand multipartite asymmetric EPR steering and have potential applications in building quantum networks [43, 44] and one-way quantum computing [11–14]. For example, in quantum networks and quantum computing, if we want to achieve that A can simultaneously manipulate B, C, and D, but B, C, and D cannot affect A in reverse, we can use the non-monogamous quantum steering state we have prepared that can be one-to-three. Or in quantum communication, A can send information to B, C, and D, but B, C, and D do not know where the information actually comes from. So this one to many non-monogamous quantum steering state can have special applications.
2. Theory
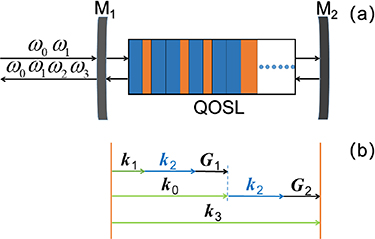
Here, we consider a cascaded nonlinear process in a one-sided input-output optical cavity which can be seen in figure 1(a). Cavity mirror M
1 partially reflects and partially transmits all frequency optical fields, and cavity mirror M
2 fully reflects all frequency optical fields. A pump with frequency ω0 and a signal beam with frequency ω1 enter into the optical cavity in which a quasiperiodic optical superlattice (QOSL) is placed as a nonlinear gain medium. Idle beam with frequency ω2 is generated by different frequency generation between the pump and the signal [40, 41]. Sum-frequency beam with frequency ω3 is generated by a cascaded sum-frequency process between the pump and the idle in the same optical superlattice [40, 41]. In this cascaded nonlinear process, energy conservation is satisfied 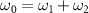 and
and 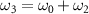 . It can be seen in figure 1(b) that the phase mismatch are compensated by the reciprocal vectors G1 and G2 provided by the QOSL through quasi-phase-matching [37] technique as
. It can be seen in figure 1(b) that the phase mismatch are compensated by the reciprocal vectors G1 and G2 provided by the QOSL through quasi-phase-matching [37] technique as 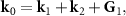 and
and 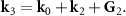
Figure 1. (a) Structure diagram of optical cavity. (b) Schematic diagram of quasi-phase-matching process.
Download figure:
Standard image High-resolution imageThe interaction Hamiltonian for the cascaded nonlinear process can be written as 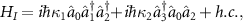 where κ1 and κ2 denotes the nonlinear coupling constants and
where κ1 and κ2 denotes the nonlinear coupling constants and 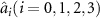 is the boson annihilation operator. The Hamiltonian for cavity pump and external input signal is
is the boson annihilation operator. The Hamiltonian for cavity pump and external input signal is  , where ε0 and ε1 are the classical pump and signal amplitude, respectively. Following the standard treatment, in the positive-P representation [45] the equations of motion for the cavity modes can be derived as
, where ε0 and ε1 are the classical pump and signal amplitude, respectively. Following the standard treatment, in the positive-P representation [45] the equations of motion for the cavity modes can be derived as
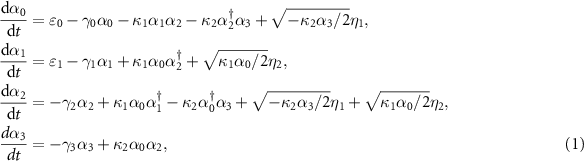
where 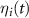 are the Gaussian noise terms with the properties
are the Gaussian noise terms with the properties  and
and 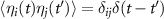 . αi
are amplitudes for the pump, signal, idle, and sum-frequency field in the positive-P representation, respectively. γi
represent the cavity loss at frequency ωi
. One can regard system variables including their mean value Ai
and small fluctuations in the steady state as
. αi
are amplitudes for the pump, signal, idle, and sum-frequency field in the positive-P representation, respectively. γi
represent the cavity loss at frequency ωi
. One can regard system variables including their mean value Ai
and small fluctuations in the steady state as 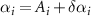
 . And we take
. And we take 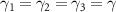 for the purpose of simplifying the calculation. Based on linear processing approach, equation (1) can be rewritten in a matrix form as
for the purpose of simplifying the calculation. Based on linear processing approach, equation (1) can be rewritten in a matrix form as

with ![$ \delta \tilde{\alpha}\!\!\! = \!\!\![\delta \alpha _{0},\delta \alpha _{0}^{\dagger },\delta \alpha _{1},\delta \alpha _{1}^{\dagger },\delta \alpha _{2},\delta \alpha _{2}^{\dagger },\delta \alpha _{3},\delta \alpha _{3}^{\dagger }]^{\mathrm{T}}, $](https://content.cld.iop.org/journals/1367-2630/26/1/013049/revision2/njpad1f0bieqn16.gif) B is the drift matrix of noise terms which contains the steady-state solutions and dW is a vector of Wiener increments [24]. The drift matrix A can be written the form as
B is the drift matrix of noise terms which contains the steady-state solutions and dW is a vector of Wiener increments [24]. The drift matrix A can be written the form as
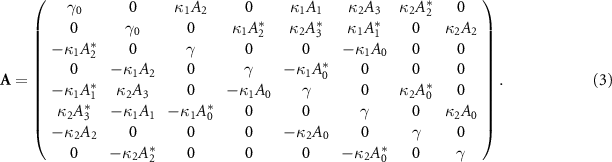
On the basis of Fourier transform, the intracavity spectrum can be obtained as
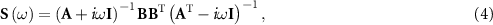
where ω is the Fourier analysis frequency and I is the identity matrix. Based on the standard input-output relationship [46], the output spectrum can be calculated.
3. Results
Because linearization methods can only be used when the system is in steady state. Under the condition that the above drift matrix A has no negative real part of eigenvalue, the system is in steady state. Therefore, we analyze the variation of the real part of the eigenvalue of A with the nonlinear parameters. As shown in figure 2, the eigenvalues are calculated with respect to the classical pump amplitude ε0, the injected signal amplitude ε1, the loss factor ratio 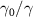 , and the nonlinear coupling constant ratio
, and the nonlinear coupling constant ratio 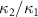 , respectively. It can be seen from figure 2 that the real part of the eigenvalues has no negative value. This shows the linearization method is effective. Therefore, we can discuss the asymmetric quantum steering within the above parameters.
, respectively. It can be seen from figure 2 that the real part of the eigenvalues has no negative value. This shows the linearization method is effective. Therefore, we can discuss the asymmetric quantum steering within the above parameters.
Figure 2. Real parts of eigenvalues of drift matrix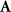 (Eigenvalues (A) versus: (a) ε0, (b) ε1, (c)
(Eigenvalues (A) versus: (a) ε0, (b) ε1, (c) 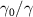 , and (d)
, and (d) 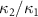 , respectively.
, respectively.
Download figure:
Standard image High-resolution imageIn order to illustrate the asymmetric EPR steering, we use Reid's criterion [38], which proves the existence of the EPR paradox when the product of two orthogonal variances is less than 1. The two orthogonal variances can be written as [38]
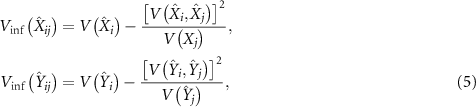
with 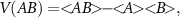 where
where 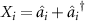 and
and 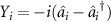 .
. 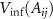 denotes the variance of Ai
inferred from the metric of Aj
. When the product of these two inferred variances is less than 1, i can be controlled by j and the EPR paradox between the two optical fields is proved. Here we take
denotes the variance of Ai
inferred from the metric of Aj
. When the product of these two inferred variances is less than 1, i can be controlled by j and the EPR paradox between the two optical fields is proved. Here we take 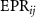 as the variances of Xij
and Yij
in equation (5). If
as the variances of Xij
and Yij
in equation (5). If 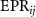 is less than 1, it means that optical field
is less than 1, it means that optical field 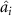 can be steered by optical field
can be steered by optical field 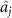 . When
. When 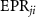 is greater than or equal to 1 in the same time, it means that optical field
is greater than or equal to 1 in the same time, it means that optical field 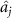 cannot be steered by optical field
cannot be steered by optical field 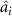 . It leads to asymmetric steering, reflecting the unique asymmetry of quantum steering which is different from quantum entanglement. Since EPR manipulable states are a strict subset of the entangled states, both symmetric and asymmetric steering prove that the two modes are bipartite entangled states. The asymmetric EPR steering properties among pump, signal, idle, and sum-frequency beams are investigated according to this determination criterion.
. It leads to asymmetric steering, reflecting the unique asymmetry of quantum steering which is different from quantum entanglement. Since EPR manipulable states are a strict subset of the entangled states, both symmetric and asymmetric steering prove that the two modes are bipartite entangled states. The asymmetric EPR steering properties among pump, signal, idle, and sum-frequency beams are investigated according to this determination criterion.
Quadripartite asymmetric steering is more complicated than the tripartite asymmetric steering in [36]. Here we mainly discuss the case of one to many asymmetric steering. Figure 3 shows one to many classification of quadripartite asymmetric steering which includes one to one, one to two and one to three asymmetric EPR steering. Through one to many asymmetric steering, one-way control of multiple components can be realized. Through calculation and analysis, we find that there is one to many asymmetric EPR steering in the quadripartite asymmetric steering generated by the cascaded nonlinear process. Next, we take the one-way control of optical field 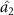 on other optical fields as an example, and analyze the influence of nonlinear parameters on asymmetric steering.
on other optical fields as an example, and analyze the influence of nonlinear parameters on asymmetric steering.
Figure 3. One to many classification of quadripartite asymmetric steering: (a) One to one; (b) One to two; (c) One to three. The green arrow indicates that steering is available, while the red arrow indicates that steering is unavailable.
Download figure:
Standard image High-resolution imageFigure 4 shows the variation of 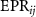 with respects to the normalized analysis frequency
with respects to the normalized analysis frequency 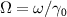 . When about
. When about 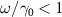 , one can see that
, one can see that 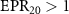 while
while  which shows that optical field
which shows that optical field 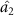 can steer
can steer 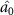 , but
, but 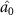 cannot steer
cannot steer 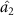 . In the whole selected parameter range,
. In the whole selected parameter range, 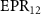 is less than 1, and
is less than 1, and 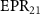 is almost all greater than 1. This indicates that there is asymmetric quantum steering correlation between optical fields
is almost all greater than 1. This indicates that there is asymmetric quantum steering correlation between optical fields  and
and 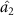 in almost the whole selected parameter range. When about
in almost the whole selected parameter range. When about 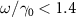 ,
, 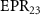 is greater than 1, while
is greater than 1, while 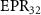 is less than 1, which indicates that there is asymmetric EPR steering between optical fields
is less than 1, which indicates that there is asymmetric EPR steering between optical fields 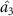 and
and 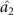 . It can be seen from figure 4 that optical field
. It can be seen from figure 4 that optical field 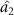 can steer optical fields
can steer optical fields 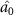 ,
, 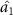 , and
, and 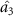 in one direction. There is a one-way quantum steering of one to three (can be seen in figure 3(c)), which is more meaningful than one-to-one steering, which can achieve one to many one-way manipulation. It is helpful to realize quantum information work such as quantum networks and one-way quantum computing.
in one direction. There is a one-way quantum steering of one to three (can be seen in figure 3(c)), which is more meaningful than one-to-one steering, which can achieve one to many one-way manipulation. It is helpful to realize quantum information work such as quantum networks and one-way quantum computing.
Figure 4.
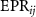 versus the normalized analysis frequency
versus the normalized analysis frequency 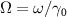 with
with 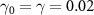 ,
, 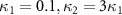 and
and 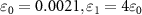 .
.
Download figure:
Standard image High-resolution imageFigure 5 shows the change of 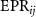 with the ratio of injection signal amplitude to pump amplitude
with the ratio of injection signal amplitude to pump amplitude 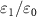 . It is obvious that
. It is obvious that 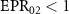 and
and 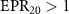 in the whole range, and
in the whole range, and 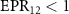 and
and 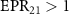 when about
when about 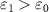 . Therefore, there is one to one bipartite asymmetric EPR steering among the three optical field pairs. When
. Therefore, there is one to one bipartite asymmetric EPR steering among the three optical field pairs. When  , there is one to two asymmetric EPR steering of optical field
, there is one to two asymmetric EPR steering of optical field 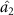 can one-way steer optical fields
can one-way steer optical fields  and
and 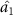 in the same time. Optical fields
in the same time. Optical fields  ,
, 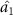 and
and 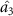 can share the information from optical field
can share the information from optical field 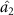 . It can be seen that the steering relationship among the four optical fields can be modulated by selecting the appropriate intensity ratio of signal and pump.
. It can be seen that the steering relationship among the four optical fields can be modulated by selecting the appropriate intensity ratio of signal and pump.
Figure 5.
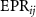 versus
versus 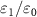 with
with 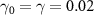 ,
, 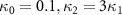 , and
, and  .
.
Download figure:
Standard image High-resolution imageFigure 6 depicts the values of 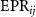 versus the nonlinear coupling constant ratio
versus the nonlinear coupling constant ratio 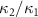 . From figure 6, it can be seen that when
. From figure 6, it can be seen that when 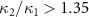 ,
, 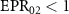 and
and 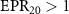 ,
, 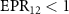 and
and 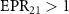 ,
, 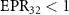 and
and 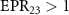 , optical field
, optical field  can simultaneously steer optical fields
can simultaneously steer optical fields 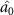 ,
, 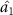 and
and 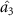 , which shows that there is one to three asymmetric EPR steering. When
, which shows that there is one to three asymmetric EPR steering. When 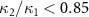 ,
, 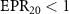 and
and 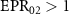 ,
, 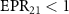 and
and 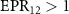 ,
, 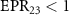 and
and 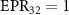 , optical fields
, optical fields 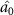 ,
, 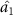 and
and 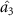 can simultaneously steer optical field
can simultaneously steer optical field 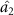 , which shows that there is three to one asymmetric EPR steering. When the value of κ2 is close to the value of κ1,
, which shows that there is three to one asymmetric EPR steering. When the value of κ2 is close to the value of κ1, 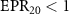 and
and 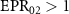 ,
, 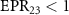 and
and 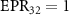 , optical field
, optical field 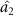 can be steered by optical fields
can be steered by optical fields  and
and 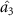 , but the asymmetric steering of one to three or three to one cannot be obtained. κ is related to the structural parameters of the optical superlattice [40]. Different kinds of asymmetric EPR steering can be obtained by designing different optical superlattice parameters.
, but the asymmetric steering of one to three or three to one cannot be obtained. κ is related to the structural parameters of the optical superlattice [40]. Different kinds of asymmetric EPR steering can be obtained by designing different optical superlattice parameters.
Figure 6.
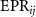 versus
versus 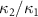 with
with  ,
,  and
and 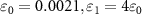 , and
, and 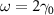 .
.
Download figure:
Standard image High-resolution imageThe values of 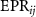 versus the damping rates ratio
versus the damping rates ratio  is shown in figure 7. When
is shown in figure 7. When 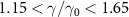 , optical field
, optical field 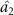 can steer optical fields
can steer optical fields 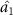 and
and 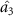 in one-way and one to two asymmetric EPR steering can be obtained. At about
in one-way and one to two asymmetric EPR steering can be obtained. At about 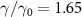 , optical field
, optical field 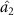 can steer optical fields
can steer optical fields 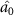 ,
, 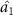 and
and 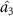 in one-way and one to three asymmetric EPR steering can be obtained. When
in one-way and one to three asymmetric EPR steering can be obtained. When 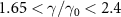 , optical field
, optical field 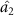 can steer optical fields
can steer optical fields 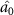 and
and 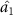 in one-way and one to two asymmetric EPR steering can be obtained. As
in one-way and one to two asymmetric EPR steering can be obtained. As 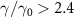 , optical field
, optical field 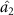 only can steer optical fields
only can steer optical fields 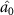 in one-way and one to one asymmetric EPR steering can be obtained. The damping rates are related to the reflection and transmission coefficients of the cavity mirror. Therefore, different asymmetric EPR steering can be obtained by designing different cavity mirrors.
in one-way and one to one asymmetric EPR steering can be obtained. The damping rates are related to the reflection and transmission coefficients of the cavity mirror. Therefore, different asymmetric EPR steering can be obtained by designing different cavity mirrors.
Figure 7. The values of 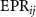 versus the damping rates ratio
versus the damping rates ratio 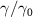 with
with 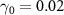 ,
, 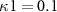 ,
,  and
and 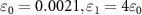 , and
, and 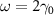 .
.
Download figure:
Standard image High-resolution image4. Conclusions
One to many non-monogamous EPR steering can be obtained by optical parametric amplification cascaded a sum-frequency generation. The cascaded nonlinear process can be achieved by quasi-phase-matching technique. Nonlinear parameters have an important influence on asymmetric EPR steering. By modulating nonlinear parameters, different kinds of asymmetric EPR steering can be obtained, such as one to one, one to two, or one to three asymmetric EPR steering. Asymmetric EPR steering can achieve one-way control, which is different from symmetric quantum steering. Here we only analyze one to many asymmetric EPR steering. In fact, quadripartite asymmetric EPR steering also has many to one asymmetric steering, such as two to one asymmetric steering in [36], or even three to one asymmetric steering. We hope that the results of this study will help people to better understand multipartite asymmetric EPR steering and have potential applications in quantum information processing, such as building quantum networks and one-way quantum computing.
Acknowledgments
This work is supported by National Natural Science Foundations of China (No. 61975184), Science Foundation of Zhejiang Sci-Tech University (No. 19062151-Y).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).