Abstract
Universality of the long-distance behavior across the Bardeen–Cooper–Schrieffer (BEC)-Bose–Einstein condensate (BCS) smooth transition for two-body density correlation functions and the Cooper-pair probability density is demonstrated in a balanced mixture of a two-component Fermi gas at T = 0. It is numerically shown at the mean-field level that these two-body quantities exhibit an exponential decay in terms of the chemical potential and the low-energy behavior of the gap. A general expression is found for the two-body distributions holding for different features of finite-range potentials, such as divergences at the origin, discontinuities at a finite radius, power-law decay, and exponential decay. The correlation length characterizing the long-distance behavior unravels the dependence on the energy needed to break pairs along the BEC-BCS crossover, a quantity meaningful to the stability of the many-body state.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Equilibrium density correlation functions are fundamental for the understanding of the spatial structure of matter [1]. They yield the next level of information beyond thermodynamics, elucidating the underlying arrangement in matter found at all scales, from astronomical galaxies to atomic conglomerates such as solids, liquids, or superfluid phases [2–8]. In addition, correlation functions are of fundamental relevance to characterize the order of a phase transition as they directly track density–density fluctuations [9–16]. Within the ubiquitous crossover of fermionic superfluids that goes from a Bardeen–Cooper–Schrieffer (BCS) state to a molecular Bose–Einstein condensate (BEC), as the s-wave scattering length is varied through a Feshbach resonance [17–24], the analysis of density correlations has been a subject of relatively recent scrutiny, both at zero and finite temperature [19, 20, 23–31], as well as varying interaction models [22, 32], and space dimension [26, 33, 34], but mostly within the context of the contact interaction that depends solely on the scattering length. The modulation of such an effective interaction between fermions gives the possibility of the emergence of different quantum states like superfluidity, or superconductivity for charged fermions, and molecular formation, giving account of the rich many-body effects that can be found in nature. And, thus, it appears as a natural question the determination of the intrinsic spatial structure of these states.
The proper scenario to address the analysis of the two-body spatial structure are the seminal works by Leggett [35] and Eagles [36] that arrived to the prominent conclusion of the BEC-BCS crossover. These works became a referent in the whole field of fermionic matter in its degenerate regime. This mean-field model envisages the understanding of more complex phenomena, as for instance, superfluids or superconductors in lower dimensions or confined in non-homogeneous environments, FFLO phases [23, 37], the cooling of neutron stars [23, 38], the formation of deuteron states in nuclear matter [23] and the rich diversity of systems belonging to the physics of quasiparticles and excitons as well [39].
The main contribution of the present paper resides on the resolution of the emerging universal character of the long-distance behavior of the spatial density correlations along the zero-temperature BEC-BCS crossover, within mean-field theory and for contact and finite-range atomic interactions. That is, while the detailed behavior of those two-body distribution functions at short distances do depend on the interatomic potential at hand, we show that asymptotically their dependence has the same functional form in terms of thermodynamic, or many-body properties such as the chemical potential and the low-momentum energy gap. More importantly, we find that the correlation length ξ, a crucial physical quantity that determines the size of the density fluctuations, can be analytically expressed in terms of the minimum threshold energy required to break a fermion pair, 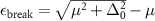 , namely, as
, namely, as 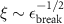 , with µ the chemical potential and Δ0 the zero-momentum gap corresponding to the given parameters of the interaction potential or, alternatively, the scattering length. This threshold energy εbreak has been identified in analyzing the breaking of pairs, both, in the spectroscopic analysis of the BCS state [20, 40–42] and in the study of dynamical collective excitations [43]. Thus, since that energy is a minimum, the correlation length is a maximum, indicating that as long as the pairs remain as Cooper pairs or bound molecules, the pair structure stays correlated within a spatial region of the size of the order of such a length. This certainly unveils a universal feature proper of the mean-field theory. In addition we also find that, accompanying the exponential decay of the distributions, there is a
, with µ the chemical potential and Δ0 the zero-momentum gap corresponding to the given parameters of the interaction potential or, alternatively, the scattering length. This threshold energy εbreak has been identified in analyzing the breaking of pairs, both, in the spectroscopic analysis of the BCS state [20, 40–42] and in the study of dynamical collective excitations [43]. Thus, since that energy is a minimum, the correlation length is a maximum, indicating that as long as the pairs remain as Cooper pairs or bound molecules, the pair structure stays correlated within a spatial region of the size of the order of such a length. This certainly unveils a universal feature proper of the mean-field theory. In addition we also find that, accompanying the exponential decay of the distributions, there is a  envelope and a oscillatory function whose wavelength is also universal.
envelope and a oscillatory function whose wavelength is also universal.
The findings we present here follow from a detailed numerical analysis of the density–density correlation functions of like and different spin species,  and
and  , and of the Cooper pair probability distribution. That is, within the BCS-Leggett variational approach, we fully analyze the BEC-BCS crossover using four finite-range potentials that show representative features of typical atomic and nuclear interactions. We analyze a square well potential [20], which shows a discontinuity at a finite radius; an exponential potential [44], which is smooth over all space; the Yukawa potential [45], which has a divergence at the origin; and we also use a van der Waals tail potential [23, 32], which bears the common atomic power-law decay. An important aspect is that we do not approximate these potentials in the gap equation and, while this introduces the inconvenience of dealing with numerical difficulties, these have been solved in [32, 46]. Indeed, as the range of the potential becomes very small, in the appropriate limit we recover the contact interaction potentials results [25]. Anyhow, we show that our conclusions are also valid for large potential ranges as well. We also discuss the high-energy behavior of the s-wave gap functions, which are highly dependent on the structure of the potentials. We will show that the gaps have a power-law decay and, in some cases, an oscillatory behavior due to the discontinuities of the given potentials.
, and of the Cooper pair probability distribution. That is, within the BCS-Leggett variational approach, we fully analyze the BEC-BCS crossover using four finite-range potentials that show representative features of typical atomic and nuclear interactions. We analyze a square well potential [20], which shows a discontinuity at a finite radius; an exponential potential [44], which is smooth over all space; the Yukawa potential [45], which has a divergence at the origin; and we also use a van der Waals tail potential [23, 32], which bears the common atomic power-law decay. An important aspect is that we do not approximate these potentials in the gap equation and, while this introduces the inconvenience of dealing with numerical difficulties, these have been solved in [32, 46]. Indeed, as the range of the potential becomes very small, in the appropriate limit we recover the contact interaction potentials results [25]. Anyhow, we show that our conclusions are also valid for large potential ranges as well. We also discuss the high-energy behavior of the s-wave gap functions, which are highly dependent on the structure of the potentials. We will show that the gaps have a power-law decay and, in some cases, an oscillatory behavior due to the discontinuities of the given potentials.
The paper is organized as follows. In section 2 we present the BCS Hamiltonian with the corresponding gap and number equations that arise from the usual variational approach. We introduce the four finite-range potentials under consideration, and show their corresponding gap functions, chemical potentials and threshold energies required to break a pair throughout the crossover. In section 3 we define the density–density correlation functions and the pair wave function, which exhibit the spatial structure of the mean-field approach. We show the numerical fits that allow us to exhibit the large-distance behavior of the two-body distributions. In particular, we discuss the role of the threshold energy required to break a pair in determining the correlation length which establishes the universal property of the mean-field approach. We address how this important physical insight is obtained from both the spectroscopic and dynamical collective excitations scenarios. Finally, in section 4 we summarize our work and elaborate on further perspectives regarding the large-distance behavior of the two-body distributions and the relevance of finite-range potentials in systems of different physical nature.
2. BEC-BCS crossover for contact and finite-range potentials
The determination of the universal properties of the long-distance behavior of two-body properties of an ultracold balanced gas mixture of Fermi atoms, interacting between pairs by a short finite-range interatomic potential, emerges from the Hamiltonian
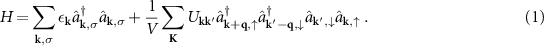
Here, 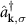 and
and 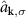 are creation and annihilation operators of free fermions with momentum k and hyperfine spin component labeled as
are creation and annihilation operators of free fermions with momentum k and hyperfine spin component labeled as 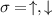 ; the kinetic energy is
; the kinetic energy is 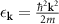 . In the interaction term the sum goes over three wave vectors
. In the interaction term the sum goes over three wave vectors 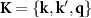 and V is the volume of the sample.
and V is the volume of the sample. 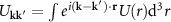 is the Fourier transform of the finite-range potential of the interparticle interaction. In addition to the contact potential
is the Fourier transform of the finite-range potential of the interparticle interaction. In addition to the contact potential  , with a the scattering length, we consider four potential models representative of short-range interatomic potentials, determined by a characteristic energy
, with a the scattering length, we consider four potential models representative of short-range interatomic potentials, determined by a characteristic energy 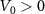 , that represents the depth, and a spatial finite range R. Note that in the Hamiltonian above we have kept the BCS interaction between atoms of different species only. It can be shown that the Hartree and Fock terms, in the ground state, do not modify the essential physics of the crossover transition, not only in the contact interaction but for the finite-range interaction case as well [32].
, that represents the depth, and a spatial finite range R. Note that in the Hamiltonian above we have kept the BCS interaction between atoms of different species only. It can be shown that the Hartree and Fock terms, in the ground state, do not modify the essential physics of the crossover transition, not only in the contact interaction but for the finite-range interaction case as well [32].
The finite-range potentials here studied are a square-well 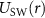 , typically used as a first approach to model interatomic interactions [20], a purely decaying exponential
, typically used as a first approach to model interatomic interactions [20], a purely decaying exponential  , a classic nuclear model [44], the Yukawa potential [45] representing a screened Coulomb interaction, and a van der Waals tail potential
, a classic nuclear model [44], the Yukawa potential [45] representing a screened Coulomb interaction, and a van der Waals tail potential 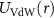 , a realistic attractive common atomic interaction at large distances [23] but, for simplicity in our calculations, assumed it constant at short distances. These are given by the following expressions,
, a realistic attractive common atomic interaction at large distances [23] but, for simplicity in our calculations, assumed it constant at short distances. These are given by the following expressions,




We mention here that the Fourier transforms of these models have an analytic expression, useful for our treatment below.
Performing the standard variational procedure in the grand potential function 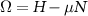 with the BCS ansatz
with the BCS ansatz 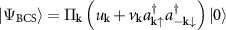 one obtains the coefficients
one obtains the coefficients  and
and 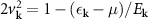 , where
, where  [23, 24]. The energy gap
[23, 24]. The energy gap  and chemical potential µ satisfy the usual coupled equations [35],
and chemical potential µ satisfy the usual coupled equations [35],


with N the total number of particles. Because of the s-wave symmetry the dependence of 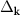 on k is on its magnitude k only and, certainly, on the potential parameters V0 and R. It is very important to emphasize here that for finite-range potentials equation (6a
) for the gap
on k is on its magnitude k only and, certainly, on the potential parameters V0 and R. It is very important to emphasize here that for finite-range potentials equation (6a
) for the gap  does not require the standard renormalization procedure, necessary in the case of the contact interaction approximation, to warrant convergence [23, 24]. In fact, such a divergence is an artifact associated with the contact approximation itself [46]. Once equations (6a
) and (6b
) are solved, one can calculate the functions
does not require the standard renormalization procedure, necessary in the case of the contact interaction approximation, to warrant convergence [23, 24]. In fact, such a divergence is an artifact associated with the contact approximation itself [46]. Once equations (6a
) and (6b
) are solved, one can calculate the functions  and
and  on which the correlation functions are expressed.
on which the correlation functions are expressed.
As broadly established in the literature of ultracold Fermi gases, the BEC-BCS crossover is generally analyzed in terms of the s-wave scattering length a, being the effective potential amplitude, as established by the contact interaction. Experimentally, the scattering length can be modulated by an external magnetic field, coupled in a Zeeman fashion to the spin degrees of freedom. This allows for tuning the value of a from the extreme attractive regime 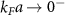 , where a BCS state of Cooper pairs develops, to the repulsive region
, where a BCS state of Cooper pairs develops, to the repulsive region  , where Bose bound pair or molecules are formed; here,
, where Bose bound pair or molecules are formed; here,  is the Fermi momentum. At the crossover the bound state appears due to a Feshbach resonance where the scattering length diverges and changes sign [20, 21, 23]. In contrast to the contact interaction, the expressions for the finite-range potentials here considered do not depend explicitly on a. This, however, is not an obstacle to investigate the mean-field many-body physics in terms of such a length. The key aspect is to have a relationship of a in terms of the potential parameters V0 and R in order to reveal the presence of bound states or dissociated pairs. In some cases, we may have an analytic expression of a as a function of V0 and R, but in general, we can find such a relationship by numerically solving the two-body Schrödinger equation in the low-energy limit [47]. We make this correspondence for the proposed interaction potentials in order to investigate the correlations along the BEC-BCS crossover, in terms of a. Based on the results of [32, 48], in this article we consider a representative value for the interatomic potential ranges
is the Fermi momentum. At the crossover the bound state appears due to a Feshbach resonance where the scattering length diverges and changes sign [20, 21, 23]. In contrast to the contact interaction, the expressions for the finite-range potentials here considered do not depend explicitly on a. This, however, is not an obstacle to investigate the mean-field many-body physics in terms of such a length. The key aspect is to have a relationship of a in terms of the potential parameters V0 and R in order to reveal the presence of bound states or dissociated pairs. In some cases, we may have an analytic expression of a as a function of V0 and R, but in general, we can find such a relationship by numerically solving the two-body Schrödinger equation in the low-energy limit [47]. We make this correspondence for the proposed interaction potentials in order to investigate the correlations along the BEC-BCS crossover, in terms of a. Based on the results of [32, 48], in this article we consider a representative value for the interatomic potential ranges  . This choice is consistent with the hypothesis of a weakly interacting gas in the dilute regime. As we show in appendix
. This choice is consistent with the hypothesis of a weakly interacting gas in the dilute regime. As we show in appendix  as functions of k and chemical potential for each potential, as functions of the wavevector k and of the scattering length a.
as functions of k and chemical potential for each potential, as functions of the wavevector k and of the scattering length a.
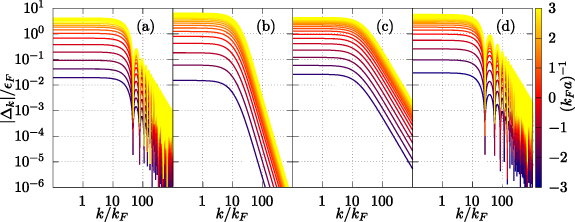
Figure 1. Dimensionless gaps 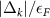 , scaled with the Fermi energy
, scaled with the Fermi energy 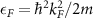 , for the (a) square well, (b) exponential, (c) Yukawa, and (d) van der Waals potentials. Each line corresponds to different values of the s-wave scattering length a with a fixed range
, for the (a) square well, (b) exponential, (c) Yukawa, and (d) van der Waals potentials. Each line corresponds to different values of the s-wave scattering length a with a fixed range 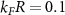 . Both axes have a logarithmic scale. The sharp oscillations of the gap in (a) and (d) are due to the discontinuity of the potential at r = R, see equations (2) and (5).
. Both axes have a logarithmic scale. The sharp oscillations of the gap in (a) and (d) are due to the discontinuity of the potential at r = R, see equations (2) and (5).
Download figure:
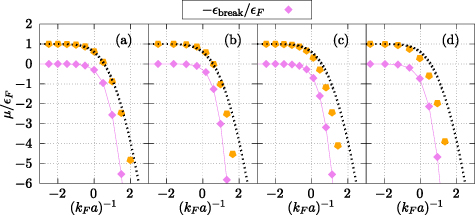
Standard image High-resolution imageFigure 2. Chemical potentials scaled with the Fermi energy  , shown with (orange) pentagons, for the (a) square well, (b) exponential, (c) Yukawa, and (d) van der Waals potentials. As in figure 1 the potential radius is fixed
, shown with (orange) pentagons, for the (a) square well, (b) exponential, (c) Yukawa, and (d) van der Waals potentials. As in figure 1 the potential radius is fixed 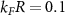 . For comparison, in each panel the dotted line corresponds to the values of the chemical potential of the contact interaction. The (pink) diamonds joined with a line correspond to the threshold energy
. For comparison, in each panel the dotted line corresponds to the values of the chemical potential of the contact interaction. The (pink) diamonds joined with a line correspond to the threshold energy 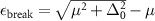 , as amply discussed in the text.
, as amply discussed in the text.
Download figure:
Standard image High-resolution imageLet us comment on the behavior of the gaps  for the different potentials under consideration, shown in figure 1. In every case the maximum value of the gap is at k = 0 in any region of the crossover, namely, for any value of a. In agreement with the inclusion of finite-range interactions, the gaps have a power law decay for large wave vectors k (high-energy behavior), which we further comment below and in appendix
for the different potentials under consideration, shown in figure 1. In every case the maximum value of the gap is at k = 0 in any region of the crossover, namely, for any value of a. In agreement with the inclusion of finite-range interactions, the gaps have a power law decay for large wave vectors k (high-energy behavior), which we further comment below and in appendix  . Therefore, as expected, in the appropriate limit where the potential range vanishes, the gap becomes a constant for all values of k, and the contact interaction case is recovered. The decreasing behavior of
. Therefore, as expected, in the appropriate limit where the potential range vanishes, the gap becomes a constant for all values of k, and the contact interaction case is recovered. The decreasing behavior of 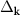 for large k renders the gap equation (6a
) convergent without the need of a renormalization procedure. One can observe that for the square well and van der Waals potentials, panels (a) and (d) of figure 1, the gaps exhibit oscillations for large values of k, which arise as a result of the discontinuity of the respective potential radius R. As this discontinuity of the potentials is situated at short distances, it influences the large-wave-vector regime with an oscillatory behavior. In appendix
for large k renders the gap equation (6a
) convergent without the need of a renormalization procedure. One can observe that for the square well and van der Waals potentials, panels (a) and (d) of figure 1, the gaps exhibit oscillations for large values of k, which arise as a result of the discontinuity of the respective potential radius R. As this discontinuity of the potentials is situated at short distances, it influences the large-wave-vector regime with an oscillatory behavior. In appendix 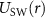 and
and  oscillate with a functional form given by
oscillate with a functional form given by 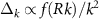 with f an oscillatory function different for each potential. For the exponential potential we have found analytically
with f an oscillatory function different for each potential. For the exponential potential we have found analytically  , while for the Yukawa potential
, while for the Yukawa potential 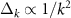 . These high-energy asymptotic behaviors may provide physical insight for BEC-BCS crossover of nucleons because, although more complex than those here, finite-range potentials are required to model the interactions between nucleons. The advantage of the model potentials we are addressing is that the gap equation can be written in terms of analytic kernels that allow for faster and more precise calculations, as has been reported in previous works [32, 46]. In contrast, more complicated potentials have to be approximated by separable forms in the gap equation, see for instance [49]. We expect the features reported here may aid in performing numerical calculations for more complicated potentials.
. These high-energy asymptotic behaviors may provide physical insight for BEC-BCS crossover of nucleons because, although more complex than those here, finite-range potentials are required to model the interactions between nucleons. The advantage of the model potentials we are addressing is that the gap equation can be written in terms of analytic kernels that allow for faster and more precise calculations, as has been reported in previous works [32, 46]. In contrast, more complicated potentials have to be approximated by separable forms in the gap equation, see for instance [49]. We expect the features reported here may aid in performing numerical calculations for more complicated potentials.
As shown in figure 2, the chemical potentials for the different potentials are qualitatively similar. The main difference arises on the BEC side, where the formation of molecules depends strongly on the features of the potential. For example, the chemical potential of the van der Waals potential, figure 2(d) becomes negative faster when 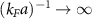 . However, on the BCS side, the values of the chemical potentials are very similar, being close to the Fermi energy εF
, in accordance with a weakly interacting Fermi gas.
. However, on the BCS side, the values of the chemical potentials are very similar, being close to the Fermi energy εF
, in accordance with a weakly interacting Fermi gas.
3. Correlation functions and the spatial structure of the gas mixture
To investigate the spatial large-distance behavior of the correlation functions for the finite-range potentials here considered, see equations (2)–(5), we recall that the density–density correlation functions are defined as [23, 25],

whereas stated above, σ and  identify different hyperfine spin states. The density operator for the spin component σ is given by
identify different hyperfine spin states. The density operator for the spin component σ is given by 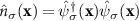 , where
, where  are the usual field operators of a uniform gas. For a balanced mixture the condition of equal population
are the usual field operators of a uniform gas. For a balanced mixture the condition of equal population 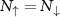 implies
implies 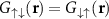 and
and  .
.
It can be straightforwardly shown that the correlation function for antiparallel spins is [20, 23, 25],

where,

And, correspondingly, the correlation function for parallel spins is given by,

where

An associated quantity in the BCS theory is the Cooper pairs wavefunction [35]

As we will illustrate below, the Cooper-pair density probability distribution  shares the same asymptotic features of the correlation functions.
shares the same asymptotic features of the correlation functions.
As stated above, we first numerically solve simultaneously the gap and number equations (6a
) and (6b
) to obtain 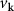 and
and  . Then, by numerical Fourier transforms, we calculate the correlation functions
. Then, by numerical Fourier transforms, we calculate the correlation functions 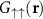 ,
,  and the density pair probability
and the density pair probability 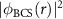 . This is a technically difficult task, specially for finding their asymptotic behavior for long distances
. This is a technically difficult task, specially for finding their asymptotic behavior for long distances 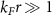 . While in the deep BCS and BEC regimes,
. While in the deep BCS and BEC regimes,  , the numerical convergence does not allow to make definite conclusions, fortunately the best fittings can be found for values near unitarity, namely
, the numerical convergence does not allow to make definite conclusions, fortunately the best fittings can be found for values near unitarity, namely 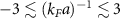 , which covers experimentally accessible values [19, 20, 23, 42]. Figure 3 show a fragment of the above functions as functions of r for the indicated values of
, which covers experimentally accessible values [19, 20, 23, 42]. Figure 3 show a fragment of the above functions as functions of r for the indicated values of 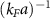 . We note that there are quite regular oscillations and, for long distances, an exponential envelope. Although below we present precise fittings of these curves, one can readily seen that in BCS the density fluctuations have a very long range, becoming quite short at BEC, with a smooth crossover.
. We note that there are quite regular oscillations and, for long distances, an exponential envelope. Although below we present precise fittings of these curves, one can readily seen that in BCS the density fluctuations have a very long range, becoming quite short at BEC, with a smooth crossover.
Figure 3. Segments of two-body distributions. Correlation functions (a) 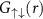 , (b)
, (b) 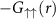 ; and (c) pair wave probability function
; and (c) pair wave probability function  . First row corresponds to square well
. First row corresponds to square well 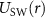 ; second to exponential
; second to exponential  ; third Yukawa
; third Yukawa 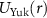 ; and fourth van der Waals
; and fourth van der Waals 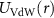 . In each plot the density (colors) indicate the value of the scattering length. The upper dark curves correspond to the BCS limit, while the lower light (yellow) curves to the BEC limit. The functions have an arbitrary normalization, and the vertical axes have a logarithmic scale.
. In each plot the density (colors) indicate the value of the scattering length. The upper dark curves correspond to the BCS limit, while the lower light (yellow) curves to the BEC limit. The functions have an arbitrary normalization, and the vertical axes have a logarithmic scale.
Download figure:
Standard image High-resolution imageFigures 4 and 5 are the main result of this article, from which we reach the following conclusion: the correlation functions and the pair probability distribution, for large distances  , can be accurately cast, as suggested above from figure 3, as distributions of the form
, can be accurately cast, as suggested above from figure 3, as distributions of the form
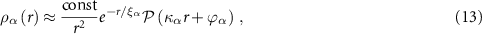
where  and
and  a periodic function to be determined and which, in principle, depends on the particular model potential. In figure 4 we show fittings of ξα
, for
a periodic function to be determined and which, in principle, depends on the particular model potential. In figure 4 we show fittings of ξα
, for 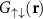 in (blue) squares,
in (blue) squares,  in (green) triangles and
in (green) triangles and 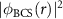 in (red) asterisks, for the four finite-range potentials considered. These fittings are obtained as the numerical slopes of the envelopes of the corresponding functions shown in figure 3. On the other hand, the solid (purple) line is the function, or correlation length
in (red) asterisks, for the four finite-range potentials considered. These fittings are obtained as the numerical slopes of the envelopes of the corresponding functions shown in figure 3. On the other hand, the solid (purple) line is the function, or correlation length  ,
,

with

and where µ is the chemical potential and Δ0 the value of the gap at k = 0, for the corresponding value of  for each potential. These values of µ and Δ0 are obtained from the curves in figures 1 and 2 and, as also shown in 2, we can observe the behavior of εbreak along the crossover, for all four finite-range potentials analyzed. In the BCS extreme
for each potential. These values of µ and Δ0 are obtained from the curves in figures 1 and 2 and, as also shown in 2, we can observe the behavior of εbreak along the crossover, for all four finite-range potentials analyzed. In the BCS extreme  , indicating in turn that
, indicating in turn that  as expected, since in such a limit the BCS state of Cooper pairs tends to the free Fermi gas, whose density correlations show Fermi oscillations and an algebraic decay only [1, 19]. In the far side of BEC one obtains the opposite, namely,
as expected, since in such a limit the BCS state of Cooper pairs tends to the free Fermi gas, whose density correlations show Fermi oscillations and an algebraic decay only [1, 19]. In the far side of BEC one obtains the opposite, namely,  and
and  , again as expected since the formation of tight pairs effectively decorrelate spin of opposite pairs, and the delta-correlation term dominates in the correlation function of same spin species, see (10), indicating a diluted very weakly interacting Bose gas of molecules. We note that the indicated limits are just asymptotic, as εbreak and
, again as expected since the formation of tight pairs effectively decorrelate spin of opposite pairs, and the delta-correlation term dominates in the correlation function of same spin species, see (10), indicating a diluted very weakly interacting Bose gas of molecules. We note that the indicated limits are just asymptotic, as εbreak and 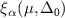 are always finite.
are always finite.
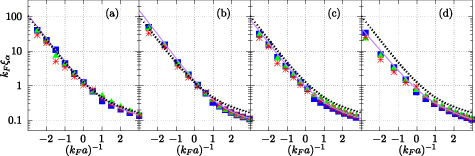
Figure 4. Large-distance correlation lengths ξα
for (a) square well, (b) exponential, (c) Yukawa, and (d) Van der Waals interatomic potentials, as functions of the scattering length a, with kF
the Fermi momentum. In each panel, squares (blue) correspond to the antiparallel spins correlation function  , triangles (green) to the parallel spins correlation function
, triangles (green) to the parallel spins correlation function  , and asterisks (red) to the pair probability distribution function
, and asterisks (red) to the pair probability distribution function 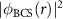 ; see text. The solid line (purple) is the length associated with the correlation length
; see text. The solid line (purple) is the length associated with the correlation length  with εbreak given in (15). In each panel the dotted (black) line corresponds to the contact interaction potential [25, 29].
with εbreak given in (15). In each panel the dotted (black) line corresponds to the contact interaction potential [25, 29].
Download figure:
Standard image High-resolution imageFigure 5. Wave vectors κα for the (a) square well, (b) exponential, (c) Yukawa, and (d) van der Waals potentials. Symbols are the same as in figure 4. The dotted (black) line corresponds to the contact potential case reported in [25].
Download figure:
Standard image High-resolution imageThe agreement, between the predicted function 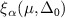 and the numerical asymptotic fittings of ξα
, is excellent for all potentials, for all distribution functions and for all calculated values of the scattering length. We thus claim that the dependence of the correlation length ξα
on the thermodynamic quantities µ and Δ0, as given by (13) and (14), is universal. Hereafter we shall drop the index α of ξ in (14). In the same figures 4 and 5, with dotted (black) lines, we also show the calculated correlation length corresponding to the contact potential in 3D. The behavior is similar and the values of ξ are similar because of the small value of the interaction range R used. For larger values of the R, while the agreement of the fitted correlation length with the calculated length remains very close, the deviation from the contact interaction is evident. See appendix
and the numerical asymptotic fittings of ξα
, is excellent for all potentials, for all distribution functions and for all calculated values of the scattering length. We thus claim that the dependence of the correlation length ξα
on the thermodynamic quantities µ and Δ0, as given by (13) and (14), is universal. Hereafter we shall drop the index α of ξ in (14). In the same figures 4 and 5, with dotted (black) lines, we also show the calculated correlation length corresponding to the contact potential in 3D. The behavior is similar and the values of ξ are similar because of the small value of the interaction range R used. For larger values of the R, while the agreement of the fitted correlation length with the calculated length remains very close, the deviation from the contact interaction is evident. See appendix  .
.
It is important to point out that the insight to find (14) as value of the correlation length was suggested from the corresponding analysis of the correlation functions and pair probability distribution with the contact potential in 3D [25] and 2D [26]. It was analytically found that the correlation length of all those quantities is indeed given by expressions (14) and (15), but with the value of the gap Δ independent of k, as occurs in such an approximation. In particular, for the contact potential in 2D there are only two characteristic lengths, the inverse of the usual Fermi momentum kF and the correlation length ξ; this may be due to the peculiar scale invariance of the contact potential in 2D [26]. We also mention that this result has also been found in [29] studying correlations at finite temperature, for the contact interaction as well. Thus, based on these previous results we searched for a similar fitting, finding that the gap in (15) must be evaluated at zero momentum for finite range interactions. It is relevant to recall that characteristic lengths of the correlation functions, as well as the Cooper pair-size have certainly been the subject of several studies, see [22, 50–53].
It remains now to envision the meaning of the characteristic energy εbreak, and its associated length ξ as the correlation length. The energy εbreak has already been identified in two instances as a minimum threshold energy to break a pair and, therefore, its associated length ξ is the largest and dominant corresponding length, thus overwhelming any other pair breaking energy length. Thus, the correlation length is the largest at which the BCS state sustains the spatial structure of pairs, being large Cooper pairs at the BCS regime or very tight bound pairs at the BEC extreme. The simplicity of the mean-field approach indicates that the density-density correlation length is the same as the pair size given by the pair probability distribution function.
One of the two cases where εbreak has been determined to be a minimum threshold to break pairs is the analysis by Ketterle et al [20, 42] in studies with RF spectroscopy; and the other by Combescot et al [43] within their determination of collective dynamical excitations in the BCS model. In the first case, it was found that εbreak is the threshold dissociation energy to break a pair when, in addition to the balanced two-component mixture with  and
and 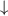 spins, a third hyperfine spin state is used to capture the energy from a pair in the BCS state when it dissociates. It is important to stress that this third state has experimental relevance since typically a radio frequency signal with a definite magnitude, arising from the transition to such an additional state, confirms the identity of the pairs along the crossover. The energy difference for an excitation minus the energy associated with the third hyperfine state ε3 may be generally written as [40, 42],
spins, a third hyperfine spin state is used to capture the energy from a pair in the BCS state when it dissociates. It is important to stress that this third state has experimental relevance since typically a radio frequency signal with a definite magnitude, arising from the transition to such an additional state, confirms the identity of the pairs along the crossover. The energy difference for an excitation minus the energy associated with the third hyperfine state ε3 may be generally written as [40, 42],
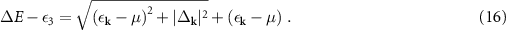
Then, one can readily find that the minimum value for the pair dissociation is found at  , see figure 1, thus yielding εbreak as expressed in (15). It is evident that this derivation is independent of the interaction potential used and, for sure, whether is of finite range or of contact nature. However, the values of the gap
, see figure 1, thus yielding εbreak as expressed in (15). It is evident that this derivation is independent of the interaction potential used and, for sure, whether is of finite range or of contact nature. However, the values of the gap 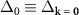 at zero momentum and the chemical potential µ do certainly depend on the details of the interaction potential.
at zero momentum and the chemical potential µ do certainly depend on the details of the interaction potential.
In the other instance, as discussed in [43] and [54], the energy εbreak also arises within the two-component mixture when analyzing the dispersion relation of collective modes of the BCS dynamics, in the contact potential approximation. In particular, in determining the critical velocity vc
using Landau's criterion, one must first find the minimum value of  , with
, with  the dispersion relation of excitations at momentum q, namely,
the dispersion relation of excitations at momentum q, namely, ![$v_c = \textrm{min}[\omega(q)/q]$](https://content.cld.iop.org/journals/1367-2630/25/11/113019/revision2/njpad0854ieqn95.gif) . It is found that the lower energy boundary for the pair-breaking continuum into the creation of two single-particle excitation is precisely εbreak, for all values of the scattering length. However, in determining the superfluid critical velocity, one must also take into account the equilibrium collective excitations, being Bogoliubov modes in the BEC side [43] and Anderson–Bogoliubov excitations in the BCS extreme [55]. Recalling that the speed of sound cs
can be calculated within the BCS model as
. It is found that the lower energy boundary for the pair-breaking continuum into the creation of two single-particle excitation is precisely εbreak, for all values of the scattering length. However, in determining the superfluid critical velocity, one must also take into account the equilibrium collective excitations, being Bogoliubov modes in the BEC side [43] and Anderson–Bogoliubov excitations in the BCS extreme [55]. Recalling that the speed of sound cs
can be calculated within the BCS model as  , the conclusion is that the superfluid critical velocity is,
, the conclusion is that the superfluid critical velocity is,

Using BCS theory one can verify [43] that in the BCS side, indeed, the critical velocity is given by εbreak but, in the BEC extreme, Bogoliubov modes take over and superfluidity is lost before pairs are broken. In any case, in the thermodynamic T = 0 state, εbreak remains as the threshold energy for pair-breaking along the whole crossover.
The additional universal feature exhibited by the two-body distributions is the oscillatory behavior at large distances, as specified in equation (13). In figure 5 we plot the fitting of the large-distance wave vector oscillations κα
, along the crossover, as a function of  . For any given value of the scattering length, and for each interatomic potential, the three functions
. For any given value of the scattering length, and for each interatomic potential, the three functions  ,
,  and
and  oscillate with the same wavelength. For this quantity, although we do not have a function that fits it, we find the general conclusion that on the BCS side the wave vector tends to the Fermi momentum, as expected,
oscillate with the same wavelength. For this quantity, although we do not have a function that fits it, we find the general conclusion that on the BCS side the wave vector tends to the Fermi momentum, as expected, 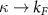 , then it falls down to zero towards the BEC side. As can be seen in figure 5, we were not able to fit the oscillations on the BEC side since they are severely arrested by the rapidly falling correlation length. As a reference, the contact interaction case do explicitly shows that the wavelength of the oscillations grows with no bound as
, then it falls down to zero towards the BEC side. As can be seen in figure 5, we were not able to fit the oscillations on the BEC side since they are severely arrested by the rapidly falling correlation length. As a reference, the contact interaction case do explicitly shows that the wavelength of the oscillations grows with no bound as 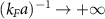 . This oscillatory behavior can be identified with the many-body configuration [56]. In the BCS limit the wave vector is similar to the Fermi wave number, in agreement with the weakly interacting regime [1, 25]. In the BEC limit the wave vector decreases allowing the pair wave function and the opposite spins correlation function to converge to a bound state distribution. As can be numerically determined from figure 3, the correlation functions
. This oscillatory behavior can be identified with the many-body configuration [56]. In the BCS limit the wave vector is similar to the Fermi wave number, in agreement with the weakly interacting regime [1, 25]. In the BEC limit the wave vector decreases allowing the pair wave function and the opposite spins correlation function to converge to a bound state distribution. As can be numerically determined from figure 3, the correlation functions  and
and 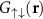 oscillate out of phase, just as in the contact interaction case [25], indicating the already identified nested structure of the different spin species, as statistically observed from any atom.
oscillate out of phase, just as in the contact interaction case [25], indicating the already identified nested structure of the different spin species, as statistically observed from any atom.
4. Final remarks
We have analyzed the density–density correlation functions for equal and different spin components, for a balanced mixture of fermions in two spin states, at T = 0 and within the mean-field BCS theory. In addition, we have also examined the pair probability distribution function. These three distribution functions can be expressed in terms of the BCS wavefunction variational parameters 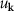 and
and  , that determine essentially all the statistical properties of the equilibrium many-body ground state, including the thermodynamic properties and the correlation functions here studied. This simplicity is certainly a consequence of the present being a mean-field theory. Furthermore, although it requires careful numerical evaluations, one can extend the theory from the use of a contact potential to interatomic potentials with finite range. Besides allowing for more realistic inclusion of interatomic potentials, these do not have the unnecessary renormalization artifacts of the contact interaction. And, as we have shown here, one can tune the interatomic potential parameters and map the results in terms of the scattering length of the corresponding binary collisions, allowing for exploring the physics at hand along the full BEC-BCS crossover.
, that determine essentially all the statistical properties of the equilibrium many-body ground state, including the thermodynamic properties and the correlation functions here studied. This simplicity is certainly a consequence of the present being a mean-field theory. Furthermore, although it requires careful numerical evaluations, one can extend the theory from the use of a contact potential to interatomic potentials with finite range. Besides allowing for more realistic inclusion of interatomic potentials, these do not have the unnecessary renormalization artifacts of the contact interaction. And, as we have shown here, one can tune the interatomic potential parameters and map the results in terms of the scattering length of the corresponding binary collisions, allowing for exploring the physics at hand along the full BEC-BCS crossover.
Our contribution here, by means of four exemplifying interatomic potentials, is that the long distance behavior of the density correlation functions and the pair probability distribution are given by an oscillatory function, times an algebraic  , accompanied with an exponentially decaying function. The corresponding oscillatory wavenumber κ and the correlation length ξ are found to be the same for the three distributions and, more importantly, expressed in terms of universal functions of thermodynamic quantities, the chemical potential µ and the zero-momentum energy gap Δ0. At this value of the momentum the gap takes its maximum value, which is what it would take in the limit of the contact interaction. The main finding of our study, following the insight gained by analyzing the contact potential, is the unambiguous identification of the energy scale
, accompanied with an exponentially decaying function. The corresponding oscillatory wavenumber κ and the correlation length ξ are found to be the same for the three distributions and, more importantly, expressed in terms of universal functions of thermodynamic quantities, the chemical potential µ and the zero-momentum energy gap Δ0. At this value of the momentum the gap takes its maximum value, which is what it would take in the limit of the contact interaction. The main finding of our study, following the insight gained by analyzing the contact potential, is the unambiguous identification of the energy scale 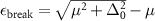 that, in turn, determines the correlation length
that, in turn, determines the correlation length 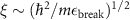 . This energy scale has previously been found to be the minimum threshold to break a pair, either from a spectroscopic excitation perspective [20, 42], or from the dispersion relation of collective modes in the BCS dynamics [43]. As this threshold energy is a minimum, the corresponding length scale ξ is a maximum, indicating that it is the largest length of the excitations that characterizes the equilibrium density fluctuations. This length, being a consequence of many-body effects is indeed independent of the interaction details.
. This energy scale has previously been found to be the minimum threshold to break a pair, either from a spectroscopic excitation perspective [20, 42], or from the dispersion relation of collective modes in the BCS dynamics [43]. As this threshold energy is a minimum, the corresponding length scale ξ is a maximum, indicating that it is the largest length of the excitations that characterizes the equilibrium density fluctuations. This length, being a consequence of many-body effects is indeed independent of the interaction details.
While the present results appear to be of relevance for the understanding of the spatial structure of an ultracold gas mixture of fermionic pairs, and for the full elucidation of the consequences of BCS theory as well, we should insist that these are predictions of a mean-field theory. In particular, since correlations depend on, at least, two-body density matrices, extensions beyond mean-field may alter the obtained universal relationships found here. Thus, the findings of this article may motivate both, further theoretical efforts using Green functions techniques for instance [23, 24], and experiments for measuring structure factors [40] to verify whether the asymptotic behavior of correlation function remains similar for different atomic systems or not.
Analyzing finite range interactions is of relevance since, while indeed, the BEC-BCS crossover has been identified in several systems, mostly in ultracold atomic clouds [23, 24, 57–60], in some others the effective interaction is fixed and the crossover is tuned by means of the density [23, 24, 28, 38, 61] and, while the strength of the interaction is still characterized by the s-wave scattering length, it has been observed that next leading-order contributions, such as the effective range, are important for the density-induced BEC-BCS crossover, even at the mean-field level [28, 38, 62]. At any rate, the main requirement is the use of a finite-range interaction, a feature of the present study, and which has been known to pose a very difficult problem for solving the gap equation [62].
To conclude, we would like to point out that several analysis of superfluidity in nucleon–nucleon mixtures have been addressed within a mean-field approach of the BEC-BCS crossover where the structure of the potentials has also to be taken into account [23, 63]. While those potentials are more complicated than the ones considered in this work, requiring special functional forms [23], some of those potentials are similar to the Yukawa potential of equation (4). We believe our results provide physical insight about the formation of pairing with finite-range interactions. However, for nucleon–nucleon interactions, the high-energy regime is influenced by a more complicated structure of finite-range interactions and, also, the free dispersion relation at high energies should be modified [63].
Acknowledgments
This work was partially funded by Grants IN108620 and IN117623 DGAPA (UNAM). G A D C and J C O J acknowledge CONAHCYT-Mexico for a scholarship.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Appendix A: High-energy behavior of the gaps
In [32, 46] the gap equation was expressed in terms of kernels,
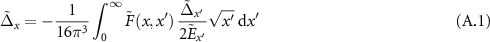
where 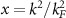 ,
,  ,
, 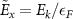 and
and 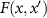 is the kernel. It is difficult to find the closed-form expression for the kernel given an arbitrary potential. Notwithstanding, in such a case an easier computation of the gap can be achieved [32, 46]. From equation (A.1), it can be noticed that the high-energy behavior of the gap
is the kernel. It is difficult to find the closed-form expression for the kernel given an arbitrary potential. Notwithstanding, in such a case an easier computation of the gap can be achieved [32, 46]. From equation (A.1), it can be noticed that the high-energy behavior of the gap 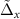 can be extracted focusing on the functional dependence of the kernels. Then we can show explicitly the power-law decay for the gaps of the square-well, exponential potential, and Yukawa potential.
can be extracted focusing on the functional dependence of the kernels. Then we can show explicitly the power-law decay for the gaps of the square-well, exponential potential, and Yukawa potential.
The corresponding kernels for each potential are the following:
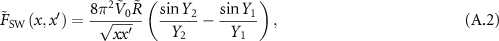
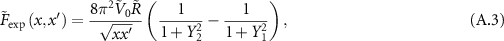
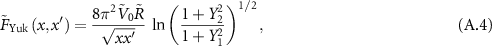
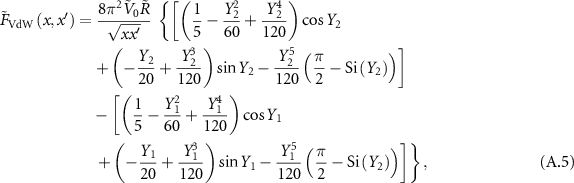
where 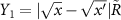 and
and 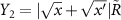 , and we are using the sine integral,
, and we are using the sine integral,

The range of the potentials are scaled with the Fermi wave number  , and the depth of the potentials are determined by
, and the depth of the potentials are determined by 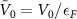 .
.
The high-energy behavior can be extracted taking the limit 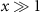 , such that the region where
, such that the region where 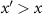 has a negligible contribution due to the decay of the factor
has a negligible contribution due to the decay of the factor 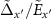 . For the square-well we have
. For the square-well we have
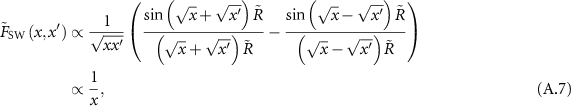
where first we removed the absolute values, since 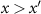 , then we added the fractions, and lastly we identify the power-law decay. For the exponential potential we can approximate
, then we added the fractions, and lastly we identify the power-law decay. For the exponential potential we can approximate
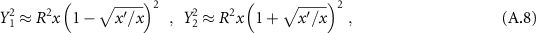
then, we can approximate
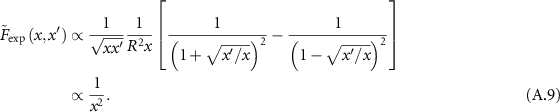
For the Yukawa potential we can approximate the argument of the logarithm in a similar way as with the previous kernels,

leading to

And for the van der Waals potential we fitted the envelopes of the gaps shown in figure 1(d), finding

Appendix B: Correlation length of the square well with 
Similar calculations can be performed for different potential ranges. Qualitatively, as we have commented above, the chemical potential and gaps have similar behaviors. Nevertheless, the features are modified by the details of the potential. For the square well  we show in figure B1 numerical calculations of the gaps
we show in figure B1 numerical calculations of the gaps  , chemical potentials µ and large-distance correlation lengths
, chemical potentials µ and large-distance correlation lengths 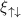 ,
,  , ξBCS. Comparing with figure 1(a) it can be noticed that the region where the gap is constant around k = 0 decreases with an increase of the range R. Also, we can see a change in the oscillations of the gap, which are also modulated by R. As commented above, in the large wave vector regime the gap of the square well has a functional form of
, ξBCS. Comparing with figure 1(a) it can be noticed that the region where the gap is constant around k = 0 decreases with an increase of the range R. Also, we can see a change in the oscillations of the gap, which are also modulated by R. As commented above, in the large wave vector regime the gap of the square well has a functional form of 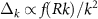 .
.
Figure B1. Numerical calculations of the gap (a), the chemical potential (b), and the large-distance correlation lengths for the square well 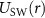 with a fixed range
with a fixed range  . In (a) each line corresponds to a different value of the scattering length
. In (a) each line corresponds to a different value of the scattering length 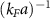 , which can be compared with figure 1(a). The chemical potentials in (b) are shown with (orange) pentagons. For comparison the dotted line corresponds to the contact interaction case, and the (pink) diamonds joined with a line are the threshold energy εbreak. The large distance correlation lengths in (c) are of
, which can be compared with figure 1(a). The chemical potentials in (b) are shown with (orange) pentagons. For comparison the dotted line corresponds to the contact interaction case, and the (pink) diamonds joined with a line are the threshold energy εbreak. The large distance correlation lengths in (c) are of  in (blue) squares, of
in (blue) squares, of 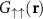 in (green) triangles, and of
in (green) triangles, and of  in (red) asterisks. The (purple) solid line is the theoretical
in (red) asterisks. The (purple) solid line is the theoretical  . The (black) dotted line is the large-distance correlation length for the contact interaction.
. The (black) dotted line is the large-distance correlation length for the contact interaction.
Download figure:
Standard image High-resolution imageThe large-distance correlation length  gets modified numerically by the details of the potential. In figure B1(c) it can be seen that on the BCS side ξ increases with the range of the potential, while on the BEC side ξ decreases faster due to the presence of a bound state in the two-body potential.
gets modified numerically by the details of the potential. In figure B1(c) it can be seen that on the BCS side ξ increases with the range of the potential, while on the BEC side ξ decreases faster due to the presence of a bound state in the two-body potential.