Abstract
We study the main intra-band and inter-band transport properties at zero temperature of free electron-like system undergoing a topological reconstruction of the Fermi surface for the two-dimensional and three-dimensional case. The calculated intra-band properties include the single-particle density of states, the total and the effective concentrations of electrons and the thermopower. As for the inter-band case, the real part of the conductivity has been calculated within the vanishing inter-band relaxation approximation as a function of the incident photon energy. Within this approach, it is shown that the optical conductivity has a nonvanishing component parallel to the reconstruction wave vector and the shape which depends on the value of the Fermi energy. Each dimensionality has its particular features in the transport quantities presented in the paper, which are discussed and compared with those in the free electron scenario. Finally, we identify the signature of the topological reconstruction of the Fermi surface in the intra-band and inter-band transport functions.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The central goal of this paper is to identify signatures of the topological reconstruction of the Fermi surface in the static and dynamic electronic response functions in the free electron-like two-dimensional (2D) and three-dimensional (3D) systems. These response functions are easily experimentally accessible. They are: the effective concentration of the intra-band charge carriers which defines the Drude weight, the thermoelectric power known as the Seebeck coefficient and the optical conductivity, namely its real part. The emergence of the quantum phase transition associated with the topological reconstruction of the Fermi surface is predicted in the 2D and 3D nearly free electron gas systems [1–3]. In the mentioned works it is shown that periodic, self-consistent perturbation of the nearly free electron system, such as a charge density wave for example, can decrease the total energy of the system thus making it unstable with respect to its formation. It is based on the fact that energy of the electron band is decreased if initially closed Fermi surfaces are related, by the self-consistent wave vector, in the way to reconstruct and undergo a topological change into an open one. In that process, two peculiar so-called 'Lifshitz points' are created in the band structure below and above the initial Fermi energy respectfully: a hyperbolic point below and an elliptic point above. The presence of the hyperbolic point in electron spectrum leads to density of states with the van Hove singularity below the initial Fermi energy and a pseudo-gap (i.e. significantly reduced electron density of states around the Fermi level) between the two 'Lifshitz points', accommodating the electrons at lower energies in turn stabilizing the charge density wave phase. Here we mention a few notable examples of systems whose ground state is well enough approximated by the free electron dispersion.
In the 2D case the recently proposed layered heterostructure LiBN [4–7] has a single parabolic conduction band. The effective mass, the Fermi energy EF and correspondingly Fermi wave vector kF depend on the type of the alkali metal and on its concentration relative to the underlying BN hexagonal net. Another way of changing the Fermi energy is by the electrostatic doping [8] to which majority of the 2D materials are susceptible. Furthermore, the real materials exhibiting the topological reconstruction of the Fermi surface, due to the spontaneous stabilization of the charge density wave ground state, are mostly effectively 2D systems such as the high-Tc superconducting cuprates [9], or certain intercalated graphite compounds [10].
Contrary to 2D, a possible 3D system with parabolic electron dispersion for the reconstruction to take place is hard to find. As it was shown [1–3], a necessary condition on the wave vector of reconstruction, relating the Fermi surfaces, is that it should be close to the integer multiple of 2kF. In the 3D metals the Fermi energy is changed by impurity doping. This in turn could invoke the nontrivial effects, leading to the conduction band renormalisation near the Fermi energy.
In order to find the signature of the topological reconstruction of the Fermi surface in the electronic transport experiments, we proceed as follows: first we define an auxiliary system which comprises of a free electron gas in the presence of a weak periodic crystal potential. This procedure is well know from the elementary solid state physics textbooks [11] and in the vicinity of a single Bragg plane it gives a two-band description of the electronic system. For simplicity we adopt the simplest approximation where such a periodic potential has only one Fourier component. In the case of the uniaxial charge/spin density wave this approximation is exact. Hence, the resulting two-band ground state develops a pseudo-gap thus defining boundary of the new Brillouin zone which now resembles the infinitely long stripe (2D), or a cylinder (3D). Also, we can shift the Fermi energy relatively to the centre of the pseudo-gap and calculate the effect of this shifting on the transport response functions which, to the knowledge of the authors, is not present in the literature. Finally, the mechanism of topological reconstruction by the density wave is revised trough the minimization of the total electronic energy by formation of the self-consistent periodic potential. A correspondence is then made between crystal and self-consistent periodic potential, whose wave vector (which also determines the Brillouin zone) is locked to the Fermi wave vector. This makes our starting problem, topologically reconstructed electron gas, just a special case of the auxiliary model of free electrons in the weak perturbing potential.
The paper is outlined as follows:
In section 2 we define the Hamiltonian along with the electron energies which are written in dimensionless units defined on the cylinder-like Brillouin zone. In sections 3 and 4 the single-particle density of state (DOS) is calculated for 2D and 3D case. Certain DOS features are to some extend visible in the effective concentration of electrons and in the Seebeck coefficient. Both quantities are calculated at near zero temperature and compared to the well-known free electron gas results. The real part of the optical conductivity is calculated using the Kubo formula in section 5. We define and evaluate the inter-band current matrix element whose only non-vanishing component is the one parallel to the wave vector of the density wave. The closed form of the optical conductivity is found and its dependence on Fermi energy and dimensionality of the system analyzed in details. Finally, the particular case of the phase with the topologically reconstructed Fermi surface is addressed.
2. Two-band Hamiltonian
The mathematical framework of this section does not depend on the system dimensionality. The generic mean-field Hamiltonian describes the free electron gas in the presence of the self-consistent, uniaxial reconstruction potential with amplitude Δ and spatial modulation vector Q
The electron dispersions have a parabolic shape ɛk = ck2 where c = ℏ2/2m, k is electron wave vector, m is the electron effective mass, while the second part in equation (2.1) is the coupling of electrons to the self-consistent reconstruction potential. Writing the Hamiltonian equation (2.1) in its matrix form in the basis of and states
we notice the resemblance to the Hamiltonian matrix found in the problem of determining the electron energies in the presence of a weak periodic crystal potential in the vicinity of a single Bragg's plane [11]. In that textbook example the crystal potential is assumed to have only a single Fourier component with the spatially-dependent form 2Δ cos(r ⋅ Q). Q is the smallest reciprocal lattice vector.
The diagonalisation of equation (2.1) is straightforward using the Bogoliubov unitary transformation UHU−1 = E, where E is the diagonal eigenvalue matrix and U is [12]
The auxiliary angle ϑk is a function of the Hamiltonian matrix elements in equation (2.1)
Utilizing equations (2.3) and (2.2) in the above-described way, the Bloch energies are obtained. They are defined within the Brillouin zone with the periodicity determined by Q and are labelled by index s ∈ {+, −}
To make the mathematical treatment as simple as possible, three modifications are done in electron dispersion equation (2.5).
First, k is defined relatively to Q. This way the Bloch wave vector may be decomposed as k = k⊥ + k∥ with respect to the Q direction.
Further, the origin of the newly-formed Brillouin zone is shifted by k → k + Q/2. That way the point of the band splitting shifts to the origin of Brillouin zone. Implementing these two changes in equation (2.5) we get
The final modifications defines the dimensionless variables, i.e. κ = 2k/Q, and scaling the energies equation (2.6) to ɛQ ,
which are shown in figure 1. The energy scale ɛQ = c(Q/2)2 in equation (2.7) is associated with the bare electronic energy at the Bragg's plane prior to the pseudo-gap opening. The dimensionless parameter η = Δ/ɛQ is a measure of the strength of the perturbating potential. In the general perturbative crystal potential approach, as well as in the case of the topological reconstruction, we expect η ≪ 1.
Figure 1. (a) The Fermi surface for increasing values of the scaled Fermi energy ωF. The blue and the red line correspond to the s = − and s = + band equation (2.7) respectively. In sub-figure 1 ωF is just above ωB, in 2 ωF = ωL, in 3 ωF = ωU, in 4 ωF is just above ωU, in 5 ωF is inbetween ωT and ωU and in 6 ωF is just below ωT. (b) Schematic depiction of the Brillouin zone in dimensionless units of κ after the reconstruction by a periodic potential. The zone is bounded in the κ∥ direction and unbounded in the κ⊥ direction. (c) The bands equation (2.7) along the direction of κ are shown in (b) with four characteristic energy values marked by the green circles.
Download figure:
Standard image High-resolution imageThe Brillouin zone, over which equation (2.7) is spanned, resembles an infinitely long cylinder in κ⊥ ∈ [−∞, ∞] direction of total width κ∥ ∈ [−1, 1]. In the forthcoming calculation, there are four energy constants which are linked to the bands equation (2.7), of particular importance.
The bottom (B) energy of the s = − band and the top (T) energy of the s = + band within the κ⊥ = 0 cross section of the Brillouin zone are located at the κ∥ = 1 (see figure 1)
Also, the values at the centre of the Brillouin zone (the pseudo-gap region) κ = 0 are important. We label them by indices L and U depending on their value
being the elliptic point in the upper and saddle point in the lower band, named the upper and the lower 'Lifshitz point' respectively [13]. So, the maximal vertical energy difference between the two bands is
while, correspondingly, the width of the pseudo-gap is
All the transport properties including the DOS to which we shall refer to in the next section, will be the piecewise functions of energy on the intervals defined by equations (2.8)–(2.11).
3. Density of states
Here we calculate the single-particle DOS per unit volume for the 2D (d = 2) and 3D (d = 3) case. The mathematical procedure outlined in this section is used throughout the rest of the paper and is presented in detail in appendix
with the bands given by equation (2.5). Changing the sum in equation (3.1) to an integral over κ and introducing the scaled energy ω = E/ɛQ , as defined in the previous section, we get
The dimensionality d enters explicitly in equation (3.2) in the prefactors, giving a correct unit of the d-dependent DOS, and also as a parameter in the integral over κ⊥. Also, we have exploited the fact that equation (2.7) is an even function of κ . The way to tackle the integral equation (3.2) which contains the Dirac delta function of another function g(x) is to decompose the δ-function as a sum over the roots x0
It is optimal to deal with the κ⊥ variable first. Applying the formula equation (3.3) to equation (3.2) we get
where is the real root of the argument of the delta function in equation (3.2)
The Heaviside step function Θ in equation (3.4) changes the integration limits (it is 1 for positive arguments and zero otherwise). This is equivalent to the constraint that equation (3.5) is real and within the interval . This in turn imposes restrictions on the integration boundaries of κ∥ making them (ω, s)-dependent, transforming (3.4) to
In appendix
First we calculate the DOS for the free electron bands in the 3D and 2D case. For consistency, the free electron DOS is also expressed in terms of ω and ɛQ
showing the usual constant or -dependence in 2D and 3D, respectively, as depicted in figure 2 by dashed lines. The 3D DOS equation (3.6) can be written down immediately since the integration is easily preformed giving
which is shown as red line in figure 2. Several features of this piecewise function stand out when compared to the free electron case. First, the onset of DOS is at ωB. Secondly, the emergence of the van Hove singularities at the points ωL and ωU, as well as a constant value of the DOS between them, ω ∈ (ωL, ωU), is in contrary to the overall shape as anticipated by equation (3.8). This constant value, as reported in [3], also deviating form the result stated in [11], has a profound influence on the DC transport properties as shown in the next section.
Figure 2. The density of electron states (DOS) of a reconstructed system described by the bands equation (2.7) as a function of the scaled energy ω in units of for η = 0.2. Full green and red lines represent the 2D and 3D case respectively. The dashed lines represent the 2D and 3D free electron DOS equation (3.8).
Download figure:
Standard image High-resolution imageFor the 2D case we obtain the DOS numerically by inserting the boundaries equation (3.7) and the root equation (3.5) into equation (3.6). The result is shown as a green line in figure 2. As in the previous 3D case here also we notice differences when compared with the constant DOS as predicted for the free electron model equation (3.8). The main distinction is visible for energies around the pseudo-gap region. At the energy ωL a logarithmic singularity is formed due to the saddle geometry of the band. Once the ωU is reached, DOS jumps abruptly to the free electron gas value equation (3.8) and continues so until ωT is reached.
4. Carrier concentrations and low-T thermopower
For the upcoming analysis, we regard the scaled Fermi energy ωF ≡ EF/ɛQ as a variable. The way the Fermi energy is changed is not of our primary concern, nor shall we go into the discussion about the possible influence that the doping procedure has on stability of the band structure. This provides an insight in the often-used charge transport quantities that depend not only on the value of the Fermi energy, but also on the direction of the applied external perturbation.
First we calculate the total concentration of electrons ntot as it depends on the Fermi energy. Second, the main component of the Drude weight, the effective concentration of conducting electrons nα , is calculated. The connection with the experiment here is simple since the Drude weight is measured in the reflectivity experiments (plasma edge). In a free electron-like system this concentration is trivially related with the total concentration of electrons [7], but in the system described by more 'exotic' bands like equation (2.6), the two may differ significantly as seen in graphene for example [14]. Finally, the Seebeck coefficient or thermoelectric power Sα is calculated in the T = 0 limit using the Mott formula.
4.1. Total concentration of electrons ntot
We start by writing the total zero-temperature concentration of electrons in the momentum representation,
where V is the system volume, and in the scaled energy representation,
where, in the later, the recently calculated DOS has been utilized. The , equation (4.2) is a function of scaled Fermi energy ωF and it is depicted in the figure 3 for 2D and 3D case ( because of the reasons given in the following subsection). On the same figure a d-dependent free electron value of electron concentration
is drawn by the green dashed lines.
Figure 3. Total and effective concentration of electrons in 2D and 3D case as a functions of scaled Fermi energy ωF in units of equation (4.3) for η = 0.2 and for m = me. It is shown that total concentration is equal to the perpendicular effective concentration ntot = n⊥ in both dimensionalities. On the other hand n∥ has features of its own. The free electron concentration n0 is represented by a green dashed line.
Download figure:
Standard image High-resolution imageThe common feature in both 2D and 3D is that the total concentration equation (4.2) and its free electron analog equation (4.3) are almost equal for energies in the interval (ωB, ωL). Above ωL they start to deviate, slightly more in 3D then in 2D.
4.2. Effective concentration of electrons nα
Here, the effective concentrations of electrons nα that participate in the DC transport are calculated. Index α denotes a Cartesian component with respect to the reconstruction wave vector, i.e. α ∈ (∥, ⊥), of the effective concentration. The DC conductivity is defined as σDC = e2 τnα /me where τ is the scattering relaxation time, me is a bare electron mass and the zero-temperature (T = 0) expression for nα [15] is given in two equivalent forms
The two expressions in equation (4.4) are obtainable from one another by partial integration. Here, as well, nα will be expressed in terms of the dimensionless units ωF.
The two distinct directions α ∈ (∥, ⊥) in electron dispersions equation (2.6) imply the difference between n⊥ and n∥. It is easy to check that and thus equation (4.4b) is the same as equation (4.1), , if m = me, which holds for the α = ⊥ case regardless of dimensionality d.
On the other hand, this is not so for the α = ∥ case. The second derivative of the electron dispersion equation (2.6) over k∥ is not a constant, but a rather complicated function of k∥. Since we have already presented the solution for the integrals involving the δ-function, we shall proceed by evaluating n∥ using equation (4.4a). Changing the sum into an integral over κ and introducing ω as defined in the previous section, the following result is obtained
which, after the δ-function evaluation by the same recipe from the section 3, gives
The differences between the effective and the total , concentration are shown in the figure 3. Unlike the or equivalently , is extremely susceptible to the features originating from the pseudo-gap. Several features are highlighted depending on the position of ωF. The main feature of 2D effective concentration is the 'shark fin' shape at ωF within the pseudo-gap. The logarithmic divergency in DOS at energy of the lower Lifshitz point, ωL (the saddle point in the lower band), corresponds to the inflection point in . Also, the discontinuity in the DOS generates the discontinuity in the slopes of at the energy of the higher Lifshitz point, ωU (bottom of the upper band). Above the pseudo-gap, gradually tends to equation (4.3) as ωF increases.
The features of the effective concentration in 3D system are more 'tamed' than those in 2D. Outside the pseud-gap, has roughly a -dependence as shown by equation (4.3). Within the pseudo-gap region, is a constant.
It is particularly visible on the example of this system how and differ. Although , they are both approximately by a factor of two larger then for ωF > ωL. Eventually they meet at higher values of ωF. The discrepancy is a result of an unphysically large value of η, chosen as such merely for the matter of presentation, for depiction of the two concentrations. This discrepancy also serves as a reminder to the fact that even a simple distortion like the pseudo-gap opening on the Fermi surface changes the concentration of electrons participating in the DC conductivity substantially comparing to their total number. As η is set to zero, nα and ntot naturally become equal to n0.
4.3. The Seebeck coefficient Sα
We use the well-known Mott formula for Sα [11, 16]. This formula is a result of the Sommerfeld expansion (kB T ≪ EF) of the Onsanger's transport coefficients and it reads
As noted in the in section 4.2, nα depends differently in α = ∥ and α = ⊥ case, so consequently will Sα . For comparison, the Seebeck coefficient for the 2D and 3D free electron gas is derived using equations (4.7) and (4.3). This gives simply
since, as noted before for the free electron gas, the total and the effective concentrations are equal. Expression (4.8) is shown in figure 4 as a green dashed line. The results for the Seebeck coefficient equation (4.7) with two different components α ∈ (⊥, ∥) are shown in figure 4 for the 2D and 3D case. The common characteristic for 2D and 3D case is that, for Fermi energies small compared to ωL, is equal to the free electron value equation (4.8). Also, in general, deviates weakly from the free electron result with the main differences located around and in the pseudo-gap region. on the other hand has a rich structure. For the 2D system, it has a logarithmic divergency at ωL and a discontinuity at ωU. Also, between these two points changes sign. In the 3D case manages to follow free electron result with minor deviations in the form of small spikes at ωL and ωU. On the other hand, vanishes in the pseudo-gap. This is due to the constant DOS equation (3.9) for this energy interval. In the ωF ≫ ωL limit, as well as for η → 0, Sα (ωF) → S0(ωF), ∀ α, both in the 2D and 3D case.
Figure 4. Direction-dependent Seebeck coefficient, S∥ and S⊥, as a function of scaled Fermi energy ωF for the 2D and 3D system described by equation (2.7) in units of for η = 0.2 and m = me. The free electron gas value S0 equation (4.8) is presented by the green dashed line.
Download figure:
Standard image High-resolution image5. Optical conductivity
Here we calculate the zero-temperature optical response of the electron system described by equation (2.1) in 2D and 3D case. The calculation consists of defining the optical conductivity tensor within the two-band picture in the limit of vanishing inter-band relaxation and with the current matrix elements derived from the Hamiltonian equation (2.1). We shall see that shape of the real part of the optical conductivity strongly depends on the values of the scaled Fermi energy ωF, and weakly on the dimensionality d of the system.
5.1. Optical conductivity Kubo formula
In the two-band model the complex inter-band conductivity tensor is defined [17] as a function of the incident photon energy
where α is index of the Cartesian component of the inter-band conductivity tensor. The only α-dependent part in the conductivity formula equation (5.1) is the inter-band current matrix element . These elements are part of the diagonalized current matrix defined as a unitary transformation of the Hamiltonian equation (2.2) matrix derivative
with the unitary matrix U given by equation (2.3). In the expression equation (5.1) Γ is a small phenomenological relaxation parameter and in the limit Γ → 0 the real part of the conductivity tensor for the incident photon energies reduces to
Once the elements equation (5.2) are derived we can use equation (5.3) for further analytical derivation.
5.2. Optical conductivity of 2D and 3D system
We begin by evaluating the inter-band current element. Inserting the unitary matrix elements equation (2.3) and the derivatives of the Hamiltonian (2.2) in equation (5.2) we get
The only non-vanishing component in the derivative of the free electron dispersion (section 2) in the above expression is α = ∥. Therefore, the optical conductivity in the presented model has only the α = ∥ component. Written in terms of dimensionless variables κ and η the inter-band current element is
We shall omit the label ∥ when addressing the real part of the optical conductivity which we calculate by inserting the equation (5.5) into equation (5.3) and changing the sum to an integral over the dimensionless variable κ within the limits given in section 2. As a general result for dimensionality d we find
In writing the above integral we have used the T = 0 Fermi–Dirac distribution function f(Eκ ) = Θ(EF − Eκ ). Also, in the above expression, the scaled dimensionless variable for the incident photon energy, , is introduced alongside the conductivity constant σ0 = e2/4ℏ.
In equation (5.6) the variable κ∥ is used for decomposing the δ-function over its roots. According to the procedure from section 3
where . The initial restriction κ∥ ∈ [0, 1] limits the range of Ω to
and so does the interval on which Re σ(d)(Ω) is defined. The effect, that the restriction equation (5.8) has on Re σ(d)(Ω), can be summarized to Re σ(d)(Ω) ∝ Θ(Ω − Ωmin)Θ(Ωmax − Ω). Limits in equation (5.8) are thus easily identified. The lower value, Ωmin, is the minimum vertical spacing between the valence and conduction band and is equal to the pseudo-gap width (see figures 1(c) and 5(a) and equation (2.8). The larger value, Ωmax, is the maximum distance from the bottom of the valence to the top of the conduction band (see figures 1(c) and 5(a) and equation (2.9)).
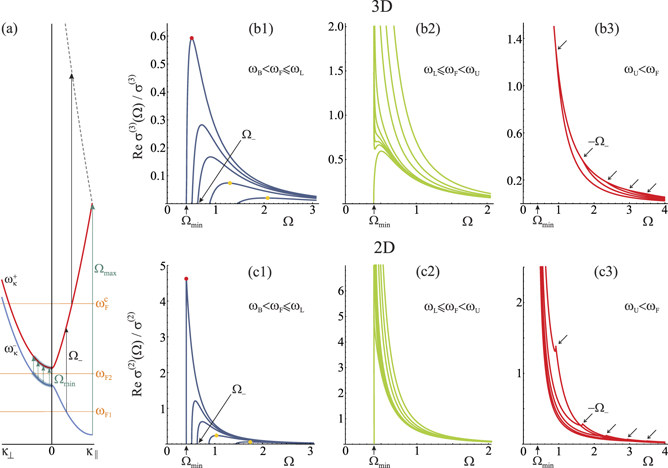
Figure 5. (a) Schematic view of the characteristic regions for optical excitations with respect to the band structure. The position of several characteristic Fermi energies ωF is shown in orange alongside with Ωmin, Ωmax and a optical threshold energy Ω− with respect to ωF1. The thick line segments on the bands around indicate filled and empty states that are shifted with respect to one another by the energy Ωmin. A hypothetical third band is shown as a dotted line together with the critical . Gray thick lines and arrows on the bands around ωF2 indicate states excited from the to band by a constant energy Ωmin leading to the divergent optical response. (b1)–(c3) Re σ(d)(Ω) plotted for several values of ωF within the three intervals as described in the main text. The conductivity is given in units of σ(d) with parameter η = 0.2 defining the position of Ωmin as indicated by an arrow. The characteristic points such as the onset of optical excitation at Ω−, the positions of maxima (at energy Ω0) and the kinks position at −Ω− are indicated on the figures by dots or arrows. For comparison, both 3D and 2D Re σ(d)(Ω) are plotted for the same values of ωF belonging to the one of three intervals as noted in figures. In (b1) and (c1) Re σ(d)(Ω) is plotted for ωF = 0.4, 0.6, 0.7, 0.75, 0.8. In (b2) and (c2) Re σ(d)(Ω) is plotted for ωF = 0.8001, 0.805, 0.807, 0.81, 0.815, 0.83, 0.9, 1, 1.2. In (b3) and (c3) Re σ(d)(Ω) is plotted for ωF = 1.5, 2, 2.5, 3, 3.5.
Download figure:
Standard image High-resolution imageInserting the δ-function equation (5.7) back into equation (5.6) and changing in the electron energies in arguments of the Θ-functions, we have
The Θ-functions within the integral in equation (5.9) are finite (equal to 1) only if their arguments are positive. We exploit that by introducing the auxiliary function
so we can factorise the arguments of the Θ-functions in equation (5.9) as
In equation (5.11) it states: if (R± is not real), then the argument of the Θ-function on the left-hand side of equation (5.11) is zero since κ⊥ > 0 and the Θ-function vanishes, as does the entire equation (5.9). If (R± is real), the argument of the Θ-function on the left-hand side of equation (5.11) is positive and can be written as a product of monomials. Since R± + κ⊥ > 0, it does not influence the value of the Θ-function, leaving effectively the result in equation (5.11). Thus, from equation (5.11) we see that the Θ-function influences only the upper limit of integration
Whether equation (5.10) is real or not and consequently equation (5.12) finite or zero, depends on the value of Ω and ωF. Of course, the allowed values of Ω should fall within the limits set by equation (5.8). With a modest effort in determining the sign of the sub-root functions in equation (5.10), the following conclusions can be made for each integral in equation (5.12) separately.
R− is real (the sub-root function equation (5.10) is positive) and hence the first integral in the curly brackets in equation (5.12) is finite for Ω within the interval
where
Also, comparing equations (5.14) and (5.8) we conclude
and Ω+ > Ωmax.
On the other hand, R+ is real (the sub-root function equation (5.10) is positive) and hence the second integral in the curly brackets in equation (5.12) is finite for Ω in the interval
From equation (5.14) we see that regardless of ωF, −Ω+ < Ωmin, while −Ω− > Ωmin if ωF > 1 + η.
When collected, the conditions and restrictions (5.13)–(5.16) are best expressed by the aid of the step function Θ. Defining a d-dependent constant of conductivity as
we arrive to the final expression for the real part of the d-dimensional optical conductivity
There are two main features in equation (5.18). The first one is the prefactor which, regardless of d, has a strong Ω−3-dependency. The second one is the part within the square brackets. Besides on Ω, it is also depends on d and ωF. To fully understand how Re σ(d)(Ω) evolves with ωF we analyze each dimensionality separately.
5.3. 3D optical conductivity features
Here we describe the 3D Ω-dependent conductivity Re σ(d)(Ω) as it depends on ωF.
Case ωF ⩽ ωL:
In figure 5(b1) Re σ(3)(Ω) is shown for several values of ωF bounded by condition ωF ⩽ ωL. The onset of the inter-band excitation begins at Ω− equation (5.3), indicated by an arrow in figure 5(b1) for a specific value of ωF = 0.7, and ends at Ωmax. Ω− is the vertical distance between the bands as shown schematically in figure 5(a). In this range of ωF values, Re σ(3)(Ω) is a humped curve expanding toward Ωmin, with increasing amplitude and spiking as ωF → ωL. For small enough ωF, the position of maximum is roughly estimated to be at
represented by orange dots in figure 5(b1). Equation (5.19) was obtained under the assumption Ω− ≫ Ωmin. Clearly this breaks as we approach ωF → ωL.
There is a steep linear dependence for photon energies just above the onset of inter-band excitations at Ω− (figure 5(b1)). The steepness increases as ωF → ωL. Finally, for ωF = ωL equation (5.18) reduces to
for energies Ω just above Ω− = Ωmin. At the particular value, ωF = ωL, we can analytically find the position of the maximum which is located at , clearly above the threshold energy Ωmin with the peak height of , depicted by the red circle in figure 5(b1). The square-root in for ωF = ωL has its origin in the shape of DOS below ωL and above ωU which has a square-root dependence (see equation (3.9) and figure (2)).
Case ωL ⩽ ωF ⩽ ωU:
For ωF slightly above ωL, two features take place in Re σ(3)(Ω). The first one is a one over a square-root divergency for Ω ⪆ Ωmin, which quickly falls off to the second feature, which is a residuum of the hump shown in figure 5(b2). As ωF increases and enters into the pseudo-gap, the hump in Re σ(3)(Ω) shifts to the left and eventually disappears leaving only a one over square-root singularity which is present for all ωF > ωL. The origin of the divergency can be easily traced from the figure 5(a) where it is shown that the upper the lower bands are parallel in κ⊥ direction, shifted by the amount Ωmin. Once the Fermi energy ωF is slightly larger than ωL (ωF2 in figure 5(a)), a finite amount of states determined by κ∥ = 0 is excited across the pseudo-gap by the photon energy of Ω = Ωmin, producing a divergent optical response. Overally, for ωF well within a pseudo-gap, the optical conductivity behaves roughly as Ω−3 over the entire interval between the points Ωmin and Ωmax, as it is shown in figure 5(b2) for several values of the ωL < ωF < ωU.
Case ωF > ωU:
In this case an additional feature appears in the optical conductivity as can been seen from figure 5(b3) plotted for several values of ωF. Now, −Ω−, which is positive equation (5.16), is the limiting value, dividing the two different Ω-dependencies which arise due to the square brackets in equation (5.18). The rough dependence on Ω can be summarized as:
In figure 5(b3) a kink in Re σ(3)(−Ω−) is indicated by an arrow. As ωF is further increased, the kink travels to the right.
5.4. 2D optical conductivity features
Similar considerations apply for the 2D optical conductivity.
Case ωF < ωL:
The 2D optical conductivity which is shown in figure 5(c1) for several values of ωF, has an onset of inter-band excitations at Ω−. Re σ(2)(Ω) is humped-like curve with a bit more pronounced amplitude then its 3D analog. The conductivity curve expands toward Ωmin, with increasing amplitude and spikes as ωF → ωL. Again, for ωF ≪ ωL, which implies Ω− ≫ Ωmin, the position of maximum is roughly estimated to be at
denoted by the orange circles in figure 5(c1). In the 2D case there is a square-root dependence for photon energies just above the onset of the inter-band excitation at Ω− as shown in figure 5(c1). The amplitude of the square-root increases as ωF → ωL. Finally, for ωF = ωL, equation (5.18) reduces to the simple approximate expression
valid for energies Ω not much larger than Ωmin. For this particular value of Fermi energy, the spike of the optical conductivity is finite, located at Ω0 = Ωmin, and has a height of (red dot in figure 5(c1)).
Although a singularity in the DOS is located at ωL (see figure 2), it does not imply the divergency of the optical conductivity as shown in figure 5(c1). The reason is the so-called 'bottle-neck' effect that the upper band creates with its parabolic bottom and a constant DOS (figures (1) and (2)) at energy ωU. There is an infinite number of electron states at ωL ready to be excited across the pseudo-gap to ωU. However, at ωU there is only a finite number of states to accept those electrons. This is the origin of a finite point-like dependence of optical conductivity equation (5.20) at photon energy Ω = Ωmin.
Case ωL ⩽ ωF ⩽ ωU:
As in the 3D case, here we also find a one over square-root divergency for Ω ⪆ Ωmin and ωF slightly above ωL. However, unlike in the 3D case, there is no hump present. As ωF increases into the pseudo-gap, the square-root divergency is more and more pronounced. This also has its roots in the existence of a finite segment of the band that can be excited (vertically) to band along the κ⊥ direction at energy Ωmin. The higher the value of ωF, the larger is the segment and so is the amplitude of the square-root divergency (figure 5(a)). The optical conductivity is shown in figure 5(c2) for several values of ωL < ωF < ωU. Overally, for ωF well within the pseudo-gap, the optical response behaves roughly as Ω−3 along the entire interval between the points Ωmin and Ωmax.
Case ωF > ωU:
Here also, as it was in the 3D case, −Ω− is the limiting value dividing the two different Ω-dependencies which arise due to the expression within the square brackets in equation (5.18) (see figure 5(c3). They are approximately given by
Comparing expressions equations (5.21) and (5.24) we can see that the overall frequency dependence is universal in 2D and 3D. At the particular point, Re σ(2)(−Ω−) has a small spike at energy −Ω−, as pointed by an arrow in figure 5(c3). As ωF is further increased, the kink (spike) travels to the right, while the overall conductivity curve moves to the left. This movement of the curve to the left is in contrast to the 3D case where the optical conductivity curve tends to move to the right as ωF is increased (see figures 5(c3) and (b3)).
5.5. Validity of the two-band model in the calculation of optical response
The optical excitations in the two-band model are limited by the minimal Ωmin and maximal Ωmax value of the incoming photon. Ωmax, which is equal to ωT, corresponds to the excitation as shown in figure 5(a). The question arises to which value of the Fermi energy, call it the critical Fermi energy , can we fill the second band so that electron excited from hits the hypothetical third band (dashed line in figure 5(a)) when absorbing the photon with the highest allowed energy Ωmax? Once being above the energy , the two-band description of the optical conductivity is not sufficient and the third band has to be included into the consideration when calculating σ(d)(Ω).
This scenario is relevant under the assumption that higher Fourier components of the crystal potential are finite. This also implies that the inter-band current matrix elements equation (5.5) between the second and the third band are finite, allowing the single-particle optical transitions.
The numerical estimate for can be done easily by taking the non-perturbative free electron dispersion of the third band ɛk−2Q , shift it and express it in dimensionless units as described in section 2 to get ω κ . Then we search for the wave vector κ for which . Neglecting η and any other equivalent gap parameter in this procedure we obtain κ ≈ 1 − ωT/8. This in turn gives
where we have taken ωT ≈ 4. Thus the result is that the optical response of the two-band model, as presented in section 5.2, is correct for the Fermi energy within the interval . For , a third band has to be taken into account for calculating the optical conductivity.
6. Signatures of the topologically reconstructed Fermi surface
In order to understand the signature of the Fermi surface reconstruction 'seen' by the optical probe, let us briefly summarize the onset of this process in physical systems. The systems that spontaneously undergo the topological reconstruction of its Fermi surface do so by lowering the total energy with respect to the initial system without reconstruction. Usually, the spontaneous self-consistent periodic potential, that initiates the reconstruction, is some form of the density wave (charge or spin). Here, mainly two scenarios can take place: (1) the 'nesting scenario' in which parts of the Fermi surface, with special open topology, get mapped to each other by a single wave vector, fully (or to the great extent) gaping the Fermi surface thus causing the corresponding density wave instability [18]; (2) the 'touching scenario' in which the closed Fermi surfaces very slightly overlap each other leading to the formation of the pseudo-gap which lowers the band energy as predicted and well described in references [1, 3]. It is also worth mentioning the type of topological reconstruction of the Fermi surface triggered (due to some external influence such as pressure) by the inter-band instability of the initial system, consisting of distant parabolic valence and conduction band, in which the latter are related by a finite wave vector and reconstructed in the way to form the self-consistent 'exciton band' which in turn lowers the overall energy of the system [19].
In this work we analyse the optical response within the intra-band 'touching scenario'. Any scenario of electron-driven instability is closely related to the Fermi wave vector, which, in turn, determines the wave vector of the density wave. It turns out that in such systems reconstruction of the Fermi surface takes place in such a way that the optimal Fermi energy 'falls' in the pseudo-gap, i.e. ωF ∈ {ωL, ωU}, between lower and upper Lifshitz point (closer to the upper one at ωU). Therefore, to change the Fermi energy significantly for the sake of optical probing does not seem to be feasible since it would compromise the stability of the system presented as such in this work. Nevertheless, in real systems it can be changed to some extent. The reason why is the crystal lattice potential (for simplicity not considered within the model under consideration). It permits the reconstruction with the wave vector which does not deviate from commensurability with the (reciprocal) crystal lattice to the great extent (see the charge ordering in the high-Tc superconducting cuprates for example [9]). In that sense we may say that the density wave ordering with reasonably small adjustments of the Fermi energy, small compared to η, are protected by the crystal symmetry.
Concerning the intra-band transport, which is a good probe once we can change the Fermi energy, the intra-band coefficients calculated in this paper are therefore evaluated only at one particular value of the Fermi energy, or its close vicinity. However, combining the knowledge about the Drude weight, which is finite, and Seebeck which is either zero (3D), or negative (2D), some information about the reconstructed phase can be obtained.
Optical probe may give a better insight. As noted in the last section, we are interested in the shape of the optical conductivity when the Fermi energy lies inside the pseudo-gap, exactly given by equation (5.18). Analysing the experimentally measured optical conductivity results, a hump-like feature, such as in figures 5(b1) and (c1), or a kink-like one in figures 5(b3) and (c3), indicate that ωF lies outside the pseudo-gap and hence we are not dealing with the topologically reconstructed Fermi surface.
Finally it is worth mentioning that, although there are some similarities in the shape of the inter-band conductivity (see figure 5) with the inter-band conductivity of the 1D density wave condensate with finite and infinite mass reported in [20], the process studied in this paper is of entirely different nature. In the afore-mentioned paper the density wave contribution to the conductivity is studied in the fully gapped 1D Fröhlich system, while in this work we deal with the 2D/3D mostly metallic system in the pseudo-gap regime.
7. Conclusions
In this paper we calculate the main zero-temperature intra-band charge transport coefficients and the real part of the (inter-band) optical conductivity for the 2D and 3D metallic system in which initially closed Fermi surface of the parabolic one-electron band undergoes the topological reconstruction into an open one. The topological reconstruction of the Fermi surface presumably takes place due to the instability of the initial electron band, with electron–phonon or electron–electron interaction, with respect to the spontaneous formation of the charge density wave with such a wave vector that relates the initial Fermi surfaces within so-called 'touching scenario' resulting in formation of the saddle point in the lower and elliptical point in the upper newly formed electron band dispersion, and opening of a pseudo-gap in electron spectrum between them. In turn, the total energy of electron band is lowered, consequently stabilizing the density wave if the coupling constant of interaction is large enough [1–3]. Such a scenario may explain an onset of the charge density wave ground state accompanied with such a reconstruction of the Fermi surface, for example in the high-Tc superconducting cuprates [9], or certain intercalated graphite compounds [10].
In order to track a signature of the specific reconstruction of the Fermi surface experimentally (for example the absence of the Hall effect in the 2D net of the closed Fermi surfaces reconstructed by a biaxial charge density wave as predicted in [21]), we calculate the above-mentioned transport properties adopting, in this work, the two-band model. Obtained quantities are complementary to the data obtained from the nowadays mostly used techniques such as ARPES for example [22]. The electron density of states after the Fermi surface reconstruction, clearly exhibiting the pseudo-gap with logarithmic van Hove singularity in the 2D and Heaviside step discontinuity in the 3D system at the energy of the saddle point in the spectrum, has a profound impact on the calculated transport properties: the effective concentration of carriers taking part in electric conductivity, the Seebeck coefficient and the real part of the optical conductivity.
In terms of the Cartesian components with respect to the reconstruction wave vector, the perpendicular effective number of carriers shows no significant change, with respect to the total concentration of electrons, in both 2D and 3D case. The effective number of carriers addresses the problem of effective electron mass in the band reconstructions process, i.e. passing through the pseudo-gap as the Fermi energy is changed. On the other hand, the parallel component shows significant deviations form the total concentration in terms of reduction of concentration of electrons, more pronounced in 2D than in 3D, especially in the region of the pseudo-gap. The signatures of the band reconstruction are even more striking in thermopower. The perpendicular component of the Seebeck coefficient, similar to the effective electron concentration, does not show the significant deviation from the free electron value as the Fermi energy is changed. However, the parallel component attains negative value along the pseudo-gap, with large spikes at the energies of saddle point and elliptical point in electron band, in the 2D case, while in the 3D case the parallel Seebeck coefficient is zero, indicating the absence of corresponding thermopower for Fermi energies within the pseudo-gap.
The real part of the optical conductivity, within the framework of vanishing inter-band relaxation approximation, is presented in the closed form as a function of an incident photon energy and position of the Fermi energy for 2D and 3D system. We present all relevant features of the optical conductivity with respect to characteristic energies: minimal and maximal single-electron energy, and energies of saddle and elliptical points in the reconstructed electron band (so-called lower and upper Lifshitz points between which the pseudo-gap is spanned). For the Fermi energy within the interval below the lower Lifshitz point, optical conductivity is a finite hump-like curve in both 2D and 3D system. However, for the Fermi energy within the interval above the lower Lifshitz point, the optical conductivity attains a one over square root energy dependence for the incident photon energies above the pseudo-gap threshold (width of the pseudo-gap), also in both 2D and 3D system. Specificity of the 2D system is seen from comparison of the electron DOS and optical conductivity, where we see that the divergency in DOS does not imply the divergency in optical conductivity due to the so-called 'bottle-neck' effect (due to the logarithmic van Hove singularity there is an infinite number of electrons to be excited into the finite number of available states). Furthermore, this implies that the oversimplified expression for real part of optical conductivity, involving the joint DOS [17], is not applicable here.
Acknowledgments
This work was supported by the Croatian Science Foundation, Project IP-2016-06-2289, and by the QuantiXLie Centre of Excellence, a project cofinanced by the Croatian Government and European Union through the European Regional Development Fund—the Competitiveness and Cohesion Operational Programme (Grant KK.01.1.1.01.0004). The authors are thankful to Dr IK for the everlasting inspiration.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix A.: DOS mathematics
We explicitly solve the d = 3 case. The d = 2 follows accordingly. We investigate the s = + case first. The equation (3.4) is
where we assumed the square root is real. Hence the sub-root function has to be positive. We solve this irrational inequality under the root to determine the boundaries of κ∥ for which it holds
where
Correspondingly, the Θ-function in (A.1) can be written in a few alternative ways
The last line in equation (A.4) follows because κ∥ > 0. The necessary condition for A−(ω) to be real gives ω > 1 + η = ωU while for it to be A(ω) < 1 yields . The Θ-function (A.4) once inserted back in (A.1) change the upper limit of integration. For those ω that give A(ω) < 1, integral (A.1) becomes
while for ω > ωT it stays
Similar reasoning applies for the s = − case. Here the irrational inequality for the boundaries of κ∥ gives
Since A+(ω) > 1, ∀ ω, we focus only on A−(ω) which is A−(ω) < 1 for and ω < 1 − η = ωL. Hence using the same recipe as in equation (A.4) the Θ-function can be written as
Now, the Θ-function (A.8) changes in the integral (A.1) only the lower limit of integration. For those ω that give A−(ω) < 1, integral (A.1) becomes
while for ω > ωL it stays
Collecting the cases of different ω values alongside with the integration limits we come to equation (3.7).


























![${\left\{{\kappa }_{\perp }\right\}}_{0}\in [0,\infty ]$](https://content.cld.iop.org/journals/1367-2630/24/5/053024/revision2/njpac696dieqn6.gif)