Abstract
We develop a theory of the magnetoplasmon resonance (MPR) in two-dimensional superconductors in the fluctuating regime, where the temperature is slightly above the critical temperature of the superconducting transition. In this regime, unpaired electrons and fluctuating Cooper pairs coexist in the system and interact with each other via long-range Coulomb forces, forming a Bose–Fermi mixture. The sample is considered to be under the influence of an external time-dependent electromagnetic field with a frequency in sub-terahertz range and a permanent magnetic field. It is shown that the MPR of the system is strongly modified in the presence of superconducting fluctuations in the vicinity of the superconducting transition. In particular, the fluctuating Cooper pairs dramatically change the broadening of the MPR, which is reflected in the optical response of the system.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The pioneering work of Bardeen, Cooper and Schrieffer devoted to the theoretical explanation of the superconductivity phenomena [1] led to a sequential study of collective modes in superconductors [2–10]. It turned out that the plasmon modes are not at all affected by the transition of the material to the superconducting (SC) state since the nearly dispersionless plasmon frequency in any three-dimensional material is much larger than the SC gap. However, if the superconductor is in the peculiar fluctuating regime [11–15] at temperatures above than but close to the critical temperature of SC transition Tc, there start to emerge fluctuating Cooper pairs, but the value of the SC gap still remains zero. It seems essential to conclude, that in this situation there is no considerable influence of any SC properties on the plasma oscillations of normal electrons in the sample. Indeed, the correction to the Drude conductivity caused by the SC fluctuations, known as paraconductivity, is as a rule small [16] albeit observable [17]. However, owing to the presence of SC fluctuations, a lot of intriguing physics occurs in superconductors above Tc [18–20], and this is of great interest specially in low-dimensional [21, 22] and high Tc [23, 24] superconductors.
Experimentally, the study of plasmons is usually based on the measurement of the electromagnetic (EM) power absorption by the sample, which is proportional to the electric current in the system. It is true that the transport of normal electrons gives the dominant contribution to the EM power absorption, and the impact of the paraconductivity terms is small. However, the fluctuations might essentially influence both the position and width of the plasmon resonance of normal electrons [21]. It stems from strong interaction between normal electrons and the fluctuating Cooper pairs in the sample via the long-range Coulomb forces, which are activated while exciting the plasmons with an EM field.
The position of the plasmon resonance is also sensitive to the presence of an external magnetic field. It gives an opportunity to control the magnetoplasmon (MP) resonance (MPR) in the experiment. In this paper, we develop a theory of MPR in two-dimensional (2D) superconductors in the fluctuating regime (at temperatures 0 < T − Tc ≪ Tc). The system we study represents a single layer of a 2D material at the temperature slightly above the Tc, exposed to an electromagnetic field and an external magnetic field. Thus, the system represents a mixture of a Fermi gas of normal electrons and a Bose gas of fluctuating Cooper pairs interacting via the Coulomb forces.
Other examples of hybrid Bose–Fermi systems comprise electron gas—superconductor [25–27], exciton gas—2D electron gas (2DEG) [28–31], and exciton–polaritons in a microcavity—2DEG systems [32]. From that perspective, a superconductor in the fluctuating regime can be looked at as a hybrid Bose–Fermi system, where two gases described by different quantum statistics coexist in one (same) 2D layer, forming a Bose–Fermi mixture.
The MPR has already been studied in some hybrid systems, in particular, a system consisting of a degenerate electron gas interacting with a dipolar exciton gas in the Bose–Einstein condensate (BEC) state has been considered [33]. There, the theoretical description of excitonic BEC in the framework of the Bogoliubov model demonstrates the existence of sound-like collective modes of the BEC. The phase velocity of these modes dramatically depends on the condensate density and can strongly interact with plasmon modes of electronic subsystem. This interaction modifies the MPR of the whole system resulting in the replacement of the standard Lorenz shape of MPR by an asymmetric profile which reminds of Fano resonance [34]. Qualitatively, this behavior can be explained by a simple harmonic oscillator model. Indeed, the two oscillatory modes (plasmon oscillation of the electron density and sound-like modes of excitonic BEC) can be looked at as harmonic oscillators coupled with each other by a spring (the Coulomb force) and exposed to an external driving (EM field). One thus have all the necessary ingredients to observe the MP Fano resonance phenomenon [34].
Returning to fluctuating superconductors (where the bosonic subsystem is fluctuating Cooper pairs but not the BEC particles as in the example before), here the situation is different. The Bose gas of fluctuating Cooper pairs does not possess its own collective modes. Thus, when an external EM field excites the plasmon oscillations of normal electron gas subsystem, the Bose subsystem (SC fluctuations) does not oscillate since the plasmon phase velocity exceeds both the Fermi velocity and the phase velocity of fluctuating Cooper pairs. Therefore, the gas of SC fluctuations plays the role of viscous media for plasmon oscillations of normal electrons. It results in the appearance of frictional force acting on the plasmon harmonic oscillator. As a result, in the vicinity of the critical temperature Tc, the shape of the plasmon resonance experiences strong modification.
2. Theory
We consider a system that resembles a standard setup for the experimental investigation of the MPR phenomenon (figure 1). It consists of a 2D conducting layer covered with a metallic grating (some other possible geometries to observe the effects in question will be discussed herein below). The grating period a determines the wave vector k = 2π/a of the effective EM field. Furthermore, the system is additionally exposed to a permanent magnetic field. Magnetoplasmons have been widely studied in 2D electron systems using different methods [35–38], paving the way for variety of applications [39, 40]. To study the MPs in the presence of SC fluctuations, we will use the approach based on the analysis of the dielectric function.
Figure 1. System schematic. A two-dimensional electron gas covered by a metallic grating. The system is exposed to an EM field of light E polarized across the grating and a uniform magnetic field B.
Download figure:
Standard image High-resolution imageFor the 2D layer placed on top of the substrate at z > 0, the Poisson equation for the scalar potential ϕ(z) due to the internal induced electric field reads
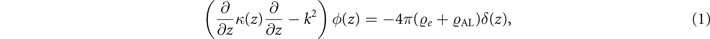
where κ is the dielectric constant, ϱe and ϱAL are the charge densities of normal electrons and fluctuating Cooper pairs in reciprocal space, respectively. We note that while solving the Poisson equation, we neglect the retardation effects. Using the solution of equation (1) and the continuity equation, we arrive at the dielectric function given by

where 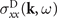 is the longitudinal part of the Drude magnetoconductivity tensor and
is the longitudinal part of the Drude magnetoconductivity tensor and 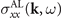 is the longitudinal part of paraconductivity or the Aslamazov–Larkin (AL) conductivity in a uniform magnetic field B. The function (2) accounts for both the spatial and temporal dispersions of the system. In general, the standard procedure to derive the dielectric function accounts for the temporal and spatial variation of normal electron (and Cooper pairs) density, which are the result of the response to external excitations [41, 42]. The optical spectra can be found from the real part of the effective longitudinal conductivity of the system, which in turn can be found from the continuity equation. However, in this work we particularly focus on the absorption spectrum, which can be inferred from the imaginary part of the plasmon dispersion. Thus, determination and analysis of this quantity will be the main aim of this work.
is the longitudinal part of paraconductivity or the Aslamazov–Larkin (AL) conductivity in a uniform magnetic field B. The function (2) accounts for both the spatial and temporal dispersions of the system. In general, the standard procedure to derive the dielectric function accounts for the temporal and spatial variation of normal electron (and Cooper pairs) density, which are the result of the response to external excitations [41, 42]. The optical spectra can be found from the real part of the effective longitudinal conductivity of the system, which in turn can be found from the continuity equation. However, in this work we particularly focus on the absorption spectrum, which can be inferred from the imaginary part of the plasmon dispersion. Thus, determination and analysis of this quantity will be the main aim of this work.
The equation which defines the dispersion of collective modes in the system reads [43–45]
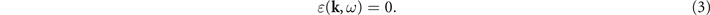
Since phase velocity of the plasmon mode is much larger than the Fermi velocity of electrons and it also exceeds the center-of-mass velocity of Cooper pairs, it allows us to neglect the spatial dispersions of both the conductivities, thus assuming k = 0 in their expressions. Then, the Drude conductivity of normal electrons takes its conventional form,
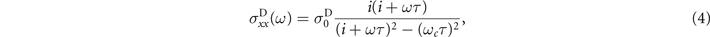
where  is the static Drude conductivity of normal electrons with e the electron charge, n the electron density, τ the scattering time, and m the effective electron mass; ωc
= eB/m is the cyclotron frequency. The experimental observation of the plasmon resonance holds under the condition ωτ ≫ 1, thus preventing the impurity-induced plasmon damping. Under this condition, the superconductor is in the clean limit, where the nonlocality effects play an essential role [46]. The general expression for paracoductivity at finite frequency, magnetic field, and non-locality corrections reads [46]
is the static Drude conductivity of normal electrons with e the electron charge, n the electron density, τ the scattering time, and m the effective electron mass; ωc
= eB/m is the cyclotron frequency. The experimental observation of the plasmon resonance holds under the condition ωτ ≫ 1, thus preventing the impurity-induced plasmon damping. Under this condition, the superconductor is in the clean limit, where the nonlocality effects play an essential role [46]. The general expression for paracoductivity at finite frequency, magnetic field, and non-locality corrections reads [46]

where 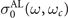 is the paraconductivity in 'local approximation', and the remaining part (the terms in square brackets) accounts for the non-local corrections.
is the paraconductivity in 'local approximation', and the remaining part (the terms in square brackets) accounts for the non-local corrections.
To find the MP dispersion in the presence of SC fluctuations, we should consider the dispersion equation (3) together with the conductivities, given by equations (4) and (5) (the renormalization of the MP dispersion in general case will be analyzed numerically below). Let us estimate here analytically the MP damping due to SC fluctuations in the limit of weak electron-impurity scattering, ωp τ ≫ 1. After some algebra, the dispersion equation (4) takes the form

where
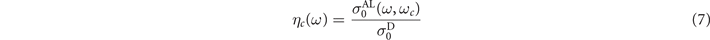
determines the strength of interaction between the normal electrons and SC fluctuations.
In the absence of SC fluctuations, ηc (ω) = 0, and equation (6) can be solved by successive approximations in the limit ωτ ≫ 1, with the result ω = ωp − i Γ, where
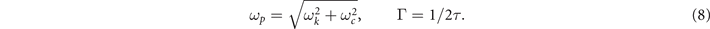
Here we introduced a bare 2D plasmon frequency

corresponding to the setup in figure 1. This holds if ωp τ ≫ 1, which is a typical condition for experimental observation of the MPR. Expression (8) shows that at vanishing magnetic fields, the MP dispersion coincides with bare 2D plasmon frequency ωk , whereas with increasing magnetic field, ωp approaches the cyclotron frequency ωc , as it is shown in figure 2.
Figure 2. MPR dispersions without the account of the SC fluctuations: normalized frequency Ω = ω/ωk
as a function of the normalized cyclotron frequency Ωc
= ωc
/ωk
. Gray dashed and red dotted lines show the asymptotic behavior 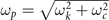 and ωp
= ωc
, respectively.
and ωp
= ωc
, respectively.
Download figure:
Standard image High-resolution imageIn the presence of SC fluctuations, the dispersion is extremely sensitive to the frequency dependence of the paraconductivity 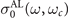 . At large frequencies, ω ≫ Tc, it rapidly decreases and the SC fluctuations produce no essential influence on the properties of plasmons. This reminds the three-dimensional case, where the SC transition does not affect the plasmon oscillations of electrons. An essential influence of SC fluctuations occurs at low frequencies when ω ≪ Tc. In this regime, the theoretical treatment can be easily performed if the paraconductivity is taken in the static limit,
. At large frequencies, ω ≫ Tc, it rapidly decreases and the SC fluctuations produce no essential influence on the properties of plasmons. This reminds the three-dimensional case, where the SC transition does not affect the plasmon oscillations of electrons. An essential influence of SC fluctuations occurs at low frequencies when ω ≪ Tc. In this regime, the theoretical treatment can be easily performed if the paraconductivity is taken in the static limit, 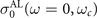 ,
,
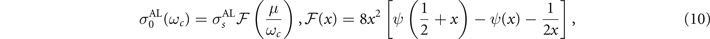
where 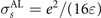 is the static AL conductivity of fluctuating Cooper pairs. In what follows, we will (naturally) assume the smallness of AL correction as compared with the static Drude conductivity,
is the static AL conductivity of fluctuating Cooper pairs. In what follows, we will (naturally) assume the smallness of AL correction as compared with the static Drude conductivity, 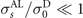 . In equation (10), μ = αTcε, where ε = (T − Tc)/Tc
is the reduced temperature, and the Ginzbug–Landau parameter α is fixed by the relation 4mαTc
ξ2 = 1. The coherence length ξ in 2D samples reads
. In equation (10), μ = αTcε, where ε = (T − Tc)/Tc
is the reduced temperature, and the Ginzbug–Landau parameter α is fixed by the relation 4mαTc
ξ2 = 1. The coherence length ξ in 2D samples reads
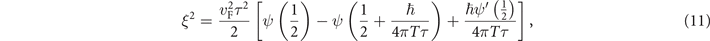
where ψ(x) is the digamma function and vF is the Fermi velocity.
Expression (6) is still exact. In the limit ωτ ≫ 1, it can also be solved by successive approximations. In the lowest order, we substitute ω = ωp in the right-hand side of this expression, and from equation (6) we again find ω = ωp − iΓ, where the MP damping reads
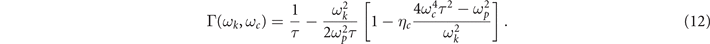
This analytical expression accounts for both the electron-impurity scattering and the influence of SC fluctuations to the MP damping (in the limit ωp τ ≫ 1). In the absence of magnetic field (ωc = 0) we find
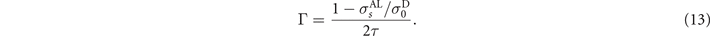
Comparing it with the dispersion of the 2D plasmon (ω = ωk
− i/2τ), we conclude that the presence of SC fluctuations results in the narrowing of the resonance since  , and thus
, and thus  in equation (13). In the case of large magnetic fields ωc
≫ ωk
, we find
in equation (13). In the case of large magnetic fields ωc
≫ ωk
, we find
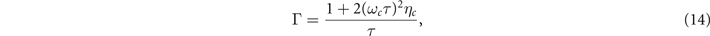
which corresponds to the broadening of the resonance in contrast with the zero-field limit. This is an interesting effect: SC fluctuations can result in both narrowing and broadening of the MPR, depending on the magnitude of the magnetic field.
It should be noted, that the function  in equation (10) is limited,
in equation (10) is limited,  . Thus, the value of ηc
is determined mainly by the prefactor
. Thus, the value of ηc
is determined mainly by the prefactor  . Despite the fact that the AL theory is applicable at
. Despite the fact that the AL theory is applicable at  , this smallness can be compensated by the 'plasmonic factor' ωc
τ ≫ 1, which linearly grows with B. Thus, strong magnetic fields may amplify the SC fluctuations contribution into the MP damping. Note also, that the absorption spectrum has a standard Lorentzian form with the width given by equation (12).
, this smallness can be compensated by the 'plasmonic factor' ωc
τ ≫ 1, which linearly grows with B. Thus, strong magnetic fields may amplify the SC fluctuations contribution into the MP damping. Note also, that the absorption spectrum has a standard Lorentzian form with the width given by equation (12).
3. Discussion
We have demonstrated that the SC fluctuations affect the plasmon resonance and produce an additional plasmon damping mechanism at low plasmon frequencies when the condition ℏω < Tc holds. Let us now discuss the possibility of experimental observation of this effect. The critical (maximal) effective frequency corresponding to Tc = 10 K is ω ∼ 1.4 × 1012 s−1. The plasmon frequencies typical for the modern semiconductor structures lie in the range 1010–1011 s−1, which falls in the range above (satisfies the condition on the critical frequency). The problem is that such 2D plasmon modes correspond to low electron densities, ∼1011 cm−2, at which the SC transition does not occur (since higher electron densities are usually required).
Indeed, the SC transition occurs at the electron densities 5 × 1013–1014 cm−2, as it has recently been shown, for example, in MoS2 monolayer structures [47, 48]. In the case of an ungated plasmon geometry, shown in figure 1, such electron densities correspond to plasmon frequencies exceeding the critical value.
One possible way to resolve this contradiction is the using of gated plasmons, when the metallic gates screen the Coulomb interaction between electrons lowering the plasmon frequency. A gated plasmon dispersion can be found from the ungated one (9), with the substitution (κ + 1)/2 → [κ1 + κ2 coth(kD)]/2 [49], such that
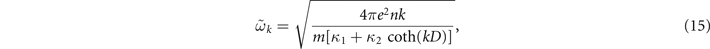
where D is the thickness of the dielectric layer, κ1 and κ2 are the dielectric constants for the substrate and the dielectric layer between the 2D electron gas and the metallic gate, correspondingly. The screening is effective in the case of thin dielectric layers, when kD ≪ 1, and thus
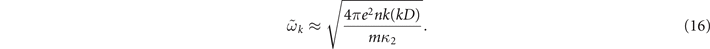
For MoS2, taking n = 1014 cm−2, m ≈ 0.5m0, kD = 10−3, k ≈ 103 cm−1 and using a dielectric layer with a relatively large dielectric constant, κ2 = 14, we can estimate 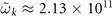 s−1 and
s−1 and 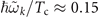 .
.
Another possibility to observe the phenomena in question is to use the proximity plasmons [50–52], which exist in 2D systems covered by the gates having more sophisticated (or complex) geometries, for instance, a strip or a disc shape. The dispersion of a proximity plasmon also behaves as 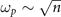 times the geometrical factor dependent on the width of the strip or the disc radius and the distance between the 2D electron gas and the gate. Then, it also becomes possible to satisfy the inequality ω < Tc by the sample design.
times the geometrical factor dependent on the width of the strip or the disc radius and the distance between the 2D electron gas and the gate. Then, it also becomes possible to satisfy the inequality ω < Tc by the sample design.
Finally, the third possibility is in using specific plasmon modes with the relativistic nature [53, 54], which may exist in the regime ωτ ≪ 1, contrast to the standard regime ωτ ≫ 1 considered here. The theory worked out in this manuscript is not directly applicable in this case since we disregard the relativistic retardation effects. However, the basic principles should remain the same.
To study the MP dispersion numerically, we took the electron densities n1 = 5 × 1013 cm−2 and n2 = 1014 cm−2, assuming the plasmon frequency is fixed by the particular geometry of the gate, and thus we took ωk = 5 × 1011 s−1.
Figure 3 shows the imaginary part of MP dispersion at different values of normal electron densities and reduced temperature, calculated numerically using equation (3). From the numerical analysis, we conclude that the effect of the presence of SC fluctuations can be neglected in the real part of the MP dispersion. Thus, we will only address the changes in the imaginary part of the MP dispersion. From figure 3 [both panels (a) and (b)], we note that the dependence of the damping on electron densities as well as temperature is strikingly different for low (inset) and high (main plot) magnetic fields. This indicates a crossover at some critical magnetic field.
Figure 3. MPR damping Im Ω = Im(ω/ωk ) as a function of the normalized cyclotron frequency Ωc = ωc /ωk . (a) The dependence of the MPR damping on the electron density: n = 5 × 1013 cm−2 (green) and 1014 cm−2 (red) at T = 10.1 K. (b) The dependence of the MPR damping on temperature: T = 10.02 K (red) and 10.9 K (green) at n = 5 × 1013 cm−2. The dashed lines in both the panels represent the dampings of the plasmons without SC fluctuations for comparison. The scattering time is τ = 5 × 10−10 s.
Download figure:
Standard image High-resolution imageFrom figure 3(a) we conclude that at low magnetic fields, the damping decreases in comparison with the bare MP damping as the normal electron density is lowered whereas at high magnetic fields it increases. At low magnetic fields, the deviation from bare MP damping is lower for electron densities near the superconducting transition.
In figure 3(b) we see that at low magnetic fields the magnitude of damping decreases as the temperature approaches the critical temperature. The deviation from the bare MP damping is more pronounced at temperatures very close to the critical temperature indicating the strong influence of SC fluctuations. This behavior is reversed at higher magnetic fields.
Overall, the behavior of the imaginary part of the renormalised MP dispersion is consistent with the theoretical predictions given by equation (12). At low magnetic fields, the term ηc
has a significant value due to the contribution of the function 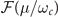 , and it dominates the nature of damping in this regime. At higher magnetic fields, the term ηc
is negligible since
, and it dominates the nature of damping in this regime. At higher magnetic fields, the term ηc
is negligible since 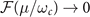 and hence, the damping in this regime shows a power–law behavior
and hence, the damping in this regime shows a power–law behavior 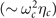 .
.
4. Conclusions
In conclusion, we studied the dielectric function of a two-dimensional material in the regime of superconducting fluctuations (in the vicinity of the transition temperature to the superconducting state from above), exposed to an electromagnetic field of sub-terahertz frequency and a constant magnetic field. We analyzed the dispersion of collective modes in the system, taking into account the interaction between the normal electrons and fluctuating Cooper pairs influenced by the magnetic field. It was shown that the width of the magnetoplasmon resonance experiences broadening and narrowing depending on the magnitude of the external magnetic field.
This paper sheds light on magnetoplasmon resonance phenomenon in two-dimensional superconductors, accounting for fluctuations. The developed theoretical approach can be especially useful in studying superconducting samples of reduced dimensionality, since the paraconductivity correction becomes more significant in low-dimensional structures [16]; it can also be employed to study multi-layer structures based on transition metal dichalcogenides or cuprates. For that, one has to modify equation (2) for the dielectric function and account for the paraconductivity term in the dielectric function for layered materials [55–57].
Acknowledgments
We acknowledge the support by the Institute for Basic Science in Korea (Project No. IBS-R024-D1), the Russian Foundation for Basic Research (Project No. 18-29-20033), and the Ministry of Science and Higher Education of the Russian Federation (Project FSUN-2020-0004).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).







