Photoionization of nS and nD Rydberg atoms of Rb and Cs from the near-infrared to the ultraviolet spectral region

Photoionization (PI), or the photoelectric effect, of atoms is one of the longest-studied processes in atomic physics, dating back to at least the Bohr model [1]. Because the outermost electron(s) of Rydberg atoms lie at high energy levels, the minimum photon energy required for Rydberg-atom PI typically is in the millieV regime. Hence, the spectral range of the ionizing radiation ranges from THz fields through the infrared (IR), visible and ultraviolet (UV) spectral regions and higher. Rydberg atoms are known to be extremely sensitive to PI by black-body radiation, a consequence of their extended electronic wavefunctions and large transition electric-dipole moments [2, 3]. Generally, as the photon energy increases, the Rydberg atoms becomes less sensitive to PI due to increasing mismatch between bound-state and free-electron wavefunctions, and the ionization cross sections drop rapidly. However, in certain PI channels this general trend is interrupted by pronounced minima in the PI cross sections as a function of wavelength λ of the ionizing field. The PI minima are quite sensitive to the assumed Rydberg-electron model potentials. Hence, experimental PI studies can serve as a method to test and to possibly fine-tune model potentials. Data on Rydberg-atom PI cross sections are also relevant to applications of Rydberg atoms in which the rate of laser-induced PI must be minimized.

PI minima in atoms can be attributed to Cooper minima or shape resonances, which are, in the following, briefly explained. Cooper minima, first reported by John Cooper in 1962 [4], occur as a result of vanishing PI matrix-element integrals. The PI matrix elements are integrals over expressions that involve a product of an initial- and a final-state electron wavefunction. The wavefunctions are quasi-periodic and have different spatial periods and phases. At certain values of λ, the matrix-element integral can vanish, in remote resemblance to destructive interference between two out-of-phase periodic functions. The free-state wavefunction on its own does not exhibit any special behavior at the Cooper minima. The associated dips in the PI cross sections as a function of λ can be hundreds of nm wide. Shape resonances, on the other hand, are due to quasi-bound scattering states within an inner well of the relevant free-electron potential. As in our case, the potential barrier that separates the outer region from the inner well can arise from the sum of a short-range attractive potential with a repulsive core and the long-range centrifugal potential, ℏ² ℓ(ℓ + 1)/(2m_e r²), with electron angular momentum ℓ, electron mass m_e, and electron radial coordinate r. As λ is varied, the free-electron wavefunction can pass through a narrow resonance in the inner well, characterized by a large-amplitude quasi-bound scattering state inside the barrier and a π phase shift outside the barrier. In certain Rydberg-atom PI channels, shape resonances cause minima in the PI cross sections; these tend to be narrower as a function of λ than Cooper minima.

Finding the wavelengths at which PI cross sections have minima is interesting from a basic atomic-physics perspective, because it represents a test of the assumed model potentials for the Rydberg and the free-electron states. Knowledge of PI minima can also be beneficial from an applications standpoint. Rydberg atoms in optical dipole traps and optical lattices can become photo-ionized by the trapping beams themselves. If the trapping- or lattice-beam wavelength is set at a PI minimum, the trapped atoms will be less prone to PI by the trapping beams. The absence of Rydberg-atom PI could be important, for instance, in experiments on quantum simulation and quantum information processing using Rydberg atoms [5–8], quantum control [9, 10], high-precision spectroscopy [11–14], and in large-scale arrays of Rydberg atoms that could potentially be trapped [15].

Various experiments and theoretical investigations have been performed over the years to find PI minima, both from Cooper minima and from shape resonances. Aymar et al investigated Cooper minima of one-electron systems (Li, Na, K, Rb, Sr⁺) using quantum defect theory [16, 17], and Msezane and Manson found Cooper minima in a wide range of atomic species (fluoride, Z = 9, to cesium, Z = 55) at lower-lying, non-Rydberg excited states (3d, 4d, 5d) [18]. More recently, Zatsarinny and Tayal computationally calculated Cooper minima in potassium [19], which were later verified experimentally by Yar, Ali, and Baig [20]. Beterov et al calculated transition probabilities and PI cross sections of alkali metals using a Coulomb approximation and a quasiclassical model [21]. Additionally, there have been measurements of the Cooper minimum of atoms in a plasma background [22–24]. Meanwhile, shape resonances have been seen in PI calculations for francium [25], observed in positronium [26] and in atom collisions [27–29], and used to form Rydberg molecules [30, 31].

In this work, we report computational findings on Cooper minima and shape resonances in Rydberg-state PI in Rb and Cs. We use model potentials [32] for rubidium and cesium to determine the initial (bound) and and final (free-state) wavefunctions of the photoionized electrons. The model potentials were developed and employed in [32] for the computation of molecular dispersion coefficients, and were further applied to compute polarizabilities [33], two-photon rates [34] involving low-lying atomic states, and Rb 5D PI cross sections [35]. In these applications, the accuracy of the potentials in the ionic core region of the atoms was important. This also is the case in our application of these potentials, in which we compute Rydberg-atom PI cross sections across a wide range of λ. We find several Cooper minima and shape resonances that are heavily reliant on the behavior of the wavefunctions (and hence the potentials) inside and near the ionic core. We evaluate our results in context with free-state wavefunction plots and the underlying model potentials, and comparisons between Cs and Rb are made. We discuss the viability of measuring these PI minima experimentally, as well as the relevance to atomic physics theory and to applications.

2.1. Atomic model potentials

We denote the initial Rydberg states |i⟩ = |n, ℓ, m_ℓ ⟩ with principal, angular-momentum and magnetic quantum numbers n, ℓ and m_ℓ , respectively, and the photo-ionized free-electron states $\vert f\rangle =\vert {{\epsilon}}^{\prime },{\ell }^{\prime },{m}_{\ell }^{\prime }\rangle$ with free-electron energy ${\epsilon}\prime$, and angular-momentum and magnetic quantum numbers $\ell \prime$ and ${m}_{\ell }^{\prime }$, 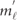respectively.

The calculation of PI cross sections requires a procedure to calculate the initial-state and free-state wavefunctions, ψ_i (r) = ⟨r|i⟩ and ψ_f (r) = ⟨r|f⟩ of the valence electron, with relative electron position r. The fine structure is neglected in the present work because it is much smaller than the Rydberg-atom binding energy and the energy of the free electron. The wavefunction calculation requires a set of model potentials. The model-potential approach aims at describing the effects of many-electron interactions via ℓ-dependent single-electron potentials for the valence electron(s). The method has been developed over many decades, including in works [36–39]. Here, we use model potentials for Rb and Cs that were developed and employed in references [32–34] to describe properties of low-lying atomic states. The model potentials account for many-electron interactions of the valence electron inside the atomic core and for the long-range perturbation due to core polarization.

The model potentials are, in atomic units,

$$\begin{equation}{V}_{\ell }\left(r\right)={V}_{0,\ell }\left(r\right)+\frac{\ell \left(\ell +1\right)}{2{r}^{2}}.\end{equation} \tag{ 1 }$$

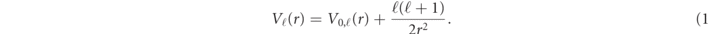
The V_ℓ (r) depend on ℓ via the centrifugal term and, more importantly, via ℓ-dependent fit parameters in

$$\begin{equation}{V}_{0,\ell }\left(r\right)=-\frac{{Z}_{\ell }\left(r\right)}{r}-\frac{{\alpha }_{c}}{2{r}^{4}}\left[1-\mathrm{exp}\left[-{\left(\frac{r}{{r}_{c}}\right)}^{6}\right]\right].\end{equation} \tag{ 2 }$$

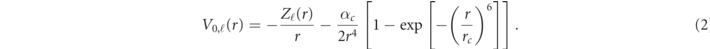
There, α_c is the ℓ-independent core polarizability, Z_ℓ (r) is an ℓ-dependent function, and r_c an ℓ-dependent parameter. There are five ℓ-dependent fit parameters, which are provided in equation (18) and table 1 in [32]. The potentials depend on atomic species. Also, for Rb and Cs V_0,ℓ>3(r) = V_0,ℓ=3.

An important property of PI matrix elements is that their values essentially accumulate within a short range (r less than several tens of a₀), with only small contributions arising from the overwhelmingly vast outer volume of the Rydberg atoms. The shape resonances discussed in our work are due to a potential well inside the centrifugal barrier of V_ℓ=3(r), at distances r ≲ 1.5 a₀. This is inside the ionic Rydberg-atom core, the radius of which is on the order of 3 a₀. The many-electron physics in the core is approximated via the effective single-electron model potentials. Spectroscopic measurements of PI features, such as shape resonances, would provide valuable tests for the model potentials and their underlying theory.

The Cooper minima discussed in our work also depend somewhat on the exact structure of the wavefunctions (and hence the model potentials) inside the core. However, this dependence is less narrow-band in PI energy than the energy width of the shape resonances. An energy-dependent long-range phase-shift of the wavefunctions, related to known quantum defects via Seaton's theorem [40], qualitatively captures the origin of the Cooper minima. In contrast, the concept of a gradual wavefunction phase-shift is not suitable for shape resonances, because those induce a π phase-shift step over a narrow energy range, as seen in the wavefunction plots in our paper.

The wavefunctions are calculated from the model potentials using a numerical method outlined by Reinhard et al [41]. The method is a finite-difference method to solve the time-independent Schrödinger equation on a variable-step-size spatial grid. The grid provides at least 500 grid points per magnitude of the position-dependent free-electron wavelength (which is complex in the classically forbidden inner region), while maintaining a minimal grid-point density near the classical tuning point (where the local electron wavelength diverges). For given free-electron energy, the free-state wavefunction boundary conditions are matched on the inside, and the wavefunction is propagated outward over the extent of the bound-state wavefunction. The spatial grids for bound and free states are identical. The energies of the lower states are fine-adjusted so as to exactly match (to within numerical errors) the boundary conditions in both the inner and outer classically forbidden regions.

The effective quantum numbers found by fine-tuning the bound-state energies agree with those obtained by inserting known quantum defects into the Rydberg-Ritz formula [2] to better than three figures after the decimal point. While this observation, which accords with an accuracy statement made in [32], is reassuring, it must be stressed that our motivation for fine-tuning the level energies is to have the exponential wavefunctions tails in the classically forbidden regions approach zero as closely as possible, and as far in or out as possible. The high degree of accuracy to which the wavefunction boundary conditions must be matched is due to the fact that the PI matrix elements are very small and accumulate over a small region inside and near the ionic core, with contributions from regions r ≳ 10 a₀ essentially canceling out due to destructive interference. An exact match of the wavefunction boundary conditions both on the inside (free and bound states) and on the outside (bound state) is required in order to avoid errors due to sloppy wavefunction truncation in the classically forbidden regions.

For context with other aspects of Rydberg-atom physics, it is worth noting that the computation of bound-bound matrix elements between Rydberg states is considerably more forgiving than that of PI matrix elements. Bound-bound matrix elements are required, for instance, to model Stark effects, electromagnetic transitions between Rydberg states, diamagnetism and long-range Rydberg molecules. An exact match of the inside boundary conditions is, typically, not important for bound-bound matrix elements, because those matrix elements tend to integrate to very large values within the outer expanses of the Rydberg-electron wavefunctions, with no significant contributions from the core region. Hence, for bound-bound matrix elements it is often sufficient to phase-shift the Rydberg wavefunctions according to known quantum defects, and to truncate the wavefunctions at a radius r ∼ 1 a₀ (without bothering to match inside boundary conditions). This simplified procedure is not allowable for PI matrix elements.

2.2. Calculating PI cross sections

PI is an effect of the 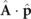$\hat{\mathbf{A}}\cdot \hat{\mathbf{p}}$-interaction of the minimal-coupling Hamiltonian [3] in first order. Given a linearly polarized plane wave with polarization unit vector 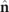$\hat{\mathbf{n}}$, wave vector k and angular frequency ω, the partial PI cross section is

$$\begin{equation}\sigma =\frac{\pi {e}^{2}{\hslash }^{2}}{{\varepsilon }_{0}{m}_{\mathrm{e}}^{2}\omega c}{\left\vert \hat{\mathbf{n}}\cdot \int {\psi }_{f}^{{\ast}}{\text{e}}^{\text{i}\mathbf{k}\cdot \mathbf{r}}\nabla {\psi }_{i}\enspace {\mathrm{d}}^{3}r\right\vert }^{2}\left(\frac{1}{{E}_{H}{a}_{0}^{2}}\right),\end{equation} \tag{ 3 }$$

with the atomic energy unit E_H ≈ 27.2 eV, and standard identifiers for other physical constants. The result is in SI units, m². The matrix element is computed in atomic units, with free states normalized in units of energy, i.e. 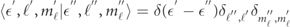$\langle {{\epsilon}}^{\prime },{\ell }^{\prime },{m}_{\ell }^{\prime }\vert {{\epsilon}}^{\prime \prime },{\ell }^{\prime \prime },{m}_{\ell }^{\prime \prime }\rangle =\delta \left({{\epsilon}}^{\prime }-{{\epsilon}}^{\prime \prime }\right){\delta }_{{\ell }^{\prime \prime },{\ell }^{\prime }}{\delta }_{{m}_{\ell }^{\prime \prime },{m}_{\ell }^{\prime }}$, and the term in parentheses within equation (2) converting the matrix-element square from atomic into SI units.

It is shown in reference [42] that for light-induced PI of Rydberg atoms the electric-dipole approximation (EDA), e^ik⋅r = 1, is valid at a level to better than 10⁻⁴, i.e. electric-dipole-forbidden transitions have cross sections that are smaller than those of the dipole-allowed ones by a factor of at least ten thousand, and the cross sections for dipole-allowed transitions are virtually unaltered by making the EDA.

Making the EDA and averaging the cross sections over the initial-state magnetic quantum number, m_ℓ , we obtain the shell-averaged partial cross section,

$$\begin{equation}{\bar{\sigma }}_{n,\ell }^{{{\epsilon}}^{\prime },{\ell }^{\prime }}=\frac{\pi {e}^{2}{\hslash }^{2}}{3{{\epsilon}}_{\text{0}}{m}_{\text{e}}^{2}\omega c}\frac{{\ell }_{{ >}}}{\left(2\ell +1\right)}\vert M{\vert }^{2}\left(\frac{1}{{E}_{H}{\mathit{\text{a}}}_{\text{0}}^{2}}\right),\end{equation} \tag{ 4 }$$

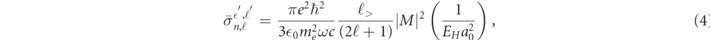
where M is the radial PI matrix element in atomic units,

$$\begin{equation}M={\int }_{0}^{\infty }{u}_{{{\epsilon}}^{\prime },{\ell }^{\prime }}\left(r\right)\left[{u}_{n,\ell }^{\prime }\left(r\right)\mp \frac{{u}_{n,\ell }\left(r\right)}{r}{\ell }_{{ >}}\right]\mathrm{d}r.\end{equation} \tag{ 5 }$$

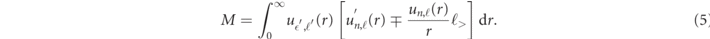
There, the upper sign is for ℓ_> = ℓ' = ℓ + 1 and the bottom sign for ℓ_> = ℓ = ℓ' + 1. The functions u_∗,ℓ (r) are given by u_∗,ℓ (r) = rR_∗,ℓ (r), with the usual radial wavefunction R_∗,ℓ (r), and ∗ = n and ∗ = ' denoting the principal quantum number of the bound- and the energy of the free-electron state, respectively. The free-state energy follows from the wavelength of the PI light, λ, and the binding energy of the Rydberg atom. The free-state energy in atomic units is ' = 2πa₀/(αλ) −|W(n, ℓ)|, with λ in meters, the fine structure constant α, and the bound-state energy W(n, ℓ) from the wavefunction calculation.

For linearly polarized light, the value of m_ℓ along the direction of the laser electric field is conserved, and the m_ℓ -dependent PI cross sections follow from the shell-averaged ones via

$$\begin{equation}{\sigma }_{z,n,\ell ,{m}_{\ell }}^{{{\epsilon}}^{\prime },{\ell }^{\prime }}=\frac{3\left({\ell }_{{ >}}^{2}-{m}_{\ell }^{2}\right)}{\left(2{\ell }_{{ >}}+1\right)\left(2{\ell }_{{ >}}-1\right)}\frac{\left(2\ell +1\right)}{{\ell }_{{ >}}}{\bar{\sigma }}_{n,\ell }^{{{\epsilon}}^{\prime },{\ell }^{\prime }},\end{equation} \tag{ 6 }$$

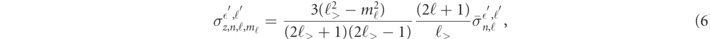
with similar expressions applicable to other light polarizations [42]. The resonances and Cooper minima in the cross sections arise from the behavior of the radial PI matrix elements in the shell-averaged expressions. In the following, it is therefore sufficient to consider the behavior of the shell-averaged PI cross sections, 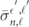${\bar{\sigma }}_{n,\ell }^{{{\epsilon}}^{\prime },{\ell }^{\prime }}$.

It is noted that the matrix element in equation (5) follows directly from the 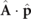$\hat{\mathbf{A}}\cdot \hat{\mathbf{p}}$-interaction in the minimal-coupling Hamiltonian, and making the EDA. The matrix-element form in equation (5), known as velocity form [3, 43], is accurate because it requires no approximation beyond the EDA (which is exquisitely well satisfied). In the case that the atomic potential also is velocity-independent (not including the centrifugal term), the matrix elements can be converted into length form [3, 43] using $\hat{\mathbf{p}}=i\left[{\hat{H}}_{0},\hat{\mathbf{r}}\right]$ (with field-free Hamiltonian ${\hat{H}}_{0}$). 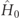This allows an alternate, commonly used method to compute atom-field interaction matrix elements. We have checked that the PI matrix elements calculated in velocity and length forms are identical for ℓ ⩾ 4, where a single ℓ-independent potential, V_0,ℓ⩾3 = V_0,ℓ=3, applies to compute both the bound- and free-state wavefunctions.

For ℓ < 4, however, the model potentials are ℓ-dependent. Noting that the PI matrix elements involve wavefunctions with ℓ-values differing by 1, PI channels with the smaller of the involved ℓ-values, ℓ_<, being less or equal 2 involve a set of two different model potentials. We should then expect the length-form results to become inaccurate (i.e., to deviate from the velocity form). Indeed, for ℓ_< ⩽ 2 the PI cross sections calculated in length form are typically off by ∼20%, with considerably larger relative deviations near the PI minima. Also, the λ-values of the Cooper minima differ by ∼50 nm between the two forms. It is important to state that the velocity-form PI matrix elements are valid for all ℓ, because they do not require the identity $\hat{\mathbf{p}}=i\left[{\hat{H}}_{0},\hat{\mathbf{r}}\right]$ to hold. For the PI cross-section calculations presented in this paper, we have chosen ℓ = 0 and ℓ = 2, because these are experimentally relevant cases. For these ℓ-values one must use the velocity-form expressions given in equations (4) and (5).

For context with spectroscopic work elsewhere, it is worth noting that the relative error of E1 transition matrix elements calculated in length form, for ℓ_< ⩽ 2, is several orders of magnitude lower for bound-bound transitions than it is for bound-free Rydberg transitions (i.e., Rydberg-atom PI). This is because the bound-bound E1 matrix elements mostly accumulate outside the atomic core region, where all model potentials are ℓ-independent, with negligible contributions from inside the core. As a result, length-form calculations of bound-bound E1 transition matrix moments are accurate enough for most purposes, even if ℓ_< ⩽ 2.

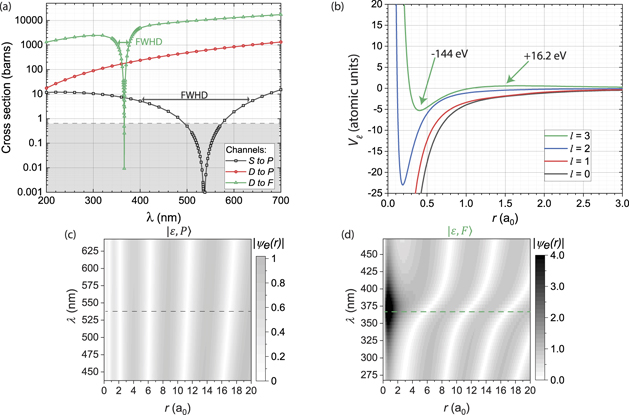
Figure 1(a) shows shell-averaged cross sections of three PI channels of Rb Rydberg atoms, namely 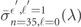${\bar{\sigma }}_{n=35,\ell =0}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=1}\left(\lambda \right)$, ${\bar{\sigma }}_{n=35,\ell =2}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=1}\left(\lambda \right)$, and ${\bar{\sigma }}_{n=35,\ell =2}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=3}\left(\lambda \right)$, 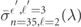for wavelengths ranging from the deep UV to the near-IR regime. Aside from the resonant features discussed later, it is seen that the S → P cross sections are fairly small over the entire range, topping out at only about 20 times the Thomson cross section, σ_T = 0.665 b. In the near-IR spectral range, nS-type Rydberg atoms have PI cross sections that are lower than those of other low-ℓ PI channels by up to about three orders of magnitude. In contrast, the D → P and D → F channels in figure 1(a) follow the generic trend that PI rates rapidly increase at longer wavelengths. Between λ = 200 nm and 700 nm, the PI cross sections of those channels increase by one to two orders of magnitude. Typically, the PI threshold will peak at the PI threshold, with depends on n and ℓ and is in the far-IR regime.

Zoom In Zoom Out Reset image size

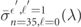The plot ${\bar{\sigma }}_{n=35,\ell =0}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=1}\left(\lambda \right)$ in figure 1(a) shows a minimum centered at λ = 536 nm. As the S → P channel is the only PI channel of S-type Rydberg atoms, the total PI cross section equals the partial cross section 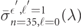${\bar{\sigma }}_{n=35,\ell =0}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=1}\left(\lambda \right)$, and is below σ_T over a range 490 nm ≲ λ ≲ 570 nm. Taking into account the asymmetry of the PI minimum in 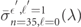${\bar{\sigma }}_{n=35,\ell =0}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=1}\left(\lambda \right)$, we define the full width at half depth (FWHD) of the minimum as the range over which the cross section dips below half of the PI maximum seen in the UV range. For the Rb Cooper minimum, the PI maximum in the UV range is 10 b, so the FWHD is the range over which the cross section dips below 5 b. The FWHD is ≈240 nm, with the FWHD-range covering the spectral region 400 ≲ λ ≲ 640 nm. The large width of the PI minimum in the S → P channel serves as an indicator that this is a Cooper minimum, as will be proven below.

The D → F channel shows a minimum centered at λ = 366 nm with an FWHD of only about 20 nm. The narrow width of this minimum is a first indicator that this minimum is different in nature from the minimum in the S → P channel; below we will show that the minimum in the D → F channel is due to a shape resonance. The D → P channel has no PI minimum within the range displayed in figure 1(a). We also did not find any minimum over an extended search across a wider range from 100 nm to 2 μm (not shown). The total shell-averaged PI cross section of Rb 35D is given by the sum of the partial cross sections, 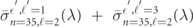${\bar{\sigma }}_{n=35,\ell =2}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=1}\left(\lambda \right)\enspace +\enspace {\bar{\sigma }}_{n=35,\ell =2}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=3}\left(\lambda \right)$. Hence, the observable cross section of the 35D-state is the sum of two of the curves in figure 1(a). The total 35D PI cross section therefore has a minimum of about 200 bs at 366 nm, and rises to about 3000 b several tens of nm away.

The physical differences between the PI minima in the Rb S → P and D → F channels become apparent when looking at the inner regions of the relevant free-electron model potentials, V_ℓ (r), and the free-electron wavefunctions. In figure 1(b) we show V_ℓ (r) for ℓ = 0 to 3 and over the range r ⩽ 3 a₀, and in figures 1(c) and (d) free-electron wave-function moduli for the S → P and D → F ionization channels, respectively, over the range r ⩽ 20 a₀. Figures 1(b)–(d) are focused on the central atomic region, where phase shifts and shape resonances determine the PI behavior. In figure 1(c), the free-electron wavefunction does not exhibit any noteworthy feature, as λ passes through the PI minimum. There merely is a gradual phase shift of the wavefunction due the slightly changing de-Broglie wavelength of the free electron. Hence, the PI minimum is due to incidental near-perfect destructive interference between bound-state and free-electron wavefunctions (where the bound-state function shows up in a modified form; see equation (5)). This fact makes the PI minimum in the Rb S → P channel a Cooper minimum. Due to the rather gradual change of the free-state wavefunction, the Cooper minimum is comparatively wide in PI wavelength and free-electron energy. The Cooper minimum relates to the fact that the bound-state and free-state quantum defects differ by about 1/2 in Rb (the quantum defects are near 3.13 for S and 2.65 for P).

The free-state wavefunction of the D → F channel exhibits a resonant structure at the PI minimum, which manifests in the region of high wavefunction amplitude near r ≈ 1a₀, as well as a phase change of ≈π in the outer, oscillatory region of the wavefunction. The phase change is spread out over a few tens of nm in λ. The resonance occurs at the λ-value of the PI minimum, and it has a width in λ of only a few tens of nm. Another piece of insight follows from the V_ℓ (r), plotted in figure 1(b). There, it is seen that V_ℓ=3(r) exhibits an inner well formed by the centrifugal potential and the core region of the model potential V_0,ℓ=3(r) for r ≲ 1.5 a₀. (Note equation (1) regarding the definition of V_0,ℓ=3 and V_ℓ=3). Of the four potentials shown, the ℓ = 3 potential is the only one with an inner potential well and a centrifugal barrier. The potential barrier peaks at an energy of about +16.2 eV, and the inner well reaches a minimal value of about −144 eV. It is apparent that the resonance, which is at about ' = 3.37 eV, is the lowest and only quasi-bound state in the inner potential well of V_ℓ=3(r). These findings sum up to the statement that the PI minimum in the D → F channel is due to a shape resonance. The phase shift of π of the scattering wavefunction across the resonance, seen in figure 1(d), is another telltale sign of a shape resonance [44].

It may seem counter-intuitive that the shape resonance manifests as a minimum in the PI cross section of the D to F channel (see figure 1(a)), while the free-state wavefunction exhibits the expected enhancement in the inner potential well (see figures 1(b) and (e)). This behavior results from destructive interference of the product under the integral in equation (5). While the free wavefunction displays only a single pronounced maximum inside the potential barrier, it is multiplied with the quasi-periodic term in the square bracket in equation (5). Here it happens to be the case that the PI matrix-element integral, M(λ), passes through a zero crossing at λ ≈ 365 nm, where it exhibits perfect destructive interference (and flips sign). The zero is almost exactly at the center of the free-state wavefunction's shape resonance peak (also located at λ ≈ 365 nm). The coincidence leads to a near-symmetric dip in the D to F PI cross section versus λ. The corresponding PI shape resonance in the case of Cs, discussed in section 4, is less symmetric.

After identifying the physical origins of the PI minima, we wish to comment on a length-form calculation of the PI cross sections, which has yielded qualitatively similar behaviors with quantitatively notable differences (not shown). For instance, the Cooper minimum in the length-form result for Rb 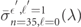${\bar{\sigma }}_{n=35,\ell =0}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=1}\left(\lambda \right)$ is shifted up in wavelength by about 50 nm relative to the velocity-form result. While the (unphysical) shift in the length-form result is less than the width of the minimum, it is large enough to be of significance. The shift represents a case in which the length-form calculation exhibits a significant error relative to the velocity-form calculation. We reiterate here that the velocity-form calculation is correct, while the length-form is expected to show an error because of the ℓ-dependence of the model potentials V_0,ℓ . For ℓ ⩾ 4 the PI cross sections obtained with the two forms agree, because the model potentials to be used for the bound (ℓ) and free-electron (ℓ' = ℓ ± 1) states are identical (namely, V_0,ℓ=3).

It is also worth commenting on free-electron photon scattering due to the A²-term in the atom-field interaction [3]. Since within the λ-range discussed the photon energy exceeds the atomic binding scale by orders of magnitude, the photon scattering has a cross section given by the Thomson scattering cross section, σ_T = 0.665 b. For a truly free electron, we would be looking at a case of low-energy Compton-scattering, and the recoil energy would be in the range of h × 10 GHz. This recoil energy would be too small to cause atomic bound-bound transitions, nor would it cause photo-ionization of the atom. Therefore, the Thomson scattering of a Rydberg electron is recoil-free and elastic (except for a very small recoil of the entire atom). In the gray regions in figures 1 and 2, the elastic (Thomson) scattering rate exceeds the PI rate, and it may be measurable. Comparing the two effects, we further note that the Thomson scattering is due to the A²-term in the atom-field interaction, and it occurs in the outer reaches of the Rydberg atom, r ≳ 10 a₀, where the Rydberg electron resides with near-unity probability, whereas PI (photo-electric effect) is due to the A ⋅p-term and it tends to occur in and near the atomic core, r ≲ 10 a₀.

Zoom In Zoom Out Reset image size

The dependence of elastic photon scattering and PI on principal quantum number n also is of interest. The elastic cross section, σ_T, is independent of n. In contrast, the PI cross sections, away from the resonances, have a generic scaling close to ∝n^*−3, with n* = n − δ_ℓ denoting the effective quantum number, and δ_ℓ the quantum defect. We have verified this scaling in additional calculations (which are not presented in detail).

Finally, expanding the A² term to leading order in the PI laser's wavenumber k_L , which is equivalent to dropping the EDA in the A ⋅p-term, PI through two-photon absorption from the PI-laser field becomes allowed. We find that the ratio between A² and A ⋅p PI rates scales with the ratio between the free-electron ponderomotive energy shift, 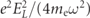${e}^{2}{E}_{L}^{2}/\left(4{m}_{\mathrm{e}}{\omega }^{2}\right)$, and the electron rest energy (E_L here is the laser field). Two-photon PI through the A² term therefore is outside the scope of the present paper, as are multi-photon effects due to higher-order A ⋅p interactions.

Figure 2(a) shows partial PI cross sections for Cs 35S and 35D, for the S → P, D → P, and D → F ionization channels. In this figure, which is organized analogous to figure 1, we see that all three partial PI cross section channels have minima, namely Cooper minima for S → P and D → P, and a shape resonance for D → F. The PI minima are 100 to 200 nm deeper in the UV than in Rb. The PI cross section of the 35S state barely rises above the elastic scattering cross section, σ_T, across the displayed range, making S-type Rydberg atoms of Cs essentially PI-free at all wavelengths shorter than about 500 nm. Otherwise the trends observed in figure 2(a) follow those of Rb. As in Rb, in Cs the shape resonance is considerably narrower than the Cooper minima. The Cooper minimum in the D → P channel is of little relevance, because in the total PI cross section it will be near-invisible against PI on the D → F channel.

The potential curves and free-state wavefunction maps for Cs, shown in figure 2(b) and figures 2(c)–(e), respectively, present a situation that is similar to that in Rb. The Cooper minima in the S → P and D → P channels have an FWHD of about 100 nm and are characterized by free-state wavefunctions with smooth, λ-dependent phase changes and without any resonant behavior. The ℓ = 3 potential is the only one that features a relevant barrier, which is located at r ≈ 1 a₀ and peaks at 39.2 eV. The potential well inside the barrier bottoms out at −335 eV. The lowest electron 'state' in the well is a quasi-bound positive-energy resonance associated with the shape resonance at λ = 150 nm in the partial PI cross section on the D → F channel.

The PI cross sections warrant an experimental investigation because of the importance of optical traps of Rb and Cs Rydberg atoms in the applications mentioned near the end of section 3, where atom loss and decoherence must be avoided. In our paper we stress that the model potentials used in the calculations play a central role. It is apparent that the positions of the PI minima are very sensitive to the potentials and the resultant phase shifts and quasi-bound states near and inside the Rydberg atoms' ionic cores. Noting the large depth and the small range of the inner wells of the ℓ = 3 potentials, one may expect that a measurement of the shape resonances will present a particularly sensitive test for the ℓ = 3 model potentials.

Considering the widths of the PI minima, one fruitful experimental approach is to use a tunable pulsed laser to photo-ionize a sample of N cold Rydberg atoms and to count the ions using a single-particle counter. The latter may utilize, for instance, a micro-channel plate or a channeltron, which are capable of single-ion counting with efficiencies of ≳30%. Considering that it will typically be desired to count at least one ion per laser pulse, so as to build up sufficient statistics, but fewer than ∼N/2 to avoid saturation, at a given σ the fluence F of the pulse should be in the range

$$\begin{equation}\frac{hc}{2\sigma \lambda }\;\gtrsim \;F\;\gtrsim \;\frac{hc}{N\sigma \lambda }\end{equation} \tag{ 7 }$$

To measure the shape resonance of 35D in Rb, this relation would have to be satisfied for σ ranging between σ_min ∼ 200 b and σ_max ∼ 10 000 b, the range of the total PI cross section of that state [see figure 2(a)]. For an assumed number of N = 10⁷ Rydberg atoms, equation (7) translates into

$$\begin{align}\frac{hc}{2{\sigma }_{\mathrm{max}}\enspace \lambda }\;\gtrsim \;& F\;\gtrsim \enspace \frac{hc}{N{\sigma }_{\mathrm{min}}\enspace \lambda }\\ 3{\times}1{0}^{3}\frac{\mathrm{m}\mathrm{J}}{{\mathrm{m}\mathrm{m}}^{2}}\enspace \gtrsim \enspace & F\;\gtrsim \enspace 2.7\enspace {\times}1{0}^{-3}\frac{\mathrm{m}\mathrm{J}}{{\mathrm{m}\mathrm{m}}^{2}}\quad .\end{align} \tag{ 8 }$$

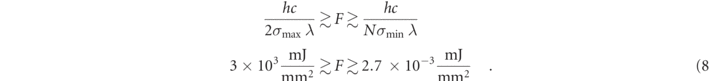
Noting that the PI laser could have an area of several mm², it is seen that the pulse fluence F required to measure the shape resonance of Rb 35D lies within fairly comfortable limits. A pulse energy of a few tens of μJ per pulse could be sufficient to map out the shape resonances.

To measure the Cooper minimum of Rb 35S, we set σ_min = σ_T = 0.67 b, the elastic photon scattering rate, and σ_max = 20 b. In this case, the limiting experimental requirement is

$$\begin{equation}F\;\gtrsim \;\frac{hc}{N{\sigma }_{\mathrm{min}}\enspace \lambda },\quad \mathrm{o}\mathrm{r},\quad F\;\gtrsim \;0.6\frac{\mathrm{m}\mathrm{J}}{{\mathrm{m}\mathrm{m}}^{2}}\quad .\end{equation} \tag{ 9 }$$

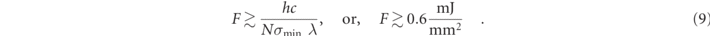
It is seen that for a beam with several mm² in cross section a pulse energy of a few mJ per pulse could be sufficient to map out the Cooper minimum. This pulse energy could be delivered, for instance, by a nanosecond pulsed dye laser (PDL), pumped with a harmonic of a pulsed YAG laser. Noting that with decreasing n the PI cross sections generally increase as n^*−3, additional experimental flexibility would be afforded by lowering n.

A main issue with measuring the PI minima is the lasers that would be required to run these experiments. The cesium shape resonance, for example, is centered at 150 nm, which is not an easily accessible wavelength. This wavelength could be reached by running a 600 nm laser through frequency-doubling crystals, but the setup would be expensive and inefficient. Additionally, 150 nm light is readily scattered in air, so the laser beam paths must be short to avoid significant beam attenuation.

Of the five PI minima we found, we surmise that the easiest one to experimentally investigate is the Rb shape resonance (see equation (8)). This minimum is centered at 366 nm, which can be accessed by running a PDL with a dye such as LDS-720, and then sending the PDL beam through a doubling crystal. The Rb and Cs S → P Cooper minima are the second-best candidates for measurement because of their accessible wavelengths, but the cross sections expected for these channels are generally low. The resultant condition on the fluence (see equation (9)) will make this effort more challenging.

The small total PI cross sections of Rb and Cs nS Rydberg states makes these states ideal for applications of optically excitable, laser-trapped Rydberg atoms. The Cooper minimum in Rb 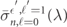${\bar{\sigma }}_{n,\ell =0}^{{{\epsilon}}^{\prime },{\ell }^{\prime }=1}\left(\lambda \right)$ is near 532 nm, the second harmonic of YAG and similar lasers, which can deliver sufficient power for dipole and optical-lattice traps for Rydberg atoms [9, 11, 12, 45]. Laser-trapped, practically PI- and decoherence-free Rydberg atoms can be useful in applications in which atomic decay and decoherence must be minimized, such as in quantum simulation, quantum information processing and high-precision spectroscopy.

We have calculated the partial PI cross sections of S- and D-type Rydberg atoms of Rb and Cs from the UV into the near-IR spectral regime. We have identified one Cooper minimum and one shape resonance in Rb, and two Cooper minima and one shape resonance in Cs. Unlike in photon scattering and PI of ground-state atoms by light, the photon energy in PI of Rydberg atoms by light exceeds the electron binding energy by several orders of magnitude, and the atoms are very large compared to the PI wavelength. Similarly unusual energy and size scaling parameters can apply in x-ray PI of regular atoms.

In future work, one may investigate these PI cross sections experimentally. The exact wavelengths of the PI minima will be useful to know for the design of optical dipole traps and optical lattices for Rydberg atoms. For instance, traps for Rb nS Rydberg atoms could benefit from the Cooper minimum of Rb near λ = 536 nm. Further, the Rb shape UV lattice would be effective for Rb nD Rydberg atoms. UV lattices are uncommon, but they have been used in the past to trap mercury [46].

Similar calculations can be performed for any element, as long as there is a model potential to use. In this vein, the same study could be conducted for other alkali metals such as potassium and sodium. While there have been articles in the past that have reported on Cooper minima in these elements, there may be other Cooper minima and shape resonances that are unknown. The studies could also be expanded out of the alkali metal group into other commonly studied species, such as Sr, Yb and Ca, which may have interesting PI behavior due to the presence of two valence electrons. The elastic photon scattering of Rydberg atoms, which has a cross section equivalent to the Thomson scattering cross section, may also deserve a future study.

Single-electron calculations in model potentials are convenient in that they are computationally less demanding, after the model potentials are known. In the future, it may be of interest to perform exact all-electron calculations on Rydberg-atom PI, possibly in an extension of all-electron calculations of sodium [47] and cesium [48].

This work was supported by NSF Grant No. PHY-1707377. We thank Callum Jones of the University of California, Los Angeles, and Shruti Paranjape of the University of Michigan for valuable discussions.

The data that support the findings of this study are available upon reasonable request from the authors.