Constructing a virtual two-qubit gate by sampling single-qubit operations

Quantum computation is completely specified with a quantum circuit, U, an initial state with its density matrix representation, ρ, and an observable, O, measured at the output. Given U, ρ, and O, any quantum computation can be represented by a tensor network [23–25]. We define the tensor representation of U, ρ, and O in the following manner.

Suppose that our quantum computer has n qubits. We define a complete set of basis in the space of 2 × 2 complex matrix and its dual as ${\left\{\vert {e}_{i}\rangle \rangle \right\}}_{i=1}^{4}$ and ${\left\{\langle \langle {e}_{i}\vert \right\}}_{i=1}^{4}$ respectively, and assume orthonormality under the trace inner product; 〈〈e_i |e_j 〉〉 = δ_ij . We use the trace inner product, that is, for matrices A and B, 〈〈A|B〉〉 = Tr(A^† B). A density matrix ρ can be decomposed into the sum of $\vert {e}_{{j}_{1}}\rangle \rangle \otimes \vert {e}_{{j}_{2}}\rangle \rangle \otimes \cdots \otimes \vert {e}_{{j}_{n}}\rangle \rangle =\vert {e}_{{j}_{1}}{e}_{{j}_{2}}\dots {e}_{{j}_{n}}\rangle \rangle$ as

$$\begin{equation}\vert \rho \rangle \rangle =\sum\limits _{{j}_{1},\dots ,{j}_{n}}{\rho }_{\boldsymbol{j}}\vert {e}_{{j}_{1}}{e}_{{j}_{2}}\dots {e}_{{j}_{n}}\rangle \rangle ,\end{equation} \tag{ 1 }$$

where j = (j₁, j₂, ..., j_n ). We refer to the elements ${\rho }_{\boldsymbol{j}}=\langle \langle {e}_{{j}_{1}}{e}_{{j}_{2}}\dots {e}_{{j}_{n}}\vert \rho \rangle \rangle$ as the tensor representation of ρ. An observable O can also be decomposed into the same form. Note that we can naturally assume tensor representations of observables and density matrices consist of real numbers because they are always Hermitian and we can choose the basis ${\left\{\vert {e}_{i}\rangle \rangle \right\}}_{i=1}^{4}$ as Hermitian, e.g. we can use the Pauli matrices {I, X, Y, Z} as the basis. Therefore, we assume ρ_i and O_i are real henceforth. The quantum circuit, U, transforms ρ into UρU^†. We define a corresponding superoperator $\mathcal{S}\left(U\right)$ whose action is defined by $\mathcal{S}\left(U\right)\rho =U\rho {U}^{{\dagger}}$. Superoperator can be decomposed as,

$$\begin{equation}\mathcal{S}\left(U\right)=\sum\limits _{{j}_{1},\dots ,{j}_{n}}\sum\limits _{{k}_{1},\dots ,{k}_{n}}\mathcal{S}{\left(U\right)}_{\boldsymbol{j},\boldsymbol{k}}\vert {e}_{{j}_{1}}\dots {e}_{{j}_{n}}\rangle \rangle \langle \langle {e}_{{k}_{1}}\dots {e}_{{k}_{n}}\vert .\end{equation} \tag{ 2 }$$

Note that this decomposition is not limited to superoperators of unitary matrices, but also is applicable for any linear operator that acts on a density matrix. We call $\mathcal{S}{\left(U\right)}_{\boldsymbol{j},\boldsymbol{k}}=\langle \langle {e}_{{j}_{1}}\dots {e}_{{j}_{n}}\vert \mathcal{S}\left(U\right)\vert {e}_{{k}_{1}}\dots {e}_{{k}_{n}}\rangle \rangle$ tensor representation of $\mathcal{S}\left(U\right)$. When we use the Pauli operators as basis set, $\mathcal{S}{\left(U\right)}_{\boldsymbol{j},\boldsymbol{k}}$ is referred as Pauli transfer matrix.

Quantum computation ends with measuring the observable O. This output can be written down as,

$$\begin{equation}\langle \langle O\vert \mathcal{S}\left(U\right)\vert \rho \rangle \rangle =\mathrm{T}\mathrm{r}\left(OU\rho {U}^{{\dagger}}\right)\end{equation} \tag{ 3 }$$

$$\begin{equation}=\sum\limits _{{j}_{1},\dots ,{j}_{n}}\sum\limits _{{k}_{1},\dots ,{k}_{n}}{O}_{\boldsymbol{j}}\mathcal{S}{\left(U\right)}_{\boldsymbol{j},\boldsymbol{k}}{\rho }_{\boldsymbol{k}},\end{equation} \tag{ 4 }$$

In many cases, U is a product of elementary gates ${\left\{{U}_{i}\right\}}_{i=1}^{L}$, that is, U = U_L ...U₁. The tensor representation of the overall gate, $\mathcal{S}\left(U\right)$, is also a product of $\mathcal{S}\left({U}_{i}\right)$; $\mathcal{S}\left(U\right)=\mathcal{S}\left({U}_{L}\right)\dots \mathcal{S}\left({U}_{1}\right)$. An important note is that as long as the tensor representation of each element is unchanged, the result of the overall computation is also unchanged. If $\mathcal{S}\left(U\right)$ can be represented by a sum of some simple operations as $\mathcal{S}\left(U\right)={\sum }_{i}{c}_{i}\mathcal{S}\left({V}_{i}\right)$ with coefficients {c_i }, the expectation value of an observable O can be computed with the following equality,

$$\begin{equation}\langle \langle O\vert \mathcal{S}\left(U\right)\vert \rho \rangle \rangle =\sum\limits _{i}{c}_{i}\langle \langle O\vert \mathcal{S}\left({V}_{i}\right)\vert \rho \rangle \rangle .\end{equation} \tag{ 5 }$$

Note that c_i can, in general, depend on the state |ρ〉〉. We use this scheme to perform the 'decomposition' of a circuit in this work.

It is noteworthy that as we perform decompositions of a superoperator rather than an operator such as U itself, the method becomes friendly for a realistic quantum device. A direct decomposition of U into some simple operators {V_i }, i.e. U = ∑_i c_i V_i , can also be utilized for the same task; however, as expectation values are calculated as ⟨0|U^† OU|0⟩ where |0⟩ is an initial state, this approach requires us to evaluate ${\sum }_{i,j}{c}_{i}{c}_{j}^{{\ast}}\langle 0\vert {V}_{j}^{{\dagger}}O{V}_{i}\vert 0\rangle$ which are rather hard for the NISQ devices. This fact demonstrates the advantage of using the above formalism. The tensor network representation of the superoperator formalism allows us to graphically understand the decompositions.

We can show the following, which can then be utilized to decompose any two-qubit gate into a sequence of single-qubit operations.

Lemma 1. For operators A₁ and A₂ such that ${A}_{1}^{2}=I$ and ${A}_{2}^{2}=I$,

$$\begin{align}\hfill \mathcal{S}\left({\text{e}}^{\text{i}\theta {A}_{1}\otimes {A}_{2}}\right)& ={\mathrm{cos}}^{2}\enspace \theta \mathcal{S}\left(I\otimes I\right)+{\mathrm{sin}}^{2}\enspace \theta \mathcal{S}\left({A}_{1}\otimes {A}_{2}\right)\hfill \\ \hfill & \quad +\frac{1}{8}\enspace \mathrm{cos}\enspace \theta \enspace \mathrm{sin}\enspace \theta \sum\limits _{\left({\alpha }_{1},{\alpha }_{2}\right)\in {\left\{{\pm}1\right\}}^{2}}{\alpha }_{1}{\alpha }_{2}\left[\mathcal{S}\left(\left(I+{\alpha }_{1}{A}_{1}\right)\otimes \left(I+i{\alpha }_{2}{A}_{2}\right)\right)\right.\hfill \\ \hfill & \quad \left.+\mathcal{S}\left(\left(I+i{\alpha }_{1}{A}_{1}\right)\otimes \left(I+{\alpha }_{2}{A}_{2}\right)\right)\right]\hfill \end{align} \tag{ 6 }$$

To prove this, we can directly check the tensor representation of both hand side is equivalent. For detailed calculation, see appendix A1. This theorem is schematically depicted in figure 1(a). Notice that the operation that is proportional to I ± A and I ± iA for A ∈ {X, Y, Z} can respectively be performed by a projective measurement and a single-qubit rotation.

Zoom In Zoom Out Reset image size

The correspondence with a single-qubit rotation is clear from the formula, ${\mathrm{e}}^{{\pm}\mathrm{i}\pi A/4}=\frac{1}{\sqrt{2}}\left(I{\pm}iA\right)$, which is the rotation of angle π/2 around the A axis. Let ${\mathcal{M}}_{A}$ be the projective measurement on the A basis (A ∈ {X, Y, Z}), that is, ${\mathcal{M}}_{A}$ acts on a density matrix ρ as,

$$\begin{equation}{\mathcal{M}}_{A}\rho =\frac{1}{\mathrm{T}\mathrm{r}\left(\rho \frac{I+\alpha A}{2}\right)}\left(\frac{I+\alpha A}{2}\right)\rho \left(\frac{I+\alpha A}{2}\right),\end{equation} \tag{ 7 }$$

depending on the result of the measurement α ∈ {1, −1}. This is equivalent to $\mathcal{S}\left(I{\pm}A\right)$ up to the factor of $4\enspace \mathrm{T}\mathrm{r}\left(\rho \frac{I+\alpha A}{2}\right)$, that is,

$$\begin{equation}\mathcal{S}\left(I+\alpha A\right)=4\enspace \mathrm{T}\mathrm{r}\left(\rho \frac{I+\alpha A}{2}\right){\mathcal{M}}_{A,\alpha },\end{equation} \tag{ 8 }$$

where ${\mathcal{M}}_{A,\alpha }$ is a measurement operation postselected with the measurement outcome α. $\mathrm{T}\mathrm{r}\left(\rho \frac{I+\alpha A}{2}\right)$ is the probability of getting the result α by measuring ρ on the A basis. Lemma 1 with this fact implies that the gate ${\text{e}}^{\text{i}\theta {A}_{1}\otimes {A}_{2}}$ can be decomposed, in a sense of equation (5), into a sum of I ⊗ I, A₁ ⊗ A₂, ${\mathcal{M}}_{{A}_{1}}\otimes {\mathrm{e}}^{{\pm}\mathrm{i}\pi {A}_{2}/4}$, and ${\mathrm{e}}^{{\pm}\mathrm{i}\pi {A}_{1}/4}\otimes {\mathcal{M}}_{{A}_{2}}$, which can be stated as lemma below. Notably, this technique can be applied for any θ, which enables us to perform continuous two-qubit gates.

Lemma 2. A quantum gate ${\text{e}}^{\text{i}\theta {A}_{1}\otimes {A}_{2}}$ with operators A₁ and A₂ such that ${A}_{1}^{2}=I$ and ${A}_{2}^{2}=I$ can be decomposed into six single-qubit operations. For any quantum state |ρ〉〉, to achieve the error of the decomposition with respect to the trace distance with probability at least 1 − δ, the required number of circuit runs is O(log(1/δ)/²).

The detailed proof is given in appendix B. Intuitively, since the error comes from the probabilistic part of the decomposition, that is the renormalization factor in equation (8) $\mathrm{T}\mathrm{r}\left(\rho \frac{I+\alpha A}{2}\right)$, if we want to estimate $\mathrm{T}\mathrm{r}\left(\rho \frac{I+\alpha A}{2}\right)$ within error , O(1/²) repetition would suffice.

Let us finally mention the case of the controlled-Z gate, which we denote by CZ. CZ can be decomposed into

$$\begin{equation}\text{C}\text{Z}={\text{e}}^{\text{i}\pi I\otimes Z/4}\enspace {\text{e}}^{\text{i}\pi Z\otimes I/4}\enspace {\text{e}}^{-\text{i}\pi Z\otimes Z/4},\end{equation} \tag{ 9 }$$

ignoring the global phase. This means we can decompose a CZ gate using lemma 2. The decomposition is shown in figure 2. Similar decompositions can be performed on some basic two-qubit gates such as CNOT. Endo et al [26] also provides such decomposition (reference [26], appendix B). However, our protocol above is slightly advantageous in that the number of single-qubit operations required is six compared to theirs which requires nine of them.

Zoom In Zoom Out Reset image size

In the previous subsection, we showed that any two-qubit rotation can be decomposed into a sum of single-qubit operations. Here, we extend the strategy to construct virtual non-destructive measurement of two-qubit operators. Similar to the previous section, we can show the following. This theorem is schematically shown in figure 1(b).

Lemma 3. For operators A₁ and A₂ such that ${A}_{1}^{2}=I$ and ${A}_{2}^{2}=I$,

$$\begin{align}\hfill \mathcal{S}\left(I+{A}_{1}\otimes {A}_{2}\right)& =\mathcal{S}\left(I\otimes I\right)+\mathcal{S}\left({A}_{1}\otimes {A}_{2}\right)+\frac{1}{8}\sum\limits _{\left({\alpha }_{1},{\alpha }_{2}\right)\in {\left\{{\pm}1\right\}}^{2}}{\alpha }_{1}{\alpha }_{2}\left[\mathcal{S}\left(\left(I+{\alpha }_{1}{A}_{1}\right)\otimes \left(I+{\alpha }_{2}{A}_{2}\right)\right)\right.\hfill \\ \hfill & \quad \left.-\mathcal{S}\left(\left(I+i{\alpha }_{1}{A}_{1}\right)\otimes \left(I+i{\alpha }_{2}{A}_{2}\right)\right)\right].\hfill \end{align} \tag{ 10 }$$

This can also be shown by the direct calculation of both hand side. See appendix A2 for detailed calculation.

The above lemma can be utilized to show the following.

Lemma 4. A non-local projection $\frac{I+{A}_{1}\otimes {A}_{2}}{2}$ with operators A₁ and A₂ such that ${A}_{1}^{2}=1$ and ${A}_{2}^{2}=2$ can be decomposed into six single-qubit operations. For any quantum state |ρ〉〉, to achieve the error of the decomposition with respect to the trace distance with probability at least 1 − δ, the required number of circuit runs is O(log(1/δ)/²).

This can be shown with exactly the same approach taken to prove lemma 2, which is provided in appendix B.

The idea of simulating a large quantum circuit by a small quantum computer has been put forward in reference [16]. Peng et al utilized the equivalence shown in figure 3. In the figure,

$$\begin{equation}\begin{aligned}\hfill {O}_{1}=I,& {\rho }_{1}=\vert 0\rangle \langle 0\vert ,\hfill & \hfill {c}_{1}=+1/2,\\ \hfill {O}_{2}=I,& {\rho }_{2}=\vert 1\rangle \langle 1\vert ,\hfill & \hfill {c}_{2}=+1/2,\\ \hfill {O}_{3}=X,& {\rho }_{3}=\vert +\rangle \langle +\vert ,\hfill & \hfill {c}_{3}=+1/2,\\ \hfill {O}_{4}=X,& {\rho }_{4}=\vert -\rangle \langle -\vert ,\hfill & \hfill {c}_{4}=-1/2,\\ \hfill {O}_{5}=Y,& {\rho }_{5}=\vert +i\rangle \langle +i\vert ,\hfill & \hfill {c}_{5}=+1/2,\\ \hfill {O}_{6}=Y,& {\rho }_{6}=\vert -i\rangle \langle -i\vert ,\hfill & \hfill {c}_{6}=-1/2,\\ \hfill {O}_{7}=Z,& {\rho }_{7}=\vert 0\rangle \langle 0\vert ,\hfill & \hfill {c}_{7}=+1/2,\\ \hfill {O}_{8}=Z,& {\rho }_{5}=\vert 1\rangle \langle 1\vert ,\hfill & \hfill {c}_{8}=-1/2,\end{aligned}\end{equation} \tag{ 11 }$$

where $\vert {\pm}\rangle =\left(\vert 0\rangle {\pm}\vert 1\rangle \right)/\sqrt{2}$ and $\vert {\pm}i\rangle =\left(\vert 0\rangle {\pm}i\vert 1\rangle \right)/\sqrt{2}$. The symbols ⊳ and ⊲ denotes the measurement of a certain observable and the preparation of a certain state, respectively. Contrasting this technique and ours, we refer to the former and the latter as 'time-like' and 'space-like' cut, respectively. More concretely, a time-like cut of a quantum channel can be defined as a decomposition of the channel in the sense of equation (5) using measure-and-prepare channels only. In contrast, a space-like cut of a non-local quantum channel is a decomposition of the channel using local quantum channels only.

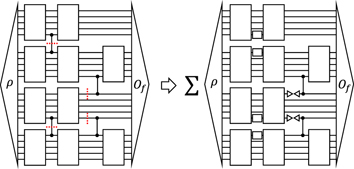
Zoom In Zoom Out Reset image size

The decomposition presented in the previous section can also be used in this direction. Let us compare the scaling of cost of our decomposition scheme and that of Peng et al by a simple example. We consider the case where we have an n-qubit quantum computer to simulate a 2n-qubit quantum circuit of figure 4, which has only one CZ gate between n-qubit 'cluster'. The task is to estimate the expectation value of a final observable O_f by measuring it in the computational basis. To simplify the discussion, we assume O_f is a string of Pauli Z's.

Zoom In Zoom Out Reset image size

Let v be a desired variance of the estimation of the expectation value of O_f . We can show a naive algorithm, which runs the equal number of circuits for each terms appearing in the decomposition, to perform the decomposition with time-like cuts, in the worst case, requires 2048/v runs of n-qubit circuit, while the space-like cut approach takes $\frac{15}{2v}$ runs. The analysis of this simple example is given in appendix D. Although the analysis given here is based on a naive algorithm and there are possibilities to improve it, this analysis somewhat shows the enhancement provided by our space-like cut protocol.

General case

We can consider a general case where we perform the time-like and space-like cuts simultaneously to make a given m-qubit quantum circuit runnable on an n-qubit quantum computer. Let the number of time-like and space-like cuts be M_t and M_s , respectively. See figure 5 for a schematic illustration. For space-like cuts, we assume they are performed only on CZ gates. The input state ρ is initialized in |0⟩⟨0|^⊗m and O_f is an output (diagonal) observable calculated from some output function f : {0, 1}^m → [−1, 1]. Our task here is to estimate the expectation $\mathbb{E}\left[f\left(y\right)\right]$ for a random bitstring y ∈ {0, 1}^m sampled from the original circuit. This model is adopted from reference [16] which originates in reference [20]. With this definition, we can get the following.

Zoom In Zoom Out Reset image size

Theorem 5. The number of n-qubit circuit runs required to estimate $\mathbb{E}\left[f\left(y\right)\right]$ within accuracy with some high probability 1 − δ is $O\left(\frac{{9}^{{M}_{s}}1{6}^{{M}_{t}}}{{{\epsilon}}^{2}}\enspace \mathrm{log}\left(\frac{1}{2\delta }\right)\right)$.

This implies that the decomposition of the circuit should be performed to minimize ${9}^{{M}_{s}}1{6}^{{M}_{t}}$. A detailed proof is given in appendix E, however, the above can roughly be explained as follows. At each space-like cut, we get six different sets of single-qubit operations, so M_s cuts induce ${6}^{{M}_{s}}$ terms. Likewise, M_t time-like cuts induce ${8}^{{M}_{t}}$ terms, which makes the total number of circuits in decomposition ${6}^{{M}_{s}}{8}^{{M}_{t}}$. With this decomposition, we can take a Monte-Carlo approach to estimate the sum, that is, we randomly choose circuits to run and average them. Hoeffding's inequality can be used to bound the error of such protocol, which states that if a magnitude of a random variable is always bounded by some constant a, then O(a²/²) samples would suffice to obtain an accuracy of . In this case, we are to estimate $\mathbb{E}\left[f\left(y\right)\right]={\sum }_{i=1}^{{6}^{{M}_{s}}{8}^{{M}_{t}}}{c}_{i}\langle \langle {O}_{f}\vert \mathcal{S}\left({V}_{i}\right)\vert \rho \rangle \rangle$ with i randomly drawn from $\left\{1,\dots ,{6}^{{M}_{s}}{8}^{{M}_{t}}\right\}$ and $\vert {c}_{i}\vert =1/{2}^{{M}_{s}+{M}_{t}}$, that is, $\mathbb{E}\left[f\left(y\right)\right]$ is estimated by ${\mathbb{E}}_{i}\left[{6}^{{M}_{s}}{8}^{{M}_{t}}{c}_{i}\langle \langle {O}_{f}\vert \mathcal{S}\left({V}_{i}\right)\vert \rho \rangle \rangle \right]$. The magnitude of random variable ${6}^{{M}_{s}}{8}^{{M}_{t}}{c}_{i}\langle \langle {O}_{f}\vert \mathcal{S}\left({V}_{i}\right)\vert \rho \rangle \rangle$ is roughly ${3}^{{M}_{s}}{4}^{{M}_{t}}$, thus we can apply the Hoeffding bound to get the result.

The theorem introduced above can be utilized to 'virtually' perform a two-qubit gate between qubits at distance. Figure 6 shows an example of such a virtual two-qubit gate. Notice that this protocol works irrespective of the distance between the qubits. Many swap gates are otherwise necessary for performing such gates, which makes them impractical on NISQ devices due to the non-negligible amount of decoherence and gate error of such devices.

Zoom In Zoom Out Reset image size

This protocol might be useful for the variational algorithms such as the variational quantum eigensolver (VQE) [9] and the quantum approximate optimization algorithms (QAOA) [12]. Here, we describe an example in the QAOA. In the QAOA, we seek to find a ground state of a Hamiltonian H on n-qubit which is a sum of Pauli Z's and its products. For example, a Hamiltonian may have the form of,

$$\begin{equation}H=\sum\limits _{ij}{J}_{ij}{Z}_{i}{Z}_{j}.\end{equation} \tag{ 12 }$$

The QAOA tries to solve the problem by converting it to an optimization problem of a continuous variable β and γ . The optimization of β and γ are performed so as to minimize the function,

$$\begin{equation}\langle H\left(\boldsymbol{\beta },\boldsymbol{\gamma }\right)\rangle =\langle +{\vert }^{\otimes n}{U}^{{\dagger}}\left(\boldsymbol{\beta },\boldsymbol{\gamma }\right)HU\left(\boldsymbol{\beta },\boldsymbol{\gamma }\right)\vert {+\rangle }^{\otimes n},\end{equation} \tag{ 13 }$$

where,

$$\begin{equation}U\left(\boldsymbol{\beta },\boldsymbol{\gamma }\right)={\text{e}}^{\text{i}{\boldsymbol{\beta }}_{p}\sum\limits _{i}{X}_{i}}\enspace {\text{e}}^{\text{i}{\boldsymbol{\gamma }}_{p}H}\dots {\text{e}}^{\text{i}{\boldsymbol{\gamma }}_{2}H}\enspace {\text{e}}^{\text{i}{\boldsymbol{\beta }}_{1}\sum\limits _{i}{X}_{i}}\enspace {\text{e}}^{\text{i}{\boldsymbol{\gamma }}_{1}H}.\end{equation} \tag{ 14 }$$

This algorithm has been experimentally demonstrated [13] with the connectivity of the target Hamiltonian being equivalent to the connectivity of the actual device.

The equivalence of the connectivity is almost necessary from the requirement to perform e^{i γ H} . This requirement can somewhat be relaxed by our protocol which enables qubits to virtually interact irrespective of the distance between them. Let us now assume that an available device has a square-lattice connectivity of figure 6, and a Hamiltonian of the QAOA which we aim to solve has an interaction between one pair of qubits that is not included in the hardware connectivity graph. In this case, to execute the QAOA circuit (equation (14)), we can use our space-like technique p times to virtually apply the unitary. The scaling of the cost can be bounded by setting M_t = 0 and M_s = p in theorem 5 which gives us a scaling of 9^{p −2} log[1/(2δ)]. The time-like cut approach of Peng et al [16] can also be utilized in this direction. However, as this approach would require 4 cuts per gate, the cost scaling is bounded by 16^{4p −2} log[1/(2δ)] by setting M_t = 4p and M_s = 0 in theorem 5. This demonstrates an advantage, albeit in this special settings, of our technique over the previous result.

In the context of the VQE, which is also an algorithm to find a ground state of a Hamiltonian but mainly targets a concrete physical system such as molecules, it has been proposed to use the same kind of quantum circuits as the QAOA [27, 28]. Our result may also be applicable in constructing such circuits.

Tensor representation of $\mathcal{S}\left({\text{e}}^{\text{i}\theta {A}_{1}\otimes {A}_{2}}\right)$ is,

$$\begin{align}\hfill & \langle \langle {e}_{i}{e}_{j}\vert \mathcal{S}\left({\text{e}}^{\text{i}\theta {A}_{1}\otimes {A}_{2}}\right)\vert {e}_{k}{e}_{l}\rangle \rangle =\langle \langle {e}_{i}{e}_{j}\vert \mathcal{S}\left(\mathrm{cos}\enspace \theta +i\enspace \mathrm{sin}\enspace \theta {A}_{1}\otimes {A}_{2}\right)\vert {e}_{k}{e}_{l}\rangle \rangle \hfill \\ \hfill & \qquad =\mathrm{T}\mathrm{r}\left({e}_{i}\otimes {e}_{j}\left(\mathrm{cos}\enspace \theta I+i\enspace \mathrm{sin}\enspace \theta {A}_{1}\otimes {A}_{2}\right){e}_{k}\otimes {e}_{l}\left(\mathrm{cos}\enspace \theta I-i\enspace \mathrm{sin}\enspace \theta {A}_{1}\otimes {A}_{2}\right)\right)\hfill \\ \hfill & \qquad ={\mathrm{cos}}^{2}\enspace \theta {a}_{1,ijkl}+i\enspace \mathrm{sin}\enspace \theta \enspace \mathrm{cos}\enspace \theta \left({a}_{6,ijkl}-{a}_{7,ijkl}\right)+{\mathrm{sin}}^{2}\enspace \theta {a}_{16,ijkl}.\hfill \end{align} \tag{ A5 }$$

Observe that,

$$\begin{equation}\begin{cases}\left\{+1,+i\right\}-\left\{+1,-i\right\}\quad \hfill \\ =2i\left({a}_{4}-{a}_{5}\right)+2i\left({a}_{6}-{a}_{7}\right)-2i\left({a}_{8}-{a}_{9}\right)+2i\left({a}_{12}-{a}_{13}\right),\quad \hfill \\ \left\{-1,+i\right\}-\left\{-1,-i\right\}\quad \hfill \\ =2i\left({a}_{4}-{a}_{5}\right)-2i\left({a}_{6}-{a}_{7}\right)+2i\left({a}_{8}-{a}_{9}\right)+2i\left({a}_{12}-{a}_{13}\right),\quad \hfill \\ \left\{+i,+1\right\}-\left\{-i,+1\right\}\quad \hfill \\ =2i\left({a}_{2}-{a}_{3}\right)+2i\left({a}_{6}-{a}_{7}\right)+2i\left({a}_{8}-{a}_{9}\right)+2i\left({a}_{12}-{a}_{13}\right),\quad \hfill \\ \left\{+i,-1\right\}-\left\{-i,-1\right\}\quad \hfill \\ =2i\left({a}_{2}-{a}_{3}\right)-2i\left({a}_{6}-{a}_{7}\right)-2i\left({a}_{8}-{a}_{9}\right)+2i\left({a}_{12}-{a}_{13}\right),\quad \hfill \end{cases}\end{equation} \tag{ A6 }$$

where we abbreviated the subscripts ijkl. We can solve the above for i(a₆ − a₇), and obtain

$$\begin{align}\hfill 8i\left({a}_{6}-{a}_{7}\right)& =\left\{+1,+i\right\}-\left\{+1,-i\right\}-\left\{-1,+i\right\}+\left\{-1,-i\right\}\hfill \\ \hfill & \quad +\left\{+i,+1\right\}-\left\{-i,+1\right\}-\left\{+i,-1\right\}+\left\{-i,-1\right\}\hfill \end{align} \tag{ A7 }$$

$$\begin{equation}=\sum\limits _{\boldsymbol{\alpha }\in {\left\{{\pm}1\right\}}^{2}}{\alpha }_{1}{\alpha }_{2}\left[\mathcal{S}\left(\left(I+{\alpha }_{1}{A}_{1}\right)\otimes \left(I+i{\alpha }_{2}{A}_{2}\right)\right)+\mathcal{S}\left(\left(I+i{\alpha }_{1}{A}_{1}\right)\otimes i\left(I+{\alpha }_{2}{A}_{2}\right)\right)\right].\end{equation} \tag{ A8 }$$

Combining this with equation (A5) completes the proof.

We first write down the tensor representation of the projective measurement, I + β A₁ ⊗ A₂ for β = ±1.

$$\begin{align}\hfill \langle \langle {e}_{i}{e}_{j}\vert \mathcal{S}\left(I+\boldsymbol{\beta }{A}_{1}\otimes {A}_{2}\right)\vert {e}_{k}{e}_{l}\rangle \rangle & =\mathrm{T}\mathrm{r}\left({e}_{i}\otimes {e}_{j}\left(I+\boldsymbol{\beta }{A}_{1}\otimes {A}_{2}\right){e}_{k}\otimes {e}_{l}\left(I+\boldsymbol{\beta }{A}_{1}\otimes {A}_{2}\right)\right)\hfill \\ \hfill & ={a}_{1,ijkl}+\boldsymbol{\beta }\left({a}_{6,ijkl}+{a}_{7,ijkl}\right)+{a}_{16,ijkl}\hfill \end{align} \tag{ A9 }$$

Similarly to the previous proof, observe that,

$$\begin{equation}\begin{cases}\left\{+1,+1\right\}-\left\{+1,-1\right\}\quad \hfill \\ =2\left({a}_{4}+{a}_{5}\right)+2\left({a}_{6}+{a}_{7}\right)+2\left({a}_{8}+{a}_{9}\right)+2\left({a}_{12}+{a}_{13}\right),\quad \hfill \\ \left\{-1,+1\right\}-\left\{-1,-1\right\}\quad \hfill \\ =2\left({a}_{4}+{a}_{5}\right)-2\left({a}_{6}+{a}_{7}\right)-2\left({a}_{8}+{a}_{9}\right)+2\left({a}_{12}+{a}_{13}\right),\quad \hfill \\ \left\{+i,+i\right\}-\left\{+i,-i\right\}\quad \hfill \\ =2i\left({a}_{4}-{a}_{5}\right)-2\left({a}_{6}+{a}_{7}\right)+2\left({a}_{8}+{a}_{9}\right)+2i\left({a}_{12}-{a}_{13}\right),\quad \hfill \\ \left\{-i,+i\right\}-\left\{-i,-i\right\}\quad \hfill \\ =2i\left({a}_{4}-{a}_{5}\right)+2\left({a}_{6}+{a}_{7}\right)-2\left({a}_{8}+{a}_{9}\right)+2i\left({a}_{12}-{a}_{13}\right),\quad \hfill \end{cases}\end{equation} \tag{ A10 }$$

We can solve the above for i(a₆ + a₇), and obtain,

$$\begin{align}\hfill 8\left({a}_{6}+{a}_{7}\right)& =\left\{+1,+1\right\}-\left\{+1,-1\right\}-\left\{-1,+1\right\}+\left\{-1,-1\right\}\hfill \\ \hfill & \quad -\left\{+i,+i\right\}+\left\{+i,-i\right\}+\left\{-i,+i\right\}-\left\{-i,-i\right\}\hfill \end{align} \tag{ A11 }$$

$$\begin{equation}=\sum\limits _{\boldsymbol{\alpha }\in {\left\{{\pm}1\right\}}^{2}}{\alpha }_{1}{\alpha }_{2}\left[\mathcal{S}\left(\left(I+{\alpha }_{1}{A}_{1}\right)\otimes \left(I+{\alpha }_{2}{A}_{2}\right)\right)-\mathcal{S}\left(\left(I+i{\alpha }_{1}{A}_{1}\right)\otimes \left(I+i{\alpha }_{2}{A}_{2}\right)\right)\right].\end{equation} \tag{ A12 }$$

Bravyi et al has considered to remove k qubits in a given n + k-qubit circuit at the cost of O(kd2^k ) classical computation, where d defined to be proportional to the number of gates applied to the k-qubit system. The technique utilized in their work, in particular, figure 2 in reference [20] can also provide a derivation to the above lemmas when combined with our recent technique developed in reference [28].

First, we consider the 'time-like' cut approach. Let us name two-qubit on which the CZ gate acts a and b, and let σ_a and σ_b be their 1-qubit reduced density matrices after the gate U₁ ⊗ V₁.

We assume,

• One n-qubit device is available.
• Qubits that are measured in the basis of an observable O_i can be reused to prepare the input state ρ_j .

We take the following naive approach to estimate ⟨O_f ⟩. First, divide the allowed number of circuit runs N into N/2 to run the divided circuit for equal times. N/2 runs are further divided into N/128 runs to run the circuit with O_i and ρ_j for i, j ∈ {1, 2, ..., 8}² [30]. With each N/128 runs with a pair (O_i , ρ_j ), we estimate the value of the tensor network below. Since we assumed O_f is a tensor product of Pauli Z's and O_i is drawn from I, X, Y, Z, from each run we obtain a measurement result o_ij,r = ±1, where r is the index to distinguish the runs. Using o_ij,r , we estimate the above tensor network by ${\tilde {o}}_{ij}=\frac{1}{N/128}{\sum }_{r=1}^{N/128}{o}_{ij,r}$. Since o_ij,r is a random variable which takes {+1, −1}, this estimator ${\tilde {o}}_{ij}$ approximately follows a normal distribution with an expectation $\mathbb{E}\left[{o}_{ij}\right]$ and a variance $\frac{1}{N/128}\left(1-\mathbb{E}{\left[{o}_{ij}\right]}^{2}\right){\leqslant}\frac{1}{N/128}$, for sufficiently large N. Therefore, with N/128 runs of a quantum circuit, we can estimate the value of the above tensor network with the variance $\frac{128}{N}$ at most. We can obtain the same result for the other cluster.

For each i, j, k, l, the tensor in the sum of figure 4 is estimated by the product of the above estimators because the measurement result is independent on each cluster. The variance of each tensor network can be evaluated because they are a product of two random variables approximately drawn from normal distribution with variance at most $\frac{128}{N}$, and it is at most $\frac{64}{N}$. We have that c_ijkl ∈ {±1/2⁴}. This reduces the variance of each term in the summation to 1/(2N). However, when we take the sum since each term can be approximated by a normal distribution with the variance at most 1/(2N) and we take summation of 8⁴ = 4096 terms, the result has the variance at most 2048/N.

For the space-like cut, we divide the allowed number of circuit runs, N, to N/6 [31]. First, we run eight circuits that do not involve the measurement in the middle and obtain estimators for these four tensor network. Each of the estimators has the variance at most 6/N. Let us now move on to the circuits with the measurement. For arbitrary density matrix ρ', the Z measurement produces the density matrix $\left(\frac{I+\alpha }{2}\right){\rho }^{\prime }\left(\frac{I+\alpha }{2}\right)/{p}_{\alpha }$ with probability p_α . Therefore, to obtain the above decomposition, we need to know the normalization factor p_α . With N/6 circuit runs, p_α is estimated to the variance p_α (1 − p_α )/(N/6) which is at most 6/(4N) = 3/(2N). Note that when N is large, the distribution of the estimator ${\tilde {p}}_{\alpha }$ can be thought of as a normal distribution. Conditioned on α, we construct an estimator of O_f . Since α is obtained with probability p_α , for each α we have p_α N/6 samples to estimate O_f . Therefore, for each α, the estimator of O_f has the variance of 6/p_α N. Since the estimator of the tensor network is the product of the estimators of conditioned O_f and p_α , its variance is $\frac{6}{N}\frac{1}{{p}_{\alpha }+1/\left[{p}_{\alpha }\left(1-{p}_{\alpha }\right)\right]}{\leqslant}\frac{3}{2N}$. Each pair of the tensor network in figure 2 is multiplied together, and if we perform this with the estimators obtained above, the variance of each term is at most $\frac{3}{N}$. We further multiply each term with ±1/2, then the variance is reduced to $\frac{3}{4N}$. Finally, the summation of 10 such term leads to the variance of $\frac{15}{2N}$.