Abstract
We report on coherent and dissipative coupling between a magnon mode and an anti-resonance of transmission in a cylindrical microwave cavity. By effectively suppressing coherent coupling, we observe the hybridized dispersion to change from level repulsion to level attraction. A careful examination reveals distinct differences in the line shape and phase evolution of transmission spectra between these coupling behaviors. For a quantitative understanding of the interactions between the magnon mode and the cavity anti-resonance, we develop a model which precisely describes our experimental observations, particularly, the signature in the line shape and phase of the microwave transmission. Our work sets a foundation for understanding strong coupling between magnon modes and cavity anti-resonances. In addition, it also confirms the ubiquity of level attraction in coupled magnon-photon systems, which may be helpful to develop future magnon-based hybrid quantum systems.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
During the last several decades, hybrid systems composed of two or more distinct components, ranging from photons, atoms, ions and spins to mesoscopic superconducting and nanomechanical devices, have been extensively studied for building future quantum technologies [1–3]. Through strong coupling interactions, such hybridized systems could combine the individual advantages of each component and build novel devices with multitasking capabilities. Although the coupling strength between a single spin and a microwave photon is very weak, stronger coupling can be achieved by the use of collective excitations (also called as magnons) in ferrimagnetic materials such as yttrium iron garnet (YIG, Y3Fe5O12) [4–9]. Various interesting phenomena, including the manipulation of spin current [10, 11], the magnon quintuplet state [12], the exceptional point [13] and the bistability of cavity magnon polaritons [14] have been demonstrated in strongly coupled magnon-photon systems. In addition to the fundamental uniform mode, coupling between photons and higher order non-uniform modes has also been studied, with coupling strength depending on the overlap between the magnon and caity modes [15, 16]. For multiple YIG samples coupled to a microwave cavity mode [17, 18], magnon dark modes have been observed, showing a way to couple distant magnetic systems. Currently, magnon-based hybrid systems have become a highly versatile platform for studying the coherent interactions between collective spin exciations and microwave photons, superconducting qubits [19], optical photons [20–22] and phonons [23, 24].
Experimentally, people often avoid placing magnetic samples at rf magnetic (h-) field nodes of a cavity mode, as here coherent magnon-photon coupling vanishes. However, dissipative coupling could dominate near this condition, where the cavity Lenz effect produces a microwave current that impedes the magnetization dynamics [25]. Instead of level repulsion with mode anticrossing seen in coherently coupled magnon-photon systems, dissipative coupled systems exhibit level attraction with a coalescence of hybridized magnon-photon modes [25–27]. Alternatively, Grigoryan and Xia have proposed an approach to explore level attraction [28] in hybrid magnon-photon systems, by modulating the relative phase [29] between coherent microwaves, and very recently Boventer et al [30] reported level attraction in these systems. Due to its potential applications in topological energy transfer, quantum sensing, and nonreciprocal photon transmission, level attraction has been of great interest in studies of other systems, such as in Bose–Einstein condensated quantum systems [31, 32], microcavity polariton systems [33] and cavity optomechanical systems [34–36].
The previous work [25], has reported the first discovery of level attraction in the coupled cavity magnon system and studied its physical origin. However, it still left a few important questions open. Firstly, the experiment of [25] was performed by using a special 1D Fabry–Perot-like cavity, which consists of a Ku-band circular waveguide with two circular-rectangular transitions. Considering the promising applications of level attraction, it is of high interest to study whether level attraction may ubiquitously exist in other cavity systems. Additionally, the previous work [25] has studied the dispersion and lineshape of level attraction, but left the phase characteristics unclear. Understanding the phase relationship in level attraction is very important because it provides a new angle to observe level attraction and may offer us an intuitive evidence to distinguish it from level repulsion.
In this paper, we report on the experimental realization of level attraction between magnon modes and microwave anti-resonances in a conventional cylindrical cavity. We confirm that the effect of level attraction is ubiquitous in hybridized magnon-photon systems and that coherent coupling must be effectively suppressed in order to observe it. As a result of competition between dissipative and coherent coupling, the coalescence of the hybridized dispersions, a signature of dissipative coupling, is not always clearly observed in experiments. After a careful examination of the phase evolution in hybridized magnon-photon systems, we provide unambiguous evidence of level attraction through the phase information of the magnon-like mode.
In the following sections, we first develop a transmission theory to explain anti-resonance as well as the coupling effects between cavity anti-resonance and magnon modes. Then experimental observations in both the level repulsion and level attraction cases are quantitatively compared to theoretical calculations in regards to the dispersion, line shape and phase of the microwave transmission.
2. Theoretical model
For a quantitative understanding of the anti-resonance in a microwave cavity as well as the strong interaction between a cavity anti-resonance and the magnon mode, we first deduce the transmission spectrum of the bare cavity based on the input–output theory [37–40]. Then, by considering the competition between the coherent and dissipative magnon-photon couplings, the transmission spectrum of the coupled anti-resonance and magnon system was obtained, which we compare with our experiment data.
2.1. The physics of an anti-resonance
In contrast to a resonance, the most important signature of an anti-resonance is a π phase jump accompanied by a pronounced low magnitude in transmission. Similar to resonances, anti-resonances widely exist in nearly all kinds of dynamic systems from mechanical oscillators [41, 42] to electrodynamic [43–47] and quantum systems [48–51]. Generally, the anti-resonance arises from destructive interference between the excitation and response of the system, which is different from the constructive interference during resonance. Both resonance and anti-resonance characterize specific response of a system to external driving.
To illustrate the nature of anti-resonance, we begin by analyzing the response of a coupled system consisting of two mechanical oscillators. The destructive interference behavior, which we highlight below, also governs the physics of a hybrid anti-resonance that is demonstrated in magnon-photon coupled systems [43]. As shown in the figure 1(a), the alternating force is directly applied on the first oscillator, and indirectly affects the second oscillator through the coupling spring between these two oscillators. Two eigenmodes exist in this coupled system, at which the oscillating amplitudes of the system reach the maximum, shown as the two peaks in figure 1(b). Correspondingly, both of their phases change from 0 to π (figure 1(c)). For each mode, the first oscillator keeps in phase with the excitation at low frequency, but becomes out of phase above the mode frequency. Besides these two resonances in this coupled system, an anti-resonance occurs at the uncoupled frequency of the second oscillator (see appendix A for mathematic details), which exhibits as a sharp dip between two resonant peaks in the response spectrum (figure 1(b)) and a rapid phase decrease from π to 0 in the phase spectrum (figure 1(c)). At this frequency, the excitation on the first oscillator destructively interferes with the back action from the second oscillator. Therefore, the first oscillator nearly keeps stationary at this frequency, which indicates the mechanical impedance of the first oscillator reaches the maximum at the anti-resonance. On the contrary, the second oscillator can still oscillate, even though its response is relatively small. By means of this unique property, anti-resonance is usually used to characterize the subsystem in a coupled system.
Figure 1. (a) Schematic picture of the anti-resonance existing in the coupled mechanical oscillator system. (b) and (c) The response and corresponding phase of the first oscillator which connects with the external excitation. (d) Schematic picture of the parallel RLC circuit with two ports, which can be viewed as the anti-resonance in microwave engineering. (e) and (f) The transmission spectrum and corresponding phase of this parallel RLC circuit.
Download figure:
Standard image High-resolution imageIn microwave engineering, the parallel RLC circuit (figure 1(d)) is sometimes also referred as the anti-resonance [45]. The impedance of the parallel circuit reaches the maximum at its resonant frequency, and therefore the incident signal is blocked by the circuit (see appendix B). As shown in the figures 1(e) and (f), the amplitude of transmission spectrum S21 reaches the minimum at the anti-resonant frequency with its phase sharply decreasing from π/2 to −π/2. Obviously, the parallel RLC circuit shows the similar properties with the anti-resonance in the coupled system both from their dynamic amplitudes and phases.
In addition, another kind of anti-resonances which exist in the multi-mode system can be derived from the destructive interference of consecutive modes such as in the mechanical structures [42]. Here, at a certain frequency between the frequencies of the two uncoupled resonances, the response of the first resonance cancels the response of the second resonance, causing a minimum response with respect to the driving force.
2.2. Input–output formalism for a cavity anti-resonance
Phenomenologically, anti-resonance in the transmission spectrum of a given microwave cavity can be treated as an equivalent parallel RLC circuit [45], which effectively blocks the incident signal at the resonant frequency due to its high impedance [45, 46]. For cavity resonance in the transmission spectrum, closed boundaries defined by discontinuous interfaces, such as the metallic walls of cavity, determine the resonant behavior. In this condition, input/output ports are perturbations of cavity resonance. However, for cavity anti-resonance in the transmission spectrum, the boundary conditions of the cavity become partially open, due to the connection between the inside and outside of the cavity via the input/output ports.
Considering the similarity between resonance and anti-resonance, for the purpose of calculating the transmission spectrum, we can use the same Hamiltonian to model the cavity photon state for both of them as:
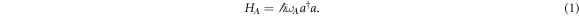
Here, 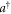 (a) represents the creation (annihilation) operator of the cavity photon, and ωA is the mode frequency. By connecting the cavity to the external photon bath, the equation of motion for the cavity photon in a Heisenberg representation can be written as:
(a) represents the creation (annihilation) operator of the cavity photon, and ωA is the mode frequency. By connecting the cavity to the external photon bath, the equation of motion for the cavity photon in a Heisenberg representation can be written as:
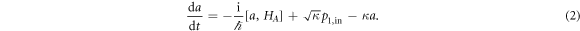
Here, 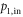 is the operator of input field from the port 1, and κ is the coupling strength between the external photon bath and cavity photon. Because of this coupling, additional port losses of cavity photon are generated, which are characterized by the last term in the equation.
is the operator of input field from the port 1, and κ is the coupling strength between the external photon bath and cavity photon. Because of this coupling, additional port losses of cavity photon are generated, which are characterized by the last term in the equation.
For a double-sided cavity, the output field from the port 2 depends on the specific properties of the cavity photon state. A cavity resonance opens a transmission channel between the input field 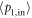 and the output field
and the output field 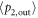 , so that the transmission reaches the maximum at this frequency. Off the resonance, the high impedance of cavity blocks the channel, and results in the decrease of transmission. This dynamic property can be well described by
, so that the transmission reaches the maximum at this frequency. Off the resonance, the high impedance of cavity blocks the channel, and results in the decrease of transmission. This dynamic property can be well described by 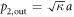 , and the resulting transmission coefficient is expressed as
, and the resulting transmission coefficient is expressed as  . For a cavity anti-resonance, in contrast, the transmission channel is blocked at the anti-resonant frequency due to the high impedance of cavity. Therefore, the transmission spectrum reaches the minimal value. Off the anti-resonance, the decrease of cavity impedance allows the input field
. For a cavity anti-resonance, in contrast, the transmission channel is blocked at the anti-resonant frequency due to the high impedance of cavity. Therefore, the transmission spectrum reaches the minimal value. Off the anti-resonance, the decrease of cavity impedance allows the input field  directly connecting with the output field
directly connecting with the output field  , and results in the increase of transmission. We adopt the input–output relation
, and results in the increase of transmission. We adopt the input–output relation 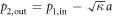 to describe the dynamic property of anti-resonance, and the transmission spectrum derived from this relation is
to describe the dynamic property of anti-resonance, and the transmission spectrum derived from this relation is 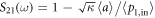 . Solving equation (2) and substituting the result into the transmission expression of the anti-resonance, we obtain:
. Solving equation (2) and substituting the result into the transmission expression of the anti-resonance, we obtain:

The parameter β is the cavity intrinsic damping rate. For other cases of anti-resonance in multi-resonance systems discussed in section 2.1, a similar transmission function can be deduced using the appropriate approximations. Note that usually κ > βωA due to the high impedance nature of the cavity anti-resonance, but the large extrinsic damping rate κ does not change the sharp phase transition feature (as shown in figure 1) that is determined by the intrinsic damping parameter β. Hence, the cavity anti-resonance may be used for studying light–matter interactions in open quantum systems characterized by a low intrinsic but a large extrinsic damping.
In the emerging field of cavity spintronics, strong coupling between cavity resonances and magnon modes have been extensively studied [4–10, 14, 15, 17, 18, 20, 24]. In the following, we present the theoretical and experimental study of strong coupling between a cavity anti-resonance and a magnon mode.
2.3. A general model of level attraction and level repulsion for magnons coupled with a cavity anti-resonance
By placing a YIG sphere in the cavity, strong interactions between cavity photons and magnons can produce not only level repulsion, but also level attraction. According to the detailed discussion in [25], the coupling features in a coupled cavity magnon system are determined by three different electrodynamic principles, i.e. Ampère's Law (KA term), Faraday's Law (KF term) and Lenz's Law (KL term). Specifically, the inductive current of the cavity circuit produces an rf-field (Ampère's Law), which drives spin precession in the magnon system. Because the magnetic flux of the cavity is altered by the spin precession, an additional current is generated in the cavity circuit (Faraday's Law). Usually, these two effects dominate, leading to coherent coupling in the cavity magnon system. However, when the YIG sphere is placed at an h-field node of the cavity mode, the coherent coupling vanishes and the cavity Lenz effect becomes dominant. As a result, the current induced by the spin precession in the cavity circuit will produce another rf h-field, which applies a drag torque to the spin and impedes the spin precession. Depending on the relative magnitudes of the drive torque and drag torque on the spin, the coupling effect in the cavity magnon system could be either coherent or dissipative. In the presence of both coherent and dissipative coupling, the coupling interaction can be generalized by an equivalent non-Hermitian Hamiltonian as
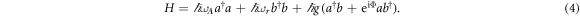
Here, 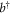 (b) represents the creation (annihilation) operator of the magnon mode and ωr is the frequency of the magnon mode. The coupling phase Φ describes the competing coherent and dissipative couplings: Φ = 0 for level repulsion and Φ = π for level attraction [25].
(b) represents the creation (annihilation) operator of the magnon mode and ωr is the frequency of the magnon mode. The coupling phase Φ describes the competing coherent and dissipative couplings: Φ = 0 for level repulsion and Φ = π for level attraction [25].
Taking into account of the intrinsic damping rate α and β for the magnon and cavity anti-resonance, respectively, the equation of motion for this coupled system isolated with the photon bath in the Heisenberg representation can be derived from equation (4), which has the following form:
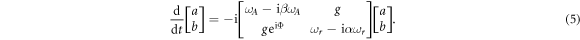
The real parts of the coupling matrix's eigenvalues are the eigen-frequencies of hybridized modes in the coupled system expressed as:
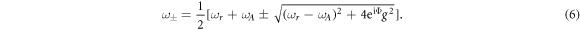
Using input–output theory for the anti-resonance, we can further obtain the transmission spectrum of the magnon-antiresonance coupled system as:

Here, the coupling term is determined by  , where KF, KA and KL are real numbers [25]. If the driven torque resulting from Ampère's Law is dominant, we have KA > KL, and hence Φ = 0 which indicates the coherent coupling is dominant. Otherwise, the drag torque resulting from Lenz's Law becomes dominant, where we have KA < KL, and hence Φ = π which means the dissipative coupling becomes dominant. By setting either Φ = 0 or Φ = π, this equation can well describe the observed transmission spectra for either level repulsion or level attraction, respectively.
, where KF, KA and KL are real numbers [25]. If the driven torque resulting from Ampère's Law is dominant, we have KA > KL, and hence Φ = 0 which indicates the coherent coupling is dominant. Otherwise, the drag torque resulting from Lenz's Law becomes dominant, where we have KA < KL, and hence Φ = π which means the dissipative coupling becomes dominant. By setting either Φ = 0 or Φ = π, this equation can well describe the observed transmission spectra for either level repulsion or level attraction, respectively.
3. Experiment results and discussion
The experiments were performed by inserting a YIG sphere (1 mm diameter) into a cylindrical microwave cavity. This cavity is a multi-mode system with both resonances and anti-resonances, and is made of oxygen free copper with an inner diameter of 25 mm. To make its mode frequencies tunable, the top of cavity is fixed with a screw, and the height of cavity can be tuned continuously from 19 to 44 mm, as shown in figure 2(a). Four ports close to the bottom are available to configure the transmission measurement using a vector network analyzer. Unless other specified, the two-port scattering parameters were measured at a parallel-port configuration.
Figure 2. (a) Schematic picture of the tunable cylindrical cavity. An YIG sphere is placed in the cavity to produce the coupling effects between the cavity anti-resonance and magnon system. (b) The transmission spectra of the cylindrical cavity measured at different heights. Resonances and anti-resonances of the cylindrical cavity are represented as blue and red colors, respectively. Both of them vary as a function of the cavity height. The dashed lines and solid lines are the simulated frequencies of resonance and anti-resonance, respectively. (c) Two typical spectra of the cylindrical cavity measured at a height of 35 mm with two parallel (solid line) or vertical (dashed line) ports. Besides the resonances labeled as TE or TM modes in the figure, several anti-resonances can be observed in the spectrum. (d) and (e) A zoomed-in view of the amplitude and phase evolution of the anti-resonance at 13.59 GHz. The purple and green circles in (d) represent the reflection  and transmission
and transmission 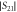 , respectively. The yellow circles in (e) represent the measured phase evolution of anti-resonance. The red solid lines are the CST simulation results, and black dashed lines are the calculated results using equation (3).
, respectively. The yellow circles in (e) represent the measured phase evolution of anti-resonance. The red solid lines are the CST simulation results, and black dashed lines are the calculated results using equation (3).
Download figure:
Standard image High-resolution image3.1. Anti-resonance characterization in a microwave cavity
Figure 2(b) maps the measured transmission spectrum of the empty cavity at different heights. Besides the cavity modes (blue color), we have also observed several anti-resonances (red color) occurring at some height ranges. Black dashed lines and solid lines indicate the simulated frequencies of resonances and anti-resonances by Computer Simulation Technology Microwave studio (CST MWS), which well reproduce experimental observations. A typical transmission spectrum at the height of 35 mm is shown as the solid line in figure 2(c). Resonant peaks in this spectrum indicate the traditional cavity modes which have been labeled as TE or TM modes according to their mode profiles. In addition, three sharp dips corresponding to anti-resonances occur at 12.52 GHz, 13.59 GHz and 14.62 GHz, respectively.
Through the CST simulation, we also found that unlike for resonances, the frequency of anti-resonance is very sensitive to the port positions. To verify this effect, we performed another experiment measuring the S21 spectrum at a perpendicular-port configuration and the result at a height of 35 mm is shown as the red dashed line in figure 2(c). It is clear to see that in both configurations the resonance frequencies are uncharged; however, anti-resonances show a significant difference. Those three anti-resonances observed in a parallel-port configuration disappear, and two new anti-resonances appear at 9.84 and 10.52 GHz with ports vertical. This observation indicates the different origins of the resonance and anti-resonance in this cylindrical cavity. The constructive interference of resonance is caused by the metallic walls of the cavity, and is not sensitive to the port position, and its maximum transmission amplitude is determined by the energy exchange rate (transmittance) between the cavity and photon bath. In contrast, the destructive interference of anti-resonance is very sensitive to the distance between the two ports and its minimum transmission amplitude is determined by the reflectivity.
In the following experiment, we select the anti-resonance at 13.59 GHz to demonstrate the coupling effects between an anti-resonance and magnon system, because it has sufficient separation from other modes. Figures 2(d) and (e) show the amplitude of the S-parameter and the phase of S21 around the anti-resonant frequency, respectively. The purple circles in figure 2(d) represent the reflection S11 of the anti-resonance, which is close to unity as expected and hence results in a large κ. From the transmission (S21), cavity anti-resonance is defined as the minimal transmission, which can be resolved on a dB scale and well fitted by equation (3) (black dashed lines). The coupling strength κ/2π and intrinsic damping factor of the cavity photon β are deduced to be 14.99 GHz and 2.96 × 10−4, respectively. Note that due to the nature of the cavity anti-resonance, κ/2π is far larger than the intrinsic damping βωA. In addition, simulation results are also plotted, which can well reproduce the amplitude and phase changes.
3.2. Dispersion of level attraction and level repulsion
After characterizing the spectrum of anti-resonances in this standard cylindrical cavity, we have designed an experiment to study the coupling effects between the anti-resonance and magnon system. Before performing the coupling experiment, the three-dimensional mode profile of the anti-resonance at 13.59 GHz was simulated, and figure 3(a) shows the strength of the rf h-field over three cross-sections. Among them, the x–y view shows a cross section of the rf h-field distribution at 28 mm above the bottom of the cavity, which exhibits a highly spatial symmetry with four nodes along x, y, −x and −y. In the coupling experiment, a 1 mm YIG sphere was placed in this cross section. Markers A and B labeled in figure 3(a) show two positions of the YIG sphere in the cavity. The external magnetic field H is applied along the x direction. The other two cross-sections correspond to the x–z plane at y = 0 and the y–z plane at x = 0, respectively. All of them clearly indicate that the rf magnetic field at position A is very weak, which is required in order to observe level attraction in coupled photon-magnon systems [25].
Figure 3. (a) The rf field distribution of the anti-resonance occurring at 13.59 GHz from three different views. The red and blue colors in the figure represent maximum and minimum field intensities, respectively. Note the field distribution in the x–y section which is 28 mm above from bottom of the cavity and exhibits high spatial symmetry. The relative positions of the YIG sphere in the rf field have been labeled as A and B. (b) and (c) Level attraction and level repulsion between the anti-resonance and the magnon mode are observed, when the YIG sphere was put at position A and position B, respectively. The white and black dashed lines in both figures represent the uncoupled magnon mode and anti-resonance at different external fields. (d) and (e) The normalized derivatives of the transmission phase with respect to the frequency (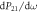 ) are plotted as a function of the external field for level attraction and level repulsion, respectively. Green dashed lines in both figures indicate the calculated dispersions of hybridized modes (possessing anti-resonant features) for these two cases using equation (6). The blue color in both mappings indicates resonance arising from the coupling effects between the anti-resonance and magnon mode. The yellow dashed lines in both figures indicate the calculated dispersions of the resonances.
) are plotted as a function of the external field for level attraction and level repulsion, respectively. Green dashed lines in both figures indicate the calculated dispersions of hybridized modes (possessing anti-resonant features) for these two cases using equation (6). The blue color in both mappings indicates resonance arising from the coupling effects between the anti-resonance and magnon mode. The yellow dashed lines in both figures indicate the calculated dispersions of the resonances.
Download figure:
Standard image High-resolution imageWe first placed the YIG sphere at position A, where the drag torque due to the cavity Lenz' Law is more dominant than the driven torque resulting from Ampère's Law, i.e. KL > KA. Therefore, the coupling effects between the cavity anti-resonance and the magnon mode is dissipative, which tends to impede magnetization dynamics. As expected, level attraction was observed, as seen in figure 3(b), where the white and black dashed lines represent the uncoupled magnon mode and the cavity anti-resonance at different external fields. The magnon mode follows the dispersion ωr = γ(H + HA), where γ = 2π × 25.3μ0 GHz/T, 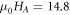 mT is the magnetocrystalline anisotropy field, and the damping factor α of the magnon mode is 1.2 × 10−4. The coupling between the cavity anti-resonance and magnon mode leads to two hybridized modes. Both of them appear as hybridized anti-resonances in spectra, and we will explain them in detail in section 3.3 by studying their phase spectra.
mT is the magnetocrystalline anisotropy field, and the damping factor α of the magnon mode is 1.2 × 10−4. The coupling between the cavity anti-resonance and magnon mode leads to two hybridized modes. Both of them appear as hybridized anti-resonances in spectra, and we will explain them in detail in section 3.3 by studying their phase spectra.
Besides the mapping of transmission spectra for level attraction (figure 3(b)), a mapping of normalized derivatives of transmission phase with respect to the frequency (dP21/dω) has also been plotted in figure 3(d), which can offer us another intuitive picture to understand level attraction in the coupled cavity anti-resonance and magnon system. dP21/dω is proportional to the reciprocal of photon group velocity in the system. Therefore, red and blue colors in the mapping can equivalently indicate the decrease or enhancement of group velocities for different modes. It is clear to see that two hybridized modes with red colors gradually merge with each other. Green dashed lines are the calculated dispersions of these two hybridized modes using equation (6) with g/2π = 21.4 MHz and Φ = π. In addition, the magnon-photon coupling also produces a resonance at the uncoupled magnon mode frequency, similar to the physics of the coupled oscillator model discussed in the section 2.1, where the coupling of two resonances produces an anti-resonance at the uncoupled frequency of the second oscillator. Here, the coupling of two anti-resonances produces a resonance due to the destructive interference effect, which enhances the photon group velocity (blue color). Indeed, it well follows the frequency of the uncoupled magnon mode (yellow dashed line).
In contrast, when the YIG sphere is placed at position B, the driven torque becomes dominant. In this case, the anti-resonance and the magnon mode are coherently coupled. Two uncoupled modes (the black and white dashed lines in figure 3(c)) hybridize with each other and shift towards opposite directions in the frequency domain. The normalized derivatives of transmission phase with respect to the frequency (dP21/dω) have been plotted in figure 3(e), which clearly indicate the frequencies of two hybridized modes in the coupled cavity anti-resonance and magnon system (red color). Using g/2π = 59 MHz and Φ = 0, the calculation result (green dashed lines) of equation (6) well reproduces the frequencies of two hybridized modes. Again, as described by the coupled oscillator model, an additional resonance appears at the uncoupled magnon frequency in this level repulsion case (blue color). The striking contrast between figures 3(b), (d) and 3(c), (e) clearly reveals the distinguished coupling features between level attraction and level repulsion.
3.3. Line shape and phase evolution of transmission spectra
To study the line shape evolution of the transmission spectra in the strongly coupled range, five pairs of typical spectra selected from figures 3(b) and (c) (indicated by the arrows) were plotted in figures 4(a) and (b). Each spectrum of either the level attraction or the level repulsion contains two dips and one peak. For these two dips, one is the cavity-photon-like hybridized mode and the other is the magnon-like hybridized mode. At the frequency of uncoupled magnon mode, a resonant peak occurs from the coupling effect. Because of the superposition of the magnon-like hybridized mode and the resonant peak, the line shape of transmission near the magnon-like hybridized mode is in general anti-symmetric5
. As shown in figure 3(d), interestingly, the dispersion of resonant peak occurs at outside of the two hybridized modes. However, in the level repulsion case, the resonant peak occurs between them (figure 3(e)). The different sequences of anti-resonant dips and the resonant peak in the frequency domain result in different polarities of the transmission line shape near the magnon-like hybridized mode. From figures 4(a) and (b) we see that (1) the polarity of the asymmetry changes as it passes through the cavity mode frequency ωA; and (2) the polarity of the line shape is opposite between the case of level attraction and level repulsion. To qualitatively explain this striking observation, we use the fact that 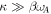 to simplify the equation (7) and obtain
to simplify the equation (7) and obtain
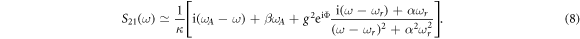
Figure 4. (a) Individual transmission spectra (dots) selected from figure 3 (indicated by arrows) are shown for level attraction (a) and level repulsion (b). Red solid lines in both figures are the calculation results using equation (7). Correspondingly, the phase of the transmission spectra shown in (a) and (b) have been plotted in (c) and (d). Dots and solid lines represent the experiment data and calculation results, respectively. Black dashed lines in both figures indicate 0° for each phase curve using equation (7).
Download figure:
Standard image High-resolution imageThe resonant feature is caused by the third term in the bracket, which includes both the symmetric and anti-symmetric line shapes [29]. The calculated result, by using either equation (7) or (8), shows that (1) the polarity of the asymmetry changes with the sign of ωA − ω for both Φ = 0 and Φ = π and (2) the polarity of the whole line shape reverses between Φ= 0 and Φ = π. Physically, in the first case, the induced field of cavity with respect to the excitation has π phase shift with respect to the cavity anti-resonance. Consequently, the magnon mode driven by this induced field has π phase difference between these two conditions of ω < ωA and ω > ωA. As for the second case, depending on whether the interaction from the cavity anti-resonance to the magnon mode is the driven torque or drag torque, a π phase difference of the magnon mode would also be induced between these two situations. In both cases, the π phase difference can result in the polarity reverse of line shape near the magnon-like hybridized mode in the spectra. As shown in figures 4(a) and (b), the agreement between experimental line shape (symbols) and the calculation (solid lines) is excellent.
Correspondingly, the phase change in these five pairs of spectra has also been plotted for comparison, as shown in figures 4(c) and (d). Near the condition of ω = ωA = ωr, a single 2π-phase jump appears for level attraction, while for level repulsion two π-phase drops, corresponding to two hybridized anti-resonance modes, can be observed along with an additional opposite π-phase jump between them. At the condition of ωr < ωA, the cascaded phase of the resonant peak and the magnon-like hybridized mode merge as a peak lying on the top of the phase background (∼π/2) for level attraction and a dip for level repulsion. In contrast, at the condition of ωr > ωA, the cascaded phase of the magnon-like hybridized mode and the resonant peak merge as a dip lying on the bottom of the phase background (∼ −π/2) for level attraction and a peak for level repulsion.
These features can be intuitively understood by considering the relative sequences of anti-resonant dips and resonant peak at different external field, shown in figures 3(d) and (e). In the case of level attraction for instance, at the condition of ωr < ωA, the frequency of resonant peak is lower than the magnon-like anti-resonance. As we have mentioned in section 2.1, resonance corresponds to a π phase increase, while anti-resonance corresponds to a π phase decrease. Therefore, the cascade phase near the magnon-like hybridized mode increases first, and then decreases. Consequently, a peak occurs on the top of the phase background. Similarly, we can easily explain the phase behavior near the magnon-like hybridized mode at the condition of ωr > ωA. Specially, the 2π phase drop in the level attraction case at the condition of ωr = ωA can be explained by the coalescence of two hybridized anti-resonance modes.
As shown in figures 4(c) and (d), the experimental line shape (symbols) and the calculation (solid lines) is in excellent agreement without any adjusting parameters. Even though the magnitude and phase spectra of the microwave transmission exhibit contrasting characteristics between level attraction and level repulsion, all of them can be well reproduced using either equation (7) or (8). This confirms the validity of our model for analyzing and fitting the transmission spectra for both coherent and dissipative coupled magnon-photon systems.
3.4. Consecutive transition from level repulsion to level attraction
To further reveal the tunability of the coupling effects in the cylindrical cavity, another experiment has been designed to observe the transition from level repulsion to level attraction. The experiment set-up is shown as the insert of figure 5(a), where the simulated rf h-field distribution clearly shows a four-fold symmetry. Therefore, by rotating the YIG sphere within the cavity a distance of 6 mm from the outer edge, the relative impact of Ampère's Law and Lenz's Law can be manipulated continuously. As a result, the coupling strength g as a function of the angular position θ for the YIG sphere should reflect such a symmetry.
Figure 5. (a) Coupling strength g between the coupled anti-resonance and magnon system measured at different angles. Green and blue dots respectively indicate the range where level repulsion and attraction occur. The red dashed line describes 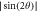 . The insert shows a schematic picture of the experiment set-up. The YIG sphere is rotated within the cavity 6 mm from the outer edge. (b) and (c) Typical transmission spectra mappings for the level repulsion at 45° and level attraction at 90°. Dashed lines in both figures are the calculation results using equation (6).
. The insert shows a schematic picture of the experiment set-up. The YIG sphere is rotated within the cavity 6 mm from the outer edge. (b) and (c) Typical transmission spectra mappings for the level repulsion at 45° and level attraction at 90°. Dashed lines in both figures are the calculation results using equation (6).
Download figure:
Standard image High-resolution imageSetting θ = 45° (or an odd multiple of 45°) at an rf h-field anti-node, level repulsion occurs as shown in figure 5(b). By fitting the dispersion (dashed lines) according to equation (6), the deduced coupling strength is g/2π = 32 MHz. Rotating to θ = 90° (or an integer multiple 90°), at an rf h-field node, level attraction appears in figure 5(c) with a coupling strength of g/2π = 16 MHz.
The determined coupling strength g as a function of the angular position θ of the YIG sphere is summarized in figure 5(a) using the solid circles for level attraction and open circles for level repulsion. The dotted line follows a simple 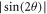 relation according to the linear dependence of the coherent coupling strength on the local h-field strength of the mode profile. It is clearly seen that this simple model cannot fully explain our experimental results because level attraction is beyond this model. In figure 5(a) we can find two distinct coupling regions: the level attraction region for θ near integer multiples of 90° (over a range of about ±6°) and level repulsion for θ near odd multiples of 45° (over a range of about ±39°). Experiments also indicate that the range of level attraction expands when the YIG is placed closer to the center of the circle. All these features are consistent with the results discussed based on the classical picture in [25], confirming that two competing magnon-photon coupling effects coexist in general experimental conditions. Only by minimizing the coherent coupling caused by the h-field torque, the dissipative magnon-photon coupling would reveal, allowing the observation of level attraction.
relation according to the linear dependence of the coherent coupling strength on the local h-field strength of the mode profile. It is clearly seen that this simple model cannot fully explain our experimental results because level attraction is beyond this model. In figure 5(a) we can find two distinct coupling regions: the level attraction region for θ near integer multiples of 90° (over a range of about ±6°) and level repulsion for θ near odd multiples of 45° (over a range of about ±39°). Experiments also indicate that the range of level attraction expands when the YIG is placed closer to the center of the circle. All these features are consistent with the results discussed based on the classical picture in [25], confirming that two competing magnon-photon coupling effects coexist in general experimental conditions. Only by minimizing the coherent coupling caused by the h-field torque, the dissipative magnon-photon coupling would reveal, allowing the observation of level attraction.
4. Conclusions
In summary, we have studied the coupling phenomena between a magnon mode and a transmission anti-resonance of a conventional cylindrical cavity. The effects of both level repulsion and level attraction have been observed by controlling the coherent coupling and dissipative coupling in such a system. While level attraction was first observed in a specially designed 1D Fabry–Perot-like microwave cavity, our results confirm that level attraction is as ubiquitous as level repulsion in cavity magnonic systems as predicted in [25]. By careful analysis, in this paper we have revealed the distinguished signatures of coherent coupling and dissipative coupling in both the line shape and phase evolution of the microwave transmission. This knowledge is important in order to explore hidden level attraction in other hybrid systems, particularly when dissipative coupling caused by negative back-action is comparable to coherent coupling. Furthermore, like electromagnetically induced transparency, where the coherent coupling renders a medium transparent within a narrow spectral range around a broad transmission line, a similar pattern accompanied by a rapid phase change (giving rise to slow light) has been also observed for dissipative coupling. As the phase evolution and hence the group velocity can be well predicted by our model, level attraction may become a new avenue for producing slow light in cavity photonic systems.
Acknowledgments
This work has been funded by NSERC, the National Natural Science Foundation of China Grant No. 11429401, the China Scholarship Council. We would like to thank H Tang, X Han, P Hyde, Y Yang, I Proskurin, R L Stamps, L H Bai, and M Harder for discussions and/or helps, and we also acknowledge CMC Microsystems for providing equipment that facilitated this research.
Appendix A.: Dynamics of the coupled oscillators
In this section, we mathematically discuss a coupled system consisting of two mechanical oscillators (or pendulums) (figure 1(a)) to clarify the dynamic properties of the anti-resonance in this kind of systems. If the amplitudes of two oscillators, θ1 and θ2, are relatively small, then both of them can be treated as linear systems. The equations of motion for them are:
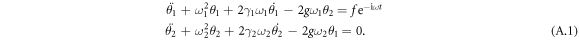
Here, γ1 and γ2 represent the damping rates of these two oscillators, respectively. g is the coupling strength between them.  is the alternating force applied on the first oscillator and normalized by its mass. By solving these equations and using the approximation (ω + ω1,2) ≈ 2ω1,2, we can get the responses of these two oscillators, R1(ω) and R2(ω), with respect to the driving force:
is the alternating force applied on the first oscillator and normalized by its mass. By solving these equations and using the approximation (ω + ω1,2) ≈ 2ω1,2, we can get the responses of these two oscillators, R1(ω) and R2(ω), with respect to the driving force:
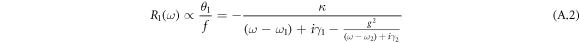

Here, κ represents the coupling strength between the driven force and the first oscillator. This coupling effect opens an additional dissipative channel for the first oscillator, and therefore enhances its damping rate. During the derivation, we used a lumped damping rate γ1 to represent the total damping of the first oscillator which satisfies the relation γ1 > κ.
By re-organizing the response function R1(ω) for a strongly coupled case (g2 > (γ1 − κ)γ2), we can get a much conciser form:
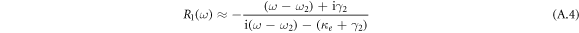
and
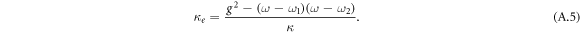
According to this new form, it is obvious to see that R1(ω) reaches a minimum at ω2 which is the uncoupled frequency of the second oscillator. Actually, this frequency corresponds the anti-resonant frequency of this coupled system. Strikingly, the intrinsic damping of the anti-resonance is exactly same as for the uncoupled second oscillator. Thus, anti-resonance in this coupled system can be used to characterize dynamic properties of the second oscillator. Additionally, κe is an equivalently extrinsic damping which is frequency dependent and results in the asymmetric line shape of the anti-resonance.
Appendix B.: Parallel RLC circuit
Besides the anti-resonance in the coupled system, the parallel RLC circuit in microwave engineering is also referred as anti-resonance [45]. Its impedance near the resonant frequency has the form:
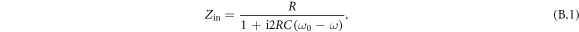
Here, R and C are the resistance and capacitance of the RLC circuit, respectively. ω0 is the resonant frequency, and the impedance of this parallel RLC circuit reaches the maximum at this frequency. Note that we assume both the current and voltage follow the form of 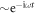 during the derivation. By using the ABCD matrix, we can calculate the transmission spectrum of the parallel RLC circuit as shown in the figure 1(d), which has the form:
during the derivation. By using the ABCD matrix, we can calculate the transmission spectrum of the parallel RLC circuit as shown in the figure 1(d), which has the form:
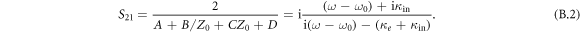
κe and κin used here respectively represent the extrinsic damping from the ports and the intrinsic damping of circuit which follow the forms of 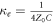 and
and 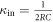 . At the resonant frequency, transmission of parallel circuit reaches the minimum, which indicates the incident signal is blocked by this circuit. Comparing the transmission spectrum S21 with the response function of the first oscillator R1(ω) in appendix A, except π/2 phase difference, they have a similarly mathematical form which indicates these two types of anti-resonances exhibit common dynamic properties, such as the minimal response and phase dive with the external excitation.
. At the resonant frequency, transmission of parallel circuit reaches the minimum, which indicates the incident signal is blocked by this circuit. Comparing the transmission spectrum S21 with the response function of the first oscillator R1(ω) in appendix A, except π/2 phase difference, they have a similarly mathematical form which indicates these two types of anti-resonances exhibit common dynamic properties, such as the minimal response and phase dive with the external excitation.
Footnotes
- 5
The anti-symmetric line shape of the magnon-like mode can be clearly observed via the decibel scale.








