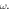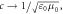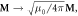Abstract
We examine the momentum and angular momentum (AM) properties of monochromatic optical fields in dispersive and inhomogeneous isotropic media, using the Abraham- and Minkowski-type approaches, as well as the kinetic (Poynting-like) and canonical (with separate spin and orbital degrees of freedom) pictures. While the kinetic Abraham–Poynting momentum describes the energy flux and the group velocity of the wave, the Minkowski-type quantities, with proper dispersion corrections, describe the actual momentum and AM carried by the wave. The kinetic Minkowski-type momentum and AM densities agree with phenomenological results derived by Philbin. Using the canonical spin–orbital decomposition, previously used for free-space fields, we find the corresponding canonical momentum, spin and orbital AM of light in a dispersive inhomogeneous medium. These acquire a very natural form analogous to the Brillouin energy density and are valid for arbitrary structured fields. The general theory is applied to a non-trivial example of a surface plasmon-polariton (SPP) wave at a metal-vacuum interface. We show that the integral momentum of the SPP per particle corresponds to the SPP wave vector, and hence exceeds the momentum of a photon in the vacuum. We also provide the first accurate calculation of the transverse spin and orbital AM of the SPP. While the intrinsic orbital AM vanishes, the transverse spin can change its sign depending on the SPP frequency. Importantly, we present both macroscopic and microscopic calculations, thereby proving the validity of the general phenomenological results. The microscopic theory also predicts a transverse magnetization in the metal (i.e. a magnetic moment for the SPP) as well as the corresponding direct magnetization current, which provides the difference between the Abraham and Minkowski momenta.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction and overview
1.1. Abraham and Minkowski momenta
The characterization of the momentum and angular momentum (AM) of light in continuous media is a long-standing problem, with the Abraham–Minkowski discussion in its center; see [1–5] for reviews. Although recently there were several works claiming the 'resolution' of the Abraham–Minkowski controversy [5–7], debates on various aspects of optical momentum in media are still continuing. Naturally, different momenta can manifest in different types of problems or experiments. For example, one can investigate optical forces acting on the medium or on a small material probe in the medium [7–10]. On the other hand, one may wonder about the momentum carried by the wave per se and characterizing wave parameters such as the velocity of its propagation (phase or group) or wave vector [11–19]. In this work we mostly stick with the second approach. Throughout this paper we consider monochromatic waves with fixed frequency  lossless isotropic media described by permittivity and permeability
lossless isotropic media described by permittivity and permeability  and
and  (which can depend on
(which can depend on 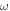 in the dispersive case), and cycle-averaged dynamical properties (energy, momentum, and AM) of waves.
in the dispersive case), and cycle-averaged dynamical properties (energy, momentum, and AM) of waves.
To recall the basics of the problem, we start with the Poynting momentum density of monochromatic light in free space [20–22]:
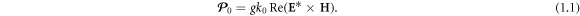
Hereafter, we use Gaussian units6
with 
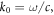 and all free-space quantities are marked by the subscript '0'. In a non-dispersive medium, the Abraham and Minkowski momentum densities are given by [1–5]:
and all free-space quantities are marked by the subscript '0'. In a non-dispersive medium, the Abraham and Minkowski momentum densities are given by [1–5]:

These two momenta are often interpreted as 'kinetic' and 'canonical' momenta of light, respectively [3–5, 7, 11, 13, 18]. In dispersive media, the Abraham momentum preserves its form, while the 'canonical' momentum should be modified with dispersion-related terms [12–14, 16, 17]:
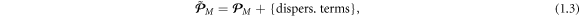
and the 'naïve' Minkowski momentum (1.2) does not make physical sense. Hereafter, we mark by tilde all quantities modified by the presence of dispersion. For simplicity, we will refer to the momentum (1.3) as to the properly modified Minkowski momentum in a dispersive medium.
For the simplest optical fields—plane waves—in a transparent medium, the Abraham and Minkowski momenta 'per photon' are reduced to the following simple form [3–5, 7, 11–14, 16–18]:
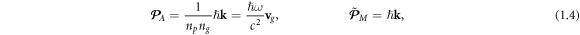
where 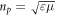 and
and 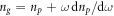 are the phase and group refractive indices of the medium, respectively,
are the phase and group refractive indices of the medium, respectively, 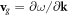 is the group velocity in the medium
is the group velocity in the medium 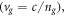 and k is the wave vector in the medium, with magnitude
and k is the wave vector in the medium, with magnitude 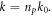
Equations (1.4) shed light on the physical meaning of the Abraham and Minkowski momenta, which can be associated with the group velocity and wave vector in the medium. This correspondence is very general [11, 18]. For example, even for inhomogeneous waves in non-transparent inhomogeneous media, such as surface plasmon-polaritons (SPPs) at metal-vacuum interfaces [23], the group velocity is still determined by the integral value of the Poynting (=Abraham) momentum [24]. At the same time, the conservation of the wave momentum and momentum matching in various resonant problems involve Minkowski momentum, i.e., the wave vector in the medium. The most known example is Snell's law in the light refraction at planar interfaces [20, 22]. Furthermore, more subtle spin and orbital Hall effects (transverse beam shifts) in the refraction at planar interfaces are intimately related to the conservation of the corresponding Minkowski AM based on the same wavevector k [25–30].
However, there are problems, where the wave vector and corresponding momentum conservation are well defined and observable, while using the Minkowski momentum faces difficulties. For instance, in evanescent or surface waves, such as SPPs, the wave vector k exceeds k0 in absolute value, and this 'super-momentum' higher than 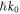 per photon is observable in momentum-transfer experiments [23, 31–35]. As we show below, the modified Minkowski momentum (1.3) can explain these features when integrated in localized SPP waves, but not locally in evanescent and other structured fields. This problem is related to another optical momentum dilemma.
per photon is observable in momentum-transfer experiments [23, 31–35]. As we show below, the modified Minkowski momentum (1.3) can explain these features when integrated in localized SPP waves, but not locally in evanescent and other structured fields. This problem is related to another optical momentum dilemma.
1.2. Canonical and kinetic pictures in free space
Besides the Abraham–Minkowski debate, the momentum and AM of light allow various descriptions even in free space. There, it is also related to the 'kinetic' and 'canonical' quantities, but in a different sense. Namely, the well-known Poynting momentum (1.1) corresponds to the kinetic momentum density, which appears in the symmetrized (kinetic) energy–momentum tensor (EMT) of the electromagnetic field [36]. In this approach, the total AM density is determined by the same Poynting vector [20–22, 36]:
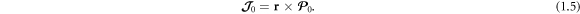
Despite its universal character, this formalism has several practical drawbacks. First, the Poynting momentum and AM do not describe separately spin and orbital degrees of freedom of light. In particular, the AM density (1.5) is extrinsic, i.e. depending on the choice of the coordinate origin, and characterizing the spin (intrinsic) AM density is problematic in the Poynting formalism. At the same time, spin and orbital AM are widely explored as independent degrees of freedom in modern optics [37–43] and also in quantum field theory [44, 45]. Second, the Poynting vector looses its clear physical meaning in the case of structured (i.e., inhomogeneous) optical fields, where it cannot explain local momentum transfer (including 'super-momentum') and optical radiation-pressure forces [31–35, 41, 46, 47].
The spin–orbital decomposition of the AM of light, described in [48–54], appears naturally in the canonical approach [35, 36, 41, 44, 45, 47, 54, 55]. Using the formalism dual-symmetric with respect to the electric and magnetic fields [35, 41, 52, 54–57], the canonical momentum density of a monochromatic light in free space is given by [35, 41, 54–56]:
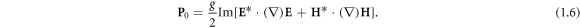
This momentum describes only the orbital part of the AM, L0, while the spin part is provided by an independent intrinsic quantity S0 [35, 41, 52, 54, 55, 57]:
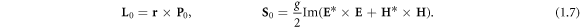
Recently, it was shown that the canonical quantities (1.6) and (1.7) are much more suitable for the description of the momentum and AM properties of free-space light than the kinetic Poynting characteristics (1.1) and (1.5). In particular, the optical force and torque on a small electric-dipole particle or an atom are given by the electric parts of the canonical momentum (1.6) and spin AM (1.7), respectively [35, 41, 46, 47, 58–60]. This makes canonical quantities directly measurable and immediately explaining numerous experiments involving spin/orbital AM [35, 41, 61–63] and structured light fields [31–35, 46, 47, 64]. Moreover, using canonical formalism enabled prediction and description of unusual phenomena, such as unusual transverse spin AM in evanescent and other structured fields [35, 41–43, 46, 65–68] and super-momentum transfer higher than 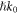 per photon [31–35].
per photon [31–35].
The canonical momentum density (1.6) can be written as a local expectation value of the quantum-mechanical momentum operator 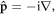 and hence can be associated with the local phase gradient or local wave vector
and hence can be associated with the local phase gradient or local wave vector 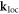 of the field [33, 56]. This elucidates its canonical character, akin to the Minkowski momentum (1.4). However, in contrast to equation (1.4), valid for a single plane wave, canonical momentum (1.6) describes the local phase gradient in an arbitrary structured field, which can consist of multiple plane waves propagating in different directions. In turn, the canonical spin AM density (1.7) describes the local ellipticity of the 3D polarization of an arbitrary structured field.
of the field [33, 56]. This elucidates its canonical character, akin to the Minkowski momentum (1.4). However, in contrast to equation (1.4), valid for a single plane wave, canonical momentum (1.6) describes the local phase gradient in an arbitrary structured field, which can consist of multiple plane waves propagating in different directions. In turn, the canonical spin AM density (1.7) describes the local ellipticity of the 3D polarization of an arbitrary structured field.
The relation between the kinetic (Poynting) momentum 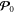 and canonical momentum P0 in free space is given by the spin–orbital momentum decomposition [35, 41, 47, 55, 56]:
and canonical momentum P0 in free space is given by the spin–orbital momentum decomposition [35, 41, 47, 55, 56]:

Here the canonical momentum P0 describes the orbital part (which determines the orbital AM L0), while the spin momentum 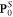 is related to the spin AM S0 via the non-local relation
is related to the spin AM S0 via the non-local relation 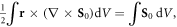 valid for any localized fields vanishing at infinity. Importantly, the spin momentum vanishes for plane waves and does not contribute to the integral (expectation) value of the wave momentum for localized fields, so that the integral kinetic and canonical momenta coincide:
valid for any localized fields vanishing at infinity. Importantly, the spin momentum vanishes for plane waves and does not contribute to the integral (expectation) value of the wave momentum for localized fields, so that the integral kinetic and canonical momenta coincide:
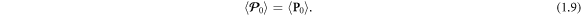
Here, 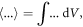 and hereafter it denotes suitable spatial integrals for localized fields.
and hereafter it denotes suitable spatial integrals for localized fields.
In terms of relativistic field theory, the canonical momentum and spin densities (1.6) and (1.7) originate from the canonical energy–momentum and AM tensors, which are directly obtained from Noether's theorem applied to the electromagnetic field Lagrangian [36, 44, 45, 54, 55]. Two points should be emphasized here. First, the original form of these canonical tensors involves the gauge-dependent electromagnetic vector potential A. The standard procedure in this case is to consider only the 'transverse' (i.e., divergence-free) gauge-invariant part of this potential, 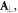 which for monochromatic fields is expressed via the wave electric field
which for monochromatic fields is expressed via the wave electric field 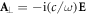 [44, 45, 47–50, 52, 54, 55, 60]. Second, the standard electromagnetic-field Lagrangian is not dual-symmetric with respect to the electric and magnetic fields. Due to this, it results in double electric-field parts of quantities (1.6) and (1.7), with no magnetic-field parts [36, 44, 47, 60]. However, an alternative Lagrangian formalism, dual-symmetrized between electric and magnetic contributions [55, 69, 70], produces the symmetric quantities (1.6) and (1.7), more natural for free Maxwell fields [35, 41, 54–57, 59]. In this paper we employ the dual-symmetric formalism [55] and show that it is more consistent with the canonical optical properties in media than the dual-asymmetric (electric-biased) approach.
[44, 45, 47–50, 52, 54, 55, 60]. Second, the standard electromagnetic-field Lagrangian is not dual-symmetric with respect to the electric and magnetic fields. Due to this, it results in double electric-field parts of quantities (1.6) and (1.7), with no magnetic-field parts [36, 44, 47, 60]. However, an alternative Lagrangian formalism, dual-symmetrized between electric and magnetic contributions [55, 69, 70], produces the symmetric quantities (1.6) and (1.7), more natural for free Maxwell fields [35, 41, 54–57, 59]. In this paper we employ the dual-symmetric formalism [55] and show that it is more consistent with the canonical optical properties in media than the dual-asymmetric (electric-biased) approach.
While the symmetrized (kinetic) EMT contains only the Poynting momentum density 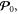 the canonical EMT is non-symmetric, and contains both the Poynting vector
the canonical EMT is non-symmetric, and contains both the Poynting vector 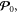 acting as the energy flux density, and the canonical momentum density P0. Remarkably, considering the EMT for electromagnetic waves in a medium, Dewar [11] and later Dodin and Fisch [18] found that the electromagnetic EMT in a (non-dispersive) medium can be modified to the Minkowski form, where the Poynting energy flux and canonical momentum are substituted by the Abraham (Poynting) and Minkowski momenta,
acting as the energy flux density, and the canonical momentum density P0. Remarkably, considering the EMT for electromagnetic waves in a medium, Dewar [11] and later Dodin and Fisch [18] found that the electromagnetic EMT in a (non-dispersive) medium can be modified to the Minkowski form, where the Poynting energy flux and canonical momentum are substituted by the Abraham (Poynting) and Minkowski momenta, 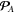 and
and 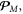 respectively. Schematically, these different forms of the EMTs in free space and in media can be presented as follows:
respectively. Schematically, these different forms of the EMTs in free space and in media can be presented as follows:

This provides a qualitative link between the Abraham–Minkowski and kinetic-canonical (in the relativistic field-theory sense) dilemmas.
Summarizing the above considerations, one should associate the Poynting–Abraham quantities with the energy flux and group velocity of the wave-packet propagation, while the canonical and Minkowski quantities are related to the momentum density carried by the wave and its wave-vector characteristics. At the same time, we emphasize that the kinetic-canonical dilemma between 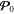 and
and 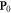 in the sense of relativistic field theory originates from the separation of the spin and orbital degrees of freedom, while the Abraham–Minkowski dilemma between
in the sense of relativistic field theory originates from the separation of the spin and orbital degrees of freedom, while the Abraham–Minkowski dilemma between 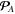 and
and 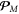 is related to the separation of the medium and field contributions to the momentum. Therefore, one can consider the spin–orbital separation in both Abraham and Minkowski momenta in a medium, as well as Abraham and Minkowski forms of the kinetic and canonical (orbital) momenta in a medium, i.e., four types of momenta in the medium. In what follows, we use the 'kinetic' and 'canonical' characteristics in the field-theory sense of the spin–orbital separation, also explicitly indicating the Abraham- and Minkowski-type quantities.
is related to the separation of the medium and field contributions to the momentum. Therefore, one can consider the spin–orbital separation in both Abraham and Minkowski momenta in a medium, as well as Abraham and Minkowski forms of the kinetic and canonical (orbital) momenta in a medium, i.e., four types of momenta in the medium. In what follows, we use the 'kinetic' and 'canonical' characteristics in the field-theory sense of the spin–orbital separation, also explicitly indicating the Abraham- and Minkowski-type quantities.
1.3. About this work
Here we aim to provide a complete Abraham–Minkowski and kinetic-canonical picture of optical momentum and AM in dispersive and inhomogeneous (but isotropic and lossless) media. For the reader's convenience, we summarize all the quantities under discussion in table 1, indicating their forms in free space, dispersion-free, and dispersive media. Our main emphasis in this work is on the Minkowski-type quantities, because these correspond to the actual wave momentum, spin, and AM in the medium, in contrast to the Abraham-type energy flux properties.
Table 1.
Four possible pictures of the optical momentum and AM densities in free space, non-dispersive isotropic media, and dispersive (generally inhomogeneous) media. The Abraham- and Minkowski-type, kinetic and canonical (spin–orbital) quantities are shown. In all cases, the kinetic Abraham–Poynting momentum density  describes the energy flux and group velocity of the wave, whereas the canonical Minkowski-type momentum and spin densities
describes the energy flux and group velocity of the wave, whereas the canonical Minkowski-type momentum and spin densities  and
and 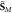 provide a clear and self-consistent picture of the momentum and AM carried by the wave. In turn, the kinetic-Minkowski and canonical-Abraham quantities have less natural forms with cumbersome dispersive and gradient corrections (indicated as {dispers.} and {grad.} here).
provide a clear and self-consistent picture of the momentum and AM carried by the wave. In turn, the kinetic-Minkowski and canonical-Abraham quantities have less natural forms with cumbersome dispersive and gradient corrections (indicated as {dispers.} and {grad.} here).

|
The paper is organized as follows. In this introductory section 1 we provided a general overview of the problem. In section 2, we discuss the general momentum and AM expressions listed in table 1 and their properties. Then, in section 3, we consider an explicit example of a SPP wave at a metal-vacuum interface.
This example (which to the best of our knowledge has never been considered in the Abraham–Minkowski context) provides a perfect test for the momentum and AM properties of structured optical fields in dispersive inhomogeneous media. The multiple advantages of the SPP system are as follows:
- (i)SPP waves are well studied and readily achievable experimentally.
- (ii)Even a single SPP wave is a structured field, for which the simplified plane-wave equation (1.4) are not applicable.
- (iii)SPPs exist at interfaces, i.e. in essentially inhomogeneous media.
- (iv)
- (v)Dispersion of the metal is crucial for the SPP properties.
Thus, SPPs provide both an accessible and highly non-trivial system to study optical momentum and AM.
In section 3 we apply the general expressions from table 1 to calculate the momentum and AM properties of SPPs. In particular, we present the first accurate calculations of the canonical and Minkowski momenta, as well as the transverse spin and orbital AM of a SPP. Notably, the integral canonical or Minkowski momentum of SPP exceeds 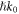 per particle, and this offers the first example of the integral super-momentum (previously known only locally). Moreover, the intrinsic orbital AM of the SPP vanishes, whereas the integral transverse spin AM can change its sign depending on parameters.
per particle, and this offers the first example of the integral super-momentum (previously known only locally). Moreover, the intrinsic orbital AM of the SPP vanishes, whereas the integral transverse spin AM can change its sign depending on parameters.
Importantly, in section 4, we provide microscopic calculations of the momentum and AM in SPPs. Taking into account both microscopic electromagnetic fields and the motion of free electrons in the metal, we obtain the Minkowski and canonical quantities previously introduced using macroscopic phenomenological considerations. This validates the use of these quantities for structured optical fields in dispersive and inhomogeneous media. Moreover, the microscopic theory predicts a transverse magnetization in the metal (i.e. a magnetic moment for the SPP) as well as the corresponding direct magnetization current , which corresponds to the difference between the Abraham and Minkowski-type momenta.
Finally, in section 5, we briefly discuss issues related to the dual symmetry between electric- and magnetic-field contributions. We show that while integral electric and magnetic conributions to the momentum and spin are equal for localized fields in free space [52, 55], this is not the case for localized fields in media. Most importantly, we find that the microscopic calculations of section 4 are only compatible with the dual-symmetric (rather than electric-biased) forms of the canonical quantities.
We should also briefly mention preceding works, which considered some of the above aspects of SPPs. First, Nakamura [71] performed microscopic calculations of the transverse AM of SPPs. Although results of that work are erroneous in several aspects (calculation errors, mixing of the spin and orbital AM, etc), its methodology inspired us to perform microscopic calculations presented in section 4. Second, Kim and Wang aimed to calculated Abraham and 'naïve' Minkowski (without dispersion terms) versions of the transverse spin AM in SPPs [72–74]. However, their results are also misleading. First, the definitions in [72–74] do not describe the Abraham-type spin, which was properly defined and calculated in [35, 65], and which corresponds to an energy-flux property rather than the actual spin AM carried by the wave. Second, the 'naïve' Minkowski expressions are not applicable to waves in dispersive media and lead to erroneous results. Thus, the first accurate calculation of the transverse spin and other 'canonical' characteristics of SPPs are provided in the present work.
2. Momentum and AM of light in dispersive inhomogeneous media
Throughout this paper we consider monochromatic electric and magnetic fields: ![${\boldsymbol{ {\mathcal E} }}({\bf{r}},t)=\mathrm{Re}[{\bf{E}}({\bf{r}}){{\rm{e}}}^{-{\rm{i}}\omega t}]$](https://content.cld.iop.org/journals/1367-2630/19/12/123014/revision2/njpaa8913ieqn39.gif) and
and ![${\boldsymbol{ {\mathcal H} }}({\bf{r}},t)=\mathrm{Re}[{\bf{H}}({\bf{r}}){{\rm{e}}}^{-{\rm{i}}\omega t}].$](https://content.cld.iop.org/journals/1367-2630/19/12/123014/revision2/njpaa8913ieqn40.gif) The main independent dynamical properties of light are: energy, momentum, as well as spin and orbital AM. One can also add here helicity, which is an independent conserved quantity [55, 57, 59, 69, 70, 75–79]. The momentum and AM characteristics, both kinetic and canonical, for monochromatic free-space fields are given by equations (1.1) and (1.5)–(1.8). For completeness, here we add the energy density [20–22]:
The main independent dynamical properties of light are: energy, momentum, as well as spin and orbital AM. One can also add here helicity, which is an independent conserved quantity [55, 57, 59, 69, 70, 75–79]. The momentum and AM characteristics, both kinetic and canonical, for monochromatic free-space fields are given by equations (1.1) and (1.5)–(1.8). For completeness, here we add the energy density [20–22]:
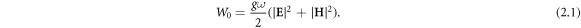
We now consider an isotropic lossless dispersive and inhomogeneous medium, which is characterized by the real frequency-dependent permittivity 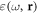 and permeability
and permeability 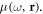 In this case, the complex field amplitudes satisfy stationary Maxwell equations:
In this case, the complex field amplitudes satisfy stationary Maxwell equations:


Note that these source-free equations are used in the decomposition of the Poynting momentum density into canonical and spin parts, equation (1.8).
The energy density of a monochromatic optical field in such a medium is described by the well-known Brillouin expression [20, 22]:

where

Describing the optical momentum density in a medium is a more sophisticated problem. On the one hand, the Abraham momentum 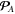 preserves its Poynting-vector form (1.2) in the medium. By analogy with the canonical decomposition (1.8), one can decompose it into orbital and spin parts,
preserves its Poynting-vector form (1.2) in the medium. By analogy with the canonical decomposition (1.8), one can decompose it into orbital and spin parts,  where:
where:
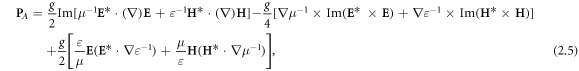
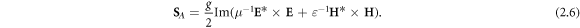
This spin–orbital decomposition was introduced in [65] (up to the missing last term in square brackets in (2.5)) and was used in [35, 46, 80] because of its convenience in homogeneous media. However, in inhomogeneous media, the canonical momentum density (2.5) acquires cumbersome gradient terms. Moreover, the physical interpretation of the quantities (2.5) and (2.6) is not quite clear. Indeed, as we discussed above, the Abraham momentum 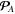 should be associated with the energy flux density and group velocity (1.10) rather than with the wave momentum density. Therefore, the Abraham-type quantities (2.5) and (2.6) correspond to the orbital and spin parts of the energy flux density, but cannot be regarded as canonical momentum and spin densities in the wave. In addition, at interfaces between media, the Abraham-type spin density (2.6) is discontinuous, and the corresponding gradient terms in equation (2.5) produce singular delta-function contributions to the canonical and spin momentum densities
should be associated with the energy flux density and group velocity (1.10) rather than with the wave momentum density. Therefore, the Abraham-type quantities (2.5) and (2.6) correspond to the orbital and spin parts of the energy flux density, but cannot be regarded as canonical momentum and spin densities in the wave. In addition, at interfaces between media, the Abraham-type spin density (2.6) is discontinuous, and the corresponding gradient terms in equation (2.5) produce singular delta-function contributions to the canonical and spin momentum densities 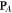 and
and 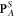 [65]. This makes the Abraham-type spin–orbital decomposition imperfect. Note also that, similarly to the free-space equations (1.8) and (1.9), the solenoidal spin part of the energy flux does not contribute to the plane-wave and integral characteristics:
[65]. This makes the Abraham-type spin–orbital decomposition imperfect. Note also that, similarly to the free-space equations (1.8) and (1.9), the solenoidal spin part of the energy flux does not contribute to the plane-wave and integral characteristics:
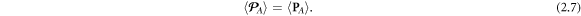
Therefore, in some plane-wave or integral calculations it could be more convenient to use equation (2.5) as the energy flux density.
To describe physically meaningful momentum and AM densities in the optical field, one should use the Minkowski momentum. Its simple form (1.2) is not valid in the presence of dispersion, and several works discussed modifications of the Minkowski-type wave momentum in a dispersive medium [12–14, 16, 17]. The most general expression, suitable for structured wave fields was derived by Philbin [16, 17] using the phenomenological Lagrangian formalism and Noether's theorem:
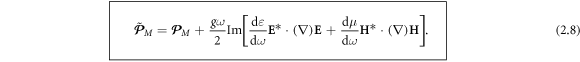
Here, the first term is the 'naïve' Minkowski momentum (1.2), while the second term describes the dispersion-related correction. For a plane wave in a transparent homogeneous medium, the Abraham and modified-Minkowski momenta 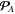 and
and 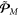 yield simplified equation (1.4) [3–5, 7, 11–14, 16–18].
yield simplified equation (1.4) [3–5, 7, 11–14, 16–18].
Since the Minkowski-type momentum (2.8) represents 'canonical' wave-vector properties of the wave, it makes sense to find the spin–orbital decomposition, similar to equation (1.8), and introduce the corresponding canonical spin and orbital properties. In doing so, we apply the standard Poynting-vector decomposition (1.8) to the first (Minkowski) term in equation (2.8) and add the second dispersive term to the orbital part (because of its natural orbital form). This results in 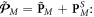
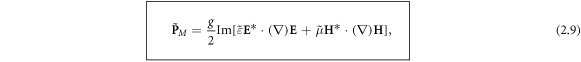
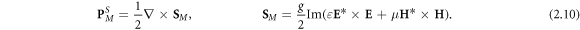
Notably, the canonical (orbital) momentum density (2.9) has a nice form similar to the free-space momentum (1.6) with the  and
and 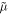 multipliers, exactly as in the Brillouin energy density (2.3). Furthermore, the momentum (2.9) is free of cumbersome gradient terms, present in the canonical Abraham-type momentum (2.5). However, the quantity
multipliers, exactly as in the Brillouin energy density (2.3). Furthermore, the momentum (2.9) is free of cumbersome gradient terms, present in the canonical Abraham-type momentum (2.5). However, the quantity 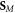 in equation (2.10) is the 'naïve' Minkowski spin AM density, which lacks dispersive corrections. As we show below, this is not the canonical spin AM density of the wave. Notably, in the SPP example considered below, the quantity
in equation (2.10) is the 'naïve' Minkowski spin AM density, which lacks dispersive corrections. As we show below, this is not the canonical spin AM density of the wave. Notably, in the SPP example considered below, the quantity 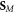 is continuous at the interface, and therefore the canonical and spin parts of the modified Minkowski momentum density,
is continuous at the interface, and therefore the canonical and spin parts of the modified Minkowski momentum density, 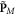 and
and 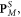 are free of delta-function singularities. This makes the Minkowski-type spin–orbital decomposition more appealing than the Abraham one.
are free of delta-function singularities. This makes the Minkowski-type spin–orbital decomposition more appealing than the Abraham one.
Akin to equations (1.8), (1.9), and (2.7), the solenoidal spin momentum (2.10) vanishes for plane waves and does not contribute to the integral momentum values. Therefore, the integral values of the kinetic and canonical Minkowski-type momenta (2.8) and (2.9) coincide for localized fields:
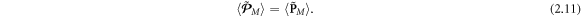
Thus, one can use either of these momenta in calculations of the integral or plane-wave properties.
To determine the canonical spin and orbital AM in a dispersive medium, we start with the kinetic (total) Minkowski-type AM. Again, the Minkowski-type analog of equation (1.5) in a dispersive medium was found by Philbin and Allanson [17]:
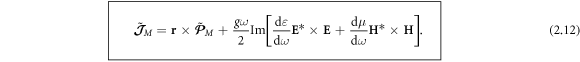
Importantly, the AM density (2.12) breaks the simple relation (1.5) between the kinetic momentum and AM densities, 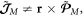 and contains a dispersion-related correction of the spin-like local form. Substituting
and contains a dispersion-related correction of the spin-like local form. Substituting 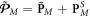 with equations (2.9) and (2.10) into equation (2.12) and using the nonlocal relation between the spin momentum and spin AM,
with equations (2.9) and (2.10) into equation (2.12) and using the nonlocal relation between the spin momentum and spin AM, 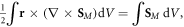 we derive the canonical orbital and spin AM densities in a dispersive medium:
we derive the canonical orbital and spin AM densities in a dispersive medium:
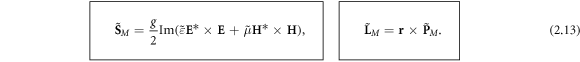
Here the dispersion terms from equation (2.12) correct the 'naïve' Minkowski spin density 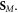 Remarkably, equations (2.13) have a very nice form, similar to the free-space equation (1.7), but now with the same
Remarkably, equations (2.13) have a very nice form, similar to the free-space equation (1.7), but now with the same  and
and 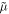 multipliers as in the Brillouin energy density (2.3) and canonical momentum density (2.9). The integral values of the kinetic and canonical AM (2.12) and (2.13) coincide for localized fields:
multipliers as in the Brillouin energy density (2.3) and canonical momentum density (2.9). The integral values of the kinetic and canonical AM (2.12) and (2.13) coincide for localized fields:
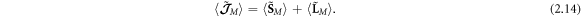
Equations (2.3), (2.9), and (2.13) constitute a set of canonical characteristics of a monochromatic light in a dispersive and inhomogeneous medium. Importantly, these can be written as local expectation values of quantum-mechanical energy 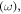 momentum
momentum 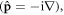 and spin-1
and spin-1 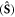 operators [35, 54–56, 59]:
operators [35, 54–56, 59]:
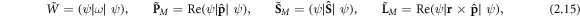
using the following wave-function:
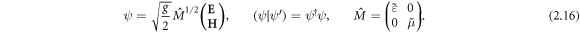
Exactly the same formalism for electromagnetic bi-linear forms (including Berry connection and other topological characteristics) in dispersive media was recently suggested in works by Silveirinha [81–83]. Thus, the above equations bring together approaches developed by (i) Philbin (kinetic Minkowski-type momentum and AM in dispersive media) [16, 17], (ii) Bliokh et al (canonical momentum and AM pictures in free space) [35, 41, 52, 55, 56], and (iii) Silveirinha (electromagnetic bi-linear forms in dispersive media) [81–83].
The natural form of the energy, momentum, and AM in equations (2.3), (2.9), (2.13), and (2.15) suggests that the canonical form of the Minkowski-type momentum and AM densities is more suitable for the description of the optical momentum and AM than the previously used kinetic Minkowski-type approach, equations (2.8) and (2.12), and the Abraham-type quantities (2.5) and (2.6). For example, consider a polarized plane wave propagating in a homogeneous dispersive medium. All field components have the same phase factor  the electric and magnetic field amplitudes are related by
the electric and magnetic field amplitudes are related by 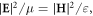 whereas the ellipticity of the polarization can be characterized by the helicity σ, such that
whereas the ellipticity of the polarization can be characterized by the helicity σ, such that 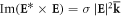 (and a similar equation for the magnetic field), where
(and a similar equation for the magnetic field), where 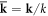 characterizes the direction of the wave propagation. Using these simple properties, from equations (2.3), (2.5), (2.6), (2.9) and (2.13), we readily obtain the ratios of the canonical Abraham- and Minkowski-type momentum and spin densities to the energy density of the wave:
characterizes the direction of the wave propagation. Using these simple properties, from equations (2.3), (2.5), (2.6), (2.9) and (2.13), we readily obtain the ratios of the canonical Abraham- and Minkowski-type momentum and spin densities to the energy density of the wave:
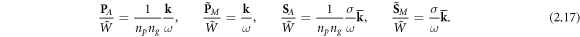
The first two of these equations exactly correspond to equation (1.4), whereas the other two equations provide their counterparts for the spin AM (see [17, 84]). In this manner, the Minkowski-type momentum 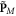 and spin AM
and spin AM 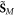 correspond to the values
correspond to the values 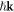 and
and 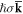 per photon, as one would expect for photons, the Abraham-type momentum
per photon, as one would expect for photons, the Abraham-type momentum 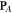 determines the group velocity (1.4), while the Abraham-type spin
determines the group velocity (1.4), while the Abraham-type spin 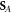 does not have a clear physical meaning.
does not have a clear physical meaning.
It is important to note that it is the Minkowski-type wave momentum and AM that are conserved in media with the corresponding translational and rotational symmetries. First, this follows in the most general form from the results of [16, 17], where the kinetic quantities (2.8) and (2.12) were derived from Noether's theorem. In view of equations (2.11) and (2.14), this is also true for the canonical Minkowski-type quantities (2.9) and (2.13). Second, in the plane-wave equation (2.17), the Minkowski-type momentum and spin exactly correspond to the tangent-momentum and normal-AM conservation laws in the wave refraction at an interface between two media [20, 22, 25–30] (Snell's law and optical beam shifts).
In this section we presented a macroscopic phenomenological introduction of these quantities. Below, considering SPPs at the vacuum-metal interface, we show that this macroscopic model is in exact agreement with microscopic calculations taking into account separate electron and field contributions. It should be also noted that in the absence of dispersion, 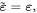
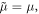 and both kinetic and canonical characteristics discussed in this section acquire simplified Minkowski forms, shown in table 1.
and both kinetic and canonical characteristics discussed in this section acquire simplified Minkowski forms, shown in table 1.
3. Macroscopic calculations for a SPP
3.1. SPP fields and parameters
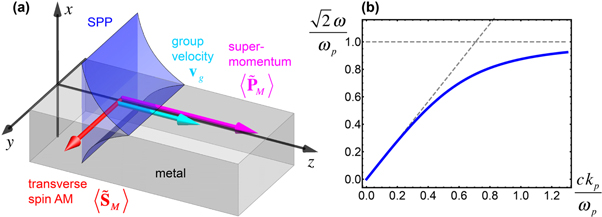
We now consider an explicit example of a structured optical field in a dispersive and inhomogeneous medium: a SPP at the metal-vacuum interface [23]. The geometry of the problem is shown in figure 1(a), where the interface is the x = 0 plane with the vacuum in the x > 0 half-space (medium 1) and metal in the x < 0 half-space (medium 2), whereas the SPP wave propagates along the z-axis with the wavevector  (hereafter,
(hereafter, 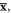
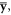 and
and 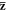 denote the unit vectors of the corresponding axes). The permittivity and permeability of the metal are given using the standard plasma model [23]:
denote the unit vectors of the corresponding axes). The permittivity and permeability of the metal are given using the standard plasma model [23]:
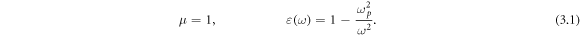
Here, 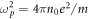 is the plasma frequency, where n0 is the volume density of free electrons in the metal,
is the plasma frequency, where n0 is the volume density of free electrons in the metal, 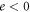 is the electron charge, and m is the electron mass. Thus, the metal is a dispersive medium with
is the electron charge, and m is the electron mass. Thus, the metal is a dispersive medium with 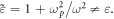 SPPs are electromagnetic surface TM waves that exist at frequencies
SPPs are electromagnetic surface TM waves that exist at frequencies 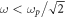 where
where 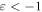 [23].
[23].
Figure 1. (a) Schematic picture of a surface plasmon-polariton (SPP) wave at the metal-vacuum interface [23]. The subluminal group velocity (3.8), super-momentum (3.9), and the transverse spin (3.14) are schematically shown. (b) The dispersion of the SPP, 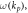 obtained from equations (3.1) and (3.3).
obtained from equations (3.1) and (3.3).
Download figure:
Standard image High-resolution imageThe electric and magnetic fields of a single SPP wave can be written as [23, 24, 65]:
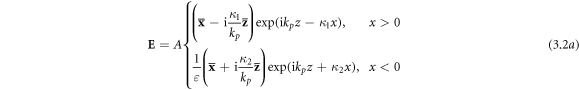
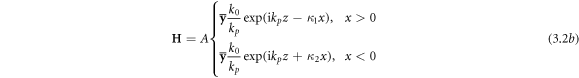
where A is the field amplitude, whereas the wave number and spatial decay constants of the SPP field are:
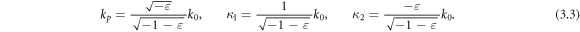
The vacuum part of the SPP fields (3.2) and (3.3) is a free-space TM-polarized evanescent wave with 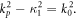 From equations (3.1) and (3.3), one can obtain the dependence
From equations (3.1) and (3.3), one can obtain the dependence 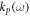 and the dispersion of the SPP,
and the dispersion of the SPP, 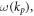 shown in figure 1(b).
shown in figure 1(b).
3.2. Energy, group velocity, and momentum of SPPs
Substituting equations (3.2) and (3.3) into equation (2.3), we obtain the energy density distribution in the SPP field:
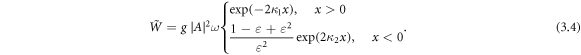
Note that the distribution (3.4) is discontinuous at the interface x = 0. Since SPP field is localized along the x coordinate, we can also calculate the integral 'expectation value' of the SPP energy integrating 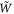 over
over 

where  In what follows, we express the integral momentum and AM characteristics of SPPs with respect to the energy (3.5), in order to highlight their values 'per plasmon'. From the energy-density distribution, we also find the position of the center of energy along the x-axis:
In what follows, we express the integral momentum and AM characteristics of SPPs with respect to the energy (3.5), in order to highlight their values 'per plasmon'. From the energy-density distribution, we also find the position of the center of energy along the x-axis:
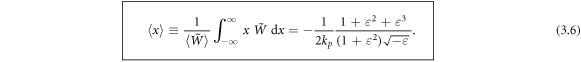
It follows from here that for 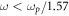 the energy centroid is located in the vacuum:
the energy centroid is located in the vacuum: 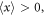 while for
while for 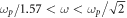 it moves into the metal:
it moves into the metal: 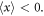 Dependences of the integral energy (3.5) and center-of-energy position (3.6) on the SPP frequency are shown in figure 2.
Dependences of the integral energy (3.5) and center-of-energy position (3.6) on the SPP frequency are shown in figure 2.
Download figure:
Standard image High-resolution imageThe Abraham–Poynting momentum density, or rather the energy flux, equations (1.1) and (1.2), for the SPP fields (3.2) and (3.3) yields
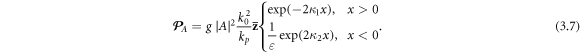
Note that this flux is negative (backward) inside the metal, producing a vortex-like energy circulation in SPP wave packets [24, 65, 85]. Nonetheless, the integral energy flux  is positive, and, in ratio to the energy (3.5), it determines the group velocity of SPPs [24, 86]:
is positive, and, in ratio to the energy (3.5), it determines the group velocity of SPPs [24, 86]:
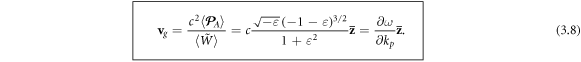
Importantly, the absolute value of the group velocity (3.8) is always subluminal: 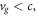 which corresponds to the subluminal propagation of a SPP wave packet. This also means that the integral Abraham momentum is smaller than
which corresponds to the subluminal propagation of a SPP wave packet. This also means that the integral Abraham momentum is smaller than 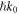 'per plasmon'. Although the plane-wave homogenous-medium equations (1.4) and (2.17) are not directly applicable to the structured SPP wave at the metal-vacuum interface, the group velocity (3.8) can be written in the form
'per plasmon'. Although the plane-wave homogenous-medium equations (1.4) and (2.17) are not directly applicable to the structured SPP wave at the metal-vacuum interface, the group velocity (3.8) can be written in the form 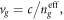 where we introduced an effective phase refractive index for SPPs,
where we introduced an effective phase refractive index for SPPs, 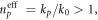 and the corresponding effective group index
and the corresponding effective group index 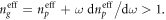 This shows that the relations (1.4) between the Abraham energy flux, group velocity, and refractive indices are rather general and can be extended, using integral expectation values, to localized states in inhomogeneous media. The frequency dependence of the SPP group velocity (3.8) is depicted in figure 3(a).
This shows that the relations (1.4) between the Abraham energy flux, group velocity, and refractive indices are rather general and can be extended, using integral expectation values, to localized states in inhomogeneous media. The frequency dependence of the SPP group velocity (3.8) is depicted in figure 3(a).
Figure 3. The group velocity (3.8) and integral Minkowski-type momentum (3.9) of a SPP versus frequency. While the group velocity is always sub-luminal, 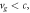 the integral momentum of SPP corresponds to the super-momentum
the integral momentum of SPP corresponds to the super-momentum 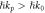 'per plasmon'.
'per plasmon'.
Download figure:
Standard image High-resolution imageThe orbital and spin parts of the energy flux (3.7), 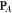 and
and 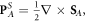 equations (2.5) and (2.6), have been analyzed for SPPs in [65], and we do not reproduce these here. We just recall that these parts have singular delta-function contributions at the interface x = 0 due to the gradient terms in equation (2.5) and discontinuity of the Abraham spin (2.6)
equations (2.5) and (2.6), have been analyzed for SPPs in [65], and we do not reproduce these here. We just recall that these parts have singular delta-function contributions at the interface x = 0 due to the gradient terms in equation (2.5) and discontinuity of the Abraham spin (2.6) 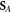 (shown below). These singular contributions are crucial to satisfy equation (2.7).
(shown below). These singular contributions are crucial to satisfy equation (2.7).
We now calculate the Minkowski-type momentum for the SPP fields. It has a more natural form in the canonical approach. Indeed, using equation (2.9), we readily obtain for the field (3.2) with the common  phase factor:
phase factor:

Note that the momentum density 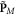 is positive both in the vacuum and in metal, in contrast to the energy flux (3.7). Moreover, it does not have delta-function singularities at the interface, in contrast to the canonical Abraham-type momentum
is positive both in the vacuum and in metal, in contrast to the energy flux (3.7). Moreover, it does not have delta-function singularities at the interface, in contrast to the canonical Abraham-type momentum 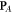 [65].
[65].
Assuming that the energy is quantized as  'per plasmon', equations (3.9) mean that the SPP carries super-momentum
'per plasmon', equations (3.9) mean that the SPP carries super-momentum 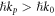 per plasmon. Remarkably, so far the super-momentum was described only locally, in evanescent waves or near optical vortices [31–35, 56, 87, 88]. At the same time, the integral momentum for any localized wave field in free space is always less than
per plasmon. Remarkably, so far the super-momentum was described only locally, in evanescent waves or near optical vortices [31–35, 56, 87, 88]. At the same time, the integral momentum for any localized wave field in free space is always less than 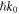 per photon [33]. Equations (3.9) show an example of the integral super-momentum. Of course, one can say that a canonical momentum higher than
per photon [33]. Equations (3.9) show an example of the integral super-momentum. Of course, one can say that a canonical momentum higher than 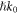 per photon appears in any medium with phase refractive index
per photon appears in any medium with phase refractive index 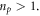 Equations (3.9) can also be written in the form of equations (1.4) and (2.17) with
Equations (3.9) can also be written in the form of equations (1.4) and (2.17) with  and effective refractive index
and effective refractive index 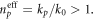 However, in the case of SPP waves, this effective refractive index originates from the inhomogeneous evanescent character of surface waves rather than from the high permittivity of the medium. Indeed, in the limit
However, in the case of SPP waves, this effective refractive index originates from the inhomogeneous evanescent character of surface waves rather than from the high permittivity of the medium. Indeed, in the limit  we have
we have 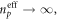 while
while 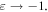 Note that although in some works the super-momentum was interpreted as a 'superluminal group velocity' [33, 88], our present analysis shows that it should rather be considered as a pure momentum property, while the group velocity is determined by the Poynting–Abraham energy flux and is always subluminal. The frequency dependence of the ratio of the SPP momentum (3.9) and energy is shown in figure 3(b).
Note that although in some works the super-momentum was interpreted as a 'superluminal group velocity' [33, 88], our present analysis shows that it should rather be considered as a pure momentum property, while the group velocity is determined by the Poynting–Abraham energy flux and is always subluminal. The frequency dependence of the ratio of the SPP momentum (3.9) and energy is shown in figure 3(b).
According to equation (2.11), the kinetic form of the Minkowski-type momentum (2.8) has the same integral value (3.9), but its local density does not exhibit the nice proportionality to the energy density as in equation (3.9):
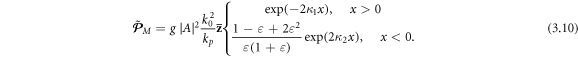
Moreover, this momentum density coincides with the Poynting–Abraham one in the vacuum. Therefore, for 
 and the kinetic Minkowski-type momentum (3.10) cannot explain the local super-momentum density in the vacuum evanescent field,
and the kinetic Minkowski-type momentum (3.10) cannot explain the local super-momentum density in the vacuum evanescent field,  which is described by the canonical momentum (3.9) and is observed experimentally [31–33]. Comparing equations (3.8)–(3.10), together with the singular character of the canonical Abraham-type momentum
which is described by the canonical momentum (3.9) and is observed experimentally [31–33]. Comparing equations (3.8)–(3.10), together with the singular character of the canonical Abraham-type momentum  [65], confirms that the canonical picture is more natural for the description of the Minkowski-type wave momentum, while the kinetic approach is more suitable for the characterization of the Abraham-type energy fluxes, see table 1.
[65], confirms that the canonical picture is more natural for the description of the Minkowski-type wave momentum, while the kinetic approach is more suitable for the characterization of the Abraham-type energy fluxes, see table 1.
3.3. Spin and orbital AM of SPPs
We are now in the position to determine the spin and orbital AM of SPPs. Akin to the momentum of SPPs, these should be described using the Minkowski-type canonical picture. However, for completeness and comparison with other approaches, we first calculate the Abraham-type spin density (2.6) and its integral value. With the SPP fields (3.2) and (3.3), we obtain:
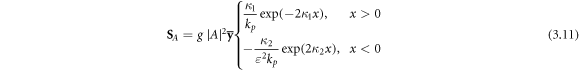
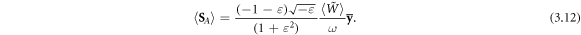
This is the transverse helicity-independent spin, first described in [65] and now attracting considerable attention [35, 41–43, 46, 66–68]. We wrote equation (3.11) using the  factors to conform with the known results for the transverse spin in an evanescent wave in free space [35, 41–43]:
factors to conform with the known results for the transverse spin in an evanescent wave in free space [35, 41–43]:  for
for 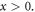 Equation (3.11) shows that the Abraham-type spin density
Equation (3.11) shows that the Abraham-type spin density 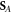 is discontinuous at the interface
is discontinuous at the interface  As a result of this, the canonical and spin parts of the Abraham–Poynting energy flux have delta-function singularities [65], originating from the gradient terms in equation (2.5). Note also that the integral value
As a result of this, the canonical and spin parts of the Abraham–Poynting energy flux have delta-function singularities [65], originating from the gradient terms in equation (2.5). Note also that the integral value 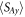 is always positive and is in agreement with calculations of [65] up to a factor of 2 missing there. (The missing factor of 2 in [65] originates from the improper application of the relation
is always positive and is in agreement with calculations of [65] up to a factor of 2 missing there. (The missing factor of 2 in [65] originates from the improper application of the relation 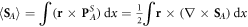 to the z-delocalized SPP wave, involving only the term
to the z-delocalized SPP wave, involving only the term 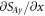 under the integral. In fact, this relation is valid only for localized wave packets involving two terms:
under the integral. In fact, this relation is valid only for localized wave packets involving two terms: 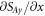 and
and 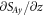 ). At the same time, calculations of the integral Abraham spin 'per particle' for surface Maxwell modes in [89] are not applicable in the SPP case because a dispersion-free model without proper Brillouin energy (2.3) was considered there. The frequency dependence of the Abraham-type spin (3.12) (in units of
). At the same time, calculations of the integral Abraham spin 'per particle' for surface Maxwell modes in [89] are not applicable in the SPP case because a dispersion-free model without proper Brillouin energy (2.3) was considered there. The frequency dependence of the Abraham-type spin (3.12) (in units of 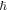 'per plasmon') is shown in figure 4(a).
'per plasmon') is shown in figure 4(a).
Figure 4. (a) The integral Abraham-type transverse spin (3.12) and proper canonical Minkowski-type transverse spin (3.14) of the SPP versus frequency. In contrast to the positive Abraham-type spin, the Minkowski-type spin can have different directions and vanishes for 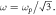 (b) The frequency dependences of the intrinsic (3.15) and extrinsic (with respect to the interface
(b) The frequency dependences of the intrinsic (3.15) and extrinsic (with respect to the interface 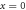 ) (3.16) orbital angular momentum (AM) of the SPP. The vanishing intrinsic part means that the canonical momentum density (3.9) does not exhibit any vortex-like circulation, in contrast to the Poynting–Abraham energy flux (3.7) [24, 65, 85]. In turn, the extrinsic orbital AM originates from the shifted energy centroid of the SPP, equation (3.6) and figure 2(b).
) (3.16) orbital angular momentum (AM) of the SPP. The vanishing intrinsic part means that the canonical momentum density (3.9) does not exhibit any vortex-like circulation, in contrast to the Poynting–Abraham energy flux (3.7) [24, 65, 85]. In turn, the extrinsic orbital AM originates from the shifted energy centroid of the SPP, equation (3.6) and figure 2(b).
Download figure:
Standard image High-resolution imageWe now calculate the properly defined canonical Minkowski-type spin and orbital AM (2.13). Substituting equations (3.2) and (3.3) into equation (2.13), we find:
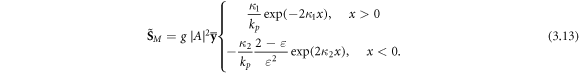
The spin AM density (3.13) is directed oppositely in the vacuum and metal: 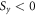 for
for 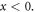 This agrees with the opposite direction of rotation of the electric field E in the metal, equation (3.2a), but is in contrast to what is obtained for the 'naïve' Minkowski spin (2.10), positive in the metal:
This agrees with the opposite direction of rotation of the electric field E in the metal, equation (3.2a), but is in contrast to what is obtained for the 'naïve' Minkowski spin (2.10), positive in the metal:  for
for 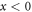 [72–74]. (Here we do not show the distribution of
[72–74]. (Here we do not show the distribution of  equation (2.10), and only note that it is continuous at the interface
equation (2.10), and only note that it is continuous at the interface  this assures the non-singular character of the canonical momentum
this assures the non-singular character of the canonical momentum 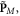 equation (2.9), which does not have any gradient corrections.) This proves that taking into account the dispersion-related corrections is crucial for determining the transverse spin and other dynamical properties of light in a dispersive medium. The integral expectation value of the spin AM (3.13) becomes:
equation (2.9), which does not have any gradient corrections.) This proves that taking into account the dispersion-related corrections is crucial for determining the transverse spin and other dynamical properties of light in a dispersive medium. The integral expectation value of the spin AM (3.13) becomes:
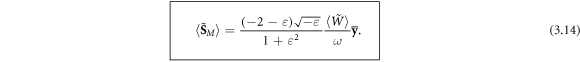
Equation (3.14) provides the first accurate calculation of the transverse spin AM carried by a SPP. In contrast to the Abraham-like spin (3.12) considered before, its direction can vary depending on the SPP frequency. Namely, it is positive,  for
for  and negative,
and negative, 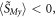 for
for 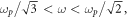 so that it vanishes at
so that it vanishes at 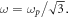 The frequency dependence of the Minkowski-type spin (3.14) (in units of
The frequency dependence of the Minkowski-type spin (3.14) (in units of 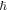 per plasmon) is shown in figure 4(a). Note that its absolute value never exceeds
per plasmon) is shown in figure 4(a). Note that its absolute value never exceeds 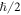 per plasmon; this is because of the pure-electric origin of the transverse spin, with no magnetic part. Interestingly, the critical zero-spin value
per plasmon; this is because of the pure-electric origin of the transverse spin, with no magnetic part. Interestingly, the critical zero-spin value 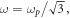 or
or  corresponds to the elliptical
corresponds to the elliptical  -polarizations of the electric field (3.2) with the axes ratios
-polarizations of the electric field (3.2) with the axes ratios 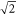 and
and 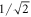 (i.e., identical ellipticities but different orientations), and opposite directions of the rotation, in the vacuum and metal, respectively.
(i.e., identical ellipticities but different orientations), and opposite directions of the rotation, in the vacuum and metal, respectively.
The orbital AM density in the SPP field is determined by equation (2.13) and the canonical momentum density (3.9): 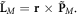 This quantity is extrinsic, i.e., depends on the choice of the coordinate origin. However, the expectation value of the orbital AM can have both extrinsic and intrinsic contributions [41]. The intrinsic orbital AM is calculated with respect to the centroid of the energy density distribution. Using the x-shifted centroid (3.6) and z-directed momentum density (3.9), we calculate the y-directed intrinsic orbital AM of the SPP:
This quantity is extrinsic, i.e., depends on the choice of the coordinate origin. However, the expectation value of the orbital AM can have both extrinsic and intrinsic contributions [41]. The intrinsic orbital AM is calculated with respect to the centroid of the energy density distribution. Using the x-shifted centroid (3.6) and z-directed momentum density (3.9), we calculate the y-directed intrinsic orbital AM of the SPP:
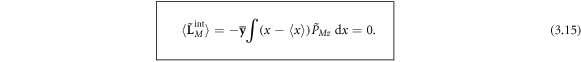
Thus, the intrinsic orbital AM of SPP vanishes. This is because of the proportionality between the canonical momentum density (3.9) and energy density (3.4), which in turn determines the centroid (3.6). The vanishing intrinsic orbital AM (3.15) reflects the non-vortex character of the canonical momentum (3.9), in contrast to the circulating Abraham-type energy fluxes [24, 65, 85]. The extrinsic part of the orbital AM, calculated with respect to the interface 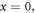 can be written as:
can be written as:
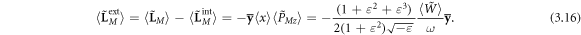
This quantity can change its sign depending on the sign of 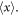 The frequency dependences of the intrinsic and extrinsic parts of the Minkowski-type orbital AM, equations (3.15) and (3.16), (in units of
The frequency dependences of the intrinsic and extrinsic parts of the Minkowski-type orbital AM, equations (3.15) and (3.16), (in units of 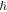 per plasmon) are shown in figure 4(b).
per plasmon) are shown in figure 4(b).
Below we examine the microscopic model of fields and electrons in the metal, which confirms the above phenomenological calculations and Minkowski-type picture of the momentum and AM of SPPs.
4. Microscopic calculations for a SPP
4.1. Microscopic fields and parameters of electron plasma
The microscopic approach is based on the separation of the microscopic electromagnetic field (E, H) and charges/currents inside the medium. In our case, the metal can be described using the Bloch hydrodynamic model for electron plasma. In this model, the electron density is written as 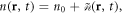 where
where 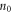 is the uniform unperturbed density of free electrons (which neutralizes positive charges of background motionless ions), and
is the uniform unperturbed density of free electrons (which neutralizes positive charges of background motionless ions), and 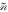 is a small perturbation of the electron density caused by the interaction with electromagnetic wave fields. The local electron velocity is given by
is a small perturbation of the electron density caused by the interaction with electromagnetic wave fields. The local electron velocity is given by 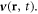 Considering a monochromatic linear problem, we introduce complex amplitudes for perturbations of electron properties,
Considering a monochromatic linear problem, we introduce complex amplitudes for perturbations of electron properties, ![$\tilde{{\mathscr{n}}}({\bf{r}},t)=\mathrm{Re}[\tilde{n}({\bf{r}}){{\rm{e}}}^{-{\rm{i}}\omega t}]$](https://content.cld.iop.org/journals/1367-2630/19/12/123014/revision2/njpaa8913ieqn167.gif) and
and ![$\pmb{\mathscr{v}}({\bf{r}},t)=\mathrm{Re}[\tilde{{\bf{v}}}({\bf{r}}){{\rm{e}}}^{-{\rm{i}}\omega t}],$](https://content.cld.iop.org/journals/1367-2630/19/12/123014/revision2/njpaa8913ieqn168.gif) and the time derivatives become
and the time derivatives become 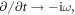 entirely similar to complex field amplitudes. Microscopic electromagnetic fields always occur in free space (i.e., there is no effective medium,
entirely similar to complex field amplitudes. Microscopic electromagnetic fields always occur in free space (i.e., there is no effective medium,  ), but the Maxwell equations are modified by the presence of charges and currents [22]:
), but the Maxwell equations are modified by the presence of charges and currents [22]:

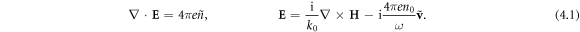
These equations describe the influence of the electrons on the fields. The back action is described by the hydrodynamic equation for the electron gas [71]:
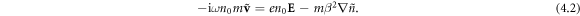
This equation is a classical equation of motion of the electron in the electric field E (the Lorentz force from the magnetic field vanishes in the linear problem) with the additional quantum pressure term involving the coefficient 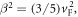 where
where  is the Fermi velocity of electrons. Our classical treatment of the SPP wave implies the limit
is the Fermi velocity of electrons. Our classical treatment of the SPP wave implies the limit 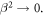 However, we cannot omit the last term in equation (4.2) from the beginning because it is crucial to satisfy the boundary conditions at the metal-vacuum discontinuity,
However, we cannot omit the last term in equation (4.2) from the beginning because it is crucial to satisfy the boundary conditions at the metal-vacuum discontinuity, 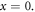
Solving equations (4.1) and (4.2) with standard boundary conditions at the metal-vacuum interface (continuity of 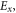
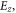
 and vanishing of
and vanishing of  ) yields the microscopic electric and magnetic fields as well as electron plasma properties in the SPP wave. The magnetic field (both in the vacuum and in the metal) and electric field in the vacuum are still described by the macroscopic equation (3.2) with parameters (3.1) and (3.3), while the electric field inside the metal becomes:
) yields the microscopic electric and magnetic fields as well as electron plasma properties in the SPP wave. The magnetic field (both in the vacuum and in the metal) and electric field in the vacuum are still described by the macroscopic equation (3.2) with parameters (3.1) and (3.3), while the electric field inside the metal becomes:
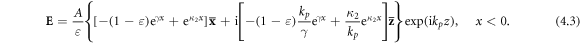
Here 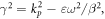 we still use
we still use  as a parameter given by equation (3.1), and
as a parameter given by equation (3.1), and 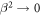 implies
implies 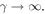 The electron density and velocity perturbations in SPPs are given by:
The electron density and velocity perturbations in SPPs are given by:
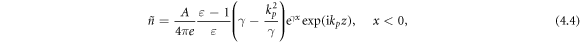
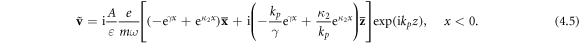
We can now consider the classical limit 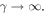 Since the γ-terms appear only in the metal half-space
Since the γ-terms appear only in the metal half-space  one can use the limiting transition
one can use the limiting transition  where the delta-function describes surface effects at the interface. After doing so, the electric field (4.3) becomes equal to the macroscopic one, equation (3.2), while the electron density vanishes in the volume,
where the delta-function describes surface effects at the interface. After doing so, the electric field (4.3) becomes equal to the macroscopic one, equation (3.2), while the electron density vanishes in the volume,  for
for 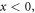 and acquires a surface delta-function singularity:
and acquires a surface delta-function singularity:
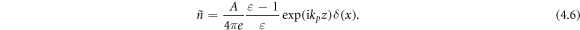
As we show below, this singularity is cancelled by another singularity in field gradients, and all dynamical properties of the SPP wave are determined by volume contributions in the metal and in the vacuum. Finally, the electron velocity (4.5) becomes proportional to the electric field (3.2) (which follows from equation (4.2) at β = 0):
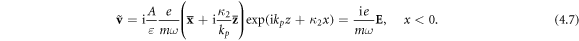
Note that it is the vanishing of the electron density perturbation  in volume that makes the microscopic fields 'transverse', i.e., divergence-free:
in volume that makes the microscopic fields 'transverse', i.e., divergence-free: 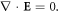 Because of this, we do not need to consider contributions of 'longitudinal' (i.e., curl-free) fields to the energy, momentum, and AM [90].
Because of this, we do not need to consider contributions of 'longitudinal' (i.e., curl-free) fields to the energy, momentum, and AM [90].
In addition to the point-charge features of electrons, we will need their electric-dipole properties. Since velocity is a time derivative of the position of the electron, we can write the complex amplitude of the electron displacement as 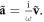 From here, the complex amplitude of the density of the electron dipole moment is:
From here, the complex amplitude of the density of the electron dipole moment is:
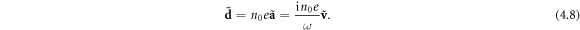
Substituting here equation (4.7), we can write the dipole-moment density (4.8) as:
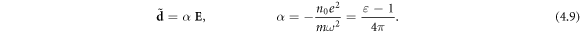
Here α is the dipole polarizability of the electron gas, and the last equality shows that it is in perfect agreement with the macroscopic theory based on the permittivity  [22]. Indeed, substituting the velocity (4.7) into Maxwell equation (4.1) for microscopic fields, we immediately obtain the source-free Maxwell equation (2.2) for macroscopic fields with permittivity
[22]. Indeed, substituting the velocity (4.7) into Maxwell equation (4.1) for microscopic fields, we immediately obtain the source-free Maxwell equation (2.2) for macroscopic fields with permittivity 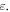
4.2. Microscopic calculations of energy and momentum densities
In the vacuum half-space 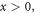 the microscopic and macroscopic electromagnetic fields and their properties coincide, so we have to compare only the macroscopic and microscopic properties in the metal. Hereafter, we consider all quantities only in the
the microscopic and macroscopic electromagnetic fields and their properties coincide, so we have to compare only the macroscopic and microscopic properties in the metal. Hereafter, we consider all quantities only in the 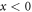 half-space.
half-space.
The cycle-averaged energy density in the system of microscopic electromagnetic fields and electrons can be written as:
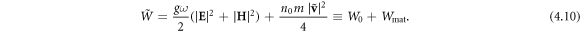
Here the first term is the microscopic-field energy (written as for free-space fields, equation (2.1)), and the second term is the kinetic energy of electrons. Note that the latter can also be presented as the energy of the dipole (4.8) and (4.9) in the electric field: 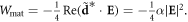 Substituting fields (3.2) and velocity (4.7) into equation (4.10) results in the macroscopic energy density
Substituting fields (3.2) and velocity (4.7) into equation (4.10) results in the macroscopic energy density 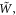 equation (3.4), at
equation (3.4), at  Thus, the microscopic and macroscopic calculations are in perfect agreement. The field and electron contributions in the metal are:
Thus, the microscopic and macroscopic calculations are in perfect agreement. The field and electron contributions in the metal are:
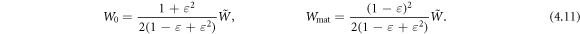
The momentum density in the microscopic approach is also the sum of the field and electron contributions. The velocity of electrons in external fields is associated with the kinetic rather than canonical momentum of electrons, and, therefore, we consider the corresponding kinetic momentum density of the field. (It is worth noticing that the canonical electron momentum in the metal vanishes:  where we used the relation
where we used the relation  for the transverse vector potential and equation (4.7).) For the microscopic field, the kinetic field momentum is given by the Poynting vector (1.1), i.e. the Abraham momentum. Below we show that adding it to the kinetic electron momentum yields the kinetic Minkowski-type momentum density (2.8) suggested by Philbin [16, 17]:
for the transverse vector potential and equation (4.7).) For the microscopic field, the kinetic field momentum is given by the Poynting vector (1.1), i.e. the Abraham momentum. Below we show that adding it to the kinetic electron momentum yields the kinetic Minkowski-type momentum density (2.8) suggested by Philbin [16, 17]:
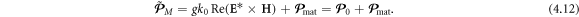
The calculation of the electron contribution 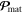 requires a more sophisticated approach. Indeed, the simple expression
requires a more sophisticated approach. Indeed, the simple expression  (with oscillating, zero-average
(with oscillating, zero-average  ) for point electrons does not provide a meaningful result; instead of this, one has to consider an optical force acting on electric dipoles (4.8) and (4.9). We follow the formalism described in the review [4], section 5.1 therein.
) for point electrons does not provide a meaningful result; instead of this, one has to consider an optical force acting on electric dipoles (4.8) and (4.9). We follow the formalism described in the review [4], section 5.1 therein.
Namely, we consider a long but finite wave packet instead of a monochromatic continuous wave. Afterwards, the length of the wave packet can be tend to infinity. Introducing slowly varying amplitudes 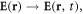
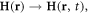 etc, with the typical scale of the t-variations much larger than
etc, with the typical scale of the t-variations much larger than 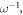 involves the corresponding narrow but finite frequency Fourier spectrum centered at
involves the corresponding narrow but finite frequency Fourier spectrum centered at 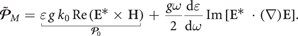 This produces the first-order Taylor-series correction to the relation (4.9) between the dipole moment and electric field:
This produces the first-order Taylor-series correction to the relation (4.9) between the dipole moment and electric field:
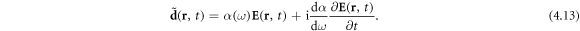
Next, we consider the cycle-averaged force density acting on the dipole moment (4.13) in an external electromagnetic field [4]:
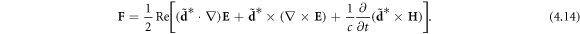
Substituting here equation (4.13), after some transformations the force can be written as:
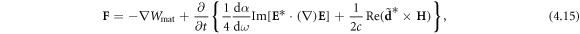
where 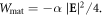 The first term in equation (4.15) represents the gradient force, while the two terms subject to the time derivative should be associated with the momentum density carried by the electrons, i.e.,
The first term in equation (4.15) represents the gradient force, while the two terms subject to the time derivative should be associated with the momentum density carried by the electrons, i.e., 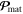 of equation (4.12). Expressing the dipole-moment density and polarizability via the electric field and
of equation (4.12). Expressing the dipole-moment density and polarizability via the electric field and 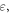 equation (4.9), we arrive at:
equation (4.9), we arrive at:
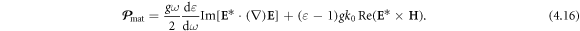
Here the second term is associated with the 'Abraham force' [22].
Substituting the electron momentum density (4.16) into equation (4.12), results in the kinetic form of the Minkowski-type momentum density (2.8) (for μ = 1):
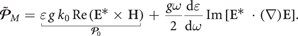
Thus, using microscopic calculations for the SPP, we rigorously derived the kinetic momentum density (2.8) suggested previously from a phenomenological formalism [16, 17].
We now trace the decomposition of the kinetic momentum (4.17) into the canonical (orbital) and spin parts (2.9) and (2.10). In principle, one substitutes the electron velocity 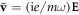 into the microscopic Maxwell equation (4.1), which results in the macroscopic Maxwell equation (2.2) with permittivity
into the microscopic Maxwell equation (4.1), which results in the macroscopic Maxwell equation (2.2) with permittivity 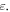 Then, the decomposition becomes straightforward as described in section 2. However, it is instructive to trace this decomposition at the microscopic level. For this purpose, we decompose the Poynting-like part of the kinetic momentum (4.17) into canonical and orbital parts using the microscopic Maxwell equation (4.1). The presence of sources,
Then, the decomposition becomes straightforward as described in section 2. However, it is instructive to trace this decomposition at the microscopic level. For this purpose, we decompose the Poynting-like part of the kinetic momentum (4.17) into canonical and orbital parts using the microscopic Maxwell equation (4.1). The presence of sources, 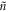 and
and 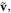 modifies this decomposition as compared to the free-space case (1.6)–(1.8):
modifies this decomposition as compared to the free-space case (1.6)–(1.8):
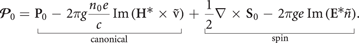
Here we ascribed the two source-related terms to the canonical and spin parts such that the final result will coincide with the macroscopic equations.
First, for the SPP fields (3.2) and velocity (4.7) the velocity-related term contains only the canonical-type contribution (because 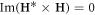 in SPPs):
in SPPs):
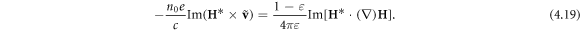
Combining the canonical part of equation (4.18) with equation (4.19) and the second term in equation (4.17), we obtain the macroscopic canonical Minkowski-type momentum (2.9) (with μ = 1):
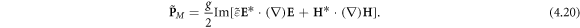
Second, the curl of the free-space-like spin S0 for the SPP fields (3.2) contains a delta-function singularity at the metal-vacuum interface x = 0. Remarkably, this singularity is exactly cancelled by the singularity (4.6) in the electron density distribution, so that the spin part in equation (4.18) becomes non-singular. This confirms the non-singular character of the spin–orbital decomposition in the Minkowski-type approach, in contrast to the Abraham one [65]. In the bulk, 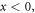 the spin part of equation (4.18) substituted in equation (4.17) immediately yields the corresponding part of the macroscopic Minkowski-type momentum involving the 'naïve' Minkowski spin (2.10):
the spin part of equation (4.18) substituted in equation (4.17) immediately yields the corresponding part of the macroscopic Minkowski-type momentum involving the 'naïve' Minkowski spin (2.10):
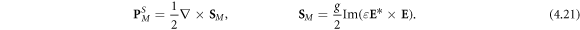
Thus, we have obtained the macroscopic Minkowski-type momentum densities (2.8)–(2.10), both kinetic and canonical, using microscopic calculations in the metal with separated field and matter contributions.
4.3. Microscopic approach to the spin and orbital AM
It might seem that the description of the AM quantities in dispersive media, given in section 2, is somewhat 'inconsistent' with the corresponding momentum quantities. Indeed, the Minkowski-type kinetic AM (2.12) is not simply determined by the corresponding kinetic momentum, 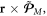 but contains additional dispersion-related terms. Furthermore, the spin momentum (2.10) is determined by the naïve Minkowski spin density SM, while the proper canonical spin AM
but contains additional dispersion-related terms. Furthermore, the spin momentum (2.10) is determined by the naïve Minkowski spin density SM, while the proper canonical spin AM 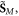 equation (2.13), differs from it in a dispersive medium. The microscopic approach sheds light on these 'inconsistencies'.
equation (2.13), differs from it in a dispersive medium. The microscopic approach sheds light on these 'inconsistencies'.
Namely, the local motion of electrons provides an intrinsic contribution to the AM density [71], in fact, to its spin part. Using the electron displacement 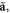 equation (4.8), and velocity
equation (4.8), and velocity 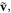 equation (4.7), one can write this part of the AM density as:
equation (4.7), one can write this part of the AM density as:
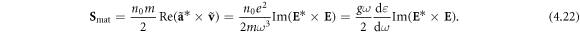
This term exactly describes the dispersion-related addition in the Minowski-type kinetic AM (2.12) for the SPP wave:
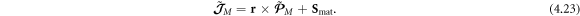
Thus, akin to the momentum density (2.8) and (4.17), microscopic calculations justify the kinetic AM density (2.12), previously obtained by Philbin within a phenomenological approach [17].
Consider now the spin and orbital AM densities. The orbital AM density is straightforwardly determined by the canonical momentum (4.20): 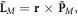 and we have already described its properties in section 3. At the same time, the intrinsic electron contribution (4.22) elucidates the difference between the naïve Minkowski spin density (4.21) and canonical spin density (2.13):
and we have already described its properties in section 3. At the same time, the intrinsic electron contribution (4.22) elucidates the difference between the naïve Minkowski spin density (4.21) and canonical spin density (2.13):
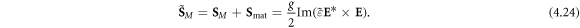
This justifies the use of the canonical spin AM in dispersive media and the transverse spin of a SPP calculated in equations (3.13) and (3.14), figure 4(a). The dispersion-related contribution is absolutely crucial in the case of SPPs, because 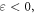
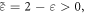 and it changes both the magnitude and sign of the spin AM density in the metal.
and it changes both the magnitude and sign of the spin AM density in the metal.
4.4. Magnetization, magnetization current, and Abraham momentum
The electron contribution (4.22) to the spin AM of a SPP corresponds to the microscopic circular motion of electrons in the SPP field. This microscopic orbital motion of the electrons produces multiple circulating currents, and, hence, the constant (non-oscillating) magnetization of the metal. Using the standard gyromagnetic ratio, we obtain the magnetization density in the metal:
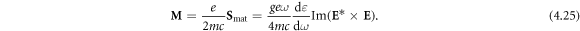
This equation exactly coincides with the results [91, 92] obtained for the magnetization of plasma by electromagnetic radiation and the inverse Faraday effect [22, 93]. For the SPP fields (3.2) and (3.3), we find:
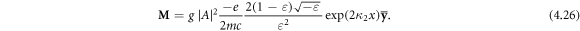
Thus, the metal is magnetized along the positive-y direction (e < 0).
The magnetization (4.26) means that the SPP, being a mixed photon-electron excitation, carries a non-zero magnetic moment. To characterize this magnetic moment 'per plasmon', we calculate the integral magnetization (4.26):
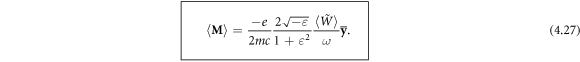
This corresponds to the magnetic moment 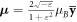 per plasmon, where
per plasmon, where 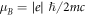 is the Bohr magneton. The absolute value of this magnetic moment grows from 0 to
is the Bohr magneton. The absolute value of this magnetic moment grows from 0 to 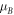 as the SPP frequency
as the SPP frequency 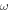 changes from 0 to
changes from 0 to 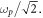
Moreover, the inhomogeneous magnetization (4.26) generates the corresponding magnetization electric current 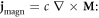
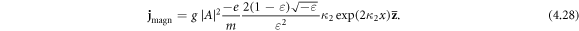
This is a direct current which flows in the metal in the z direction, i.e., along the SPP propagation. It should be emphasized that the current (4.28) is obtained as a quadratic form of the SPP fields. Indeed, the linear-approximation current is determined by the electron velocity 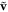 and vanishes after cycle averaging.
and vanishes after cycle averaging.
We also note that the magnetization current is solenoidal (divergenceless). Therefore, it does not contribute to the charge transport and cannot be measured by an ammeter or voltmeter. Nonetheless, one can determine the electron velocity  and momentum density
and momentum density  corresponding to the direct current (4.28). Using equation (3.3), we write it as:
corresponding to the direct current (4.28). Using equation (3.3), we write it as:
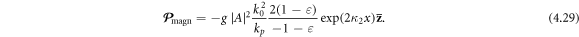
Thus, the magnetization momentum (4.29) is directed oppositely to the SPP propagation. Remarkably, it is exactly equal to the difference between the kinetic Abraham and Minkowski-type momentum densities in the metal, equations (3.7) and (3.10):
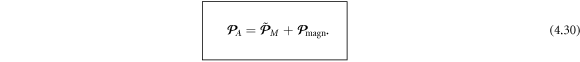
Equation (4.30) completes the microscopic picture and explains the origin of the difference between the Abraham and Minkowski momenta in the medium. Since this difference is produced by the direct magnetization current, it cannot be attributed to the wave (Minkowski-type) momentum but it does contribute to the energy flux (Abraham–Poynting momentum) and the group velocity of SPPs. Note that the Abraham momentum density can also be obtained as a pure microscopic-field momentum  see equation (4.12) [19]. It follows from here that the total momentum of the metal vanishes in the problem under consideration: the electron contribution to the wave momentum is exactly cancelled by the magnetization-current momentum:
see equation (4.12) [19]. It follows from here that the total momentum of the metal vanishes in the problem under consideration: the electron contribution to the wave momentum is exactly cancelled by the magnetization-current momentum: 
5. Helicity and duality aspects
5.1. Helicity density and flux in a medium
Here we briefly consider problems related to the dual symmetry between electric and magnetic fields in Maxwell equations [52, 54–57, 69, 70, 75, 76, 79]. This symmetry is exact in free-space Maxwell equations, but the presence of electric charges and currents in matter breaks it. The dual symmetry corresponds to the conservation of electromagnetic helicity via Noether's theorem [55, 57, 69, 70, 75, 76, 94–97]. Using the same phenomenological Lagrangian formalism as for the derivation of Minkowski-type momentum and AM densities (2.8) and (2.12), Philbin obtained the helicity density in a dispersive medium [77]:
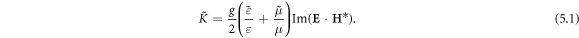
In a dispersion-free medium, 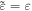 and
and 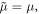 and equation (5.1) yields the free-space result
and equation (5.1) yields the free-space result  [55, 57, 59, 69]. It should be emphasized that
[55, 57, 59, 69]. It should be emphasized that  is the helicity density, but not the chirality density (Lipkin's zilch); these quantities are simply proportional to each other only in free space [57, 77, 98–102]. Similarly to equation (2.17), for a plane wave in a homogeneous transparent medium, equation (5.1) yields:
is the helicity density, but not the chirality density (Lipkin's zilch); these quantities are simply proportional to each other only in free space [57, 77, 98–102]. Similarly to equation (2.17), for a plane wave in a homogeneous transparent medium, equation (5.1) yields:
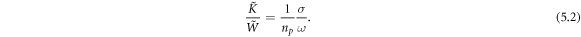
This means that the helicity 'per photon' in units of  is limited in the medium by the
is limited in the medium by the  range. This is a strange result without clear physical meaning. Using the quantum wavefunction formalism (2.15) and (2.16) with the helicity operator [55, 59]
range. This is a strange result without clear physical meaning. Using the quantum wavefunction formalism (2.15) and (2.16) with the helicity operator [55, 59]  would produce a more natural result:
would produce a more natural result:
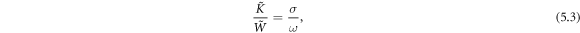
but only in the case of a non-dispersive medium. Therefore, the helicity density in a dispersive medium is still controversial and requires further investigation. In any case, for the SPP fields (3.2), the helicity vanishes [65] due to the orthogonality of the electric and magnetic fields.
Note also that in free space the dual-symmetric spin AM density (1.7) determines the helicity flux density [55, 57, 69, 70, 99]. In a dispersive medium, calculations in [77] showed that the flux density of the helicity (5.1) is determined by the Abraham spin density  equation (2.6). In this case, the helicity flux density does not coincide with the proper Minkowski-type spin AM density (2.13) in a medium, and these are two different physical quantities. Even considering the Lipkin's chirality density, its flux becomes proportional to the 'naïve' Minkowski spin density
equation (2.6). In this case, the helicity flux density does not coincide with the proper Minkowski-type spin AM density (2.13) in a medium, and these are two different physical quantities. Even considering the Lipkin's chirality density, its flux becomes proportional to the 'naïve' Minkowski spin density  [77, 101], which is different from the canonical spin density (2.13) in dispersive media.
[77, 101], which is different from the canonical spin density (2.13) in dispersive media.
5.2. Dual-symmetric and asymmetric quantities
So far, we considered all definitions of the optical energy, momentum, and AM using forms symmetric with respect to the electric and magnetic fields (and, correspondingly, indices  and μ) [35, 41, 42, 46, 52, 54–57, 59, 65, 69, 70]. However, in standard electromagnetic field theory (or QED) the field Lagrangian is not dual-symmetric [36, 44, 55, 69, 70]. Due to this, the canonical momentum, spin, and orbital AM densities are often defined using dual-asymmetric field-theory expressions, which contain only the electric-field parts [36, 44, 47–50, 60, 90]. In such 'standard' formalism in free space, the energy density and kinetic Poynting momentum density are still given by the dual-symmetric expressions (1.1) and (2.1), whereas the canonical momentum, spin, and spin AM densities (1.6)–(1.8) become [54, 55]:
and μ) [35, 41, 42, 46, 52, 54–57, 59, 65, 69, 70]. However, in standard electromagnetic field theory (or QED) the field Lagrangian is not dual-symmetric [36, 44, 55, 69, 70]. Due to this, the canonical momentum, spin, and orbital AM densities are often defined using dual-asymmetric field-theory expressions, which contain only the electric-field parts [36, 44, 47–50, 60, 90]. In such 'standard' formalism in free space, the energy density and kinetic Poynting momentum density are still given by the dual-symmetric expressions (1.1) and (2.1), whereas the canonical momentum, spin, and spin AM densities (1.6)–(1.8) become [54, 55]:
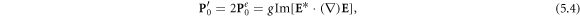
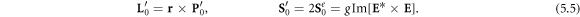
Here, we introduced the electric and magnetic parts of the momentum and spin densities (1.6) and (1.7): 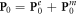 and
and 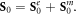 Adopting the definitions (5.4) and (5.5) would mean that only the phase gradients of the electric (but not magnetic) field produce momentum and orbital AM, and only rotations of the electric (but not magnetic) field generate the spin AM. On the one hand, this is not satisfactory from a general physical perspective, where electromagnetic waves involve electric and magnetic fields on equal footing [52, 55–57, 81–83]. On the other hand, the electric-biased quantities (5.4) and (5.5) can be useful in some practical problems considering interactions of fields with electric-dipole particles or atoms, which are not sensitive to magnetic fields [47–49, 59, 60]. However, for magnetic-dipole particles, the electric-biased quantities (5.4) and (5.5) do not make sense.
Adopting the definitions (5.4) and (5.5) would mean that only the phase gradients of the electric (but not magnetic) field produce momentum and orbital AM, and only rotations of the electric (but not magnetic) field generate the spin AM. On the one hand, this is not satisfactory from a general physical perspective, where electromagnetic waves involve electric and magnetic fields on equal footing [52, 55–57, 81–83]. On the other hand, the electric-biased quantities (5.4) and (5.5) can be useful in some practical problems considering interactions of fields with electric-dipole particles or atoms, which are not sensitive to magnetic fields [47–49, 59, 60]. However, for magnetic-dipole particles, the electric-biased quantities (5.4) and (5.5) do not make sense.
Note that in free space, the dual-asymmetric densities (5.4) and (5.5) do not cause significant problems because: (i) the Poynting-vector decomposition still has the same form (1.8): 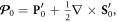 and (ii) the integral values of all these quantities for localized free-space fields coincide with the dual-symmetric definitions [52, 55]:
and (ii) the integral values of all these quantities for localized free-space fields coincide with the dual-symmetric definitions [52, 55]:

However, in a medium, which is dual-asymmetric  in the generic case, the difference between the dual-symmetric and asymmetric definitions becomes crucial. We again consider the example of a SPP wave at a metal-vacuum interface. First, the electric and magnetic contributions to the energy density (2.3) and (3.4) for the macroscopic SPP fields (3.2) equal:
in the generic case, the difference between the dual-symmetric and asymmetric definitions becomes crucial. We again consider the example of a SPP wave at a metal-vacuum interface. First, the electric and magnetic contributions to the energy density (2.3) and (3.4) for the macroscopic SPP fields (3.2) equal:
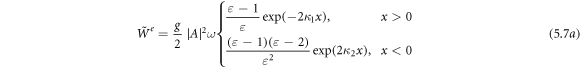
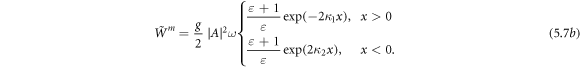
Obviously, these contributions are different and result in different integral electric and magnetic energy parts:

Then, the electric and magnetic parts of the canonical Minkowski-type momentum (2.9) and (3.9) become proportional to the corresponding energy parts:
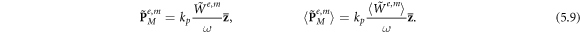
From here and the difference in the integral electric and magnetic energies (5.8), it follows that using an electric-biased momentum density similar to equation (5.4), ![${\tilde{{\bf{P}}}}_{M}^{{\prime} }=2{\tilde{{\bf{P}}}}_{M}^{e}=g\text{Im}[\tilde{\varepsilon }\,{{\bf{E}}}^{* }\cdot ({\rm{\nabla }}){\bf{E}}],$](https://content.cld.iop.org/journals/1367-2630/19/12/123014/revision2/njpaa8913ieqn248.gif) would yield:
would yield:
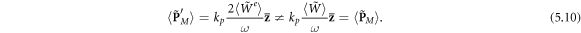
Thus, the dual-asymmetric definitions in a medium do not satisfy the convenient free-space relations (5.6). In the case of equation (5.10), this breaks the natural proportionality (3.9) and the momentum of the SPP becomes not equal to 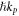 per plasmon. Obviously, this is a physically unsatisfactory result. Therefore, we conclude that dual-symmetric definitions of momentum and AM densities are crucial for structured waves in inhomogeneous optical media.
per plasmon. Obviously, this is a physically unsatisfactory result. Therefore, we conclude that dual-symmetric definitions of momentum and AM densities are crucial for structured waves in inhomogeneous optical media.
Moreover, the validity of the dual-symmetric (rather than electric-biased) formalism follows from the microscopic calculations of section 4. Indeed, the dispersion-related material correction in equation (4.17) has the form 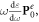 independently of the formalism. It is naturally combined with the corresponding electric term
independently of the formalism. It is naturally combined with the corresponding electric term 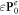 of the dual-symmetric spin–orbital decomposition of the first term of (4.17), yielding the electric part of the canonical dual-symmetric Minkowski-type momentum (2.9):
of the dual-symmetric spin–orbital decomposition of the first term of (4.17), yielding the electric part of the canonical dual-symmetric Minkowski-type momentum (2.9): 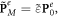 see equations (4.18)–(4.20). However, using the electric-biased decomposition (5.4) and (5.5) doubles the non-dispersive term:
see equations (4.18)–(4.20). However, using the electric-biased decomposition (5.4) and (5.5) doubles the non-dispersive term: 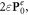 and then it cannot be combined with the same dispersive term into a meaningful result proportional to
and then it cannot be combined with the same dispersive term into a meaningful result proportional to 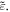 The same situation occurs in the microscopic derivation of the spin AM. The dispersive material term
The same situation occurs in the microscopic derivation of the spin AM. The dispersive material term 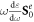 (4.22) is naturally combined with the electric part of the dual-symmetric spin density
(4.22) is naturally combined with the electric part of the dual-symmetric spin density 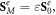 producing the electric part of the canonical dual-symmetric Minkowski-type spin (2.13):
producing the electric part of the canonical dual-symmetric Minkowski-type spin (2.13):  see equation (4.24). In turn, the electric-biased non-dispersive spin
see equation (4.24). In turn, the electric-biased non-dispersive spin 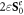 cannot be combined with the fixed dispersive term. Thus, the dual-symmetric forms of the canonical momentum and AM densities are justified on the microscopic level by fixed dispersive material terms in the momentum and AM densities.
cannot be combined with the fixed dispersive term. Thus, the dual-symmetric forms of the canonical momentum and AM densities are justified on the microscopic level by fixed dispersive material terms in the momentum and AM densities.
The transverse spin AM of SPPs is a quantity which is extremely sensitive to the duality. Indeed, for the metal-vacuum interface considered here, the transverse spin has a purely electric nature: only the electric field rotates in solutions (3.2), while the transverse magnetic field yields no contribution to the spin AM [65]. Using an electric-biased definition of the spin AM, similar to equation (5.5), 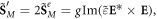 we would obtain a transverse spin twice as large as equations (3.13) and (3.14):
we would obtain a transverse spin twice as large as equations (3.13) and (3.14): 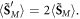 However, one could also consider surface waves at an interface between the vacuum and a magnetic medium with
However, one could also consider surface waves at an interface between the vacuum and a magnetic medium with  and
and  In this case, the surface wave would be given by equation (3.2) with swapped electric and magnetic fields, and the transverse spin would have a purely magnetic nature. Obviously, the electric-biased definition would yield no spin AM at all:
In this case, the surface wave would be given by equation (3.2) with swapped electric and magnetic fields, and the transverse spin would have a purely magnetic nature. Obviously, the electric-biased definition would yield no spin AM at all:  This is a clear evidence that the equality of integral electric and magnetic spins for localized states in free space [52] does not hold true in media:
This is a clear evidence that the equality of integral electric and magnetic spins for localized states in free space [52] does not hold true in media:
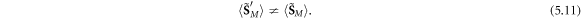
Overall, we conclude that only the dual-symmetric definitions of the momentum, spin, and orbital AM properties of optical fields in dispersive media provide physically consistent and satisfactory results.
6. Concluding remarks
We have examined momentum and AM properties of monochromatic optical fields in dispersive and inhomogeneous media. The two major problems that lie at the heart of this study are: (i) the Abraham–Minkowski dilemma and (ii) the canonical spin–orbital decomposition of optical momentum and AM. We have shown that, in principle, one can formulate four momentum-AM pictures using Abraham-type and Minkowski-type quantities in kinetic (i.e. Poynting-like, without spin–orbital separation) and canonical (i.e. with spin–orbital separation) approaches. These four pictures are summarized in table 1. However, two of these sets of quantities are more physically meaningful.
First, the Abraham–Poynting kinetic momentum density (1.1) and (1.2),  should be associated with the energy flux density rather than the momentum density. This quantity determines the energy transport and group velocity of a wave packet in the medium.
should be associated with the energy flux density rather than the momentum density. This quantity determines the energy transport and group velocity of a wave packet in the medium.
Second, the canonical Minkowski-type momentum density (2.9),  together with the corresponding spin and orbital AM densities (2.13),
together with the corresponding spin and orbital AM densities (2.13), 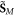 and
and 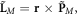 provide a physically meaningful and self-consistent description of the momentum and AM of light in the medium. To the best of our knowledge, these quantities were derived for the first time in the present work, but these are consistent with several previously used approaches. On the one hand, the kinetic counterpart of this canonical picture, momentum (2.8),
provide a physically meaningful and self-consistent description of the momentum and AM of light in the medium. To the best of our knowledge, these quantities were derived for the first time in the present work, but these are consistent with several previously used approaches. On the one hand, the kinetic counterpart of this canonical picture, momentum (2.8), 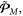 and total AM (2.12),
and total AM (2.12), 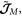 exactly coincide with those obtained in the most general form by Philbin and Allanson [16, 17]. On the other hand, our canonical characteristics (2.9) and (2.13) have a more elegant form, exhibiting a pleasing similarity with the Brillouin energy density (2.3),
exactly coincide with those obtained in the most general form by Philbin and Allanson [16, 17]. On the other hand, our canonical characteristics (2.9) and (2.13) have a more elegant form, exhibiting a pleasing similarity with the Brillouin energy density (2.3), 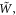 in the medium. As a result, the energy, momentum, spin, and orbital AM densities in the medium can be written in a laconic unified form (2.15) using the corresponding quantum-mechanical operators and proper inner product modified by the
in the medium. As a result, the energy, momentum, spin, and orbital AM densities in the medium can be written in a laconic unified form (2.15) using the corresponding quantum-mechanical operators and proper inner product modified by the  and
and 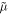 indices of the medium. This coincides with the general approach to electromagnetic bi-linear forms developed by Silveirinha [81–83].
indices of the medium. This coincides with the general approach to electromagnetic bi-linear forms developed by Silveirinha [81–83].
We applied the above general theory to a SPP wave at a metal-vacuum interface. This example provides a deep physical insight because it involves essentially inhomogeneous fields as well as an inhomogeneous, non-transparent, and dispersive medium. This is in sharp contrast to plane waves in homogeneous transparent media, which are considered in the majority of the Abraham–Minkowski studies. We have shown that in the non-trivial SPP field, the integral Abraham–Poynting momentum 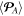 describes the group velocity
describes the group velocity  of SPPs, equation (3.8), while the integral canonical momentum
of SPPs, equation (3.8), while the integral canonical momentum 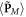 corresponds to the super-momentum
corresponds to the super-momentum 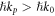 per plasmon, equation (3.9). This is the first example of a wave, which carries an integral momentum larger than that of a photon in vacuum, and this originates from the inhomogeneous-evanescent character of the surface wave rather than from the medium refractive index (
per plasmon, equation (3.9). This is the first example of a wave, which carries an integral momentum larger than that of a photon in vacuum, and this originates from the inhomogeneous-evanescent character of the surface wave rather than from the medium refractive index (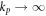 at
at 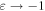 in the metal).
in the metal).
We have also provided the first accurate calculation of the transverse spin 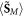 of a SPP, equation (3.14). The result differs considerably from previous calculations using the Abraham-type definition of the spin [65]. In particular, the integral transverse spin AM of a SPP can vanish (at
of a SPP, equation (3.14). The result differs considerably from previous calculations using the Abraham-type definition of the spin [65]. In particular, the integral transverse spin AM of a SPP can vanish (at  ), change its sign and reach the value
), change its sign and reach the value 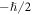 per plasmon, figure 4(a). In turn the intrinsic orbital AM (calculated with respect to the center of energy) of a SPP vanishes, equation (3.15). This agrees with the non-vortex character of the canonical momentum density (phase gradient) in the SPP field, and is in contrast to the Abraham–Poynting circulating energy flux [65].
per plasmon, figure 4(a). In turn the intrinsic orbital AM (calculated with respect to the center of energy) of a SPP vanishes, equation (3.15). This agrees with the non-vortex character of the canonical momentum density (phase gradient) in the SPP field, and is in contrast to the Abraham–Poynting circulating energy flux [65].
Thus, the SPP example shows that the Abraham-type kinetic and Minkowski-type canonical properties provide intuitively clear and consistent description of complex optical fields in complex media. Importantly, we have also provided microscopic calculations of the momentum and AM densities for the SPP field, considering the microscopic electromagnetic fields and motion of free electrons in the metal. These calculations resulted precisely in the Minkowski-type momentum and AM densities, previously suggested from macroscopic phenomenological approaches [16, 17]. This proves the validity of our approach and illuminates its physical origin. Importantly, the dispersion 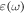 in the metal was absolutely crucial in the above calculations, affecting not only the magnitudes but also the signs of the dynamical quantities (because of
in the metal was absolutely crucial in the above calculations, affecting not only the magnitudes but also the signs of the dynamical quantities (because of 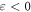 and
and 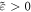 ).
).
Using the microscopic theory, we have also predicted a transverse magnetization of the metal (the inverse Faraday effect) corresponding to the transverse spin of a SPP. This means that a SPP wave carries not only the spin AM but also the transverse magnetic moment, up to a Bohr magneton per plasmon. Furthermore, an inhomogeneous magnetization produces the direct magnetization current flowing along the metal surface in the SPP propagation direction. Remarkably, the momentum density corresponding to this current is exactly equal to the difference between the Abraham and Minkowski-type momenta in the metal, thereby providing one more 'resolution' of this longstanding problem [1–7].
Finally, we briefly discussed the optical helicity and duality problems in dispersive media. The analysis of the SPP example leads us to conclude that the dual-symmetric description of the canonical momentum, spin and orbital AM, with symmetric electric- and magnetic-field contributions, is crucially important for the physically meaningful and consistent picture of these properties in dispersive media. In particular, we found that microscopic calculations, including dispersion-related material terms, are consistent with the dual-symmetric (rather than electric-biased) formalism.
Thus, the present study provides a complete analysis and description of the momentum and AM of light in dispersive and inhomogeneos (but isotropic and lossless) media. We have considered SPPs only as the simplest example of the application of our theory, where other approaches fail. Taking into account both material and structured-light properties is crucial in a variety of nanooptical and photonic systems, including photonic crystals, metamaterials, and optomechanical systems. Our theory provides an efficient toolbox for the description of dynamical properties of light in such systems. One of the main tasks for future studies is to extend this analysis to other classes of materials, including dissipation or gain and anisotropy. In particular, it is not clear if one can separate the spin and orbital degrees of freedom in anisotropic media. Close correspondence of our approach to some of the results of [18, 81–83, 101] (dealing with quite general bi-anisotropic media), suggests that the analysis presented in this work can be extended to more complex cases.
Another important direction for future consideration is whether the fundamental wave characteristics introduced in this work can be observed in experiments. There were experiments measuring Minkowski-type momentum 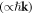 for plane waves in dispersive media [13, 103, 104]. In addition, the canonical momentum and spin AM densities in structured optical fields in free space are directly observable via the optical force and torque on dipole particles or atoms [31–35, 41, 46, 47, 59–63, 66]. Therefore, now it would be important to calculate and measure optical forces and torques on small particles in dispersive media (e.g. liquids or gases), and check if these are proportional to the canonical momentum and spin densities in dispersive media. Furthermore, it would be important to find an experimental setup where the integral super-momentum and transverse spin of SPPs, derived in this work, could be detected. So far, only local densities of these quantities were accessible via local free-space measurements using small particles or atoms [31–35, 41, 66, 67, 105–108].
for plane waves in dispersive media [13, 103, 104]. In addition, the canonical momentum and spin AM densities in structured optical fields in free space are directly observable via the optical force and torque on dipole particles or atoms [31–35, 41, 46, 47, 59–63, 66]. Therefore, now it would be important to calculate and measure optical forces and torques on small particles in dispersive media (e.g. liquids or gases), and check if these are proportional to the canonical momentum and spin densities in dispersive media. Furthermore, it would be important to find an experimental setup where the integral super-momentum and transverse spin of SPPs, derived in this work, could be detected. So far, only local densities of these quantities were accessible via local free-space measurements using small particles or atoms [31–35, 41, 66, 67, 105–108].
Acknowledgments
We acknowledge helpful discussions with: T G Philbin, F J Rodríguez-Fortuño, I Fernandez-Corbaton, M Silveirinha, M Masuripur, E Leader, Y P Bliokh, M Durach, and N Noginova. This work was supported by the RIKEN iTHES Project, MURI Center for Dynamic Magneto-Optics via the AFOSR Award No. FA9550-14-1-0040, the Japan Society for the Promotion of Science (KAKENHI), the IMPACT program of JST, CREST grant No. JPMJCR1676, the John Templeton Foundation, the RIKEN-AIST 'Challenge Research' program, and the Australian Research Council.
A short (letter) version of this work, highlighting its main results without derivations, has recently been published in [109]. After the submission of this work, we became aware of the recent preprint [110], where material corrections to the electromagnetic spin density, similar to those obtained in our work, were found in the form of a torque in the spin continuity equation.
Footnotes
- 6
For the conversion between Gaussian and SI units see appendix 4 in [20]. For the quantities used in this work, this conversion is realized via



 and
and