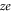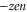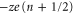Abstract
Biological ion channels are protein nanotubes embedded in, and passing through, the bilipid membranes of cells. Physiologically, they are of crucial importance in that they allow ions to pass into and out of cells, fast and efficiently, though in a highly selective way. Here we show that the conduction and selectivity of calcium/sodium ion channels can be described in terms of ionic Coulomb blockade in a simplified electrostatic and Brownian dynamics model of the channel. The Coulomb blockade phenomenon arises from the discreteness of electrical charge, the strong electrostatic interaction, and an electrostatic exclusion principle. The model predicts a periodic pattern of Ca2+ conduction versus the fixed charge Qf at the selectivity filter (conduction bands) with a period equal to the ionic charge. It thus provides provisional explanations of some observed and modelled conduction and valence selectivity phenomena, including the anomalous mole fraction effect and the calcium conduction bands. Ionic Coulomb blockade and resonant conduction are similar to electronic Coulomb blockade and resonant tunnelling in quantum dots. The same considerations may also be applicable to other kinds of channel, as well as to charged artificial nanopores.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Biological ion channels are natural nanopores providing fast and highly selective permeation of physiologically important ions (e.g. cations such as Na+, K+ and Ca2+) through the bilipid membranes of biological cells [1–3]. The channel proteins carrying the pores are embedded in the cellular membrane, and are complicated structures consisting of thousands of atoms.
More than three decades after their discovery, and following a vast number of experiments, a great deal is now known about ion channels. Yet there remain many features of their function—including some quite basic features—that are still not properly understood. Examples include: the selectivity in which e.g. a calcium channel favours Ca2+ over Na+ by up to 1000:1, even though the ions are essentially the same size; that this selectivity is combined with fast permeation in which the ion goes through the channel almost at the rate of free diffusion (as though the channel were an open hole); the anomalous mole fraction effect (AMFE) where, in a pure NaCl solution, a Na+ ion can pass easily through a calcium channel, but its passage is blocked by tiny traces of Ca2+; the exact role of the fixed electric charge at the so-called selectivity filter in determining the selectivity; and, associated with that, the mechanism by which mutations that alter the fixed charge can result either in destruction of the channel, so that it no longer conducts, or in conversion of e.g. a sodium channel into a calcium channel or vice versa. We will account for these and other experimentally observed features of channel conduction in terms of a novel vision of the permeation process inspired by well-understood phenomena in a quite different area of physics, associated with quantum dots and tunnel diodes.
The conduction and selectivity of a cation-selective channel are determined by the ions' movements and interactions inside a short, narrow selectivity filter lined with negatively charged protein residues that provide the net fixed negative charge Qf; correspondingly, anion-conducting channels possess positive fixed charge [1, 4]. Ions in solution are surrounded by hydration shells with associated dehydration potential barriers that are also crucial for selectivity in many cases [5–9]. Selectivity frequently involves a 'knock on' mechanism or, more generally, the correlated motion of several ions [10–13]. The protein residues forming the 'locus' of the selectivity filter are amino acids, of which aspartate (D) and glutamate (E) have negatively charged side chains ( where e is the proton charge), lysine (K) has a positively charged side chain (
where e is the proton charge), lysine (K) has a positively charged side chain (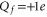 ), and alanine (A) has a neutral side chain. The nominal Qf value is defined by which amino acid residues are present. Calcium L-type channels possess EEEE selectivity filter loci (
), and alanine (A) has a neutral side chain. The nominal Qf value is defined by which amino acid residues are present. Calcium L-type channels possess EEEE selectivity filter loci ( ) [14–16]. Mammalian Na+ channels have DEKA inner site loci (and DDEE outer sites) [1, 17] and hence different Qf. Bacterial NaChBac [18] and NavAb [19, 20] Na+ channels have selectivity filters with EEEE loci like Ca2+ channels but select Na+ ions over Ca2+: an apparent anomaly that awaits explanation.
) [14–16]. Mammalian Na+ channels have DEKA inner site loci (and DDEE outer sites) [1, 17] and hence different Qf. Bacterial NaChBac [18] and NavAb [19, 20] Na+ channels have selectivity filters with EEEE loci like Ca2+ channels but select Na+ ions over Ca2+: an apparent anomaly that awaits explanation.
The modern study of ion channels is based on the existence of the distinct open and closed states of channels, evident in thousands of experiments as discrete levels of current flow measured from individual channel proteins [21]. Site-directed mutagenesis provides a method for systematically varying the structure and net charge of their selectivity filter loci. The resultant changes in conduction and selectivity as functions of Qf can then be measured by use of the patch-clamp technique. Such mutant studies [18, 22–29] have demonstrated that Qf is a key determinant of conduction and selectivity in the calcium/sodium family of channels, with the Ca2+/Na+ selectivity growing with increasing 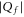 [30–33]. However, the underlying mechanism has remained obscure.
[30–33]. However, the underlying mechanism has remained obscure.
Discovery of the structures of the bacterial potassium KcsA [34] and sodium NavAb [19] channels and the application of all-atom molecular dynamics simulations [20, 28, 35–37] have yielded deep insight into fine details of the ionic permeation processes, including the reproduction of currents [38, 39]. However, a multi-scale analysis is still needed [40–42] to build up a full picture. Self-consistent electrostatic and Brownian dynamics simulations [15, 30, 43–45] describe ionic motion as an electro-diffusion process, leading to fast and direct estimation of the currents under non-equilibrium conditions. Such simulations have shown very clearly that the permeation and selectivity features of many channels are defined by just the basic electrostatics of narrow water-filled channels, rather than by the details of the channel structures themselves.
The discreteness of the ionic charge plays a significant role in ion channel conduction [8, 46–48]. An electrostatic theory of ionic transport in water-filled periodically charged nanopores [49, 50], treating the ions as a 1D Coulomb gas [50], revealed ion-exchange through low-barrier phase transitions as the ion concentration and Qf were varied [51]. It has recently been shown that nanopores can exhibit ionic Coulomb blockade [52], an electrostatic phenomenon similar to electronic Coulomb blockade in mesoscopic systems [53–56].
Our earlier simulations of a simple electrostatic model of calcium/sodium ion channels revealed a periodic set of Ca2+ conduction-bands and stop-bands as a function of the fixed charge Qf at the selectivity filter [57–59] similar to transitions [51]. The energetics of that phenomenon has been derived from electrostatics as single- and multi-ion barrier-less conduction and results were compared with the experimental data available to date [58, 59].
In this paper we demonstrate that the origin of these conduction bands lies in ionic Coulomb blockade [52], closely similar to its electronic counterpart in quantum dots [53]. We thus introduce a Coulomb blockade model of permeation and selectivity in biological ion channels, describing them as discrete electrostatic devices [56]. The applicability of Coulomb blockade to biological ion channels follows naturally from an earlier discussion of the crucial role of electrostatics and the suggestion that there might be 'eigenstates' for conduction [60, 61] in biological ion channels. We will show that the Coulomb blockade model predicts the positions and shapes of the conduction bands, defines the channel occupancy as a Fermi–Dirac distribution, and thereby provides an explanation of divalent block and AMFE, including the exponential dependence of the divalent block threshold IC50 on Qf.
We will focus on the sodium/calcium family of channels including the voltage-gated Ca2+ [14, 28] and Na+ channels [19, 62]. These channels exhibit strong valence selectivity and can undergo a wide range of transformations as the result of site-directed mutagenesis, enabling us to test many of the predictions of our model. The picture that we will develop may, however, be more generally applicable. Section 2 describes a generic model of calcium/sodium channels, its geometry (2.1), electrostatics (2.2), Brownian dynamics (2.3) and validity (2.4). Section 3 introduces and verifies the ionic Coulomb blockade model of ion channel conduction and selectivity; it reviews multi-ion conduction bands (3.1), describes the Coulomb blockade model (3.2), identifies real channels and mutants (3.3), derives the shape of Coulomb blockade oscillations (3.4) and explains the selectivity and AMFE (3.5). Section 3.6 contains further considerations. Section 4 draws the results together and presents concluding remarks.
In what follows, with SI units e is the proton charge, T the temperature, z the ionic valence, kB Boltzmann's constant and  0 the electric permittivity of the vacuum. We use dimensionless units for energy assuming
0 the electric permittivity of the vacuum. We use dimensionless units for energy assuming  .
.
2. A generic electrostatic and Brownian dynamics model of the calcium channel
2.1. Geometry and general features of the model
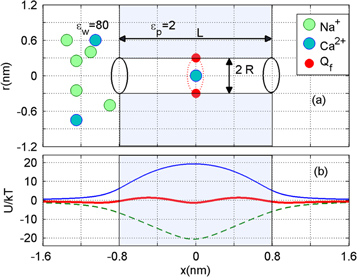
Figure 1(a) shows the generic, self-consistent, electrostatic model of the selectivity filter of a calcium/sodium channel whose properties we will analyse. We consider it as a negatively charged, axisymmetric, water-filled, cylindrical pore through the protein hub in the cellular membrane; and, to match the dimensions of the selectivity filters of the Na+/Ca2+ channels on which we focus, we suppose it to be of radius R = 0.3 nm and length L = 1.6 nm [14, 15, 63]. The x-axis is coincident with the channel axis, with x = 0 in the center of channel. There is a centrally placed, uniformly charged, rigid ring of negative charge 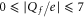 embedded in the wall at
embedded in the wall at  . The left-hand bath, modeling the extracellular space, contains non-zero concentrations of Ca2+ and/or Na+ ions. For the Brownian dynamics simulations, the computational domain length Ld = 10 nm, its radius Rd = 10 nm, the grid size h = 0.05 nm, and a potential difference in the range
. The left-hand bath, modeling the extracellular space, contains non-zero concentrations of Ca2+ and/or Na+ ions. For the Brownian dynamics simulations, the computational domain length Ld = 10 nm, its radius Rd = 10 nm, the grid size h = 0.05 nm, and a potential difference in the range 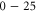 mV (corresponding to the depolarized membrane state) was applied between the left and right domain boundaries.
mV (corresponding to the depolarized membrane state) was applied between the left and right domain boundaries.
Figure 1. (a) Generic electrostatic model of the selectivity filter of a Ca2+ or Na+ channel. It is treated as an axisymmetric, water-filled, cylindrical pore of radius R = 0.3 nm and length L = 1.6 nm through the protein hub in the cellular membrane. A centrally placed, uniform, rigid ring of negative charge Qf in the range  is embedded in the wall at
is embedded in the wall at  . Ions inside the channel move in single file along its axis. (b) Energetics of a moving Ca2+ ion for fixed charge
. Ions inside the channel move in single file along its axis. (b) Energetics of a moving Ca2+ ion for fixed charge  . The dielectric self-energy barrier Us (blue solid line) is balanced by site attraction (green dashed line) resulting in an almost barrier-less energy profile (red solid line).
. The dielectric self-energy barrier Us (blue solid line) is balanced by site attraction (green dashed line) resulting in an almost barrier-less energy profile (red solid line).
Download figure:
Standard image High-resolution imageThe mobile sodium and calcium ions are described as charged spheres of radius 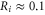 nm for both ions (allowing use of the implicit solvent model [64, 65] with neglible ion radii), with diffusion coefficients of
nm for both ions (allowing use of the implicit solvent model [64, 65] with neglible ion radii), with diffusion coefficients of 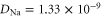 m2 s−1 [15, 66] and
m2 s−1 [15, 66] and  m2 s−1 [15], respectively.
m2 s−1 [15], respectively.
We take both the water and the protein to be homogeneous continua describable by relative permittivities 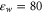 and
and  , respectively, together with an implicit model of ion hydration whose validity is discussed elsewhere [58]. We approximate
, respectively, together with an implicit model of ion hydration whose validity is discussed elsewhere [58]. We approximate  w, DNa, and DCa as being equal to their bulk values throughout the whole computational domain (see below, section 2.4).
w, DNa, and DCa as being equal to their bulk values throughout the whole computational domain (see below, section 2.4).
2.2. Self-consistent electrostatics of the model
The electrostatic potential U for an ion, and the potential gradients, were derived by numerical solution of Poisson's electrostatic equation within the computational domain shown in figure 1:
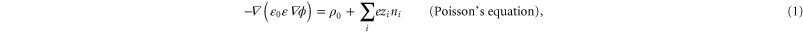
where  is the relative permittivity of the medium (water or protein), ρ0 is the density of fixed charge, zi is the charge number (valence), and ni is the number density of moving ions.
is the relative permittivity of the medium (water or protein), ρ0 is the density of fixed charge, zi is the charge number (valence), and ni is the number density of moving ions.
Self-consistent electrostatics within the narrow, water-filled, channel in the protein differs significantly from bulk electrostatics [49, 67, 68]. The huge gradient between 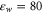 and
and  , the discreteness of ionic charge and the specific channel geometry, lead to permeation, quasi-1D axial behaviour of ions inside the channel [49, 50, 69], and hence to single-filing. Consequently, we use a 1D dynamical model to simulate the axial single-file movement of cations (only) inside the selectivity filter and in its close vicinity.
, the discreteness of ionic charge and the specific channel geometry, lead to permeation, quasi-1D axial behaviour of ions inside the channel [49, 50, 69], and hence to single-filing. Consequently, we use a 1D dynamical model to simulate the axial single-file movement of cations (only) inside the selectivity filter and in its close vicinity.
Figure 1(b) shows axial single-ion potential energy profiles for 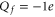 , including the repulsive self-energy barrier Us and the attraction energy Ua attributable to the fixed negative charge. The dielectric self-energy Us plays a crucial role in controlling ion permeation through the narrow channel. It will be shown below that Us defines the strength of Coulomb blockade for an ion of particular valence z, and that it determines the condition for strong valence selectivity [30, 58]. The site attraction is proportional to
, including the repulsive self-energy barrier Us and the attraction energy Ua attributable to the fixed negative charge. The dielectric self-energy Us plays a crucial role in controlling ion permeation through the narrow channel. It will be shown below that Us defines the strength of Coulomb blockade for an ion of particular valence z, and that it determines the condition for strong valence selectivity [30, 58]. The site attraction is proportional to 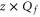 , so that a variation of Qf can significantly change the resultant profile. In particular for
, so that a variation of Qf can significantly change the resultant profile. In particular for 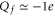 , the self-potential barrier of the dielectric boundary force can be balanced by electrostatic attraction to the fixed charge Qf, resulting in almost barrier-less conduction [58].
, the self-potential barrier of the dielectric boundary force can be balanced by electrostatic attraction to the fixed charge Qf, resulting in almost barrier-less conduction [58].
2.3. Brownian dynamics simulation of the ionic current
The ions' motion through a channel can be described as an electro-diffusion process and investigated through Brownian dynamics simulations [15, 30, 44, 45, 57, 70–73] of the ionic trajectories. Taking account of the single-filing required by electrostatics, we can solve the over-damped, time-discretized, Langevin equation numerically. An axial step 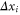 of the ith ion is defined as [74],
of the ith ion is defined as [74],

where Di is the ionic diffusion coefficient,  is the time step,
is the time step, 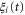 is normalized white noise, zi is the valence of the ith ion, and the potential
is normalized white noise, zi is the valence of the ith ion, and the potential 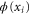 is calculated self-consistently from (1) at each simulation step.
is calculated self-consistently from (1) at each simulation step.
Brownian dynamics simulations of the ion current J and occupancy P were performed separately for CaCl2 and NaCl solutions, and also for a mixed-salt configuration, with concentrations ![$[\mathrm{Na}]=30$](https://content.cld.iop.org/journals/1367-2630/17/8/083021/revision1/njp517214ieqn26.gif) mM and
mM and 
![$\leqslant \;[\mathrm{Ca}]\leqslant 80$](https://content.cld.iop.org/journals/1367-2630/17/8/083021/revision1/njp517214ieqn28.gif) mM.
mM.
2.4. Validity and limitations of the generic model
Our reduced model obviously represents a considerable simplification of the actual electrostatics and dynamics of moving ions and water molecules within the narrow selectivity filter. The validity and range of applicability of this kind of model have been discussed in detail elsewhere [35, 58, 75, 76]. The most significant simplifications are probably: the use of continuum electrostatics; the use of the implicit solvent model; the use of Brownian dynamics with uncorrelated noise sources for the charged particles; and the assumption of 1D (i.e. single-file) movement of ions inside the selectivity filter. We can partially accommodate these simplifications by use of effective values [58].
3. Coulomb blockade model of permeation and selectivity
In this section we introduce the Coulomb blockade picture of permeation and selectivity and show that the phenomenon manifests itself in the model of figure 1 when its geometrical parameters are appropriate for calcium/sodium channels. We will show that the model describes well both the simulated conduction bands and many experimentally measured phenomena of valence selectivity in calcium/sodium channels. The Coulomb blockade model provides significant generalization of our earlier explanation of conduction bands [58] and connects them with mesoscopic transport and single-electron devices [52, 54, 56].
We start by reviewing the main outcome of our earlier Brownian dynamics simulations of conduction bands [57, 58] in order to summarise some of the results that need to be explained including, in particular, the observation of conduction bands.
3.1. Multi-ion conduction bands
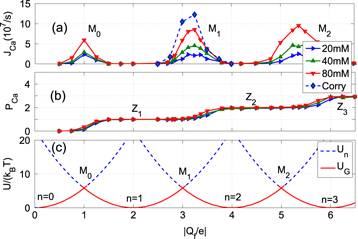
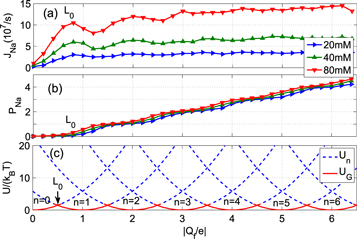
Figures 2(a), (b) and 3(a), (b) present the Brownian dynamics results [57–59] for permeation of the model channel figure 1(a) by calcium and sodium ions, respectively, in pure baths of different concentration, plotted in each case as a function of Qf.
Figure 2. Multi-ion Ca2+ conduction and occupancy in the Ca2+/Na+ channel model versus the effective fixed charge Qf; the Brownian dynamics (BD) simulation results (a), (b) are reworked from [57, 59]. (a) Plots of the Ca2+ current JCa for pure Ca2+ baths of concentration 20, 40 and 80 mM. The BD results of Corry et al [15] are shown for comparison (blue, dashed, diamonds, in arbitrary units). (b) The channel occupancy PCa. (c) Plots of the electrostatic energy Un (blue, dashed) and the ground state (i.e. minimum) energy 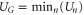 (red, solid) versus Qf for channels with
(red, solid) versus Qf for channels with 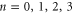 . Ca2+ ions inside. The conduction bands M0, M1, M2 and the stop bands Z1, Z2, Z3 (indicated by labels) are discussed in the text.
. Ca2+ ions inside. The conduction bands M0, M1, M2 and the stop bands Z1, Z2, Z3 (indicated by labels) are discussed in the text.
Download figure:
Standard image High-resolution imageFigure 3. Multi-ion Na+ conduction and occupancy in the Ca2+/Na+ channel model versus the effective fixed charge Qf; the Brownian dynamics simulation results (a), (b) are reworked from [59]. (a) Plots of the Na+ current JNa for pure Na+ baths of concentration 20, 40 and 80 mM. (b) The occupancy PNa. (c) Plots of the electrostatic energy Un (blue, dashed) and resulting oscillations of the ground state energy 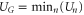 (red, solid) versus Qf for channels with
(red, solid) versus Qf for channels with 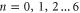 Na+ ions inside. The conduction band L0 is discussed in the text.
Na+ ions inside. The conduction band L0 is discussed in the text.
Download figure:
Standard image High-resolution imageFigure 2(a) exhibits a sequence of narrow conduction bands M0, M1, M2, separated by stop-bands of almost zero-conductance centred on the blockade points Z1, Z2, Z3. Figure 2(b) shows that the Mn peaks in JCa correspond to transition regimes where the channel occupancy PCa jumps from one integer value to the next, and that the stop-bands correspond to saturated regions with integer 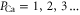 .
.
The band M0 corresponds to single-ion low-barrier conduction (see red curve in figure 1(b)). Band M1 corresponds to double-ion knock-on conduction, which is well-established for L-type Ca2+ channels [14, 77, 78]; a similar peak was obtained by Corry et al [15] in Brownian dynamics simulations of the Ca2+ channel. Band M2 corresponds to triple-ion conduction, a process that can be identified with the permeation of ryanodine receptor calcium channels [7] (see table 1 below for further detail). These bands can be considered as examples of self-organization in ion channels [16, 73].
Table 1. Putative identification of ionic Coulomb blockade model bands with some known wild type (WT) channels and mutants sequences (extended from [58]).
| N | Channel/mutant | Site locus | Nom. 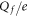
|
Band | Band's 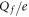
|
|---|---|---|---|---|---|
| (a) | WT Na+-selective Nav channel [22] | DEKA |
|
L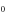 |
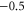
|
| WT Non-selective OmpF [27] | KRRRDE |

|
M0 |

|
|
| WT Ca2+-selective L-type channel [23] | EEEE |
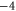
|
M1 |
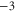
|
|
| WT NaChBac[18], NavAB [28] | EEEE |
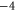
|
Z2 |
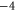
|
|
| WT Ca2+-selective RyR channel [7] | DDDD(ED) |
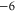
|
M2 |
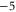
|
|
| (b) | WT Na+-selective Nav channel [22] | DEKA |
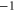
|
L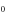 |
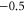
|
| Ca2+-blocked Nav mutant |
 DEKE DEKE |
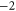
|
M0 |
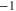
|
|
| Ca2+-permeable Nav mutant |
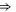 DEEA DEEA |

|
Z1 |

|
|
| Ca2+-selective Nav mutant |
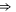 EEEE EEEE |
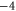
|
M1 |
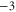
|
|
| (c) | WT Ca2+-selective L-type channel [23] | EEEE |

|
M1 |
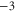
|
| Ca2+-blocked Cav mutant |
 EEQE EEQE |
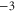
|
Z1 |
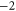
|
|
| Na+-conductive Cav mutant |
 EEKE EEKE |
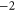
|
M0 |
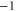
|
|
| Na+-selective Cav mutant |
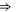 EEKA EEKA |
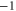
|
L0 |
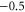
|
|
| (d) | WT Na+-selective NaChBac [18] | EEEE |
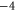
|
Z2 |
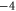
|
| Ca2+-selective CaChBac mutant |
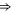 EEEE+DDDD EEEE+DDDD |

|
M3 |
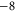
|
|
| (e) | WT Na+-selective NavAB [28] | EEEE |
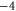
|
Z2 |
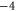
|
| Ca2+-selective CavAB mutant |
 EEEE+DDDD EEEE+DDDD |

|
M3 |

|
Comparison of the JCa and PCa plots in figures 2(a) and (b) shows that for the Mn points near which conduction occurs, 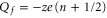 ; whereas the non-conducting regions of constant P correspond to Zn points with
; whereas the non-conducting regions of constant P correspond to Zn points with 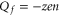 , i.e. to the neutralized state [59]. These bands will be interpreted below as strong Coulomb blockade.
, i.e. to the neutralized state [59]. These bands will be interpreted below as strong Coulomb blockade.
Figures 3 (a) and (b) plot the equivalent results for sodium ions in pure NaCl baths of different concentration showing (a) the sodium current and (b) the occupancy as functions of Qf. The current JNa exhibits a single-ion peak L0 that would appear to be analogous to the calcium conduction band M0 of figure 2(a). For larger Qf there are weak, strongly overlapping, conduction bands between which the current does not fall to zero, making the sodium conductance relatively independent of Qf. The separations of the JNa band maxima are approximately half the size of those for the calcium bands, reflecting the charge difference between Na+ and Ca2+ ions. We will refer to this scenario as an example of weak Coulomb blockade.
Figures 2(c) and 3(c) plot the ground state energies characteristic of Coulomb blockade graphs [56]. They will be discussed in the next section. Note that we use ground state in the physics sense, implying the state of minimum energy.
3.2. Coulomb blockade oscillations of conductance
We are now in position to introduce the Coulomb blockade model of conduction and selectivity in Ca2+/Na+ ion channels. We will find that it is able to account for the pattern of calcium and sodium bands seen in figures 2 and 3 in terms of strong and weak Coulomb blockade oscillations [55], respectively .
The discreteness and entity of the ionic charge allow to us to introduce exclusive 'eigenstates' 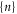 of the channel for fixed integer numbers of ions inside its selectivity filter, with total electrostatic energy Un. The transition
of the channel for fixed integer numbers of ions inside its selectivity filter, with total electrostatic energy Un. The transition 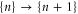 corresponds to the entry of a new ion, whereas
corresponds to the entry of a new ion, whereas 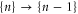 corresponds to the escape of a trapped ion. The n ions' eigenstates form a discrete exclusive set of
corresponds to the escape of a trapped ion. The n ions' eigenstates form a discrete exclusive set of 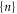 -states [79] :
-states [79] :
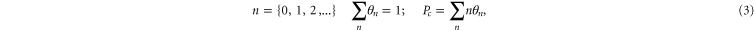
The electrostatic exclusion principle (3) leads to Fermi–Dirac statistical distributions [80] for θn and Pc, as will be derived below.
The total energy Un for a channel in state  can be expressed as:
can be expressed as:
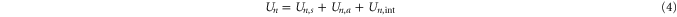
where 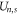 is the self-energy,
is the self-energy, 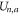 is the energy of attraction, and
is the energy of attraction, and 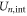 is the ions' mutual interaction energy.
is the ions' mutual interaction energy.
We approximate Un as the dielectric self-energy  of the excess charge Qn, based on the assumption that both the ions and Qf are located within the central part of the selectivity filter, so that application of Gauss's theorem to the n similar ions captured within its volume gives a Coulomb blockade-like quadratic dependence of Un on Qf [51]:
of the excess charge Qn, based on the assumption that both the ions and Qf are located within the central part of the selectivity filter, so that application of Gauss's theorem to the n similar ions captured within its volume gives a Coulomb blockade-like quadratic dependence of Un on Qf [51]:
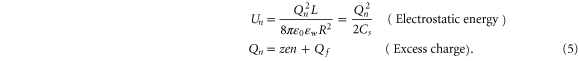
Here, Cs stands for the geometry-dependent self-capacitance of the channel, and Qn represents the excess charge at the selectivity filter for the n ions as a function of Qf. A binomial expansion Qn2 in (5) gives first approximations for  ,
, 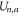 and
and 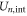 that are consistent with the energetics analysis in [58] and with the 1D Coulomb gas model of ion–ion and ion-fixed charge interactions [49, 50]. A more realistic account of the interactions would result in corrections to (5) and to the formulæ derived from it.
that are consistent with the energetics analysis in [58] and with the 1D Coulomb gas model of ion–ion and ion-fixed charge interactions [49, 50]. A more realistic account of the interactions would result in corrections to (5) and to the formulæ derived from it.
With (5) we arrive at an equation identical to that for electronic Coulomb blockade (except for the presence of z), and our further consideration follows standard Coulomb blockade theory [53, 55]. Remarkably, however, the ionic version of the phenomenon exhibits valence selectivity precisely because it contains the valence z.
To interpret the conduction bands in terms of Coulomb blockade, we calculate Un as a function of Qf for 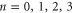 and examine the minimum (i.e. ground state) energy
and examine the minimum (i.e. ground state) energy
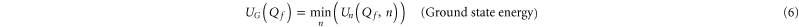
for the ground state occupancy nG, and the excess charge QG, all as functions of Qf (see figures 2(c) and 3(c)). The ground state (6) is by definition a stable state in thermal equilibrium.
Coulomb blockade appears in low-capacitance systems on account of quantization of the quadratic energy in (5) on a grid of discrete states (3), provided that the ground state {nG} is separated from neighbouring  states by large Coulomb energy gaps as function of geometry (
states by large Coulomb energy gaps as function of geometry (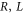 ) and ion valence z:
) and ion valence z:

where 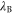 stands for Bjerrum length [49] (0.7 nm for water at T = 298K). This is the applicability condition for the strong electrostatic exclusion principle. Ion channels are extremely small and have tiny capacitance: the dimensionless self-energies of monovalent and divalent ions are
stands for Bjerrum length [49] (0.7 nm for water at T = 298K). This is the applicability condition for the strong electrostatic exclusion principle. Ion channels are extremely small and have tiny capacitance: the dimensionless self-energies of monovalent and divalent ions are 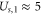 and
and 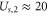 , respectively, providing strong Coulomb blockade effects for divalent ions.
, respectively, providing strong Coulomb blockade effects for divalent ions.
It follows from (5) that Un versus Qf for given z is described by an equidistant set of identical parabolæ of period equal to the ionic charge 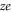 . These patterns are plotted for Ca2+ in figure 2(c) and for Na+ in figure 3(c). We note that
. These patterns are plotted for Ca2+ in figure 2(c) and for Na+ in figure 3(c). We note that  exhibits two different kinds of ground state singular points, marked as Mn and Zn. The minima of Un (and correspondingly the blockade regions) appear around the neutralization points Z
exhibits two different kinds of ground state singular points, marked as Mn and Zn. The minima of Un (and correspondingly the blockade regions) appear around the neutralization points Z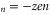 where the net charge at the selectivity filter Qn = 0 and the occupancy Pc is saturated at an integer value [51, 58].
where the net charge at the selectivity filter Qn = 0 and the occupancy Pc is saturated at an integer value [51, 58].
Figure 2(c) illustrates the fact that for Ca2+ the ground state 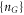 Zn points are separated from neighbouring
Zn points are separated from neighbouring 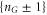 states by an impermeable Coulomb gap of
states by an impermeable Coulomb gap of  (see (7)) hence providing strong Coulomb blockade. At the neutralized (Qn = 0) blockade points Zn, Ca2+ ions are prohibited by the self-energy barrier from entering the uncharged channel. The crossover points Mn (
(see (7)) hence providing strong Coulomb blockade. At the neutralized (Qn = 0) blockade points Zn, Ca2+ ions are prohibited by the self-energy barrier from entering the uncharged channel. The crossover points Mn (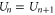 ) allow low-barrier (almost barrier-less)
) allow low-barrier (almost barrier-less)  transitions (see figure 1 (b)); they correspond to the Pc transition regions and to the conduction peaks in J [58]. The Mn points are separated from higher energy states by impermeable barriers of
transitions (see figure 1 (b)); they correspond to the Pc transition regions and to the conduction peaks in J [58]. The Mn points are separated from higher energy states by impermeable barriers of 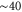 ; these points are equivalent to the ion-exchange transitions reported by Zhang et al [51].
; these points are equivalent to the ion-exchange transitions reported by Zhang et al [51].
The pattern of sodium ground states in figure 3(c) arises from energy gaps Uc that are 4× smaller than for calcium, They are too small to prevent thermally activated transitions between neighbouring states and they allow the coexistence of more then two  -states; correspondingly there is only a weak exclusion principle, in turn giving rise to weak Coulomb blockade.
-states; correspondingly there is only a weak exclusion principle, in turn giving rise to weak Coulomb blockade.
The positions of the singular Qf points in figure 2(a) can be written as:

where  ,
,  are possible corrections for the singular parts of the affinity and ion–ion interaction (see above) and possible electrostatic field leakage. Equations (8) describe two interleaved periodic sets of points having periods equal to the ionic charge
are possible corrections for the singular parts of the affinity and ion–ion interaction (see above) and possible electrostatic field leakage. Equations (8) describe two interleaved periodic sets of points having periods equal to the ionic charge 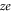 , very similar to their counterparts in electronic Coulomb blockade [54].
, very similar to their counterparts in electronic Coulomb blockade [54].
The points Z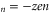 are neutralization points, where the excess charge Qn = 0 and UG takes minimal values. Such points are stable and current is prohibited. Charge neutrality is important, but it is not the only factor that influences channel conductance: the term
are neutralization points, where the excess charge Qn = 0 and UG takes minimal values. Such points are stable and current is prohibited. Charge neutrality is important, but it is not the only factor that influences channel conductance: the term 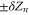 accounts formally for the other factors (unaccounted parts of ion–ion/ion-ligand interactions and hydration energy, fields leaks etc).
accounts formally for the other factors (unaccounted parts of ion–ion/ion-ligand interactions and hydration energy, fields leaks etc).
The points 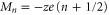 are where barrier-less conduction occurs, for which
are where barrier-less conduction occurs, for which 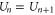 . Similarly, the terms
. Similarly, the terms  account formally for any unconsidered perturbations.
account formally for any unconsidered perturbations.
We may therefore interpret the Brownian dynamics-simulated calcium conduction bands of figure 2(a) as Coulomb blockade conductance oscillations [55] which appear in this case as 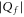 is being increased, and the corresponding occupancy steps in figure 2(b) as a Coulomb staircase [56]. The deviations in the precise positions of Mn and Zn can be attributed to field leaks and the model simplifications.
is being increased, and the corresponding occupancy steps in figure 2(b) as a Coulomb staircase [56]. The deviations in the precise positions of Mn and Zn can be attributed to field leaks and the model simplifications.
3.3. Identification of bands with real calcium channels
Table 1, showing the putative identifications of the bands/singularities in the Coulomb blockade model with real channels, wild type and mutants in the Ca2+/Na+ family, has been extended from [57, 58].
Table 1(a) describes shows identifications of conduction bands with wild type channels.
The single-ion Na+ barrier-less point L0 can be speculatively identified with the non-selective DEKA sodium channel ( ) [1, 17]. The single-ion Ca2+ barrier-less point M0 can be identified with the non-selective OmpF porin (
) [1, 17]. The single-ion Ca2+ barrier-less point M0 can be identified with the non-selective OmpF porin (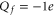 ) [27], or with nonselective Na+–K channel [81].
) [27], or with nonselective Na+–K channel [81].
Mammalian calcium channels exist in several modifications. Some of them (L-type, T-type) share the same highly conserved four-glutamate (EEEE) locus at the selectivity filter with nominal 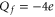 [14]. The permeation properties (sharp selectivity, AMFE, double-ion nature of calcium permeation) of these channels are consistent with the double-ion M1 Ca2+ conduction band [57, 58]. The double-ion knock-on mechanism of conduction and selectivity in the L-type calcium channel has been derived from the experimentally observed double-affinity of AMFE [14, 78]. The same M1 peak can be also identified with the Ca2+-selective mutant of the Nav sodium channel (
[14]. The permeation properties (sharp selectivity, AMFE, double-ion nature of calcium permeation) of these channels are consistent with the double-ion M1 Ca2+ conduction band [57, 58]. The double-ion knock-on mechanism of conduction and selectivity in the L-type calcium channel has been derived from the experimentally observed double-affinity of AMFE [14, 78]. The same M1 peak can be also identified with the Ca2+-selective mutant of the Nav sodium channel (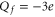 ) [22] and a calcium-selective mutant of OmpF porin (
) [22] and a calcium-selective mutant of OmpF porin ( ) [27].
) [27].
The Ryanodine receptor RyR calcium channel has  and relatively weak selectivity [7]. We connect it with M
and relatively weak selectivity [7]. We connect it with M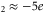 three-ion conduction point [57, 58].
three-ion conduction point [57, 58].
Bacterial sodium channels, NaChBac [18] and NavAB [28] possess EEEE loci (with nominal 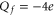 ), typical of mammalian calcium channels but nonetheless exhibit Na+-selective features and divalent blockade. We connect them (speculatively) with the Z2 Ca2+ blockade point for
), typical of mammalian calcium channels but nonetheless exhibit Na+-selective features and divalent blockade. We connect them (speculatively) with the Z2 Ca2+ blockade point for 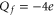 .
.
It is evident that the nominal charges of the channel loci exceed the charge of the model bands by nearly 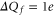 . For example, at M1 we have
. For example, at M1 we have 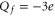 from the Coulomb blockade model, whereas the nominal
from the Coulomb blockade model, whereas the nominal 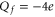 for the EEEE loci of L-type calcium channels (and there are corresponding discrepancies at the M2 and M3 points). We speculate that these systematic discrepancies may be connected to field leaks, to the distant influence of the positive charges of the other ends of the amino acids buried in the rest of the protein, or to possible protonation of the side chains [82]. Molecular dynamics simulations [28, 35, 38] could be particularly helpful in determining the effective values of Qf for wild type and mutant channels.
for the EEEE loci of L-type calcium channels (and there are corresponding discrepancies at the M2 and M3 points). We speculate that these systematic discrepancies may be connected to field leaks, to the distant influence of the positive charges of the other ends of the amino acids buried in the rest of the protein, or to possible protonation of the side chains [82]. Molecular dynamics simulations [28, 35, 38] could be particularly helpful in determining the effective values of Qf for wild type and mutant channels.
The above identification scheme can thus account for many mutation transformations observed in the Ca2+/Na+ channels family. The main test and validation of the Coulomb blockade model is the correct prediction that single 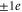 mutations should lead to sharp changes of calcium conductance from resonance to blockade and vice versa.
mutations should lead to sharp changes of calcium conductance from resonance to blockade and vice versa.
Similarly, table 1(b) describes the radical mutation-induced transformation of the Nav sodium channel to a calcium channel, when the DEKA locus has been sequentially changed by point mutations [22].
Table 1(c) shows that the downward mutations of EEEE calcium channels described in [23] lead to a moderate decrease of divalent/monovalent (Ba2+/Na+) selectivity for EEEE  mutation and a sharp, two-order decrease for the EEEE
mutation and a sharp, two-order decrease for the EEEE 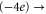 EKEE
EKEE 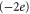 mutation (though see discussion below).
mutation (though see discussion below).
Tables 1(d), (e) show that the upward mutations of the EEEE loci of bacterial sodium channels (EEEE 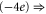 EEEE+DDDD
EEEE+DDDD  calcium channels described in [18, 28] lead to channel transformation to a calcium-selective mutant CaChBac and CavAB, respectively. Ca2+ selective mutants demonstrate selectivities of up to
calcium channels described in [18, 28] lead to channel transformation to a calcium-selective mutant CaChBac and CavAB, respectively. Ca2+ selective mutants demonstrate selectivities of up to 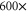 in favour of Ca2+ ions over Na+, and AMFE. We putatively connect these transformations with the jump
in favour of Ca2+ ions over Na+, and AMFE. We putatively connect these transformations with the jump 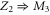 . Note, that the model predicts rather high numbers of ions inside the channel (between 3 and 4 for M3) but there is no experimental evidence to support these specific occupancy numbers.
. Note, that the model predicts rather high numbers of ions inside the channel (between 3 and 4 for M3) but there is no experimental evidence to support these specific occupancy numbers.
One of the most striking consequences of the Coulomb blockade oscillations is that, for channels having  , adding one negative charge should dramatically decrease the Ca2+ conductance. So far, all mutation chains showed increase of calcium selectivity with growth of negative Qf which can also, however, be explained by alternative models [32]. On the other hand these experiments are limited to
, adding one negative charge should dramatically decrease the Ca2+ conductance. So far, all mutation chains showed increase of calcium selectivity with growth of negative Qf which can also, however, be explained by alternative models [32]. On the other hand these experiments are limited to 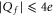 where the Coulomb blockade model also predicts an experimental increase of calcium selectivity with growth of
where the Coulomb blockade model also predicts an experimental increase of calcium selectivity with growth of 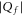 in the range
in the range 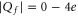 (see figure 11 of [58)] but predicts a sharp drop in calcium selectivity near the neutralization blockade point Z2.
(see figure 11 of [58)] but predicts a sharp drop in calcium selectivity near the neutralization blockade point Z2.
We can suppose that the NavAB/NaChBac EEEE locus has an effective 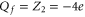 , and hence a 1e mutation of the EEEE ring (or a
, and hence a 1e mutation of the EEEE ring (or a  mutation of the neighbouring ring of residues) should lead to increase of S for both directions of mutation. The currently available data (see tables (d), (e)) were obtained for mutation steps of
mutation of the neighbouring ring of residues) should lead to increase of S for both directions of mutation. The currently available data (see tables (d), (e)) were obtained for mutation steps of 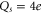 and thus cannot resolve the effect of the smaller 1e jumps.
and thus cannot resolve the effect of the smaller 1e jumps.
These identifications can be seen as an initial verification of the Coulomb blockade model predictions, albeit with some discrepancies. Further investigations are needed to confirm the channel identifications, to understand why the nominal Qf is systematically slightly smaller than the Qf values of band maxima in the model, and to establish the reason why mammalian and bacterial channels with EEEE-loci have opposite selectivity properties.
3.4. Shapes of the Coulomb blockade oscillations
We now develop a description of the (interconnected) shapes of the Coulomb blockade oscillations in J, and the Coulomb staircase in P. We consider the case of divalent Ca2+ bands arising from strong Coulomb blockade (figure 2).
The equilibrium distribution of Pc in the vicinity of the Mn points (and hence calculation of the shapes of Pc(U) or 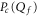 ) follows from standard Coulomb blockade theory. As mentioned above, the energy level separation for divalent Ca2+ is so large
) follows from standard Coulomb blockade theory. As mentioned above, the energy level separation for divalent Ca2+ is so large  that the general set of eigenstates (3) reduces to a simple two-state exclusive set:
that the general set of eigenstates (3) reduces to a simple two-state exclusive set:
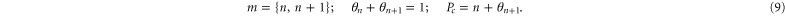
The electrostatic exclusion principle (9) plays the same role here as that of the Pauli exclusion principle in quantum mechanics [83–85]; the standard derivation via the partition function, taking account of exclusion principle (9) leads [86–88] to Fermi–Dirac statistics for θn+1 and an excess (fractional) occupancy  :
:

where  is the chemical potential, Pb is a reference occupancy related to the bulk concentration, and μ0 is a constant potential assumed here to be
is the chemical potential, Pb is a reference occupancy related to the bulk concentration, and μ0 is a constant potential assumed here to be 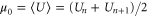 . Hence:
. Hence:
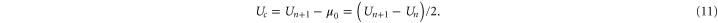
The Fermi–Dirac equation (10) is equivalent to the Langmuir isotherm [86] and to Michaelis–Menten saturation. A similar Fermi function was obtained earlier [51] for the variation of Pc with concentration.
Note that the Fermi–Dirac distribution needed for cases where the exclusion principle is based on volume exclusion, and the ions have unequal diameters, has been investigated by Liu and Eisenberg [85, 89, 90].
It follows from (5) that Uc is a linear function of Qf:
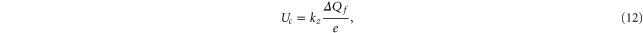
where 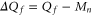 and
and  . Hence the Fermi–Dirac function (10) also describes the dependence of P* on Qf:
. Hence the Fermi–Dirac function (10) also describes the dependence of P* on Qf:

where for our geometry with z = 2 (Ca2+ ions) the dimensionless scaling coefficient 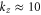 . This is the final result for the shape of the Coulomb staircase of occupancy as a function of Qf. Figure 2(b) shows qualitative agreement of
. This is the final result for the shape of the Coulomb staircase of occupancy as a function of Qf. Figure 2(b) shows qualitative agreement of 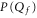 shapes with (13), including the concentration-dependent shift between curves with different Pb. We will make a more detailed comparison below.
shapes with (13), including the concentration-dependent shift between curves with different Pb. We will make a more detailed comparison below.
Approximate forms of the current as a function of energy (or fixed charge) can be found via the variance σ of the Fermi–Dirac occupancy P due to thermal fluctuations, as follows from the fluctuation–dissipation theorem and linear response theory [91]. The ability of an energy level to contribute to the current/conductance is then proportional to 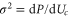 via the Landauer approximation [54, 55]:
via the Landauer approximation [54, 55]:
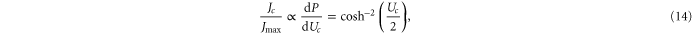
where Jmax is the barrier-less diffusive current. Taking account of scattering, one reaches the standard Coulomb blockade theory approximation [55, 92]:
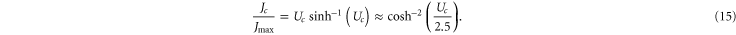
Alternatively (15) can be derived by the quasi-equilibrium (or nonequilibrium reaction rate [93]) approach with explicit solution of the Nernst–Planck equation (i.e. the Goldman–Hodgkin–Katz (GHK) solution ) taking account of the Fermi–Dirac occupancy (10), so (15) can thus be called the Fermi-GHK approximation; a similar result was obtained earlier by Mott [94, 95].
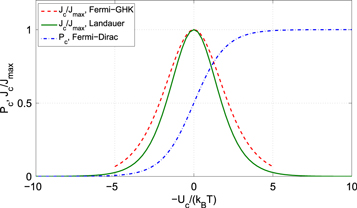
Figure 4 reveals a resonant conductivity as Uc is varied, for both the Landauer (14) and Fermi-GHK (15) approximations: in each case there is a peak coinciding with the maximum in the derivative of Pc,  . (Note that, from (5), variation of Uc is equivalent to variation of Qf.) In practical terms, the difference between the two approximations is small: they both represent double-exponential peaks of half-width
. (Note that, from (5), variation of Uc is equivalent to variation of Qf.) In practical terms, the difference between the two approximations is small: they both represent double-exponential peaks of half-width 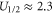 . The form of this current is similar to that of the tunneling current in a quantum dot [54]: an even, double-exponential function of Uc, reflecting the symmetry of the escape and relaxation trajectories [96]. Note that even small asymmetries, easy to overlook, can have disquieting effects [97].
. The form of this current is similar to that of the tunneling current in a quantum dot [54]: an even, double-exponential function of Uc, reflecting the symmetry of the escape and relaxation trajectories [96]. Note that even small asymmetries, easy to overlook, can have disquieting effects [97].
Figure 4. The calculated occupancy P and current J as Uc (or equivalently Qf) is varied. The occupancy Pc (blue, dash–dot) shows the Fermi–Dirac transition from Pc = 0 to Pc = 1. The currents calculated in the Landauer 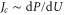 (green, solid) and Fermi-GHK (red, dashed) approximations both exhibit resonant peaks in the transition region.
(green, solid) and Fermi-GHK (red, dashed) approximations both exhibit resonant peaks in the transition region.
Download figure:
Standard image High-resolution imageFor a quantitative comparison of the theory with Pc as obtained from the Brownian dynamics simulations, we calculate the effective (excess) well depth 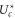 as:
as:
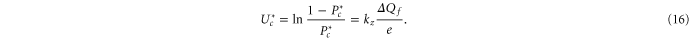
The Fermi–Dirac function (10) predicts that 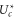 should be linear in Qf, i.e. (16) represents linearising coordinates for the Fermi–Dirac equation (10); the Coulomb blockade model also predicts the geometry-dependent coefficient kz.
should be linear in Qf, i.e. (16) represents linearising coordinates for the Fermi–Dirac equation (10); the Coulomb blockade model also predicts the geometry-dependent coefficient kz.
Figure 5(a) shows a sawtooth-like dependence of 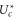 on Qf, confirming that the
on Qf, confirming that the  transitions obey the Fermi–Dirac function (10) of Uc. For M1, the slope corresponds well with analytic kz; the discrepancies in slope at M2 and M3 are attributable to our neglect of ion–ion interactions.
transitions obey the Fermi–Dirac function (10) of Uc. For M1, the slope corresponds well with analytic kz; the discrepancies in slope at M2 and M3 are attributable to our neglect of ion–ion interactions.
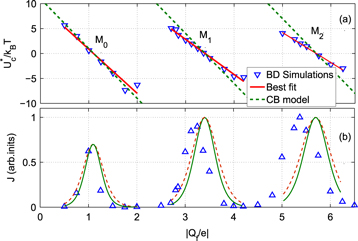
Figure 5. Comparisons of the ionic Coulomb blockade model with Brownian dynamics (BD) simulation results as Qf is varied. (a) The effective well depth 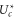 (blue point-down triangles) fitted by Fermi–Dirac function (16) with best-fit slopes (full red lines) and with analytical slopes kz (green dashed lines). (b) The full green curves representing the Landauer approximation (14), and the red-dashed lines representing the Fermi-GHK approximation (15), are compared with the Brownian dynamics simulations (blue, point-up triangles).
(blue point-down triangles) fitted by Fermi–Dirac function (16) with best-fit slopes (full red lines) and with analytical slopes kz (green dashed lines). (b) The full green curves representing the Landauer approximation (14), and the red-dashed lines representing the Fermi-GHK approximation (15), are compared with the Brownian dynamics simulations (blue, point-up triangles).
Download figure:
Standard image High-resolution imageFigure 5(b) compares the predictions of the Coulomb blockade model with the conduction bands M0, M1, M2 obtained from the simulations [57]. The Landauer and Fermi-GHK peaks are calculated using (14) and (15) respectively with the values of 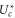 taken from plot (a), and there are no adjustable parameters. The BD peak shapes and positions are described reasonably well by the model, extending the simpler fitting in [58, 59]. Again, the agreement is very good for M1, and less good for M2 and M3 on account of our neglect of field leaks and the singular parts of the interactions.
taken from plot (a), and there are no adjustable parameters. The BD peak shapes and positions are described reasonably well by the model, extending the simpler fitting in [58, 59]. Again, the agreement is very good for M1, and less good for M2 and M3 on account of our neglect of field leaks and the singular parts of the interactions.
In general, the results of Brownian dynamics simulations [57, 58] correspond well with the predictions of the Coulomb blockade model.
3.5. Valence selectivity and AMFE
Comparison of the Ca2+ (z = 2) bands pattern (figure 2) with the Na+ (z = 1) picture (figure 3 ) clearly shows that, unlike its electronic counterpart, ionic Coulomb blockade is valence-dependent: the positions of the bands 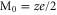 , and their period
, and their period  , shift in proportion to z as described by equation (8) and they broaden/narrow in proportion to z2 (5) [58].
, shift in proportion to z as described by equation (8) and they broaden/narrow in proportion to z2 (5) [58].
The ionic Coulomb blockade model attributes selectivity to modification of the UG dependences on Qf. Valence selectivity is provided by the electrostatic z-dependent shift of 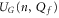 curves and the corresponding shifts of the Mn and Zn singular points. Alike-charge selectivity can in principle be accounted for by hydration-dependent shifts of Mn and Zn.
curves and the corresponding shifts of the Mn and Zn singular points. Alike-charge selectivity can in principle be accounted for by hydration-dependent shifts of Mn and Zn.
The model also predicts that a monovalent (e.g. sodium) ionic current can be effectively blocked by a few divalent (e.g. calcium) ions, an effect well-known in calcium and sodium channels. Calcium blockade is an aspect of AMFE, which is a signature of EEEE calcium channels [14]. The threshold of the divalent block IC50 is defined as the Ca2+ concentration which results in a 50% decrease in the monovalent current [14]. We can estimate IC50 on the assumption that the sodium current is proportional to (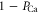 ), i.e. to the fraction of time when the channel is not blocked by calcium ionc. Hence equations (12, 13) result in an exponential dependence of IC50 on Qf:
), i.e. to the fraction of time when the channel is not blocked by calcium ionc. Hence equations (12, 13) result in an exponential dependence of IC50 on Qf:

which is a prediction that can be tested.
Mutant studies of the DEKA sodium channel [22, 24, 26] have measured the dependence of AMFE on the selectivity filter locus and its Qf, and it was shown that log(IC50) can successfully be fitted by a linear function of Qf (figure 6), in agreement with the prediction (17) of the Coulomb blockade model, or

where a and b are constants. The best-fit line gives b = 2.29 [24] which does not agree well with the 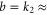 10 calculated for our model. This discrepancy can be interpreted as evidence that the geometrical parameters (R and L) of the selectivity filter of a DEKA sodium channel differ from values taken in our model (R = 0.3 nm, L = 1.6 nm). To be compatible with experiments the selectivity filter would need to be shorter and/or wider. We can get good agreement for e.g. R = 3.5 nm and L = 0.4 nm (such a short selectivity filter would in fact correspond well to the model of [70]) for which k2 = 2.28. Because the exact values are not yet known, our fitting can be used to estimate these parameters. Note, however, that the fitting (18) is not unique to the Coulomb blockade model but follows from the dominance of electrostatics for divalent ions [24].
10 calculated for our model. This discrepancy can be interpreted as evidence that the geometrical parameters (R and L) of the selectivity filter of a DEKA sodium channel differ from values taken in our model (R = 0.3 nm, L = 1.6 nm). To be compatible with experiments the selectivity filter would need to be shorter and/or wider. We can get good agreement for e.g. R = 3.5 nm and L = 0.4 nm (such a short selectivity filter would in fact correspond well to the model of [70]) for which k2 = 2.28. Because the exact values are not yet known, our fitting can be used to estimate these parameters. Note, however, that the fitting (18) is not unique to the Coulomb blockade model but follows from the dominance of electrostatics for divalent ions [24].
Figure 6. Calcium block as a function of the net charge Qf of the sodium channel inner ring mutants (relative to the wild type (DEKA)). For the indicated mutants  (i.e. the concentration [Ca2+] necessary to block 50% of sodium inward current) is plotted as a function of the net charge of the inner ring Qf. Data points are taken from [24] (blue open circles) and [22] (green open squares). The continuous red line indicates an exponential function
(i.e. the concentration [Ca2+] necessary to block 50% of sodium inward current) is plotted as a function of the net charge of the inner ring Qf. Data points are taken from [24] (blue open circles) and [22] (green open squares). The continuous red line indicates an exponential function 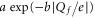 , with b = 2.29, corresponding to a least-squares fit to all the data.
, with b = 2.29, corresponding to a least-squares fit to all the data.
Download figure:
Standard image High-resolution image3.6. Further considerations
Although an ion moving inside a channel is a room-temperature classical system described by Newtonian dynamics, we see that it exhibits some quantum-like mesoscopic features [52]. They include the appearance of strong Coulomb blockade oscillations in conductance, a Coulomb staircase, and a Fermi–Dirac distribution of occupancy for Ca2+ ions. We attribute such behavior to the charge discreteness, to the strong electrostatic interaction in confinement [52] and to the electrostatic exclusion principle. It has been shown rigorously that, in the presence of an exclusion principle, Brownian motion leads to a Fermi–Dirac distribution of the Brownian particles [84].
A parametric study [57] based on Brownian dynamics modelling has shown that, in accordance with (7), strong Coulomb blockade may be expected in channels of radii 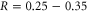 nm for ions having z = 2, e.g. for Ca+ ions in calcium/sodium channels. It is an interesting and significant question whether or not strong blockade and the corresponding oscillations may also arise in the conduction of monovalent ions in K+ channels. The latter have a selectivity filter of appropriate radius,
nm for ions having z = 2, e.g. for Ca+ ions in calcium/sodium channels. It is an interesting and significant question whether or not strong blockade and the corresponding oscillations may also arise in the conduction of monovalent ions in K+ channels. The latter have a selectivity filter of appropriate radius,  nm [34]. Furthermore, K+ ions are fully hydrated, which should lead to a stronger electrostatic interaction and hence to a marked decrease in the effective
nm [34]. Furthermore, K+ ions are fully hydrated, which should lead to a stronger electrostatic interaction and hence to a marked decrease in the effective  w, bringing it close to
w, bringing it close to 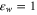 . In such a case equation (7) suggests that we could expect an observable Coulomb blockade effect, even for monovalent ions in potassium channels [40, 41], a speculation that needs to be tested.
. In such a case equation (7) suggests that we could expect an observable Coulomb blockade effect, even for monovalent ions in potassium channels [40, 41], a speculation that needs to be tested.
The relationship of the stop bands in the model to the subconductance states seen in experiments, and to the noise of closed channels, remains to be determined. Subconductance states and unusual baseline noise are found in a wide variety of natural biological channels [98].
4. Conclusions
We conclude that ionic Coulomb blockade manifests itself in a simple electrostatic and Brownian dynamics model of a water-filled charged nanopore with parameters chosen to correspond to those of biological ion channels. It is a fundamental electrostatic phenomenon based on charge discreteness, an electrostatic exclusion principle and linear response theory. For divalent Ca2+ ions in calcium/sodium channels, the blockade is strong, so that the ionic permeation process is closely analogous to low-temperature mesoscopic transport in quantum dots. The several similarities include the applicability of Fermi–Dirac statistics and the appearance of Coulomb blockade oscillations, i.e. the calcium ion channel can behave as a single-charge discrete electrostatic device.
For the parameter range where it is applicable and strong, the ionic Coulomb blockade picture leads to several explicit predictions that are unique to the model:
- Periodic oscillations of conductance versus Qf with a period close to the ionic charge
 , with stop-bands Zn centred on positions
, with stop-bands Zn centred on positions  , and conduction-bands Mn centred on
, and conduction-bands Mn centred on  .
. - Hence, a valence dependence of the pattern of bands, leading to valence selectivity.
- Fermi–Dirac occupancy statistics and corresponding shapes of the occupancy bands.
- The barrier-less character of conduction at the Mn points.
The approach also provides straightforward (provisional) explanations of many experimentally observed phenomena in the Ca2+/Na+ channels family including:
- Fast permeation, which can be accounted for through barrier-less single- and multi-ion conductivity.
- The strong valence selectivity of calcium channels.
- Divalent block of a monovalent current and the AMFE.
- The mutation transformations of conduction and selectivity.
The ionic Coulomb blockade model of ionic permeation provides a simple and transparent explanation of a wide range of experimental data that hitherto had not seemed to be connected, and it reinterprets the calcium conduction bands as manifestations of a quite general electrostatic phenomenon, common to ion channels, quantum-dots, and tunnel diodes.
Currently available experimental data do not allow for full validation of the Coulomb blockade model and, moreover, there are some small discrepancies. Therefore, we present this theory as something still awaiting full verification through comparison with experimental results from real biological channels, rather than as something already 'verified'. Further investigations are needed to confirm/refute the tentative channel identifications, to understand why the nominal Qf is systematically slightly smaller than the Qf values of band maxima in the model, and to explain why mammalian and bacterial EEEE-loci channels have different selectivity properties.
Finally, we remark that the results could also be applicable to other ion channels and to biomimetic nanopores with charged walls.
Acknowledgments
We acknowledge valuable discussions with M I Dykman, W A T Gibby, I A Khovanov, D G Luchinsky, A Stefanovska and R Tindjong. IKK is also grateful to B Shklovskii and M Di Ventra for helpful comments and discussions. The research was supported by the Engineering and Physical Sciences Research Council UK (grants Nos. EP/G070660/1 and EP/M015831/1).