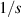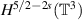Paper • The following article is Open access

Phase transitions in the fractional three-dimensional Navier–Stokes equations

and

Published 11 March 2024 • © 2024 The Author(s). Published by IOP Publishing Ltd
, , Citation Daniel W Boutros and John D Gibbon 2024 Nonlinearity 37 045010 DOI 10.1088/1361-6544/ad25be

Download Article PDF

Article metrics

83 Total downloads

Share this article

Author e-mails

dwb42@cam.ac.uk

Author affiliations

1 Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, United Kingdom

2 Department of Mathematics, Imperial College London, London SW7 2AZ, United Kingdom

Author notes

3 Author to whom any correspondence should be addressed.

ORCID iDs

Dates

  1. Received 6 May 2023
  2. Accepted 1 February 2024
  3. Published

Check for updates using Crossmark

Buy this article in print

Journal RSS
Sign up for new issue notifications
0951-7715/37/4/045010

Abstract

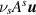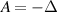The fractional Navier–Stokes equations on a periodic domain $[0,\,L]^{3}$ differ from their conventional counterpart by the replacement of the $-\nu\Delta{\boldsymbol{u}}$ Laplacian term by $\nu_{s}A^{s}{\boldsymbol{u}}$, where $A = - \Delta$ is the Stokes operator and 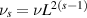$\nu_{s} = \nu L^{2(s-1)}$ is the viscosity parameter. Four critical values of the exponent 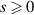$s\unicode{x2A7E} 0$ have been identified where functional properties of solutions of the fractional Navier–Stokes equations change. 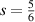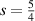These values are: $s = \frac{1}{3}$; $s = \frac{3}{4}$; $s = \frac{5}{6}$ and $s = \frac{5}{4}$. In particular: (i) for 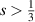$s \gt \frac{1}{3}$ we prove an analogue of one of the Prodi–Serrin regularity criteria; (ii) for $s \unicode{x2A7E} \frac{3}{4}$ we find an equation of local energy balance and; (iii) for $s \gt \frac{5}{6}$ we find an infinite hierarchy of weak solution time averages. The existence of our analogue of the Prodi–Serrin criterion for $s \gt \frac{1}{3}$ suggests the sharpness of the construction using convex integration of Hölder continuous solutions with epochs of regularity in the range 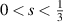$0 \lt s \lt \frac{1}{3}$.

Export citation and abstract BibTeX RIS

Previous article in issue
Next article in issue

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.

Recommended by Dr Theodore Dimitrios Drivas

Footnotes

  • 3 

    Somewhat confusingly, because of the $1/s$ exponent on t, the hyper-viscous case s > 1 corresponds to sub-diffusion in the theory of random walks while the hypo-viscous case s < 1 corresponds to super-diffusion.

  • 4 

    In addition to the general regularity criteria on the velocity field for the three dimensional Navier–Stokes equations [49, 50], $\int_{0}^{t}\|\nabla{\boldsymbol{u}}\|_{\infty}\,d\tau$ is another sufficient regularity condition which is applicable in both two and three dimensions. This time integral also applies to the Euler equations. Beale et al [51] then showed how this result for the three dimensional Euler equations could be converted to control over $\int_{0}^{t}\|{\boldsymbol{\omega}}\|_{\infty}\,d\tau$ at the price of making the upper bound super-exponential in time. In this paper we consider our result in theorem 2 to be an analogue of that of Prodi and Serrin.

  • 5 

    The origin of the exponent $s = \frac{5}{6}$ is as follows: it is elementary to show that the critical space for the fractional Navier–Stokes equations is $H^{5/2-2s}(\mathbb{T}^3)$. This coincides with $H^{s}(\mathbb{T}^3)$ (which is part of the Leray–Hopf regularity) when $s = \frac{5}{6}$.

Please wait… references are loading.
10.1088/1361-6544/ad25be