Abstract
We explore the interplay between nematicity (spontaneous breaking of the sixfold rotational symmetry), superconductivity, and non-Fermi liquid behavior in partially flat-band (PFB) models on the triangular lattice. A key result is that the nematicity (Pomeranchuk instability), which is driven by many-body effect and stronger in flat-band systems, enhances superconducting transition temperature in a systematic manner on the Tc dome. There, a plausible  -wave symmetry, in place of the conventional
-wave symmetry, in place of the conventional 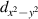 -wave, governs the nematicity-enhanced pairing with a sharp rise in the Tc dome on the filling axis. When the sixfold symmetry is spontaneously broken, the pairing interaction is shown to become stronger with more compact pairs in real space than when the symmetry is enforced. These are accompanied by a non-Fermi character of electrons in the PFBs with many-body interactions.
-wave, governs the nematicity-enhanced pairing with a sharp rise in the Tc dome on the filling axis. When the sixfold symmetry is spontaneously broken, the pairing interaction is shown to become stronger with more compact pairs in real space than when the symmetry is enforced. These are accompanied by a non-Fermi character of electrons in the PFBs with many-body interactions.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Strongly correlated systems have become an epitome in the condensed-matter physics, as exemplified by the high-temperature superconductivity in the cuprate [1], and iron-based [2] families. These compounds exhibit rich phase diagrams as hallmarked by the emergence of unconventional superconductivity, and a plethora of symmetry-broken phases such as spin and charge nematicity and stripe orders.
Quest for finding novel high-temperature superconductors spurs interests in exploring many-body systems with short-range repulsions but with (nearly) flat subregions in the band dispersion arising from hopping beyond nearest neighbors or from lattice structures [3, 4]. These systems with dispersionless band portions permit numerous scattering channels for the electrons and can give rise to various exotic quantum phases such as spin and charge density waves [5, 6], Mott insulating [7], and bad-metallic phases [8], as well as the formation of spatially extended Cooper pairs [9, 10].
Interaction and the flatness of the band structure can be intimately related to geometric and quantum frustration in producing strong correlation effects. The spin liquid behavior in hexagonal lattices, such as organic compounds [11, 12] and inorganic Herbertsmithites [13, 14], are typical examples. In these exotic liquids, the classical picture is no longer valid, and their quantum phase transitions cannot be described within Landau's phase transition theory.
Aside from these many-body phenomena, the electron nematicity, i.e. spontaneous breaking of spatial rotational symmetry triggered by many-body interactions, is another manifestation of the correlation effects [15, 16]. It is an intriguing direction to pursue the physical origins of these symmetry-broken phases [17–19], and to grasp the interplay between nematicity and other phases such as superconductivity [10, 20–24] and non-Fermi liquid [25]. Various studies report different roles of nematic fluctuations on the superconductivity including the competition between these two phases, e.g. in doped 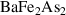 [26], the assistance of nematicity to enhance the superconductivity transition temperature, e.g. in twisted bilayer graphene [27], and the negligible effect of nematicity on the superconducting phase, e.g. in
[26], the assistance of nematicity to enhance the superconductivity transition temperature, e.g. in twisted bilayer graphene [27], and the negligible effect of nematicity on the superconducting phase, e.g. in 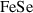 [28]. One crucial aspect is figuring out which of these possibilities occur in systems that have a flat or partially flat band (PFB) in their dispersions [5, 6, 29, 30].
[28]. One crucial aspect is figuring out which of these possibilities occur in systems that have a flat or partially flat band (PFB) in their dispersions [5, 6, 29, 30].
In this paper, we bring these features together to explore the interplay between the nematicity and superconductivity in PFB models on the triangular lattice, effective model for Moire-produced basis states [31]. Here the lattice structure frustrates magnetic orders, thereby giving opportunities for nematic instabilities to arise. As a key finding, we shall demonstrate that nematicity can significantly enhance transition temperatures (Tc) in the superconducting phase, with a 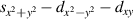 -wave pairing symmetry. This occurs for an intermediate Hubbard repulsion and in a non-Fermi liquid regime.
-wave pairing symmetry. This occurs for an intermediate Hubbard repulsion and in a non-Fermi liquid regime.
2. Model
The Hubbard Hamiltonian on the isotropic triangular lattice reads

where  creates (annihilates) an electron with momentum
creates (annihilates) an electron with momentum 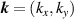 and spin σ at site i,
and spin σ at site i,  . The repulsive Hubbard interaction is denoted as
. The repulsive Hubbard interaction is denoted as  , and µ is the chemical potential. The non-interacting band dispersion for the triangular lattice is given as
, and µ is the chemical potential. The non-interacting band dispersion for the triangular lattice is given as
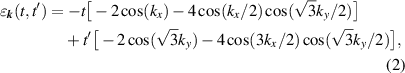
where t is the nearest-neighbor hopping (taken as a unit of energy) and tʹ is the second-neighbor hopping. Here, we consider 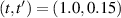 , which possesses a nearly flat region along
, which possesses a nearly flat region along  , see dashed line in figure 1. For the interaction, we set an intermediate
, see dashed line in figure 1. For the interaction, we set an intermediate 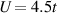 , with the inverse temperature set to be
, with the inverse temperature set to be  except in figure 3(c).
except in figure 3(c).
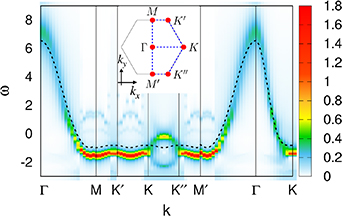
Figure 1. Momentum-dependent spectral function along high-symmetry momenta (see labels in the inset) in the PFB system with 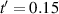 for
for 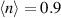 and U = 4.5. Dashed black lines represents the shifted noninteracting band structure (
and U = 4.5. Dashed black lines represents the shifted noninteracting band structure (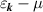 ) with a chemical potential
) with a chemical potential  . (Inset) Hexagonal Brillouin zone for the triangular lattice with high symmetry points marked, i.e. Γ at
. (Inset) Hexagonal Brillouin zone for the triangular lattice with high symmetry points marked, i.e. Γ at 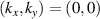 , K at
, K at  , Kʹ at
, Kʹ at 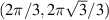 , Kʹʹ at
, Kʹʹ at  , M at
, M at 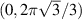 , and Mʹ at
, and Mʹ at  . M and Mʹ are equivalent, in both of twofold (in the presence of the nematicity) and sixfold (in its absence) rotational symmetries. In the presence of sixfold symmetry, Kʹ and Kʹʹ are equivalent as well.
. M and Mʹ are equivalent, in both of twofold (in the presence of the nematicity) and sixfold (in its absence) rotational symmetries. In the presence of sixfold symmetry, Kʹ and Kʹʹ are equivalent as well.
Download figure:
Standard image High-resolution image3. Numerical method
To study paramagnetic phases with no spin imbalance, we employ the dynamical mean-field theory (DMFT) combined with the fluctuation exchange approximation (FLEX), known as the FLEX+DMFT [32]. This method comprises DMFT and FLEX double loops, solved self-consistently at each FLEX+DMFT iteration. In this work, we solve the DMFT impurity problem by the modified iterative perturbation theory [33, 34]. The momentum-dependent FLEX self-energy is constructed from the bubble and ladder diagrams. After removing the doubly-counted diagrams in the local FLEX self-energy, the FLEX+DMFT self-energy is updated. The momentum-dependent self-energy in the FLEX+DMFT incorporates vertex corrections generated from the DMFT iterations into the local part of the FLEX self-energy. Even though our FLEX+DMFT method does not deal with spatial vertex corrections, larger coordination number and frustrated magnetic fluctuations in the triangular lattice give rise to more local self-energies and less dominant spatial vertex corrections than in the square lattice [35]. As a result, the FLEX+DMFT is considered to be a reliable approach that incorporates local and nonlocal correlations.
When we start from the non-interacting tight-binding Hamiltonian, equation (1), that has the sixfold rotational (C6) lattice symmetry, the solution of the many-body problem may exhibit a lower symmetry. To study the phases with/without C6 symmetry, we solve the FLEX+DMFT loops with/without imposing the C6 constraints. To explore the Pomeranchuk instability with the broken C6 symmetry, we take an initial self-energy as ![$\Sigma_{\textrm{in}} = 0.05 [\cos(k_{x}) - \cos(\sqrt{3}k_{y}/2) \cos(k_{x}/2) ]$](https://content.cld.iop.org/journals/0953-8984/35/24/245605/revision3/cmacc6afieqn24.gif) which acts as a seed for distorting the Fermi surface for the FLEX+DMFT iterations. The FLEX+DMFT calculations are here performed on a
which acts as a seed for distorting the Fermi surface for the FLEX+DMFT iterations. The FLEX+DMFT calculations are here performed on a 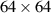 momentum grid and an energy mesh with 2048 points.
momentum grid and an energy mesh with 2048 points.
4. Nematicity and non-Fermi liquid behavior
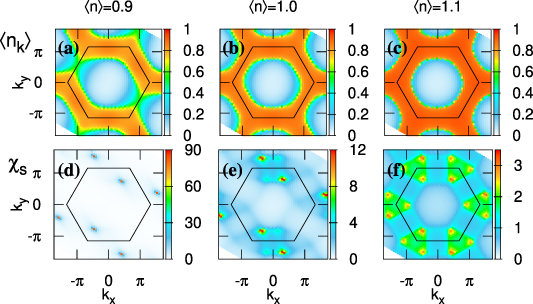
We start with presenting the momentum distribution function plotted in panels (a–c) in figure 2 (top rows). For a system with a well-defined Fermi surface,  should take the value of unity (zero) inside (outside) the Fermi surface for
should take the value of unity (zero) inside (outside) the Fermi surface for 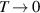 . For all band fillings in our results, the maxima of the momentum-dependent distribution function are below unity. The system exhibits a filling-dependent degrading of C6 down to a twofold C2 symmetry in
. For all band fillings in our results, the maxima of the momentum-dependent distribution function are below unity. The system exhibits a filling-dependent degrading of C6 down to a twofold C2 symmetry in 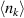 . Namely, we have here an emergence of nematicity, or a Pomeranchuk instability. The breaking of C6 is seen to occur even right at half-filling, while the electron-doped case shows a preserved C6.
. Namely, we have here an emergence of nematicity, or a Pomeranchuk instability. The breaking of C6 is seen to occur even right at half-filling, while the electron-doped case shows a preserved C6.
Figure 2. Momentum distribution functions (top panels) and spin susceptibilities (bottom) are displayed in momentum space for band fillings 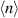 = 0.9 (a), (d), 1.0 (b), (e), and 1.1 (c), (f). All results are calculated for the PFB systems with
= 0.9 (a), (d), 1.0 (b), (e), and 1.1 (c), (f). All results are calculated for the PFB systems with  and U = 4.5. The black hexagon in each panel indicates the Brillouin zone. Note different color bars between different band fillings.
and U = 4.5. The black hexagon in each panel indicates the Brillouin zone. Note different color bars between different band fillings.
Download figure:
Standard image High-resolution imageFigure 3. (a) Pomeranchuk order parameter ξ.  for
for 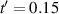 is represented by purple lines.
is represented by purple lines.  is shown by magenta lines. (b) Exponent α of the impurity self-energy for systems with (dashed curves) and without (solid) imposed sixfold symmetry. (c) The largest eigenvalue λ of the linearized Eliashberg equation for the singlet pairing symmetry against band filling for the PFB system with
is shown by magenta lines. (b) Exponent α of the impurity self-energy for systems with (dashed curves) and without (solid) imposed sixfold symmetry. (c) The largest eigenvalue λ of the linearized Eliashberg equation for the singlet pairing symmetry against band filling for the PFB system with 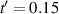 and U = 4.5, with the broken (dark blue curves) or unbroken (sky-blue) sixfold symmetry. Black horizontal line marks λ = 1, and an arrow points to the dip in λ when C6 is enforced. Vertical blue solid lines indicate
and U = 4.5, with the broken (dark blue curves) or unbroken (sky-blue) sixfold symmetry. Black horizontal line marks λ = 1, and an arrow points to the dip in λ when C6 is enforced. Vertical blue solid lines indicate  (see text). Vertical dotted sky-blue lines are at
(see text). Vertical dotted sky-blue lines are at  .
.
Download figure:
Standard image High-resolution imageTo quantify the broken C6 symmetry, we introduce point-group resolved Pomeranchuk order parameters defined as  and
and 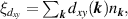 with
with  [36]. The form factors,
[36]. The form factors, 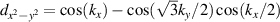 and
and 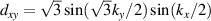 , describe the distortion of the Fermi surface in the point group C6, and ξ is a real number with values between zero (when C6 is preserved) and unity.
, describe the distortion of the Fermi surface in the point group C6, and ξ is a real number with values between zero (when C6 is preserved) and unity.
Figure 3(a) displays ξ against the band filling. We can see that, as the band filling is reduced, ξ starts to grow, and at a critical band filling  (vertical blue line in figure 3(a)),
(vertical blue line in figure 3(a)),  undergoes a first-order phase transition [37, 38]. At this filling, the onset of nematicity is accompanied by a Lifshitz transition, where the Fermi surface delineated by the ridges in
undergoes a first-order phase transition [37, 38]. At this filling, the onset of nematicity is accompanied by a Lifshitz transition, where the Fermi surface delineated by the ridges in  (not shown) is not only distorted but undergoes a topological change from closed to open structures.
(not shown) is not only distorted but undergoes a topological change from closed to open structures.
We further notice that the filling dependence of the nematicity differs between  and
and  in the PFB model; compare purple and magenta lines in figure 3(a). For
in the PFB model; compare purple and magenta lines in figure 3(a). For  ,
,  is dominant, while
is dominant, while 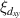 takes over below
takes over below 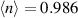 , which we call the second characteristic band filling,
, which we call the second characteristic band filling, 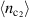 (vertical dashed sky-blue line in figure 3(a)). While
(vertical dashed sky-blue line in figure 3(a)). While  displays a first-order transition at
displays a first-order transition at 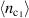 ,
,  exhibits a crossover at
exhibits a crossover at  . This suggests that thermodynamic parameters such as temperature at which
. This suggests that thermodynamic parameters such as temperature at which 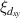 and
and  experience the first-order transitions are different from each other.
experience the first-order transitions are different from each other.
To trace back the origin of the nematic phases, let us next present the momentum-dependent spin susceptibility 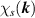 for the PFB model in figures 2(d)–(f). In the electron-doped regime where the Pomeranchuk instability is absent, χs
respects the sixfold rotational symmetry of the lattice, with peaks at
for the PFB model in figures 2(d)–(f). In the electron-doped regime where the Pomeranchuk instability is absent, χs
respects the sixfold rotational symmetry of the lattice, with peaks at 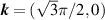 and its equivalent positions under C6. As band filling is decreased below the half-filling, the spin susceptibility develops spikes around
and its equivalent positions under C6. As band filling is decreased below the half-filling, the spin susceptibility develops spikes around  and the equivalent places under a C2 subgroup of the original C6 rotational symmetry. The appearance of spikes at mid-momenta in the spin susceptibilities indicates the presence of long-range spin fluctuations in our systems [39].
and the equivalent places under a C2 subgroup of the original C6 rotational symmetry. The appearance of spikes at mid-momenta in the spin susceptibilities indicates the presence of long-range spin fluctuations in our systems [39].
In general, an electronic nematicity without breaking the translational symmetry can be driven by structural transitions, charge [40] or spin [41] fluctuations. Our Hamiltonian does not deal with the distortion of the lattice or phonons and thus precludes structural transitions. We have checked that the charge susceptibility is at least an order of magnitude smaller than the spin susceptibility. Thus the spin-mediated correlations should be responsible for the emergence of the Pomeranchuk instability [24].
Now let us turn to a non-Fermi liquid character of the present electronic systems, since the flat portions of the band may well exert peculiar effects. We can quantify this in terms of the impurity self-energy in DMFT by fitting the imaginary part of the self-energy on Matsubara axis to  , and present the result for the exponent α in figure 3(b). In general, α = 1 at small ωn
(c.f., α = 2 on real frequency axis as
, and present the result for the exponent α in figure 3(b). In general, α = 1 at small ωn
(c.f., α = 2 on real frequency axis as 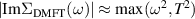 at small T) characterizes the Fermi liquid, while α < 0.5 will signify a non-Fermi liquid (bad metal) behavior [42–45]. Above the first order Pomeranchuk transition for
at small T) characterizes the Fermi liquid, while α < 0.5 will signify a non-Fermi liquid (bad metal) behavior [42–45]. Above the first order Pomeranchuk transition for 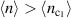 , α's computed for systems with (dashed lines) and without (solid lines) the enforced C6 constraint trivially coincide with each other. We can see that both systems display strong non-Fermi liquid behavior with α well below 1. If we turn to
, α's computed for systems with (dashed lines) and without (solid lines) the enforced C6 constraint trivially coincide with each other. We can see that both systems display strong non-Fermi liquid behavior with α well below 1. If we turn to 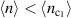 for which we have revealed the nematicity, figure 3(b) shows notable differences in α between the cases where C6 is enforced or not. After a sharp drop at
for which we have revealed the nematicity, figure 3(b) shows notable differences in α between the cases where C6 is enforced or not. After a sharp drop at 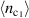 as the band filling is reduced, α gradually increases (decreases) in the presence (absence) of the imposed sixfold constraint. Eventually α starts to decrease with decreasing
as the band filling is reduced, α gradually increases (decreases) in the presence (absence) of the imposed sixfold constraint. Eventually α starts to decrease with decreasing  at
at  in the PFB system. The persistent α < 0.5 for
in the PFB system. The persistent α < 0.5 for  implies that the nematic phase resides in the non-Fermi liquid regime.
implies that the nematic phase resides in the non-Fermi liquid regime.
5. Superconductivity
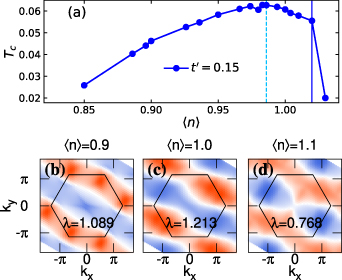
Now let us come to our key interest in pairing instabilities, for which we solve the linearized Eliashberg equation,  to find the largest eigenvalue λ for the spin-singlet, even-frequency superconducting gap function Δ. Here,
to find the largest eigenvalue λ for the spin-singlet, even-frequency superconducting gap function Δ. Here,  with ωn
the fermionic Matsubara frequency, and the effectiv interaction for singlets given as
with ωn
the fermionic Matsubara frequency, and the effectiv interaction for singlets given as  . The pairing is identified when λ exceeds unity [46]. Figure 3(c) depicts λ in the presence (dashed green lines) or absence (solid blue) of imposed C6 symmetry in PFB.
. The pairing is identified when λ exceeds unity [46]. Figure 3(c) depicts λ in the presence (dashed green lines) or absence (solid blue) of imposed C6 symmetry in PFB.
When the sixfold rotational symmetry is enforced, we get λ < 0.8 in PFB model, indicating that the singlet superconductivity does not arise for the temperature (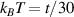 ) considered here. We can still notice that λ displays a double-peak structure with a minimum at
) considered here. We can still notice that λ displays a double-peak structure with a minimum at  . The dip is shown to occur at the band filling at which the
. The dip is shown to occur at the band filling at which the  gap function with two-nodal lines for
gap function with two-nodal lines for  changes into a more complicated multi-nodal-line gap functions for
changes into a more complicated multi-nodal-line gap functions for 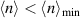 , see [47] supplemental material for details. This behavior of the gap function reflects a crossover from the antiferromagnetic spin structure with a single nesting vector for
, see [47] supplemental material for details. This behavior of the gap function reflects a crossover from the antiferromagnetic spin structure with a single nesting vector for 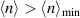 , to a more complex spin structure for
, to a more complex spin structure for 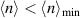 where single peaks in the spin susceptibility evolve into extended structures (see figures 2(d)–(f)). Thus the system for
where single peaks in the spin susceptibility evolve into extended structures (see figures 2(d)–(f)). Thus the system for 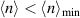 goes beyond the conventional nesting physics. Similar structure in λ and associated gap function have also been reported for PFB systems on the square lattice [9], again in the absence of nematicity.
goes beyond the conventional nesting physics. Similar structure in λ and associated gap function have also been reported for PFB systems on the square lattice [9], again in the absence of nematicity.
In a dramatic contrast, if we allow the C6 symmetry to be broken spontaneously, λ soars from those with C6 restriction, as seen for  . This occurs concomitantly with the Pomeranchuk order parameters (ξ's), which grow precisely in this filling region. Just below
. This occurs concomitantly with the Pomeranchuk order parameters (ξ's), which grow precisely in this filling region. Just below  , λ in the systems with broken C6 (solid blue lines in figure 3(c)) exhibits a rapid growth and exceeds unity. This is inherited in the superconducting transition temperatures
, λ in the systems with broken C6 (solid blue lines in figure 3(c)) exhibits a rapid growth and exceeds unity. This is inherited in the superconducting transition temperatures 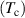 , presented in figure 4(a).
, presented in figure 4(a).
Figure 4. (a) Superconducting transition temperature Tc
against band filling for the PFB. Vertical solid line indicates  , while vertical dotted line indicates
, while vertical dotted line indicates  . (b)–(d) Gap functions in momentum-space with singlet pairing for the PFB system with
. (b)–(d) Gap functions in momentum-space with singlet pairing for the PFB system with  for U = 4.5 and β = 30 for
for U = 4.5 and β = 30 for  (a), 1.0 (b) and 1.1 (c). Black hexagons indicate the Brillouin zone. Color code for the gap function is bluish (reddish) for negative (positive) values, for which we have omitted the color bars since the linearized Eliashberg equation does not indicate magnitudes of Δ.
(a), 1.0 (b) and 1.1 (c). Black hexagons indicate the Brillouin zone. Color code for the gap function is bluish (reddish) for negative (positive) values, for which we have omitted the color bars since the linearized Eliashberg equation does not indicate magnitudes of Δ.
Download figure:
Standard image High-resolution image
Tc, with the broken C6, exhibits a single-dome structure as a function of band filling. We can observe that the presence of a flat portion in PFB or a van Hove singularity for  have similar effects on the largest values of Tc when
have similar effects on the largest values of Tc when  . One should note that, while a van Hove singularity at EF
only occurs at a single point on the filling axis, a flat portion of the band can accommodate a range of band filling. This difference is reflected in the width of the Tc dome at a given temperature; see figure 4(a) and SM. The maximum of Tc in the PFB is seen to take place close to
. One should note that, while a van Hove singularity at EF
only occurs at a single point on the filling axis, a flat portion of the band can accommodate a range of band filling. This difference is reflected in the width of the Tc dome at a given temperature; see figure 4(a) and SM. The maximum of Tc in the PFB is seen to take place close to  at which
at which 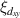 exceeds
exceeds  . Note that the superconducting transition temperature becomes almost doubled as we pass through
. Note that the superconducting transition temperature becomes almost doubled as we pass through  , see figure 4(a), which should come from the interplay between nematicity, spin fluctuations, and superconductivity.
, see figure 4(a), which should come from the interplay between nematicity, spin fluctuations, and superconductivity.
Let us now delve into the gap function in momentum space in figures 4(b)–(d). In the electron-doped regime, the PFB model exhibits a conventional  paring symmetry [48]. This behavior of the gap function persists for
paring symmetry [48]. This behavior of the gap function persists for  . On the other hand, below
. On the other hand, below 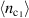 where the C6 symmetry is broken down to its C2 subgroup, the dominant channel of instability is a mixture of
where the C6 symmetry is broken down to its C2 subgroup, the dominant channel of instability is a mixture of  ,
, 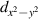 and dxy
-wave symmetries, see figure S16 in SM.
and dxy
-wave symmetries, see figure S16 in SM.
To better understand the role of nematicity in superconducting phases, we can look at  , where
, where  is the effective interaction with the imposed C6 constraint. As shown in figure S19 in SM, Veff is much intensified when C6 is lifted. Since χc
is much smaller than χs
, the effective pairing interaction reflects the momentum-dependence of the spin-susceptibility under the Pomeranchuk distortions. This effective interaction assists electrons to nonlocally form Cooper pairs [15, 38, 49]. The deformation in
is the effective interaction with the imposed C6 constraint. As shown in figure S19 in SM, Veff is much intensified when C6 is lifted. Since χc
is much smaller than χs
, the effective pairing interaction reflects the momentum-dependence of the spin-susceptibility under the Pomeranchuk distortions. This effective interaction assists electrons to nonlocally form Cooper pairs [15, 38, 49]. The deformation in  allows first-order perturbation corrections in the distortion, which should be responsible for the drastic changes in λ below
allows first-order perturbation corrections in the distortion, which should be responsible for the drastic changes in λ below 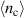 . This contrasts with the previous study on the interplay between nematicity and superconductivity, where the enhancement of λ originates from the second-order perturbation corrections and thus results in much smaller changes [24].
. This contrasts with the previous study on the interplay between nematicity and superconductivity, where the enhancement of λ originates from the second-order perturbation corrections and thus results in much smaller changes [24].
6. Discussion and summary
We have studied whether and how an emergent nematicity affects superconductivity in PFBs on the regular triangular lattice. We have shown with the FLEX+DMFT that nematicity dramatically affects pairing symmetry, and the TC
is significantly enhanced by the lowered point-group symmetry in the electronic structure. This is shown to occur in a non-Fermi liquid regime, which is characterized by blurred Fermi surfaces, momentum-dependent fractional occupations of the band, and a fractional power-law in the self-energy. In the presence of nematic order, the superconducting symmetry changes from an (extended)  -wave to a
-wave to a  -wave, where unlike the conventional nesting-driven case, the pairing interaction is governed by an intricate spin susceptibility structure.
-wave, where unlike the conventional nesting-driven case, the pairing interaction is governed by an intricate spin susceptibility structure.
Future works should include the elaboration of the way in which the non-Fermi liquid property affects the superconductivity, and exploration of the interplay between Pomeranchuk instability and superconductivity in multi-band/orbital systems with flat regions.
Acknowledgments
Sh S acknowledges financial support from the ANR under the Grant ANR-18-CE30-0001-01 (TOPODRIVE) and the European Union Horizon 2020 research and innovation program under Grant Agreement No. 829044 (SCHINES). M K was supported by JSPS KAKENHI Grand Numbers JP20K22342 and JP21K13887. H A thanks CREST (Core Research for Evolutional Science and Technology) 'Topology' project (Grant Number JPMJCR18T4) from Japan Science and Technology Agency, and JSPS KAKENHI Grant JP17H06138.
Data availability statement
The data cannot be made publicly available upon publication because they are not available in a format that is sufficiently accessible or reusable by other researchers. The data that support the findings of this study are available upon reasonable request from the authors. The data that support the findings of this study are available upon request from the authors.
Supplementary data (8.0 MB PDF)