1. INTRODUCTION
In the hierarchical model of galaxy formation, low-mass dwarf-sized galaxies collapse and merge to form the massive galactic structures that we observe today. Minor mergers in the present-day universe continue to influence the properties of stellar halos (Bullock & Johnston 2005) and perhaps the appearance of galactic disks (Gilmore et al. 2002; Abadi et al. 2003; Yoachim & Dalcanton 2005). How this process of minor merging works in detail is not well understood. The Local Group is a prime locale for studying minor merging events. In the Milky Way, three satellites are undergoing tidal disruption and accretion: the Magellanic Stream (Mathewson et al. 1974; Connors et al. 2006), Sagittarius dwarf (Ibata et al. 1994; Majewski et al. 2003; Newberg et al. 2003), and Canis Major dwarf (Martin et al. 2005). The Andromeda spiral galaxy (M31), our nearest large neighbor, also hosts a number of tidally distorted and disrupted satellites. These include the dwarf elliptical galaxy NGC 205 (Kent 1987; Choi et al. 2002; Geha et al. 2006), the compact elliptical galaxy M32 (Kent 1987; Choi et al. 2002), the Giant Southern Stream (Ibata et al. 2001; Font et al. 2006; Fardal et al. 2007), and possibly the satellite galaxy Andromeda VIII (Morrison et al. 2003). In this paper we present a detailed study of the tidal interaction between M31 and the dwarf elliptical galaxy NGC 205.
In addition to being building blocks of larger galaxies, dwarf galaxies are interesting in their own right. Of the various dwarf galaxy types, dwarf elliptical (dE) galaxies are the least understood, and their origin is heavily debated. What is known about dE's is that they are a galaxy population found exclusively in denser regions, accounting for more than 75% of the objects in cluster environments (Binney & Tremaine 1987; Trentham & Tully 2002). They are typically dark matter-poor in their inner regions and predominantly gas-poor. The two general dE formation theories postulate that these galaxies are primordial building blocks or an evolved/transformed population, but neither theory is capable of explaining all the observables. The first theory, based on cold dark matter models, asserts that these are low-mass, primordial building blocks that formed early ( ) in their present locale. If dE's formed by this scenario, we could gain insight into the very first galaxies to form by studying these relics. The second theory postulates that dE's are born as more massive spiral galaxies which are subsequently altered as a result of interactions with other galaxies through tidal effects (Moore et al. 1998; Ricotti & Gnedin 2005). If dE's are transformed spirals, then this transformation is expected to cause an increase in the velocity dispersion and induce some rotation (Moore et al. 1998). However, this scenario is unable to explain the observed distribution of rotation speeds and velocity dispersions among Virgo Cluster dE's. Specifically, it cannot explain the presence of a substantial population of dE's with no detectable rotation and relatively low velocity dispersion (Geha et al. 2002, 2003). To complicate matters further, the faint underlying disks are found in both rotating and nonrotating dE's (Geha et al. 2003; Lisker et al. 2006). It is also possible that the dE's result from some combination of the above two mechanisms. A complete model explaining dE formation is still needed. Local group dE galaxies offer an excellent resource for the exploration of these and other formation scenarios.
) in their present locale. If dE's formed by this scenario, we could gain insight into the very first galaxies to form by studying these relics. The second theory postulates that dE's are born as more massive spiral galaxies which are subsequently altered as a result of interactions with other galaxies through tidal effects (Moore et al. 1998; Ricotti & Gnedin 2005). If dE's are transformed spirals, then this transformation is expected to cause an increase in the velocity dispersion and induce some rotation (Moore et al. 1998). However, this scenario is unable to explain the observed distribution of rotation speeds and velocity dispersions among Virgo Cluster dE's. Specifically, it cannot explain the presence of a substantial population of dE's with no detectable rotation and relatively low velocity dispersion (Geha et al. 2002, 2003). To complicate matters further, the faint underlying disks are found in both rotating and nonrotating dE's (Geha et al. 2003; Lisker et al. 2006). It is also possible that the dE's result from some combination of the above two mechanisms. A complete model explaining dE formation is still needed. Local group dE galaxies offer an excellent resource for the exploration of these and other formation scenarios.
 ) in their present locale. If dE's formed by this scenario, we could gain insight into the very first galaxies to form by studying these relics. The second theory postulates that dE's are born as more massive spiral galaxies which are subsequently altered as a result of interactions with other galaxies through tidal effects (Moore et al. 1998; Ricotti & Gnedin 2005). If dE's are transformed spirals, then this transformation is expected to cause an increase in the velocity dispersion and induce some rotation (Moore et al. 1998). However, this scenario is unable to explain the observed distribution of rotation speeds and velocity dispersions among Virgo Cluster dE's. Specifically, it cannot explain the presence of a substantial population of dE's with no detectable rotation and relatively low velocity dispersion (Geha et al. 2002, 2003). To complicate matters further, the faint underlying disks are found in both rotating and nonrotating dE's (Geha et al. 2003; Lisker et al. 2006). It is also possible that the dE's result from some combination of the above two mechanisms. A complete model explaining dE formation is still needed. Local group dE galaxies offer an excellent resource for the exploration of these and other formation scenarios.
) in their present locale. If dE's formed by this scenario, we could gain insight into the very first galaxies to form by studying these relics. The second theory postulates that dE's are born as more massive spiral galaxies which are subsequently altered as a result of interactions with other galaxies through tidal effects (Moore et al. 1998; Ricotti & Gnedin 2005). If dE's are transformed spirals, then this transformation is expected to cause an increase in the velocity dispersion and induce some rotation (Moore et al. 1998). However, this scenario is unable to explain the observed distribution of rotation speeds and velocity dispersions among Virgo Cluster dE's. Specifically, it cannot explain the presence of a substantial population of dE's with no detectable rotation and relatively low velocity dispersion (Geha et al. 2002, 2003). To complicate matters further, the faint underlying disks are found in both rotating and nonrotating dE's (Geha et al. 2003; Lisker et al. 2006). It is also possible that the dE's result from some combination of the above two mechanisms. A complete model explaining dE formation is still needed. Local group dE galaxies offer an excellent resource for the exploration of these and other formation scenarios.Unlike the Milky Way, which does not host any dE satellites, M31 hosts a total of three: NGC 185, NGC 147, and NGC 205. NGC 185 and NGC 147 lie far enough away from M31 to escape present tidal distortion. NGC 205 lies a projected  from M31 and is our nearest example of a tidally distorted dE galaxy. It is a gas-poor, low-luminosity, early-type galaxy with an exponential surface brightness profile (Choi et al. 2002), defining features of dE galaxies. The little gas and dust in NGC 205 is concentrated within a
from M31 and is our nearest example of a tidally distorted dE galaxy. It is a gas-poor, low-luminosity, early-type galaxy with an exponential surface brightness profile (Choi et al. 2002), defining features of dE galaxies. The little gas and dust in NGC 205 is concentrated within a 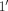 radius, beyond which the satellite is essentially gas and dustfree (Young & Lo 1997; Welch et al. 1998). The current line-of-sight distance estimate between NGC 205 and M31 is about 39 kpc, with M31 residing
radius, beyond which the satellite is essentially gas and dustfree (Young & Lo 1997; Welch et al. 1998). The current line-of-sight distance estimate between NGC 205 and M31 is about 39 kpc, with M31 residing  kpc and NGC 205 at
kpc and NGC 205 at  (McConnachie et al. 2005). Throughout this paper we adopt this distance of 824 kpc to NGC 205. The absolute
(McConnachie et al. 2005). Throughout this paper we adopt this distance of 824 kpc to NGC 205. The absolute 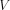 -band magnitude of NGC 205 is
-band magnitude of NGC 205 is 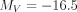 , corresponding to a few percent of M31’s luminosity (Hodge 1992; Choi et al. 2002). Bender et al. (1991) reports a mass-to-light ratio for NGC 205 of
, corresponding to a few percent of M31’s luminosity (Hodge 1992; Choi et al. 2002). Bender et al. (1991) reports a mass-to-light ratio for NGC 205 of  . This value is consistent with dynamical models of dE's that suggest a global mass-to-light ratio of
. This value is consistent with dynamical models of dE's that suggest a global mass-to-light ratio of  and is indicative of an intermediate-to-old stellar population containing little to no dark matter within an effective radius (Geha et al. 2002). De Rijcke et al. (2006) finds a
and is indicative of an intermediate-to-old stellar population containing little to no dark matter within an effective radius (Geha et al. 2002). De Rijcke et al. (2006) finds a  -band mass-to-light ratio within
-band mass-to-light ratio within  (1.04 kpc) of
(1.04 kpc) of  . This supports the conclusion that there is little dark matter contained within the inner regions of NGC 205. It is not known whether NGC 205 resides in an extended dark matter halo.
. This supports the conclusion that there is little dark matter contained within the inner regions of NGC 205. It is not known whether NGC 205 resides in an extended dark matter halo.
 from M31 and is our nearest example of a tidally distorted dE galaxy. It is a gas-poor, low-luminosity, early-type galaxy with an exponential surface brightness profile (Choi et al. 2002), defining features of dE galaxies. The little gas and dust in NGC 205 is concentrated within a
from M31 and is our nearest example of a tidally distorted dE galaxy. It is a gas-poor, low-luminosity, early-type galaxy with an exponential surface brightness profile (Choi et al. 2002), defining features of dE galaxies. The little gas and dust in NGC 205 is concentrated within a 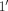 radius, beyond which the satellite is essentially gas and dustfree (Young & Lo 1997; Welch et al. 1998). The current line-of-sight distance estimate between NGC 205 and M31 is about 39 kpc, with M31 residing
radius, beyond which the satellite is essentially gas and dustfree (Young & Lo 1997; Welch et al. 1998). The current line-of-sight distance estimate between NGC 205 and M31 is about 39 kpc, with M31 residing  kpc and NGC 205 at
kpc and NGC 205 at  (McConnachie et al. 2005). Throughout this paper we adopt this distance of 824 kpc to NGC 205. The absolute
(McConnachie et al. 2005). Throughout this paper we adopt this distance of 824 kpc to NGC 205. The absolute 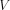 -band magnitude of NGC 205 is
-band magnitude of NGC 205 is 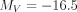 , corresponding to a few percent of M31’s luminosity (Hodge 1992; Choi et al. 2002). Bender et al. (1991) reports a mass-to-light ratio for NGC 205 of
, corresponding to a few percent of M31’s luminosity (Hodge 1992; Choi et al. 2002). Bender et al. (1991) reports a mass-to-light ratio for NGC 205 of  . This value is consistent with dynamical models of dE's that suggest a global mass-to-light ratio of
. This value is consistent with dynamical models of dE's that suggest a global mass-to-light ratio of  and is indicative of an intermediate-to-old stellar population containing little to no dark matter within an effective radius (Geha et al. 2002). De Rijcke et al. (2006) finds a
and is indicative of an intermediate-to-old stellar population containing little to no dark matter within an effective radius (Geha et al. 2002). De Rijcke et al. (2006) finds a  -band mass-to-light ratio within
-band mass-to-light ratio within  (1.04 kpc) of
(1.04 kpc) of  . This supports the conclusion that there is little dark matter contained within the inner regions of NGC 205. It is not known whether NGC 205 resides in an extended dark matter halo.
. This supports the conclusion that there is little dark matter contained within the inner regions of NGC 205. It is not known whether NGC 205 resides in an extended dark matter halo.There is strong evidence that NGC 205 is tidally distorted by M31. Choi et al. (2002) measure twisting of elliptical isophotes, along with a subtle break in the surface brightness profile, providing confirmation of tidal distortion found in earlier studies. A radial velocity survey of red giant branch (RGB) stars in NGC 205 by Geha et al. (2006) notes an abrupt turnover in the semimajor axis velocity profile coincident with the tidal distortion reported by Choi et al. (2002). McConnachie et al. (2004) postulates that the ∼1° (15 kpc) long, arclike feature seen in the northwest quadrant of M31 could be a stellar stream associated with NGC 205. Demers et al. (2003), in their study of C stars in the system, report possible evidence of tidal debris to the west of NGC 205 beyond its tidal radius. Within an effective radius, NGC 205 appears to be undistorted. However, beyond this radius, there is strong evidence for distortion.
In this paper we investigate the large parameter space defining the orbit and history of NGC 205 using a restricted  -body code and a genetic algorithm for optimization. Modeling satellite/parent galaxy interactions is extremely difficult when there are no gaseous or stellar streams to directly constrain the path of the satellite’s orbit. In the absence of tidal trails, as is the case for NGC 205, there is a limited set of observable quantities that can be used as constraints: stellar radial velocities, projected sky position, and constraints on the line-of-sight distance. To complicate matters further, large parameter spaces with inherent degeneracies typically define galaxy encounters. Hence, in weakly distorted systems it is difficult to find unique, qualified fits to the observables. For this reason, few optimized
-body code and a genetic algorithm for optimization. Modeling satellite/parent galaxy interactions is extremely difficult when there are no gaseous or stellar streams to directly constrain the path of the satellite’s orbit. In the absence of tidal trails, as is the case for NGC 205, there is a limited set of observable quantities that can be used as constraints: stellar radial velocities, projected sky position, and constraints on the line-of-sight distance. To complicate matters further, large parameter spaces with inherent degeneracies typically define galaxy encounters. Hence, in weakly distorted systems it is difficult to find unique, qualified fits to the observables. For this reason, few optimized  -body studies of mildly distorted galaxies have been carried out. In our simulations we employ a genetic algorithm to achieve optimization (Holland 1975; Goldberg 1989). This particular optimization technique has been successfully used in similar studies of more heavily distorted dwarf galaxies (Theis & Kohle 2001; Theis et al. 2001). Using a restricted
-body studies of mildly distorted galaxies have been carried out. In our simulations we employ a genetic algorithm to achieve optimization (Holland 1975; Goldberg 1989). This particular optimization technique has been successfully used in similar studies of more heavily distorted dwarf galaxies (Theis & Kohle 2001; Theis et al. 2001). Using a restricted  -body code, we explore three distinct, initially stable configurations of 1000 test particles representing NGC 205: a (cold) rotating disk without velocity dispersion, a (warm) rotating disk with velocity dispersion, and a (hot) spheroid supported completely by randomly distributed, isotropic velocities. Detailed photometric and kinematic observations enable this unique study by providing strong constraints on the simulated system (Choi et al. 2002; Geha et al. 2006).
-body code, we explore three distinct, initially stable configurations of 1000 test particles representing NGC 205: a (cold) rotating disk without velocity dispersion, a (warm) rotating disk with velocity dispersion, and a (hot) spheroid supported completely by randomly distributed, isotropic velocities. Detailed photometric and kinematic observations enable this unique study by providing strong constraints on the simulated system (Choi et al. 2002; Geha et al. 2006).
 -body code and a genetic algorithm for optimization. Modeling satellite/parent galaxy interactions is extremely difficult when there are no gaseous or stellar streams to directly constrain the path of the satellite’s orbit. In the absence of tidal trails, as is the case for NGC 205, there is a limited set of observable quantities that can be used as constraints: stellar radial velocities, projected sky position, and constraints on the line-of-sight distance. To complicate matters further, large parameter spaces with inherent degeneracies typically define galaxy encounters. Hence, in weakly distorted systems it is difficult to find unique, qualified fits to the observables. For this reason, few optimized
-body code and a genetic algorithm for optimization. Modeling satellite/parent galaxy interactions is extremely difficult when there are no gaseous or stellar streams to directly constrain the path of the satellite’s orbit. In the absence of tidal trails, as is the case for NGC 205, there is a limited set of observable quantities that can be used as constraints: stellar radial velocities, projected sky position, and constraints on the line-of-sight distance. To complicate matters further, large parameter spaces with inherent degeneracies typically define galaxy encounters. Hence, in weakly distorted systems it is difficult to find unique, qualified fits to the observables. For this reason, few optimized  -body studies of mildly distorted galaxies have been carried out. In our simulations we employ a genetic algorithm to achieve optimization (Holland 1975; Goldberg 1989). This particular optimization technique has been successfully used in similar studies of more heavily distorted dwarf galaxies (Theis & Kohle 2001; Theis et al. 2001). Using a restricted
-body studies of mildly distorted galaxies have been carried out. In our simulations we employ a genetic algorithm to achieve optimization (Holland 1975; Goldberg 1989). This particular optimization technique has been successfully used in similar studies of more heavily distorted dwarf galaxies (Theis & Kohle 2001; Theis et al. 2001). Using a restricted  -body code, we explore three distinct, initially stable configurations of 1000 test particles representing NGC 205: a (cold) rotating disk without velocity dispersion, a (warm) rotating disk with velocity dispersion, and a (hot) spheroid supported completely by randomly distributed, isotropic velocities. Detailed photometric and kinematic observations enable this unique study by providing strong constraints on the simulated system (Choi et al. 2002; Geha et al. 2006).
-body code, we explore three distinct, initially stable configurations of 1000 test particles representing NGC 205: a (cold) rotating disk without velocity dispersion, a (warm) rotating disk with velocity dispersion, and a (hot) spheroid supported completely by randomly distributed, isotropic velocities. Detailed photometric and kinematic observations enable this unique study by providing strong constraints on the simulated system (Choi et al. 2002; Geha et al. 2006).The paper is laid out as follows: In § 2 we discuss the photometric and kinematic observational data used to constrain our system. In § 3 we give the details of the parameters, galaxy models, and methods used in our numerical simulations. In § 4 we present the results of the numerical simulations. In § 5 we discuss the implications of our results. Finally, in § 6 we discuss the observational and computational improvements that could be applied to this study.
2. OBSERVATIONAL DATA
Our study of NGC 205 is unique because we enforce both photometric and kinematic constraints on our simulated system. Although this cannot ensure that we converge on the correct orbital history of NGC 205, it does remove a significant amount of the degeneracy inherent in studies that only use photometric constraints. Strong evidence of tidal distortion is seen both in the photometry and the kinematics of NGC 205 at a major-axis distance of  -
- (1.1-1.2 kpc) (Choi et al. 2002; Geha et al. 2006). A discussion of the surface photometry by Choi et al. (2002) is included in § 2.1, and a discussion of the internal kinematics by Geha et al. (2006) is included in § 2.2. These observations are summarized in Figure 1.
(1.1-1.2 kpc) (Choi et al. 2002; Geha et al. 2006). A discussion of the surface photometry by Choi et al. (2002) is included in § 2.1, and a discussion of the internal kinematics by Geha et al. (2006) is included in § 2.2. These observations are summarized in Figure 1.
 -
- (1.1-1.2 kpc) (Choi et al. 2002; Geha et al. 2006). A discussion of the surface photometry by Choi et al. (2002) is included in § 2.1, and a discussion of the internal kinematics by Geha et al. (2006) is included in § 2.2. These observations are summarized in Figure 1.
(1.1-1.2 kpc) (Choi et al. 2002; Geha et al. 2006). A discussion of the surface photometry by Choi et al. (2002) is included in § 2.1, and a discussion of the internal kinematics by Geha et al. (2006) is included in § 2.2. These observations are summarized in Figure 1.Figure 1.
Observed properties of the M31-NGC 205 system. The colored dots represent NGC 205’s semimajor axis velocity relative to its systemic velocity of –246 km s–1 as measured by Geha et al. (2006). Note the turnover in velocity at the semimajor axis distance of ∼  (1.08 kpc) is coincident with the isophotal twisting radius measured by Choi et al. (2002). The labels A-F are defined as follows: A=center of NGC 205, B=radius at which the use Choi et al. (2002) data begins (internal to this we use an exponential surface brightness profile), C=radius at which isophotal twisting and radial velocity turnover occurs, D=radius at which the use of Choi et al. (2002) data ends (external to this we use an exponential law), E=center of M31, and F=center of M32. The projected distance between NGC 205 and M31 (points A and E) is
(1.08 kpc) is coincident with the isophotal twisting radius measured by Choi et al. (2002). The labels A-F are defined as follows: A=center of NGC 205, B=radius at which the use Choi et al. (2002) data begins (internal to this we use an exponential surface brightness profile), C=radius at which isophotal twisting and radial velocity turnover occurs, D=radius at which the use of Choi et al. (2002) data ends (external to this we use an exponential law), E=center of M31, and F=center of M32. The projected distance between NGC 205 and M31 (points A and E) is  , or 8.8 kpc if we take NGC 205 to be at a distance of 824 kpc (McConnachie et al. 2005). The photometric contours B, C, and D lie at semimajor axis distances of
, or 8.8 kpc if we take NGC 205 to be at a distance of 824 kpc (McConnachie et al. 2005). The photometric contours B, C, and D lie at semimajor axis distances of  (0.40 kpc),
(0.40 kpc),  (1.04 kpc), and
(1.04 kpc), and  (2.68 kpc), respectively. (Image courtesy of Phil Choi.)
(2.68 kpc), respectively. (Image courtesy of Phil Choi.) |
2.1. Photometric Data
The surface photometry of NGC 205 in the  and
and  bands was obtained by Choi et al. (2002) using the Kitt Peak National Observatory 0.9/0.6 m Burrell Schmidt telescope. Due to the incompleteness of the
bands was obtained by Choi et al. (2002) using the Kitt Peak National Observatory 0.9/0.6 m Burrell Schmidt telescope. Due to the incompleteness of the  -band coverage, Choi et al. (2002) employed the
-band coverage, Choi et al. (2002) employed the  -band data and IRAF’s ellipse task to determine the surface brightness contours of NGC 205 out to a limiting magnitude of
-band data and IRAF’s ellipse task to determine the surface brightness contours of NGC 205 out to a limiting magnitude of  mag arcsec–2, coinciding with a semimajor axis distance of
mag arcsec–2, coinciding with a semimajor axis distance of  (2.88 kpc).
(2.88 kpc).
 and
and  bands was obtained by Choi et al. (2002) using the Kitt Peak National Observatory 0.9/0.6 m Burrell Schmidt telescope. Due to the incompleteness of the
bands was obtained by Choi et al. (2002) using the Kitt Peak National Observatory 0.9/0.6 m Burrell Schmidt telescope. Due to the incompleteness of the  -band coverage, Choi et al. (2002) employed the
-band coverage, Choi et al. (2002) employed the  -band data and IRAF’s ellipse task to determine the surface brightness contours of NGC 205 out to a limiting magnitude of
-band data and IRAF’s ellipse task to determine the surface brightness contours of NGC 205 out to a limiting magnitude of  mag arcsec–2, coinciding with a semimajor axis distance of
mag arcsec–2, coinciding with a semimajor axis distance of  (2.88 kpc).
(2.88 kpc).Choi et al. (2002) report that NGC 205 is well fit by two different exponential profiles at various semimajor axis radii. One profile, covering a semimajor axis range of  (
( ), has a disk scale length of
), has a disk scale length of  (0.60 kpc), where
(0.60 kpc), where  is defined as the radius at which the intensity has decreased by a factor of
is defined as the radius at which the intensity has decreased by a factor of  ; the other profile, covering a semimajor axis range of
; the other profile, covering a semimajor axis range of  (
( kpc) and
kpc) and  (2.00 kpc), has a disk scale length of
(2.00 kpc), has a disk scale length of  (0.68 kpc). Also reported was a “subtle downward break” at
(0.68 kpc). Also reported was a “subtle downward break” at  (1.20 kpc), which correlates nicely with the semimajor axis distance of
(1.20 kpc), which correlates nicely with the semimajor axis distance of  (1.04 kpc) that marks the location where the isophotal position angle and ellipticity stop increasing and begin decreasing, leading to an
(1.04 kpc) that marks the location where the isophotal position angle and ellipticity stop increasing and begin decreasing, leading to an  -shaped semimajor axis profile for NGC 205. The location of this isophotal twisting matches the radial velocity turnover radius of
-shaped semimajor axis profile for NGC 205. The location of this isophotal twisting matches the radial velocity turnover radius of  (
( or 1.08 kpc) observed by Geha et al. (2006), thus supporting the conclusion that NGC 205 is interacting tidally with M31.
or 1.08 kpc) observed by Geha et al. (2006), thus supporting the conclusion that NGC 205 is interacting tidally with M31.
 (
( ), has a disk scale length of
), has a disk scale length of  (0.60 kpc), where
(0.60 kpc), where  is defined as the radius at which the intensity has decreased by a factor of
is defined as the radius at which the intensity has decreased by a factor of  ; the other profile, covering a semimajor axis range of
; the other profile, covering a semimajor axis range of  (
( kpc) and
kpc) and  (2.00 kpc), has a disk scale length of
(2.00 kpc), has a disk scale length of  (0.68 kpc). Also reported was a “subtle downward break” at
(0.68 kpc). Also reported was a “subtle downward break” at  (1.20 kpc), which correlates nicely with the semimajor axis distance of
(1.20 kpc), which correlates nicely with the semimajor axis distance of  (1.04 kpc) that marks the location where the isophotal position angle and ellipticity stop increasing and begin decreasing, leading to an
(1.04 kpc) that marks the location where the isophotal position angle and ellipticity stop increasing and begin decreasing, leading to an  -shaped semimajor axis profile for NGC 205. The location of this isophotal twisting matches the radial velocity turnover radius of
-shaped semimajor axis profile for NGC 205. The location of this isophotal twisting matches the radial velocity turnover radius of  (
( or 1.08 kpc) observed by Geha et al. (2006), thus supporting the conclusion that NGC 205 is interacting tidally with M31.
or 1.08 kpc) observed by Geha et al. (2006), thus supporting the conclusion that NGC 205 is interacting tidally with M31.We perform our own exponential fit of the form
 to the intermediate parts of Choi et al. (2002) intensity profile in order to estimate the disk scale length of the galaxy if it were tidally undistorted. We exclude the nucleus (interior to
to the intermediate parts of Choi et al. (2002) intensity profile in order to estimate the disk scale length of the galaxy if it were tidally undistorted. We exclude the nucleus (interior to  , or 0.40 kpc), where the data follows neither an exponential law [
, or 0.40 kpc), where the data follows neither an exponential law [ ] nor a de Vaucouleurs law [
] nor a de Vaucouleurs law [ ], and the outer regions (exterior to
], and the outer regions (exterior to  , or 2.68 kpc), where the surface brightness and sky become comparable. We measure a disk scale length of
, or 2.68 kpc), where the surface brightness and sky become comparable. We measure a disk scale length of  (0.59 kpc) and a central (nucleus-free) surface brightness of
(0.59 kpc) and a central (nucleus-free) surface brightness of  mag arcsec–2. These results are used as a basis for generating an undistorted NGC 205 and modeling the inner and outer regions of NGC 205 in its final, integrated state. Hence, we are able to remove the nucleus from NGC 205 by extrapolating the exponential surface brightness profile from the intermediate region (
mag arcsec–2. These results are used as a basis for generating an undistorted NGC 205 and modeling the inner and outer regions of NGC 205 in its final, integrated state. Hence, we are able to remove the nucleus from NGC 205 by extrapolating the exponential surface brightness profile from the intermediate region ( -
- ) to the central region (
) to the central region ( -
- ). The surface brightness profile of Choi et al. (2002) our exponential surface brightness fit, and the data used in our simulations are summarized in Figure 2.
). The surface brightness profile of Choi et al. (2002) our exponential surface brightness fit, and the data used in our simulations are summarized in Figure 2.

 , or 0.40 kpc), where the data follows neither an exponential law [
, or 0.40 kpc), where the data follows neither an exponential law [ ] nor a de Vaucouleurs law [
] nor a de Vaucouleurs law [ ], and the outer regions (exterior to
], and the outer regions (exterior to  , or 2.68 kpc), where the surface brightness and sky become comparable. We measure a disk scale length of
, or 2.68 kpc), where the surface brightness and sky become comparable. We measure a disk scale length of  (0.59 kpc) and a central (nucleus-free) surface brightness of
(0.59 kpc) and a central (nucleus-free) surface brightness of  mag arcsec–2. These results are used as a basis for generating an undistorted NGC 205 and modeling the inner and outer regions of NGC 205 in its final, integrated state. Hence, we are able to remove the nucleus from NGC 205 by extrapolating the exponential surface brightness profile from the intermediate region (
mag arcsec–2. These results are used as a basis for generating an undistorted NGC 205 and modeling the inner and outer regions of NGC 205 in its final, integrated state. Hence, we are able to remove the nucleus from NGC 205 by extrapolating the exponential surface brightness profile from the intermediate region ( -
- ) to the central region (
) to the central region ( -
- ). The surface brightness profile of Choi et al. (2002) our exponential surface brightness fit, and the data used in our simulations are summarized in Figure 2.
). The surface brightness profile of Choi et al. (2002) our exponential surface brightness fit, and the data used in our simulations are summarized in Figure 2.Figure 2.
Surface brightness profile of NGC 205 in magnitudes per square arcsecond vs. semimajor axis distance. The solid line illustrates the brightness profile in B magnitudes measured by Choi et al. (2002) the dashed line represents the exponential fit performed using the intermediate regions of Choi et al. (2002) data (  to
to  ), and the blue line defines the data used in our simulations. Note that in the intermediate regions (
), and the blue line defines the data used in our simulations. Note that in the intermediate regions ( to
to  ) we use Choi et al. (2002) measurements, and in the inner (>
) we use Choi et al. (2002) measurements, and in the inner (> ) and outer (<
) and outer (< ) regions we use our exponential fit. This effectively removes the nucleus from the inner region and models the data in the outer region where the surface brightness of the galaxy and the sky brightness become comparable.
) regions we use our exponential fit. This effectively removes the nucleus from the inner region and models the data in the outer region where the surface brightness of the galaxy and the sky brightness become comparable. |
2.2. Kinematic Data
A recent kinematic study of NGC 205 by Geha et al. (2006) using the Keck DEIMOS multislit spectrograph resulted in the collection of radial velocities for 725 RGB stars. The stellar spectra were obtained using four masks, each covering an area of ≈ (
( kpc). Two of these masks were centered on NGC 205 along the major axis, while the other two were placed off center along the tidally distorted major axis, one in southeast (SE) and one in northwest (NW). These observations extend out to
kpc). Two of these masks were centered on NGC 205 along the major axis, while the other two were placed off center along the tidally distorted major axis, one in southeast (SE) and one in northwest (NW). These observations extend out to  (4.79 kpc), well beyond the tidal radius of NGC 205, and are spatially well distributed. The contamination by M31 field stars is estimated to be only a few percent.
(4.79 kpc), well beyond the tidal radius of NGC 205, and are spatially well distributed. The contamination by M31 field stars is estimated to be only a few percent.
 (
( kpc). Two of these masks were centered on NGC 205 along the major axis, while the other two were placed off center along the tidally distorted major axis, one in southeast (SE) and one in northwest (NW). These observations extend out to
kpc). Two of these masks were centered on NGC 205 along the major axis, while the other two were placed off center along the tidally distorted major axis, one in southeast (SE) and one in northwest (NW). These observations extend out to  (4.79 kpc), well beyond the tidal radius of NGC 205, and are spatially well distributed. The contamination by M31 field stars is estimated to be only a few percent.
(4.79 kpc), well beyond the tidal radius of NGC 205, and are spatially well distributed. The contamination by M31 field stars is estimated to be only a few percent.The systemic velocity of NGC 205, as measured by Geha et al. (2006), is – km s–1, while the systemic velocity of M31 is –
km s–1, while the systemic velocity of M31 is – km s–1 (de Vaucouleurs 1991). This results in a velocity for NGC 205 of
km s–1 (de Vaucouleurs 1991). This results in a velocity for NGC 205 of  km s–1 relative to M31. The velocities of the northwest tail of the satellite are more positive, while the southeast tail, which is closer to M31, are more negative as compared to NGC 205’s systemic velocity. The opposite is true in the central regions (<
km s–1 relative to M31. The velocities of the northwest tail of the satellite are more positive, while the southeast tail, which is closer to M31, are more negative as compared to NGC 205’s systemic velocity. The opposite is true in the central regions (< ).
).
 km s–1, while the systemic velocity of M31 is –
km s–1, while the systemic velocity of M31 is – km s–1 (de Vaucouleurs 1991). This results in a velocity for NGC 205 of
km s–1 (de Vaucouleurs 1991). This results in a velocity for NGC 205 of  km s–1 relative to M31. The velocities of the northwest tail of the satellite are more positive, while the southeast tail, which is closer to M31, are more negative as compared to NGC 205’s systemic velocity. The opposite is true in the central regions (<
km s–1 relative to M31. The velocities of the northwest tail of the satellite are more positive, while the southeast tail, which is closer to M31, are more negative as compared to NGC 205’s systemic velocity. The opposite is true in the central regions (< ).
).Geha et al. (2006) maps the semimajor axis velocity profile of NGC 205 by binning the RGB stars perpendicular to the  -shaped major axis into ≥
-shaped major axis into ≥ (0.24 kpc) radial bins. The velocity of each bin, containing a minimum of 25 stars, is determined by fitting a Gaussian profile to its stars. The resulting fit is plotted in Figure 3. The major-axis rotation curve of NGC 205 shows a distinct velocity turnover (with
(0.24 kpc) radial bins. The velocity of each bin, containing a minimum of 25 stars, is determined by fitting a Gaussian profile to its stars. The resulting fit is plotted in Figure 3. The major-axis rotation curve of NGC 205 shows a distinct velocity turnover (with  km s–1) at
km s–1) at 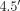 , which is coincident with the estimated tidal radius (∼
, which is coincident with the estimated tidal radius (∼ ) and onset of isophotal twisting (see § 2.1). Geha et al. (2006) suggests that this feature is due to gravitational interaction between NGC 205 and M31, and infers that NGC 205 is on a prograde encounter. If correct, over half of Geha et al.'s (2006) evenly sampled RGB stars lie outside NGC 205’s tidal radius, meaning they have been tidally stripped from the satellite and are no longer bound. The ratio of the maximum rotational velocity to the average velocity dispersion of NGC 205 (assuming an average ellipticity of
) and onset of isophotal twisting (see § 2.1). Geha et al. (2006) suggests that this feature is due to gravitational interaction between NGC 205 and M31, and infers that NGC 205 is on a prograde encounter. If correct, over half of Geha et al.'s (2006) evenly sampled RGB stars lie outside NGC 205’s tidal radius, meaning they have been tidally stripped from the satellite and are no longer bound. The ratio of the maximum rotational velocity to the average velocity dispersion of NGC 205 (assuming an average ellipticity of 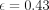 ) is
) is 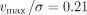 (Geha et al. 2006). Given that the expected ratio for an isotropic, oblate, rotational-flattened galaxy with
(Geha et al. 2006). Given that the expected ratio for an isotropic, oblate, rotational-flattened galaxy with  is
is  and that similar anisotropic Virgo dE’s on average have
and that similar anisotropic Virgo dE’s on average have  , NGC 205 falls somewhere between a rotational-supported body and an anisotropic object (Binney & Tremaine 1987; Geha et al. 2006).
, NGC 205 falls somewhere between a rotational-supported body and an anisotropic object (Binney & Tremaine 1987; Geha et al. 2006).
 -shaped major axis into ≥
-shaped major axis into ≥ (0.24 kpc) radial bins. The velocity of each bin, containing a minimum of 25 stars, is determined by fitting a Gaussian profile to its stars. The resulting fit is plotted in Figure 3. The major-axis rotation curve of NGC 205 shows a distinct velocity turnover (with
(0.24 kpc) radial bins. The velocity of each bin, containing a minimum of 25 stars, is determined by fitting a Gaussian profile to its stars. The resulting fit is plotted in Figure 3. The major-axis rotation curve of NGC 205 shows a distinct velocity turnover (with  km s–1) at
km s–1) at 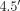 , which is coincident with the estimated tidal radius (∼
, which is coincident with the estimated tidal radius (∼ ) and onset of isophotal twisting (see § 2.1). Geha et al. (2006) suggests that this feature is due to gravitational interaction between NGC 205 and M31, and infers that NGC 205 is on a prograde encounter. If correct, over half of Geha et al.'s (2006) evenly sampled RGB stars lie outside NGC 205’s tidal radius, meaning they have been tidally stripped from the satellite and are no longer bound. The ratio of the maximum rotational velocity to the average velocity dispersion of NGC 205 (assuming an average ellipticity of
) and onset of isophotal twisting (see § 2.1). Geha et al. (2006) suggests that this feature is due to gravitational interaction between NGC 205 and M31, and infers that NGC 205 is on a prograde encounter. If correct, over half of Geha et al.'s (2006) evenly sampled RGB stars lie outside NGC 205’s tidal radius, meaning they have been tidally stripped from the satellite and are no longer bound. The ratio of the maximum rotational velocity to the average velocity dispersion of NGC 205 (assuming an average ellipticity of 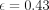 ) is
) is 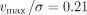 (Geha et al. 2006). Given that the expected ratio for an isotropic, oblate, rotational-flattened galaxy with
(Geha et al. 2006). Given that the expected ratio for an isotropic, oblate, rotational-flattened galaxy with  is
is  and that similar anisotropic Virgo dE’s on average have
and that similar anisotropic Virgo dE’s on average have  , NGC 205 falls somewhere between a rotational-supported body and an anisotropic object (Binney & Tremaine 1987; Geha et al. 2006).
, NGC 205 falls somewhere between a rotational-supported body and an anisotropic object (Binney & Tremaine 1987; Geha et al. 2006).Figure 3.
NGC 205’s semimajor axis radial velocity (relative to M31) and dispersion profile as reported by Geha et al. (2006). (a) The black dots represent the combined velocity measurements of RGB stars. At distances of ∼  (1.08 kpc) from the center of NGC 205 tidal distortion becomes evident. (b) The slope interior to the distortion of NGC 205. The ranges used to constrain our simulations are illustrated in the insert and correspond to a lower limit of –0.08 km s–1 arcsec–1 and an upper limit slope of 0.0 km s–1 arcsec–1 (or –20 and 0 km s–1 kpc–1, respectively, when NGC 205 lies at a distance of 824 kpc). (c) The velocity dispersion of NGC 205 along the semimajor axis.
(1.08 kpc) from the center of NGC 205 tidal distortion becomes evident. (b) The slope interior to the distortion of NGC 205. The ranges used to constrain our simulations are illustrated in the insert and correspond to a lower limit of –0.08 km s–1 arcsec–1 and an upper limit slope of 0.0 km s–1 arcsec–1 (or –20 and 0 km s–1 kpc–1, respectively, when NGC 205 lies at a distance of 824 kpc). (c) The velocity dispersion of NGC 205 along the semimajor axis. |
We perform a linear fit to the interior regions (< ) of NGC 205 where significant tidal distortion has not yet occurred. Using Geha et al. (2006) error bars for each velocity measurement, we determine a maximum and minimum slope for the satellite’s central velocity profile of 0.0 and –0.08 km s–1 arcsec–1, respectively. This significance level corresponds to 1.83 σ and is plotted in Figure 3. We use both this subset and the full data set to constrain the motion of test particles in our numerical simulations (see §§ 3.6.2 and 3.6.3).
) of NGC 205 where significant tidal distortion has not yet occurred. Using Geha et al. (2006) error bars for each velocity measurement, we determine a maximum and minimum slope for the satellite’s central velocity profile of 0.0 and –0.08 km s–1 arcsec–1, respectively. This significance level corresponds to 1.83 σ and is plotted in Figure 3. We use both this subset and the full data set to constrain the motion of test particles in our numerical simulations (see §§ 3.6.2 and 3.6.3).
 ) of NGC 205 where significant tidal distortion has not yet occurred. Using Geha et al. (2006) error bars for each velocity measurement, we determine a maximum and minimum slope for the satellite’s central velocity profile of 0.0 and –0.08 km s–1 arcsec–1, respectively. This significance level corresponds to 1.83 σ and is plotted in Figure 3. We use both this subset and the full data set to constrain the motion of test particles in our numerical simulations (see §§ 3.6.2 and 3.6.3).
) of NGC 205 where significant tidal distortion has not yet occurred. Using Geha et al. (2006) error bars for each velocity measurement, we determine a maximum and minimum slope for the satellite’s central velocity profile of 0.0 and –0.08 km s–1 arcsec–1, respectively. This significance level corresponds to 1.83 σ and is plotted in Figure 3. We use both this subset and the full data set to constrain the motion of test particles in our numerical simulations (see §§ 3.6.2 and 3.6.3).3. NUMERICAL SIMULATIONS
The previous section discusses the photometric and kinematic observations of NGC 205. In order to reproduce the observed features of NGC 205, we trace it’s center of mass back half an orbit, set up an initial configuration of test particles (to represent the undistorted NGC 205), and allow it to interact under the influence of both NGC 205’s and M31’s potential. The final, integrated galaxy is then compared to photometric and kinematic observations. Strict upper and lower limits are placed on the variable parameters and a genetic algorithm is employed to effectively search our parameter space. In the following sections we discuss the explorable parameters of the system (§ 3.1), the potentials of both galaxies (§ 3.2), the initial configurations of NGC 205’s test particles (§ 3.3), the integration scheme (§ 3.4), the genetic algorithm used to improve on the initial guesses (§ 3.5), and, finally, our method of comparing the integrated system to observations (§ 3.6). The goal of these simulations is to determine the orbital parameters of NGC 205.
For our simulations, the units are chosen such that the distance unit is  (or 10 kpc if we assume NGC 205 lies at a distance of 824 kpc), the velocity unit is 280 km s–1, and
(or 10 kpc if we assume NGC 205 lies at a distance of 824 kpc), the velocity unit is 280 km s–1, and  . This roughly results in a mass unit of
. This roughly results in a mass unit of 
 and a time unit of 35 Myr.
and a time unit of 35 Myr.
 (or 10 kpc if we assume NGC 205 lies at a distance of 824 kpc), the velocity unit is 280 km s–1, and
(or 10 kpc if we assume NGC 205 lies at a distance of 824 kpc), the velocity unit is 280 km s–1, and  . This roughly results in a mass unit of
. This roughly results in a mass unit of 
 and a time unit of 35 Myr.
and a time unit of 35 Myr.3.1. System Parameters and Constraints
There are a total of 10 free parameters in our numerical simulation. Six of these parameters define the initial conditions of the undistorted NGC 205 system, while the other four define the final conditions of the present-day observed system. The six initial condition parameters are the mass of NGC 205 (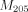 ), the disk scale length (
), the disk scale length ( ), the relative orientation (in
), the relative orientation (in  ,
,  ) of NGC 205’s initial, undistorted disk, whether NGC 205 is on a prograde or retrograde orbit about M31 (
) of NGC 205’s initial, undistorted disk, whether NGC 205 is on a prograde or retrograde orbit about M31 ( ), and the Hernquist (1990) scale length (the radius at which a quarter mass is enclosed) of NGC 205’s potential (
), and the Hernquist (1990) scale length (the radius at which a quarter mass is enclosed) of NGC 205’s potential ( ). The four final constraints are the three-component final velocity vector of NGC 205’s center of mass relative to M31’s center of mass (
). The four final constraints are the three-component final velocity vector of NGC 205’s center of mass relative to M31’s center of mass ( ), and the line-of-sight distance between NGC 205 and M31 (
), and the line-of-sight distance between NGC 205 and M31 ( ). A detailed discussion of the upper and lower limits placed on each of these parameters is motivated and discussed in detail below. The parameters are discretized into 256 steps within their given constraints, with the sole exception of the prograde/retrograde parameter,
). A detailed discussion of the upper and lower limits placed on each of these parameters is motivated and discussed in detail below. The parameters are discretized into 256 steps within their given constraints, with the sole exception of the prograde/retrograde parameter,  , which can take on a value of either 0 or 1. This number of steps is chosen such that the genetic algorithm can thoroughly explore our defined parameter space, while limiting the time needed to perform the simulations. These given parameter values define approximately 1022
possible orbits. In the continuous real world, there are an infinite number of orbits. A summary of the constraints is given in Table 1.
, which can take on a value of either 0 or 1. This number of steps is chosen such that the genetic algorithm can thoroughly explore our defined parameter space, while limiting the time needed to perform the simulations. These given parameter values define approximately 1022
possible orbits. In the continuous real world, there are an infinite number of orbits. A summary of the constraints is given in Table 1.
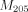 ), the disk scale length (
), the disk scale length ( ), the relative orientation (in
), the relative orientation (in  ,
,  ) of NGC 205’s initial, undistorted disk, whether NGC 205 is on a prograde or retrograde orbit about M31 (
) of NGC 205’s initial, undistorted disk, whether NGC 205 is on a prograde or retrograde orbit about M31 ( ), and the Hernquist (1990) scale length (the radius at which a quarter mass is enclosed) of NGC 205’s potential (
), and the Hernquist (1990) scale length (the radius at which a quarter mass is enclosed) of NGC 205’s potential ( ). The four final constraints are the three-component final velocity vector of NGC 205’s center of mass relative to M31’s center of mass (
). The four final constraints are the three-component final velocity vector of NGC 205’s center of mass relative to M31’s center of mass ( ), and the line-of-sight distance between NGC 205 and M31 (
), and the line-of-sight distance between NGC 205 and M31 ( ). A detailed discussion of the upper and lower limits placed on each of these parameters is motivated and discussed in detail below. The parameters are discretized into 256 steps within their given constraints, with the sole exception of the prograde/retrograde parameter,
). A detailed discussion of the upper and lower limits placed on each of these parameters is motivated and discussed in detail below. The parameters are discretized into 256 steps within their given constraints, with the sole exception of the prograde/retrograde parameter,  , which can take on a value of either 0 or 1. This number of steps is chosen such that the genetic algorithm can thoroughly explore our defined parameter space, while limiting the time needed to perform the simulations. These given parameter values define approximately 1022
possible orbits. In the continuous real world, there are an infinite number of orbits. A summary of the constraints is given in Table 1.
, which can take on a value of either 0 or 1. This number of steps is chosen such that the genetic algorithm can thoroughly explore our defined parameter space, while limiting the time needed to perform the simulations. These given parameter values define approximately 1022
possible orbits. In the continuous real world, there are an infinite number of orbits. A summary of the constraints is given in Table 1.Mass.—The mass of NGC 205 is not currently well known. A recent constraint was placed on the mass contained within a  radius sphere by De Rijcke et al. (2006) of
radius sphere by De Rijcke et al. (2006) of 
 . We use the De Rijcke et al. (2006) minimum of
. We use the De Rijcke et al. (2006) minimum of 
 as a lower limit on the total mass of NGC 205 (i.e., if all the mass were contained within
as a lower limit on the total mass of NGC 205 (i.e., if all the mass were contained within  ) and set a very liberal upper limit of
) and set a very liberal upper limit of 
 .
.
 radius sphere by De Rijcke et al. (2006) of
radius sphere by De Rijcke et al. (2006) of 
 . We use the De Rijcke et al. (2006) minimum of
. We use the De Rijcke et al. (2006) minimum of 
 as a lower limit on the total mass of NGC 205 (i.e., if all the mass were contained within
as a lower limit on the total mass of NGC 205 (i.e., if all the mass were contained within  ) and set a very liberal upper limit of
) and set a very liberal upper limit of 
 .
.Disk scale length.—This parameter is used when NGC 205 is modeled as a disk. In § 2.1 we determined that the observable disk scale length of NGC 205 is  . We assume that at earlier times NGC 205’s surface brightness profile followed an exponential law governed by a different
. We assume that at earlier times NGC 205’s surface brightness profile followed an exponential law governed by a different  , which has since been affected by its interaction with M31. We therefore allow the genetic algorithm to explore the range
, which has since been affected by its interaction with M31. We therefore allow the genetic algorithm to explore the range  for the initial disk scale length in order to model the undistorted NGC 205. If NGC 205 indeed lies at a distance of 824 kpc, then this
for the initial disk scale length in order to model the undistorted NGC 205. If NGC 205 indeed lies at a distance of 824 kpc, then this  range corresponds to
range corresponds to  . The disk scale length is also used to determine the maximum distance an initial test particle can be placed in the disk of NGC 205. We chose a maximum distance of
. The disk scale length is also used to determine the maximum distance an initial test particle can be placed in the disk of NGC 205. We chose a maximum distance of 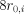 ; however, at this distance we expect to find very few particles, since the initial distribution follows an exponential law.
; however, at this distance we expect to find very few particles, since the initial distribution follows an exponential law.
 . We assume that at earlier times NGC 205’s surface brightness profile followed an exponential law governed by a different
. We assume that at earlier times NGC 205’s surface brightness profile followed an exponential law governed by a different  , which has since been affected by its interaction with M31. We therefore allow the genetic algorithm to explore the range
, which has since been affected by its interaction with M31. We therefore allow the genetic algorithm to explore the range  for the initial disk scale length in order to model the undistorted NGC 205. If NGC 205 indeed lies at a distance of 824 kpc, then this
for the initial disk scale length in order to model the undistorted NGC 205. If NGC 205 indeed lies at a distance of 824 kpc, then this  range corresponds to
range corresponds to  . The disk scale length is also used to determine the maximum distance an initial test particle can be placed in the disk of NGC 205. We chose a maximum distance of
. The disk scale length is also used to determine the maximum distance an initial test particle can be placed in the disk of NGC 205. We chose a maximum distance of 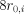 ; however, at this distance we expect to find very few particles, since the initial distribution follows an exponential law.
; however, at this distance we expect to find very few particles, since the initial distribution follows an exponential law.Initial disk orientation.—These orientation parameters are used when NGC 205 is modeled as a disk. We assume axisymmetry for NGC 205’s initial, undistorted disk and describe its orientation in three-dimensional space by two of the three Euler angles. We define the plane of the sky as the  plane centered on M31 with the positive
plane centered on M31 with the positive  -axis in the direction of increasing right ascension, the positive
-axis in the direction of increasing right ascension, the positive  -axis pointing toward the observed NGC 205 and the negative
-axis pointing toward the observed NGC 205 and the negative  -axis pointing toward us. In our defined coordinate system, the Euler angle
-axis pointing toward us. In our defined coordinate system, the Euler angle  describes turning the galaxy’s
describes turning the galaxy’s  -axis clockwise in the
-axis clockwise in the  plane and is also allowed to vary from
plane and is also allowed to vary from 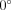 to
to  . The inclination angle
. The inclination angle  describes tilting the galaxy about the rotated
describes tilting the galaxy about the rotated  -axis and is allowed to vary from
-axis and is allowed to vary from 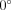 to
to  . An inclination angle of
. An inclination angle of  means the initial galaxy appears edge on, while an inclination angle of either
means the initial galaxy appears edge on, while an inclination angle of either 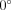 or
or 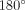 means the initial galaxy appears face on. Note the visual symmetry about
means the initial galaxy appears face on. Note the visual symmetry about  , which does not translate into dynamical symmetry. The Euler angle
, which does not translate into dynamical symmetry. The Euler angle  describes the revolution about the rotation axis and is meaningless due to the axisymmetry of NGC 205’s disk. Similarly, the axisymmetry of NGC 205 makes visual searches in the range
describes the revolution about the rotation axis and is meaningless due to the axisymmetry of NGC 205’s disk. Similarly, the axisymmetry of NGC 205 makes visual searches in the range  to
to  for
for  and
and  redundant. Thus, the position (but not the dynamics) of NGC 205’s initial disk is completely described by the parameters
redundant. Thus, the position (but not the dynamics) of NGC 205’s initial disk is completely described by the parameters  and
and  in the range
in the range 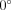 or
or  .
.
 plane centered on M31 with the positive
plane centered on M31 with the positive  -axis in the direction of increasing right ascension, the positive
-axis in the direction of increasing right ascension, the positive  -axis pointing toward the observed NGC 205 and the negative
-axis pointing toward the observed NGC 205 and the negative  -axis pointing toward us. In our defined coordinate system, the Euler angle
-axis pointing toward us. In our defined coordinate system, the Euler angle  describes turning the galaxy’s
describes turning the galaxy’s  -axis clockwise in the
-axis clockwise in the  plane and is also allowed to vary from
plane and is also allowed to vary from 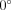 to
to  . The inclination angle
. The inclination angle  describes tilting the galaxy about the rotated
describes tilting the galaxy about the rotated  -axis and is allowed to vary from
-axis and is allowed to vary from 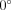 to
to  . An inclination angle of
. An inclination angle of  means the initial galaxy appears edge on, while an inclination angle of either
means the initial galaxy appears edge on, while an inclination angle of either 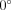 or
or 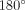 means the initial galaxy appears face on. Note the visual symmetry about
means the initial galaxy appears face on. Note the visual symmetry about  , which does not translate into dynamical symmetry. The Euler angle
, which does not translate into dynamical symmetry. The Euler angle  describes the revolution about the rotation axis and is meaningless due to the axisymmetry of NGC 205’s disk. Similarly, the axisymmetry of NGC 205 makes visual searches in the range
describes the revolution about the rotation axis and is meaningless due to the axisymmetry of NGC 205’s disk. Similarly, the axisymmetry of NGC 205 makes visual searches in the range  to
to  for
for  and
and  redundant. Thus, the position (but not the dynamics) of NGC 205’s initial disk is completely described by the parameters
redundant. Thus, the position (but not the dynamics) of NGC 205’s initial disk is completely described by the parameters  and
and  in the range
in the range 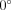 or
or  .
.Prograde vs. retrograde.—This parameter is used when NGC 205 is modeled as a disk. Since the initial sense of rotation of NGC 205 is unknown, it is important to explore both prograde and retrograde orbits. A prograde orbit means that the galaxy is rotating in the direction of the encounter, while a retrograde orbit means it is rotating in the direction against the encounter. As mentioned in the previous paragraph, exploring  in the range of
in the range of 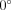 to
to  provides a complete visual search, but not a complete dynamical search. For completeness, we introduce the rotation parameter
provides a complete visual search, but not a complete dynamical search. For completeness, we introduce the rotation parameter  into our simulation whose purpose is to determine whether the Euler angle
into our simulation whose purpose is to determine whether the Euler angle  will be flipped about
will be flipped about  . The rotation parameter can be set to either
. The rotation parameter can be set to either 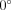 or
or  , where
, where  means
means  is unchanged and
is unchanged and  changes
changes  to
to  . Hence, this parameter essentially allows
. Hence, this parameter essentially allows  to vary from –
to vary from – to
to  so that both prograde and retrograde orbits can be explored. The motivation for using this separate parameter,
so that both prograde and retrograde orbits can be explored. The motivation for using this separate parameter,  , rather than just allowing
, rather than just allowing  to vary initially from –
to vary initially from – to
to  is that
is that  ’s binary nature provides an easy means for the genetic algorithm to instantly change the direction of the encounter via mutation or reproduction (see § 3.5 for more information on the genetic algorithm). That is, the genetic algorithm is capable of changing the rotation of the disk by merely turning this parameter off or on. Note, this effect could have also been achieved using the
’s binary nature provides an easy means for the genetic algorithm to instantly change the direction of the encounter via mutation or reproduction (see § 3.5 for more information on the genetic algorithm). That is, the genetic algorithm is capable of changing the rotation of the disk by merely turning this parameter off or on. Note, this effect could have also been achieved using the  parameter instead.
parameter instead.
 in the range of
in the range of 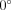 to
to  provides a complete visual search, but not a complete dynamical search. For completeness, we introduce the rotation parameter
provides a complete visual search, but not a complete dynamical search. For completeness, we introduce the rotation parameter  into our simulation whose purpose is to determine whether the Euler angle
into our simulation whose purpose is to determine whether the Euler angle  will be flipped about
will be flipped about  . The rotation parameter can be set to either
. The rotation parameter can be set to either 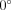 or
or  , where
, where  means
means  is unchanged and
is unchanged and  changes
changes  to
to  . Hence, this parameter essentially allows
. Hence, this parameter essentially allows  to vary from –
to vary from – to
to  so that both prograde and retrograde orbits can be explored. The motivation for using this separate parameter,
so that both prograde and retrograde orbits can be explored. The motivation for using this separate parameter,  , rather than just allowing
, rather than just allowing  to vary initially from –
to vary initially from – to
to  is that
is that  ’s binary nature provides an easy means for the genetic algorithm to instantly change the direction of the encounter via mutation or reproduction (see § 3.5 for more information on the genetic algorithm). That is, the genetic algorithm is capable of changing the rotation of the disk by merely turning this parameter off or on. Note, this effect could have also been achieved using the
’s binary nature provides an easy means for the genetic algorithm to instantly change the direction of the encounter via mutation or reproduction (see § 3.5 for more information on the genetic algorithm). That is, the genetic algorithm is capable of changing the rotation of the disk by merely turning this parameter off or on. Note, this effect could have also been achieved using the  parameter instead.
parameter instead.Hernquist scale length.—We model NGC 205’s potential as a spherical symmetric distribution of matter governed by a Hernquist profile (§ 3.2, eq. [2]). The concentration of the combined dark and baryonic matter in NGC 205 is governed by Hernquist scale length parameter,  (or
(or  in eq. [2]). We set a lower limit on
in eq. [2]). We set a lower limit on  of
of  , corresponding to a Keplerian potential, and an upper limit of
, corresponding to a Keplerian potential, and an upper limit of  , which at a distance of 824 kpc would correspond to a scale length of 10 kpc.
, which at a distance of 824 kpc would correspond to a scale length of 10 kpc.
 (or
(or  in eq. [2]). We set a lower limit on
in eq. [2]). We set a lower limit on  of
of  , corresponding to a Keplerian potential, and an upper limit of
, corresponding to a Keplerian potential, and an upper limit of  , which at a distance of 824 kpc would correspond to a scale length of 10 kpc.
, which at a distance of 824 kpc would correspond to a scale length of 10 kpc.Velocity.—The mean radial velocities of M31 and NGC 205 are – km s–1 (de Vaucouleurs 1991) and –
km s–1 (de Vaucouleurs 1991) and – km s–1 (Geha et al. 2006), respectively, resulting in a relative radial velocity for NGC 205 of
km s–1 (Geha et al. 2006), respectively, resulting in a relative radial velocity for NGC 205 of  km s–1 with respect to M31 (see § 2.2). Thus the radial velocity component,
km s–1 with respect to M31 (see § 2.2). Thus the radial velocity component,  , is given a lower limit of 49 km s–1 and an upper limit of 59 km s–1. The transverse velocity components,
, is given a lower limit of 49 km s–1 and an upper limit of 59 km s–1. The transverse velocity components,  and
and  , are given upper and lower limits dictated by the escape velocity of NGC 205’s center of mass relative to M31, and are therefore not only functions of z and
, are given upper and lower limits dictated by the escape velocity of NGC 205’s center of mass relative to M31, and are therefore not only functions of z and  , but also of M31’s mass. In order to explore both bound and unbound orbits, we allow
, but also of M31’s mass. In order to explore both bound and unbound orbits, we allow  and
and  to explore the full range of NGC 205’s escape velocity, with a maximum escape velocity of 500 km s–1 if NGC 205’s line-of-sight distance and velocity (
to explore the full range of NGC 205’s escape velocity, with a maximum escape velocity of 500 km s–1 if NGC 205’s line-of-sight distance and velocity ( and
and  ) are at their minimums.
) are at their minimums.
 km s–1 (de Vaucouleurs 1991) and –
km s–1 (de Vaucouleurs 1991) and – km s–1 (Geha et al. 2006), respectively, resulting in a relative radial velocity for NGC 205 of
km s–1 (Geha et al. 2006), respectively, resulting in a relative radial velocity for NGC 205 of  km s–1 with respect to M31 (see § 2.2). Thus the radial velocity component,
km s–1 with respect to M31 (see § 2.2). Thus the radial velocity component,  , is given a lower limit of 49 km s–1 and an upper limit of 59 km s–1. The transverse velocity components,
, is given a lower limit of 49 km s–1 and an upper limit of 59 km s–1. The transverse velocity components,  and
and  , are given upper and lower limits dictated by the escape velocity of NGC 205’s center of mass relative to M31, and are therefore not only functions of z and
, are given upper and lower limits dictated by the escape velocity of NGC 205’s center of mass relative to M31, and are therefore not only functions of z and  , but also of M31’s mass. In order to explore both bound and unbound orbits, we allow
, but also of M31’s mass. In order to explore both bound and unbound orbits, we allow  and
and  to explore the full range of NGC 205’s escape velocity, with a maximum escape velocity of 500 km s–1 if NGC 205’s line-of-sight distance and velocity (
to explore the full range of NGC 205’s escape velocity, with a maximum escape velocity of 500 km s–1 if NGC 205’s line-of-sight distance and velocity ( and
and  ) are at their minimums.
) are at their minimums.Line-of-sight distance.—The reported distances to M31 and NGC 205 are  and
and  kpc, respectively (McConnachie et al. 2004). By adding the errors in quadrature, we approximate the line-of-sight distance to be
kpc, respectively (McConnachie et al. 2004). By adding the errors in quadrature, we approximate the line-of-sight distance to be  kpc and allow the genetic algorithm to search within the range of 2 to 76 kpc for the final position of NGC 205. We recognize that this is a generous range to search, but decide to err on the side conservatism.
kpc and allow the genetic algorithm to search within the range of 2 to 76 kpc for the final position of NGC 205. We recognize that this is a generous range to search, but decide to err on the side conservatism.
 and
and  kpc, respectively (McConnachie et al. 2004). By adding the errors in quadrature, we approximate the line-of-sight distance to be
kpc, respectively (McConnachie et al. 2004). By adding the errors in quadrature, we approximate the line-of-sight distance to be  kpc and allow the genetic algorithm to search within the range of 2 to 76 kpc for the final position of NGC 205. We recognize that this is a generous range to search, but decide to err on the side conservatism.
kpc and allow the genetic algorithm to search within the range of 2 to 76 kpc for the final position of NGC 205. We recognize that this is a generous range to search, but decide to err on the side conservatism.3.2. Galaxy Potential Models
The close proximity of M31 to NGC 205 stipulates that fairly accurate potentials are necessary in modeling the interaction between the galaxies. However, there is an implied limit to the level of complexity of the models resulting from the large number of orbits searched by the genetic algorithm. That is, using too simple of a model can result in incorrect final integrated positions and velocities, and, if the model is too complex, the genetic algorithm will spend large amounts of time attempting to complete a single orbit. Hence it is essential to find balance between the two requirements in order to come up with an optimal model. In this subsection we discuss the potential models used in our simulations. We assume that the galaxy potentials are not changing significantly during the course of the interaction and thus remain static.
Previous studies suggest dwarf elliptical galaxies do not contain a significant amount of dark matter in their inner regions. The amount of dark matter in the outer regions of dE's is completely unknown. Thus, one of the goals of this project is to probe the dark matter content of NGC 205. We make the simple, but appropriate, approximation that the potential of NGC 205 is a spherically symmetric spheroid with a Hernquist profile (Hernquist 1990). However, it should be noted that the ideal model for NGC 205 is a stellar population orbiting in a fully consistent potential with a brightness profile lying somewhere in between an exponential disk and exponential bulge (i.e., a hot, exponential disk). The difficulty of constructing such a model is demonstrated by the complex photometry discussed in § 2.1. For the purpose of this paper we model NGC 205’s potential as
 where
where  is the total mass of NGC 205 (stars, interstellar gas, dark matter),
is the total mass of NGC 205 (stars, interstellar gas, dark matter),  is the Hernquist scale length that defines the concentration of matter in NGC 205, and
is the Hernquist scale length that defines the concentration of matter in NGC 205, and  is the distance from the center of NGC 205. Both the mass and the Hernquist scale length are variables probed by the genetic algorithm.
is the distance from the center of NGC 205. Both the mass and the Hernquist scale length are variables probed by the genetic algorithm.

 is the total mass of NGC 205 (stars, interstellar gas, dark matter),
is the total mass of NGC 205 (stars, interstellar gas, dark matter),  is the Hernquist scale length that defines the concentration of matter in NGC 205, and
is the Hernquist scale length that defines the concentration of matter in NGC 205, and  is the distance from the center of NGC 205. Both the mass and the Hernquist scale length are variables probed by the genetic algorithm.
is the distance from the center of NGC 205. Both the mass and the Hernquist scale length are variables probed by the genetic algorithm.The potential of M31 is best represented by a three-component model containing a bulge, a disk, and a halo. Geehan et al. (2006) derives a “simple analytic bulge-disk-halo model” using a spherical symmetric Hernquist profile for the bulge (eq. [2]), an infinitesimally thin, exponential disk and a spherically symmetric NFW profile for the extended dark halo given by
 where
where  is a dimensionless density parameter,
is a dimensionless density parameter, 
 kpc–3 is today’s critical density with Hubble constant
kpc–3 is today’s critical density with Hubble constant  in units of 100 km–1 s–1 Mpc–1, and
in units of 100 km–1 s–1 Mpc–1, and 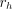 is the halo scale radius (Navarro et al. 1996).
is the halo scale radius (Navarro et al. 1996).

 is a dimensionless density parameter,
is a dimensionless density parameter, 
 kpc–3 is today’s critical density with Hubble constant
kpc–3 is today’s critical density with Hubble constant  in units of 100 km–1 s–1 Mpc–1, and
in units of 100 km–1 s–1 Mpc–1, and 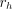 is the halo scale radius (Navarro et al. 1996).
is the halo scale radius (Navarro et al. 1996).The exponential disk model used by Geehan et al. (2006) is presently without a known analytic solution. Although the equation and its spatial derivatives can easily be solved numerically, the amount of time required to integrate a set of particles through a complete orbit becomes unreasonable for our purposes. An alternative approach is to construct a large table of values for the spatial derivatives and perform a bicubic interpolation in both  and
and  in order to find the force on a single particle at each step in the integration. Unfortunately, this latter method is unable to significantly decrease the amount of computation time required for a single orbit. Thus, we use a Miyamoto & Nagai (1975) disk which provides results that are comparable to those from the exponential disk used by Geehan et al. (2006):
in order to find the force on a single particle at each step in the integration. Unfortunately, this latter method is unable to significantly decrease the amount of computation time required for a single orbit. Thus, we use a Miyamoto & Nagai (1975) disk which provides results that are comparable to those from the exponential disk used by Geehan et al. (2006):
 where
where  is the disk scale length and
is the disk scale length and  is the vertical scale factor.
is the vertical scale factor.
 and
and  in order to find the force on a single particle at each step in the integration. Unfortunately, this latter method is unable to significantly decrease the amount of computation time required for a single orbit. Thus, we use a Miyamoto & Nagai (1975) disk which provides results that are comparable to those from the exponential disk used by Geehan et al. (2006):
in order to find the force on a single particle at each step in the integration. Unfortunately, this latter method is unable to significantly decrease the amount of computation time required for a single orbit. Thus, we use a Miyamoto & Nagai (1975) disk which provides results that are comparable to those from the exponential disk used by Geehan et al. (2006):

 is the disk scale length and
is the disk scale length and  is the vertical scale factor.
is the vertical scale factor.We use the “best-fit model” values derived by Geehan et al. (2006) to describe the various parameters of M31, with the sole exception of  , the vertical scale factor, which was not a reported parameter. For
, the vertical scale factor, which was not a reported parameter. For  we use the vertical scale height of the dust at a value of 0.1 kpc (Hatano et al. 1997). The values reported by Geehan et al. (2006) include the bulge mass, with
we use the vertical scale height of the dust at a value of 0.1 kpc (Hatano et al. 1997). The values reported by Geehan et al. (2006) include the bulge mass, with 
 , the bulge scale factor, with
, the bulge scale factor, with  kpc, the disk central surface density, with
kpc, the disk central surface density, with 
 kpc–2, the disk scale radius, with
kpc–2, the disk scale radius, with  kpc, the halo scale radius, with
kpc, the halo scale radius, with  kpc, and the total mass enclosed inside 125 kpc, with
kpc, and the total mass enclosed inside 125 kpc, with 
 . To compute the mass of the disk we use
. To compute the mass of the disk we use
 for the halo mass we use
for the halo mass we use
 and to find the dimensionless density parameter
and to find the dimensionless density parameter  we use the values for
we use the values for  and
and  at
at  kpc, and solve the mass profile for a NFW halo
kpc, and solve the mass profile for a NFW halo
 This results in a dimensionless density parameter value of
This results in a dimensionless density parameter value of
 A summary of these parameters is given in Table 2.
A summary of these parameters is given in Table 2.
 , the vertical scale factor, which was not a reported parameter. For
, the vertical scale factor, which was not a reported parameter. For  we use the vertical scale height of the dust at a value of 0.1 kpc (Hatano et al. 1997). The values reported by Geehan et al. (2006) include the bulge mass, with
we use the vertical scale height of the dust at a value of 0.1 kpc (Hatano et al. 1997). The values reported by Geehan et al. (2006) include the bulge mass, with 
 , the bulge scale factor, with
, the bulge scale factor, with  kpc, the disk central surface density, with
kpc, the disk central surface density, with 
 kpc–2, the disk scale radius, with
kpc–2, the disk scale radius, with  kpc, the halo scale radius, with
kpc, the halo scale radius, with  kpc, and the total mass enclosed inside 125 kpc, with
kpc, and the total mass enclosed inside 125 kpc, with 
 . To compute the mass of the disk we use
. To compute the mass of the disk we use


 we use the values for
we use the values for  and
and  at
at  kpc, and solve the mass profile for a NFW halo
kpc, and solve the mass profile for a NFW halo


3.3. Arrangement of NGC 205’s Test Particles
In addition to the parameters discussed in § 3.1 and the potentials outlined in § 3.2, the satellite’s initial, undistorted particle configuration (both in position and velocity space) directly affects the appearance of the final, integrated distribution of particles. The particles are used as tracers of surface brightness and to map the radial velocity profile of the galaxy. The present true brightness profile of NGC 205 lies in between an exponential and  law (Kent 1987; Choi et al. 2002), while the galaxy’s support is thought to come from a mix of both rotational and anisotropic velocities (Geha et al. 2006). As mentioned in § 2.2, the current observed ratio of the maximum rotational velocity to the average velocity dispersion is
law (Kent 1987; Choi et al. 2002), while the galaxy’s support is thought to come from a mix of both rotational and anisotropic velocities (Geha et al. 2006). As mentioned in § 2.2, the current observed ratio of the maximum rotational velocity to the average velocity dispersion is  . Hence the current structure of particles in the satellite lies somewhere between an exponential bulge and exponential disk.
. Hence the current structure of particles in the satellite lies somewhere between an exponential bulge and exponential disk.
 law (Kent 1987; Choi et al. 2002), while the galaxy’s support is thought to come from a mix of both rotational and anisotropic velocities (Geha et al. 2006). As mentioned in § 2.2, the current observed ratio of the maximum rotational velocity to the average velocity dispersion is
law (Kent 1987; Choi et al. 2002), while the galaxy’s support is thought to come from a mix of both rotational and anisotropic velocities (Geha et al. 2006). As mentioned in § 2.2, the current observed ratio of the maximum rotational velocity to the average velocity dispersion is  . Hence the current structure of particles in the satellite lies somewhere between an exponential bulge and exponential disk.
. Hence the current structure of particles in the satellite lies somewhere between an exponential bulge and exponential disk.The morphology of NGC 205 before tidal distortion is unknown, while a wide range of internal dynamics has been observed for cluster dE's, ranging from non-rotating to rotational flattened dE's (Geha et al. 2003). Furthermore, it is unclear which features of NGC 205 are due to intrinsic properties, projection, or tidally interaction. For this reason, we test three configurations for NGC 205: a rotating cold exponential disk (§ 3.3.1), a nonrotating hot spheroid (§ 3.3.3), and a rotating warm exponential disk (§ 3.3.2). These configurations explore the two extremes, a rotationally supported satellite with 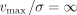 and an isotropically supported satellite with
and an isotropically supported satellite with  , as well as an intermediate construction, a warm disk with
, as well as an intermediate construction, a warm disk with  . These three models are outlined in detail below.
. These three models are outlined in detail below.
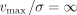 and an isotropically supported satellite with
and an isotropically supported satellite with  , as well as an intermediate construction, a warm disk with
, as well as an intermediate construction, a warm disk with  . These three models are outlined in detail below.
. These three models are outlined in detail below.3.3.1. Rotating Cold Disk
Our most basic model for NGC 205 places massless test particles in an infinitely thin, flat disk. The particles are randomly distributed in accordance with an exponential surface brightness profile, as given in equation (1). We assume that the central (nucleus free) surface brightness,  , has not evolved and that the undistorted NGC 205 follows an exponential characterized by a variable scale length,
, has not evolved and that the undistorted NGC 205 follows an exponential characterized by a variable scale length,  . We set the maximum radius of NGC 205 to
. We set the maximum radius of NGC 205 to  , a location at which very few particles are expected. In addition to
, a location at which very few particles are expected. In addition to  , the particle positions in NGC 205’s initial disk are also defined by the disk’s clockwise rotation in the
, the particle positions in NGC 205’s initial disk are also defined by the disk’s clockwise rotation in the  plane,
plane,  , and inclination angle,
, and inclination angle,  . The values of these three parameters (
. The values of these three parameters ( ,
,  ,
,  ) are obtained from the genetic algorithm.
) are obtained from the genetic algorithm.
 , has not evolved and that the undistorted NGC 205 follows an exponential characterized by a variable scale length,
, has not evolved and that the undistorted NGC 205 follows an exponential characterized by a variable scale length,  . We set the maximum radius of NGC 205 to
. We set the maximum radius of NGC 205 to  , a location at which very few particles are expected. In addition to
, a location at which very few particles are expected. In addition to  , the particle positions in NGC 205’s initial disk are also defined by the disk’s clockwise rotation in the
, the particle positions in NGC 205’s initial disk are also defined by the disk’s clockwise rotation in the  plane,
plane,  , and inclination angle,
, and inclination angle,  . The values of these three parameters (
. The values of these three parameters ( ,
,  ,
,  ) are obtained from the genetic algorithm.
) are obtained from the genetic algorithm.Initially, the cold disk is completely supported by rotation, such that  . Each particle moves in a circular orbit about the satellite’s center under the influence of a Hernquist profile. This results in a circular velocity, in the plane of NGC 205’s disk, of
. Each particle moves in a circular orbit about the satellite’s center under the influence of a Hernquist profile. This results in a circular velocity, in the plane of NGC 205’s disk, of
 where
where  is the mass of NGC 205,
is the mass of NGC 205,  is the Hernquist scale length of NGC 205, and
is the Hernquist scale length of NGC 205, and  is the particle’s distance from the center of NGC 205. The direction of rotation in the disk is determined by the parameter
is the particle’s distance from the center of NGC 205. The direction of rotation in the disk is determined by the parameter  . Hence, the particle’s circular velocities are very simply defined by their distance from the satellite’s center and by the three variable parameters:
. Hence, the particle’s circular velocities are very simply defined by their distance from the satellite’s center and by the three variable parameters:  ,
,  , and
, and  . Any dispersion found in the final, integrated system is a direct result of tidal interaction with M31.
. Any dispersion found in the final, integrated system is a direct result of tidal interaction with M31.
 . Each particle moves in a circular orbit about the satellite’s center under the influence of a Hernquist profile. This results in a circular velocity, in the plane of NGC 205’s disk, of
. Each particle moves in a circular orbit about the satellite’s center under the influence of a Hernquist profile. This results in a circular velocity, in the plane of NGC 205’s disk, of

 is the mass of NGC 205,
is the mass of NGC 205,  is the Hernquist scale length of NGC 205, and
is the Hernquist scale length of NGC 205, and  is the particle’s distance from the center of NGC 205. The direction of rotation in the disk is determined by the parameter
is the particle’s distance from the center of NGC 205. The direction of rotation in the disk is determined by the parameter  . Hence, the particle’s circular velocities are very simply defined by their distance from the satellite’s center and by the three variable parameters:
. Hence, the particle’s circular velocities are very simply defined by their distance from the satellite’s center and by the three variable parameters:  ,
,  , and
, and  . Any dispersion found in the final, integrated system is a direct result of tidal interaction with M31.
. Any dispersion found in the final, integrated system is a direct result of tidal interaction with M31.3.3.2. Rotating Warm Disk
A more realistic model for NGC 205 arranges massless test particles in a disk with some vertical thickness. We employ the method prescribed by Hernquist (1993) using cylindrical coordinates and distribute the particles in an exponentially decaying density profile given by
 where
where  is the cylindrical radius,
is the cylindrical radius,  is the mass of the satellite,
is the mass of the satellite,  is the disk scale length, and
is the disk scale length, and  is the vertical scale thickness. For our simulations, we set vertical scale thickness,
is the vertical scale thickness. For our simulations, we set vertical scale thickness,  , equal to the scale radius,
, equal to the scale radius,  , in order to create a “puffier” disk. As with the cold disk model outlined in § 3.3.1, the maximum radius of NGC 205 is constrained to
, in order to create a “puffier” disk. As with the cold disk model outlined in § 3.3.1, the maximum radius of NGC 205 is constrained to  and the disk is oriented using the
and the disk is oriented using the  and θ parameters obtained from the genetic algorithm.
and θ parameters obtained from the genetic algorithm.

 is the cylindrical radius,
is the cylindrical radius,  is the mass of the satellite,
is the mass of the satellite,  is the disk scale length, and
is the disk scale length, and  is the vertical scale thickness. For our simulations, we set vertical scale thickness,
is the vertical scale thickness. For our simulations, we set vertical scale thickness,  , equal to the scale radius,
, equal to the scale radius,  , in order to create a “puffier” disk. As with the cold disk model outlined in § 3.3.1, the maximum radius of NGC 205 is constrained to
, in order to create a “puffier” disk. As with the cold disk model outlined in § 3.3.1, the maximum radius of NGC 205 is constrained to  and the disk is oriented using the
and the disk is oriented using the  and θ parameters obtained from the genetic algorithm.
and θ parameters obtained from the genetic algorithm.The warm disk is supported by a combination of rotational and anisotropic velocities. Using the method outlined by Hernquist (1993) self-consistent disks are approximated using the moments of the collisionless Boltzmann equation. In order to avoid imaginary streaming velocities ( ) near the center, the softened version of the radial dispersion equation is used
) near the center, the softened version of the radial dispersion equation is used
 where
where  is the disk softening radius and
is the disk softening radius and  is the normalization constant. As prescribed by Hernquist (1993) the softening radius is set to
is the normalization constant. As prescribed by Hernquist (1993) the softening radius is set to  . The normalization factor,
. The normalization factor,  , can then be easily computed by specifying
, can then be easily computed by specifying  at
at 
 However, we cannot simply set the radial dispersion at one scale length equal to the observed dispersion in NGC 205 of
However, we cannot simply set the radial dispersion at one scale length equal to the observed dispersion in NGC 205 of  km s–1 (Geha et al. 2006). This would cause the streaming velocities to become imaginary for much of the parameter space. To avoid this potential problem, the maximum allowed radial dispersion that imposes
km s–1 (Geha et al. 2006). This would cause the streaming velocities to become imaginary for much of the parameter space. To avoid this potential problem, the maximum allowed radial dispersion that imposes  is used, with the caveat that
is used, with the caveat that  cannot exceed 29 km s–1. The vertical dispersion perpendicular to the plane of the disk is given by
cannot exceed 29 km s–1. The vertical dispersion perpendicular to the plane of the disk is given by
 where
where  is the disk surface density given by the local Hernquist density (Hernquist 1990),
is the disk surface density given by the local Hernquist density (Hernquist 1990),
 and
and  is the Hernquist scale length. Using the epicyclic approximation, the azimuthal dispersion can be related to the radial dispersion
is the Hernquist scale length. Using the epicyclic approximation, the azimuthal dispersion can be related to the radial dispersion
 where the epicyclic and angular frequencies are respectively given by
where the epicyclic and angular frequencies are respectively given by
 and
and
 with the circular velocity
with the circular velocity  given by equation (9) and the potential energy
given by equation (9) and the potential energy  of a Hernquist profile given by equation (2). If we assume that the velocity ellipsoid stays aligned with the coordinate axes, the streaming velocity becomes
of a Hernquist profile given by equation (2). If we assume that the velocity ellipsoid stays aligned with the coordinate axes, the streaming velocity becomes

 ) near the center, the softened version of the radial dispersion equation is used
) near the center, the softened version of the radial dispersion equation is used

 is the disk softening radius and
is the disk softening radius and  is the normalization constant. As prescribed by Hernquist (1993) the softening radius is set to
is the normalization constant. As prescribed by Hernquist (1993) the softening radius is set to  . The normalization factor,
. The normalization factor,  , can then be easily computed by specifying
, can then be easily computed by specifying  at
at 

 km s–1 (Geha et al. 2006). This would cause the streaming velocities to become imaginary for much of the parameter space. To avoid this potential problem, the maximum allowed radial dispersion that imposes
km s–1 (Geha et al. 2006). This would cause the streaming velocities to become imaginary for much of the parameter space. To avoid this potential problem, the maximum allowed radial dispersion that imposes  is used, with the caveat that
is used, with the caveat that  cannot exceed 29 km s–1. The vertical dispersion perpendicular to the plane of the disk is given by
cannot exceed 29 km s–1. The vertical dispersion perpendicular to the plane of the disk is given by

 is the disk surface density given by the local Hernquist density (Hernquist 1990),
is the disk surface density given by the local Hernquist density (Hernquist 1990),

 is the Hernquist scale length. Using the epicyclic approximation, the azimuthal dispersion can be related to the radial dispersion
is the Hernquist scale length. Using the epicyclic approximation, the azimuthal dispersion can be related to the radial dispersion



 given by equation (9) and the potential energy
given by equation (9) and the potential energy  of a Hernquist profile given by equation (2). If we assume that the velocity ellipsoid stays aligned with the coordinate axes, the streaming velocity becomes
of a Hernquist profile given by equation (2). If we assume that the velocity ellipsoid stays aligned with the coordinate axes, the streaming velocity becomes

Once these low-order moments are determined, the radial and vertical velocities for individual particles can be drawn randomly from Gaussians with widths  and
and  , while the azimuthal velocity is determined by adding the streaming velocity,
, while the azimuthal velocity is determined by adding the streaming velocity,  , to the velocity value drawn from a Gaussian with width
, to the velocity value drawn from a Gaussian with width  . This configuration results in observable ratios of the maximum rotational velocity to the average velocity dispersion dispersions of
. This configuration results in observable ratios of the maximum rotational velocity to the average velocity dispersion dispersions of  . Since the satellite still contains rotational support, the parameter
. Since the satellite still contains rotational support, the parameter  is used to specify the direction of this rotation.
is used to specify the direction of this rotation.
 and
and  , while the azimuthal velocity is determined by adding the streaming velocity,
, while the azimuthal velocity is determined by adding the streaming velocity,  , to the velocity value drawn from a Gaussian with width
, to the velocity value drawn from a Gaussian with width  . This configuration results in observable ratios of the maximum rotational velocity to the average velocity dispersion dispersions of
. This configuration results in observable ratios of the maximum rotational velocity to the average velocity dispersion dispersions of  . Since the satellite still contains rotational support, the parameter
. Since the satellite still contains rotational support, the parameter  is used to specify the direction of this rotation.
is used to specify the direction of this rotation.3.3.3. Nonrotating Hot Spheroid
The third model for NGC 205 configures the satellite as a dynamically hot, pressure supported spheroid. Hence, the velocities of this model are completely isotropic. This construction is essentially the counter to the rotationally supported, cold disk model outlined in § 3.3.1. The density profile follows the analytical model for spherical galaxies outlined by Hernquist (1990):
 where
where  is the mass of the satellite,
is the mass of the satellite,  is the Hernquist scale length of NGC 205, and
is the Hernquist scale length of NGC 205, and  is the particle’s distance from the center of NGC 205. As with the previous two models, the maximum radius of NGC 205 is constrained to
is the particle’s distance from the center of NGC 205. As with the previous two models, the maximum radius of NGC 205 is constrained to  .
.

 is the mass of the satellite,
is the mass of the satellite,  is the Hernquist scale length of NGC 205, and
is the Hernquist scale length of NGC 205, and  is the particle’s distance from the center of NGC 205. As with the previous two models, the maximum radius of NGC 205 is constrained to
is the particle’s distance from the center of NGC 205. As with the previous two models, the maximum radius of NGC 205 is constrained to  .
.Using the energy dependent distribution function,  , for a Hernquist profile, a spheroid supported by isotropic velocities can be constructed using random realizations (Hernquist 1990; Ascasibar & Binney 2005). The phase-space density as a function of specific energy is
, for a Hernquist profile, a spheroid supported by isotropic velocities can be constructed using random realizations (Hernquist 1990; Ascasibar & Binney 2005). The phase-space density as a function of specific energy is
 with the dimensionless variable
with the dimensionless variable  defined as
defined as
 The specific energy
The specific energy  of a particle at position
of a particle at position  and velocity
and velocity  is
is
 with
with  , the potential energy for a Hernquist profile, given by equation (2). We normalize the distribution function in a volume element
, the potential energy for a Hernquist profile, given by equation (2). We normalize the distribution function in a volume element  , centered on (
, centered on ( ,
,  ), by dividing
), by dividing 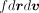 by its maximum. This maximum corresponds to the point in parameter space containing the largest amount of mass (and in our case, mass-less test particles). Using spherical symmetry,
by its maximum. This maximum corresponds to the point in parameter space containing the largest amount of mass (and in our case, mass-less test particles). Using spherical symmetry,  becomes
becomes  . Hence, the maximum of
. Hence, the maximum of  is easily found numerically and resides at
is easily found numerically and resides at  and
and  , where
, where  is the circular velocity given by equation (9).
is the circular velocity given by equation (9).
 , for a Hernquist profile, a spheroid supported by isotropic velocities can be constructed using random realizations (Hernquist 1990; Ascasibar & Binney 2005). The phase-space density as a function of specific energy is
, for a Hernquist profile, a spheroid supported by isotropic velocities can be constructed using random realizations (Hernquist 1990; Ascasibar & Binney 2005). The phase-space density as a function of specific energy is

 defined as
defined as

 of a particle at position
of a particle at position  and velocity
and velocity  is
is

 , the potential energy for a Hernquist profile, given by equation (2). We normalize the distribution function in a volume element
, the potential energy for a Hernquist profile, given by equation (2). We normalize the distribution function in a volume element  , centered on (
, centered on ( ,
,  ), by dividing
), by dividing 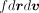 by its maximum. This maximum corresponds to the point in parameter space containing the largest amount of mass (and in our case, mass-less test particles). Using spherical symmetry,
by its maximum. This maximum corresponds to the point in parameter space containing the largest amount of mass (and in our case, mass-less test particles). Using spherical symmetry,  becomes
becomes  . Hence, the maximum of
. Hence, the maximum of  is easily found numerically and resides at
is easily found numerically and resides at  and
and  , where
, where  is the circular velocity given by equation (9).
is the circular velocity given by equation (9).Using the normalized  , particles are placed in phase space using a von Neumann rejection technique (Press et al. 1992). Tentative values for
, particles are placed in phase space using a von Neumann rejection technique (Press et al. 1992). Tentative values for  and
and  are randomly chosen within the range
are randomly chosen within the range  and
and ![0\leq v\leq v_{\mathrm{esc}\,}=\left[-2\Phi \left(r\right)\right]^{1/ 2}](https://content.cld.iop.org/journals/0004-637X/683/2/722/revision1/eq-00276.gif) , and a tentative
, and a tentative  is computed. Next a random number
is computed. Next a random number  between 0 and 1 is selected (where 1 corresponds to the normalized peak of
between 0 and 1 is selected (where 1 corresponds to the normalized peak of  ). The provisional values for
). The provisional values for  and
and  are kept only if
are kept only if  , else the process is reinitiated until the condition is satisfied. Once
, else the process is reinitiated until the condition is satisfied. Once  and
and  are generated, position and velocity angular coordinates are randomly chosen from
are generated, position and velocity angular coordinates are randomly chosen from  and –
and – , and the particle is placed in the satellite. The procedure is then repeated until the satellite is completely populated with the desired number of particles. This configuration results in a galaxy with a density profile given by equation (9) and that is completely supported by isotropic velocities (
, and the particle is placed in the satellite. The procedure is then repeated until the satellite is completely populated with the desired number of particles. This configuration results in a galaxy with a density profile given by equation (9) and that is completely supported by isotropic velocities ( ). Note that, unlike the rotating cold disk and warm disk, the symmetry of the nonrotating spheroid negates the need for parameters
). Note that, unlike the rotating cold disk and warm disk, the symmetry of the nonrotating spheroid negates the need for parameters  ,
,  , and
, and  , while the density profile’s dependence on
, while the density profile’s dependence on  reduces the use of
reduces the use of  values to setting the maximum radius for placing particles.
values to setting the maximum radius for placing particles.
 , particles are placed in phase space using a von Neumann rejection technique (Press et al. 1992). Tentative values for
, particles are placed in phase space using a von Neumann rejection technique (Press et al. 1992). Tentative values for  and
and  are randomly chosen within the range
are randomly chosen within the range  and
and ![0\leq v\leq v_{\mathrm{esc}\,}=\left[-2\Phi \left(r\right)\right]^{1/ 2}](https://content.cld.iop.org/journals/0004-637X/683/2/722/revision1/eq-00276.gif) , and a tentative
, and a tentative  is computed. Next a random number
is computed. Next a random number  between 0 and 1 is selected (where 1 corresponds to the normalized peak of
between 0 and 1 is selected (where 1 corresponds to the normalized peak of  ). The provisional values for
). The provisional values for  and
and  are kept only if
are kept only if  , else the process is reinitiated until the condition is satisfied. Once
, else the process is reinitiated until the condition is satisfied. Once  and
and  are generated, position and velocity angular coordinates are randomly chosen from
are generated, position and velocity angular coordinates are randomly chosen from  and –
and – , and the particle is placed in the satellite. The procedure is then repeated until the satellite is completely populated with the desired number of particles. This configuration results in a galaxy with a density profile given by equation (9) and that is completely supported by isotropic velocities (
, and the particle is placed in the satellite. The procedure is then repeated until the satellite is completely populated with the desired number of particles. This configuration results in a galaxy with a density profile given by equation (9) and that is completely supported by isotropic velocities ( ). Note that, unlike the rotating cold disk and warm disk, the symmetry of the nonrotating spheroid negates the need for parameters
). Note that, unlike the rotating cold disk and warm disk, the symmetry of the nonrotating spheroid negates the need for parameters  ,
,  , and
, and  , while the density profile’s dependence on
, while the density profile’s dependence on  reduces the use of
reduces the use of  values to setting the maximum radius for placing particles.
values to setting the maximum radius for placing particles.3.4. Restricted N-Body Simulations
The simulations are carried out using a restricted N-body approach (Pfleiderer & Siedentopf 1961; Toomre & Toomre 1972) in a Cartesian coordinate system. The use of a Cartesian coordinate system is motivated by the format of the available observations: Choi et al. (2002) photometric observations are defined in the  plane and Geha et al. (2006) velocity observations are defined in the
plane and Geha et al. (2006) velocity observations are defined in the  direction. We center our coordinate system on M31 and define the
direction. We center our coordinate system on M31 and define the  plane as the plane of the sky, with
plane as the plane of the sky, with  pointing north, along a line of increasing declination (decl.), and
pointing north, along a line of increasing declination (decl.), and  pointing east, along a line of increasing right ascension (R.A.). The positive
pointing east, along a line of increasing right ascension (R.A.). The positive  -axis, which is also centered on M31, is therefore along our line-of-sight pointing away from us. By this definition, an object moving toward us is defined to have a negative
-axis, which is also centered on M31, is therefore along our line-of-sight pointing away from us. By this definition, an object moving toward us is defined to have a negative  -velocity, while an object moving away from us is defined to have a positive
-velocity, while an object moving away from us is defined to have a positive  -velocity.
-velocity.
 plane and Geha et al. (2006) velocity observations are defined in the
plane and Geha et al. (2006) velocity observations are defined in the  direction. We center our coordinate system on M31 and define the
direction. We center our coordinate system on M31 and define the  plane as the plane of the sky, with
plane as the plane of the sky, with  pointing north, along a line of increasing declination (decl.), and
pointing north, along a line of increasing declination (decl.), and  pointing east, along a line of increasing right ascension (R.A.). The positive
pointing east, along a line of increasing right ascension (R.A.). The positive  -axis, which is also centered on M31, is therefore along our line-of-sight pointing away from us. By this definition, an object moving toward us is defined to have a negative
-axis, which is also centered on M31, is therefore along our line-of-sight pointing away from us. By this definition, an object moving toward us is defined to have a negative  -velocity, while an object moving away from us is defined to have a positive
-velocity, while an object moving away from us is defined to have a positive  -velocity.
-velocity.The center of M31 lies at the center of this coordinate system  . The spherical symmetry of the bulge and the halo require no rotation, while the axisymmetry of the disk requires a rotation of
. The spherical symmetry of the bulge and the halo require no rotation, while the axisymmetry of the disk requires a rotation of  around the
around the  -axis followed by a
-axis followed by a 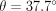 rotation about the
rotation about the  -axis. Thus, if we define a disk as edge on along the
-axis. Thus, if we define a disk as edge on along the  -axis at angles of
-axis at angles of  and
and  then the orientation of the M31 disk in the projected plane of the sky is given by
then the orientation of the M31 disk in the projected plane of the sky is given by
 For computational purposes, the inverse of the matrix above is used to rotate each particle into the frame of M31 (with the disk lying in the
For computational purposes, the inverse of the matrix above is used to rotate each particle into the frame of M31 (with the disk lying in the  plane) in order to compute the particle acceleration due to the disk, and then rotated back into our coordinate system as defined above.
plane) in order to compute the particle acceleration due to the disk, and then rotated back into our coordinate system as defined above.
 . The spherical symmetry of the bulge and the halo require no rotation, while the axisymmetry of the disk requires a rotation of
. The spherical symmetry of the bulge and the halo require no rotation, while the axisymmetry of the disk requires a rotation of  around the
around the  -axis followed by a
-axis followed by a 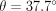 rotation about the
rotation about the  -axis. Thus, if we define a disk as edge on along the
-axis. Thus, if we define a disk as edge on along the  -axis at angles of
-axis at angles of  and
and  then the orientation of the M31 disk in the projected plane of the sky is given by
then the orientation of the M31 disk in the projected plane of the sky is given by

 plane) in order to compute the particle acceleration due to the disk, and then rotated back into our coordinate system as defined above.
plane) in order to compute the particle acceleration due to the disk, and then rotated back into our coordinate system as defined above.There are five major steps involved in the simulation. For each individual orbit, the values of the unknown parameters described in § 3.1 are obtained from the genetic algorithm as discussed in § 3.5. Each step in a simulated orbit is outlined in Figure 4 and described below:
-
First, the center of mass (COM) of NGC 205 is integrated back in time approximately half an orbit using a Bulirsch Stoer integration scheme (Press et al. 1992). The presence of M31’s disk presents difficulties for performing straightforward calculations of the orbital period. Hence, we approximate the orbital period as twice the circular velocity period of NGC 205. Although this approximation is far from exact, we intentionally overcompensate for the period to ensure that the satellite travels at least half an orbit or descends from a reasonably large radii. If the integration time is longer than 6.8 Gyr the orbit is fixed to 6.7 Gyr, since such orbits are much longer than the dynamical timescale for NGC 205. Since only the COM’s
 and
and  positions are known precisely, the final
positions are known precisely, the final  position and the velocity vector (
position and the velocity vector ( ) must be taken from the genetic algorithm’s initial parameter space. The acceleration is computed using a three-component potential model for M31 consisting of a bulge, a disk and a halo as described in § 3.2. We set the required accuracy per time step to one part in 107
.
) must be taken from the genetic algorithm’s initial parameter space. The acceleration is computed using a three-component potential model for M31 consisting of a bulge, a disk and a halo as described in § 3.2. We set the required accuracy per time step to one part in 107
. -
At this earlier time, we assume tidal distortion of NGC 205 has not yet taken place. After successful integration back in time, the initial, undistorted NGC 205 galaxy is created and populated with 1000 massless test particles in a preselected configuration, as discussed in § 3.3. The distribution of test particles is not intended to be a self-consistent tracer of the mass, rather, it is constructed to be a tracer of the expected surface brightness profile of NGC 205 prior to its distortion.
-
Next, the undistorted system of particles is integrated forward in time to the present day under the influence of both galaxies’ potentials. As discussed in § 3.2, we model NGC 205 as a spherically symmetric static potential and M31 as a three-component static potential. The mass,
 , and Hernquist scale length,
, and Hernquist scale length,  , used to construct NGC 205’s potential are unknown parameters and are obtained from the genetic algorithm. We set the required accuracy per particle per time step in our integration to one part in 107
.
, used to construct NGC 205’s potential are unknown parameters and are obtained from the genetic algorithm. We set the required accuracy per particle per time step in our integration to one part in 107
. -
After the integration is complete, the final, simulated system is compared to the known, observed system. The comparison involves a total of six to seven tests, depending on the model used for NGC 205. Although, individually, these tests report a probability measurement, their true purpose is to provide information to the GA instructing it on how to improve subsequent guesses. An outline of each test is provided in § 3.6.
-
Steps 1-4 are repeated until the desired number of orbits is reached. We then use a genetic algorithm to improve our initial conditions and repeat the process until we can match our observations. For each orbit, parameters resulting in a goodness-of-fit value higher than the previous value are recorded. Steps 1-5 are then repeated using a new guesses for the free parameters.
Figure 4.
Schematic overview of the simulated interaction between a cold NGC 205 and M31. In step 1 the center of mass of NGC 205 is integrated back in time approximately half an orbit. In step 2 a cold disk representing the undistorted NGC 205 is created. In step 3 the undistorted disk is integrated forward in time in response to NGC 205’s and M31’s potentials. In step 4 a photometric and kinematic comparison is done between the integrated system and the observed NGC 205 system. |
3.5. The Genetic Algorithm
Our 10-dimensional parameter space discussed in § 3.1 contains approximately 1022
possible orbits. At an average of 6.25 CPU seconds an orbit for our simplest model, the cold disk, an iterative search of the space would take on order 106
CPU Gyr. For this reason, we must efficiently search the parameter space with an optimization algorithm. We have chosen to use the optimization technique invented by Holland (1975) called a genetic algorithm (GA) for two pragmatic reasons. The first is that GAs have the distinct advantage of not getting stuck in local optima, a problem that plagues hill-climbing techniques which exploit gradient information. The second benefit is that GAs are reasonably effective at reducing the amount of searching needed to converge on a solution in a given parameter space. Hence, GAs are especially useful in problems in which iterative searches are computational unreasonable. These two features make genetic algorithms ideal for searching parameter spaces containing an unknown distribution of local optima.
The inspiration behind the GA is biological evolution. The idea follows that evolution is a process determined by chromosomes and natural selection. In the GA application, an individual point in parameter space is equivalent to a chromosome, and the parameters making up that chromosome are analogous to genes. As dictated by biology, evolution occurs at the point of reproduction and individuals with genes advantageous to their species are more likely to reproduce. Mutations of genes and recombination of chromosomes (crossover) can result in offspring that are very different than their biological parents, and if these mutations and recombinations result in a higher level of success for the offspring, they become more likely to reproduce. With each new generation, a new population is created and the old population is replaced.
There are three general modules that define and drive all genetic algorithms, including the evaluation, population, and reproduction modules. Within any particular application, the details of each module can vary. The purpose of the evaluation module is to determine the fitness of a particular individual. Fitness is a measure of an individual’s feasibility as a solution to the problem at hand and is commonly determined by a mathematical function. The fitness is the only information fed into the genetic algorithm and is used in the population and reproduction modules. At any given time, the population module hosts the current population of individuals, called a generation. Encoded in this module are the existing population’s chromosomes and the methods used for creating new generations (e.g., how many children are produced by a set of parents). The method of parent selection (e.g., roulette wheel, stochastic tournament, deterministic sampling) is often contained in this module as well, but can alternatively be a component in the reproduction module. The population module begins by creating an initial population (the first generation), which generally consists of random, single-point guesses in parameter space. The success of a given GA run only weakly depends on this initial first guess. The successive replacements of this population by the reproduction module results in new generations. The reproduction module determines the method by which new chromosomes will be created. The amount of mutation and the method of crossover (the way the parent’s chromosomes are combined to produce offspring) are defined in this module. The resulting offspring becomes an individual of the next generation (Goldberg 1989; Davis 1991).
We use a micro-genetic algorithm (micro-GA) driver designed by D. L. Carroll,4 which employs a tournament selection scheme with a shuffling technique to select individuals for reproduction. Carroll’s micro-GA is characterized by a small population (five individuals), with uniform crossover, elitism, and no mutation or niching. The algorithm works by first arranging individuals in the current population in some arbitrary order (shuffling). Two individuals are then randomly chosen from the population, and the fittest among the pair is selected as a parent (tournament selection). Tournament selection is then repeated to select the second parent. Next, genes are picked at random from the first or second parent to create an offspring (uniform crossover), which subsequently becomes a new member of the next generation. The process of selection and reproduction continues until the new generation is completely populated. In Carroll’s micro-GA configuration, elitism ensures that the best individual from the previous generation is replicated into the new generation and the absence of niching means that only one local optima can exist in a population at any given time.
3.6. Measuring Fitness (The Evaluation Module)
As previously discussed, the only interface between the GA and our  -body simulation is the evaluation module, which determines the fitness of an individual. For our problem, we use the photometric and kinematic observations discussed in § 2 to measure the fitness of each simulated orbit. Since the fitness is a solitary number fed into the genetic algorithm, each simulated galaxy has its photometric and kinematic goodness-of-fit measurements weighted and combined into a single value. The goal of the fitness value is to tell the GA when and how to improve. Hence, it is not advantageous to use a straightforward
-body simulation is the evaluation module, which determines the fitness of an individual. For our problem, we use the photometric and kinematic observations discussed in § 2 to measure the fitness of each simulated orbit. Since the fitness is a solitary number fed into the genetic algorithm, each simulated galaxy has its photometric and kinematic goodness-of-fit measurements weighted and combined into a single value. The goal of the fitness value is to tell the GA when and how to improve. Hence, it is not advantageous to use a straightforward  method (especially since the simulated photometric and kinematic results are dependent on the same parameters); it is, in fact, more effective to weight and combine individual tests that measure the qualities of a given orbit. In our simulation a total of six to seven tests are used. After testing many orders and weighting schemes we find the following configuration to be most effective: two-dimensional two-sided Kolmogorov-Smirnov (2DKS) test with a weight of
method (especially since the simulated photometric and kinematic results are dependent on the same parameters); it is, in fact, more effective to weight and combine individual tests that measure the qualities of a given orbit. In our simulation a total of six to seven tests are used. After testing many orders and weighting schemes we find the following configuration to be most effective: two-dimensional two-sided Kolmogorov-Smirnov (2DKS) test with a weight of  (§ 3.6.1), slope measurement with a weight of
(§ 3.6.1), slope measurement with a weight of  (§ 3.6.2), weighted velocity profile
(§ 3.6.2), weighted velocity profile  probability with a weight of
probability with a weight of  (§ 3.6.3), and surface brightness profile
(§ 3.6.3), and surface brightness profile  probabilities with weights of
probabilities with weights of  each (§ 3.6.4). The weights and criteria for each of these evaluations is discussed below and summarized in Table 3.
each (§ 3.6.4). The weights and criteria for each of these evaluations is discussed below and summarized in Table 3.
 -body simulation is the evaluation module, which determines the fitness of an individual. For our problem, we use the photometric and kinematic observations discussed in § 2 to measure the fitness of each simulated orbit. Since the fitness is a solitary number fed into the genetic algorithm, each simulated galaxy has its photometric and kinematic goodness-of-fit measurements weighted and combined into a single value. The goal of the fitness value is to tell the GA when and how to improve. Hence, it is not advantageous to use a straightforward
-body simulation is the evaluation module, which determines the fitness of an individual. For our problem, we use the photometric and kinematic observations discussed in § 2 to measure the fitness of each simulated orbit. Since the fitness is a solitary number fed into the genetic algorithm, each simulated galaxy has its photometric and kinematic goodness-of-fit measurements weighted and combined into a single value. The goal of the fitness value is to tell the GA when and how to improve. Hence, it is not advantageous to use a straightforward  method (especially since the simulated photometric and kinematic results are dependent on the same parameters); it is, in fact, more effective to weight and combine individual tests that measure the qualities of a given orbit. In our simulation a total of six to seven tests are used. After testing many orders and weighting schemes we find the following configuration to be most effective: two-dimensional two-sided Kolmogorov-Smirnov (2DKS) test with a weight of
method (especially since the simulated photometric and kinematic results are dependent on the same parameters); it is, in fact, more effective to weight and combine individual tests that measure the qualities of a given orbit. In our simulation a total of six to seven tests are used. After testing many orders and weighting schemes we find the following configuration to be most effective: two-dimensional two-sided Kolmogorov-Smirnov (2DKS) test with a weight of  (§ 3.6.1), slope measurement with a weight of
(§ 3.6.1), slope measurement with a weight of  (§ 3.6.2), weighted velocity profile
(§ 3.6.2), weighted velocity profile  probability with a weight of
probability with a weight of  (§ 3.6.3), and surface brightness profile
(§ 3.6.3), and surface brightness profile  probabilities with weights of
probabilities with weights of  each (§ 3.6.4). The weights and criteria for each of these evaluations is discussed below and summarized in Table 3.
each (§ 3.6.4). The weights and criteria for each of these evaluations is discussed below and summarized in Table 3.3.6.1. Two-Dimensional Two-Sided Kolmogorov-Smirnov Test
Our first evaluation uses the two-dimensional two-sided 2DKS test (Press et al. 1992). The observed surface brightness profile of NGC 205 system is modeled as a distribution of particles placed as tracers of the projected surface brightness profile. The number of particles in the “observed” distribution is chosen such that it equals the number of particles in the simulated distribution. The 2DKS test probability,  , is measured using the statistic from Numerical Recipes (Press et al. 1992).
, is measured using the statistic from Numerical Recipes (Press et al. 1992).
 , is measured using the statistic from Numerical Recipes (Press et al. 1992).
, is measured using the statistic from Numerical Recipes (Press et al. 1992).Simulations resulting a probability ≥0.01 are given a fitness value of 0.01 and allowed to proceed to the next test. Those with values <0.01 return a fitness value equal to the 2DKS probability value. The 2DKS test fitness value is thus
 A weight of only
A weight of only  (or a maximum fitness value of 0.01) is given to the 2DKS test because it is most effective at recognizing bad fits, rather than quantifying good fits. That is, the two disadvantages of this test are that it has only a 0.20 significance level and a bias toward the center (since this is where most of the particles are located).
(or a maximum fitness value of 0.01) is given to the 2DKS test because it is most effective at recognizing bad fits, rather than quantifying good fits. That is, the two disadvantages of this test are that it has only a 0.20 significance level and a bias toward the center (since this is where most of the particles are located).

 (or a maximum fitness value of 0.01) is given to the 2DKS test because it is most effective at recognizing bad fits, rather than quantifying good fits. That is, the two disadvantages of this test are that it has only a 0.20 significance level and a bias toward the center (since this is where most of the particles are located).
(or a maximum fitness value of 0.01) is given to the 2DKS test because it is most effective at recognizing bad fits, rather than quantifying good fits. That is, the two disadvantages of this test are that it has only a 0.20 significance level and a bias toward the center (since this is where most of the particles are located).3.6.2. Interior Velocity Slope (Disk Models Only)
We ensure that NGC 205 has the correct tidally undistorted central semimajor axis velocity profile by using the velocity slope interior to ∼ for the second fitness evaluation. This test is performed only on the disk models, since the nonrotating spheroid contains no preservable internal rotation. To determine the simulated semimajor axis velocity profile (and measure its slope), the minimum distance between each test particle and the
for the second fitness evaluation. This test is performed only on the disk models, since the nonrotating spheroid contains no preservable internal rotation. To determine the simulated semimajor axis velocity profile (and measure its slope), the minimum distance between each test particle and the  -shaped major axis of NGC 205 is computed. The slit masks used by Geha et al. (2006) to observe NGC 205’s velocity profile are adjacent to the semimajor axis, with dimensions
-shaped major axis of NGC 205 is computed. The slit masks used by Geha et al. (2006) to observe NGC 205’s velocity profile are adjacent to the semimajor axis, with dimensions  (3.8 kpc) long by
(3.8 kpc) long by  (1.0 kpc) wide. Based on the Geha et al. (2006) collection method, simulated particles whose perpendicular distance to the major axis is less than
(1.0 kpc) wide. Based on the Geha et al. (2006) collection method, simulated particles whose perpendicular distance to the major axis is less than  (1 kpc) are selected, and their velocities are binned and average with neighboring particles to create a simulated velocity profile. The radial size of each velocity bin along the semimajor axis is roughly
(1 kpc) are selected, and their velocities are binned and average with neighboring particles to create a simulated velocity profile. The radial size of each velocity bin along the semimajor axis is roughly  (0.24 kpc).
(0.24 kpc).
 for the second fitness evaluation. This test is performed only on the disk models, since the nonrotating spheroid contains no preservable internal rotation. To determine the simulated semimajor axis velocity profile (and measure its slope), the minimum distance between each test particle and the
for the second fitness evaluation. This test is performed only on the disk models, since the nonrotating spheroid contains no preservable internal rotation. To determine the simulated semimajor axis velocity profile (and measure its slope), the minimum distance between each test particle and the  -shaped major axis of NGC 205 is computed. The slit masks used by Geha et al. (2006) to observe NGC 205’s velocity profile are adjacent to the semimajor axis, with dimensions
-shaped major axis of NGC 205 is computed. The slit masks used by Geha et al. (2006) to observe NGC 205’s velocity profile are adjacent to the semimajor axis, with dimensions  (3.8 kpc) long by
(3.8 kpc) long by  (1.0 kpc) wide. Based on the Geha et al. (2006) collection method, simulated particles whose perpendicular distance to the major axis is less than
(1.0 kpc) wide. Based on the Geha et al. (2006) collection method, simulated particles whose perpendicular distance to the major axis is less than  (1 kpc) are selected, and their velocities are binned and average with neighboring particles to create a simulated velocity profile. The radial size of each velocity bin along the semimajor axis is roughly
(1 kpc) are selected, and their velocities are binned and average with neighboring particles to create a simulated velocity profile. The radial size of each velocity bin along the semimajor axis is roughly  (0.24 kpc).
(0.24 kpc).The allowed slope ( ) range is determined from Geha et al. (2006) velocity observations of NGC 205 (see § 2.2). We set a generous slope range for our simulations of –0.80 to 0.0 km s–1 arcsec–1 (see Fig. 3), corresponding to a –20 to 0.0 km s–1 kpc–1 gradient, if NGC 205 lies at a distance of 824 kpc. The significance level is chosen such that the slope has the maximum range to vary, without ever going positive, and corresponds to 1.83
) range is determined from Geha et al. (2006) velocity observations of NGC 205 (see § 2.2). We set a generous slope range for our simulations of –0.80 to 0.0 km s–1 arcsec–1 (see Fig. 3), corresponding to a –20 to 0.0 km s–1 kpc–1 gradient, if NGC 205 lies at a distance of 824 kpc. The significance level is chosen such that the slope has the maximum range to vary, without ever going positive, and corresponds to 1.83  .
.
 ) range is determined from Geha et al. (2006) velocity observations of NGC 205 (see § 2.2). We set a generous slope range for our simulations of –0.80 to 0.0 km s–1 arcsec–1 (see Fig. 3), corresponding to a –20 to 0.0 km s–1 kpc–1 gradient, if NGC 205 lies at a distance of 824 kpc. The significance level is chosen such that the slope has the maximum range to vary, without ever going positive, and corresponds to 1.83
) range is determined from Geha et al. (2006) velocity observations of NGC 205 (see § 2.2). We set a generous slope range for our simulations of –0.80 to 0.0 km s–1 arcsec–1 (see Fig. 3), corresponding to a –20 to 0.0 km s–1 kpc–1 gradient, if NGC 205 lies at a distance of 824 kpc. The significance level is chosen such that the slope has the maximum range to vary, without ever going positive, and corresponds to 1.83  .
.If the slope falls within the range specified above, it is given a probability of 1 and a weight of  (or a value of 0.09). This is then added to the 2DKS result of 0.01 (for a total fitness value of 0.10) and the code proceeds to the next test. If it does not fall within the range, it is compared with the slope of a previous run in order to determine if the GA is improving and assigned a fitness value. Improvement is defined by how the inner slope is changing with respect to previous orbits and is symbolized by the parameter
(or a value of 0.09). This is then added to the 2DKS result of 0.01 (for a total fitness value of 0.10) and the code proceeds to the next test. If it does not fall within the range, it is compared with the slope of a previous run in order to determine if the GA is improving and assigned a fitness value. Improvement is defined by how the inner slope is changing with respect to previous orbits and is symbolized by the parameter  . The parameter
. The parameter  is set equal to 1 if the absolute value of the slope minus the observationally best-fit slope of –0.40 km s–1 arcsec–1 is less than the previous orbit’s value [i.e.,
is set equal to 1 if the absolute value of the slope minus the observationally best-fit slope of –0.40 km s–1 arcsec–1 is less than the previous orbit’s value [i.e.,  ], and is otherwise set equal to 0. The fitness value at this step is thus given by
], and is otherwise set equal to 0. The fitness value at this step is thus given by
 This results in a minimum fitness value of 0.01 for a slope of
This results in a minimum fitness value of 0.01 for a slope of  , and a maximum fitness value of 0.10 for a slope very close to 0.0 or 0.80 km s–1 arcsec–1. If, instead, the absolute value of the slope minus the best-fit slope is greater than the previous orbit’s value [i.e.,
, and a maximum fitness value of 0.10 for a slope very close to 0.0 or 0.80 km s–1 arcsec–1. If, instead, the absolute value of the slope minus the best-fit slope is greater than the previous orbit’s value [i.e.,  ], then the parameter
], then the parameter  and the GA returns a fitness value of 0.01. The ultimate goal of this evaluation is to inform the GA if it is improving on the internal velocity profile. In the case of the nonrotating spheroid, the fitness is automatically set to 0.10 before proceeding to the next test.
and the GA returns a fitness value of 0.01. The ultimate goal of this evaluation is to inform the GA if it is improving on the internal velocity profile. In the case of the nonrotating spheroid, the fitness is automatically set to 0.10 before proceeding to the next test.
 (or a value of 0.09). This is then added to the 2DKS result of 0.01 (for a total fitness value of 0.10) and the code proceeds to the next test. If it does not fall within the range, it is compared with the slope of a previous run in order to determine if the GA is improving and assigned a fitness value. Improvement is defined by how the inner slope is changing with respect to previous orbits and is symbolized by the parameter
(or a value of 0.09). This is then added to the 2DKS result of 0.01 (for a total fitness value of 0.10) and the code proceeds to the next test. If it does not fall within the range, it is compared with the slope of a previous run in order to determine if the GA is improving and assigned a fitness value. Improvement is defined by how the inner slope is changing with respect to previous orbits and is symbolized by the parameter  . The parameter
. The parameter  is set equal to 1 if the absolute value of the slope minus the observationally best-fit slope of –0.40 km s–1 arcsec–1 is less than the previous orbit’s value [i.e.,
is set equal to 1 if the absolute value of the slope minus the observationally best-fit slope of –0.40 km s–1 arcsec–1 is less than the previous orbit’s value [i.e.,  ], and is otherwise set equal to 0. The fitness value at this step is thus given by
], and is otherwise set equal to 0. The fitness value at this step is thus given by

 , and a maximum fitness value of 0.10 for a slope very close to 0.0 or 0.80 km s–1 arcsec–1. If, instead, the absolute value of the slope minus the best-fit slope is greater than the previous orbit’s value [i.e.,
, and a maximum fitness value of 0.10 for a slope very close to 0.0 or 0.80 km s–1 arcsec–1. If, instead, the absolute value of the slope minus the best-fit slope is greater than the previous orbit’s value [i.e.,  ], then the parameter
], then the parameter  and the GA returns a fitness value of 0.01. The ultimate goal of this evaluation is to inform the GA if it is improving on the internal velocity profile. In the case of the nonrotating spheroid, the fitness is automatically set to 0.10 before proceeding to the next test.
and the GA returns a fitness value of 0.01. The ultimate goal of this evaluation is to inform the GA if it is improving on the internal velocity profile. In the case of the nonrotating spheroid, the fitness is automatically set to 0.10 before proceeding to the next test.3.6.3. Weighted Semimajor Axis Radial Velocity Profile
If the 2DKS test and central slope requirements are satisfied, a weighted  statistic is determined for the semimajor axis velocity profile and a probability
statistic is determined for the semimajor axis velocity profile and a probability  inferred. Similar to the method outlined in § 3.6.2, simulated particles with a perpendicular distance to NGC 205’s semimajor axis less than
inferred. Similar to the method outlined in § 3.6.2, simulated particles with a perpendicular distance to NGC 205’s semimajor axis less than  (1 kpc) are collected and binned. The only difference is that the radial length of the velocity bins are slightly larger than those used to measure the slope. Each bin is chosen to be in accordance with those used by Geha et al. (2006) resulting in an average bin width of approximately
(1 kpc) are collected and binned. The only difference is that the radial length of the velocity bins are slightly larger than those used to measure the slope. Each bin is chosen to be in accordance with those used by Geha et al. (2006) resulting in an average bin width of approximately  (0.48 kpc).
(0.48 kpc).
 statistic is determined for the semimajor axis velocity profile and a probability
statistic is determined for the semimajor axis velocity profile and a probability  inferred. Similar to the method outlined in § 3.6.2, simulated particles with a perpendicular distance to NGC 205’s semimajor axis less than
inferred. Similar to the method outlined in § 3.6.2, simulated particles with a perpendicular distance to NGC 205’s semimajor axis less than  (1 kpc) are collected and binned. The only difference is that the radial length of the velocity bins are slightly larger than those used to measure the slope. Each bin is chosen to be in accordance with those used by Geha et al. (2006) resulting in an average bin width of approximately
(1 kpc) are collected and binned. The only difference is that the radial length of the velocity bins are slightly larger than those used to measure the slope. Each bin is chosen to be in accordance with those used by Geha et al. (2006) resulting in an average bin width of approximately  (0.48 kpc).
(0.48 kpc).The  weights are constructed so that more weight is given to the tidally distorted regions beyond ∼
weights are constructed so that more weight is given to the tidally distorted regions beyond ∼ . Ergo, this externally weighted velocity profile compliments the interior velocity slope discussed in § 3.6.2 to provide a complete description of the semimajor axis velocity profile. We use the weighting function,
. Ergo, this externally weighted velocity profile compliments the interior velocity slope discussed in § 3.6.2 to provide a complete description of the semimajor axis velocity profile. We use the weighting function,
 where
where  determines steepness of the function, and
determines steepness of the function, and  corresponds to the semimajor axis distance at which the weight is equal to
corresponds to the semimajor axis distance at which the weight is equal to  . In our model we set
. In our model we set  and
and 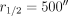 in order to produce
in order to produce  weights that turn on at ∼
weights that turn on at ∼ and rise rapidly. Since the weights are discretely sampled in accordance with Geha et al. (2006) bins, we normalize the weights to the number of available bins:
and rise rapidly. Since the weights are discretely sampled in accordance with Geha et al. (2006) bins, we normalize the weights to the number of available bins:
 where
where  is the semimajor axis value corresponding to the center of each velocity bin, and
is the semimajor axis value corresponding to the center of each velocity bin, and  is the total number of bins. These weights are then used to determine the
is the total number of bins. These weights are then used to determine the  statistic,
statistic,
 where
where  is the average radial velocity found by the simulation in the ith bin, and both
is the average radial velocity found by the simulation in the ith bin, and both  and
and  are the observed average radial velocity and error, respectively, in the ith bin.
are the observed average radial velocity and error, respectively, in the ith bin.
 weights are constructed so that more weight is given to the tidally distorted regions beyond ∼
weights are constructed so that more weight is given to the tidally distorted regions beyond ∼ . Ergo, this externally weighted velocity profile compliments the interior velocity slope discussed in § 3.6.2 to provide a complete description of the semimajor axis velocity profile. We use the weighting function,
. Ergo, this externally weighted velocity profile compliments the interior velocity slope discussed in § 3.6.2 to provide a complete description of the semimajor axis velocity profile. We use the weighting function,

 determines steepness of the function, and
determines steepness of the function, and  corresponds to the semimajor axis distance at which the weight is equal to
corresponds to the semimajor axis distance at which the weight is equal to  . In our model we set
. In our model we set  and
and 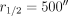 in order to produce
in order to produce  weights that turn on at ∼
weights that turn on at ∼ and rise rapidly. Since the weights are discretely sampled in accordance with Geha et al. (2006) bins, we normalize the weights to the number of available bins:
and rise rapidly. Since the weights are discretely sampled in accordance with Geha et al. (2006) bins, we normalize the weights to the number of available bins:

 is the semimajor axis value corresponding to the center of each velocity bin, and
is the semimajor axis value corresponding to the center of each velocity bin, and  is the total number of bins. These weights are then used to determine the
is the total number of bins. These weights are then used to determine the  statistic,
statistic,

 is the average radial velocity found by the simulation in the ith bin, and both
is the average radial velocity found by the simulation in the ith bin, and both  and
and  are the observed average radial velocity and error, respectively, in the ith bin.
are the observed average radial velocity and error, respectively, in the ith bin.Once the  value is obtained, its statistical significance can be determined using the
value is obtained, its statistical significance can be determined using the  probability function,
probability function,  (Press et al. 1992), where the degrees of freedom value,
(Press et al. 1992), where the degrees of freedom value,  , is given by
, is given by  . If the weighted radial velocity profile probability is ≥10−10
it is considered an adequate fit and a value of
. If the weighted radial velocity profile probability is ≥10−10
it is considered an adequate fit and a value of  is added to the slope and 2DKS fitness. The code then proceeds to the next set of tests. However, if the weighted radial velocity profile probability is <10−10
, then a new fitness is computed by subtracting the inverse logarithm of the probability from the slope and 2DKS fitness. So, based on the probability, the orbit has an updated fitness value of
is added to the slope and 2DKS fitness. The code then proceeds to the next set of tests. However, if the weighted radial velocity profile probability is <10−10
, then a new fitness is computed by subtracting the inverse logarithm of the probability from the slope and 2DKS fitness. So, based on the probability, the orbit has an updated fitness value of
 This results in a minimum fitness value of 0.10 for a
This results in a minimum fitness value of 0.10 for a  probability of 0 and a maximum fitness value of 0.28 for a
probability of 0 and a maximum fitness value of 0.28 for a  probability of 1. The contribution of the weighted radial velocity profile test to the total fitness is 18%.
probability of 1. The contribution of the weighted radial velocity profile test to the total fitness is 18%.
 value is obtained, its statistical significance can be determined using the
value is obtained, its statistical significance can be determined using the  probability function,
probability function,  (Press et al. 1992), where the degrees of freedom value,
(Press et al. 1992), where the degrees of freedom value,  , is given by
, is given by  . If the weighted radial velocity profile probability is ≥10−10
it is considered an adequate fit and a value of
. If the weighted radial velocity profile probability is ≥10−10
it is considered an adequate fit and a value of  is added to the slope and 2DKS fitness. The code then proceeds to the next set of tests. However, if the weighted radial velocity profile probability is <10−10
, then a new fitness is computed by subtracting the inverse logarithm of the probability from the slope and 2DKS fitness. So, based on the probability, the orbit has an updated fitness value of
is added to the slope and 2DKS fitness. The code then proceeds to the next set of tests. However, if the weighted radial velocity profile probability is <10−10
, then a new fitness is computed by subtracting the inverse logarithm of the probability from the slope and 2DKS fitness. So, based on the probability, the orbit has an updated fitness value of

 probability of 0 and a maximum fitness value of 0.28 for a
probability of 0 and a maximum fitness value of 0.28 for a  probability of 1. The contribution of the weighted radial velocity profile test to the total fitness is 18%.
probability of 1. The contribution of the weighted radial velocity profile test to the total fitness is 18%.3.6.4. Weighted and Unweighted Radial and Angular Brightness Profile
If the previous three tests (2DKS, slope, weighted radial velocity profile) are satisfied, the weighted and unweighted  statistics for the projected surface brightness profile are obtained and probabilities,
statistics for the projected surface brightness profile are obtained and probabilities,  , inferred. Since NGC 205 is undergoing tidal distortion, information from both the radial and angular profiles can be used as constraints. It is advantageous to look at the weighted and unweighted, radial and angular profiles independently, since they each provide unique information about the satellite’s orbit. That is, the weighted
, inferred. Since NGC 205 is undergoing tidal distortion, information from both the radial and angular profiles can be used as constraints. It is advantageous to look at the weighted and unweighted, radial and angular profiles independently, since they each provide unique information about the satellite’s orbit. That is, the weighted  statistics give information about the exterior, tidally distorted regions of the satellite, whereas the unweighted
statistics give information about the exterior, tidally distorted regions of the satellite, whereas the unweighted  statistics inform about the interior, undistorted regions of NGC 205. Likewise, the radial profile reveals the extent that the satellite is being compressed or expanded, while the angular profile describes the twisting and elongation of NGC 205.
statistics inform about the interior, undistorted regions of NGC 205. Likewise, the radial profile reveals the extent that the satellite is being compressed or expanded, while the angular profile describes the twisting and elongation of NGC 205.
 statistics for the projected surface brightness profile are obtained and probabilities,
statistics for the projected surface brightness profile are obtained and probabilities,  , inferred. Since NGC 205 is undergoing tidal distortion, information from both the radial and angular profiles can be used as constraints. It is advantageous to look at the weighted and unweighted, radial and angular profiles independently, since they each provide unique information about the satellite’s orbit. That is, the weighted
, inferred. Since NGC 205 is undergoing tidal distortion, information from both the radial and angular profiles can be used as constraints. It is advantageous to look at the weighted and unweighted, radial and angular profiles independently, since they each provide unique information about the satellite’s orbit. That is, the weighted  statistics give information about the exterior, tidally distorted regions of the satellite, whereas the unweighted
statistics give information about the exterior, tidally distorted regions of the satellite, whereas the unweighted  statistics inform about the interior, undistorted regions of NGC 205. Likewise, the radial profile reveals the extent that the satellite is being compressed or expanded, while the angular profile describes the twisting and elongation of NGC 205.
statistics inform about the interior, undistorted regions of NGC 205. Likewise, the radial profile reveals the extent that the satellite is being compressed or expanded, while the angular profile describes the twisting and elongation of NGC 205.In our simulation, massless test particles are used as tracers of surface brightness. The weighted and unweighted angular and radial distribution of test particles is compared with the surface brightness profile given in Figure 2, which uses the data from Choi et al. (2002) in the range  to
to  and our fitted exponential surface brightness profile interior to
and our fitted exponential surface brightness profile interior to  and exterior to
and exterior to  . In addition to this surface brightness profile, we use the position angles and ellipticities measured by Choi et al. (2002) from
. In addition to this surface brightness profile, we use the position angles and ellipticities measured by Choi et al. (2002) from  to
to  . The position angle and ellipticities of the isophotes internal to
. The position angle and ellipticities of the isophotes internal to  and external to
and external to  are held fixed, since interior to this we have removed the nucleus and exterior to this the surface brightness and sky become comparable.
are held fixed, since interior to this we have removed the nucleus and exterior to this the surface brightness and sky become comparable.
 to
to  and our fitted exponential surface brightness profile interior to
and our fitted exponential surface brightness profile interior to  and exterior to
and exterior to  . In addition to this surface brightness profile, we use the position angles and ellipticities measured by Choi et al. (2002) from
. In addition to this surface brightness profile, we use the position angles and ellipticities measured by Choi et al. (2002) from  to
to  . The position angle and ellipticities of the isophotes internal to
. The position angle and ellipticities of the isophotes internal to  and external to
and external to  are held fixed, since interior to this we have removed the nucleus and exterior to this the surface brightness and sky become comparable.
are held fixed, since interior to this we have removed the nucleus and exterior to this the surface brightness and sky become comparable.For the  tests, we step in semimajor axis units of
tests, we step in semimajor axis units of  (∼
(∼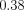 kpc) and in angular units of
kpc) and in angular units of  . We measure out to a maximum semimajor axis distance of
. We measure out to a maximum semimajor axis distance of  (∼
(∼ kpc) and use the center of each areal bin to determine the corresponding surface brightness. Since our semimajor axis steps are not coincident with those of Choi et al. (2002) isophotes, we interpolate to obtain an intermediate ellipticity and position angle that is complementary to our step. The unweighted radial surface brightness profile of the simulated distribution is then found by summing the number of tracer particles within each predetermined isophotal annulus, while the unweighted angular surface brightness profile is measured by totaling the number of tracer particles contained within each angular beam. The unweighted
kpc) and use the center of each areal bin to determine the corresponding surface brightness. Since our semimajor axis steps are not coincident with those of Choi et al. (2002) isophotes, we interpolate to obtain an intermediate ellipticity and position angle that is complementary to our step. The unweighted radial surface brightness profile of the simulated distribution is then found by summing the number of tracer particles within each predetermined isophotal annulus, while the unweighted angular surface brightness profile is measured by totaling the number of tracer particles contained within each angular beam. The unweighted  statistic for both the radial and angular surface brightness profiles can then be computed using equation (28), setting each weight
statistic for both the radial and angular surface brightness profiles can then be computed using equation (28), setting each weight  equal to 1, normalizing our observed distribution
equal to 1, normalizing our observed distribution  to total the number of tracer particles used in the simulation, and setting
to total the number of tracer particles used in the simulation, and setting  equal to
equal to  , the number of expected particles in the bin. For the weighted
, the number of expected particles in the bin. For the weighted  tests, the same formula is followed, except that the weighting function given by equation (26) is used to determine
tests, the same formula is followed, except that the weighting function given by equation (26) is used to determine  .
.
 tests, we step in semimajor axis units of
tests, we step in semimajor axis units of  (∼
(∼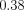 kpc) and in angular units of
kpc) and in angular units of  . We measure out to a maximum semimajor axis distance of
. We measure out to a maximum semimajor axis distance of  (∼
(∼ kpc) and use the center of each areal bin to determine the corresponding surface brightness. Since our semimajor axis steps are not coincident with those of Choi et al. (2002) isophotes, we interpolate to obtain an intermediate ellipticity and position angle that is complementary to our step. The unweighted radial surface brightness profile of the simulated distribution is then found by summing the number of tracer particles within each predetermined isophotal annulus, while the unweighted angular surface brightness profile is measured by totaling the number of tracer particles contained within each angular beam. The unweighted
kpc) and use the center of each areal bin to determine the corresponding surface brightness. Since our semimajor axis steps are not coincident with those of Choi et al. (2002) isophotes, we interpolate to obtain an intermediate ellipticity and position angle that is complementary to our step. The unweighted radial surface brightness profile of the simulated distribution is then found by summing the number of tracer particles within each predetermined isophotal annulus, while the unweighted angular surface brightness profile is measured by totaling the number of tracer particles contained within each angular beam. The unweighted  statistic for both the radial and angular surface brightness profiles can then be computed using equation (28), setting each weight
statistic for both the radial and angular surface brightness profiles can then be computed using equation (28), setting each weight  equal to 1, normalizing our observed distribution
equal to 1, normalizing our observed distribution  to total the number of tracer particles used in the simulation, and setting
to total the number of tracer particles used in the simulation, and setting  equal to
equal to  , the number of expected particles in the bin. For the weighted
, the number of expected particles in the bin. For the weighted  tests, the same formula is followed, except that the weighting function given by equation (26) is used to determine
tests, the same formula is followed, except that the weighting function given by equation (26) is used to determine  .
.Each of the four surface brightness profile tests discussed above are evaluated independently and combined to update the GA fitness. Similar to the velocity profile test in § 3.6.3, tests with probabilities ≥10−10
are considered reasonable fits and are assigned a value of  . Profiles resulting in probabilities <10−10
are designated bad fits and assigned a value of –
. Profiles resulting in probabilities <10−10
are designated bad fits and assigned a value of –![1.0/ \mathrm{log}\,[ Q_{j}( \chi ^{2}\vert \nu ) ]](https://content.cld.iop.org/journals/0004-637X/683/2/722/revision1/eq-00409.gif) . The updated fitness then becomes
. The updated fitness then becomes

 where the
where the  index specifies which of the four surface brightness profile tests, and
index specifies which of the four surface brightness profile tests, and  refers to the weighted velocity profile fitness from equation (29). Hence, each
refers to the weighted velocity profile fitness from equation (29). Hence, each  test can contribute a maximum of
test can contribute a maximum of  to the total fitness, resulting in a maximum fitness value of 1. Once the fitness of a orbit has been determined, the GA can use the information to create new, improved orbits.
to the total fitness, resulting in a maximum fitness value of 1. Once the fitness of a orbit has been determined, the GA can use the information to create new, improved orbits.
 . Profiles resulting in probabilities <10−10
are designated bad fits and assigned a value of –
. Profiles resulting in probabilities <10−10
are designated bad fits and assigned a value of –![1.0/ \mathrm{log}\,[ Q_{j}( \chi ^{2}\vert \nu ) ]](https://content.cld.iop.org/journals/0004-637X/683/2/722/revision1/eq-00409.gif) . The updated fitness then becomes
. The updated fitness then becomes


 index specifies which of the four surface brightness profile tests, and
index specifies which of the four surface brightness profile tests, and  refers to the weighted velocity profile fitness from equation (29). Hence, each
refers to the weighted velocity profile fitness from equation (29). Hence, each  test can contribute a maximum of
test can contribute a maximum of  to the total fitness, resulting in a maximum fitness value of 1. Once the fitness of a orbit has been determined, the GA can use the information to create new, improved orbits.
to the total fitness, resulting in a maximum fitness value of 1. Once the fitness of a orbit has been determined, the GA can use the information to create new, improved orbits.4 See the Fortran Genetic Algorithm Driver V1.7a, at http://cuaerospace.com/carroll/ga.html.
4. RESULTS
In this section we present the genetic algorithm’s results for the three NGC 205 models outlined in § 3.3: the rotating cold disk (§ 4.1), the rotating warm disk (§ 4.2), and the nonrotating hot spheroid (§ 4.3). We perform 1000 GA runs on each model (with different initial random number seeds for each run) in order to thoroughly explore the parameter space and expose possible degeneracies. Each GA run consists of 1000 generations of 5 individual orbits and produces a best orbit (highest fitness) from these 5000 orbits. Hence, for each model,  orbits are explored and 103
best orbits are returned. Below the resulting direction of NGC 205’s approach on the sky plane, parameter values and single best orbit are given for these three models.
orbits are explored and 103
best orbits are returned. Below the resulting direction of NGC 205’s approach on the sky plane, parameter values and single best orbit are given for these three models.
 orbits are explored and 103
best orbits are returned. Below the resulting direction of NGC 205’s approach on the sky plane, parameter values and single best orbit are given for these three models.
orbits are explored and 103
best orbits are returned. Below the resulting direction of NGC 205’s approach on the sky plane, parameter values and single best orbit are given for these three models.4.1. Rotating Cold Disk
We initialize NGC 205 as a rotating, cold exponential disk of massless test particles, serving as tracers of surface brightness. The resulting direction of approach (§ 4.1.1), preferred parameter values (§ 4.1.2), and best orbit (§ 4.1.3) for the cold disk simulations are outlined below.
4.1.1. Direction of NGC 205’s Approach (Cold Disk)
Figure 5 shows histograms of NGC 205’s varying directions of approach on the plane of the sky and selected spatial projections for the cold, rotating disk model. The histogram in Figure 5a depicts the best orbit from each of the 1000 GA runs. Even without any further constraints, a clear directional preference emerges from the 1000 orbits. The histogram peaks at 148 orbits with NGC 205 advancing from the west (W), followed closely by 140 orbits from the west-northwest (WNW) and 130 orbits from the northwest. Of these 1000 orbits, 752 are bound to M31, 500 are prograde, 280 are retrograde and 220 are radial (with radial orbits defined by  ).
).
 ).
).Figure 5.
Cold disk model. Direction of approach for NGC 205 modeled as an initially rotating, cold disk. (a) The best orbit from each of the 1000 GA runs. (b) Orbits with additional photometric, kinematic, and fitness constraints. Included is the resulting best orbit from a single GA run with 3000 particles (dashed line). (c) The sky-projected (  ) orbits from the shaded region of the histogram. Also plotted are M31’s bulge and disk at 2 scale radii (subtending
) orbits from the shaded region of the histogram. Also plotted are M31’s bulge and disk at 2 scale radii (subtending  and
and  , respectively), an approximation of McConnachie et al. (2004) stellar arc and two surface brightness isophotes, one at
, respectively), an approximation of McConnachie et al. (2004) stellar arc and two surface brightness isophotes, one at  (the onset of NGC 205’s tidal distortion) and the other at
(the onset of NGC 205’s tidal distortion) and the other at  (NGC 205’s tidal radius). Note that none of these orbits trace the stellar arc observed in M31’s northwest quadrant. (d) The line-of-sight (
(NGC 205’s tidal radius). Note that none of these orbits trace the stellar arc observed in M31’s northwest quadrant. (d) The line-of-sight ( ) orbits from the shaded region of the histogram. Also included are M31’s bulge and disk at 2 scale radii and the investigated
) orbits from the shaded region of the histogram. Also included are M31’s bulge and disk at 2 scale radii and the investigated  -values (2-76 kpc).
-values (2-76 kpc). |
Figure 5b shows orbits with additional photometric, kinematic, and fitness constraints. The outlined histogram imposes a weighted velocity  probability ≥10−10
and return values ≥
probability ≥10−10
and return values ≥ for each of the four surface brightness
for each of the four surface brightness  probabilities (§ 3.6.3-§ 3.6.4). This constraint significantly reduces the initial 1000 orbits to 32 orbits and returns a direction of approach that lies somewhere between the north-northwest (NNW) and west, with the peak lying in the northwest. Furthermore, none of these orbits is retrograde (in fact, none of the retrograde orbits has a fitness >0.25). The enclosed shaded region further imposes the condition that fitness ≥
probabilities (§ 3.6.3-§ 3.6.4). This constraint significantly reduces the initial 1000 orbits to 32 orbits and returns a direction of approach that lies somewhere between the north-northwest (NNW) and west, with the peak lying in the northwest. Furthermore, none of these orbits is retrograde (in fact, none of the retrograde orbits has a fitness >0.25). The enclosed shaded region further imposes the condition that fitness ≥ , a value selected to be just below that of the top 10 orbits (or
, a value selected to be just below that of the top 10 orbits (or  ). This results in a reduction from 32 orbits to 9, meaning that one of the top 10 orbits fails to satisfy all the imposed photometric and kinematic constraints. The remaining directions of approach continue to peak in the northwest, with only west approaches now ruled out. Hence, the directional preference initially suggested by the histogram of 1000 orbits is reinforced by the addition of photometric, kinematic and fitness requirements.
). This results in a reduction from 32 orbits to 9, meaning that one of the top 10 orbits fails to satisfy all the imposed photometric and kinematic constraints. The remaining directions of approach continue to peak in the northwest, with only west approaches now ruled out. Hence, the directional preference initially suggested by the histogram of 1000 orbits is reinforced by the addition of photometric, kinematic and fitness requirements.
 probability ≥10−10
and return values ≥
probability ≥10−10
and return values ≥ for each of the four surface brightness
for each of the four surface brightness  probabilities (§ 3.6.3-§ 3.6.4). This constraint significantly reduces the initial 1000 orbits to 32 orbits and returns a direction of approach that lies somewhere between the north-northwest (NNW) and west, with the peak lying in the northwest. Furthermore, none of these orbits is retrograde (in fact, none of the retrograde orbits has a fitness >0.25). The enclosed shaded region further imposes the condition that fitness ≥
probabilities (§ 3.6.3-§ 3.6.4). This constraint significantly reduces the initial 1000 orbits to 32 orbits and returns a direction of approach that lies somewhere between the north-northwest (NNW) and west, with the peak lying in the northwest. Furthermore, none of these orbits is retrograde (in fact, none of the retrograde orbits has a fitness >0.25). The enclosed shaded region further imposes the condition that fitness ≥ , a value selected to be just below that of the top 10 orbits (or
, a value selected to be just below that of the top 10 orbits (or  ). This results in a reduction from 32 orbits to 9, meaning that one of the top 10 orbits fails to satisfy all the imposed photometric and kinematic constraints. The remaining directions of approach continue to peak in the northwest, with only west approaches now ruled out. Hence, the directional preference initially suggested by the histogram of 1000 orbits is reinforced by the addition of photometric, kinematic and fitness requirements.
). This results in a reduction from 32 orbits to 9, meaning that one of the top 10 orbits fails to satisfy all the imposed photometric and kinematic constraints. The remaining directions of approach continue to peak in the northwest, with only west approaches now ruled out. Hence, the directional preference initially suggested by the histogram of 1000 orbits is reinforced by the addition of photometric, kinematic and fitness requirements.More importantly, these constraints rule out other possible orbits for the cold disk model. This includes McConnachie et al. (2004) favored  long stellar arclike feature (observed in the northwest quadrant of M31) as a tidal stellar stream originating from NGC 205. Modeling this trail as tidal debris from the satellite suggests encroachment from somewhere in between the north-northeast (NNE) and east (E) region (
long stellar arclike feature (observed in the northwest quadrant of M31) as a tidal stellar stream originating from NGC 205. Modeling this trail as tidal debris from the satellite suggests encroachment from somewhere in between the north-northeast (NNE) and east (E) region ( -
- ) on the plane of the sky. While
) on the plane of the sky. While  of the orbits from the 1000 GA runs fall within this four-bin region, we find that these orbits all have poor angular surface brightness distributions (i.e., they cannot simultaneously match both a weighted and unweighted angular
of the orbits from the 1000 GA runs fall within this four-bin region, we find that these orbits all have poor angular surface brightness distributions (i.e., they cannot simultaneously match both a weighted and unweighted angular  probability constraint of 0.1). This result indicates that orbits approaching from the north-northeast through east are ruled out as solutions by the observed isophotal twisting in NGC 205 (§ 2.1).
probability constraint of 0.1). This result indicates that orbits approaching from the north-northeast through east are ruled out as solutions by the observed isophotal twisting in NGC 205 (§ 2.1).
 long stellar arclike feature (observed in the northwest quadrant of M31) as a tidal stellar stream originating from NGC 205. Modeling this trail as tidal debris from the satellite suggests encroachment from somewhere in between the north-northeast (NNE) and east (E) region (
long stellar arclike feature (observed in the northwest quadrant of M31) as a tidal stellar stream originating from NGC 205. Modeling this trail as tidal debris from the satellite suggests encroachment from somewhere in between the north-northeast (NNE) and east (E) region ( -
- ) on the plane of the sky. While
) on the plane of the sky. While  of the orbits from the 1000 GA runs fall within this four-bin region, we find that these orbits all have poor angular surface brightness distributions (i.e., they cannot simultaneously match both a weighted and unweighted angular
of the orbits from the 1000 GA runs fall within this four-bin region, we find that these orbits all have poor angular surface brightness distributions (i.e., they cannot simultaneously match both a weighted and unweighted angular  probability constraint of 0.1). This result indicates that orbits approaching from the north-northeast through east are ruled out as solutions by the observed isophotal twisting in NGC 205 (§ 2.1).
probability constraint of 0.1). This result indicates that orbits approaching from the north-northeast through east are ruled out as solutions by the observed isophotal twisting in NGC 205 (§ 2.1).To further test this conclusion, we perform a single cold disk GA run with 3000 particles. While numerous GA runs with >1000 particles are too expensive for our purposes, a single GA run allows us to check our results against a more complex system. The 3000 particle GA run returns a direction of approach from the north-northwest, an orbit in qualitative agreement with our 1000 particle runs. This result is denoted in Figure 5b with a dashed line.
The plots at the bottom of Figure 5 show the trajectories of the constrained 9 orbits corresponding to the shaded region in Figure 5b. All 9 orbits have very large tangential motions and are not bound to M31. Included in the  sky projection plot (Fig. 5c) are tracers of the 9 orbits, an approximation of McConnachie et al. (2004) stellar arc, M31’s bulge and disk at 2 scale radii (subtending
sky projection plot (Fig. 5c) are tracers of the 9 orbits, an approximation of McConnachie et al. (2004) stellar arc, M31’s bulge and disk at 2 scale radii (subtending  and
and  , respectively), and two surface brightness isophotes, one at
, respectively), and two surface brightness isophotes, one at  corresponding to the onset of NGC 205’s tidal distortion and the other at
corresponding to the onset of NGC 205’s tidal distortion and the other at  indicating NGC 205’s tidal radius. As discussed, none of the constrained orbits trace the stellar arc observed in the northwest quadrant of M31. Included in the
indicating NGC 205’s tidal radius. As discussed, none of the constrained orbits trace the stellar arc observed in the northwest quadrant of M31. Included in the  line-of-sight plot (Fig. 5d) are tracers of the 9 orbits, M31’s bulge and disk at 2 scale radii, and the range of allowed
line-of-sight plot (Fig. 5d) are tracers of the 9 orbits, M31’s bulge and disk at 2 scale radii, and the range of allowed  -values (2-76 kpc). All nine orbits converge at distances very close to M31 and follow roughly similar trajectories. Furthermore, the nine orbits begin on nearly radial courses with
-values (2-76 kpc). All nine orbits converge at distances very close to M31 and follow roughly similar trajectories. Furthermore, the nine orbits begin on nearly radial courses with  , where
, where  is the angle between
is the angle between  and
and  , the position vector from the center of NGC 205 to M31 and the velocity vector of NGC 205, respectively. Ergo, the radial paths of these nine simulated satellites precludes prograde or retrograde encounters.
, the position vector from the center of NGC 205 to M31 and the velocity vector of NGC 205, respectively. Ergo, the radial paths of these nine simulated satellites precludes prograde or retrograde encounters.
 sky projection plot (Fig. 5c) are tracers of the 9 orbits, an approximation of McConnachie et al. (2004) stellar arc, M31’s bulge and disk at 2 scale radii (subtending
sky projection plot (Fig. 5c) are tracers of the 9 orbits, an approximation of McConnachie et al. (2004) stellar arc, M31’s bulge and disk at 2 scale radii (subtending  and
and  , respectively), and two surface brightness isophotes, one at
, respectively), and two surface brightness isophotes, one at  corresponding to the onset of NGC 205’s tidal distortion and the other at
corresponding to the onset of NGC 205’s tidal distortion and the other at  indicating NGC 205’s tidal radius. As discussed, none of the constrained orbits trace the stellar arc observed in the northwest quadrant of M31. Included in the
indicating NGC 205’s tidal radius. As discussed, none of the constrained orbits trace the stellar arc observed in the northwest quadrant of M31. Included in the  line-of-sight plot (Fig. 5d) are tracers of the 9 orbits, M31’s bulge and disk at 2 scale radii, and the range of allowed
line-of-sight plot (Fig. 5d) are tracers of the 9 orbits, M31’s bulge and disk at 2 scale radii, and the range of allowed  -values (2-76 kpc). All nine orbits converge at distances very close to M31 and follow roughly similar trajectories. Furthermore, the nine orbits begin on nearly radial courses with
-values (2-76 kpc). All nine orbits converge at distances very close to M31 and follow roughly similar trajectories. Furthermore, the nine orbits begin on nearly radial courses with  , where
, where  is the angle between
is the angle between  and
and  , the position vector from the center of NGC 205 to M31 and the velocity vector of NGC 205, respectively. Ergo, the radial paths of these nine simulated satellites precludes prograde or retrograde encounters.
, the position vector from the center of NGC 205 to M31 and the velocity vector of NGC 205, respectively. Ergo, the radial paths of these nine simulated satellites precludes prograde or retrograde encounters.4.1.2. Preferred Parameter Values (Cold Disk)
Figure 6 shows the evolved parameter values resulting from the 1000 cold disk GA runs. Each best orbit’s parameter and corresponding fitness are plotted. Since the fitness is determined by combining numerous tests, the line illustrating passing criteria for each fitness step is also included, with the sole exception of the 2DKS test for which all 1000 orbits quantitatively pass. The 9 constrained orbits from Figure 5b and the cutoff fitness value line for the top 10 orbits are highlighted in red. In addition, the resulting best orbit’s parameter values from the 3000 particle GA run are included (dashed line).
Figure 6.
Cold disk model. Plotted are the parameter values vs. fitness from the 1000 GA runs when NGC 205 is modeled as a rotating, cold disk. Each point corresponds to the best orbit from an individual GA run and a particular initial configuration (structure, dynamics, orientation) of the progenitor. The included lines denote passing criteria for the various fitness tests: slope test (  ), weighted velocity
), weighted velocity  test (
test ( ), all five
), all five  tests (
tests ( ), top 10 (
), top 10 ( ) orbits (red line,
) orbits (red line, 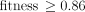 ), and nine constrained orbits (highlighted in red). Orbits that fail are poor fits to photometry and/or kinematics and reside below the
), and nine constrained orbits (highlighted in red). Orbits that fail are poor fits to photometry and/or kinematics and reside below the  line. Also included are the parameter values of the resulting best orbit from a single GA run with 3000 particles (dashed line).
line. Also included are the parameter values of the resulting best orbit from a single GA run with 3000 particles (dashed line). |
The GA’s preference for certain parameter values emerges in Figure 6. The most notable concentration is in the initial scale radius  of NGC 205, shown in detail in Figure 7 (top row). The 1000 simulations converge at
of NGC 205, shown in detail in Figure 7 (top row). The 1000 simulations converge at  (
( kpc), with orbits passing all five
kpc), with orbits passing all five  tests (
tests ( ) at
) at  (
( kpc) and the constrained 9 orbits (highlighted in red) focused at
kpc) and the constrained 9 orbits (highlighted in red) focused at  (
(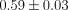 kpc), a value equivalent to the satellite’s present scale radius. This implies that a large portion of NGC 205 is unaffected by tides and the internal regions of the satellite have experienced little, if any, distortion. The remaining parameters experience a greater amount of scatter. However, definite trends still exist in the data. For example, the simulations favor orbits with very large velocities of
kpc), a value equivalent to the satellite’s present scale radius. This implies that a large portion of NGC 205 is unaffected by tides and the internal regions of the satellite have experienced little, if any, distortion. The remaining parameters experience a greater amount of scatter. However, definite trends still exist in the data. For example, the simulations favor orbits with very large velocities of  km s–1 (Fig. 7, middle row;
km s–1 (Fig. 7, middle row;  ), preferentially moving NGC 205 toward the south (
), preferentially moving NGC 205 toward the south ( km s–1) and to the east (
km s–1) and to the east ( km s–1). In addition, the GA prefers
km s–1). In addition, the GA prefers  distances very close to M31 with
distances very close to M31 with  kpc (Fig. 7, bottom row;
kpc (Fig. 7, bottom row;  ). An orbit’s fitness beyond this distance declines rapidly. Also included in Figure 7 are the resulting best orbit’s
). An orbit’s fitness beyond this distance declines rapidly. Also included in Figure 7 are the resulting best orbit’s  ,
,  , and
, and  -values from the 3000 particle GA run (dashed line). Note that these values are in qualitative agreement with the 1000 particle GA runs, with a slightly higher
-values from the 3000 particle GA run (dashed line). Note that these values are in qualitative agreement with the 1000 particle GA runs, with a slightly higher  value that is comparable to the velocities of the nine constrained orbits.
value that is comparable to the velocities of the nine constrained orbits.
 of NGC 205, shown in detail in Figure 7 (top row). The 1000 simulations converge at
of NGC 205, shown in detail in Figure 7 (top row). The 1000 simulations converge at  (
( kpc), with orbits passing all five
kpc), with orbits passing all five  tests (
tests ( ) at
) at  (
( kpc) and the constrained 9 orbits (highlighted in red) focused at
kpc) and the constrained 9 orbits (highlighted in red) focused at  (
(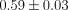 kpc), a value equivalent to the satellite’s present scale radius. This implies that a large portion of NGC 205 is unaffected by tides and the internal regions of the satellite have experienced little, if any, distortion. The remaining parameters experience a greater amount of scatter. However, definite trends still exist in the data. For example, the simulations favor orbits with very large velocities of
kpc), a value equivalent to the satellite’s present scale radius. This implies that a large portion of NGC 205 is unaffected by tides and the internal regions of the satellite have experienced little, if any, distortion. The remaining parameters experience a greater amount of scatter. However, definite trends still exist in the data. For example, the simulations favor orbits with very large velocities of  km s–1 (Fig. 7, middle row;
km s–1 (Fig. 7, middle row;  ), preferentially moving NGC 205 toward the south (
), preferentially moving NGC 205 toward the south ( km s–1) and to the east (
km s–1) and to the east ( km s–1). In addition, the GA prefers
km s–1). In addition, the GA prefers  distances very close to M31 with
distances very close to M31 with  kpc (Fig. 7, bottom row;
kpc (Fig. 7, bottom row;  ). An orbit’s fitness beyond this distance declines rapidly. Also included in Figure 7 are the resulting best orbit’s
). An orbit’s fitness beyond this distance declines rapidly. Also included in Figure 7 are the resulting best orbit’s  ,
,  , and
, and  -values from the 3000 particle GA run (dashed line). Note that these values are in qualitative agreement with the 1000 particle GA runs, with a slightly higher
-values from the 3000 particle GA run (dashed line). Note that these values are in qualitative agreement with the 1000 particle GA runs, with a slightly higher  value that is comparable to the velocities of the nine constrained orbits.
value that is comparable to the velocities of the nine constrained orbits.Figure 7.
Cold disk model. Shown here are three parameters for the rotating, cold disk model that are well constrained by the GA. Top to bottom: Initial scale length  , velocity magnitude
, velocity magnitude  , and line-of-sight distance
, and line-of-sight distance  . Left to right: Parameter values vs. fitness for the 1000 GA runs, histograms, and fitted Gaussians (except
. Left to right: Parameter values vs. fitness for the 1000 GA runs, histograms, and fitted Gaussians (except  ) for all 1000 GA runs, and histograms and fitted Gaussians for orbits satisfying
) for all 1000 GA runs, and histograms and fitted Gaussians for orbits satisfying  . Orbits with
. Orbits with  give
give  ,
,  km s–1,
km s–1,  kpc. Also included are the parameter values of the resulting best orbit from a single GA run with 3000 particles (dashed line).
kpc. Also included are the parameter values of the resulting best orbit from a single GA run with 3000 particles (dashed line). |
Conversely, some of the parameters cannot be further reduced by the simulations. The huge scatter in the radial velocity,  , indicates that the GA is unable to constrain this value beyond current observations (Fig. 6, middle row, first column). This result is not surprising, since the observed error on
, indicates that the GA is unable to constrain this value beyond current observations (Fig. 6, middle row, first column). This result is not surprising, since the observed error on  is quite small. In addition, the GA is unable to reach convergence for the satellite’s mass,
is quite small. In addition, the GA is unable to reach convergence for the satellite’s mass,  , and Hernquist scale length,
, and Hernquist scale length,  . One explanation for this is that significant degeneracies might exist for
. One explanation for this is that significant degeneracies might exist for  and
and  in the parameter space. A second possibility is that perhaps the photometric and kinematic fitness tests are not as sensitive to
in the parameter space. A second possibility is that perhaps the photometric and kinematic fitness tests are not as sensitive to  and
and  as they are to the other parameters. Hence, the GA both produces inconclusive results for
as they are to the other parameters. Hence, the GA both produces inconclusive results for  and
and  and does not further reduce the observed error on
and does not further reduce the observed error on  . However, it is able to tightly constrain NGC 205’s initial scale radius and place more general bounds on the remaining five parameters.
. However, it is able to tightly constrain NGC 205’s initial scale radius and place more general bounds on the remaining five parameters.
 , indicates that the GA is unable to constrain this value beyond current observations (Fig. 6, middle row, first column). This result is not surprising, since the observed error on
, indicates that the GA is unable to constrain this value beyond current observations (Fig. 6, middle row, first column). This result is not surprising, since the observed error on  is quite small. In addition, the GA is unable to reach convergence for the satellite’s mass,
is quite small. In addition, the GA is unable to reach convergence for the satellite’s mass,  , and Hernquist scale length,
, and Hernquist scale length,  . One explanation for this is that significant degeneracies might exist for
. One explanation for this is that significant degeneracies might exist for  and
and  in the parameter space. A second possibility is that perhaps the photometric and kinematic fitness tests are not as sensitive to
in the parameter space. A second possibility is that perhaps the photometric and kinematic fitness tests are not as sensitive to  and
and  as they are to the other parameters. Hence, the GA both produces inconclusive results for
as they are to the other parameters. Hence, the GA both produces inconclusive results for  and
and  and does not further reduce the observed error on
and does not further reduce the observed error on  . However, it is able to tightly constrain NGC 205’s initial scale radius and place more general bounds on the remaining five parameters.
. However, it is able to tightly constrain NGC 205’s initial scale radius and place more general bounds on the remaining five parameters.4.1.3. Best Orbit (Cold Disk)
Figure 8 shows the resulting best orbit from the 1000 GA runs using the cold disk model. This best orbit approaches from the northwest, is unbound to M31 (with  and
and  km s–1) and has a fitness value of 0.90. Figure 8a displays the simulated galaxy and its trajectory on the plane of the sky (in black). Also included (in red) are M31’s bulge and disk, at
km s–1) and has a fitness value of 0.90. Figure 8a displays the simulated galaxy and its trajectory on the plane of the sky (in black). Also included (in red) are M31’s bulge and disk, at  and
and  , and the predicted particle distribution for NGC 205, derived from Choi et al. (2002) isophotes and our surface brightness profile (see § 2, Fig. 2). Figure 8b shows this same orbit in the
, and the predicted particle distribution for NGC 205, derived from Choi et al. (2002) isophotes and our surface brightness profile (see § 2, Fig. 2). Figure 8b shows this same orbit in the  plane, with the addition of a vertical red line denoting the allowed
plane, with the addition of a vertical red line denoting the allowed  parameter values (
parameter values ( kpc). Shown in the bottom plots are the simulated galaxy’s velocity dispersion (circles) and performance on the five
kpc). Shown in the bottom plots are the simulated galaxy’s velocity dispersion (circles) and performance on the five  tests, with Choi et al. (2002) isophotes and Geha et al. (2006) velocity profile+errors depicted in red. The simulated surface brightness
tests, with Choi et al. (2002) isophotes and Geha et al. (2006) velocity profile+errors depicted in red. The simulated surface brightness  tests result in probabilities of 0.979, 0.856, 0.999, and 0.852 for the radial, angular, weighted radial and weighted angular tests, respectively, and in a
tests result in probabilities of 0.979, 0.856, 0.999, and 0.852 for the radial, angular, weighted radial and weighted angular tests, respectively, and in a  probability of
probability of  for the weighted velocity profile. Note that while the weighted velocity profile probability seems quite low, it satisfies the goal of the simulation by matching the turnover and reversal in the semimajor axis velocity profile. Furthermore, although this satellite began as a purely rotating disk with no dispersion, after the simulated interaction with M31 a Gaussian fit to the combined velocity distribution for all particles along the semimajor axis is 3 km s–1. Even though this simulated average dispersion is much lower than the observed average dispersion of 42 km s–1 (Geha et al. 2006), its presence indicates that some of the observed dispersion could have been tidally induced by M31. In order to reduce the Poisson noise in the dispersion profile, we reran the orbit with 5500 particles. The resulting 5500 particle Gaussian fitted velocity dispersion profile is given in Figure 8e (solid black line). The parameter values of the 1000 particle orbit are as follows:
for the weighted velocity profile. Note that while the weighted velocity profile probability seems quite low, it satisfies the goal of the simulation by matching the turnover and reversal in the semimajor axis velocity profile. Furthermore, although this satellite began as a purely rotating disk with no dispersion, after the simulated interaction with M31 a Gaussian fit to the combined velocity distribution for all particles along the semimajor axis is 3 km s–1. Even though this simulated average dispersion is much lower than the observed average dispersion of 42 km s–1 (Geha et al. 2006), its presence indicates that some of the observed dispersion could have been tidally induced by M31. In order to reduce the Poisson noise in the dispersion profile, we reran the orbit with 5500 particles. The resulting 5500 particle Gaussian fitted velocity dispersion profile is given in Figure 8e (solid black line). The parameter values of the 1000 particle orbit are as follows: 
 ;
;  ,
,  ,
,  km s–1;
km s–1;  ,
,  kpc;
kpc;  ,
,  ; and
; and  kpc. This orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. However, the radial path of the orbit precludes any sense of a prograde or retrograde encounter.
kpc. This orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. However, the radial path of the orbit precludes any sense of a prograde or retrograde encounter.
 and
and  km s–1) and has a fitness value of 0.90. Figure 8a displays the simulated galaxy and its trajectory on the plane of the sky (in black). Also included (in red) are M31’s bulge and disk, at
km s–1) and has a fitness value of 0.90. Figure 8a displays the simulated galaxy and its trajectory on the plane of the sky (in black). Also included (in red) are M31’s bulge and disk, at  and
and  , and the predicted particle distribution for NGC 205, derived from Choi et al. (2002) isophotes and our surface brightness profile (see § 2, Fig. 2). Figure 8b shows this same orbit in the
, and the predicted particle distribution for NGC 205, derived from Choi et al. (2002) isophotes and our surface brightness profile (see § 2, Fig. 2). Figure 8b shows this same orbit in the  plane, with the addition of a vertical red line denoting the allowed
plane, with the addition of a vertical red line denoting the allowed  parameter values (
parameter values ( kpc). Shown in the bottom plots are the simulated galaxy’s velocity dispersion (circles) and performance on the five
kpc). Shown in the bottom plots are the simulated galaxy’s velocity dispersion (circles) and performance on the five  tests, with Choi et al. (2002) isophotes and Geha et al. (2006) velocity profile+errors depicted in red. The simulated surface brightness
tests, with Choi et al. (2002) isophotes and Geha et al. (2006) velocity profile+errors depicted in red. The simulated surface brightness  tests result in probabilities of 0.979, 0.856, 0.999, and 0.852 for the radial, angular, weighted radial and weighted angular tests, respectively, and in a
tests result in probabilities of 0.979, 0.856, 0.999, and 0.852 for the radial, angular, weighted radial and weighted angular tests, respectively, and in a  probability of
probability of  for the weighted velocity profile. Note that while the weighted velocity profile probability seems quite low, it satisfies the goal of the simulation by matching the turnover and reversal in the semimajor axis velocity profile. Furthermore, although this satellite began as a purely rotating disk with no dispersion, after the simulated interaction with M31 a Gaussian fit to the combined velocity distribution for all particles along the semimajor axis is 3 km s–1. Even though this simulated average dispersion is much lower than the observed average dispersion of 42 km s–1 (Geha et al. 2006), its presence indicates that some of the observed dispersion could have been tidally induced by M31. In order to reduce the Poisson noise in the dispersion profile, we reran the orbit with 5500 particles. The resulting 5500 particle Gaussian fitted velocity dispersion profile is given in Figure 8e (solid black line). The parameter values of the 1000 particle orbit are as follows:
for the weighted velocity profile. Note that while the weighted velocity profile probability seems quite low, it satisfies the goal of the simulation by matching the turnover and reversal in the semimajor axis velocity profile. Furthermore, although this satellite began as a purely rotating disk with no dispersion, after the simulated interaction with M31 a Gaussian fit to the combined velocity distribution for all particles along the semimajor axis is 3 km s–1. Even though this simulated average dispersion is much lower than the observed average dispersion of 42 km s–1 (Geha et al. 2006), its presence indicates that some of the observed dispersion could have been tidally induced by M31. In order to reduce the Poisson noise in the dispersion profile, we reran the orbit with 5500 particles. The resulting 5500 particle Gaussian fitted velocity dispersion profile is given in Figure 8e (solid black line). The parameter values of the 1000 particle orbit are as follows: 
 ;
;  ,
,  ,
,  km s–1;
km s–1;  ,
,  kpc;
kpc;  ,
,  ; and
; and  kpc. This orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. However, the radial path of the orbit precludes any sense of a prograde or retrograde encounter.
kpc. This orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. However, the radial path of the orbit precludes any sense of a prograde or retrograde encounter.Figure 8.
Cold disk model. The resulting best orbit, with a fitness of 0.90, from the 1000 GA runs when NGC 205 is modeled as a rotating, cold disk. (a) Illustration of the orbit on the sky plane (black) plus observations of M31, NGC 205, and the stellar loop (red). (b) Orbit in the  plane (black) plus allowed
plane (black) plus allowed  -values (vertical red). (c) Integrated massless test particles (black) plus Choi et al. (2002) isophotes (red). (d) Simulated radial velocity profile (black) plus Geha et al. (2006) corresponding radial velocity profile (red). (e) Simulated velocity dispersion plus Geha et al. (2006) corresponding dispersion profile (red). Note that the open circles in the simulated velocity dispersion profile denote radii bins with velocity distributions that cannot be fit with a Gaussian. Instead, the standard deviation of the distribution is given. The solid black line denotes the results of a simulation using identical parameter values and 5500 test particles.
-values (vertical red). (c) Integrated massless test particles (black) plus Choi et al. (2002) isophotes (red). (d) Simulated radial velocity profile (black) plus Geha et al. (2006) corresponding radial velocity profile (red). (e) Simulated velocity dispersion plus Geha et al. (2006) corresponding dispersion profile (red). Note that the open circles in the simulated velocity dispersion profile denote radii bins with velocity distributions that cannot be fit with a Gaussian. Instead, the standard deviation of the distribution is given. The solid black line denotes the results of a simulation using identical parameter values and 5500 test particles. |
Using these orbital parameters, we roughly predict the position of the satellite and its particles at given points in time. Figure 9 illustrates the past, present, and future predictions for NGC 205 when it is modeled as a cold, rotating disk. The distribution of particles and positions in space are given for times –338 Myr, –169 Myr, present, 169 Myr and 338 Myr. The panel to the far right in Figure 9 shows NGC 205 in the plane of the sky at 338 Myr. The simulated satellite experiences a significant amount tidal distortion after passing through the disk of M31.
Figure 9.
Cold disk model. Past, present, and future projections of NGC 205 when the satellite is modeled as a initially rotating, cold disk. The left panel shows the predictions in the plane of the sky. The middle panel views the same orbit in the  plane. Note that the apparent kink in the orbit is merely a resolution effect and not indicative of an abrupt change in velocity. The positions are given at times –338 Myr, –169 Myr, present, 169 Myr, and 338 Myr. The panel on the right is a zoomed-in view of NGC 205 at 338 Myr on the plane of the sky.
plane. Note that the apparent kink in the orbit is merely a resolution effect and not indicative of an abrupt change in velocity. The positions are given at times –338 Myr, –169 Myr, present, 169 Myr, and 338 Myr. The panel on the right is a zoomed-in view of NGC 205 at 338 Myr on the plane of the sky. |
4.2. Rotating Warm Disk
This section is identical to § 4.1, but for NGC 205 modeled as a rotating, warm exponential disk of massless test particles supported by a combination or rotational and anisotropic velocities.
4.2.1. Direction of NGC 205’s Approach (Warm Disk)
In Figure 10a a distinct directional preference emerges. The histogram peaks at 228 orbits with NGC 205 advancing from the northwest, followed by 151 orbits from the north-northwest and 89 orbits from the west-northwest. Almost half the orbits are contained within these three directional bins. Furthermore, these directions of approach reinforce those from the 1000 cold disk model runs, which peaked in the west. Of these 1000 orbits, 808 are bound to M31, 233 are prograde, 593 are retrograde, and 174 are radial.
Figure 10.
Warm disk model. Same as Fig. 5, but for NGC 205 modeled as a warm disk with both rotational and anisotropic velocities. Note that the directions of approach on the plane of the sky are similar to those from the cold disk models. |
Figure 10b shows an effective reduction of 1000 orbits to 5 and returns a direction of approach lying somewhere between the north and northwest, with the peaks in both the northwest and north-northwest. Of these 5 orbits, 2 are prograde, 1 is retrograde, and 2 are radial. The shaded region enclosed within the histogram further imposes that the  , a value selected to be just below that of the top 10 orbits (or
, a value selected to be just below that of the top 10 orbits (or  ). This constraint eliminates the retrograde orbit and reduces the 5 orbits to 3, indicating that 7 of the top 10 orbits fail to satisfy all the imposed photometric and kinematic constraints given above. The remaining directions of approach continue to peak in the north-northwest, with only north approaches now ruled out, a result similar to that of the cold disk model’s. Hence, the initial directional preference from the 1000 orbits histogram is reinforced with the addition of photometric, kinematic and fitness constraints.
). This constraint eliminates the retrograde orbit and reduces the 5 orbits to 3, indicating that 7 of the top 10 orbits fail to satisfy all the imposed photometric and kinematic constraints given above. The remaining directions of approach continue to peak in the north-northwest, with only north approaches now ruled out, a result similar to that of the cold disk model’s. Hence, the initial directional preference from the 1000 orbits histogram is reinforced with the addition of photometric, kinematic and fitness constraints.
 , a value selected to be just below that of the top 10 orbits (or
, a value selected to be just below that of the top 10 orbits (or  ). This constraint eliminates the retrograde orbit and reduces the 5 orbits to 3, indicating that 7 of the top 10 orbits fail to satisfy all the imposed photometric and kinematic constraints given above. The remaining directions of approach continue to peak in the north-northwest, with only north approaches now ruled out, a result similar to that of the cold disk model’s. Hence, the initial directional preference from the 1000 orbits histogram is reinforced with the addition of photometric, kinematic and fitness constraints.
). This constraint eliminates the retrograde orbit and reduces the 5 orbits to 3, indicating that 7 of the top 10 orbits fail to satisfy all the imposed photometric and kinematic constraints given above. The remaining directions of approach continue to peak in the north-northwest, with only north approaches now ruled out, a result similar to that of the cold disk model’s. Hence, the initial directional preference from the 1000 orbits histogram is reinforced with the addition of photometric, kinematic and fitness constraints.These restrictions rule out other possible orbits, including those tracing the stellar arclike feature seen to the north of M31. The warm disk model simulations place  of the 1000 GA orbits in bins north-northeast through east. However, only 2 of these 153 orbits meet both a weighted and unweighted angular
of the 1000 GA orbits in bins north-northeast through east. However, only 2 of these 153 orbits meet both a weighted and unweighted angular  constraint of 0.1 and fail to meet a weighted and unweighted radial
constraint of 0.1 and fail to meet a weighted and unweighted radial  constraint of 0.1. As with the cold disk model, orbits tracing the observed stellar arc are ruled out as solutions by NGC 205’s photometric profile.
constraint of 0.1. As with the cold disk model, orbits tracing the observed stellar arc are ruled out as solutions by NGC 205’s photometric profile.
 of the 1000 GA orbits in bins north-northeast through east. However, only 2 of these 153 orbits meet both a weighted and unweighted angular
of the 1000 GA orbits in bins north-northeast through east. However, only 2 of these 153 orbits meet both a weighted and unweighted angular  constraint of 0.1 and fail to meet a weighted and unweighted radial
constraint of 0.1 and fail to meet a weighted and unweighted radial  constraint of 0.1. As with the cold disk model, orbits tracing the observed stellar arc are ruled out as solutions by NGC 205’s photometric profile.
constraint of 0.1. As with the cold disk model, orbits tracing the observed stellar arc are ruled out as solutions by NGC 205’s photometric profile.4.2.2. Preferred Parameter Values (Warm Disk)
Preferences by the GA for various parameter values can be seen in Figure 11. As with the cold disk model, the most notable focus is in the initial scale radius  of NGC 205, shown in detail in Figure 12 (top row). Both the 1000 simulations and the orbits passing all five
of NGC 205, shown in detail in Figure 12 (top row). Both the 1000 simulations and the orbits passing all five  tests (
tests ( ) converge at
) converge at  (
( kpc), with the constrained three orbits (highlighted in red) focused at
kpc), with the constrained three orbits (highlighted in red) focused at 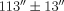 (
( kpc). These GA selected scale radii are close to the satellite’s present scale radius of
kpc). These GA selected scale radii are close to the satellite’s present scale radius of  (0.59 kpc), which implies that the internal regions of the satellite have experienced very little distortion. There is a greater amount of scatter in the remaining parameters, however, distinct trends still exist in the data. Shown in the middle row of Figure 12, orbits with very large velocities of
(0.59 kpc), which implies that the internal regions of the satellite have experienced very little distortion. There is a greater amount of scatter in the remaining parameters, however, distinct trends still exist in the data. Shown in the middle row of Figure 12, orbits with very large velocities of  km s–1 (
km s–1 ( ) are favored, moving NGC 205 primarily toward the southeast (
) are favored, moving NGC 205 primarily toward the southeast ( and
and  km s–1). In addition, the GA prefers
km s–1). In addition, the GA prefers  distances very close to M31 with
distances very close to M31 with 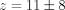 kpc (Fig. 12, bottom row;
kpc (Fig. 12, bottom row;  ). Beyond this distance an orbit’s fitness declines rapidly.
). Beyond this distance an orbit’s fitness declines rapidly.
 of NGC 205, shown in detail in Figure 12 (top row). Both the 1000 simulations and the orbits passing all five
of NGC 205, shown in detail in Figure 12 (top row). Both the 1000 simulations and the orbits passing all five  tests (
tests ( ) converge at
) converge at  (
( kpc), with the constrained three orbits (highlighted in red) focused at
kpc), with the constrained three orbits (highlighted in red) focused at 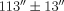 (
( kpc). These GA selected scale radii are close to the satellite’s present scale radius of
kpc). These GA selected scale radii are close to the satellite’s present scale radius of  (0.59 kpc), which implies that the internal regions of the satellite have experienced very little distortion. There is a greater amount of scatter in the remaining parameters, however, distinct trends still exist in the data. Shown in the middle row of Figure 12, orbits with very large velocities of
(0.59 kpc), which implies that the internal regions of the satellite have experienced very little distortion. There is a greater amount of scatter in the remaining parameters, however, distinct trends still exist in the data. Shown in the middle row of Figure 12, orbits with very large velocities of  km s–1 (
km s–1 ( ) are favored, moving NGC 205 primarily toward the southeast (
) are favored, moving NGC 205 primarily toward the southeast ( and
and  km s–1). In addition, the GA prefers
km s–1). In addition, the GA prefers  distances very close to M31 with
distances very close to M31 with 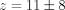 kpc (Fig. 12, bottom row;
kpc (Fig. 12, bottom row;  ). Beyond this distance an orbit’s fitness declines rapidly.
). Beyond this distance an orbit’s fitness declines rapidly.Figure 11.
Warm disk model. Same as Fig. 6, but for the warm disk model with only three constrained orbits, highlighted in red. |
Figure 12.
Warm disk model. Same as Fig. 7, but for the warm disk model. Orbits with  give
give  ,
,  km s–1, and
km s–1, and  kpc, values nearly identical to those from the cold disk models.
kpc, values nearly identical to those from the cold disk models. |
However, some parameters are not well constrained by the simulations. As with the cold disk model, the radial velocity  contains a significant amount of scatter among the allowed parameter values. In addition, the satellite’s mass,
contains a significant amount of scatter among the allowed parameter values. In addition, the satellite’s mass,  , and Hernquist scale length,
, and Hernquist scale length,  , are also unresolved parameters. Hence, as with the cold disk results, the GA both produces inconclusive results for
, are also unresolved parameters. Hence, as with the cold disk results, the GA both produces inconclusive results for  and
and  and does not further reduce the observed error on
and does not further reduce the observed error on  . However, it is able to tightly constrain NGC 205’s initial scale radius and place more general bounds on the remaining five parameters, which also happen to closely match the values from the cold disk simulations.
. However, it is able to tightly constrain NGC 205’s initial scale radius and place more general bounds on the remaining five parameters, which also happen to closely match the values from the cold disk simulations.
 contains a significant amount of scatter among the allowed parameter values. In addition, the satellite’s mass,
contains a significant amount of scatter among the allowed parameter values. In addition, the satellite’s mass,  , and Hernquist scale length,
, and Hernquist scale length,  , are also unresolved parameters. Hence, as with the cold disk results, the GA both produces inconclusive results for
, are also unresolved parameters. Hence, as with the cold disk results, the GA both produces inconclusive results for  and
and  and does not further reduce the observed error on
and does not further reduce the observed error on  . However, it is able to tightly constrain NGC 205’s initial scale radius and place more general bounds on the remaining five parameters, which also happen to closely match the values from the cold disk simulations.
. However, it is able to tightly constrain NGC 205’s initial scale radius and place more general bounds on the remaining five parameters, which also happen to closely match the values from the cold disk simulations.4.2.3. Best Orbit (Warm Disk)
Figure 13 displays the resulting best orbit from the 1000 GA runs for the warm disk model. This orbit approaches M31 from the north-northwest, is unbound (with  and
and  km s–1), and has a fitness of 0.87. The simulated surface brightness
km s–1), and has a fitness of 0.87. The simulated surface brightness  tests result in probabilities of 0.730, 0.994, 0.999, and 0.657 for the radial, angular, weighted radial, and weighted angular tests, respectively, and in a
tests result in probabilities of 0.730, 0.994, 0.999, and 0.657 for the radial, angular, weighted radial, and weighted angular tests, respectively, and in a  probability of
probability of  for the weighted velocity profile. This satellite is initialized with a radial dispersion at one scale length of
for the weighted velocity profile. This satellite is initialized with a radial dispersion at one scale length of  km s–1 and a vertical dispersion of
km s–1 and a vertical dispersion of  km s–1. After the simulated interaction with M31, the semimajor axis velocity profile contains an average observable dispersion of 6 km s–1 (which is slightly greater than its initial dispersion), with a maximum dispersion of 4 km s–1 at a radius of 2.1 kpc. The parameter values of this orbit are as follows:
km s–1. After the simulated interaction with M31, the semimajor axis velocity profile contains an average observable dispersion of 6 km s–1 (which is slightly greater than its initial dispersion), with a maximum dispersion of 4 km s–1 at a radius of 2.1 kpc. The parameter values of this orbit are as follows: 
 ;
;  ,
,  ,
,  km s–1;
km s–1; 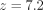 ,
,  ;
;  ,
,  ; and
; and  kpc. As with the cold disk model, this orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. Also, the radial path of this orbit precludes any sense of a prograde or retrograde encounter.
kpc. As with the cold disk model, this orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. Also, the radial path of this orbit precludes any sense of a prograde or retrograde encounter.
 and
and  km s–1), and has a fitness of 0.87. The simulated surface brightness
km s–1), and has a fitness of 0.87. The simulated surface brightness  tests result in probabilities of 0.730, 0.994, 0.999, and 0.657 for the radial, angular, weighted radial, and weighted angular tests, respectively, and in a
tests result in probabilities of 0.730, 0.994, 0.999, and 0.657 for the radial, angular, weighted radial, and weighted angular tests, respectively, and in a  probability of
probability of  for the weighted velocity profile. This satellite is initialized with a radial dispersion at one scale length of
for the weighted velocity profile. This satellite is initialized with a radial dispersion at one scale length of  km s–1 and a vertical dispersion of
km s–1 and a vertical dispersion of  km s–1. After the simulated interaction with M31, the semimajor axis velocity profile contains an average observable dispersion of 6 km s–1 (which is slightly greater than its initial dispersion), with a maximum dispersion of 4 km s–1 at a radius of 2.1 kpc. The parameter values of this orbit are as follows:
km s–1. After the simulated interaction with M31, the semimajor axis velocity profile contains an average observable dispersion of 6 km s–1 (which is slightly greater than its initial dispersion), with a maximum dispersion of 4 km s–1 at a radius of 2.1 kpc. The parameter values of this orbit are as follows: 
 ;
;  ,
,  ,
,  km s–1;
km s–1; 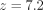 ,
,  ;
;  ,
,  ; and
; and  kpc. As with the cold disk model, this orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. Also, the radial path of this orbit precludes any sense of a prograde or retrograde encounter.
kpc. As with the cold disk model, this orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. Also, the radial path of this orbit precludes any sense of a prograde or retrograde encounter.Figure 13.
Warm disk model. Same as Fig. 8, but for the warm disk model whose resulting best orbit has a fitness of 0.87. |
Figure 14 illustrates the past, present, and future predictions for NGC 205 when it is modeled as a warm disk supported by rotation and anisotropic velocities. The distribution of particles and positions in space are given for times –338 Myr, –169 Myr, present, 169 Myr, and 338 Myr. The panel to the far right in Figure 14 shows NGC 205 in the plane of the sky at 338 Myr. The simulated satellite experiences a significant amount of tidal distortion after passing through the disk of M31.
Figure 14.
Warm disk model. Same as Fig. 9, but for the warm disk model. |
4.3. Nonrotating Hot Spheroid
This section is similar to § 4.1 and § 4.2, except that here NGC 205 is modeled as a nonrotating, hot spheroid of massless test particles supported by isotropic velocities. Since this configuration of particles has increased velocity dispersion (compared to the disk models), we include and additional discussion about our ability to match this observed component in § 4.3.4.
4.3.1. Direction of NGC 205’s Approach (Hot Spheroid)
In Figure 15 a clear directional preference is seen in the initial histogram of 1000 orbits. The histogram peaks at 432 orbits with NGC 205 advancing from the north-northwest, followed by 178 orbits from the north. More than half the orbits are contained within these two directional bins. Furthermore, these directions of approach reinforce those from the disk model runs, which peaked in the west (cold) and northwest (warm). Of these 1000 orbits, 653 are bound to M31 and 308 are on radial trajectories.
Figure 15.
Hot spheroid model. Similar to Figs. 5 and 10, but for NGC 205 modeled as a nonrotating hot spheroid. For the spheroid model the unweighted photometric constraints are set to 10−10
, which are more relaxed than the disk models’ constraint of 0.1. Note that the directions of approach on the plane of the sky are similar to those found for the disk models. |
The top-right panel of Figure 15 shows a histogram of orbits with added photometric, kinematic, and fitness constraints. The outlined histogram requires that weighted surface brightness  probabilities return values ≥
probabilities return values ≥ and that the unweighted surface brightness and weighted velocity
and that the unweighted surface brightness and weighted velocity  probabilities ≥10−10
. Notice that these constraints differ from those applied to the exponential disk models. Since the hot spheroidal model follows a Hernquist profile characterized by an
probabilities ≥10−10
. Notice that these constraints differ from those applied to the exponential disk models. Since the hot spheroidal model follows a Hernquist profile characterized by an  law (and not an exponential profile), we relax the surface brightness
law (and not an exponential profile), we relax the surface brightness  conditions that are more sensitive to the satellite’s inner regions, a portion that has experienced little, if any, tidal distortion. These imposed constraints reduce 1000 orbits to 5 and return a direction of approach lying somewhere between the north and north-northwest, with a peak of 4 orbits in the north-northwest. The shaded region enclosed within the histogram further imposes that the
conditions that are more sensitive to the satellite’s inner regions, a portion that has experienced little, if any, tidal distortion. These imposed constraints reduce 1000 orbits to 5 and return a direction of approach lying somewhere between the north and north-northwest, with a peak of 4 orbits in the north-northwest. The shaded region enclosed within the histogram further imposes that the  , a value selected to be just below that of the top 10 orbits (or
, a value selected to be just below that of the top 10 orbits (or  ). This constraint reduces the 5 orbits to 3, indicating that 7 of the top 10 orbits fail to satisfy all the imposed photometric and kinematic constraints given above. The remaining directions of approach all fall in the north-northwest, ruling out north approaches, a result similar to the disk models’ findings. Hence, the initial directional preference suggested by the 1000 orbits histogram is reinforced with the addition of photometric, kinematic, and fitness constraints.
). This constraint reduces the 5 orbits to 3, indicating that 7 of the top 10 orbits fail to satisfy all the imposed photometric and kinematic constraints given above. The remaining directions of approach all fall in the north-northwest, ruling out north approaches, a result similar to the disk models’ findings. Hence, the initial directional preference suggested by the 1000 orbits histogram is reinforced with the addition of photometric, kinematic, and fitness constraints.
 probabilities return values ≥
probabilities return values ≥ and that the unweighted surface brightness and weighted velocity
and that the unweighted surface brightness and weighted velocity  probabilities ≥10−10
. Notice that these constraints differ from those applied to the exponential disk models. Since the hot spheroidal model follows a Hernquist profile characterized by an
probabilities ≥10−10
. Notice that these constraints differ from those applied to the exponential disk models. Since the hot spheroidal model follows a Hernquist profile characterized by an  law (and not an exponential profile), we relax the surface brightness
law (and not an exponential profile), we relax the surface brightness  conditions that are more sensitive to the satellite’s inner regions, a portion that has experienced little, if any, tidal distortion. These imposed constraints reduce 1000 orbits to 5 and return a direction of approach lying somewhere between the north and north-northwest, with a peak of 4 orbits in the north-northwest. The shaded region enclosed within the histogram further imposes that the
conditions that are more sensitive to the satellite’s inner regions, a portion that has experienced little, if any, tidal distortion. These imposed constraints reduce 1000 orbits to 5 and return a direction of approach lying somewhere between the north and north-northwest, with a peak of 4 orbits in the north-northwest. The shaded region enclosed within the histogram further imposes that the  , a value selected to be just below that of the top 10 orbits (or
, a value selected to be just below that of the top 10 orbits (or  ). This constraint reduces the 5 orbits to 3, indicating that 7 of the top 10 orbits fail to satisfy all the imposed photometric and kinematic constraints given above. The remaining directions of approach all fall in the north-northwest, ruling out north approaches, a result similar to the disk models’ findings. Hence, the initial directional preference suggested by the 1000 orbits histogram is reinforced with the addition of photometric, kinematic, and fitness constraints.
). This constraint reduces the 5 orbits to 3, indicating that 7 of the top 10 orbits fail to satisfy all the imposed photometric and kinematic constraints given above. The remaining directions of approach all fall in the north-northwest, ruling out north approaches, a result similar to the disk models’ findings. Hence, the initial directional preference suggested by the 1000 orbits histogram is reinforced with the addition of photometric, kinematic, and fitness constraints.These restrictions rule out other possible orbits, including those tracing the stellar arclike feature seen to the north of M31. The hot spheroid simulations place a mere  of the 1000 GA orbits in the four bins north-northeast through east. None of these orbits meet a weighted angular
of the 1000 GA orbits in the four bins north-northeast through east. None of these orbits meet a weighted angular  constraint of 0.1. Hence, orbits tracing the observed stellar arc are ruled out as solutions by the twisting of elliptical isophotes in the tidally distorted regions of NGC 205.
constraint of 0.1. Hence, orbits tracing the observed stellar arc are ruled out as solutions by the twisting of elliptical isophotes in the tidally distorted regions of NGC 205.
 of the 1000 GA orbits in the four bins north-northeast through east. None of these orbits meet a weighted angular
of the 1000 GA orbits in the four bins north-northeast through east. None of these orbits meet a weighted angular  constraint of 0.1. Hence, orbits tracing the observed stellar arc are ruled out as solutions by the twisting of elliptical isophotes in the tidally distorted regions of NGC 205.
constraint of 0.1. Hence, orbits tracing the observed stellar arc are ruled out as solutions by the twisting of elliptical isophotes in the tidally distorted regions of NGC 205.4.3.2. Preferred Parameter Values (Hot Spheroid)
The resulting parameter values from the 1000 hot spheroid GA runs are shown in Figure 16. The spherical nature and density profile of this model effectively reduces the number of parameters from nine to six, eliminating  ,
,  , and
, and  .
.
 ,
,  , and
, and  .
.The GA’s preference for certain parameter values is quantified in Figure 17. The top two rows ( ) show the well-resolved tangential components of the velocity vector with
) show the well-resolved tangential components of the velocity vector with  and
and  km s–1, effectively moving NGC 205 toward the southeast. This results in a net velocity of
km s–1, effectively moving NGC 205 toward the southeast. This results in a net velocity of  km s–1 (
km s–1 ( ). In contrast, only the magnitude of the velocity could be well resolved in the case of the cold disk model. The GA also prefers
). In contrast, only the magnitude of the velocity could be well resolved in the case of the cold disk model. The GA also prefers  distances very close to M31 with
distances very close to M31 with  kpc (Fig. 17, bottom row;
kpc (Fig. 17, bottom row;  ). As with the disk models, an orbit’s fitness beyond this distance declines rapidly. In the bottom-right plot of Figure 16, a correlation of higher fitness to lower
). As with the disk models, an orbit’s fitness beyond this distance declines rapidly. In the bottom-right plot of Figure 16, a correlation of higher fitness to lower  values can be seen. This is a result of the initial particle distribution’s dependence on
values can be seen. This is a result of the initial particle distribution’s dependence on  in equation (19), a dependence that did not exist for the disk models. Hence, the GA’s attempt to reproduce the exponential surface brightness profile results in this correlation.
in equation (19), a dependence that did not exist for the disk models. Hence, the GA’s attempt to reproduce the exponential surface brightness profile results in this correlation.
 ) show the well-resolved tangential components of the velocity vector with
) show the well-resolved tangential components of the velocity vector with  and
and  km s–1, effectively moving NGC 205 toward the southeast. This results in a net velocity of
km s–1, effectively moving NGC 205 toward the southeast. This results in a net velocity of  km s–1 (
km s–1 ( ). In contrast, only the magnitude of the velocity could be well resolved in the case of the cold disk model. The GA also prefers
). In contrast, only the magnitude of the velocity could be well resolved in the case of the cold disk model. The GA also prefers  distances very close to M31 with
distances very close to M31 with  kpc (Fig. 17, bottom row;
kpc (Fig. 17, bottom row;  ). As with the disk models, an orbit’s fitness beyond this distance declines rapidly. In the bottom-right plot of Figure 16, a correlation of higher fitness to lower
). As with the disk models, an orbit’s fitness beyond this distance declines rapidly. In the bottom-right plot of Figure 16, a correlation of higher fitness to lower  values can be seen. This is a result of the initial particle distribution’s dependence on
values can be seen. This is a result of the initial particle distribution’s dependence on  in equation (19), a dependence that did not exist for the disk models. Hence, the GA’s attempt to reproduce the exponential surface brightness profile results in this correlation.
in equation (19), a dependence that did not exist for the disk models. Hence, the GA’s attempt to reproduce the exponential surface brightness profile results in this correlation.However, Figure 16 also demonstrates that some of the parameters are not well constrained by the simulations. As with the disk models, the radial velocity  contains a significant amount of scatter and is likely not constrainable beyond observations. In addition, the satellite’s mass,
contains a significant amount of scatter and is likely not constrainable beyond observations. In addition, the satellite’s mass,  is unresolved. Hence, as with the disk results, the GA produces inconclusive results for
is unresolved. Hence, as with the disk results, the GA produces inconclusive results for  and does not further reduce the observed error on
and does not further reduce the observed error on  . However, it is able to reasonable constrain NGC 205’s tangential velocity and line-of-sight distance, values which also happen to closely match those from the disk simulations.
. However, it is able to reasonable constrain NGC 205’s tangential velocity and line-of-sight distance, values which also happen to closely match those from the disk simulations.
 contains a significant amount of scatter and is likely not constrainable beyond observations. In addition, the satellite’s mass,
contains a significant amount of scatter and is likely not constrainable beyond observations. In addition, the satellite’s mass,  is unresolved. Hence, as with the disk results, the GA produces inconclusive results for
is unresolved. Hence, as with the disk results, the GA produces inconclusive results for  and does not further reduce the observed error on
and does not further reduce the observed error on  . However, it is able to reasonable constrain NGC 205’s tangential velocity and line-of-sight distance, values which also happen to closely match those from the disk simulations.
. However, it is able to reasonable constrain NGC 205’s tangential velocity and line-of-sight distance, values which also happen to closely match those from the disk simulations.4.3.3. Best Orbit (Hot Spheroid)
Figure 18 displays the hot spheroid’s resulting best orbit from the 1000 GA runs. This orbit approaches M31 from the north-northwest, is just barely bound (with  and
and  km s–1), and has a fitness of 0.73. Notice that on the bottom-right plot the inner velocity profile is hatched out, indicating that the slope test was not used for this model. The simulated surface brightness
km s–1), and has a fitness of 0.73. Notice that on the bottom-right plot the inner velocity profile is hatched out, indicating that the slope test was not used for this model. The simulated surface brightness  tests result in probabilities of
tests result in probabilities of  ,
,  , 0.757, and 0.83 for the radial, angular, weighted radial, and weighted angular tests, respectively, and in a
, 0.757, and 0.83 for the radial, angular, weighted radial, and weighted angular tests, respectively, and in a  probability of 0.002 for the weighted velocity profile. The orbit’s poor performance on the unweighted surface brightness
probability of 0.002 for the weighted velocity profile. The orbit’s poor performance on the unweighted surface brightness  tests is a direct result of comparing the simulated spheroid, constructed using a Hernquist density profile, to the observed NGC 205, which follows an exponential profile. Despite this fact, the orbit performs quite well on the weighted
tests is a direct result of comparing the simulated spheroid, constructed using a Hernquist density profile, to the observed NGC 205, which follows an exponential profile. Despite this fact, the orbit performs quite well on the weighted  tests that model the tidally distorted regions of NGC 205. After the simulated interaction with M31, the semimajor axis velocity profile contains an average observable dispersion of 17 km s–1 (which is lower than the observed dispersion of 42 km s–1), with a maximum dispersion of 36 km s–1 at a radius of 1.0 kpc. The parameter values of this orbit are as follows:
tests that model the tidally distorted regions of NGC 205. After the simulated interaction with M31, the semimajor axis velocity profile contains an average observable dispersion of 17 km s–1 (which is lower than the observed dispersion of 42 km s–1), with a maximum dispersion of 36 km s–1 at a radius of 1.0 kpc. The parameter values of this orbit are as follows: 
 ;
;  ,
,  ,
,  km s–1; and
km s–1; and  and
and 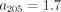 kpc. As with both disk models, this orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. Since this satellite is not rotating, prograde or retrograde definitions do not apply.
kpc. As with both disk models, this orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. Since this satellite is not rotating, prograde or retrograde definitions do not apply.
 and
and  km s–1), and has a fitness of 0.73. Notice that on the bottom-right plot the inner velocity profile is hatched out, indicating that the slope test was not used for this model. The simulated surface brightness
km s–1), and has a fitness of 0.73. Notice that on the bottom-right plot the inner velocity profile is hatched out, indicating that the slope test was not used for this model. The simulated surface brightness  tests result in probabilities of
tests result in probabilities of  ,
,  , 0.757, and 0.83 for the radial, angular, weighted radial, and weighted angular tests, respectively, and in a
, 0.757, and 0.83 for the radial, angular, weighted radial, and weighted angular tests, respectively, and in a  probability of 0.002 for the weighted velocity profile. The orbit’s poor performance on the unweighted surface brightness
probability of 0.002 for the weighted velocity profile. The orbit’s poor performance on the unweighted surface brightness  tests is a direct result of comparing the simulated spheroid, constructed using a Hernquist density profile, to the observed NGC 205, which follows an exponential profile. Despite this fact, the orbit performs quite well on the weighted
tests is a direct result of comparing the simulated spheroid, constructed using a Hernquist density profile, to the observed NGC 205, which follows an exponential profile. Despite this fact, the orbit performs quite well on the weighted  tests that model the tidally distorted regions of NGC 205. After the simulated interaction with M31, the semimajor axis velocity profile contains an average observable dispersion of 17 km s–1 (which is lower than the observed dispersion of 42 km s–1), with a maximum dispersion of 36 km s–1 at a radius of 1.0 kpc. The parameter values of this orbit are as follows:
tests that model the tidally distorted regions of NGC 205. After the simulated interaction with M31, the semimajor axis velocity profile contains an average observable dispersion of 17 km s–1 (which is lower than the observed dispersion of 42 km s–1), with a maximum dispersion of 36 km s–1 at a radius of 1.0 kpc. The parameter values of this orbit are as follows: 
 ;
;  ,
,  ,
,  km s–1; and
km s–1; and  and
and 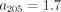 kpc. As with both disk models, this orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. Since this satellite is not rotating, prograde or retrograde definitions do not apply.
kpc. As with both disk models, this orbit is projected to pass within ≈9 kpc of M31’s center in the plane of M31’s disk. Since this satellite is not rotating, prograde or retrograde definitions do not apply.Figure 19 illustrates the past, present, and future predictions for NGC 205 when it is modeled as a hot spheroid supported by isotropic velocities. The distribution of particles are given for times –384 Myr, present, 76 Myr, and 384 Myr. The gravitationally bound satellite traces out a loop orbit. The panel to the far right in Figure 19 shows NGC 205 in the plane of the sky at 384 Myr. The simulated satellite experiences a significant amount of tidal distortion after passing through the disk of M31.
4.3.4. Semimajor Axis Velocity Dispersion
Figures 8, 13, and 18 show the best-fit orbit for each of the three models. However, none these orbits produce profiles that match the observed velocity dispersion profile. This is expected, since our fitness tests do not contain a velocity dispersion profile test, meaning our orbits are not encouraged to match this observable. The main reason this feature is not used is because the low number of particles ( ) used for each orbit makes it nearly impossible to fit a histogram and recover an accurate measurement for the velocity dispersion at all points along the semimajor axis of NGC 205.
) used for each orbit makes it nearly impossible to fit a histogram and recover an accurate measurement for the velocity dispersion at all points along the semimajor axis of NGC 205.
 ) used for each orbit makes it nearly impossible to fit a histogram and recover an accurate measurement for the velocity dispersion at all points along the semimajor axis of NGC 205.
) used for each orbit makes it nearly impossible to fit a histogram and recover an accurate measurement for the velocity dispersion at all points along the semimajor axis of NGC 205.We expect that of the three models the hot spheroid model, supported completely by isotropic velocities, is most capable of reproducing the observed dispersion. To test this, we use  massless test particles plus the best-fit hot spheroid model’s velocity and line-of-sight distance parameters given in § 4.3.3, and we conduct a coarse, iterative search in the mass (
massless test particles plus the best-fit hot spheroid model’s velocity and line-of-sight distance parameters given in § 4.3.3, and we conduct a coarse, iterative search in the mass ( ) and Hernquist scale length (
) and Hernquist scale length ( ) dimensions. We search these two parameters because they are unconstrained in all three models and heavily influence the simulated velocity dispersion profile. After producing discrete relations between
) dimensions. We search these two parameters because they are unconstrained in all three models and heavily influence the simulated velocity dispersion profile. After producing discrete relations between  and the mean velocity dispersion, we fit a power-law line and interpolate to find the values of
and the mean velocity dispersion, we fit a power-law line and interpolate to find the values of  , at each value of
, at each value of  , that result in a mean dispersion of 35 km s–1. This result is displayed as circles in the top panel of Figure 20. The solid line in the top panel of Figure 20 indicates the analytic solution for these parameter values in a tidally undistorted satellite with a projected velocity dispersion of 35 km s–1 at a radius of 1 kpc (Hernquist (1990, eq. [42]). Although this line measures the velocity dispersion at a given radius, rather than the mean velocity dispersion, the result suggests that tidal interactions between at hot spheroid progenitor and parent galaxy have not significantly impacted the velocity dispersion within a 1 kpc radius.
, that result in a mean dispersion of 35 km s–1. This result is displayed as circles in the top panel of Figure 20. The solid line in the top panel of Figure 20 indicates the analytic solution for these parameter values in a tidally undistorted satellite with a projected velocity dispersion of 35 km s–1 at a radius of 1 kpc (Hernquist (1990, eq. [42]). Although this line measures the velocity dispersion at a given radius, rather than the mean velocity dispersion, the result suggests that tidal interactions between at hot spheroid progenitor and parent galaxy have not significantly impacted the velocity dispersion within a 1 kpc radius.
 massless test particles plus the best-fit hot spheroid model’s velocity and line-of-sight distance parameters given in § 4.3.3, and we conduct a coarse, iterative search in the mass (
massless test particles plus the best-fit hot spheroid model’s velocity and line-of-sight distance parameters given in § 4.3.3, and we conduct a coarse, iterative search in the mass ( ) and Hernquist scale length (
) and Hernquist scale length ( ) dimensions. We search these two parameters because they are unconstrained in all three models and heavily influence the simulated velocity dispersion profile. After producing discrete relations between
) dimensions. We search these two parameters because they are unconstrained in all three models and heavily influence the simulated velocity dispersion profile. After producing discrete relations between  and the mean velocity dispersion, we fit a power-law line and interpolate to find the values of
and the mean velocity dispersion, we fit a power-law line and interpolate to find the values of  , at each value of
, at each value of  , that result in a mean dispersion of 35 km s–1. This result is displayed as circles in the top panel of Figure 20. The solid line in the top panel of Figure 20 indicates the analytic solution for these parameter values in a tidally undistorted satellite with a projected velocity dispersion of 35 km s–1 at a radius of 1 kpc (Hernquist (1990, eq. [42]). Although this line measures the velocity dispersion at a given radius, rather than the mean velocity dispersion, the result suggests that tidal interactions between at hot spheroid progenitor and parent galaxy have not significantly impacted the velocity dispersion within a 1 kpc radius.
, that result in a mean dispersion of 35 km s–1. This result is displayed as circles in the top panel of Figure 20. The solid line in the top panel of Figure 20 indicates the analytic solution for these parameter values in a tidally undistorted satellite with a projected velocity dispersion of 35 km s–1 at a radius of 1 kpc (Hernquist (1990, eq. [42]). Although this line measures the velocity dispersion at a given radius, rather than the mean velocity dispersion, the result suggests that tidal interactions between at hot spheroid progenitor and parent galaxy have not significantly impacted the velocity dispersion within a 1 kpc radius.Figure 20.
Hot spheroid model. The circles in the top panel show, for the tidally distorted best-fit hot spheroid orbit, the combinations of the mass  and Hernquist scale length
and Hernquist scale length  parameters that reproduce the observed mean velocity dispersion of 35 km s–1. The solid line gives analytic predictions for these parameter in a tidally undistorted satellite with a projected velocity dispersion of 35 km s–1 at a radius of 1 kpc. The bottom four panels correspond to the orbit denoted by the black point in the top panel and are similar to Fig. 18, but with 3000 particles, a mass of
parameters that reproduce the observed mean velocity dispersion of 35 km s–1. The solid line gives analytic predictions for these parameter in a tidally undistorted satellite with a projected velocity dispersion of 35 km s–1 at a radius of 1 kpc. The bottom four panels correspond to the orbit denoted by the black point in the top panel and are similar to Fig. 18, but with 3000 particles, a mass of 
 , and Hernquist scale length of 1.2 kpc. Note that this model progenitor reproduces the observed velocity dispersion profile.
, and Hernquist scale length of 1.2 kpc. Note that this model progenitor reproduces the observed velocity dispersion profile. |
In addition to matching the observed mean dispersion, we find that all these combinations of  and
and  sufficiently reproduce the velocity dispersion profile, including the observed dip at the center. We randomly select one of these points (
sufficiently reproduce the velocity dispersion profile, including the observed dip at the center. We randomly select one of these points (
 ,
,  kpc), denote it with a black circle, and display the orbit in the bottom four panels of Figure 20. The poor fitness values reported by this orbit are not a matter of concern, since this orbit was not a true result of the optimization scheme. Hence, while the mass and Hernquist scale length parameters are not constrained in the optimized parameter space search, their relative values are suggested by the observed velocity dispersion.
kpc), denote it with a black circle, and display the orbit in the bottom four panels of Figure 20. The poor fitness values reported by this orbit are not a matter of concern, since this orbit was not a true result of the optimization scheme. Hence, while the mass and Hernquist scale length parameters are not constrained in the optimized parameter space search, their relative values are suggested by the observed velocity dispersion.
 and
and  sufficiently reproduce the velocity dispersion profile, including the observed dip at the center. We randomly select one of these points (
sufficiently reproduce the velocity dispersion profile, including the observed dip at the center. We randomly select one of these points (
 ,
,  kpc), denote it with a black circle, and display the orbit in the bottom four panels of Figure 20. The poor fitness values reported by this orbit are not a matter of concern, since this orbit was not a true result of the optimization scheme. Hence, while the mass and Hernquist scale length parameters are not constrained in the optimized parameter space search, their relative values are suggested by the observed velocity dispersion.
kpc), denote it with a black circle, and display the orbit in the bottom four panels of Figure 20. The poor fitness values reported by this orbit are not a matter of concern, since this orbit was not a true result of the optimization scheme. Hence, while the mass and Hernquist scale length parameters are not constrained in the optimized parameter space search, their relative values are suggested by the observed velocity dispersion.5. DISCUSSION
This paper presents the methods and results of an optimized, restricted  -body search for NGC 205’s orbit and system parameters. We account for uncertainties in the parameter space by placing very liberal upper and lower limits on our parameters, using three dynamically distinct models for the initial configuration of NGC 205, and running our optimization algorithm (GA) 1000 times on each model. We find that out of the 1022
possible orbits, not only are certain orbits and portions of parameter space carved out, but this convergence is also model independent. These findings are outlined below:
-body search for NGC 205’s orbit and system parameters. We account for uncertainties in the parameter space by placing very liberal upper and lower limits on our parameters, using three dynamically distinct models for the initial configuration of NGC 205, and running our optimization algorithm (GA) 1000 times on each model. We find that out of the 1022
possible orbits, not only are certain orbits and portions of parameter space carved out, but this convergence is also model independent. These findings are outlined below:
 -body search for NGC 205’s orbit and system parameters. We account for uncertainties in the parameter space by placing very liberal upper and lower limits on our parameters, using three dynamically distinct models for the initial configuration of NGC 205, and running our optimization algorithm (GA) 1000 times on each model. We find that out of the 1022
possible orbits, not only are certain orbits and portions of parameter space carved out, but this convergence is also model independent. These findings are outlined below:
-body search for NGC 205’s orbit and system parameters. We account for uncertainties in the parameter space by placing very liberal upper and lower limits on our parameters, using three dynamically distinct models for the initial configuration of NGC 205, and running our optimization algorithm (GA) 1000 times on each model. We find that out of the 1022
possible orbits, not only are certain orbits and portions of parameter space carved out, but this convergence is also model independent. These findings are outlined below:-
The simulations indicate that NGC 205 is approaching from the northwest region on the plane of the sky, moving toward the southeast (i.e., increasing in right ascension, decreasing in declination), with the cold disk model favoring an approach from the northwest and the warm disk and hot spheroid models favoring the north-northwest.
-
These orbits do not trace out nor do they intersect the
 long stellar arc observed to north of M31, which was hypothesized as a tidal stream emanating from NGC 205 by McConnachie et al. (2004). Orbits that trace out this region on the plane of the sky (i.e., approaches from the north-northeast through east region) poorly match the photometry of NGC 205, specifically, the isophotal twisting. Instead, approaches from the northwest through north-northwest region are preferred, thus ruling out the stellar arc as a trail of debris from NGC 205.
long stellar arc observed to north of M31, which was hypothesized as a tidal stream emanating from NGC 205 by McConnachie et al. (2004). Orbits that trace out this region on the plane of the sky (i.e., approaches from the north-northeast through east region) poorly match the photometry of NGC 205, specifically, the isophotal twisting. Instead, approaches from the northwest through north-northwest region are preferred, thus ruling out the stellar arc as a trail of debris from NGC 205. -
Large velocities in the range 300-500 km s–1 are highly favored for NGC 205. While the majority of the orbits found by the GA are bound, the best fitting orbits are either very close to escape velocity or unbound. However, such velocities are not completely uncommon for local group satellites. Proper-motion measurements reveal that the Large Magellanic Cloud is very near escape velocity and likely on its first passage about the Milky Way (Kallivayalil et al. 2006; Besla et al. 2007). The dwarf spheroidal galaxies And XIV and And XII are near, or exceed, their local escape speeds and are presumably falling into the Local Group for the first time (Majewski et al. 2007; Chapman et al. 2007). The large tangential component of NGC 205’s simulated velocities translates into a proper motion of ∼0.1 mas yr–1.
-
The GA is able to better fit NGC 205’s observed kinematic profile when the satellite’s line-of-sight distance is very close to M31. The resulting fits report relative distances between NGC 205 and M31 in the range 2-20 kpc. Note that 2 kpc is our lower bound on the line-of-sight distance parameter. These distances correspond to a change of
 mag in McConnachie et al. (2005) measurements of NGC 205’s red giant branch tip (TRGB), analogous to either an increase in their adopted TRGB absolute magnitude (
mag in McConnachie et al. (2005) measurements of NGC 205’s red giant branch tip (TRGB), analogous to either an increase in their adopted TRGB absolute magnitude ( ) and/or reddening correction (
) and/or reddening correction ( ), or in a decrease in the TRGB observed magnitude (
), or in a decrease in the TRGB observed magnitude (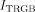 ). Furthermore, this magnitude difference is in agreement with the ±0.07 mag errors quoted by McConnachie et al. (2005) on the individual distance measurements to NGC 205 and M31. As an aside, a magnitude difference could also be accounted for by NGC 205’s composite stellar population (Salaris & Girardi 2005) resulting from a recent (∼0.5 Gyr) burst of star formation (Marleau et al. 2006). Given these possible corrections and the close relative distances found by the simulation, the question is raised: Could NGC 205 be in front of M31 rather than behind it?
). Furthermore, this magnitude difference is in agreement with the ±0.07 mag errors quoted by McConnachie et al. (2005) on the individual distance measurements to NGC 205 and M31. As an aside, a magnitude difference could also be accounted for by NGC 205’s composite stellar population (Salaris & Girardi 2005) resulting from a recent (∼0.5 Gyr) burst of star formation (Marleau et al. 2006). Given these possible corrections and the close relative distances found by the simulation, the question is raised: Could NGC 205 be in front of M31 rather than behind it? -
The disk models return tightly constrained initial scale lengths in the range 0.39-0.55 kpc, values approximately equal to NGC 205’s current scale length of 0.59 kpc. This result is consistent with the photometric and kinematic observations which suggest the central region of NGC 205 is largely unaffected by tides. Hence, both the inner kinematics and photometry are determined by the initial parameters of the system.
-
The cold disk model demonstrates its plausibility as a configuration for NGC 205 by the induction of velocity dispersions into its initially cold profile via tidal interactions. Hence, all three models contain some dispersion along their final semimajor axis velocity profile.
-
For the best-fit hot spheroid model, we can reproduce the observed mean velocity dispersion of 35 km s–1 and the semimajor axis velocity dispersion profile by using specific combinations of two otherwise unconstrained parameters, satellite mass (
 ) and Hernquist scale length (
) and Hernquist scale length ( ).
). -
For all three models, NGC 205’s large tangential velocities and close approaches to M31 indicate that it is difficult to distort a satellite to the extent that NGC 205 is observed. In order to reproduce the abrupt turnover and reversal in the velocity profile, NGC 205 must come very near to M31. While the photometric profile can be reproduced at large distances, the resulting velocity turnover is less abrupt and the reversal is not as steep. However, at very close approaches (<20 kpc), it is very easy to disrupt NGC 205. In order to avoid complete disruption and/or long tidal streamers, the satellite must approach M31 with a very high velocity. Hence, the combined photometric and kinematic observations have managed to remove degeneracies in some of the parameter space.
-
The constrained orbits are primarily radial and projected to pass within 10 kpc of M31’s center. For the cold disk model, orbits that are not radial and have a fitness >0.25 are prograde. In contrast, a larger fraction of the warm disk model’s orbits with fitness >0.25 are retrograde. This result is not surprising since the warm disk model contains some initial velocity dispersion, allowing its satellites to be more easily distorted. Thus, some of the warm disk satellites are able to reproduced milder photometric distortions by approaching on retrograde orbits (Read et al. 2006).
-
Given that many of the best fitting orbits are both radial and unbound, it is not surprising that NGC 205 has only experienced a small amount of distortion. That is, an unbound orbit indicates that NGC 205 is on its first passage while satellites on radial orbits are more difficult to disrupt than those on prograde orbits (Read et al. 2006). Although the future projections show NGC 205 whizzing through M31, inclusion of dynamical friction would change this result by slowing the satellite after hitting M31 for the first time (Seguin & Dupraz 1994). This braking mechanism is so efficient that it is likely NGC 205 will eventually merge with M31.
Although the GA’s search was quite successful, it was unable to constrain the mass and dark matter content. This latter result could be due to either degeneracies in the parameter space or an insensitivity to these parameters by the fitness tests. Furthermore, it appears that to some degree the algorithm did get stuck in local optima, a result evidenced by the scatter in the solutions and the fact that some orbits had very low fitness. Although we attempt to circumvent this undesirable result by running the GA numerous times, we cannot be 100% certain that we converge on the “best orbit” in the parameter space. However, we do find that other GA and fitness test configurations result in declining levels of a best orbit fitness and are thus confident that our method is effective. While other optimization tools are available (i.e., simulated annealing), they too have their problems and limitations, and cannot offer guaranteed improvements.
6. FUTURE DIRECTIONS
We have presented the results of optimized restricted  -body simulations of NGC 205’s tidal interaction with M31 using initially self-consistent satellite models and parameter spaces tailored specifically to the system. Although this simple model produces satisfactory results, improvements to the simulations will generate a more detailed and accurate account of the interaction, possibly produce tighter constraints on the parameters, and provide greater insight into the past, present and future of NGC 205. In this final section we discuss two observational advances that can be made and a handful of numerical improvements that can be applied to the NGC 205-M31 system in order to better and more accurately model their interaction.
-body simulations of NGC 205’s tidal interaction with M31 using initially self-consistent satellite models and parameter spaces tailored specifically to the system. Although this simple model produces satisfactory results, improvements to the simulations will generate a more detailed and accurate account of the interaction, possibly produce tighter constraints on the parameters, and provide greater insight into the past, present and future of NGC 205. In this final section we discuss two observational advances that can be made and a handful of numerical improvements that can be applied to the NGC 205-M31 system in order to better and more accurately model their interaction.
 -body simulations of NGC 205’s tidal interaction with M31 using initially self-consistent satellite models and parameter spaces tailored specifically to the system. Although this simple model produces satisfactory results, improvements to the simulations will generate a more detailed and accurate account of the interaction, possibly produce tighter constraints on the parameters, and provide greater insight into the past, present and future of NGC 205. In this final section we discuss two observational advances that can be made and a handful of numerical improvements that can be applied to the NGC 205-M31 system in order to better and more accurately model their interaction.
-body simulations of NGC 205’s tidal interaction with M31 using initially self-consistent satellite models and parameter spaces tailored specifically to the system. Although this simple model produces satisfactory results, improvements to the simulations will generate a more detailed and accurate account of the interaction, possibly produce tighter constraints on the parameters, and provide greater insight into the past, present and future of NGC 205. In this final section we discuss two observational advances that can be made and a handful of numerical improvements that can be applied to the NGC 205-M31 system in order to better and more accurately model their interaction.The simulations can be significantly improved by reducing the observational errors. As discussed, the current value for the line-of-sight distance between NGC 205 and M31 is estimated to be  kpc (McConnachie et al. 2005). An improvement on the relative distance between NGC 205 and M31 would significantly constrain the parameter space. In addition, if NGC 205 indeed has a large tangential motion of 300-500 km s–1, the satellite’s proper motion could be resolved at long wavelengths over the course of a decade or two, thus providing another significant constraint on the system. These two measurements, in conjunction with current sky positions, radial velocities, and models of M31’s mass distribution, would provide a complete description of NGC 205’s orbit.
kpc (McConnachie et al. 2005). An improvement on the relative distance between NGC 205 and M31 would significantly constrain the parameter space. In addition, if NGC 205 indeed has a large tangential motion of 300-500 km s–1, the satellite’s proper motion could be resolved at long wavelengths over the course of a decade or two, thus providing another significant constraint on the system. These two measurements, in conjunction with current sky positions, radial velocities, and models of M31’s mass distribution, would provide a complete description of NGC 205’s orbit.
 kpc (McConnachie et al. 2005). An improvement on the relative distance between NGC 205 and M31 would significantly constrain the parameter space. In addition, if NGC 205 indeed has a large tangential motion of 300-500 km s–1, the satellite’s proper motion could be resolved at long wavelengths over the course of a decade or two, thus providing another significant constraint on the system. These two measurements, in conjunction with current sky positions, radial velocities, and models of M31’s mass distribution, would provide a complete description of NGC 205’s orbit.
kpc (McConnachie et al. 2005). An improvement on the relative distance between NGC 205 and M31 would significantly constrain the parameter space. In addition, if NGC 205 indeed has a large tangential motion of 300-500 km s–1, the satellite’s proper motion could be resolved at long wavelengths over the course of a decade or two, thus providing another significant constraint on the system. These two measurements, in conjunction with current sky positions, radial velocities, and models of M31’s mass distribution, would provide a complete description of NGC 205’s orbit.Our simple model of NGC 205’s interaction with M31 yields results that are consistent and relatively independent of model type. An obvious improvement to the current simulation is to use velocity dispersion as a constraint on the system. Another improvement, applying to only the spheroid model, would be to weight the brightness of the massless test particles such that the initial surface brightness profile matches the observed exponential profile of NGC 205. Furthermore, this system can be better modeled with the inclusion of dynamical friction and mass loss, effects which act to slow the system down and increase the level of distortion in the satellite. The addition of these processes effectively transforms our time-independent model into a time-dependent problem. Another modification is to construct NGC 205 as a self-gravitating model with both dark and luminous particles, thus switching from a restricted  -body to a full
-body to a full  -body simulation. However, this more realistic model changes the problem from
-body simulation. However, this more realistic model changes the problem from  to
to  , leading to a notable increase in computation time and making it extremely costly to run the simulation along with a genetic algorithm. Despite this complication, a self-gravitating model has a significant advantage in that it allows for evolution in NGC 205. This construction provides the necessary platform to test various formation scenarios for the satellite, since it can be initialized as a spiral or dwarf irregular and then transformed into a dwarf elliptical through tidal interactions. If this improvement were to be made, one might also consider adding an initial gas mass to the progenitor galaxy and performing hydrodynamic simulations for completeness. Last but not least, NGC 205’s orbit can be improved by adding the perturbations from M31’s other satellites, such as M32, as well as the potential of the Milky Way.
, leading to a notable increase in computation time and making it extremely costly to run the simulation along with a genetic algorithm. Despite this complication, a self-gravitating model has a significant advantage in that it allows for evolution in NGC 205. This construction provides the necessary platform to test various formation scenarios for the satellite, since it can be initialized as a spiral or dwarf irregular and then transformed into a dwarf elliptical through tidal interactions. If this improvement were to be made, one might also consider adding an initial gas mass to the progenitor galaxy and performing hydrodynamic simulations for completeness. Last but not least, NGC 205’s orbit can be improved by adding the perturbations from M31’s other satellites, such as M32, as well as the potential of the Milky Way.
 -body to a full
-body to a full  -body simulation. However, this more realistic model changes the problem from
-body simulation. However, this more realistic model changes the problem from  to
to  , leading to a notable increase in computation time and making it extremely costly to run the simulation along with a genetic algorithm. Despite this complication, a self-gravitating model has a significant advantage in that it allows for evolution in NGC 205. This construction provides the necessary platform to test various formation scenarios for the satellite, since it can be initialized as a spiral or dwarf irregular and then transformed into a dwarf elliptical through tidal interactions. If this improvement were to be made, one might also consider adding an initial gas mass to the progenitor galaxy and performing hydrodynamic simulations for completeness. Last but not least, NGC 205’s orbit can be improved by adding the perturbations from M31’s other satellites, such as M32, as well as the potential of the Milky Way.
, leading to a notable increase in computation time and making it extremely costly to run the simulation along with a genetic algorithm. Despite this complication, a self-gravitating model has a significant advantage in that it allows for evolution in NGC 205. This construction provides the necessary platform to test various formation scenarios for the satellite, since it can be initialized as a spiral or dwarf irregular and then transformed into a dwarf elliptical through tidal interactions. If this improvement were to be made, one might also consider adding an initial gas mass to the progenitor galaxy and performing hydrodynamic simulations for completeness. Last but not least, NGC 205’s orbit can be improved by adding the perturbations from M31’s other satellites, such as M32, as well as the potential of the Milky Way. kpc behind M31 moving at very large velocities: 300-500 km s–1 on primarily radial orbits. Given that the observed radial component is only 54 km s–1, this implies a large tangential motion for NGC 205, moving from northwest to southeast. This suggests NGC 205 is not associated with the observed stellar arc northeast of NGC 205. Furthermore, NGC 205's velocity appears near escape velocity, signifying NGC 205 is likely on its first M31 passage.
kpc behind M31 moving at very large velocities: 300-500 km s–1 on primarily radial orbits. Given that the observed radial component is only 54 km s–1, this implies a large tangential motion for NGC 205, moving from northwest to southeast. This suggests NGC 205 is not associated with the observed stellar arc northeast of NGC 205. Furthermore, NGC 205's velocity appears near escape velocity, signifying NGC 205 is likely on its first M31 passage.



















 for the hot spheroid model. Orbits with
for the hot spheroid model. Orbits with  give
give  ,
,  , and
, and  km s–1 (not shown), and
km s–1 (not shown), and  kpc, values nearly identical to those from the disk models.
kpc, values nearly identical to those from the disk models. 

