1. INTRODUCTION
Since their discovery, gamma-ray burst (GRB) afterglows have been attributed to synchrotron radiation from the forward shock wave (Meszaros & Rees 1997), although it has been recently argued (Uhm & Beloborodov 2007; Genet et al. 2007) that observations might support a model in which the forward shock is invisible and the afterglow is emitted by a long-lived reverse shock in the burst ejecta. Assuming anyway a forward-shock origin for the afterglow emission, it is difficult to account for the magnetic energy density behind the forward shock by simple compression of the preshock field. Interstellar magnetic energy densities are typically comparable to thermal pressures and are therefore a fraction  to 10–7 of the total internal energy density when rest mass is included. It is possible that the preshock medium is the stellar wind of the burst progenitor; while the magnetic energy fraction in winds is less well known, it is unlikely to be much larger than this. Simply compressing the medium would produce approximately the same ratio
to 10–7 of the total internal energy density when rest mass is included. It is possible that the preshock medium is the stellar wind of the burst progenitor; while the magnetic energy fraction in winds is less well known, it is unlikely to be much larger than this. Simply compressing the medium would produce approximately the same ratio  behind the shock. Instead, phenomenological models of afterglow light curves typically require
behind the shock. Instead, phenomenological models of afterglow light curves typically require  to 10–1 (Panaitescu & Kumar 2002; Yost et al. 2003; Panaitescu 2005). It follows that the magnetic energy per baryon must be increased by ∼104-108.
to 10–1 (Panaitescu & Kumar 2002; Yost et al. 2003; Panaitescu 2005). It follows that the magnetic energy per baryon must be increased by ∼104-108.
 to 10–7 of the total internal energy density when rest mass is included. It is possible that the preshock medium is the stellar wind of the burst progenitor; while the magnetic energy fraction in winds is less well known, it is unlikely to be much larger than this. Simply compressing the medium would produce approximately the same ratio
to 10–7 of the total internal energy density when rest mass is included. It is possible that the preshock medium is the stellar wind of the burst progenitor; while the magnetic energy fraction in winds is less well known, it is unlikely to be much larger than this. Simply compressing the medium would produce approximately the same ratio  behind the shock. Instead, phenomenological models of afterglow light curves typically require
behind the shock. Instead, phenomenological models of afterglow light curves typically require  to 10–1 (Panaitescu & Kumar 2002; Yost et al. 2003; Panaitescu 2005). It follows that the magnetic energy per baryon must be increased by ∼104-108.
to 10–1 (Panaitescu & Kumar 2002; Yost et al. 2003; Panaitescu 2005). It follows that the magnetic energy per baryon must be increased by ∼104-108.In fact, GRB afterglows present the most compelling case among astrophysical collisionless shocks for prompt creation of magnetic energy. The synchrotron emission from supernova remnants is generally consistent with compression of the interstellar field, although some modest additional amplification may be required in particular cases (Völk et al. 2005). We focus here on GRB afterglows rather than GRB prompt emission, because the latter is generally believed to be produced within the ejecta (but see Dermer & Mitman 1999), which may be magnetically dominated from the start (Coburn & Boggs 2003; Zhang et al. 2003).
The leading hypothesis for field amplification in GRB afterglows is the relativistic Weibel instability, which extracts free energy from the anisotropy of the particles’ velocity distribution function, producing filamentary currents aligned with the shock normal; these currents are responsible for the creation of transverse magnetic fields (Medvedev & Loeb 1999). This process is able to violate MHD flux-freezing because it occurs on a microscopic scale—the relativistic electron or ion skin depth—where the inertia of individual charged particles is significant. While the Weibel instability provides a plausible mechanism to isotropize the particle velocities, it is unclear whether the small-scale fields that it produces can survive mutual annihilation long enough to explain the observed synchrotron afterglow emission. Several groups (Silva et al. 2003; Frederiksen et al. 2004; Spitkovsky 2005) have attempted to simulate the long-term nonlinear outcome of the instability, but a consensus on this question has not been achieved yet (Waxman 2006 and references therein); recent results (Spitkovsky 2007) seem to indicate that the small-scale field produced by the Weibel instability decays rapidly over a few tens of ion skin depths and does not persist over distances from the shock transition where the emission originates. One might have thought that if this instability were the source of postshock fields, then  should have a universal value for highly relativistic, highly collisionless shocks. Yet, while
should have a universal value for highly relativistic, highly collisionless shocks. Yet, while  is modeled by a constant for individual GRB afterglows, it seems to vary from one afterglow to another (Panaitescu & Kumar 2002; Yost et al. 2003; Panaitescu 2005).
is modeled by a constant for individual GRB afterglows, it seems to vary from one afterglow to another (Panaitescu & Kumar 2002; Yost et al. 2003; Panaitescu 2005).
 should have a universal value for highly relativistic, highly collisionless shocks. Yet, while
should have a universal value for highly relativistic, highly collisionless shocks. Yet, while  is modeled by a constant for individual GRB afterglows, it seems to vary from one afterglow to another (Panaitescu & Kumar 2002; Yost et al. 2003; Panaitescu 2005).
is modeled by a constant for individual GRB afterglows, it seems to vary from one afterglow to another (Panaitescu & Kumar 2002; Yost et al. 2003; Panaitescu 2005).In this paper we explore a traditional MHD explanation for magnetic field growth: turbulence. It is well known in nonrelativistic fluid dynamics that oblique shocks produce or alter the vorticity of a fluid (Ishizuka et al. 1964). In this paper we show that the same is true for an ultrarelativistic shock passing over density inhomogeneities in the preshock circumburst medium. The formalism described in a previous paper (Goodman & MacFadyen 2007, hereafter Paper I) has let us define the vorticity created in an ultrarelativistic fluid in which the energy-momentum tensor can be approximated by that of an ideal fluid with pressure equal to one-third of the proper energy density ( ). In the same work, we have introduced a remarkably simple but accurate general approximation for the local modulation of the shock Lorentz factor (Γ) by preshock density inhomogeneities; within this approximation, it is not necessary to follow the details of the flow far downstream in order to predict the evolution of the shock, provided that
). In the same work, we have introduced a remarkably simple but accurate general approximation for the local modulation of the shock Lorentz factor (Γ) by preshock density inhomogeneities; within this approximation, it is not necessary to follow the details of the flow far downstream in order to predict the evolution of the shock, provided that  , that the preshock pressure is negligible, and that the postshock pressure satisfies
, that the preshock pressure is negligible, and that the postshock pressure satisfies  . This approximation, which is modeled on nonrelativistic results described by Whitham (1974), reproduces exactly the self-similar evolution of Γ for a shock advancing into a cold preshock medium with a power-law density profile in planar, cylindrical, or spherical symmetry (Sari 2006). More importantly for the present purpose, it allows us to estimate the postshock vorticity resulting from a prescribed preshock density that varies along as well as perpendicular to the shock normal. Given the vorticity, we divide the postshock velocities, which are marginally nonrelativistic in the average postshock rest frame, into vortical and nonvortical parts. We presume that the energy density in vortical motions is a measure of the magnetic energy density that will eventually result after the eddies wind up the field to the point where its backreaction on the turbulence becomes important. These methods are described in § 2.
. This approximation, which is modeled on nonrelativistic results described by Whitham (1974), reproduces exactly the self-similar evolution of Γ for a shock advancing into a cold preshock medium with a power-law density profile in planar, cylindrical, or spherical symmetry (Sari 2006). More importantly for the present purpose, it allows us to estimate the postshock vorticity resulting from a prescribed preshock density that varies along as well as perpendicular to the shock normal. Given the vorticity, we divide the postshock velocities, which are marginally nonrelativistic in the average postshock rest frame, into vortical and nonvortical parts. We presume that the energy density in vortical motions is a measure of the magnetic energy density that will eventually result after the eddies wind up the field to the point where its backreaction on the turbulence becomes important. These methods are described in § 2.
 ). In the same work, we have introduced a remarkably simple but accurate general approximation for the local modulation of the shock Lorentz factor (Γ) by preshock density inhomogeneities; within this approximation, it is not necessary to follow the details of the flow far downstream in order to predict the evolution of the shock, provided that
). In the same work, we have introduced a remarkably simple but accurate general approximation for the local modulation of the shock Lorentz factor (Γ) by preshock density inhomogeneities; within this approximation, it is not necessary to follow the details of the flow far downstream in order to predict the evolution of the shock, provided that  , that the preshock pressure is negligible, and that the postshock pressure satisfies
, that the preshock pressure is negligible, and that the postshock pressure satisfies  . This approximation, which is modeled on nonrelativistic results described by Whitham (1974), reproduces exactly the self-similar evolution of Γ for a shock advancing into a cold preshock medium with a power-law density profile in planar, cylindrical, or spherical symmetry (Sari 2006). More importantly for the present purpose, it allows us to estimate the postshock vorticity resulting from a prescribed preshock density that varies along as well as perpendicular to the shock normal. Given the vorticity, we divide the postshock velocities, which are marginally nonrelativistic in the average postshock rest frame, into vortical and nonvortical parts. We presume that the energy density in vortical motions is a measure of the magnetic energy density that will eventually result after the eddies wind up the field to the point where its backreaction on the turbulence becomes important. These methods are described in § 2.
. This approximation, which is modeled on nonrelativistic results described by Whitham (1974), reproduces exactly the self-similar evolution of Γ for a shock advancing into a cold preshock medium with a power-law density profile in planar, cylindrical, or spherical symmetry (Sari 2006). More importantly for the present purpose, it allows us to estimate the postshock vorticity resulting from a prescribed preshock density that varies along as well as perpendicular to the shock normal. Given the vorticity, we divide the postshock velocities, which are marginally nonrelativistic in the average postshock rest frame, into vortical and nonvortical parts. We presume that the energy density in vortical motions is a measure of the magnetic energy density that will eventually result after the eddies wind up the field to the point where its backreaction on the turbulence becomes important. These methods are described in § 2.In § 3 we briefly review the present state of knowledge concerning the density inhomogeneities that may exist ahead of the shock. Both the amplitude and the length scale of the inhomogeneities are important. The former controls the amount of vortical energy—and then of magnetic energy—that is produced, while the latter determines the eddy turnover time of the turbulence, which—when multiplied by the number of eddy rotations necessary to amplify the field up to the observed  —must be less than the shock deceleration time, so that the field can be significantly amplified before adiabatic expansion reduces the particle energies available to be radiated. The uncertainties are large because one does not know whether the preshock medium is more like a stellar wind or like some component of the Galactic interstellar medium (ISM) and because the length scales of interest are too small (≲1014 cm) to be directly resolved even in the ISM. Inhomogeneities on somewhat larger scales have been invoked to explain undulations in afterglow light curves (Wang & Loeb 2000; Lazzati et al. 2002; Schaefer et al. 2003; Nakar et al. 2003).
—must be less than the shock deceleration time, so that the field can be significantly amplified before adiabatic expansion reduces the particle energies available to be radiated. The uncertainties are large because one does not know whether the preshock medium is more like a stellar wind or like some component of the Galactic interstellar medium (ISM) and because the length scales of interest are too small (≲1014 cm) to be directly resolved even in the ISM. Inhomogeneities on somewhat larger scales have been invoked to explain undulations in afterglow light curves (Wang & Loeb 2000; Lazzati et al. 2002; Schaefer et al. 2003; Nakar et al. 2003).
 —must be less than the shock deceleration time, so that the field can be significantly amplified before adiabatic expansion reduces the particle energies available to be radiated. The uncertainties are large because one does not know whether the preshock medium is more like a stellar wind or like some component of the Galactic interstellar medium (ISM) and because the length scales of interest are too small (≲1014 cm) to be directly resolved even in the ISM. Inhomogeneities on somewhat larger scales have been invoked to explain undulations in afterglow light curves (Wang & Loeb 2000; Lazzati et al. 2002; Schaefer et al. 2003; Nakar et al. 2003).
—must be less than the shock deceleration time, so that the field can be significantly amplified before adiabatic expansion reduces the particle energies available to be radiated. The uncertainties are large because one does not know whether the preshock medium is more like a stellar wind or like some component of the Galactic interstellar medium (ISM) and because the length scales of interest are too small (≲1014 cm) to be directly resolved even in the ISM. Inhomogeneities on somewhat larger scales have been invoked to explain undulations in afterglow light curves (Wang & Loeb 2000; Lazzati et al. 2002; Schaefer et al. 2003; Nakar et al. 2003).In § 4 we use the formalism of § 2 to characterize the density contrasts and length scales that preshock clumps should have in order to amplify the magnetic field up to the observed value, in the light of the circumburst picture outlined in § 3. We find that, for smaller shock Lorentz factors, the constraints on clump sizes and overdensities become less stringent; as a consequence, the magnetic energy fraction produced by preshock clumps via macroscopic turbulence is expected to evolve as the shock slows down. In § 5 we comment on the plausibility of our proposed mechanism to explain the magnetic field amplification in GRB afterglows, and we discuss how the results obtained in § 4 could be tested by inferring the time dependence of  from the time evolution of the observed synchrotron cooling frequency as the shock ages.
from the time evolution of the observed synchrotron cooling frequency as the shock ages.
 from the time evolution of the observed synchrotron cooling frequency as the shock ages.
from the time evolution of the observed synchrotron cooling frequency as the shock ages.2. GEOMETRICAL SHOCK DYNAMICS
The evolution of a shock advancing into an inhomogeneous medium depends, in principle, on the details of the downstream flow behind the shock and of the “piston” that drives it. Geometrical shock dynamics (GSD) is an approximation for this evolution in which only the conditions at the shock appear explicitly. Originally formulated by Whitham (1974) for nonrelativistic fluids, GSD has been extended by Paper I to strong ( ) ultrarelativistic shocks advancing into an ideal fluid whose pressure is negligible ahead of the shock, but one-third of its proper energy density behind the shock (
) ultrarelativistic shocks advancing into an ideal fluid whose pressure is negligible ahead of the shock, but one-third of its proper energy density behind the shock ( ).
).
 ) ultrarelativistic shocks advancing into an ideal fluid whose pressure is negligible ahead of the shock, but one-third of its proper energy density behind the shock (
) ultrarelativistic shocks advancing into an ideal fluid whose pressure is negligible ahead of the shock, but one-third of its proper energy density behind the shock ( ).
).The fundamental approximation of GSD is to evaluate the forward-going Riemann characteristics in the postshock flow as if that flow were (1) isentropic and (2) homogeneous far downstream with properties determined by the mean shock speed and the mean preshock density. Actually, preshock density inhomogeneities lead to postshock entropy variations, so assumption 1 is wrong in principle, but it turns out to be a useful fiction. In this respect, an ultrarelativistic flow has the advantage that since pressure depends only on energy density and not on any other thermodynamic variable (such as the proper number density of baryons, N), the actual entropy is irrelevant to the Riemann characteristics, which therefore enjoy exact Riemann invariants. So assumption 1 is well justified except insofar as it may be compromised by secondary shocks created by the inhomogeneities themselves behind the main shock. Assumption 2 is reasonable when preshock density inhomogeneities are small in length scale, so that they may be expected to average out far downstream.
With assumption 1, the Riemann invariant on the forward characteristics has the same value just behind the shock as it does far downstream and, therefore, with assumption 2, the same value that it would have in the mean flow. Together with the jump conditions across the shock, this provides a relation between the local Lorentz factor of the shock, Γ, and the proper preshock energy density  , in which
, in which  is the proper number density of nucleons ahead of the shock and m is the rest mass per nucleon. In the essentially one-dimensional case that
is the proper number density of nucleons ahead of the shock and m is the rest mass per nucleon. In the essentially one-dimensional case that  varies along the shock normal but not perpendicular to it, the ultrarelativistic GSD relation for the response of the shock Lorentz factor Γ to localized and transitory variations in the preshock density
varies along the shock normal but not perpendicular to it, the ultrarelativistic GSD relation for the response of the shock Lorentz factor Γ to localized and transitory variations in the preshock density  becomes (Paper I)
becomes (Paper I)
 and the corresponding change in the postshock pressure is
and the corresponding change in the postshock pressure is
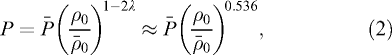 where the overbars indicate mean values. As in nonrelativistic GSD, these relations can be extended to multidimensional flows in which
where the overbars indicate mean values. As in nonrelativistic GSD, these relations can be extended to multidimensional flows in which  varies laterally as well as longitudinally (with respect to the shock normal), causing convergence or divergence of the shock normals. Equations (1) and (2) are then modified by factors involving the ratio of the local shock area to its mean value (Paper I). It is shown, however, that these corrections are of higher order in
varies laterally as well as longitudinally (with respect to the shock normal), causing convergence or divergence of the shock normals. Equations (1) and (2) are then modified by factors involving the ratio of the local shock area to its mean value (Paper I). It is shown, however, that these corrections are of higher order in  unless the density contrasts are ∼
unless the density contrasts are ∼ . For the conditions contemplated in this paper, equations (1) and (2) are adequate even in two or three dimensions.
. For the conditions contemplated in this paper, equations (1) and (2) are adequate even in two or three dimensions.
 , in which
, in which  is the proper number density of nucleons ahead of the shock and m is the rest mass per nucleon. In the essentially one-dimensional case that
is the proper number density of nucleons ahead of the shock and m is the rest mass per nucleon. In the essentially one-dimensional case that  varies along the shock normal but not perpendicular to it, the ultrarelativistic GSD relation for the response of the shock Lorentz factor Γ to localized and transitory variations in the preshock density
varies along the shock normal but not perpendicular to it, the ultrarelativistic GSD relation for the response of the shock Lorentz factor Γ to localized and transitory variations in the preshock density  becomes (Paper I)
becomes (Paper I)

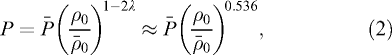
 varies laterally as well as longitudinally (with respect to the shock normal), causing convergence or divergence of the shock normals. Equations (1) and (2) are then modified by factors involving the ratio of the local shock area to its mean value (Paper I). It is shown, however, that these corrections are of higher order in
varies laterally as well as longitudinally (with respect to the shock normal), causing convergence or divergence of the shock normals. Equations (1) and (2) are then modified by factors involving the ratio of the local shock area to its mean value (Paper I). It is shown, however, that these corrections are of higher order in  unless the density contrasts are ∼
unless the density contrasts are ∼ . For the conditions contemplated in this paper, equations (1) and (2) are adequate even in two or three dimensions.
. For the conditions contemplated in this paper, equations (1) and (2) are adequate even in two or three dimensions.As in the original nonrelativistic theory, rigorous error estimates for ultrarelativistic GSD are difficult. Informally, the following conditions are probably necessary for the approximation to be useful. First, the preshock medium should be cold, meaning that preshock pressure satisfies  and that internal velocities are ≪
and that internal velocities are ≪ ; this is very likely true of the external forward shocks of GRBs. Second, the length scales of the preshock inhomogeneities should be small compared to the shock radius, so that the shock responds to local perturbations before conditions far downstream have time to react. Third, since
; this is very likely true of the external forward shocks of GRBs. Second, the length scales of the preshock inhomogeneities should be small compared to the shock radius, so that the shock responds to local perturbations before conditions far downstream have time to react. Third, since  is used as a small parameter, the preshock density fluctuations should not be so large as to cause the shock to become subrelativistic, i.e., one requires
is used as a small parameter, the preshock density fluctuations should not be so large as to cause the shock to become subrelativistic, i.e., one requires  . Finally, transitions in density should not be so abrupt as to cause strong reverse shocks, which would alter the forward shock dynamics. Paper I describes tests of ultrarelativistic GSD by comparison with exact self-similar solutions (some of which it reproduces exactly) and with numerical simulations. The latter indicate, for example, that equations (1) and (2) are in error by only a few percent for a
. Finally, transitions in density should not be so abrupt as to cause strong reverse shocks, which would alter the forward shock dynamics. Paper I describes tests of ultrarelativistic GSD by comparison with exact self-similar solutions (some of which it reproduces exactly) and with numerical simulations. The latter indicate, for example, that equations (1) and (2) are in error by only a few percent for a  shock encountering overdensities as large as
shock encountering overdensities as large as  .
.
 and that internal velocities are ≪
and that internal velocities are ≪ ; this is very likely true of the external forward shocks of GRBs. Second, the length scales of the preshock inhomogeneities should be small compared to the shock radius, so that the shock responds to local perturbations before conditions far downstream have time to react. Third, since
; this is very likely true of the external forward shocks of GRBs. Second, the length scales of the preshock inhomogeneities should be small compared to the shock radius, so that the shock responds to local perturbations before conditions far downstream have time to react. Third, since  is used as a small parameter, the preshock density fluctuations should not be so large as to cause the shock to become subrelativistic, i.e., one requires
is used as a small parameter, the preshock density fluctuations should not be so large as to cause the shock to become subrelativistic, i.e., one requires  . Finally, transitions in density should not be so abrupt as to cause strong reverse shocks, which would alter the forward shock dynamics. Paper I describes tests of ultrarelativistic GSD by comparison with exact self-similar solutions (some of which it reproduces exactly) and with numerical simulations. The latter indicate, for example, that equations (1) and (2) are in error by only a few percent for a
. Finally, transitions in density should not be so abrupt as to cause strong reverse shocks, which would alter the forward shock dynamics. Paper I describes tests of ultrarelativistic GSD by comparison with exact self-similar solutions (some of which it reproduces exactly) and with numerical simulations. The latter indicate, for example, that equations (1) and (2) are in error by only a few percent for a  shock encountering overdensities as large as
shock encountering overdensities as large as  .
.2.1. Relativistic Vorticity
This subsection is independent of GSD. We review the meaning of enthalpy current and vorticity in ideal relativistic fluids, especially those with the ultrarelativistic equation of state 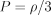 .
.
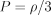 .
.When the shock passes over a local density excess—considered, for simplicity, in isolation from other inhomogeneities—the resulting postshock velocities are of two kinds. First, since the shocked clump is overpressured compared to its postshock surroundings (eq. [2]), it will expand and drive an outgoing pressure wave. If the density contrast of the clump is small, then the wave is essentially a linear disturbance from the start and travels at the sound speed,  , in the rest frame of the mean postshock flow; waves launched by large overdensities will be somewhat faster and may steepen into secondary shocks, but whatever its strength, the pressure wave rapidly departs from its source. Overlapping pressure waves launched by many distant clumps may contribute significant local velocity perturbations, but because of their oscillatory nature, intuition suggests that these velocities will not secularly amplify the magnetic field (except insofar as secondary shocks may contribute to vorticity; see § 4). It would be interesting to test this expectation in numerical simulations.
, in the rest frame of the mean postshock flow; waves launched by large overdensities will be somewhat faster and may steepen into secondary shocks, but whatever its strength, the pressure wave rapidly departs from its source. Overlapping pressure waves launched by many distant clumps may contribute significant local velocity perturbations, but because of their oscillatory nature, intuition suggests that these velocities will not secularly amplify the magnetic field (except insofar as secondary shocks may contribute to vorticity; see § 4). It would be interesting to test this expectation in numerical simulations.
 , in the rest frame of the mean postshock flow; waves launched by large overdensities will be somewhat faster and may steepen into secondary shocks, but whatever its strength, the pressure wave rapidly departs from its source. Overlapping pressure waves launched by many distant clumps may contribute significant local velocity perturbations, but because of their oscillatory nature, intuition suggests that these velocities will not secularly amplify the magnetic field (except insofar as secondary shocks may contribute to vorticity; see § 4). It would be interesting to test this expectation in numerical simulations.
, in the rest frame of the mean postshock flow; waves launched by large overdensities will be somewhat faster and may steepen into secondary shocks, but whatever its strength, the pressure wave rapidly departs from its source. Overlapping pressure waves launched by many distant clumps may contribute significant local velocity perturbations, but because of their oscillatory nature, intuition suggests that these velocities will not secularly amplify the magnetic field (except insofar as secondary shocks may contribute to vorticity; see § 4). It would be interesting to test this expectation in numerical simulations.Unless the density excess is constant along the shock front, the postshock velocity field will also contain a vortical component, whose strength is estimated below for an initially spherical overdensity with a Gaussian radial profile. As shown in Paper I, the equation of state  allows some freedom in how one defines relativistic vorticity, but to be useful in constraining the evolution of the flow, the vorticity should be associated with a conservation law such as Kelvin’s circulation theorem,
allows some freedom in how one defines relativistic vorticity, but to be useful in constraining the evolution of the flow, the vorticity should be associated with a conservation law such as Kelvin’s circulation theorem,
 where C is a closed contour comoving with the fluid four-velocity
where C is a closed contour comoving with the fluid four-velocity  , and
, and  for an appropriate thermodynamic function h (see below). Equation (3) is equivalent to
for an appropriate thermodynamic function h (see below). Equation (3) is equivalent to
 where
where  is the three-velocity of the fluid, and
is the three-velocity of the fluid, and  is the spatial part of
is the spatial part of  . Although formally identical to the nonrelativistic vorticity equation and written with three-vectors, equation (4) is actually relativistically covariant.
. Although formally identical to the nonrelativistic vorticity equation and written with three-vectors, equation (4) is actually relativistically covariant.
 allows some freedom in how one defines relativistic vorticity, but to be useful in constraining the evolution of the flow, the vorticity should be associated with a conservation law such as Kelvin’s circulation theorem,
allows some freedom in how one defines relativistic vorticity, but to be useful in constraining the evolution of the flow, the vorticity should be associated with a conservation law such as Kelvin’s circulation theorem,

 , and
, and  for an appropriate thermodynamic function h (see below). Equation (3) is equivalent to
for an appropriate thermodynamic function h (see below). Equation (3) is equivalent to

 is the three-velocity of the fluid, and
is the three-velocity of the fluid, and  is the spatial part of
is the spatial part of  . Although formally identical to the nonrelativistic vorticity equation and written with three-vectors, equation (4) is actually relativistically covariant.
. Although formally identical to the nonrelativistic vorticity equation and written with three-vectors, equation (4) is actually relativistically covariant.Because vorticity and circulation travel with the local flow velocity and are nonoscillatory in the local fluid frame, they have the potential to twist up and secularly amplify any magnetic field frozen into the flow. A fundamental assumption of this paper is that the magnetic energy will eventually reach equipartition with the kinetic energy invested in the vortical part of the flow. This assumption would also be well worth testing numerically.
For a general equation of state  , where N is the proper number density of conserved particles (e.g., baryons), it is conventional to take the quantity h in the relation
, where N is the proper number density of conserved particles (e.g., baryons), it is conventional to take the quantity h in the relation  to be the enthalpy per particle,
to be the enthalpy per particle, 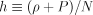 . One assumes an ideal fluid, so that the energy-momentum tensor is
. One assumes an ideal fluid, so that the energy-momentum tensor is
 where
where  in Minkowski coordinates, and the equations of motion are
in Minkowski coordinates, and the equations of motion are
 The first law of thermodynamics
The first law of thermodynamics  implies
implies  if the fluid is isentropic; the first equation of motion in equation (6) can then be recast as
if the fluid is isentropic; the first equation of motion in equation (6) can then be recast as
 the “curl” of which implies equations (3) and (4) (e.g., Eshraghi 2003; Paper I). These relations do not hold across shocks, of course, since there is an entropy jump. But if the preshock medium is inhomogeneous, then even if the flow behind the shock is smooth, it will not be isentropic in general; that is,
the “curl” of which implies equations (3) and (4) (e.g., Eshraghi 2003; Paper I). These relations do not hold across shocks, of course, since there is an entropy jump. But if the preshock medium is inhomogeneous, then even if the flow behind the shock is smooth, it will not be isentropic in general; that is,  (for an ultrarelativistic equation of state) will not be uniform. Therefore, the conventional choice of h does not lead to a conserved circulation under the circumstances contemplated in this paper. Fortunately, as pointed out in Paper I, if one defines
(for an ultrarelativistic equation of state) will not be uniform. Therefore, the conventional choice of h does not lead to a conserved circulation under the circumstances contemplated in this paper. Fortunately, as pointed out in Paper I, if one defines  using
using  instead of the true enthalpy, then equation (7) always holds in smooth parts of the flow. This is a consequence of the equation of state
instead of the true enthalpy, then equation (7) always holds in smooth parts of the flow. This is a consequence of the equation of state  , which is “barytropic” if not isentropic. It is convenient to choose the constant of proportionality so that
, which is “barytropic” if not isentropic. It is convenient to choose the constant of proportionality so that  reduces to the fluid four-velocity when pressure is uniform. Therefore, we replace the conventional enthalpy current with
reduces to the fluid four-velocity when pressure is uniform. Therefore, we replace the conventional enthalpy current with
 With this choice, circulation is conserved (eqs. [3] and [4]) everywhere except across shocks.
With this choice, circulation is conserved (eqs. [3] and [4]) everywhere except across shocks.
 , where N is the proper number density of conserved particles (e.g., baryons), it is conventional to take the quantity h in the relation
, where N is the proper number density of conserved particles (e.g., baryons), it is conventional to take the quantity h in the relation  to be the enthalpy per particle,
to be the enthalpy per particle, 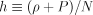 . One assumes an ideal fluid, so that the energy-momentum tensor is
. One assumes an ideal fluid, so that the energy-momentum tensor is

 in Minkowski coordinates, and the equations of motion are
in Minkowski coordinates, and the equations of motion are

 implies
implies  if the fluid is isentropic; the first equation of motion in equation (6) can then be recast as
if the fluid is isentropic; the first equation of motion in equation (6) can then be recast as

 (for an ultrarelativistic equation of state) will not be uniform. Therefore, the conventional choice of h does not lead to a conserved circulation under the circumstances contemplated in this paper. Fortunately, as pointed out in Paper I, if one defines
(for an ultrarelativistic equation of state) will not be uniform. Therefore, the conventional choice of h does not lead to a conserved circulation under the circumstances contemplated in this paper. Fortunately, as pointed out in Paper I, if one defines  using
using  instead of the true enthalpy, then equation (7) always holds in smooth parts of the flow. This is a consequence of the equation of state
instead of the true enthalpy, then equation (7) always holds in smooth parts of the flow. This is a consequence of the equation of state  , which is “barytropic” if not isentropic. It is convenient to choose the constant of proportionality so that
, which is “barytropic” if not isentropic. It is convenient to choose the constant of proportionality so that  reduces to the fluid four-velocity when pressure is uniform. Therefore, we replace the conventional enthalpy current with
reduces to the fluid four-velocity when pressure is uniform. Therefore, we replace the conventional enthalpy current with

2.2. Vorticity Production by Shocks
The goal of this subsection is to use the one-dimensional GSD approximation to derive equations (15)-(16), which relate the postshock vorticity to the preshock fractional overdensity  . Figure 1 illustrates four stages in the interaction of an ultrarelativistic shock with a density clump.
. Figure 1 illustrates four stages in the interaction of an ultrarelativistic shock with a density clump.
 . Figure 1 illustrates four stages in the interaction of an ultrarelativistic shock with a density clump.
. Figure 1 illustrates four stages in the interaction of an ultrarelativistic shock with a density clump.Figure 1.
History of a density clump overrun by an ultrarelativistic shock (mean Lorentz factor  ), viewed in the shock rest frame. (a) Lorentz-contracted (by a factor ∼
), viewed in the shock rest frame. (a) Lorentz-contracted (by a factor ∼ ) spherical clump approaches the shock (thick line) with
) spherical clump approaches the shock (thick line) with  . (b) After the shock, the clump contracts further by
. (b) After the shock, the clump contracts further by  [or
[or  in its rest frame] and moves downstream at
in its rest frame] and moves downstream at  . (c) The clump reexpands to reach pressure equilibrium and emits sound waves or weak shocks. (d) Vorticity created by the shock passage begins to roll up the clump.
. (c) The clump reexpands to reach pressure equilibrium and emits sound waves or weak shocks. (d) Vorticity created by the shock passage begins to roll up the clump. |
We begin by recalling some basic consequences of the shock jump conditions that will be needed below. Let ![[ Q]](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00052.gif) denote the discontinuity in a fluid property Q across the shock front. In the instantaneous local rest frame of the shock, where the outward unit normal to the shock front is
denote the discontinuity in a fluid property Q across the shock front. In the instantaneous local rest frame of the shock, where the outward unit normal to the shock front is  , the jump conditions are
, the jump conditions are ![[ \mathstrut{\cal T} ^{\mu j}n_{j}] =0](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00054.gif) . Using equation (5) for
. Using equation (5) for  (ideal fluid) and assuming that
(ideal fluid) and assuming that  ahead of the shock and
ahead of the shock and  behind it, one finds that the postshock three-velocity of the fluid is
behind it, one finds that the postshock three-velocity of the fluid is  in the shock frame (hence subsonic, since the sound speed is
in the shock frame (hence subsonic, since the sound speed is  ). The postshock energy density is
). The postshock energy density is  , where
, where  is the local Lorentz factor of the shock in the rest frame of the preshock fluid. Similarly, conservation of particles implies
is the local Lorentz factor of the shock in the rest frame of the preshock fluid. Similarly, conservation of particles implies ![[ NU^{i}n_{i}] =0](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00062.gif) , whence
, whence  . The quantities ρ, P, and N always denote proper values, meaning that they are defined in the local fluid rest frame and are therefore Lorentz invariants by fiat, with subscript “0” denoting a preshock value rather than a spacetime index.
. The quantities ρ, P, and N always denote proper values, meaning that they are defined in the local fluid rest frame and are therefore Lorentz invariants by fiat, with subscript “0” denoting a preshock value rather than a spacetime index.
![[ Q]](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00052.gif) denote the discontinuity in a fluid property Q across the shock front. In the instantaneous local rest frame of the shock, where the outward unit normal to the shock front is
denote the discontinuity in a fluid property Q across the shock front. In the instantaneous local rest frame of the shock, where the outward unit normal to the shock front is  , the jump conditions are
, the jump conditions are ![[ \mathstrut{\cal T} ^{\mu j}n_{j}] =0](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00054.gif) . Using equation (5) for
. Using equation (5) for  (ideal fluid) and assuming that
(ideal fluid) and assuming that  ahead of the shock and
ahead of the shock and  behind it, one finds that the postshock three-velocity of the fluid is
behind it, one finds that the postshock three-velocity of the fluid is  in the shock frame (hence subsonic, since the sound speed is
in the shock frame (hence subsonic, since the sound speed is  ). The postshock energy density is
). The postshock energy density is  , where
, where  is the local Lorentz factor of the shock in the rest frame of the preshock fluid. Similarly, conservation of particles implies
is the local Lorentz factor of the shock in the rest frame of the preshock fluid. Similarly, conservation of particles implies ![[ NU^{i}n_{i}] =0](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00062.gif) , whence
, whence  . The quantities ρ, P, and N always denote proper values, meaning that they are defined in the local fluid rest frame and are therefore Lorentz invariants by fiat, with subscript “0” denoting a preshock value rather than a spacetime index.
. The quantities ρ, P, and N always denote proper values, meaning that they are defined in the local fluid rest frame and are therefore Lorentz invariants by fiat, with subscript “0” denoting a preshock value rather than a spacetime index.To facilitate Lorentz boosts between the preshock and postshock or shock frames, it is often convenient to use the rapidity parameter  , where v is the three-velocity in the preshock frame. The relativistic addition of colinear three-velocities is equivalent to addition of the corresponding rapidity parameters. Thus, for example, using
, where v is the three-velocity in the preshock frame. The relativistic addition of colinear three-velocities is equivalent to addition of the corresponding rapidity parameters. Thus, for example, using  for the rapidity parameter of the shock and φ for the rapidity of the postshock fluid, it follows from the above that
for the rapidity parameter of the shock and φ for the rapidity of the postshock fluid, it follows from the above that  , whence
, whence  . The Lorentz factor of the postshock fluid relative to the preshock frame is
. The Lorentz factor of the postshock fluid relative to the preshock frame is 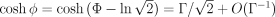 .
.
 , where v is the three-velocity in the preshock frame. The relativistic addition of colinear three-velocities is equivalent to addition of the corresponding rapidity parameters. Thus, for example, using
, where v is the three-velocity in the preshock frame. The relativistic addition of colinear three-velocities is equivalent to addition of the corresponding rapidity parameters. Thus, for example, using  for the rapidity parameter of the shock and φ for the rapidity of the postshock fluid, it follows from the above that
for the rapidity parameter of the shock and φ for the rapidity of the postshock fluid, it follows from the above that  , whence
, whence  . The Lorentz factor of the postshock fluid relative to the preshock frame is
. The Lorentz factor of the postshock fluid relative to the preshock frame is 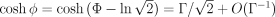 .
.Preshock clumps will typically have comparable longitudinal and lateral dimensions (meaning along and perpendicular to the mean direction of shock propagation) in their own rest frame. In the shock and postshock frames, the clumps will be longitudinally contracted by factors ∼ . During the transit of the shock over a clump and even during the subsequent expansion of the shocked clump as it comes to pressure equilibrium with the surrounding postshock fluid, there will not be enough time for signals (sound waves) to communicate laterally from one end of the clump to the other. Therefore, the interaction of the shock with the clump can be calculated in a one-dimensional approximation, in which the area of the shock is constant and the preshock mass density (
. During the transit of the shock over a clump and even during the subsequent expansion of the shocked clump as it comes to pressure equilibrium with the surrounding postshock fluid, there will not be enough time for signals (sound waves) to communicate laterally from one end of the clump to the other. Therefore, the interaction of the shock with the clump can be calculated in a one-dimensional approximation, in which the area of the shock is constant and the preshock mass density ( ) is stratified on planes parallel to the shock front.
) is stratified on planes parallel to the shock front.
 . During the transit of the shock over a clump and even during the subsequent expansion of the shocked clump as it comes to pressure equilibrium with the surrounding postshock fluid, there will not be enough time for signals (sound waves) to communicate laterally from one end of the clump to the other. Therefore, the interaction of the shock with the clump can be calculated in a one-dimensional approximation, in which the area of the shock is constant and the preshock mass density (
. During the transit of the shock over a clump and even during the subsequent expansion of the shocked clump as it comes to pressure equilibrium with the surrounding postshock fluid, there will not be enough time for signals (sound waves) to communicate laterally from one end of the clump to the other. Therefore, the interaction of the shock with the clump can be calculated in a one-dimensional approximation, in which the area of the shock is constant and the preshock mass density ( ) is stratified on planes parallel to the shock front.
) is stratified on planes parallel to the shock front.Nevertheless, lateral density gradients do produce postshock vorticity,  , even in our one-dimensional approximation. First of all, the longitudinal component
, even in our one-dimensional approximation. First of all, the longitudinal component  of the nonconventional enthalpy current defined in equation (8) varies with lateral position behind the shock. Second, since the shock itself is delayed differently at different lateral positions, the shock normal develops a lateral component, which leads to a small lateral current,
of the nonconventional enthalpy current defined in equation (8) varies with lateral position behind the shock. Second, since the shock itself is delayed differently at different lateral positions, the shock normal develops a lateral component, which leads to a small lateral current,  . Although the magnitude of
. Although the magnitude of  is
is  compared to
compared to  for a given clump amplitude, its longitudinal derivative makes a contribution to
for a given clump amplitude, its longitudinal derivative makes a contribution to  that is comparable to the lateral derivative of
that is comparable to the lateral derivative of  , as a consequence of Lorentz contraction.
, as a consequence of Lorentz contraction.
 , even in our one-dimensional approximation. First of all, the longitudinal component
, even in our one-dimensional approximation. First of all, the longitudinal component  of the nonconventional enthalpy current defined in equation (8) varies with lateral position behind the shock. Second, since the shock itself is delayed differently at different lateral positions, the shock normal develops a lateral component, which leads to a small lateral current,
of the nonconventional enthalpy current defined in equation (8) varies with lateral position behind the shock. Second, since the shock itself is delayed differently at different lateral positions, the shock normal develops a lateral component, which leads to a small lateral current,  . Although the magnitude of
. Although the magnitude of  is
is  compared to
compared to  for a given clump amplitude, its longitudinal derivative makes a contribution to
for a given clump amplitude, its longitudinal derivative makes a contribution to  that is comparable to the lateral derivative of
that is comparable to the lateral derivative of  , as a consequence of Lorentz contraction.
, as a consequence of Lorentz contraction.Let  be the density contrast of the clump:
be the density contrast of the clump: ![\rho _{0}( \boldsymbol{r}) =\overline{\rho }_{0}[ 1+\delta ( \boldsymbol{r}) ]](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00080.gif) , where
, where  is the mean preshock value. The shock propagates along z on average; let us choose a Cartesian coordinate system
is the mean preshock value. The shock propagates along z on average; let us choose a Cartesian coordinate system  in the preshock rest frame, where the subscript “0” is used to distinguish between the postshock (z) and preshock (
in the preshock rest frame, where the subscript “0” is used to distinguish between the postshock (z) and preshock ( ) longitudinal coordinates. In our one-dimensional GSD approximation, it follows from equation (1) that
) longitudinal coordinates. In our one-dimensional GSD approximation, it follows from equation (1) that
 if
if  is the value for a smooth preshock medium. As discussed at the beginning of this section, it will be assumed that
is the value for a smooth preshock medium. As discussed at the beginning of this section, it will be assumed that  so that
so that  at all times; since
at all times; since  is fairly small, rather hefty density contrasts can be compatible with this condition.
is fairly small, rather hefty density contrasts can be compatible with this condition.
 be the density contrast of the clump:
be the density contrast of the clump: ![\rho _{0}( \boldsymbol{r}) =\overline{\rho }_{0}[ 1+\delta ( \boldsymbol{r}) ]](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00080.gif) , where
, where  is the mean preshock value. The shock propagates along z on average; let us choose a Cartesian coordinate system
is the mean preshock value. The shock propagates along z on average; let us choose a Cartesian coordinate system  in the preshock rest frame, where the subscript “0” is used to distinguish between the postshock (z) and preshock (
in the preshock rest frame, where the subscript “0” is used to distinguish between the postshock (z) and preshock ( ) longitudinal coordinates. In our one-dimensional GSD approximation, it follows from equation (1) that
) longitudinal coordinates. In our one-dimensional GSD approximation, it follows from equation (1) that

 is the value for a smooth preshock medium. As discussed at the beginning of this section, it will be assumed that
is the value for a smooth preshock medium. As discussed at the beginning of this section, it will be assumed that  so that
so that  at all times; since
at all times; since  is fairly small, rather hefty density contrasts can be compatible with this condition.
is fairly small, rather hefty density contrasts can be compatible with this condition.First of all, let us focus on the contribution of  to the postshock vorticity. Let
to the postshock vorticity. Let  be the time in the preshock frame at which the shock reaches preshock position
be the time in the preshock frame at which the shock reaches preshock position  ,
,
 where we have assumed that the typical size of a density clump is small compared to the characteristic length scale for variations in
where we have assumed that the typical size of a density clump is small compared to the characteristic length scale for variations in  . The shock surface at time t is determined implicitly by
. The shock surface at time t is determined implicitly by  , so that the shock normal is
, so that the shock normal is  (the subscript reminds that derivatives are taken ahead of the shock). To leading order in
(the subscript reminds that derivatives are taken ahead of the shock). To leading order in  , the lateral components of the normal are therefore
, the lateral components of the normal are therefore
 where
where  is shorthand for
is shorthand for 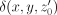 and
and  is the same in the preshock and postshock reference frames. The lateral part of the postshock fluid four-velocity is
is the same in the preshock and postshock reference frames. The lateral part of the postshock fluid four-velocity is  . With use of equations (8) and (9), the postshock lateral enthalpy current becomes
. With use of equations (8) and (9), the postshock lateral enthalpy current becomes
 Of course the lateral components of the enthalpy current take the same values in the mean postshock and preshock frames, since these frames differ by a longitudinal boost. However, in order to compute the vorticity in the mean postshock fluid frame, we should remember that the longitudinal derivative in this reference system
Of course the lateral components of the enthalpy current take the same values in the mean postshock and preshock frames, since these frames differ by a longitudinal boost. However, in order to compute the vorticity in the mean postshock fluid frame, we should remember that the longitudinal derivative in this reference system  is related to the corresponding derivative
is related to the corresponding derivative  in the preshock frame by
in the preshock frame by  because of Lorentz contraction. Thus, the contribution of
because of Lorentz contraction. Thus, the contribution of  to the postshock vorticity is
to the postshock vorticity is
 where
where  is the mean shock normal and clearly the differential operator
is the mean shock normal and clearly the differential operator  is the same in the preshock and postshock mean rest frames.
is the same in the preshock and postshock mean rest frames.
 to the postshock vorticity. Let
to the postshock vorticity. Let  be the time in the preshock frame at which the shock reaches preshock position
be the time in the preshock frame at which the shock reaches preshock position  ,
,

 . The shock surface at time t is determined implicitly by
. The shock surface at time t is determined implicitly by  , so that the shock normal is
, so that the shock normal is  (the subscript reminds that derivatives are taken ahead of the shock). To leading order in
(the subscript reminds that derivatives are taken ahead of the shock). To leading order in  , the lateral components of the normal are therefore
, the lateral components of the normal are therefore

 is shorthand for
is shorthand for 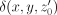 and
and  is the same in the preshock and postshock reference frames. The lateral part of the postshock fluid four-velocity is
is the same in the preshock and postshock reference frames. The lateral part of the postshock fluid four-velocity is  . With use of equations (8) and (9), the postshock lateral enthalpy current becomes
. With use of equations (8) and (9), the postshock lateral enthalpy current becomes

 is related to the corresponding derivative
is related to the corresponding derivative  in the preshock frame by
in the preshock frame by  because of Lorentz contraction. Thus, the contribution of
because of Lorentz contraction. Thus, the contribution of  to the postshock vorticity is
to the postshock vorticity is

 is the mean shock normal and clearly the differential operator
is the mean shock normal and clearly the differential operator  is the same in the preshock and postshock mean rest frames.
is the same in the preshock and postshock mean rest frames.A comparable contribution to the postshock vorticity comes from  . The longitudinal component of the postshock four-velocity is
. The longitudinal component of the postshock four-velocity is  when measured in the mean postshock frame. Since
when measured in the mean postshock frame. Since 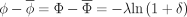 ,
,
 in the mean postshock frame. This tends to be quite subluminal; for unit overdensity (
in the mean postshock frame. This tends to be quite subluminal; for unit overdensity ( ), for example,
), for example,  , and the corresponding fluid Lorentz factor is ≈1.013. The longitudinal postshock enthalpy current is
, and the corresponding fluid Lorentz factor is ≈1.013. The longitudinal postshock enthalpy current is  . Taking the lateral derivative of this and combining with equation (13) and the definition of I in equation (10), we can write the total postshock vorticity as
. Taking the lateral derivative of this and combining with equation (13) and the definition of I in equation (10), we can write the total postshock vorticity as
 where the coordinate system is in the preshock rest frame and the derivatives are taken ahead of the shock. We have introduced the function
where the coordinate system is in the preshock rest frame and the derivatives are taken ahead of the shock. We have introduced the function
 For
For  ,
,  . It is interesting that in the total postshock vorticity there are no surviving factors of
. It is interesting that in the total postshock vorticity there are no surviving factors of  .
.
 . The longitudinal component of the postshock four-velocity is
. The longitudinal component of the postshock four-velocity is  when measured in the mean postshock frame. Since
when measured in the mean postshock frame. Since 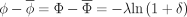 ,
,

 ), for example,
), for example,  , and the corresponding fluid Lorentz factor is ≈1.013. The longitudinal postshock enthalpy current is
, and the corresponding fluid Lorentz factor is ≈1.013. The longitudinal postshock enthalpy current is  . Taking the lateral derivative of this and combining with equation (13) and the definition of I in equation (10), we can write the total postshock vorticity as
. Taking the lateral derivative of this and combining with equation (13) and the definition of I in equation (10), we can write the total postshock vorticity as


 ,
,  . It is interesting that in the total postshock vorticity there are no surviving factors of
. It is interesting that in the total postshock vorticity there are no surviving factors of  .
.2.3. Vortical Energy
We have not been able to formulate a rigorous relativistically covariant way of dividing the energy of the postshock flow into vortical and nonvortical parts. In a nonrelativistic flow, however, this would be straightforward. One would divide the three-velocity field into potential and solenoidal parts,
 and then define the vortical energy by
and then define the vortical energy by
 where
where  is the nonrelativistic mass density. To make the decomposition from equation (17) unique, some mild additional restrictions are necessary: for example, that the region of interest is simply connected and that ψ and
is the nonrelativistic mass density. To make the decomposition from equation (17) unique, some mild additional restrictions are necessary: for example, that the region of interest is simply connected and that ψ and  have some specified behavior on the boundary or at infinity. Then one can impose
have some specified behavior on the boundary or at infinity. Then one can impose  and solve for
and solve for  from
from
 with
with  , using an appropriate Green’s function to invert
, using an appropriate Green’s function to invert  . The nonvortical part follows similarly from
. The nonvortical part follows similarly from  .
.


 is the nonrelativistic mass density. To make the decomposition from equation (17) unique, some mild additional restrictions are necessary: for example, that the region of interest is simply connected and that ψ and
is the nonrelativistic mass density. To make the decomposition from equation (17) unique, some mild additional restrictions are necessary: for example, that the region of interest is simply connected and that ψ and  have some specified behavior on the boundary or at infinity. Then one can impose
have some specified behavior on the boundary or at infinity. Then one can impose  and solve for
and solve for  from
from

 , using an appropriate Green’s function to invert
, using an appropriate Green’s function to invert  . The nonvortical part follows similarly from
. The nonvortical part follows similarly from  .
.It is not clear how to proceed in the relativistic case, because the coordinate energy density  is not simply quadratic in
is not simply quadratic in  , in general. However, for the applications we have in mind, the vortical motions are plausibly subsonic in the mean postshock frame (as long as δ is not too large) and, therefore, only mildly relativistic,
, in general. However, for the applications we have in mind, the vortical motions are plausibly subsonic in the mean postshock frame (as long as δ is not too large) and, therefore, only mildly relativistic,  . Therefore, we use the decomposition from equation (17), except for three changes: (1)
. Therefore, we use the decomposition from equation (17), except for three changes: (1)  replaces
replaces  , and therefore,
, and therefore,  in equation (19); (2)
in equation (19); (2)  , the nonrelativistic mass density, is replaced by
, the nonrelativistic mass density, is replaced by  , where ρ is the proper internal energy density; (3) the factor
, where ρ is the proper internal energy density; (3) the factor  in equation (18) is replaced by
in equation (18) is replaced by  . The reason for change 3 is that if
. The reason for change 3 is that if  and
and  , then
, then  , and we assume that
, and we assume that  derives from the second term.1
derives from the second term.1
 is not simply quadratic in
is not simply quadratic in  , in general. However, for the applications we have in mind, the vortical motions are plausibly subsonic in the mean postshock frame (as long as δ is not too large) and, therefore, only mildly relativistic,
, in general. However, for the applications we have in mind, the vortical motions are plausibly subsonic in the mean postshock frame (as long as δ is not too large) and, therefore, only mildly relativistic,  . Therefore, we use the decomposition from equation (17), except for three changes: (1)
. Therefore, we use the decomposition from equation (17), except for three changes: (1)  replaces
replaces  , and therefore,
, and therefore,  in equation (19); (2)
in equation (19); (2)  , the nonrelativistic mass density, is replaced by
, the nonrelativistic mass density, is replaced by  , where ρ is the proper internal energy density; (3) the factor
, where ρ is the proper internal energy density; (3) the factor  in equation (18) is replaced by
in equation (18) is replaced by  . The reason for change 3 is that if
. The reason for change 3 is that if  and
and  , then
, then  , and we assume that
, and we assume that  derives from the second term.1
derives from the second term.1A preshock density clump will experience, after the transit across the shock front, a contraction of its longitudinal size by a factor  , where
, where  . What was an approximately spherical clump becomes a pancake, with all of its associated vorticity in or near the interior. We adopt postshock cylindrical coordinates
. What was an approximately spherical clump becomes a pancake, with all of its associated vorticity in or near the interior. We adopt postshock cylindrical coordinates  with the z-axis parallel to the mean direction of propagation of the shock. Taking the origin at the center of the clump, assuming the clump to be axisymmetric, and recalling that the vorticity computed in equation (15) has been expressed in preshock coordinates, we may write
with the z-axis parallel to the mean direction of propagation of the shock. Taking the origin at the center of the clump, assuming the clump to be axisymmetric, and recalling that the vorticity computed in equation (15) has been expressed in preshock coordinates, we may write  , where
, where  is the Dirac delta function, and
is the Dirac delta function, and
 is referred to as the “projected vorticity.”
is referred to as the “projected vorticity.”
 , where
, where  . What was an approximately spherical clump becomes a pancake, with all of its associated vorticity in or near the interior. We adopt postshock cylindrical coordinates
. What was an approximately spherical clump becomes a pancake, with all of its associated vorticity in or near the interior. We adopt postshock cylindrical coordinates  with the z-axis parallel to the mean direction of propagation of the shock. Taking the origin at the center of the clump, assuming the clump to be axisymmetric, and recalling that the vorticity computed in equation (15) has been expressed in preshock coordinates, we may write
with the z-axis parallel to the mean direction of propagation of the shock. Taking the origin at the center of the clump, assuming the clump to be axisymmetric, and recalling that the vorticity computed in equation (15) has been expressed in preshock coordinates, we may write  , where
, where  is the Dirac delta function, and
is the Dirac delta function, and

Just after the shock passage, a clump will be at higher pressure than its surroundings, as discussed above, and will therefore expand until it reaches approximate pressure equilibrium. Since the sound crossing time in the longitudinal direction will be much less than that in lateral directions, equilibrium will be reached with only a small fractional change in the lateral size. The fractional change in the longitudinal size will be of order unity, but for  and clump overdensities
and clump overdensities  (
( is the adiabatic index appropriate for the one-dimensional expansion of an ultrarelativistic fluid), the clump will remain highly flattened even after equilibration. Since the vortex lines lie parallel to the clump midplane (i.e., in the direction
is the adiabatic index appropriate for the one-dimensional expansion of an ultrarelativistic fluid), the clump will remain highly flattened even after equilibration. Since the vortex lines lie parallel to the clump midplane (i.e., in the direction  ) and are “frozen” into the clump (as a consequence of Kelvin’s circulation theorem), the expansion will have little effect on the projected vorticity in equation (20). We may therefore solve equation (19) in the approximation that the vorticity is confined to a thin sheet with the projected vorticity computed in equation (20). The problem is mathematically equivalent to finding the vector potential due to an axisymmetric current sheet carrying a toroidal current,
) and are “frozen” into the clump (as a consequence of Kelvin’s circulation theorem), the expansion will have little effect on the projected vorticity in equation (20). We may therefore solve equation (19) in the approximation that the vorticity is confined to a thin sheet with the projected vorticity computed in equation (20). The problem is mathematically equivalent to finding the vector potential due to an axisymmetric current sheet carrying a toroidal current,
 where
where  is the Bessel function of order 1 and
is the Bessel function of order 1 and  is the Hankel transform of the projected vorticity
is the Hankel transform of the projected vorticity  ,
,
 As soon as the clump is at the same pressure as its surroundings, if the vortical motions are subrelativistic, we can use the decomposition from equation (17) with
As soon as the clump is at the same pressure as its surroundings, if the vortical motions are subrelativistic, we can use the decomposition from equation (17) with  . Moreover, pressure equilibrium between the clump and the average postshock medium implies2 that the clump proper energy density ρ is approximately equal [neglecting terms of order
. Moreover, pressure equilibrium between the clump and the average postshock medium implies2 that the clump proper energy density ρ is approximately equal [neglecting terms of order  ] to the mean postshock value
] to the mean postshock value  . Then the vortical energy of a single clump becomes
. Then the vortical energy of a single clump becomes
 In accordance with the discussion following equation (19), we have replaced the factor
In accordance with the discussion following equation (19), we have replaced the factor  in equation (18) with
in equation (18) with  . In addition, we have used integration by parts to replace the integral over all space with an integral over the source of vorticity only. This is particularly convenient when the source is represented by a vortex sheet, because we may express the energy as an integral in k-space,
. In addition, we have used integration by parts to replace the integral over all space with an integral over the source of vorticity only. This is particularly convenient when the source is represented by a vortex sheet, because we may express the energy as an integral in k-space,

 and clump overdensities
and clump overdensities  (
( is the adiabatic index appropriate for the one-dimensional expansion of an ultrarelativistic fluid), the clump will remain highly flattened even after equilibration. Since the vortex lines lie parallel to the clump midplane (i.e., in the direction
is the adiabatic index appropriate for the one-dimensional expansion of an ultrarelativistic fluid), the clump will remain highly flattened even after equilibration. Since the vortex lines lie parallel to the clump midplane (i.e., in the direction  ) and are “frozen” into the clump (as a consequence of Kelvin’s circulation theorem), the expansion will have little effect on the projected vorticity in equation (20). We may therefore solve equation (19) in the approximation that the vorticity is confined to a thin sheet with the projected vorticity computed in equation (20). The problem is mathematically equivalent to finding the vector potential due to an axisymmetric current sheet carrying a toroidal current,
) and are “frozen” into the clump (as a consequence of Kelvin’s circulation theorem), the expansion will have little effect on the projected vorticity in equation (20). We may therefore solve equation (19) in the approximation that the vorticity is confined to a thin sheet with the projected vorticity computed in equation (20). The problem is mathematically equivalent to finding the vector potential due to an axisymmetric current sheet carrying a toroidal current,

 is the Bessel function of order 1 and
is the Bessel function of order 1 and  is the Hankel transform of the projected vorticity
is the Hankel transform of the projected vorticity  ,
,

 . Moreover, pressure equilibrium between the clump and the average postshock medium implies2 that the clump proper energy density ρ is approximately equal [neglecting terms of order
. Moreover, pressure equilibrium between the clump and the average postshock medium implies2 that the clump proper energy density ρ is approximately equal [neglecting terms of order  ] to the mean postshock value
] to the mean postshock value  . Then the vortical energy of a single clump becomes
. Then the vortical energy of a single clump becomes

 in equation (18) with
in equation (18) with  . In addition, we have used integration by parts to replace the integral over all space with an integral over the source of vorticity only. This is particularly convenient when the source is represented by a vortex sheet, because we may express the energy as an integral in k-space,
. In addition, we have used integration by parts to replace the integral over all space with an integral over the source of vorticity only. This is particularly convenient when the source is represented by a vortex sheet, because we may express the energy as an integral in k-space,

We assume that the vortical energies of different clumps can simply be added. This is justified if the clumps are well separated compared to their larger (i.e., lateral) dimensions. Then if the number density of clumps in the preshock frame is  and all the clumps have the same axisymmetric density profile, the vortical energy density in the average postshock frame is
and all the clumps have the same axisymmetric density profile, the vortical energy density in the average postshock frame is  , and the vortical energy fraction becomes
, and the vortical energy fraction becomes
 Recall from equation (20) that the projected vorticity is proportional to
Recall from equation (20) that the projected vorticity is proportional to  . Since this factor is squared in computing the vortical energy, it follows from equation (25) that
. Since this factor is squared in computing the vortical energy, it follows from equation (25) that  for a fixed preshock density field. This scaling is perhaps the most important conclusion of our analysis up to this point.
for a fixed preshock density field. This scaling is perhaps the most important conclusion of our analysis up to this point.
 and all the clumps have the same axisymmetric density profile, the vortical energy density in the average postshock frame is
and all the clumps have the same axisymmetric density profile, the vortical energy density in the average postshock frame is  , and the vortical energy fraction becomes
, and the vortical energy fraction becomes

 . Since this factor is squared in computing the vortical energy, it follows from equation (25) that
. Since this factor is squared in computing the vortical energy, it follows from equation (25) that  for a fixed preshock density field. This scaling is perhaps the most important conclusion of our analysis up to this point.
for a fixed preshock density field. This scaling is perhaps the most important conclusion of our analysis up to this point.1 Why  rather than
rather than  , as one might expect in the nonrelativistic limit? The answer is that the rest-mass density of nonrelativistic fluid mechanics is actually
, as one might expect in the nonrelativistic limit? The answer is that the rest-mass density of nonrelativistic fluid mechanics is actually  , where m is the mass per particle and
, where m is the mass per particle and  , whereas the proper energy density is
, whereas the proper energy density is  , where mu is the internal energy per particle. Thus, for a general equation of state,
, where mu is the internal energy per particle. Thus, for a general equation of state,  . For
. For  , this reduces to
, this reduces to ![\mathstrut{\cal T} ^{00}\approx \rho _{m}c^{2}+\rho _{m}( v^{2}/ 2+u) +[ ( v/ c) ^{2}( \rho _{m}u/ 2+P) ]](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00163.gif) . The middle term is now recognizable as the nonrelativistic kinetic-plus-internal energy density. The term in square brackets would normally be negligible for a cold fluid because
. The middle term is now recognizable as the nonrelativistic kinetic-plus-internal energy density. The term in square brackets would normally be negligible for a cold fluid because  ; however, for an ultrarelativistic ideal fluid
; however, for an ultrarelativistic ideal fluid  , and the result is
, and the result is  , of which the first two terms are now negligible.
, of which the first two terms are now negligible.
 rather than
rather than  , as one might expect in the nonrelativistic limit? The answer is that the rest-mass density of nonrelativistic fluid mechanics is actually
, as one might expect in the nonrelativistic limit? The answer is that the rest-mass density of nonrelativistic fluid mechanics is actually  , where m is the mass per particle and
, where m is the mass per particle and  , whereas the proper energy density is
, whereas the proper energy density is  , where mu is the internal energy per particle. Thus, for a general equation of state,
, where mu is the internal energy per particle. Thus, for a general equation of state,  . For
. For  , this reduces to
, this reduces to ![\mathstrut{\cal T} ^{00}\approx \rho _{m}c^{2}+\rho _{m}( v^{2}/ 2+u) +[ ( v/ c) ^{2}( \rho _{m}u/ 2+P) ]](https://content.cld.iop.org/journals/0004-637X/671/2/1858/revision1/eq-00163.gif) . The middle term is now recognizable as the nonrelativistic kinetic-plus-internal energy density. The term in square brackets would normally be negligible for a cold fluid because
. The middle term is now recognizable as the nonrelativistic kinetic-plus-internal energy density. The term in square brackets would normally be negligible for a cold fluid because  ; however, for an ultrarelativistic ideal fluid
; however, for an ultrarelativistic ideal fluid  , and the result is
, and the result is  , of which the first two terms are now negligible.
, of which the first two terms are now negligible.2 In the mean postshock rest frame, if  is the energy-momentum tensor of the fluid in turbulent motion and
is the energy-momentum tensor of the fluid in turbulent motion and  is that of the mean fluid (whose four-velocity has spatial components
is that of the mean fluid (whose four-velocity has spatial components  in this reference frame), pressure equilibrium requires
in this reference frame), pressure equilibrium requires  ; under the assumption of spatial statistical isotropy for the turbulent motions, this implies
; under the assumption of spatial statistical isotropy for the turbulent motions, this implies  , which yields, for an ultrarelativistic fluid (
, which yields, for an ultrarelativistic fluid ( ), the equality
), the equality  ; then, since
; then, since  , if the vortical motions are subrelativistic we obtain
, if the vortical motions are subrelativistic we obtain  .
.
 is the energy-momentum tensor of the fluid in turbulent motion and
is the energy-momentum tensor of the fluid in turbulent motion and  is that of the mean fluid (whose four-velocity has spatial components
is that of the mean fluid (whose four-velocity has spatial components  in this reference frame), pressure equilibrium requires
in this reference frame), pressure equilibrium requires  ; under the assumption of spatial statistical isotropy for the turbulent motions, this implies
; under the assumption of spatial statistical isotropy for the turbulent motions, this implies  , which yields, for an ultrarelativistic fluid (
, which yields, for an ultrarelativistic fluid ( ), the equality
), the equality  ; then, since
; then, since  , if the vortical motions are subrelativistic we obtain
, if the vortical motions are subrelativistic we obtain  .
.3. THE CIRCUMBURST MEDIUM
Observations support the idea that long-duration GRBs are associated with the deaths of massive Wolf-Rayet (WR) stars, presumably arising from their core collapse (Woosley & Bloom 2006 and references therein). Then the circumburst environment is determined by the star’s mass-loss history. At the onset of the WR phase, the WR stellar wind is expected to expand with a typical velocity  inside the preexisting slower wind emitted during the red supergiant (RSG) phase, whose characteristic speed is
inside the preexisting slower wind emitted during the red supergiant (RSG) phase, whose characteristic speed is  . The winds from massive RSGs are characterized by a mass-loss rate
. The winds from massive RSGs are characterized by a mass-loss rate  between 10–6 and 10–4 M⊙ yr–1 (Chevalier et al. 2006), while the mass-loss rates
between 10–6 and 10–4 M⊙ yr–1 (Chevalier et al. 2006), while the mass-loss rates  of WR stars are between 10–5 and 10–4 M⊙ yr–1 (Crowther 2007). Several solar masses are shed by the star during these evolutionary phases. The mass equivalent to the energy of a GRB, on the other hand, is only ≈
of WR stars are between 10–5 and 10–4 M⊙ yr–1 (Crowther 2007). Several solar masses are shed by the star during these evolutionary phases. The mass equivalent to the energy of a GRB, on the other hand, is only ≈ . Therefore, the GRB forward shock is expected to become nonrelativistic long before it escapes the wind to encounter the ISM. There are at least four regions of the wind that are relevant to the relativistic phase of the afterglow (Ramirez-Ruiz et al. 2005): from the inside out, these are an expanding WR wind (
. Therefore, the GRB forward shock is expected to become nonrelativistic long before it escapes the wind to encounter the ISM. There are at least four regions of the wind that are relevant to the relativistic phase of the afterglow (Ramirez-Ruiz et al. 2005): from the inside out, these are an expanding WR wind ( , where r is the distance from the star), the shocked WR wind (
, where r is the distance from the star), the shocked WR wind ( ), the shocked RSG wind (
), the shocked RSG wind ( ), and a freely expanding RSG wind (
), and a freely expanding RSG wind ( ). Beyond these lie another shocked part of the RSG wind, the shocked ISM, and finally the unshocked ISM.
). Beyond these lie another shocked part of the RSG wind, the shocked ISM, and finally the unshocked ISM.
 inside the preexisting slower wind emitted during the red supergiant (RSG) phase, whose characteristic speed is
inside the preexisting slower wind emitted during the red supergiant (RSG) phase, whose characteristic speed is  . The winds from massive RSGs are characterized by a mass-loss rate
. The winds from massive RSGs are characterized by a mass-loss rate  between 10–6 and 10–4 M⊙ yr–1 (Chevalier et al. 2006), while the mass-loss rates
between 10–6 and 10–4 M⊙ yr–1 (Chevalier et al. 2006), while the mass-loss rates  of WR stars are between 10–5 and 10–4 M⊙ yr–1 (Crowther 2007). Several solar masses are shed by the star during these evolutionary phases. The mass equivalent to the energy of a GRB, on the other hand, is only ≈
of WR stars are between 10–5 and 10–4 M⊙ yr–1 (Crowther 2007). Several solar masses are shed by the star during these evolutionary phases. The mass equivalent to the energy of a GRB, on the other hand, is only ≈ . Therefore, the GRB forward shock is expected to become nonrelativistic long before it escapes the wind to encounter the ISM. There are at least four regions of the wind that are relevant to the relativistic phase of the afterglow (Ramirez-Ruiz et al. 2005): from the inside out, these are an expanding WR wind (
. Therefore, the GRB forward shock is expected to become nonrelativistic long before it escapes the wind to encounter the ISM. There are at least four regions of the wind that are relevant to the relativistic phase of the afterglow (Ramirez-Ruiz et al. 2005): from the inside out, these are an expanding WR wind ( , where r is the distance from the star), the shocked WR wind (
, where r is the distance from the star), the shocked WR wind ( ), the shocked RSG wind (
), the shocked RSG wind ( ), and a freely expanding RSG wind (
), and a freely expanding RSG wind ( ). Beyond these lie another shocked part of the RSG wind, the shocked ISM, and finally the unshocked ISM.
). Beyond these lie another shocked part of the RSG wind, the shocked ISM, and finally the unshocked ISM.Density inhomogeneities in such a stratified structure could be produced by several processes. First of all, the acceleration region of the WR wind, which extends to a few times the stellar radius, is known to be clumpy. Emission-line data indicate accelerating “blobs” (Moffat et al. 1988) with density filling factors  (Crowther 2007 and references therein). These must occur where the continuum is optically thin and must be large enough transversely to cover an appreciable part (≳10%) of the stellar photosphere. The clumpiness of this region is in accord with theory, since the line-driving mechanism of Castor et al. (1975), which explains the gross properties of WR and main-sequence O-star winds rather satisfactorily, is known to be unstable both radially and nonradially on scales larger than the “Sobolev length”
(Crowther 2007 and references therein). These must occur where the continuum is optically thin and must be large enough transversely to cover an appreciable part (≳10%) of the stellar photosphere. The clumpiness of this region is in accord with theory, since the line-driving mechanism of Castor et al. (1975), which explains the gross properties of WR and main-sequence O-star winds rather satisfactorily, is known to be unstable both radially and nonradially on scales larger than the “Sobolev length”  (Dessart & Owocki 2005 and references therein), where
(Dessart & Owocki 2005 and references therein), where  is the thermal velocity in the wind. Clump dimensions at least as small as ∼1010 cm with density contrasts ∼
is the thermal velocity in the wind. Clump dimensions at least as small as ∼1010 cm with density contrasts ∼ are therefore expected. These clumps may dissolve beyond the acceleration region (
are therefore expected. These clumps may dissolve beyond the acceleration region ( ) if the optically thin wind maintains a uniform temperature comparable to the color temperature of the star; the clumps are then at higher pressure than their surroundings and will expand on their sound crossing time. After crossing the reverse shock, the wind reaches temperatures ∼108 K, a regime that is thermally unstable (Field 1965). Beyond the contact discontinuity, the shocked RSG wind lies at
) if the optically thin wind maintains a uniform temperature comparable to the color temperature of the star; the clumps are then at higher pressure than their surroundings and will expand on their sound crossing time. After crossing the reverse shock, the wind reaches temperatures ∼108 K, a regime that is thermally unstable (Field 1965). Beyond the contact discontinuity, the shocked RSG wind lies at  , which is even more unstable. Thermal instability may give rise to new clumps, whose minimum size is controlled by thermal conduction and is therefore very uncertain, because the conduction rate is probably sensitive to magnetic field. Furthermore, the contact discontinuity is subject to Rayleigh-Taylor instability as the shocked RSG wind is accelerated by the less dense WR wind; however, Garcia-Segura & Franco (1996) found that clump formation is not efficient for the case of pure Rayleigh-Taylor instabilities in thick shells and concluded that a necessary condition for clump development to occur is that the shocked shell be thin enough to allow Vishniac-like instabilities (Vishniac 1983). Ramirez-Ruiz et al. (2005) point out that rapid cooling of the shocked RSG wind is indeed likely to lead to a thin shell. Clump development in the shell is controlled by the Kelvin-Helmholtz damping of the coupling between the Rayleigh-Taylor and Vishniac instabilities, while the lifetime of small dense clumps, once formed, probably again depends on conduction.
, which is even more unstable. Thermal instability may give rise to new clumps, whose minimum size is controlled by thermal conduction and is therefore very uncertain, because the conduction rate is probably sensitive to magnetic field. Furthermore, the contact discontinuity is subject to Rayleigh-Taylor instability as the shocked RSG wind is accelerated by the less dense WR wind; however, Garcia-Segura & Franco (1996) found that clump formation is not efficient for the case of pure Rayleigh-Taylor instabilities in thick shells and concluded that a necessary condition for clump development to occur is that the shocked shell be thin enough to allow Vishniac-like instabilities (Vishniac 1983). Ramirez-Ruiz et al. (2005) point out that rapid cooling of the shocked RSG wind is indeed likely to lead to a thin shell. Clump development in the shell is controlled by the Kelvin-Helmholtz damping of the coupling between the Rayleigh-Taylor and Vishniac instabilities, while the lifetime of small dense clumps, once formed, probably again depends on conduction.
 (Crowther 2007 and references therein). These must occur where the continuum is optically thin and must be large enough transversely to cover an appreciable part (≳10%) of the stellar photosphere. The clumpiness of this region is in accord with theory, since the line-driving mechanism of Castor et al. (1975), which explains the gross properties of WR and main-sequence O-star winds rather satisfactorily, is known to be unstable both radially and nonradially on scales larger than the “Sobolev length”
(Crowther 2007 and references therein). These must occur where the continuum is optically thin and must be large enough transversely to cover an appreciable part (≳10%) of the stellar photosphere. The clumpiness of this region is in accord with theory, since the line-driving mechanism of Castor et al. (1975), which explains the gross properties of WR and main-sequence O-star winds rather satisfactorily, is known to be unstable both radially and nonradially on scales larger than the “Sobolev length”  (Dessart & Owocki 2005 and references therein), where
(Dessart & Owocki 2005 and references therein), where  is the thermal velocity in the wind. Clump dimensions at least as small as ∼1010 cm with density contrasts ∼
is the thermal velocity in the wind. Clump dimensions at least as small as ∼1010 cm with density contrasts ∼ are therefore expected. These clumps may dissolve beyond the acceleration region (
are therefore expected. These clumps may dissolve beyond the acceleration region ( ) if the optically thin wind maintains a uniform temperature comparable to the color temperature of the star; the clumps are then at higher pressure than their surroundings and will expand on their sound crossing time. After crossing the reverse shock, the wind reaches temperatures ∼108 K, a regime that is thermally unstable (Field 1965). Beyond the contact discontinuity, the shocked RSG wind lies at
) if the optically thin wind maintains a uniform temperature comparable to the color temperature of the star; the clumps are then at higher pressure than their surroundings and will expand on their sound crossing time. After crossing the reverse shock, the wind reaches temperatures ∼108 K, a regime that is thermally unstable (Field 1965). Beyond the contact discontinuity, the shocked RSG wind lies at  , which is even more unstable. Thermal instability may give rise to new clumps, whose minimum size is controlled by thermal conduction and is therefore very uncertain, because the conduction rate is probably sensitive to magnetic field. Furthermore, the contact discontinuity is subject to Rayleigh-Taylor instability as the shocked RSG wind is accelerated by the less dense WR wind; however, Garcia-Segura & Franco (1996) found that clump formation is not efficient for the case of pure Rayleigh-Taylor instabilities in thick shells and concluded that a necessary condition for clump development to occur is that the shocked shell be thin enough to allow Vishniac-like instabilities (Vishniac 1983). Ramirez-Ruiz et al. (2005) point out that rapid cooling of the shocked RSG wind is indeed likely to lead to a thin shell. Clump development in the shell is controlled by the Kelvin-Helmholtz damping of the coupling between the Rayleigh-Taylor and Vishniac instabilities, while the lifetime of small dense clumps, once formed, probably again depends on conduction.
, which is even more unstable. Thermal instability may give rise to new clumps, whose minimum size is controlled by thermal conduction and is therefore very uncertain, because the conduction rate is probably sensitive to magnetic field. Furthermore, the contact discontinuity is subject to Rayleigh-Taylor instability as the shocked RSG wind is accelerated by the less dense WR wind; however, Garcia-Segura & Franco (1996) found that clump formation is not efficient for the case of pure Rayleigh-Taylor instabilities in thick shells and concluded that a necessary condition for clump development to occur is that the shocked shell be thin enough to allow Vishniac-like instabilities (Vishniac 1983). Ramirez-Ruiz et al. (2005) point out that rapid cooling of the shocked RSG wind is indeed likely to lead to a thin shell. Clump development in the shell is controlled by the Kelvin-Helmholtz damping of the coupling between the Rayleigh-Taylor and Vishniac instabilities, while the lifetime of small dense clumps, once formed, probably again depends on conduction.In short, there are ample reasons to expect a strongly inhomogeneous medium ahead of the GRB forward shock, but the sizes of the smallest clumps are uncertain. We make no attempt to estimate these sizes, but simply state below the properties (length scale, density contrast, and number density) that the clumps would have to have in order to produce postshock turbulence capable of amplifying the magnetic field sufficiently.
It is of course essential for our proposed mechanism that a seed field exist in the preshock medium. Magnetic and thermal energy densities are generally comparable in the ISM, but much less is known about the magnetic component of the winds of early-type stars. Since such winds are believed to be driven by radiative rather than centrifugal forces, as in late-type main-sequence stars, and since such stars do not possess surface convection zones, the magnetic field might be very small a priori . However, magnetic effects have been invoked to explain X-ray emission and anisotropy in the winds of early-type stars (Wolf et al. 1999; ud-Doula & Owocki 2002; Schulz et al. 2003). Furthermore, since the amplification of a weak (kinematic) magnetic energy density by turbulence proceeds exponentially on the timescale of the energy-bearing eddies (Schekochihin et al. 2002 and references therein), the number  of eddy turnover times required to reach saturation is only logarithmically dependent on the strength of the seed field. Therefore, in the estimates of the required turnover time made below, we simply assume that the magnetic energy fraction
of eddy turnover times required to reach saturation is only logarithmically dependent on the strength of the seed field. Therefore, in the estimates of the required turnover time made below, we simply assume that the magnetic energy fraction  in the preshock medium is comparable to that in the ISM, ∼10–8, so that the number of eddy rotations necessary to explain the value of
in the preshock medium is comparable to that in the ISM, ∼10–8, so that the number of eddy rotations necessary to explain the value of  inferred from afterglow observations is of order
inferred from afterglow observations is of order  . The microscopic magnetic field created by plasma instabilities at the shock might serve as a seed field for turbulent amplification if it cascades to larger scales before dissipation; fewer (if any) eddy turnovers would then be required, since the Weibel magnetic energy fraction at the shock peaks at a few tens of percent (Spitkovsky 2007). Under these circumstances, however, the Weibel instability might produce the required fields without the benefit of macroscopic amplification.
. The microscopic magnetic field created by plasma instabilities at the shock might serve as a seed field for turbulent amplification if it cascades to larger scales before dissipation; fewer (if any) eddy turnovers would then be required, since the Weibel magnetic energy fraction at the shock peaks at a few tens of percent (Spitkovsky 2007). Under these circumstances, however, the Weibel instability might produce the required fields without the benefit of macroscopic amplification.
 of eddy turnover times required to reach saturation is only logarithmically dependent on the strength of the seed field. Therefore, in the estimates of the required turnover time made below, we simply assume that the magnetic energy fraction
of eddy turnover times required to reach saturation is only logarithmically dependent on the strength of the seed field. Therefore, in the estimates of the required turnover time made below, we simply assume that the magnetic energy fraction  in the preshock medium is comparable to that in the ISM, ∼10–8, so that the number of eddy rotations necessary to explain the value of
in the preshock medium is comparable to that in the ISM, ∼10–8, so that the number of eddy rotations necessary to explain the value of  inferred from afterglow observations is of order
inferred from afterglow observations is of order  . The microscopic magnetic field created by plasma instabilities at the shock might serve as a seed field for turbulent amplification if it cascades to larger scales before dissipation; fewer (if any) eddy turnovers would then be required, since the Weibel magnetic energy fraction at the shock peaks at a few tens of percent (Spitkovsky 2007). Under these circumstances, however, the Weibel instability might produce the required fields without the benefit of macroscopic amplification.
. The microscopic magnetic field created by plasma instabilities at the shock might serve as a seed field for turbulent amplification if it cascades to larger scales before dissipation; fewer (if any) eddy turnovers would then be required, since the Weibel magnetic energy fraction at the shock peaks at a few tens of percent (Spitkovsky 2007). Under these circumstances, however, the Weibel instability might produce the required fields without the benefit of macroscopic amplification.4. RESULTS
The formalism described in § 2 can be used to predict the eddy turnover time and vortical energy fraction of the turbulent motions produced by an ultrarelativistic shock sweeping up a clumpy medium; if the preshock average (i.e., smoothed over clumps) density profile is known, a comparison with afterglow models will then let us constrain the length scale, overdensity, and volume filling factor of the circumburst inhomogeneities. Unfortunately, observations have not yet clearly determined the density profile ahead of the GRB forward shock (Chevalier & Li 2000; Panaitescu & Kumar 2001, 2002; Chevalier et al. 2004), so that we consider both free winds (energy density  ) and shocked uniform winds (
) and shocked uniform winds ( ) as possible circumburst media, keeping in mind that, as described by Ramirez-Ruiz et al. (2005) and outlined in § 3, the actual surrounding environment is much more complex.
) as possible circumburst media, keeping in mind that, as described by Ramirez-Ruiz et al. (2005) and outlined in § 3, the actual surrounding environment is much more complex.
 ) and shocked uniform winds (
) and shocked uniform winds ( ) as possible circumburst media, keeping in mind that, as described by Ramirez-Ruiz et al. (2005) and outlined in § 3, the actual surrounding environment is much more complex.
) as possible circumburst media, keeping in mind that, as described by Ramirez-Ruiz et al. (2005) and outlined in § 3, the actual surrounding environment is much more complex.Assuming that the blast wave is adiabatic and effectively spherical and that  is its isotropic equivalent energy, as derived from the gamma-ray output, we can compute the deceleration radius of the GRB forward shock when about half of the initial energy has been transferred to the shocked matter; for an initial Lorentz factor
is its isotropic equivalent energy, as derived from the gamma-ray output, we can compute the deceleration radius of the GRB forward shock when about half of the initial energy has been transferred to the shocked matter; for an initial Lorentz factor  , the typical swept-up mass where this happens is
, the typical swept-up mass where this happens is
 For the two circumburst density profiles mentioned above, the deceleration radius of the shock is then
For the two circumburst density profiles mentioned above, the deceleration radius of the shock is then
 where in the first case we have chosen typical WR parameters (
where in the first case we have chosen typical WR parameters ( and
and  ), whereas in the second case a baryon number density comparable to the ISM value (
), whereas in the second case a baryon number density comparable to the ISM value ( ) has been assumed. This corresponds to a deceleration time in the postshock rest frame
) has been assumed. This corresponds to a deceleration time in the postshock rest frame
 since the Lorentz factor of the postshock material in the preshock rest frame is
since the Lorentz factor of the postshock material in the preshock rest frame is  .
.
 is its isotropic equivalent energy, as derived from the gamma-ray output, we can compute the deceleration radius of the GRB forward shock when about half of the initial energy has been transferred to the shocked matter; for an initial Lorentz factor
is its isotropic equivalent energy, as derived from the gamma-ray output, we can compute the deceleration radius of the GRB forward shock when about half of the initial energy has been transferred to the shocked matter; for an initial Lorentz factor  , the typical swept-up mass where this happens is
, the typical swept-up mass where this happens is


 and
and  ), whereas in the second case a baryon number density comparable to the ISM value (
), whereas in the second case a baryon number density comparable to the ISM value ( ) has been assumed. This corresponds to a deceleration time in the postshock rest frame
) has been assumed. This corresponds to a deceleration time in the postshock rest frame

 .
.4.1. Clump Properties
We consider a preshock medium with number density  of identical clumps. Each clump is characterized by a Gaussian overdensity profile with central density contrast
of identical clumps. Each clump is characterized by a Gaussian overdensity profile with central density contrast  and typical size L; if the origin of the axes is in the center of the clump and R,
and typical size L; if the origin of the axes is in the center of the clump and R,  , and θ are preshock cylindrical coordinates, we choose a clump energy density profile
, and θ are preshock cylindrical coordinates, we choose a clump energy density profile
 where
where  is the energy density of the interclump homogeneous medium. In order to use the formalism introduced in § 2—where the density contrast δ was defined with respect to the mean preshock energy density
is the energy density of the interclump homogeneous medium. In order to use the formalism introduced in § 2—where the density contrast δ was defined with respect to the mean preshock energy density  (averaged over clumps), whereas here the interclump density
(averaged over clumps), whereas here the interclump density  has been used—we should set
has been used—we should set
 however, the ratio between
however, the ratio between  and
and  can be easily computed for the density profile in equation (29),
can be easily computed for the density profile in equation (29),
 provided that
provided that  . In this section we always assume
. In this section we always assume  , so that the formulae in § 2 can be used with a preshock overdensity profile
, so that the formulae in § 2 can be used with a preshock overdensity profile

 of identical clumps. Each clump is characterized by a Gaussian overdensity profile with central density contrast
of identical clumps. Each clump is characterized by a Gaussian overdensity profile with central density contrast  and typical size L; if the origin of the axes is in the center of the clump and R,
and typical size L; if the origin of the axes is in the center of the clump and R,  , and θ are preshock cylindrical coordinates, we choose a clump energy density profile
, and θ are preshock cylindrical coordinates, we choose a clump energy density profile

 is the energy density of the interclump homogeneous medium. In order to use the formalism introduced in § 2—where the density contrast δ was defined with respect to the mean preshock energy density
is the energy density of the interclump homogeneous medium. In order to use the formalism introduced in § 2—where the density contrast δ was defined with respect to the mean preshock energy density  (averaged over clumps), whereas here the interclump density
(averaged over clumps), whereas here the interclump density  has been used—we should set
has been used—we should set

 and
and  can be easily computed for the density profile in equation (29),
can be easily computed for the density profile in equation (29),

 . In this section we always assume
. In this section we always assume  , so that the formulae in § 2 can be used with a preshock overdensity profile
, so that the formulae in § 2 can be used with a preshock overdensity profile

For small density contrasts, we can perform analytical calculations taking into account just the leading-order (first-order) term in δ within equation (15); the corresponding vorticity is referred to as the “leading-order vorticity”  , and the Hankel transform of its projected vorticity is used in equation (25) to analytically compute the leading (second) order in
, and the Hankel transform of its projected vorticity is used in equation (25) to analytically compute the leading (second) order in  of the vortical energy fraction (
of the vortical energy fraction (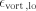 ). This approximation is certainly well justified for
). This approximation is certainly well justified for  , but Figure 2 shows that the full numerical computation for
, but Figure 2 shows that the full numerical computation for  is still in reasonable agreement with our analytical approximation
is still in reasonable agreement with our analytical approximation  even for
even for  . For larger central overdensities, a numerical calculation is required, and we could fit the numerical results with a fitting function
. For larger central overdensities, a numerical calculation is required, and we could fit the numerical results with a fitting function
 (
( and
and  are fitting parameters), so that for small overdensities (
are fitting parameters), so that for small overdensities ( ) we recover the result of the analytical computation.
) we recover the result of the analytical computation.
 , and the Hankel transform of its projected vorticity is used in equation (25) to analytically compute the leading (second) order in
, and the Hankel transform of its projected vorticity is used in equation (25) to analytically compute the leading (second) order in  of the vortical energy fraction (
of the vortical energy fraction (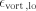 ). This approximation is certainly well justified for
). This approximation is certainly well justified for  , but Figure 2 shows that the full numerical computation for
, but Figure 2 shows that the full numerical computation for  is still in reasonable agreement with our analytical approximation
is still in reasonable agreement with our analytical approximation  even for
even for  . For larger central overdensities, a numerical calculation is required, and we could fit the numerical results with a fitting function
. For larger central overdensities, a numerical calculation is required, and we could fit the numerical results with a fitting function

 and
and  are fitting parameters), so that for small overdensities (
are fitting parameters), so that for small overdensities ( ) we recover the result of the analytical computation.
) we recover the result of the analytical computation.Figure 2.
Ratio between the exact numerical calculation of the vortical energy fraction (  ) and its analytical approximation (
) and its analytical approximation ( in eq. [36], keeping only the leading order in the central overdensity
in eq. [36], keeping only the leading order in the central overdensity  within the vorticity
within the vorticity  ) as a function of
) as a function of  ; deviations from the analytical calculation are significant only for
; deviations from the analytical calculation are significant only for  . Dotted line: Taking into account, in the numerical calculation, only the nonintegral contribution to the vorticity. Solid line: Full numerical calculation, including both the integral and nonintegral terms in eq. (15); the nonintegral contribution is found to be dominant even for large overdensities.
. Dotted line: Taking into account, in the numerical calculation, only the nonintegral contribution to the vorticity. Solid line: Full numerical calculation, including both the integral and nonintegral terms in eq. (15); the nonintegral contribution is found to be dominant even for large overdensities. |
4.2. Eddy Turnover Time
Vorticity embedded in clumps by the passage of the GRB forward shock can be responsible for the magnetic fraction inferred from afterglow models only if vortical motions are fast and energetic enough to amplify the field up to the observed value before the shock deceleration time, when adiabatic expansion would significantly reduce the particle energies available for the afterglow emission. In the leading-order approximation described above, an estimate of the eddy turnover time for the density contrast in equation (32) is
 where
where  ; the reference value chosen for the central overdensity
; the reference value chosen for the central overdensity  is in agreement with observations (see § 3) and reasonably satisfies the requirements for the leading-order approximation (see Fig. 2). If
is in agreement with observations (see § 3) and reasonably satisfies the requirements for the leading-order approximation (see Fig. 2). If  is the number of eddy rotations necessary to explain the observed
is the number of eddy rotations necessary to explain the observed  , the requirement
, the requirement  for a windlike or ISM-like circumburst medium gives, respectively,
for a windlike or ISM-like circumburst medium gives, respectively,
 Let us emphasize that, for smaller initial shock Lorentz factors
Let us emphasize that, for smaller initial shock Lorentz factors  , a larger size L and weaker overdensity
, a larger size L and weaker overdensity  are enough to satisfy the constraint
are enough to satisfy the constraint  .
.

 ; the reference value chosen for the central overdensity
; the reference value chosen for the central overdensity  is in agreement with observations (see § 3) and reasonably satisfies the requirements for the leading-order approximation (see Fig. 2). If
is in agreement with observations (see § 3) and reasonably satisfies the requirements for the leading-order approximation (see Fig. 2). If  is the number of eddy rotations necessary to explain the observed
is the number of eddy rotations necessary to explain the observed  , the requirement
, the requirement  for a windlike or ISM-like circumburst medium gives, respectively,
for a windlike or ISM-like circumburst medium gives, respectively,

 , a larger size L and weaker overdensity
, a larger size L and weaker overdensity  are enough to satisfy the constraint
are enough to satisfy the constraint  .
.4.3. Vortical Energy Fraction
The kinetic energy density invested in the vortical part of the postshock flow should be a significant fraction of its proper energy density, since—as stated in § 2—we assume that the amplified magnetic fraction, which is required to match the observational inference  , will eventually be comparable to the vortical fraction,
, will eventually be comparable to the vortical fraction,  . However,
. However,  might be smaller than
might be smaller than  if the backreaction of magnetic field on turbulent motions is important well before equipartition between the magnetic and vortical energy densities; on the other hand,
if the backreaction of magnetic field on turbulent motions is important well before equipartition between the magnetic and vortical energy densities; on the other hand,  may also be a lower limit for
may also be a lower limit for  if secondary shocks created by the overlapping sound waves of many different overpressured clumps significantly contribute to magnetic field amplification.
if secondary shocks created by the overlapping sound waves of many different overpressured clumps significantly contribute to magnetic field amplification.
 , will eventually be comparable to the vortical fraction,
, will eventually be comparable to the vortical fraction,  . However,
. However,  might be smaller than
might be smaller than  if the backreaction of magnetic field on turbulent motions is important well before equipartition between the magnetic and vortical energy densities; on the other hand,
if the backreaction of magnetic field on turbulent motions is important well before equipartition between the magnetic and vortical energy densities; on the other hand,  may also be a lower limit for
may also be a lower limit for  if secondary shocks created by the overlapping sound waves of many different overpressured clumps significantly contribute to magnetic field amplification.
if secondary shocks created by the overlapping sound waves of many different overpressured clumps significantly contribute to magnetic field amplification.The results of a numerical calculation for the vortical fraction of clumps with overdensity profile in equation (32) are shown in Figure 3 (solid line), but for small central overdensities, the leading-order analytical computation described above gives a reliable estimate of the magnetic energy fraction produced by turbulence in GRB afterglows,
 where
where  and the reference values for the central overdensity
and the reference values for the central overdensity  and the clump volume filling factor
and the clump volume filling factor  have been chosen in order to match the observational constraint
have been chosen in order to match the observational constraint  . So, clumps with moderate density contrasts (
. So, clumps with moderate density contrasts ( , in agreement with the observational evidences reviewed in § 3) can justify the lower limit of the magnetic energy fraction inferred from afterglow models. Higher density contrasts (see Fig. 3) would be necessary to achieve larger magnetic fractions; however, it is worth recalling that our model is applicable only under the assumptions that the clump overdensity is not larger than
, in agreement with the observational evidences reviewed in § 3) can justify the lower limit of the magnetic energy fraction inferred from afterglow models. Higher density contrasts (see Fig. 3) would be necessary to achieve larger magnetic fractions; however, it is worth recalling that our model is applicable only under the assumptions that the clump overdensity is not larger than  (see § 2) and that
(see § 2) and that  , so that the overdensity profile can actually be described by equation (32).
, so that the overdensity profile can actually be described by equation (32).

 and the reference values for the central overdensity
and the reference values for the central overdensity  and the clump volume filling factor
and the clump volume filling factor  have been chosen in order to match the observational constraint
have been chosen in order to match the observational constraint  . So, clumps with moderate density contrasts (
. So, clumps with moderate density contrasts ( , in agreement with the observational evidences reviewed in § 3) can justify the lower limit of the magnetic energy fraction inferred from afterglow models. Higher density contrasts (see Fig. 3) would be necessary to achieve larger magnetic fractions; however, it is worth recalling that our model is applicable only under the assumptions that the clump overdensity is not larger than
, in agreement with the observational evidences reviewed in § 3) can justify the lower limit of the magnetic energy fraction inferred from afterglow models. Higher density contrasts (see Fig. 3) would be necessary to achieve larger magnetic fractions; however, it is worth recalling that our model is applicable only under the assumptions that the clump overdensity is not larger than  (see § 2) and that
(see § 2) and that  , so that the overdensity profile can actually be described by equation (32).
, so that the overdensity profile can actually be described by equation (32).Figure 3.
Solid line: Full numerical calculation of the vortical energy fraction  as a function of the central overdensity
as a function of the central overdensity  , assuming an average shock Lorentz factor
, assuming an average shock Lorentz factor  and a clump volume filling factor
and a clump volume filling factor  (a different choice for this parameter would simply shift the curve). Dotted line: Analytical best fit with the fitting function in eq. (33) and fitting parameters
(a different choice for this parameter would simply shift the curve). Dotted line: Analytical best fit with the fitting function in eq. (33) and fitting parameters  and
and  . The area between the dashed lines gives the region allowed by afterglow observations for the magnetic energy fraction
. The area between the dashed lines gives the region allowed by afterglow observations for the magnetic energy fraction  .
. |
Equation (36) suggests that smaller overdensities would be enough to satisfy the observational constraints on  as the forward shock slows down, since
as the forward shock slows down, since  ; the magnetic fraction is then expected to change during the afterglow stage, whereas it is usually supposed constant, especially in models that invoke collisionless plasma instabilities to create the field. Therefore, the time dependence of
; the magnetic fraction is then expected to change during the afterglow stage, whereas it is usually supposed constant, especially in models that invoke collisionless plasma instabilities to create the field. Therefore, the time dependence of  might be used as a test of our model. In § 5 we discuss the prospects for constraining the evolution of
might be used as a test of our model. In § 5 we discuss the prospects for constraining the evolution of  from afterglow observations.
from afterglow observations.
 as the forward shock slows down, since
as the forward shock slows down, since  ; the magnetic fraction is then expected to change during the afterglow stage, whereas it is usually supposed constant, especially in models that invoke collisionless plasma instabilities to create the field. Therefore, the time dependence of
; the magnetic fraction is then expected to change during the afterglow stage, whereas it is usually supposed constant, especially in models that invoke collisionless plasma instabilities to create the field. Therefore, the time dependence of  might be used as a test of our model. In § 5 we discuss the prospects for constraining the evolution of
might be used as a test of our model. In § 5 we discuss the prospects for constraining the evolution of  from afterglow observations.
from afterglow observations.5. SUMMARY AND DISCUSSION
We have proposed that the postshock magnetic fields of GRB afterglows may arise from macroscopic MHD turbulence rather than microscopic plasma instabilities. The source of turbulence is vorticity produced when the shock encounters density inhomogeneities in the preshock medium. We presume that the magnetic energy fraction ( ) that results is comparable to the energy fraction of the turbulence. The ultrarelativistic geometrical shock dynamics formalism of Paper I allows an easy, although approximate, calculation of the vorticity produced by a given density inhomogeneity in the limit that the shock Lorentz factor
) that results is comparable to the energy fraction of the turbulence. The ultrarelativistic geometrical shock dynamics formalism of Paper I allows an easy, although approximate, calculation of the vorticity produced by a given density inhomogeneity in the limit that the shock Lorentz factor  .
.
 ) that results is comparable to the energy fraction of the turbulence. The ultrarelativistic geometrical shock dynamics formalism of Paper I allows an easy, although approximate, calculation of the vorticity produced by a given density inhomogeneity in the limit that the shock Lorentz factor
) that results is comparable to the energy fraction of the turbulence. The ultrarelativistic geometrical shock dynamics formalism of Paper I allows an easy, although approximate, calculation of the vorticity produced by a given density inhomogeneity in the limit that the shock Lorentz factor  .
.In this picture, the observational inference that  constrains both the amplitude and the length scale of inhomogeneities. Equations (33) and (36) roughly relate the total energy fraction in vortical motions to the volume filling factor and density contrast of the clumps; this energy fraction must be comparable to the inferred postshock
constrains both the amplitude and the length scale of inhomogeneities. Equations (33) and (36) roughly relate the total energy fraction in vortical motions to the volume filling factor and density contrast of the clumps; this energy fraction must be comparable to the inferred postshock  . Filling factors and density contrasts of order unity are required when the shock is still highly relativistic. Equation (35), on the other hand, express the constraint on the length scale and density contrast of individual clumps (independently of their volume filling factor) so that the eddies can wind the magnetic field up to the observed value in less than the expansion time of the shock. This second constraint favors small length scales, so that the clumps responsible for field amplification would probably be too small, at least individually, to modulate the afterglow light curve unless the density contrasts of those clumps are very large. Dermer & Mitman (1999) have indeed proposed very dense clumps (
. Filling factors and density contrasts of order unity are required when the shock is still highly relativistic. Equation (35), on the other hand, express the constraint on the length scale and density contrast of individual clumps (independently of their volume filling factor) so that the eddies can wind the magnetic field up to the observed value in less than the expansion time of the shock. This second constraint favors small length scales, so that the clumps responsible for field amplification would probably be too small, at least individually, to modulate the afterglow light curve unless the density contrasts of those clumps are very large. Dermer & Mitman (1999) have indeed proposed very dense clumps ( ) in their model for prompt emission by the forward shock. While their scenario might also produce strong turbulence and field amplification, the density contrasts maybe beyond the range of validity of our approximations.
) in their model for prompt emission by the forward shock. While their scenario might also produce strong turbulence and field amplification, the density contrasts maybe beyond the range of validity of our approximations.
 constrains both the amplitude and the length scale of inhomogeneities. Equations (33) and (36) roughly relate the total energy fraction in vortical motions to the volume filling factor and density contrast of the clumps; this energy fraction must be comparable to the inferred postshock
constrains both the amplitude and the length scale of inhomogeneities. Equations (33) and (36) roughly relate the total energy fraction in vortical motions to the volume filling factor and density contrast of the clumps; this energy fraction must be comparable to the inferred postshock  . Filling factors and density contrasts of order unity are required when the shock is still highly relativistic. Equation (35), on the other hand, express the constraint on the length scale and density contrast of individual clumps (independently of their volume filling factor) so that the eddies can wind the magnetic field up to the observed value in less than the expansion time of the shock. This second constraint favors small length scales, so that the clumps responsible for field amplification would probably be too small, at least individually, to modulate the afterglow light curve unless the density contrasts of those clumps are very large. Dermer & Mitman (1999) have indeed proposed very dense clumps (
. Filling factors and density contrasts of order unity are required when the shock is still highly relativistic. Equation (35), on the other hand, express the constraint on the length scale and density contrast of individual clumps (independently of their volume filling factor) so that the eddies can wind the magnetic field up to the observed value in less than the expansion time of the shock. This second constraint favors small length scales, so that the clumps responsible for field amplification would probably be too small, at least individually, to modulate the afterglow light curve unless the density contrasts of those clumps are very large. Dermer & Mitman (1999) have indeed proposed very dense clumps ( ) in their model for prompt emission by the forward shock. While their scenario might also produce strong turbulence and field amplification, the density contrasts maybe beyond the range of validity of our approximations.
) in their model for prompt emission by the forward shock. While their scenario might also produce strong turbulence and field amplification, the density contrasts maybe beyond the range of validity of our approximations.There is a question whether a fluid treatment of the postshock flow is justified at all, since the plasma is collisionless. The same question arises in supernova remnants, to which the standard answer is that magnetization of the plasma ensures a short effective mean free path. The present case is more extreme because the particles are relativistic, the length scales on which fluidlike behavior is required are smaller, especially in the present work, and the preshock field is energetically negligible. The relativistic Larmor radius of the postshock ions based on the compressed ambient field is  , where
, where  is the preshock field strength. This is smaller than the maximum tolerable clump size for field amplification at the beginning of the afterglow phase, although only barely so (§ 4.2). Furthermore, whether or not the Weibel instability can produce persistent magnetic fields, it should enforce fluidlike behavior by isotropizing particle distribution functions whenever counterstreaming plasmas overlap.
is the preshock field strength. This is smaller than the maximum tolerable clump size for field amplification at the beginning of the afterglow phase, although only barely so (§ 4.2). Furthermore, whether or not the Weibel instability can produce persistent magnetic fields, it should enforce fluidlike behavior by isotropizing particle distribution functions whenever counterstreaming plasmas overlap.
 , where
, where  is the preshock field strength. This is smaller than the maximum tolerable clump size for field amplification at the beginning of the afterglow phase, although only barely so (§ 4.2). Furthermore, whether or not the Weibel instability can produce persistent magnetic fields, it should enforce fluidlike behavior by isotropizing particle distribution functions whenever counterstreaming plasmas overlap.
is the preshock field strength. This is smaller than the maximum tolerable clump size for field amplification at the beginning of the afterglow phase, although only barely so (§ 4.2). Furthermore, whether or not the Weibel instability can produce persistent magnetic fields, it should enforce fluidlike behavior by isotropizing particle distribution functions whenever counterstreaming plasmas overlap.A basic conclusion of this work is that vortical turbulence becomes easier to produce with decreasing shock Lorentz factor. Both the energy and timescale constraints become easier to satisfy as Γ decreases (however, our ultrarelativistic approximations break down as  ). Therefore, if the postshock magnetic energy density is produced by macroscopic turbulence, it is likely that
). Therefore, if the postshock magnetic energy density is produced by macroscopic turbulence, it is likely that  will evolve as the shock ages, complicating the task of drawing physical inferences about the GRB environment from the observational data. The abundance of early X-ray light curves provided by the Swift satellite has already led to models that are more complicated than the rather simple theoretical description of the sparser BeppoSAX results (Galama et al. 1998). The light curves are not single power laws in time, but show breaks and sometimes “flares,” suggesting a need for extended energy input from the central source (Zhang et al. 2006 and references therein). But, to date, most modelers have assumed constant
will evolve as the shock ages, complicating the task of drawing physical inferences about the GRB environment from the observational data. The abundance of early X-ray light curves provided by the Swift satellite has already led to models that are more complicated than the rather simple theoretical description of the sparser BeppoSAX results (Galama et al. 1998). The light curves are not single power laws in time, but show breaks and sometimes “flares,” suggesting a need for extended energy input from the central source (Zhang et al. 2006 and references therein). But, to date, most modelers have assumed constant  and
and  (the postshock energy fraction in relativistic
(the postshock energy fraction in relativistic  ) within individual afterglows, although these parameters are often allowed to vary from one afterglow to another.
) within individual afterglows, although these parameters are often allowed to vary from one afterglow to another.
 ). Therefore, if the postshock magnetic energy density is produced by macroscopic turbulence, it is likely that
). Therefore, if the postshock magnetic energy density is produced by macroscopic turbulence, it is likely that  will evolve as the shock ages, complicating the task of drawing physical inferences about the GRB environment from the observational data. The abundance of early X-ray light curves provided by the Swift satellite has already led to models that are more complicated than the rather simple theoretical description of the sparser BeppoSAX results (Galama et al. 1998). The light curves are not single power laws in time, but show breaks and sometimes “flares,” suggesting a need for extended energy input from the central source (Zhang et al. 2006 and references therein). But, to date, most modelers have assumed constant
will evolve as the shock ages, complicating the task of drawing physical inferences about the GRB environment from the observational data. The abundance of early X-ray light curves provided by the Swift satellite has already led to models that are more complicated than the rather simple theoretical description of the sparser BeppoSAX results (Galama et al. 1998). The light curves are not single power laws in time, but show breaks and sometimes “flares,” suggesting a need for extended energy input from the central source (Zhang et al. 2006 and references therein). But, to date, most modelers have assumed constant  and
and  (the postshock energy fraction in relativistic
(the postshock energy fraction in relativistic  ) within individual afterglows, although these parameters are often allowed to vary from one afterglow to another.
) within individual afterglows, although these parameters are often allowed to vary from one afterglow to another.The effect of an evolving  depends on the relationship between the observed frequency and certain critical frequencies in the assumed spectrum. In our model, the coherence length of the field should be comparable to that of the eddies responsible for amplifying it (provided that the coherence length of the seed field is even larger), which is plausibly larger than the relativistic Larmor radius as noted above, so that standard synchrotron emission should dominate. On the other hand, for the small-scale field generated by Weibel-like plasma instabilities, the electron gyroradii are often larger than the magnetic field structures, so that jitter radiation (Medvedev 2000) might be the actual emission mechanism. A detailed analysis of the observed spectra at frequencies below the spectral peak, where jitter and synchrotron spectra are predicted to differ most strongly, might therefore distinguish between these two models for the amplification of magnetic field.
depends on the relationship between the observed frequency and certain critical frequencies in the assumed spectrum. In our model, the coherence length of the field should be comparable to that of the eddies responsible for amplifying it (provided that the coherence length of the seed field is even larger), which is plausibly larger than the relativistic Larmor radius as noted above, so that standard synchrotron emission should dominate. On the other hand, for the small-scale field generated by Weibel-like plasma instabilities, the electron gyroradii are often larger than the magnetic field structures, so that jitter radiation (Medvedev 2000) might be the actual emission mechanism. A detailed analysis of the observed spectra at frequencies below the spectral peak, where jitter and synchrotron spectra are predicted to differ most strongly, might therefore distinguish between these two models for the amplification of magnetic field.
 depends on the relationship between the observed frequency and certain critical frequencies in the assumed spectrum. In our model, the coherence length of the field should be comparable to that of the eddies responsible for amplifying it (provided that the coherence length of the seed field is even larger), which is plausibly larger than the relativistic Larmor radius as noted above, so that standard synchrotron emission should dominate. On the other hand, for the small-scale field generated by Weibel-like plasma instabilities, the electron gyroradii are often larger than the magnetic field structures, so that jitter radiation (Medvedev 2000) might be the actual emission mechanism. A detailed analysis of the observed spectra at frequencies below the spectral peak, where jitter and synchrotron spectra are predicted to differ most strongly, might therefore distinguish between these two models for the amplification of magnetic field.
depends on the relationship between the observed frequency and certain critical frequencies in the assumed spectrum. In our model, the coherence length of the field should be comparable to that of the eddies responsible for amplifying it (provided that the coherence length of the seed field is even larger), which is plausibly larger than the relativistic Larmor radius as noted above, so that standard synchrotron emission should dominate. On the other hand, for the small-scale field generated by Weibel-like plasma instabilities, the electron gyroradii are often larger than the magnetic field structures, so that jitter radiation (Medvedev 2000) might be the actual emission mechanism. A detailed analysis of the observed spectra at frequencies below the spectral peak, where jitter and synchrotron spectra are predicted to differ most strongly, might therefore distinguish between these two models for the amplification of magnetic field.In order to compare our prediction of an evolving  with the observed afterglow spectra, particularly important is the synchrotron cooling frequency, the Doppler-shifted synchrotron frequency of a postshock electron or positron that radiates much of its energy on a timescale comparable to the age of the shock. For a preshock medium with mass density profile
with the observed afterglow spectra, particularly important is the synchrotron cooling frequency, the Doppler-shifted synchrotron frequency of a postshock electron or positron that radiates much of its energy on a timescale comparable to the age of the shock. For a preshock medium with mass density profile  averaged over clumps and for an adiabatic relativistic shock with constant isotropically equivalent energy
averaged over clumps and for an adiabatic relativistic shock with constant isotropically equivalent energy  (notwithstanding the above-cited inferences from Swift data), the cooling frequency evolves as (up to dimensionless constants of order unity)
(notwithstanding the above-cited inferences from Swift data), the cooling frequency evolves as (up to dimensionless constants of order unity)
 where
where  is the shock radius, t is the astronomical observer’s time, and
is the shock radius, t is the astronomical observer’s time, and  is the GRB cosmological redshift. Evidently, the shock energy and Lorentz factor scale out of the cooling frequency when the latter is expressed in terms of the shock radius. If one could be confident that the early afterglow evolves in a freely expanding wind (
is the GRB cosmological redshift. Evidently, the shock energy and Lorentz factor scale out of the cooling frequency when the latter is expressed in terms of the shock radius. If one could be confident that the early afterglow evolves in a freely expanding wind ( ), which seems a priori likely in collapsar models, then the evolution of
), which seems a priori likely in collapsar models, then the evolution of  could be inferred by measuring that of
could be inferred by measuring that of  .
.
 with the observed afterglow spectra, particularly important is the synchrotron cooling frequency, the Doppler-shifted synchrotron frequency of a postshock electron or positron that radiates much of its energy on a timescale comparable to the age of the shock. For a preshock medium with mass density profile
with the observed afterglow spectra, particularly important is the synchrotron cooling frequency, the Doppler-shifted synchrotron frequency of a postshock electron or positron that radiates much of its energy on a timescale comparable to the age of the shock. For a preshock medium with mass density profile  averaged over clumps and for an adiabatic relativistic shock with constant isotropically equivalent energy
averaged over clumps and for an adiabatic relativistic shock with constant isotropically equivalent energy  (notwithstanding the above-cited inferences from Swift data), the cooling frequency evolves as (up to dimensionless constants of order unity)
(notwithstanding the above-cited inferences from Swift data), the cooling frequency evolves as (up to dimensionless constants of order unity)

 is the shock radius, t is the astronomical observer’s time, and
is the shock radius, t is the astronomical observer’s time, and  is the GRB cosmological redshift. Evidently, the shock energy and Lorentz factor scale out of the cooling frequency when the latter is expressed in terms of the shock radius. If one could be confident that the early afterglow evolves in a freely expanding wind (
is the GRB cosmological redshift. Evidently, the shock energy and Lorentz factor scale out of the cooling frequency when the latter is expressed in terms of the shock radius. If one could be confident that the early afterglow evolves in a freely expanding wind ( ), which seems a priori likely in collapsar models, then the evolution of
), which seems a priori likely in collapsar models, then the evolution of  could be inferred by measuring that of
could be inferred by measuring that of  .
.Present evidence suggests that the cooling frequency lies below the X-ray regime in the early afterglow phase. This conclusion rests on the usual assumption that the synchrotron-emitting electrons are injected with a power-law distribution of energies,  for
for  , in which
, in which  so that the total energy is dominated by electron energies near
so that the total energy is dominated by electron energies near  , whose characteristic observed frequency is
, whose characteristic observed frequency is  . The observed specific flux is often described as a power law in time and frequency,
. The observed specific flux is often described as a power law in time and frequency,  , despite various breaks and the aforementioned flares. If synchrotron emission dominates and
, despite various breaks and the aforementioned flares. If synchrotron emission dominates and  (slow-cooling regime), the spectral index is
(slow-cooling regime), the spectral index is  if
if  and
and  if
if  . It is believed that the acceleration index p is not much larger than 2, perhaps
. It is believed that the acceleration index p is not much larger than 2, perhaps  , which is then consistent with the observed X-ray indices
, which is then consistent with the observed X-ray indices  observed by Swift (Zhang et al. 2006 and references therein) only if
observed by Swift (Zhang et al. 2006 and references therein) only if 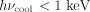 . Evaluating equation (37) at the deceleration radius appropriate for a Wolf-Rayet wind (see eq. [27]), we find that the afterglow phase begins with a cooling frequency that is plausibly consistent with this constraint,
. Evaluating equation (37) at the deceleration radius appropriate for a Wolf-Rayet wind (see eq. [27]), we find that the afterglow phase begins with a cooling frequency that is plausibly consistent with this constraint,
 Unless the cooling frequency passes through the observed band, one cannot learn much about the evolution of
Unless the cooling frequency passes through the observed band, one cannot learn much about the evolution of  from observations at
from observations at  , because (up to numerical factors of order unity)
, because (up to numerical factors of order unity)
 in this regime, where
in this regime, where  is the luminosity distance;
is the luminosity distance;  enters the above expression only via the correspondence
enters the above expression only via the correspondence  between observed frequency ν and electron Lorentz factor γ and, hence, is raised to the small exponent
between observed frequency ν and electron Lorentz factor γ and, hence, is raised to the small exponent  . On the other hand, equation (39) indicates that the flux above the cooling frequency provides an excellent measure of the energy in the electron population (Freedman & Waxman 2001).
. On the other hand, equation (39) indicates that the flux above the cooling frequency provides an excellent measure of the energy in the electron population (Freedman & Waxman 2001).
 for
for  , in which
, in which  so that the total energy is dominated by electron energies near
so that the total energy is dominated by electron energies near  , whose characteristic observed frequency is
, whose characteristic observed frequency is  . The observed specific flux is often described as a power law in time and frequency,
. The observed specific flux is often described as a power law in time and frequency,  , despite various breaks and the aforementioned flares. If synchrotron emission dominates and
, despite various breaks and the aforementioned flares. If synchrotron emission dominates and  (slow-cooling regime), the spectral index is
(slow-cooling regime), the spectral index is  if
if  and
and  if
if  . It is believed that the acceleration index p is not much larger than 2, perhaps
. It is believed that the acceleration index p is not much larger than 2, perhaps  , which is then consistent with the observed X-ray indices
, which is then consistent with the observed X-ray indices  observed by Swift (Zhang et al. 2006 and references therein) only if
observed by Swift (Zhang et al. 2006 and references therein) only if 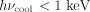 . Evaluating equation (37) at the deceleration radius appropriate for a Wolf-Rayet wind (see eq. [27]), we find that the afterglow phase begins with a cooling frequency that is plausibly consistent with this constraint,
. Evaluating equation (37) at the deceleration radius appropriate for a Wolf-Rayet wind (see eq. [27]), we find that the afterglow phase begins with a cooling frequency that is plausibly consistent with this constraint,

 from observations at
from observations at  , because (up to numerical factors of order unity)
, because (up to numerical factors of order unity)

 is the luminosity distance;
is the luminosity distance;  enters the above expression only via the correspondence
enters the above expression only via the correspondence  between observed frequency ν and electron Lorentz factor γ and, hence, is raised to the small exponent
between observed frequency ν and electron Lorentz factor γ and, hence, is raised to the small exponent  . On the other hand, equation (39) indicates that the flux above the cooling frequency provides an excellent measure of the energy in the electron population (Freedman & Waxman 2001).
. On the other hand, equation (39) indicates that the flux above the cooling frequency provides an excellent measure of the energy in the electron population (Freedman & Waxman 2001).

