Abstract
The effectiveness of conservation efforts ultimately depends on the recognition that decision making, and the systems that it is designed to affect, are inherently dynamic and characterized by multiple sources of uncertainty. To cope with these challenges, conservation planners are increasingly turning to the tools of decision analysis, especially dynamic optimization methods. Here we provide a general framework for optimal, dynamic conservation and then explore its capacity for coping with various sources and degrees of uncertainty. In broadest terms, the dynamic optimization problem in conservation is choosing among a set of decision options at periodic intervals so as to maximize some conservation objective over the planning horizon. Planners must account for immediate objective returns, as well as the effect of current decisions on future resource conditions and, thus, on future decisions. Undermining the effectiveness of such a planning process are uncertainties concerning extant resource conditions (partial observability), the immediate consequences of decision choices (partial controllability), the outcomes of uncontrolled, environmental drivers (environmental variation), and the processes structuring resource dynamics (structural uncertainty). Where outcomes from these sources of uncertainty can be described in terms of probability distributions, a focus on maximizing the expected objective return, while taking state-specific actions, is an effective mechanism for coping with uncertainty. When such probability distributions are unavailable or deemed unreliable, a focus on maximizing robustness is likely to be the preferred approach. Here the idea is to choose an action (or state-dependent policy) that achieves at least some minimum level of performance regardless of the (uncertain) outcomes. We provide some examples of how the dynamic optimization problem can be framed for problems involving management of habitat for an imperiled species, conservation of a critically endangered population through captive breeding, control of invasive species, construction of biodiversity reserves, design of landscapes to increase habitat connectivity, and resource exploitation. Although these decision making problems and their solutions present significant challenges, we suggest that a systematic and effective approach to dynamic decision making in conservation need not be an onerous undertaking. The requirements are shared with any systematic approach to decision making—a careful consideration of values, actions, and outcomes.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Biodiversity conservation is characteristically both dynamic and uncertain. It is dynamic because it depends not on the protection of static biodiversity features or attributes, but on maintenance of the ecological and evolutionary processes that sustain that biodiversity (Sarkar et al 2006, Pressey et al 2007). This, in turn, requires conservation actions that reflect the state of ecological systems as they change over time in response to both controlled and uncontrolled factors. Conservation is uncertain because ecological systems are inherently stochastic, and because any understanding of resource conditions and dynamics is inevitably incomplete (Williams 2001). The effectiveness of conservation thus depends on how well these dynamics and their associated uncertainties can be accounted for in the planning process. To that end, conservation planners increasingly rely on the tools of decision analysis.
Decision analysis has been widely used in business and government decision making (Keefer et al 2004), but its application to problems in natural resource conservation has mostly been a phenomenon of the last two decades (Huang et al 2011). Though decision-analytic approaches vary considerably, decision making in conservation typically involves (1) properly formulating the decision problem; (2) specifying feasible alternative actions; and (3) selecting criteria for evaluating potential outcomes (Tonn et al 2000). Traditional approaches to decision making, which tend to focus on alternatives and predicted ecological outcomes, can be distinguished from modern methods that emphasize fundamental values and the multiple-objective tradeoffs inherent in natural resource management (Keeney 1992, Arvai et al 2001, Burgman 2005, Gregory et al 2012). The emphasis on values rather than outcomes helps decision makers understand whether disagreements are over predicted outcomes or how those outcomes are valued (Lee 1993). It also helps promote a role for analysts and scientists in conservation decision making as 'honest brokers' rather than as advocates for a particular course of action (Pielke 2007). Multi-criteria decision analysis that accounts for outcomes and values is now widely used in conservation, and is seen as contributing to better decisions through a formal structuring of decision problems that accommodates conflicts in fundamental values among stakeholders (Kiker et al 2005, Mendoza and Martins 2006, Hajkowicz and Collins 2007, Huang et al 2011).
A particularly noteworthy aspect of the trend toward more decision analysis in conservation has been the increasing application of dynamic optimization methods to analyze recurrent decisions (Anderson 1975, Walters and Hilborn 1978, Williams 1982, Cohen 1987, Williams 1989, Possingham 1997, 2001, Williams 2001, Westphal et al 2003). Problems that require recurrent decisions are ubiquitous in conservation, ranging from examples like harvesting or prescribed burning, to the development of a biological reserve system or the control of invasive plants and animals. The growing number of conservation examples that rely on dynamic optimization methods is testament to the general applicability of these methods (table 1), and the rapid increase in computing power has made it feasible to analyze problems of at least moderate complexity.
Table 1. Examples of the problems in natural resource management addressed with dynamic optimization methods.
| Resource problem | Goal | Source |
|---|---|---|
| Harvesting | Sustainable use | Milner-Gulland (1997), Kulmala et al (2008), Johnson (2011) |
| Translocation | Endangered species persistence | Tenhumberg et al (2004) |
| Pest management | Control | Sells (1995), Bogich and Shea (2008) |
| Management of human disturbance | Endangered species occupancy | Martin et al (2011) |
| Fire management | Biodiversity conservation | Richards et al (1999), McCarthy et al (2001) |
| Endangered species persistence | Johnson et al (2011) | |
| Forest management | Endangered species persistence | Moore and Conroy (2006) |
| Reservoir management | Water supply | Alaya et al (2003), Eum et al (2011) |
| Landscape reconstruction | Endangered species persistence | Westphal et al (2003) |
| Allocation of conservation resources | Biodiversity conservation | Wilson et al (2006) |
| Reserve design | Multiple species persistence | Schapaugh and Tyre (2012) |
Table 2. Description of mathematical notation used to describe dynamic decision problems.
| Focus | Description |
|---|---|
| Common parameters | |
| xt | State of the natural resource system at time t |
| at | Action taken at time t |
| At | Strategy specifying a state-specific action at each time starting at time t |
| U(at|xt) | Utility corresponding to action at, given system state xt |
| P(xt+1|xt,at) | Probability of transition from state xt at time t to state xt+1 at t + 1, given action at |
| V(At|xt) | Value corresponding to strategy At, given system state xt at time t |
| V[xt] | Optimal value for system state xt at time t |
| Structural uncertainty | |
| qt | Model state (distribution of model confidence weights qt(k) at time t) |
| U(at|xt,qt) | Utility corresponding to action at, given system state xt and model state qt |
| Pk(xt+1|xt,at) | Model-specific probability of transition between system states, given action at |
| V(At|xt,qt) | Value corresponding to strategy At, given system state xt and model state qt at time t |
| V[xt,qt] | Optimal value for system state xt and model state qt at time t |
| Partial observability | |
| bt | Belief state (probability distribution for possible system states at time t) |
| U(at|bt) | Utility corresponding to action at, given belief state bt |
| P(bt+1|bt,at) | Probability of transition between belief states, given action at |
| V(At|bt) | Value corresponding to strategy At, given belief state qt at time t |
| V[bt] | Optimal value for belief state bt at time t |
| Robust decision making | |
| αt | Uncertainty horizon (range of belief states around a guesstimate 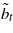 of belief state) of belief state) |
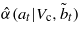
|
For action at, the largest uncertainty horizon around guesstimate 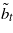 within which value is guaranteed to exceed Vc within which value is guaranteed to exceed Vc |
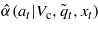
|
For action at and system state xt, the largest uncertainty horizon around guesstimate 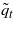 within which value is guaranteed to exceed Vc within which value is guaranteed to exceed Vc |
Dynamic optimization combines models of system change with objective functions that value present and future consequences of alternative management actions. The general management problem involves a temporal sequence of decisions, where the action at each decision point may differ depending on time and/or system state (Possingham 1997). The goal of the manager is to develop a decision rule or policy that prescribes a management action for each system state at each decision point that is optimal with respect to the objective function. A key advantage of dynamic optimization is its ability to produce a feedback policy specifying optimal decisions for possible future system states rather than expected future states (Walters and Hilborn 1978). In practice this makes optimization appropriate for systems that behave stochastically, absent any assumptions about the system remaining in a desired equilibrium or the production of a constant stream of resource returns. By properly framing problems, dynamic optimization methods have been used successfully to address a broad array of important conservation issues.
The imperative to adopt a more dynamic perspective to conservation has never been greater. While the simplifying assumptions of systems in equilibrium or of stationary system dynamics may have been acceptable in the past, the scale and rate of change in ecosystems and the services they provide have increased to unprecedented levels (Carpenter 2009, Polasky et al 2011). Those concerned with biodiversity conservation must now focus not only on enabling the processes (like periodic disturbance) which generate and maintain biodiversity, but on large-scale changes in the environment (e.g., climate) and in linked social and ecological systems that produce dynamic threats to biodiversity (Pressey et al 2007, Carpenter 2009, Possingham et al 2009, Sutherland et al 2009, Polasky et al 2011). A more forward-looking approach to conservation therefore involves a consideration of the future consequences of present actions, the timeframe over which socio-ecological processes operate and choices are made, and the uncertainty attendant to future conditions (Carpenter 2002, Polasky et al 2011).
We believe there is considerable value in a framework for decision making that accounts for the influence and uncertainty of decisions made over time. An objective driven, science-based approach that incorporates system dynamics can better highlight and distinguish the roles of science and values in decision making. Such an approach allows one to recognize and assess the elements of a conservation problem and the connections among these elements in a more systematic and effective way. By focusing on optimal strategy and the system understanding on which it is based, the approach promotes a comparative assessment of strategy interventions and highlights the value of learning about their impacts through time. Finally, the emphasis on future consequences of present actions leads naturally to less myopic, and hence more strategic, decision making. Accounting for system dynamics rather than assuming stationarity or steady state conditions can easily lead to more effective and efficient decisions that also are more relevant to biodiversity conservation.
Here we provide a general framework for optimal, dynamic conservation, and explore its capacity to cope with various sources and degrees of uncertainty. We conclude with some thoughts about its applicability to a variety of conservation problems, as well as some challenges confronting its use.
2. Formulation of the dynamic conservation problem
2.1. A general framework for optimal conservation
In broadest terms, the generic optimization problem in conservation is to choose among a set of decision options so as to maximize some objective expressed in terms of the decision choices. Decision making typically includes the following elements:
- (1)A range of decision options is needed, from which an option can be selected. The options might focus on resource exploitation, as in harvest rates or amounts; or resource enhancement, as in captive rearing, habitat management, or reserve development; or restrictions on use of a resource for recreation or economic production; or combinations of these and other actions that could influence resource outputs and conditions. We note that options may be different in kind, representing for example land acquisition and existing habitat enhancement, in which case the problem is similar to prioritization. Or individual actions might be specified as portfolios, representing different allocations of conservation resources to various activities (Wilson et al 2007, Pouzols et al 2012).
- (2)Utilities associated with key resource inputs, outputs, and services must be identified. The utilities may be based on the costs of material and energy inputs, or the output of waste products, or the economic benefits of valuable outputs, or ecological features of the system, or aggregates of these and other attributes. In some cases utilities are tied to resource conditions at the time the decision is made, and they may be time specific. Utility can be thought of as measures of preferences of a decision maker for decision-specific outputs.
- (3)An objective must be specified that aggregates attribute utilities, possibly in a time-dependent way. The objective provides valuation that typically is dependent on the strategy selected and the condition of the resource when it is implemented. Objectives often are expressed in terms of minimizing costs, or maximizing benefits, or maximizing benefits net of costs, or other forms that can be linked to the aggregation of utilities. In what follows we will refer to an objective or value function, to emphasize its relationship to the resource condition and/or strategy that is selected.
- (4)Decision making for natural resources, especially renewable natural resources, usually requires some accounting for the effect of decisions on resource status and condition. The potential consequences of a decision might be immediate, as in harvest that reduces a size of a population, or longer term, as in the effect a decision has on moving a population toward some desired status. The projection of the future consequences of present actions is described with a system model.
A great many conservation problems involve recurrent decision making, in which decisions are made at multiple times over some timeframe, usually but not always at regular intervals. Recurrent decision making is especially challenging, not least because of the need to account for the future consequences of present actions. Thus, in addition to the elements of decision making described above there must be a monitoring program that can track both objective values and system state.
The remainder of this section and section 3 focus on the mathematical structure of dynamic decision making, and on how various sources of uncertainty in system state or dynamics can be accommodated. Section 4 focuses on both the applicability of this framework and key challenges confronting its use. In particular, we discuss how some of the most common problems in conservation, such as habitat management and reserve design, can be framed to make them amenable to formal analysis.
2.2. Structure and notation for the resource control problem
Because of the complexity involved in the control of resources that are subject to environmental and other sources of variation, it is useful to provide some notation for dynamic decision making, and then describe a general framework for decisions over time (table 2). Our purpose in doing so is to clarify the decision making process, recognizing that there are a great many ways to represent the role and impacts of decisions in natural resources conservation.
Decision making is assumed to occur over a discrete time frame {0,1,...,T}, beginning at some initial time 0 and terminating at a terminal time T that may be infinite. To simplify notation, we can think of decisions as being made at regular intervals, for example monthly, seasonally or yearly. A resource system that is subjected to management is characterized by a system state xt at each time t over the time frame. System state represents the resource in terms of key resource elements, features, and attributes that evolve through time. Examples might include population size or density, species counts, structural features of habitats, environmental conditions, and ecological relationships. The state xt can be univariate or multivariate. We assume for now that the state of the system at any given time can be observed, and structural components of the system that influence dynamics are at least stochastically known. We consider the relaxation of these assumptions later.
A conservation action at is assumed to be chosen at time t from a set of options that are available at that time. The action may be multivariate, and typically (though not necessarily) varies through time. Policy A0 prescribes actions to be taken at each time starting at time 0 and continuing to the terminal time T. A policy covering only part of the time frame, starting at some time t after the initial time 0 and continuing until T, is expressed as At.
System dynamics are assumed in what follows to be Markovian, that is, the system state at time t + 1 is determined stochastically by the state at time t and action taken at time t. These transitions are specified by a probability P(xt+1|xt,at) of transition from xt to xt+1 assuming action at is taken. If there is uncertainty about the transition structure, several candidate models can be used to describe state transitions, with Pk(xt+1|xt,at) representing a particular model k∈{1,2,..,K}. Structural (or model) uncertainty can be characterized by a distribution qt of model likelihoods or weights, with elements qt(k) that may or may not be stationary. Here we refer to the distribution of model weights as the model state.
Assuming the transition structure is known, an objective or value function V(At|xt) captures the value of decisions made over the time frame in terms of the transition probabilities P(xt+1|xt,at) and accumulated utilities U(at|xt). This notation suggests that utility is influenced (at least potentially) by both the action at taken at time t as well as the system state xt at that time. Dynamic decision making typically is based on an objective or value function that accumulates utilities from the current time to the terminal time T:
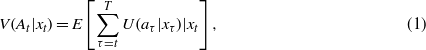
where the value V(At|xt) corresponding to strategy At is conditional on the resource state xt and the expectation is with respect to environmental variation and other measures of uncertainty.
One way to characterize the importance of future values is to include a weighting factor λ for the time-specific utilities in equation (1) that discounts future utilities relative to the present:
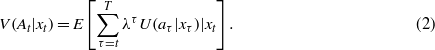
Assuming 0 < λ < 1, the effect of including λ in the value function is to reduce the influence of anticipated utilities exponentially over time. As λ converges to unity, future utilities converge in their importance to current utility, and the discounted value function shown in equation (2) converges to equation (1). As λ converges to 0, future utilities become unimportant in guiding decisions, and the summation in equation (2) includes only a single term for current utility. Discounting is broadly recognized as an indicator of social importance of the future relative to the present. The impact of discounting on both the value V(At|xt) and the strategy used to achieve it can be profound (Williams 1985). A focus on social valuation, and the larger role of stakeholders and the public in identifying and framing natural resource problems, are important but under-addressed issues in resource conservation.
On condition that there is uncertainty about transition structure, a value function Vk(At|xt,qt) accumulates utilities over time based on the transition probabilities Pk(xt+1|xt,at). In this situation, an overall value function V(At|xt,qt) for the problem can incorporate the model-specific value functions in different ways (see below).
With this notation the generic control problem can be stated thus:

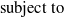


Two points in this framework are noteworthy. First, the random variable zt represents a white-noise process that combines with demographic stochasticity to induce stochasticity in the transition function xt+1 = fk(xt,at,zt), and thus to produce the Markovian probabilities Pk(xt+1|xt,at). Second, the updating function g(qt,xt+1) for qt is typically (but not necessarily) Bayes' theorem.
In what follows we consider variations in this decision making framework, focusing on the need to account for uncertainty as to system state and dynamics. In particular, we discuss the influence of nonstationary model weights, the effects of only partially observed system state, and robust decision making for cases of 'deep' uncertainty in system state or dynamics.
3. Coping with uncertainty
3.1. Model uncertainty
A key issue in determining the way optimal decisions are identified concerns the updating of the model state in the decision process. Decision making at each time uses the current model state qt in the decision making algorithm, along with an update of the model state for the next time step based on qt and the system response xt+1. This is the essence of adaptive management, which has 2 familiar forms:
Passive adaptive management—here decision making at a given time t utilizes the model state qt to weight both the immediate utilities and their anticipated accumulation over the remainder of the time frame. An example is
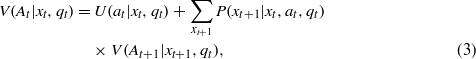
where the model weights qt(k) are used to compute an average utility U(at|xt,qt) = ∑kqt(k)Uk(at|xt), probability P(xt+1|xt,at,qt) = ∑kqt(k)Pk(xt+1|xt,at), and future value V(At+1|xt+1,qt) = ∑kqt(k)Vk(At+1|xt+1). The corresponding optimization form is
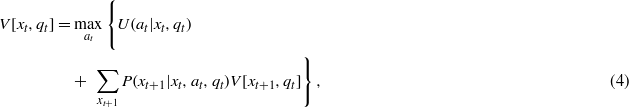
with optimization proceeding by standard backward induction starting at the terminal time T. From equation (4) the model state qt can be seen as essentially a fixed parameter over the timeframe [t,T] of the optimization. The updating of the model state occurs outside the optimization algorithm, after a decision is implemented and system response xt+1 is recorded. At that time a new model state qt+1 is derived from xt+1, and another optimization is conducted over the new timeframe [t + 1,T] based on the updated system and model states.
With this sequence it is clear that at any particular time the choice of an action is influenced by both the current system state and model state. However, the choice is not influenced by the anticipated impacts of decisions on future model state (i.e., learning). In this sense, decision making is held to be 'passive'. A long-running and successful application of passive adaptive management is the regulation of mallard (Anas platyrhynchos) harvests in the United States (Johnson 2011).
Active adaptive management—in this case decision making at a given time t utilizes the model state qt for immediate utilities and transition probabilities, and model state qt+1 for the anticipated accumulation of utilities over the remainder of the time frame. Thus, the model state qt is used to compute the average utility U(at|xt,qt) and probability P(xt+1|xt,at,qt) at time t, whereas the model state qt+1 is used to compute the average future value V(At+1|xt+1,qt+1):

where P(xt+1|xt,at,qt) is the average of model-specific transition probabilities based on the model state. Optimal strategy is produced inductively from equation (5), by
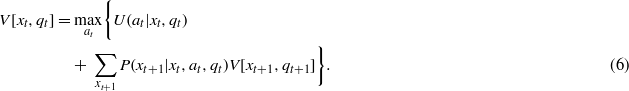
As indicated in equation (6), optimization over the timeframe [t,T] again proceeds by standard backward induction starting at the terminal time T, but in this case the potential transitions of both system and model states are included in calculation of the average future values used in the optimization algorithm. After a decision is implemented, the system response xt+1 is recorded and a new model state qt+1 is derived from xt+1, whereupon an optimal action is identified for the new system and model state at time t + 1 without resorting to a new optimization.
The main difference between this sequence and the one for passive adaptive management is that an updated model state is computed and incorporated directly into decision making. Thus, with active adaptive management the choice of an action at any particular time is influenced by its anticipated impacts on future model state (i.e., learning). It is the integration of learning directly into the optimization algorithm that differentiates active adaptive management from passive adaptive management. The decision making is held to be 'active', in that it is influenced by the anticipated effect of decisions on both system behavior and learning. In this sense adaptive management exemplifies the dual control problem of simultaneously controlling and identifying the system that is subjected to decision making (Walters 1986). Nevertheless, optimal management consists of actions that maximize objective returns, not learning per se, with model discrimination (i.e., learning) pursued only to the extent that it increases long-term returns.
By incorporating the model state qt as a parameter in the value function V[xt,qt] and accounting for the effect of learning on decision making, the challenge of identifying optimal strategies tailored to model uncertainty is increased dramatically. This is one reason why the common approach to active adaptive management is simply to use interventions in the context of classical experimentation (Walters and Holling 1990). However, there are a growing number of examples in the literature that rely on the optimization of active adaptive management strategies, including wetlands management (Williams 2011), invasive species control (Moore 2008), pest management and weed control (Shea et al 2002), habitat restoration (McCarthy and Possingham 2007), and harvest management (Hauser and Possingham 2008, Moore et al 2008).
3.2. Partial observability
In the foregoing it was assumed that the resource system being managed is completely observable, in that the system state xt is known with certainty at each decision point in the time frame. This assumption simplifies the optimal control problem, by eliminating partial observability as a source of uncertainty that must be addressed. Partial observability refers to an inability to observe a system fully, so that state-dependent decisions must be made under uncertainty as to the actual state of the system at the time the decision is made.
Partial observability presents a ubiquitous challenge in natural resources management, because the system state is almost never known with certainty, and is almost always estimated through sampling. Thus, state-dependent decision making is subject to the additional stochastic component of sampling variability. Here we represent uncertainty about system state at time t by a belief state bt that describes the strength of belief one has that the system is in each of its possible states. The belief state is essentially a distribution of state-specific probabilities that evolves through time, based on observations that are stochastically associated with, but not the same as, system states.
To clarify the issue, assume for the moment that the process is known, though not fully observed. Then a natural form of the value function that captures partial observability averages the value function for each state using the distribution probabilities b(xt) for the possible states at time t:
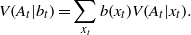
The belief state evolves as the system changes and observations accumulate through time, and the evolving belief state is used in computing the expected sum of current and future utilities
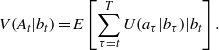
This form of the value function can be expressed recursively in terms of current and future utilities, by
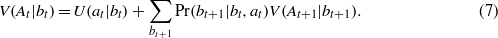
A comparison of value functions that include only partial observability or only structural uncertainty reveals both similarities and differences (Williams 2009). Thus, the presence of partial observability means that one must account for two stochastic sources, namely environmental or demographic stochasticity and sampling variability. This increases the complexity of computing the transition probabilities Pr(bt+1|bt,at) in equation (7). On the other hand, the presence of structural uncertainty means that one must account for both system state and model state in the value functions as in equations (3) and (5), which increases computational demands significantly. Which of these represents the greater challenge is likely to be problem specific.
Of course, it is possible to incorporate both structural uncertainty and partial controllability into the same algorithm for decision making (Williams 2009). Though the notation for such a case becomes rather cumbersome, the basic idea is simply to include both components of uncertainty in the value function, i.e., V(At|bt,qt). The difficulty in actually computing optimal strategies and values increases dramatically in the simultaneous presence of both forms of uncertainty. New approaches involving simulation, sub-optimality analysis, neural networking, reinforcement learning, and other methods are required to address such problems.
In recent years a great deal of work has been done on partial observability in the context of partially observable Markov decision processes. Approaches include value iteration (Monahan 1982; Lovejoy 1991a; White 1991; Cassandra 1994; Poupart 2005), discretization of belief space (Lovejoy 1991b, Hauskrecht 2000, Zhou and Hansen 2001), exploitation of the geometric structure of the value function (Smallwood and Sondik 1973; Zhang and Liu 1996; Kaelbling et al 1998), and point-based value iteration (Zhang and Zhang 2001, Pineau et al 2003). Examples in natural resources include the control of an invasive species (Moore 2008, Haight and Polasky 2010), endangered species management (Tomberlin 2010a), decision making by fishermen (Lane 1989), multi-stock fisheries management (Tomberlin 2010b), and survey and management of cryptic threatened species (Chadès et al 2008).
3.3. Robust decision making
Finally, consider a problem in which the process structure is understood, but uncertainty about the system state is so deep that it is not known even stochastically. This situation might correspond to the lack of any observation data, or a monitoring protocol that is flawed in some unrecognizable and/or uncorrectable way. Then it no longer is meaningful to maximize an average of utilities, because there is no known distribution on which to base the averaging. A different criterion is needed to guide decision making.
One such candidate is 'good enough' or robust decision making. Here the idea is not to maximize a measure of utility, but rather to produce values exceeding some specified lower limit Vc over as large a range of belief states as possible. Robust decision making involves the choice of an action that will maximize the range of belief states for which the expected utility for every belief state in that range will be 'good enough'. This shifts the focus from maximizing expected utility to maximizing coverage of 'good enough' value. The operative question is 'how wrong can one be about the belief state and still produce an adequate value?'
Robust decision making for dynamic conservation is defined in terms of a range of belief states  in the vicinity of a 'guesstimate'
in the vicinity of a 'guesstimate'  of belief state, within a range given by a parameter α called the uncertainty horizon. The range essentially specifies a set of belief states located around
of belief state, within a range given by a parameter α called the uncertainty horizon. The range essentially specifies a set of belief states located around  , with an extent given by α. More belief states are included in a range corresponding to a larger uncertainty horizon α. A key question is how large α should be.
, with an extent given by α. More belief states are included in a range corresponding to a larger uncertainty horizon α. A key question is how large α should be.
The idea of robust decision making is to identify a value for α such that every belief state in  will produce a value that exceeds some critical value Vc. This condition is specified by
will produce a value that exceeds some critical value Vc. This condition is specified by
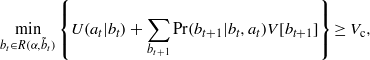
where V[bt+1] is the optimal value of the value function V(b) for belief state bt+1. The largest possible range that satisfies the condition is found by maximizing over the choice of α:
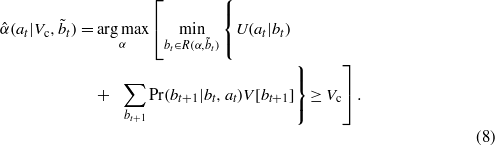
The 'robustness function'  in equation (8) gives the uncertainty horizon corresponding to action at around
in equation (8) gives the uncertainty horizon corresponding to action at around  . Robust decision making is defined for a given critical value Vc and guesstimate
. Robust decision making is defined for a given critical value Vc and guesstimate  by the selection of the action at with the largest uncertainty horizon produced by the robustness function: choose at to maximize
by the selection of the action at with the largest uncertainty horizon produced by the robustness function: choose at to maximize  .
.
A similar decision making approach can be formulated when the system is observable but there is deep uncertainty about its structure. In that case a range can be defined that is centered on a guesstimate  of the model state, with extent again given by an uncertainty horizon α. An action-specific robustness function
of the model state, with extent again given by an uncertainty horizon α. An action-specific robustness function  that gives the uncertainty horizon identified by
that gives the uncertainty horizon identified by
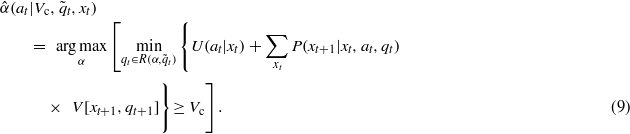
Robust decision making with uncertain model state is then defined for a given critical value Vc and guesstimate  by the selection of the action at with the largest uncertainty horizon produced by the robustness function: choose at to maximize
by the selection of the action at with the largest uncertainty horizon produced by the robustness function: choose at to maximize  . As above, deep uncertainty about system state requires one to account for two stochastic sources, which increases the complexity of computing the transition probabilities Pr(bt+1|bt,at) in equation (8). On the other hand, deep uncertainty about process structure requires one to account for system state as well as model state in the value function shown in equation (9).
. As above, deep uncertainty about system state requires one to account for two stochastic sources, which increases the complexity of computing the transition probabilities Pr(bt+1|bt,at) in equation (8). On the other hand, deep uncertainty about process structure requires one to account for system state as well as model state in the value function shown in equation (9).
The approach described here builds on the work of Ben-Haim (2000) on info-gap, robust optimization theory (Ben-Tal and Nemirovski 2002), computer assisted reasoning (Bankes et al 2001), and others. The recognition and treatment of deep uncertainties expands the decision making framework, requiring new objectives, system characterizations, and decision-analytic approaches. Examples in natural resources include climate-related decision making (Lempert and Schlesinger 2000, Lempert 2002) and water management (Hipel and Ben-Haim 1999, McCarthy and Lindenmayer 2007).
4. Framework applicability and challenges
In the foregoing we described a decision-oriented framework that accounts for system dynamics and uncertainties of various kinds and degrees. The framework has many features to recommend it for conservation and management of natural resources. Ecological systems are fundamentally dynamic, with behaviors that can be strongly influenced by management interventions. Management typically occurs through time, with iterative decision making based on system status at the time decisions are made. Finally, there is almost always considerable uncertainty about the resource status, the processes that influence resource change, and the influence of management interventions on them. The role of time is especially relevant. Decision making, environmental variation, resource status, and uncertainty are all expressed over time, which offers the possibility of learning and improved decision making. These features are captured in the models and decision apparatus presented above.
In what follows we address some generic conservation problems and discuss how they can be framed to make them amenable to decision analysis. We focus on the conservation of biodiversity, building on the rapidly developing field of conservation biology and the decision making problems it presents. Specifically, we address the problems of habitat and population management for imperiled species, the control of invasive exotic species, the design of landscapes and reserves to maintain biodiversity, and sustainable resource exploitation. First, however, we offer some general comments about modeling ecological processes and the valuation of conservation outcomes.
4.1. Applicability
Important in biodiversity conservation efforts is the recognition that it may not be species richness per se that enhances ecosystem function and resilience, but the way in which species interact with each other and with their environments (Peterson et al 1998). Thus, the issue in biodiversity conservation is how to maintain ecological processes rather than patterns, i.e., how best to influence the processes that affect change in pattern through time. A focus on enabling and maintaining the processes that enhance biodiversity is becoming more commonplace in the published literature (Margules and Pressey 2000, Whittaker et al 2005, Sarkar et al 2006, Pressey et al 2007) and in turn, conservation planners are increasingly turning to spatio-temporal processes like island biogeography, metapopulation dynamics, source-sink processes, competition, plant and animal succession, and disturbance regimes (Margules and Pressey 2000). While these approaches may suggest statistical associations and equilibrium conditions, more important are their implications for rates of mortality, reproduction, immigration, emigration, colonization, or local extinction influenced by controlled and uncontrolled variation in the environment.
We acknowledge the inherent difficulties in modeling ecological processes. However, a systematic approach to formulating useful models need not depend on a thorough mechanistic understanding or precise model parameterization, as long as uncertainty is acknowledged and treated in a systematic manner (Conroy et al 2011, Nichols et al 2011). The critical point is that informed decisions require predictions about the outcomes of potential actions, and these predictions must come from some sort of model of system dynamics. Models are not optional components of decision making, and the challenges associated with modeling and predictions simply cannot be used as reasons to abandon modeling efforts.
Another critical, yet difficult, aspect of conservation is the need to express conservation objectives in terms of tangible performance metrics, whose values change through time as a result of conservation actions and uncontrolled environmental drivers. The dynamic decision making framework we describe is amenable to a wide array of objective functions that consider the dynamic nature of conservation. For conservation of threatened species, one may wish to minimize the probability of extinction over a specified time frame, maximize the cumulative years that a species is extant, maximize the expected time to extinction, maximize the proportion of an area occupied by a species, or minimize the temporal variance of small populations. For invasive and pest species, conservation efforts might focus on maximizing the number of years when abundance is below some threshold, minimizing cumulative abundance, or minimizing the cumulative sum of the logarithm of the population growth rate. For resource exploitation, the objective function might seek to maximize the cumulate sum of harvest over an extended time frame, recognizing that such maximization depends on resource sustainability. The key point is that the objective function should express the accrual of conservation benefits over some (possibly infinite) timeframe.
Whatever the measure of benefit in biodiversity conservation, both direct and indirect costs must be considered if conservation is to be cost effective (Naidoo et al 2006, Murdoch et al 2007, Polasky 2008). That the costs of conservation can be both dynamic and uncertain has important implications (McDonald-Madden et al 2008, Carwardine et al 2010). These features of conservation value can be recognized in our decision making framework as aspects of the system to be modeled. Perhaps more problematic are efforts to conduct cost-benefit analyses by assigning dollar values to conservation. Although there has been notable work in this regard (Farber et al 2002, Naidoo and Ricketts 2006), it has been criticized because biodiversity values are incomplete, markets for some important values do not exist, and efficiency does not necessarily imply sustainability (Bishop 1993, Nunes and van den Bergh 2001). When benefits and costs cannot be reduced to the same currency (e.g., dollars) there are several possible approaches to assessing the tradeoff. One is to attempt to maximize biodiversity benefits for a fixed conservation budget (Wilson et al 2006, Murdoch et al 2007). Another is to minimize the costs of sustaining biodiversity at a prescribed level. Yet another is to rely on the notion of Pareto optimality (Kennedy et al 2008). For biodiversity conservation, Pareto-optimal solutions are those in which the conservation outcome cannot be improved without a reduction in other socio-economic values (Bishop 1993, Polasky et al 2005, 2008). Although there can be no single, optimal solution (because there is no agreement on objectives or how they are weighted), Pareto-optimal solutions provide a basis for negotiating a solution among stakeholders by first ruling out solutions that do not perform well on any of the objectives.
Here we describe six generic conservation problems and how they might be conceptualized within our decision making framework. In particular, we focus on the dynamic nature of the problem, and how objectives, system dynamics, and uncertainty might be expressed.
Habitat management—managers of conservation lands often strive to provide vegetative composition and structure that is favorable for an imperiled species, usually by mimicking natural disturbance processes such as fire. While a variety of sensible objective functions are possible, one reasonable alternative is to maximize the temporal sum of the logarithm of the finite population growth rate of the imperiled species:
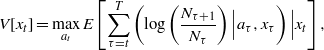
where population size Nτ is a component of system state xτ. This is equivalent to maximizing the population growth rate over the entire planning horizon. Alternative actions at at each time step might include doing nothing, conducting a prescribed burn, mechanical cutting, or perhaps treating the vegetation with herbicide. Each of these actions would be expected to have different costs as well as benefits, and the ability of the manager to meet her objective would likely be constrained by her budget. Vegetation growth and succession might be characterized in matrix form, with the entries representing the probabilities P(xt+1|xt,at) of transitioning from one vegetative state to another, conditional on the action chosen. Importantly, the complete system model would need to connect the vegetative states and actions to the expected population growth rate or to one or more demographic rates of the imperiled species. Possible sources of uncertainty likely include (1) environmental variation (e.g., periodic drought) that may affect the state transition probabilities; and (2) partial controllability where treatments may randomly vary in their effectiveness. In this case a state-dependent management strategy, which accounts for stochastic changes in system state, is superior to the traditional approach of using treatments at fixed time intervals. In the case of structural uncertainty about the relationship between habitat states and demographic rates of the imperiled species, adaptive management is a viable candidate, assuming that alternative hypotheses Pk(xt+1|xt,at) suggest different management strategies and that system monitoring is capable of distinguishing state-specific responses in the imperiled species' growth rates. Examples concerning the dynamic management of habitat include those of Richards et al (1999), McCarthy et al (2001), Moore and Conroy (2006), Johnson et al (2011), and Tyre et al (2011).
Captive rearing and stocking—imagine a critically endangered species or population in which its habitat is mostly suitable, but the extinction risk is primarily the result of small population size. Managers often consider a captive-breeding program, with the idea that releases into the wild can minimize the probability of extinction of the wild population. The objective function for this situation might be to minimize the probability that the species is extinct in the wild at the end of some arbitrarily defined planning horizon:
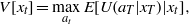
where utility U is unity if the species is extant at the end of the time frame and zero otherwise. For stochastic systems, the optimal value V[xt] is equivalent to the probability that the species will be extant at time T assuming the optimal management strategy is followed. Alternative actions at involve either capturing varying numbers of wild animals for the captive-breeding program, or releasing varying numbers of captive-reared animals into the wild. The system state would include both the number of animals in wild and captive populations, and the system model P(xt+1|xt,at) must specify expected demographic rates for both the captive and wild populations, as well as any direct mortality associated with capture and release. A key source of uncertainty is demographic stochasticity, resulting from a small number of animals being exposed to random mortality; a binomial distribution can be used to specify probabilistic predictions of survival for a specified number of captures or releases. There may also be considerable uncertainty about demographic rates in the wild population, as well as uncertainty about potential Allee effects (Berec et al 2007). In the case of critically endangered species, robust decision making that seeks to maximize the uncertainty horizon for which some critical level of success is assured ( ) may be more appropriate than an adaptive management approach. Tenhumberg et al (2004) provide an interesting case study in the dynamic, state-dependent management of captive rearing and stocking.
) may be more appropriate than an adaptive management approach. Tenhumberg et al (2004) provide an interesting case study in the dynamic, state-dependent management of captive rearing and stocking.
Control of invasives—within the constraints of their budgets, responsible agencies must routinely make tradeoffs inherent in controlling the spread of invasives; e.g., monitoring abundance in well-established areas versus monitoring potential sites for colonization, eradicating large infestations versus eradicating newly colonized sites, and monitoring populations versus implementing control measures. There are also temporal tradeoffs that must be considered because decisions made at any point in time produce a legacy for the future (e.g., how long to wait before implementing controls). Assume for example that a landscape is comprised of patches with known infestations and patches with the potential for infestation but where none has been observed. Assume that the manager is able to conduct reconnaissance surveys at periodic intervals to identify infested patches, but that the detection process is not perfect (i.e., some infestations are missed). Following each survey, the manager can choose to: (1) do nothing until time for the next reconnaissance; (2) attempt control of the infested patches that were detected; or (3) re-survey apparently empty patches and control whatever infestations are found ('search and destroy'). The actions at have different costs, with the 'do nothing' option having the lowest cost and search and destroy having the highest cost. The goal of the manager is to choose an action after each reconnaissance survey that would be expected to minimize the number of infested patches over time (or, equivalently, maximize the number of empty patches) at the lowest possible cost. One way to express these competing objectives is in a loss function, in which the total loss is the sum of direct costs of management activities and the opportunity costs of infested patches. Opportunity costs represent the ecosystem values forgone by allowing an infested patch to persist. An appropriate objective function is:
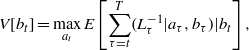
where L represents total cost. Sources of uncertainty meriting attention might include: (1) partial observability, in that infestations have some probability of being missed in the reconnaissance surveys; (2) partial controllability, in that control actions may only be partially effective at eliminating the invasive from a landscape patch; and possibly (3) structural uncertainty concerning the invasive species' rate of colonization. State dependent, adaptive decision making seems especially appropriate for such highly dynamic and uncertain systems. Taylor and Hastings (2004), Mehta et al (2007), Bogich and Shea (2008), and Haight and Polasky (2010) provide useful examples of optimal control strategies for invasives.
Reserve design—another application that highlights both uncertainty and change is the design and construction of reserve networks. Imagine a landscape consisting of planning units, each supporting a different subset of target species, and a conservation goal to maximize the number of target species on the landscape at the end of the planning horizon. It is the rare occasion (at least in terrestrial systems) when a reserve design can be implemented all at once, and changes in the socio-ecological system during the period of implementation can profoundly affect the eventual structure and functioning of the reserve (Possingham et al 2009). For example, there may be the phenomenon known as 'leakage', in which development of a reserve either displaces threats to surrounding landscapes (Ewers and Rodrigues 2008) or effects the market value of desirable properties (Armsworth et al 2006). Accounting for these dynamics and uncertainties (e.g., in real estate values or budgets) can be accommodated in the framework as random noise, as part of the modeled system state, or both (Costello and Polasky 2004, Meir et al 2004, McBride et al 2007, McDonald-Madden et al 2008). Key sources of uncertainty may include: (1) environmental variation in the direct and opportunity costs of planning units; (2) partial controllability in that the effort to acquire a planning unit may be unsuccessful; and (3) structural uncertainty concerning the assumption that acquisition of a planning unit is sufficient to protect its complement of target species. Optimal reserve design is extremely challenging because of the spatial and temporal complexity inherent in these problems. State-dependent decision making combined with a passively adaptive or robust decision making approach may be most appropriate, especially if the capacity for understanding system response is limited. Insightful examples of a dynamic approach to reserve design are provided by Moilanen and Cabeza (2007), McDonald-Madden et al (2008), and Schapaugh and Tyre (2012).
Landscape connectivity—maintaining or increasing the connectivity of habitat patches has emerged as a favored conservation approach in the face of anthropogenic habitat fragmentation and climate change (Calabrese and Fagan 2004, Hodgson et al 2009). In this case we might envision a landscape comprised of protected habitat patches embedded in a matrix of other patches, each of which can exist in one of four possible states: developed, protected, unprotected and available for acquisition, or unprotected and unavailable. Assume that each unprotected patch has a connectivity index, perhaps derived using circuit theory (Mcrae et al 2008), as well as a cost of acquisition. The conservation planner is faced with a decision to acquire an unprotected patch as it becomes available on the market, or to forgo the opportunity and wait for a more desirable patch to become available. Unprotected patches have some risk of being developed before they can be protected, and this complicates decision making over time because development of an unprotected patch will cause changes in the connectivity index for the remaining unprotected but undeveloped patches. The modeling of system dynamics may also be made more difficult by the phenomenon of extinction debt, in which the responses of metapopulations to changes in the landscape are not immediate (Hylander and Ehrlén 2013). Such time lags mean that the system is not Markovian, a feature that complicates but does not prohibit the search for optimal solutions (Williams 2007). Perhaps even more problematic is specification of an objective function. How much connectivity is enough? Too little and there will not be enough landscape connectivity to facilitate the dispersal necessary to keep local species from becoming extinct or to facilitate re-colonization. Too much landscape connectivity might have negative consequences for conservation targets by facilitating invasion by exotics or the spread of disease. Ultimately, one must make assumptions (i.e., develop models) concerning the degree of landscape connectivity and the ability of metapopulations to sustain themselves (e.g., Westphal et al 2003). Landscape planning for conservation, whether concerned with the design of reserves or their connectivity, is plagued with uncertainties concerning how the size, distribution, and connectivity of habitats influence the processes sustaining biodiversity. In the case of such over-whelming uncertainty, we suggest that approaches to decision making focusing on robustness rather than the maximum expected return (or minimum expected loss) might be the better choice.
Resource exploitation—exploitation is well recognized as an important concern for biodiversity conservation (Mace and Reynolds 2001). Yet much of the history of harvest management is characterized by application of equilibrium approaches that failed to provide sustainable harvests (Larkin 1977, Holling and Meffe 1996, Berkes 2010). To help address these failures we need a dynamic approach, in which harvesting strategies explicitly account for uncontrolled environmental variation, limited control over harvest, and other sources of stochasticity that manifest themselves over time. Also required is the need to recognize that current harvests affect future harvest opportunities, and that the future must not be discounted beyond the renewal capacity of the resource if harvests are to be sustainable (Clark and Munro 1978). Ideally, resource exploitation problems incorporate an ability to regulate (perhaps imperfectly) the magnitude of the harvest, and a monitoring program that provides information about resource status (and perhaps relevant environmental conditions) at periodic intervals. The goal of the manager may be to maximize the cumulative sum of harvests over an infinite time horizon, possibly subject to various constraints (e.g., an acceptable range of resource abundance to meet non-consumptive uses). For example, the objective function might be:
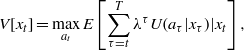
where
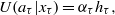
where h is harvest, and α discounts harvest according to

and g is a fixed population goal. Unless the objective incorporates biologically excessive discounting, this objective inherently recognizes the importance of future harvest opportunity and thus enhances the prospect of sustainability. Another noteworthy problem in resource exploitation is determining the level of incidental take of an imperiled or otherwise vulnerable species that might be acceptable (Runge et al 2004). Here the objective is not concerned with maximizing harvest, but on allowing a minimal level of take that does not significantly jeopardize population status. Other examples include systems of interacting species or ecosystem services, in which culling is used to generate a variety of societal benefits (Bode and Possingham 2007, White et al 2012). System models for resource exploitation might be based on simple logistic models of population growth (e.g., Johnson et al 2012) or on models that recognize significant age and sex-specific differences in rates of mortality and reproduction (Ludwig 2001). A fundamental concept in harvesting theory is density dependence (Hilborn et al 1995), and adaptive management strategies are appropriate if there is considerable uncertainty in the relationship between density and population growth rates (e.g., Hauser et al 2006, Johnson 2011).
Whatever the particular conservation problem, we suggest that a systematic approach to dynamic decision making need not be an onerous undertaking. The requirements are those for any systematic approach to decision making—a careful consideration of values, actions, and outcomes. In particular, there needs to be thoughtful deliberation among stakeholders to specify conservation and other socio-ecological objectives, and how tradeoffs among them are to be accommodated. And while the modeling of system dynamics to support conservation decision making continues to be challenging, conservationists possess a rich body of ecological theory from which plausible models can be developed. In many cases empirical information will be lacking to precisely parameterize a model, or more than one model may be a suitable candidate for describing system dynamics. As we have indicated, parameter and/or functional uncertainty can be accommodated readily with either an adaptive or robust approach to decision making. These arguments notwithstanding, we acknowledge that a decision-analytic approach to dynamic conservation faces some difficult challenges. We turn our attention to those in the following section.
4.2. Key challenges
Stakeholder engagement—stakeholders bring different perspectives, preferences, and values to decision making. A critical challenge is to find ways to engage stakeholders in framing a resource problem and identifying its objectives and management alternatives, and to continue that engagement throughout the project (Wondolleck and Yaffe 2000). In particular, it is important to find common ground that will promote decision making despite disagreements among stakeholders about what actions to take and why. The failure to create an institutional environment that promotes stakeholder involvement is a common stumbling block that can impede progress and ultimately undermine a project.
Many observers think that the major impediments to more open, adaptive management are fundamentally institutional (Stankey et al 2005). Institutions are built on major premises and long-held beliefs that are deeply embedded in educational systems, laws, policies, and norms of professional behavior (Miller 1999). There is a natural tension between the tendency of large, long-standing organizations to maintain a strong institutional framework for deliberation and decision making, versus more open decision making that relies on collaboration, flexibility, and participatory decision making (Gunderson 1999). One consequence is that not enough attention is paid to institutional barriers, and not enough effort is spent on designing organizational structures and processes to accommodate an open, adaptive style of resource conservation and management. Underlying such a framework is the recognition of evolving institutional and resource conditions, and the continuing need to assess and adapt to these changes though time.
Scale—there needs to be careful attention to problem framing as it relates to matching the scale of the problem with the scale at which conservationists (or society) can address it (Cumming et al 2006, Carpenter 2009). Though a decision problem may have a relatively narrow focal scale for implementation of alternatives, a consideration of both smaller and larger scales is often necessary to adequately predict and value outcomes. At relatively large spatial scales conservation actions will sometimes conflict with other socio-economic goals. In these cases a more open and inclusive decision making process is required, where a broader range of values and their tradeoffs are explicitly considered. To be successful at these scales conservationists must be transparent in how they account for the diverse concerns of stakeholders (through, e.g., the quantification of opportunity costs) (Naidoo et al 2006).
From an analytical perspective, a principal concern is how conservation decisions can be linked across spatial and temporal scales. For example, conservation decisions made over space can be linked to promote biodiversity at a variety of scales (Poiani et al 2000), and there have been some attempts to look at decisions linked over both time and space (Meir et al 2004). The challenge for decision analysts is to understand when linkages need to be treated explicitly (i.e., one decision depends in part on another and both decisions are under the control of the planner) and when some decisions can be treated implicitly as noise (in the case of smaller-scale decisions) or constraints (in the case of larger-scale decisions) relative to the focal scale of decision making.
Nonstationarity—one of the most significant challenges in applying optimal decision making for conservation is the possibility (indeed, the likelihood) that system dynamics are not stationary. By this we mean systemic change in process structure, resulting in directional shifts in its moments (e.g., means and variances) over time. It is important to appropriately represent the nature of such change; i.e., is it expected to be long-term and ongoing, or relatively short term with a shift to a new, stationary mean and variance? With short-term change, the key issue for optimization is how to manage through the change (Conroy et al 2011, McDonald-Madden et al 2011) until the system dynamics are again stationary. With long-term change, the challenge is to adapt to a continually evolving system. In both situations, the optimal policy will be both state and time dependent. In some cases, the nonstationarity of key structuring processes will be unrecognized, or else there may be no clear idea of how to model the changing dynamics. One way to cope with this issue would be to assume stationarity for relatively short periods, while being particularly attentive to the adequacy of the system models and revising them as their predictive ability declines (Nichols et al 2011).
Potential regime shifts—another concern about system models relates to the possibility of ecological thresholds and alternative stability regimes. The idea of unforeseen changes in ecological systems that are resistant to reversal has been at the core of 'resilience thinking' (Holling 1973, Ludwig et al 1997, Carpenter et al 2001, Ludwig et al 2002, Folke et al 2004, Walker and Salt 2006). Resilience is defined as the magnitude of disturbance a system can absorb while still retaining essentially the same function, structure, identity, and feedbacks (Walker et al 2004), or as the disturbance that can be absorbed without shifting the system to an alternative stability regime (or 'domain of attraction') (Holling 1973). Important concerns for ecosystem management are (1) the loss of resilience as the system state approaches a (perhaps unknown) threshold, and the attendant increase in probability that some disturbance will shift the system to a less desirable stability regime; and (2) changes in the parameters governing the size and shape of the domains of attraction that make system shifts more or less likely (Beisner et al 2003). Systems with alternative stable states can exhibit hysteresis, in which a loss of resilience is followed by a system change and thereafter an increase in resilience so that reversing the change is difficult (Ludwig et al 1997, Scheffer et al 2001). Although a number of researchers have begun to formulate simple models that can be used to explore these properties (Ludwig et al 1997, Scheffer et al 2001, Carpenter 2002, Scheffer and Carpenter 2003), more needs to be done to develop models that can be used to provide practical advice for those concerned with biodiversity conservation.
Monitoring—monitoring of system state variables and associated vital rates serves four primary roles in decision processes with uncertainty (Yoccoz et al 2001, Nichols and Williams 2006). Estimates of system state are required to (1) make state-dependent decisions, and (2) assess the degree to which objectives are being met. Such estimates also provide (3) a basis for learning, as estimates of key variables are compared against model-based predictions in order to update measures of confidence in system models (Williams et al 2002). Finally, monitoring data are used to provide (4) updated or better estimates of key system vital rates. Predictions of thresholds based on system models will be improved by better estimates of the vital rates governing the model processes. One way to address the potential for thresholds and regime shifts is to monitor the drivers of system change. For example, models producing extinction thresholds (Lande 1987, 1988) highlight the need for monitoring to assess changes in habitat quality (MacKenzie et al 2011, Miller et al 2012). Rapid climate change should encourage the modeling and monitoring of key environmental drivers that affect managed systems. Monitoring programs for these driver variables will be required in order to track and model system dynamics (Milly et al 2008, Nichols et al 2011).
Computation—combined with these challenges are computational limitations. There are no theoretical limits to problem dimensionality, but the time required for calculating optimal policies for problems of even moderate complexity can be prohibitive. This problem has stimulated the exploration of quasi-optimization methods like simulated annealing or reinforcement learning, which sample the policy or state space rather than conducting a comprehensive search among all possible values and states (Fonnesbeck 2005). The computational burden of dynamic analysis has also fostered the search for simple heuristic algorithms that can produce acceptable policies when an exact, optimal solution cannot be computed in a reasonable amount of time; e.g., Wilson et al (2006) and Moilanen and Cabeza (2007).
5. Conclusions
Conservation problems are often formulated as static problems, as if conservation plans can be implemented all at once (as in the construction of a reserve) or else only short-term consequences need to be considered. In our opinion, too often conservation plans are depicted as static maps of priority conservation areas or as prescribed actions that lack any state dependency. But many decision problems in conservation are inherently dynamic, with time horizons that are long, if not infinite. In some cases, a static or myopic formulation of the conservation problem may provide an adequate approximation of the optimal solution, but this cannot be known a priori. We suggest that planners need to formulate problems in a way that explicitly recognizes the interaction of periodic conservation actions and the ecological processes they are meant to influence.
A key consideration in dynamic optimization of conservation problems is the uncertainty attendant to management outcomes, which adds to the demographic and environmental variation of stochastic resource changes. This uncertainty may stem from errors in measurement and sampling of ecological systems (partial observability), incomplete control of management actions (partial controllability), and incomplete knowledge of system behavior (structural uncertainty). A failure to recognize and account for these uncertainties can significantly depress management performance and lead to severe environmental and economic losses (Ludwig et al 1993). Thus, the recent emphasis on optimization methods that account for uncertainty about the dynamics of ecological systems and their response to intervention is encouraging. Stochastic dynamic optimization is a long-standing approach for dealing with most forms of uncertainty (Williams 1989). For problems involving structural uncertainty, both passive and active adaptive management approaches are amenable to many conservation problems in which uncertainty about system dynamics is a key impediment to effective decision making. Adaptive management is fundamentally concerned with dynamic decision making, so much so that learning and adaptation become impossible without tracking the consequences of management interventions and adjusting management strategy based on results. Indeed, the defining characteristic of adaptive management is the attempt to account for the dynamics of uncertainty in making evidence-based conservation decisions. Finally, robust decision making offers considerable promise in the case of 'deep' uncertainties, which plague many of today's most pressing conservation problems.
The complexity of conservation problems that are both dynamic and stochastic can be substantial; conservation decisions are often made over both time and space, and an explicit accounting for the various sources of uncertainty makes more difficult the search for optimal solutions. On the other hand, a solution that is a bona fide optimum often is not needed, and there are a number of both formal and heuristic approaches that can be used to find 'good' solutions to conservation problems of high complexity. In our experience what is often lacking in conservation planning is not a computational apparatus for optimization, but careful thinking about how to characterize the benefits and costs of conservation to society, how to identify the full suite of potential actions that could be used to enhance the benefits net of costs, and how to represent ways that the ecological system could change as a result of those actions and other uncontrolled factors. The framework we describe facilitates this sort of systematic thinking, regardless of whether optimal solutions are ultimately available. To be effective, however, a systematic approach to conservation decision making must build on a sustained partnership between scientists and managers, have sufficient institutional flexibility to explore novel problem-solving approaches, and include a commitment of decision makers to a transparent and inclusive decision making process (Knight 2008).
Acknowledgments
We thank Drs Vanessa Adams, Michael Bode, and Edward Game for encouraging us to submit a manuscript for this focus issue. We are grateful to Dr James Nichols for useful discussions and for contributing ideas for this manuscript. Funding for this research was provided by the US Geological Survey. We thank three anonymous reviewers and the editorial board for suggestions that improved the manuscript. Any use of trade, product, or firm names in this paper is for descriptive purposes only and does not imply endorsement by the US Government.
