RECONNECTION OF QUASI-SINGULAR CURRENT SHEETS: THE "IDEAL" TEARING MODE

Recently, both numerical simulations and linear instability analyses have confirmed the possibility of fast reconnection within the framework of resistive magnetohydrodynamics. As commented by Biskamp (1986), the Sweet–Parker (hereafter SP) stationary reconnecting current sheet (Sweet 1958; Parker 1957) is unstable to an extremely fast super-tearing, or plasmoid, instability even when taking into account the stabilizing effect of the reconnection outflows (Bulanov et al. 1978). This was studied in detailed by Loureiro et al. (2007), who showed how outflows effectively introduce a critical value for the Lundquist number S = LV_A/η_m ∼ 10⁴–10⁵ for this fast instability to occur (here L is the current sheet length or breadth, which we take to be equivalent and macroscopic, V_A the Alfvén speed based on the equilibrium field far from the sheet, and η_m is the magnetic diffusivity). For large values of S a growth rate scaling as γτ_A ∼ S^1/4, with τ_A = L/V_A the ideal Alfvèn timescale, was found. Lapenta (2008) carried out simulations showing the spontaneous development of a fast reconnection mechanism on macroscopic scales. A two-dimensional (2D) current sheet evolved through two different stages: an initial slow stage with the development of a very elongated Sweet–Parker type layer was followed by a rapid transition to a fast chaotic reconnection process, without the need for anomalous resistivity or driven flows to undergo this evolution. This was also confirmed in other numerical simulations (see, e.g., Bhattacharjee et al. 2009).

From the linear point of view, the existence of instabilities with a growth rate that increases with increasing Lundquist number is problematic. In ideal MHD, magnetic reconnection is prohibited, and finding an "infinitely unstable" mode in the limit of an infinite Lundquist number points to a strong singularity in the behavior of the MHD equations. Diffusive terms change the order of the equations, even for the linearized equations, and although it would not be too surprising to find a different physical behavior between systems described by ideal MHD and those described by the resistive equations with S → ∞, the presence in the latter case of infinitely fast growing instabilities has only one possible interpretation: the impossibility of constructing the corresponding equilibrium configurations (one could also argue that an infinite growth rate is non-causal and unphysical). This Letter describes how to resolve this dilemma, by showing that in the asymptotic S → ∞ regime an effectively "ideal" tearing mode survives, in the sense that its growth rate does not depend on the Lundquist number. The instability also defines a maximum critical aspect ratio (or a ratio between the current sheet's length and width) L/a ∼ S^1/3, above which any current configuration must be intrinsically unstable and turbulent and for which it is impossible to obtain a laminar configuration.

The SP current sheet has an inverse aspect ratio a/L ∼ S^−1/2 and this dependence is such that, in the absence of a convective flow keeping the configuration stationary, it would diffuse on the ideal timescale τ_A. For this reason, an inflow–outflow velocity field must be in place to keep the sheet in a steady state and a meaningful study of the stability of the SP current sheet therefore requires consideration of this flow. The stability study of the SP sheet is different from that usually performed for resistive instabilities, where the sheet thickness or aspect ratio does not scale with the Lundquist number. In the SP case, however, the equilibrium scaling with the Lundquist number is at the heart of the paradoxical result of diverging growth rates. A study of scaling approaching the ideal limit must therefore allow the current sheet thickness to scale with the Lundquist number, but allowing for a different dependence of the inverse aspect ratio on S. Imagine therefore the formation of a current sheet characterized by an intermediate scaling of the inverse aspect ratio with respect to the Lundquist number

$$\begin{equation} \frac{a}{L}\sim S^{-\alpha }. \end{equation} \tag{ 1 }$$

In this case the diffusion time scale for the magnetic field generated by the sheet is

$$\begin{equation} \tau _D \simeq \tau _A S^{1-2\alpha } \end{equation} \tag{ 2 }$$

so we see that as long as α < 1/2, i.e., as long as the inverse current sheet aspect ratio is greater than the one defined by the SP scaling, it makes sense to study the stability of such a sheet in the absence of flows—especially if we are looking for a fast instability—because τ_D/τ_A → ∞ when S → ∞.

Recall that for the tearing mode the typical length scale, which is used to define both the Lundquist number as well as the Alfvén crossing time, is the current sheet thickness a, rather than the current sheet length L, so that the classic tearing mode dispersion relation is written in terms of S* = aV_A/η_m, and growth rates are normalized to 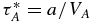$\tau ^*_A = a/V_A$. The growth rate depends on the Lundquist number as well as the wavenumber of the mode along the direction of the equilibrium magnetic field outside the current sheet k; the well-known result for the maximum growth rate is (Furth et al. 1963; Velli & Hood 1989):

$$\begin{equation} \gamma \,\tau ^*_A \sim {S^*}^{-1/2}, \qquad ka{S^*}^{1/4} \simeq 1. \end{equation} \tag{ 3 }$$

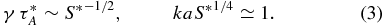
Translating this to the Lundquist numbers and Alfvén times defined by the macroscopic length L now yields

$$\begin{equation} \gamma \tau _A \sim \frac{L}{a} {S^*}^{-1/2}=\left (\frac{L}{a}\right)^{3/2} \left (\frac{LV_A}{\eta }\right)^{-1/2}=\left (\frac{L}{a}\right)^{3/2}S^{-1/2}. \end{equation} \tag{ 4 }$$

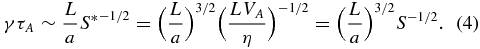
Consider then current sheets with inverse aspect ratios a/L defined by Equation (1): the expected growth rate becomes

$$\begin{equation} \gamma \tau _A \sim S^{-1/2}S^{3\alpha /2}. \end{equation} \tag{ 5 }$$

One sees that for values of α greater than α = 1/3, the growth rate tends to diverge with increasing S (and for the SP sheet the γτ_A ∼ S^1/4 scaling is confirmed). On the other hand, if we make the minimal request that the growth rate becomes at most independent of S at large S one finds that current sheets can at most become as thin as a/L ∼ S^−1/3. In other words, as a current sheet thins from a macroscopic thickness, we can imagine it as evolving through a set of α growing from 0: the growth rate, which for α < 1/3 decreases with increasing Lundquist number and is negligible for large S, quickly grows and becomes "ideal," i.e., independent of S, once α reaches the value α = 1/3. Any larger value of α will never be attained, as the instability becomes so fast that the corresponding equilibrium would be impossible to form. In other words α = 1/3 is a critical exponent separating slowly unstable sheets from a reconnection instability growing on an ideal time scale. From Equation (3), we correspondingly expect that the wavenumber of this ideally fast tearing mode should scale as kL ∼ S^1/6, leading to the formation of a large number of islands for large Lundquist numbers.

We now verify this conjecture by resolving the tearing mode equations for the Harris current sheet equilibrium, with a magnetic field aligned with the x-direction and dependent only on the y coordinate (the equilibrium is maintained either by an appropriate pressure structure or by a component in the field in the direction orthogonal to both the x and y directions):

$$\begin{equation} \boldsymbol {B}(y) = B(y)\hat{i}= B_0 \tanh \left(\frac{y}{a}\right)\hat{i}. \end{equation} \tag{ 6 }$$

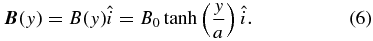
Starting from the incompressible MHD equations, we expand to first order, and write the linearized equations in terms of the y components of both the magnetic field perturbation, b, and of the velocity perturbation, v, where fluctuations are written as

$$\begin{equation} v(x,y,t)=v(y)e^{ik x+\gamma t} \end{equation} \tag{ 7 }$$

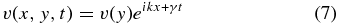
and similarly for b.

The equations are non-dimensionalized by normalizing the magnetic field and its perturbation in terms of the mean field B₀, the wavenumber k with a⁻¹, and we introduce the non-dimensional displacement ξ = iv/(γa). The growth rate is normalized to the macroscopic Alfvén time τ_A = L/V_A where the Alfvén speed is defined by (ρ is the plasma density) 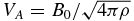$V_A = B_0/\sqrt{4 \pi \rho }$. Consider now that the equilibrium current sheet aspect ratio is taken to scale as a/L ∼ S^−α: we therefore also define a new independent variable z = y/a = (y/L)S^α, and denote derivatives with respect to z with '. The tearing mode equations become:

$$\begin{equation*} \left\lbrace \begin{array}{@{}l}\gamma ^{2}\,S^{-2\alpha }({\xi }^{\prime \prime }-{k^{2}} {\xi })= -{k}[ {B}(z)({b}^{\prime \prime }-{k}^{2}{b})-{B}^{\prime \prime }(z){b}\, ]\quad\;\,{(8a)} \\ \quad\quad{b}={k}{B}(z){\xi }+\,{1\over {\gamma } }S^{(2\alpha -1)}({b}^{\prime \prime }-{k}^{2}{b}).\quad\quad\quad\quad\quad\quad\;\;\,{(8b)}\end{array}\right. \end{equation*} \tag{ 8 }$$

The system of Equations (8) is a fourth order two-point eigenvalue problem which develops a boundary layer around the x-axis for large S. Here we solve the system numerically using the Lentini–Pereyra method (Lentini & Pereyra 1974). Because the solution to the equations outside the boundary layer may be found analytically (see Velli & Hood 1989), boundary conditions are applied well outside the current sheet by imposing the corresponding values of the asymptotic solutions, their derivatives, and a normalization condition (the overall amplitude of the perturbed magnetic field). A well-known instability criterion stems from the resolution of the simplified equation which is valid outside the boundary layer (obtained by setting the right-hand side of the momentum equation (8a) to zero). The solution to this equation for b which vanishes at ±∞ presents a discontinuity of the derivative at the origin: the jump in derivative normalized with the current sheet width, a, and the value b(0) is known as Δ' and the instability criterion, Δ' > 0, does not depend directly on the value of α but only on the a-normalized wavevector k, in terms of which it may be written as 0 < k < 1.

The system depends on three parameters, S, k, and α, and as mentioned instability is found only for 1 > k > 0. As α is varied we find maximal growth rates following the power law Equation (5) for increasing values of the Lundquist number S, (which we explore all the way up to values S ≃ 10¹³). In particular, when α < 1/3, we find that the maximal growth rate is a decreasing function of the Lundquist number, while larger α lead to diverging growth rates. Figure 1 shows the growth rate as a function of the a-normalized wavevector k, for different values of the Lundquist number S for α = 1/3. As one can see, each individual curve grows at small k, reaches a maximum, and then decreases again for increasing k. In addition, for increasing S, the maximums shift to decreasing k, as expected from the estimate of Equation (3) which, when corrected for the redefinition of S, leads to the scaling of the maximum ka ∼ S^−1/6. The fundamental result however is that the peak growth rate for increasing S shows only a very slight increase for S ∼ 10⁸–10⁹ and tends to an asymptotic value at greater S, which we find to be γ_maxτ_A ≃ 0.623.

Zoom In Zoom Out Reset image size

Integration of the tearing mode equations therefore confirms that a critical scaling with the Lundquist number exists which provides a limiting current sheet aspect ratio above which the instability becomes faster than ideal, so that it would be impossible to realize in a natural system, and this aspect ratio is significantly smaller than that of the SP sheet for large S.

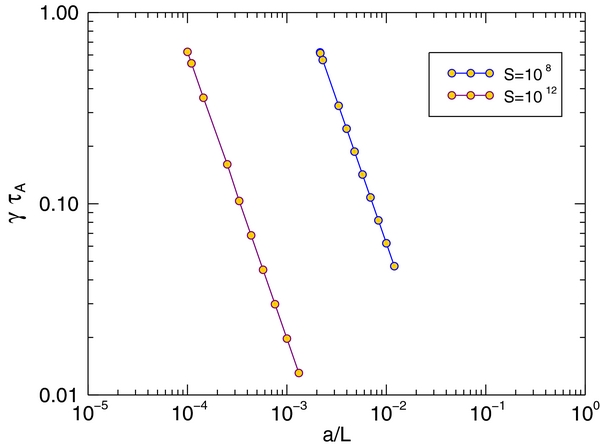
From the physical point of view it is also very interesting to inspect how the growth rate actually changes as the current sheet aspect ratio changes due to whatever driving mechanism is in place. This is shown in Figure 2 where the growth rate of the fastest tearing mode as a function of the inverse current sheet aspect ratio is plotted for two different values of the Lundquist number S = 10⁷ (blue) and S = 10¹² (red). As the inverse aspect ratio decreases, both follow the scaling Equation (5), namely γτ_A ∼ (a/L)^−3/2, very well. Consider now the slow rise of a prominence in the solar corona, or the gradual shearing of magnetic fields due to entraining by the solar wind (in the magnetosphere). In the case of a prominence eruption, one could imagine a multiple time scale evolution related to the evolution of the current sheet transitioning from slow to fast tearing (in this regard it would be appropriate to re-examine, for example, the details of x-point collapse as examined, e.g., in Cassak & Drake 2009). In our interpretation the triggering of flare-like phenomena would be associated with the growth rate reaching values close to the asymptotic ideal value as the critical sheet thickness is approached (corresponding to the maximal values in Figure 2). Another case is that associated with field line tangling by photospheric motions (as in the nanoflare scenario for heating coronal loops, Rappazzo et al. 2007, 2008). The dynamics in these cases could be different, depending on the time scale associated with current sheet formation and thinning. It has been shown recently that the current sheet collapse itself may occur on an ideal time scale once a threshold in magnetic perturbation is reached (Rappazzo & Parker 2013). In this case, the existence of "ideal tearing" would seem to provide a firmer foundation for the nanoflare scenario of coronal heating: the formation of tangential discontinuities as envisioned by Parker (1972) would end up in fast tearing of the corresponding current sheets and consequent complex dynamics.

Zoom In Zoom Out Reset image size

Let us return to the physical significance of the SP aspect ratio. As is well known, the tearing mode has a singular layer structure, where the antisymmetric ideally diverging velocity eigenfunction ξ (perfectly antisymmetric only in the case of a completely symmetric current sheet) breaks and decelerates into the stagnation point at the center of the sheet. We plot in Figure 3 the thickness of this internal layer δ/L as a function of Lundquist number S for α = 1/3. The straight line through the points corresponds to the power law scaling δ/L ∼ S^−1/2, i.e., the tearing mode singular layer for the critical thickness current sheet has an aspect ratio scaling as SP. Though this might seem a coincidence at first sight, the meaning is quickly understood: because the tearing mode now has an ideal growth rate, it must be capable of locally diffusing the field in the center of the layer where the advecting velocity stagnates on an ideal time-scale. The requirement τ_D = τ_A on the scale δ then reads δ²/η_m = L/V_A or (δ/L)² = η_m/(LV_A) = 1/S, corresponding precisely to the aspect ratio of a SP current sheet.

Zoom In Zoom Out Reset image size

The "ideal tearing" instability on the critical current sheet may still be called a super-tearing or plasmoid instability; the number of islands that develop is smaller, however, than based on super-critical SP sheets, for in the latter case the number of islands scales as N ∼ S^3/8 whereas in our case from Equation (3) we have N ∼ S^1/6. Subsequent evolution of the instability leads to a turbulent picture of collapsing x-points and coalescing islands, with differences between 2D and 3D related to differing modes dominating subsequent secondary instabilities depending on the presence or absence of a guide field (Landi et al. 2008; Landi & Bettarini 2012). Very large S simulations are required to follow the complete evolution of such a system and many reconnection simulations based on the original SP sheet configuration, and corresponding parameter studies and scaling laws (Cassak & Shay 2012; Cassak & Drake 2013; Daughton & Roytershteyn 2012), most probably need to be revisited in light of the above results.

Because of the greater thickness of the a/L ∼ S^−1/3 current sheet, the "ideal" tearing mode may be triggered at least in some contexts without invoking kinetic effects. Such effects will however play a role in defining the dynamics of the internal, singular layer. Take for example the case of the solar corona, with a 100 G magnetic field, a density of around 10⁹ cm⁻³, and temperatures around 10⁶ K. For a current sheet of length L ∼ 10⁴ km, S ≃ 5 10¹³, the ratio of our critical current sheet aspect ratio to the SP aspect ratio becomes a/δ ≃ 200, so that the critical "ideally" tearing sheet would have a thickness of the order of 300 m, while its inner, singular layer, would have a thickness of 1.5 m, in between the ion skin depth (12 m) and Larmor radius (10 cm). It therefore remains to be explored whether reconnection at the onset of instability is collisionless or not.

We have shown in this Letter that in astrophysical plasma with large Lundquist numbers (i.e., S ⩾ 10⁷) there is a critical aspect ratio for current sheets at which an ideally growing tearing mode intervenes to stop further laminar thinning, and that this critical thickness can be orders of magnitude thicker than SP current sheets. The inner diffusion region of the "ideal" tearing mode on the other hand follows the SP scaling. The persistence of an "ideal" tearing mode in the limit of large Lundquist numbers provides a solution to the paradoxical nature of diverging growth rates at high S, when one knows that in ideal MHD reconnection is prohibited. The existence of an ideal growth rate in the limit of infinite S is allowed by the singular nature of the diffusive term in the induction equation. In this Letter we have studied the stability of 1D current sheet configurations, in the sense that the equilibrium sheet was a function of only one coordinate. A generalization of our scaling study to families of 2D equilibrium configurations including inflows and outflows, generalizing the SP case, would be interesting and relevant to better understand the appearance of critical Lundquist numbers. Because resistive MHD is scale-free, direct application of the "ideal tearing" result to the physics of solar and stellar coronae requires observational inputs on the characteristic length-scale of current sheet formation, for example the length of the loops involved in reconnection, and this in turn will determine the extent to which kinetic effects are relevant at the linear level.

We wish to thank Simone Landi, Bill Matthaeus, and Francesco Pegoraro for useful discussions. This work was carried out in part by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. M.V. was supported by the NASA Solar Probe Observatory Scientist grant. The research leading to these results has received funding from the European Commissions Seventh Framework Programme (FP7/2007-2013) under the grant agreement SHOCK (project number 284515).