Abstract
In this paper, using the techniques of Gauge/gravity duality we explore the hydrodynamic regime of z = 3 Lifshitz fixed points in 1 + 1 dimensions. The speed of sound in the non relativistic plasma turns out to be 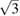 , which clearly violates the conjectured upper bound. We identify this as a natural consequence of the Lorentz symmetry breakdown at z = 3 Lifshitz fixed point. In our analysis, we compute bulk viscosity to entropy ratio for quantum field theory dual to Lifshitz gravity in 2 + 1 dimensions and it turns out that for this particular holographic model this ratio is above the conjectured lower bound.
, which clearly violates the conjectured upper bound. We identify this as a natural consequence of the Lorentz symmetry breakdown at z = 3 Lifshitz fixed point. In our analysis, we compute bulk viscosity to entropy ratio for quantum field theory dual to Lifshitz gravity in 2 + 1 dimensions and it turns out that for this particular holographic model this ratio is above the conjectured lower bound.
Export citation and abstract BibTeX RIS
1. Overview and motivation
Fluid dynamics is the low energy effective description of finite temperature QFTs perturbed from their usual thermal equilibrium by means of small fluctuations [1]. In recent times, the Gauge/gravity duality has been found to shed enough light on various key aspects of hydrodynamic transports in a strongly coupled fluid [2]. In other words, the Gauge/gravity duality provides a unique framework to explore the low frequency behavior of two point correlators between different components of the stress tensor in the strong coupling regime.
Among various remarkable outcomes of the Gauge/gravity duality, it is the existence of the sound modes in a strongly coupled plasma [3] that turns out to be the prime focus of our current analysis. It is the standard lesson of fluid dynamics which tells us that sound waves can always propagate through a finite temperature fluid medium. The information regarding the sound velocity could be extracted by knowing the poles in the expression for the retarded two point correlators between some of the components of the stress tensor [3].
The purpose of the present analysis would be to employ holographic techniques in order to compute transports, namely the bulk viscosity to entropy ratio for  dimensional QFTs dual to Lifshitz gravity in (2 + 1) dimensions. In our analysis we consider the bulk construction to be the z = 3 Lifshitz black hole solutions of new massive gravity (NMG) in (2 + 1) dimensions [4]. There are in fact several motivations behind our present analysis which we quote systematically.
dimensional QFTs dual to Lifshitz gravity in (2 + 1) dimensions. In our analysis we consider the bulk construction to be the z = 3 Lifshitz black hole solutions of new massive gravity (NMG) in (2 + 1) dimensions [4]. There are in fact several motivations behind our present analysis which we quote systematically.
- (i)Since the Lorentz symmetry is explicitly broken for the dual fluid dynamical system under consideration, therefore one should expect some natural violation of the conjectured upper bound on the speed of sound [5, 6] particularly in 1 + 1 dimensions [7]. In fact, we argue that the conjectured upper bound on the speed of sound in 1 + 1 dimensions is the consequence of the conformal invariance which might get violated in case of broken scale invariance i.e. when
 . The present calculation is a concrete example in favour of the above argument.
. The present calculation is a concrete example in favour of the above argument. - (ii)It turns out to be an interesting issue to explore the effect of genuine higher derivative (NMG) corrections on the bulk viscosity to entropy (
 ) ratio in 1 + 1 dimensions and to see whether we get a bound violation just like the case for the shear viscosity to entropy ratio [8]3. Interestingly this issue is completely unexplored for non relativistic strongly coupled fluids (particularly in lower dimensions) and the present calculation is the first non trivial example to the best of our knowledge.4
) ratio in 1 + 1 dimensions and to see whether we get a bound violation just like the case for the shear viscosity to entropy ratio [8]3. Interestingly this issue is completely unexplored for non relativistic strongly coupled fluids (particularly in lower dimensions) and the present calculation is the first non trivial example to the best of our knowledge.4 - (iii)
2. The bulk solution
We start our analysis with a brief introduction to the bulk construction, namely the Lifshitz solution in the context of NMG [13]. The corresponding action in the NMG reads as [13],
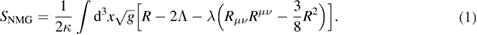
Here Λ is the cosmological constant and λ is the NMG coupling constant. The above action (1) admits a Lifshitz solution of the type [4],

where [4],

together with,

The horizon is located at  For convenience, we set l = 1 in the subsequent calculations. In our analysis the equations of motion corresponding to the hydrodynamic (spin 0) fluctuations turn out to be fourth order linear differential equations which thereby invite a completely different as well as challenging platform to compute the hydrodynamic transports for the non relativistic z = 3 plasma at strong coupling.
For convenience, we set l = 1 in the subsequent calculations. In our analysis the equations of motion corresponding to the hydrodynamic (spin 0) fluctuations turn out to be fourth order linear differential equations which thereby invite a completely different as well as challenging platform to compute the hydrodynamic transports for the non relativistic z = 3 plasma at strong coupling.
3. Thermodynamics
In this section we provide a brief discussion to the basic thermodynamic principles and/or identities which any fluid dynamical system must obey. These are the so called first law of fluid mechanics and the Euler relation [1]. Before we actually come to these issues, let us first note that the Wald entropy density (s) for the above black hole solution (2) turns out to be [14],

which also matches with [15] in the appropriate limit.
The energy density ( ) could be formally obtained by integrating over the Noether charge associated with the time like Killing symmetry
) could be formally obtained by integrating over the Noether charge associated with the time like Killing symmetry

The Hawking temperature (Th) associated with the black hole solution (2) turns out to be [4, 15],

It is now in fact a quite trivial task to check that the above entities (5)–(7) trivially satisfy the first law [1],

Next, we compute the pressure density (p) using the Euler relation [1],

Finally, using (6) and (9) the velocity of sound (vs) turns out to be

Equation (10) is precisely the speed of sound propagation from the perspective of the boundary hydrodynamics. The fact that vs > 1 should not come as a surprise since we are dealing with a non relativistic system corresponding to z = 3 fixed point where in principle there should not be any upper bound on the speed of light.
Finally, using (6) and (7) the heat capacity turns out to be,

which turns out to be positive definite. Equation (11) is an important ingredient in order to estimate the speed of sound (vs) inside a fluid medium [16].
4. Sound velocity in Lifshitz hydrodynamics
The purpose of the present section is to provide a systematic derivation of the hydrodynamic dispersion relation in the context of Lifshitz hydrodynamics and to compute the speed of sound as well as the coefficient of bulk viscosity directly from the dispersion relation itself.
In the standard framework of fluid dynamics, the velocity for sound modes are obtained by knowing the pole(s) in the expression for the retarded correlator(s) of the type 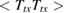 [3, 17]. As far as the current analysis is concerned, the stress tensor corresponding to the boundary non conformal fluid could be formally expressed as following [18],
[3, 17]. As far as the current analysis is concerned, the stress tensor corresponding to the boundary non conformal fluid could be formally expressed as following [18],

where  (for the present case) is the 2-velocity of the fluid satisfying
(for the present case) is the 2-velocity of the fluid satisfying  and ζ is the coefficient of bulk viscosity which appears as a consequence of the broken conformal invariance in the boundary theory. At this stage it is noteworthy to mention that for uncharged Lifshitz fluids in general there exist two transport coefficients (at the level of first order viscous hydrodynamics) namely the coefficient of bulk viscosity (
and ζ is the coefficient of bulk viscosity which appears as a consequence of the broken conformal invariance in the boundary theory. At this stage it is noteworthy to mention that for uncharged Lifshitz fluids in general there exist two transport coefficients (at the level of first order viscous hydrodynamics) namely the coefficient of bulk viscosity ( ) and an additional transport α that comes from the antisymmetric part of (12) which could be formally expressed as [18],
) and an additional transport α that comes from the antisymmetric part of (12) which could be formally expressed as [18],

This additional transport appears due to the broken Lorentz boost invariance at a Lifshitz fixed point.
In order to find pole(s) in the expression for the retarded correlator(s), we first perturb the fluid in its rest frame as [7],
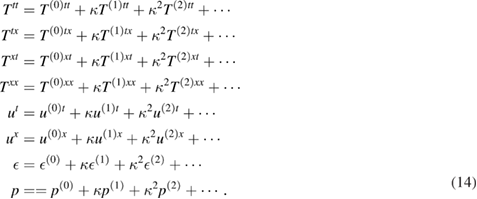
We have expanded all the quantities order by order in fluctuations around their respective equilibrium values. κ denotes the perturbation parameter. In our analysis we keep only linear order terms in the fluctuations i.e. only terms 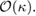 Also
Also 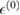 and p(0) denote the zeroth order energy density and pressure and independent of x and t.
and p(0) denote the zeroth order energy density and pressure and independent of x and t.
Due to the presence of the constraint,  , one could show that,
, one could show that,
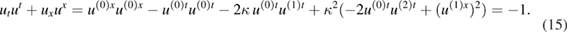
Since we are expanding around a static equilibrium solution, therefore we can fix, u(0)t = 1 and u(0)x = 0 and it follows,

So upto  we have
we have 
Next we concentrate on the anti-symmetric part of (12). Using (14) we get,

where we have neglected 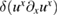 and
and  as these terms are second order in fluctuations (
as these terms are second order in fluctuations (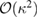 ).
).
From (14) we note,

which could be further expressed as keeping only linear order terms,
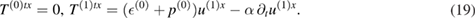
Proceeding in the same way we get,

which solves u(1)x as,

Next we simplify(19) further which finally yields,
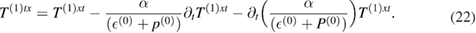
Notice that when  we get
we get 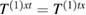 and which is thereby consistent. The last term vanishes as the derivative of the
and which is thereby consistent. The last term vanishes as the derivative of the  and p(0) vanish. So,
and p(0) vanish. So,
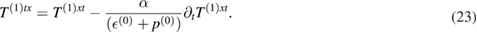
Furthermore, we can also write down the following two equations namely using the same logic,
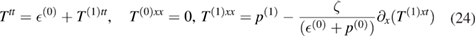
where we have used (21) to eliminate u(1)x. Note that, here we have neglected all the derivatives of the thermodynamical quantities in (23) and (24) as they are themselves first order in the fluctuations and thereby contribute at the level of second order in the fluctuations.
Next, we plug all these in the conservation equations which yields,

and

We have used the fact that  The zeroth order variation of energy is zero.
The zeroth order variation of energy is zero.
Then following [7] from (25) we obtain,
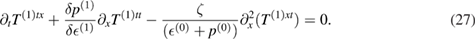
We have used the fact  and used the chain rule.
and used the chain rule.
In the next step, using (23) we first replace T(1)tx in (27) and then take the Fourier transform of the above set of equations (25) and (26) which finally yields,
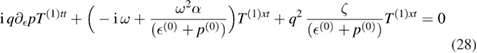
and

Using (29) one can replace T(1)tt in (28) to obtain,

So we have,
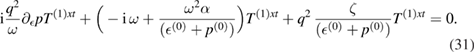
We futher simplify to obtain,
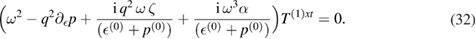
Our next task would be to solve this equation for the frequency ω perturbatively upto  , where q is the spatial momentum. For this we make the following ansatz for ω in terms of q to get the dispersion relation of the following form,
, where q is the spatial momentum. For this we make the following ansatz for ω in terms of q to get the dispersion relation of the following form,

We plug this into (32) and match the coefficients of q2 term to obtain,

which is the speed of sound in the (Lifshitz) fluid medium. Next, we match the coefficients of q2 terms in order to obtain the damping constant,

Finally, using the so called Euler relation,

one can in fact express (33) in a more sophisticated form as,

which immediately suggests that for Lifshitz like fluids one should be able to define an effective bulk viscosity  as,
as,

such that,

Equation (38) is one of the major observations of the present paper. It immediately suggests that for Lifshitz like fluids the effective value of the bulk viscosity is enhanced due to the broken Lorentz invariance. Therefore, it also confirms the fact that the bulk viscosity to entropy ratio ( ) for Lifshitz like systems should also be above the conjectured lower bound [7]. Our goal for the next section would be to compute this from the gravity calculations in the bulk, where we will consider a particular model of z = 3 Lifshitz black holes in (2 + 1) dimensions [4].
) for Lifshitz like systems should also be above the conjectured lower bound [7]. Our goal for the next section would be to compute this from the gravity calculations in the bulk, where we will consider a particular model of z = 3 Lifshitz black holes in (2 + 1) dimensions [4].
5. Dispersion relation and holography
The first step towards computing the holographic sound modes is to turn on the following (with respect to boundary rotational symmetry) perturbations in the bulk namely [3],

where we have fixed the gauge  . This gauge fixing does not fully exhaust all the gauge freedoms of the full theory and one is still left with the residual gauge freedom under the diffeomorphism
. This gauge fixing does not fully exhaust all the gauge freedoms of the full theory and one is still left with the residual gauge freedom under the diffeomorphism 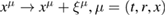 . As a consequence of this the equations of motion corresponding to the above fluctuations exhibit residual gauge and/or diffeomorphism invariance (
. As a consequence of this the equations of motion corresponding to the above fluctuations exhibit residual gauge and/or diffeomorphism invariance ( ) [3]. As a result the most general gauge invariant fluctuation turns out to be,
) [3]. As a result the most general gauge invariant fluctuation turns out to be,
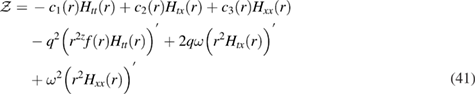
where the individual coefficients (ci) turn out to be,
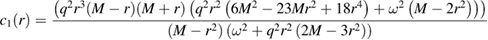
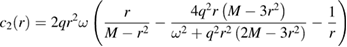
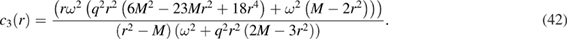
In order to arrive at (41) we have used the following metric redefinitions namely,

Note that here prime denotes derivative with respect to the radial coordinate (r).
Using the linearized equations of motion of individual scalar perturbations, it is indeed quite interesting to note that unlike the previous examples in the literature [3], the gauge invariant combination (41) satisfies a sixth order linear differential equation of the type,
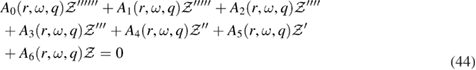
where details of the coefficients (Ai) are too cumbersome and not quite illuminating. However, in the following we explain in details how one could in principle arrive an equation of the above type (44). Using (41), we first take a linear combination of various powers of derivatives of  (with some arbitrary coefficients Ai(r)) starting from the sixth derivative level. This will contain derivatives of various powers of H's. Now one uses the equations of motion for H's and replace all the higher order derivatives in terms of lower order derivatives. Finally, we end up an equation which contain three second order derivatives in the metric, two first order derivatives in the metric and three metric coefficients with zero derivative level. All of these (altogether) seven different metric components and their derivatives will be associated with some specific combination of the coefficients Ai's. Each of those combinations has to vanish in order to satisfy (44) which yield seven algebraic relations for Ai's that determine them uniquely.
(with some arbitrary coefficients Ai(r)) starting from the sixth derivative level. This will contain derivatives of various powers of H's. Now one uses the equations of motion for H's and replace all the higher order derivatives in terms of lower order derivatives. Finally, we end up an equation which contain three second order derivatives in the metric, two first order derivatives in the metric and three metric coefficients with zero derivative level. All of these (altogether) seven different metric components and their derivatives will be associated with some specific combination of the coefficients Ai's. Each of those combinations has to vanish in order to satisfy (44) which yield seven algebraic relations for Ai's that determine them uniquely.
Next, we explore (44) in two asymptotic regions namely, near the boundary ( ) of the spacetime and at the horizon (r = rh = 1). We first consider the following ansatz for
) of the spacetime and at the horizon (r = rh = 1). We first consider the following ansatz for 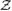 ,
,

Considering the near horizon expansion and considering the ingoing wave boundary condition [3], the parameter α could be read off as,

Next, considering the large r limit we expand  in the frequency (
in the frequency (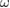 ) as well as in the momentum (q),
) as well as in the momentum (q),
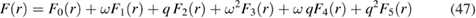
and extract the finite piece in the limit  . Keeping those finite pieces intact and considering the asymptotic normalization condition [3],
. Keeping those finite pieces intact and considering the asymptotic normalization condition [3],

we get the following quadratic equation for ω,
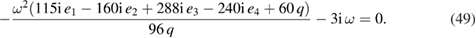
Solving (49) equation upto  we finally arrive at the cherished dispersion relation of the following form,
we finally arrive at the cherished dispersion relation of the following form,

where,
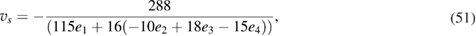
and
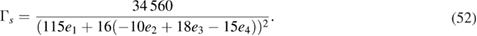
 and e4 are the four left over integrating constants. Combining (51) and (52) it is evident that5,
and e4 are the four left over integrating constants. Combining (51) and (52) it is evident that5,

So this suggest that  and vs are not independent.
and vs are not independent.
As the gauge invariant combination satisfies a six order differential equation (44) and there are in fact two boundary conditions namely, the in going wave boundary condition and the asymptotic boundary condition (48), therefore in principle we can uniquely fix two of the six unknown coefficients. Therefore, finally we are left with four undetermined constants those appear above in the expressions for vs and  . Next, we compare (50) with the dispersion relation previously obtained in (33). In (33) we have identified
. Next, we compare (50) with the dispersion relation previously obtained in (33). In (33) we have identified  as the speed of sound which is computed in (10) using the gravity solution. So equating (51) and (10) one can uniquely fix the combination of the remaining four constants as,
as the speed of sound which is computed in (10) using the gravity solution. So equating (51) and (10) one can uniquely fix the combination of the remaining four constants as,
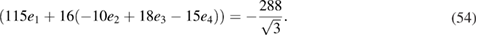
Surprisingly once this special combination of four integrating constants get (uniquely) fixed one can uniquely calculate the 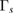 . Using (52) and (54) we finally obtain,
. Using (52) and (54) we finally obtain,

which finally yields,
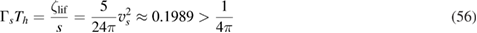
which clearly seems to preserve the conjectured lower bound [7] as we expected from our analysis in the previous section.
6. Summary and final remarks
Let us now summarize the key findings of our analysis. The present analysis has two major outcomes. The first observation tells us that for this particular holographic model under consideration the speed of sound propagation (vs) inside a z = 3 strongly coupled plasma in 1 + 1 dimensions clearly exceeds the conjectured upper bound. This observation is not surprising in the context of non relativistic hydrodynamics where the Lorentz boost symmetry is explicitly broken near the UV fixed point of the theory. We further use this value of vs obtained in (10) to show that the  which is above the conjectured lower bound [7]. But we should also note that, since
which is above the conjectured lower bound [7]. But we should also note that, since  and vs are not independent variables as shown in (53), indicating that the holographic setup considered here may not be the most general, therefore in the present calculation the value of
and vs are not independent variables as shown in (53), indicating that the holographic setup considered here may not be the most general, therefore in the present calculation the value of 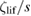 is constrained by the corresponding value of vs. The holographic calculations provide us some exact value for this ratio which for our present gravity set up turns out to be approximately 0.1989.
is constrained by the corresponding value of vs. The holographic calculations provide us some exact value for this ratio which for our present gravity set up turns out to be approximately 0.1989.
Acknowledgments
Authors acknowledge Aninda Sinha and Justin David for useful discussions. We also thank our anonymous referees for valuable comments on the manuscript. DR was supported through the Newton-Bhahba Fund and he would like to acknowledge the Royal Society UK and the Science and Engineering Research Board India (SERB) for financial assistance. AB acknowledges support form JSPS fellowship (P17023) and Yukawa Institute of Theoretical Physics.
Footnotes
- 3
Dual CFT may or may not be a unitary one. It is most likely a non-relativistic verison of logarithimic CFT as shown in [9]. This kind of CFT's is also interesting though sometimes there are problems regarding unitarity as the central charge takes negative value. But still these CFT's have many applications as interesting mathematical models as a well as describing some condensed matter systems away from unitarity [10]4. In this paper we are actually making a prediction about the hydrodynamic transport of these non-relativistic logarithmic CFT's using the AdS/CFT dictionary for the first time.
- 4
For example interested readers are referred to these references and the references there in see [10].
- 5
We thank anonymous referee for pointing this out to us.



