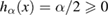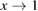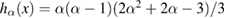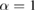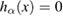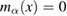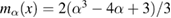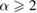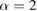Abstract
In an article in 2010, Kim et al introduced the definition of Rényi-α entanglement for bipartite quantum states and established an analytic formula of Rényi-α entanglement for arbitrary two-qubit states with  . They also derived a monogamy of entanglement in multi-qubit systems in terms of Rényi-α entanglement for
. They also derived a monogamy of entanglement in multi-qubit systems in terms of Rényi-α entanglement for 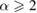 Kim et al (2010 J. Phys. A: Math. Theor. 43 445305). We find the proofs of theorems 2 and 3 contain some errors and we also present an improved derivation to overcome this flaw. The alternative derivation shows that the main conclusions remain valid despite the invalidity of the proofs.
Kim et al (2010 J. Phys. A: Math. Theor. 43 445305). We find the proofs of theorems 2 and 3 contain some errors and we also present an improved derivation to overcome this flaw. The alternative derivation shows that the main conclusions remain valid despite the invalidity of the proofs.
Export citation and abstract BibTeX RIS
In 2010, Kim et al [1] introduced the concept of Rényi-α entanglement as a generalization of the entanglement of formation, and it reduces to the standard entanglement of formation when α tends to 1 [1, 2]. Recently, it has been proved [3] that the squared Rényi-α entanglement obeys a general monogamy inequality in an arbitrary N-qubit mixed state. Correspondingly, we can construct the multipartite entanglement indicators in terms of Rényi-α entanglement which still work well even when the indicators based on the concurrence and entanglement of formation lose their efficacy. In [1] Kim et al first derived an analytic formula for the bipartite entanglement measure based on Rényi-α entanglement in two-qubit systems for  . Based on this analytic formula, they further established the monogamy inequalities of multi-qubit entanglement in terms of Rényi-α entanglement for all
. Based on this analytic formula, they further established the monogamy inequalities of multi-qubit entanglement in terms of Rényi-α entanglement for all 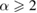 . In [1] theorems 2 and 3 are fundamental results in establishing the monogamy inequalities in terms of Rényi-α entanglement. However, we find the proofs of theorems 2 and 3 contain some errors and we also present an alternative derivation to overcome this flaw. It is shown that the main conclusions remain unchanged despite the invalidity of the proofs of theorems 2 and 3.
. In [1] theorems 2 and 3 are fundamental results in establishing the monogamy inequalities in terms of Rényi-α entanglement. However, we find the proofs of theorems 2 and 3 contain some errors and we also present an alternative derivation to overcome this flaw. It is shown that the main conclusions remain unchanged despite the invalidity of the proofs of theorems 2 and 3.
During the proof of theorem 2 in [1], the author claim that equation (35) holds for any 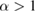 due to equation (33) in [1]. However, this derivation is incorrect because equation 33 does not hold for any
due to equation (33) in [1]. However, this derivation is incorrect because equation 33 does not hold for any 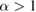 . Notice that the binomial series for
. Notice that the binomial series for 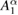 and
and  are given by
are given by
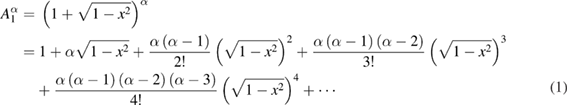
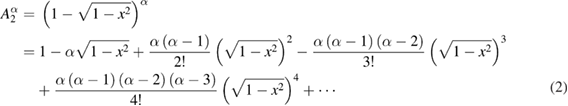
and thus


In the limit of 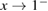 , C1 and C2 can be written as
, C1 and C2 can be written as 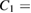
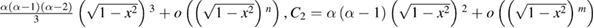 with
with 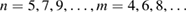 . It is obviously that C1 is non-negative under the condition
. It is obviously that C1 is non-negative under the condition 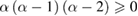 , and C2 is non-negative under the condition
, and C2 is non-negative under the condition 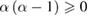 . Thus we conclude that equation (35) in [1] does not hold for
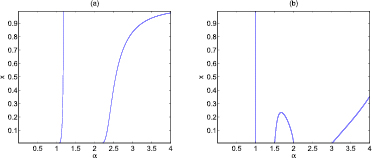
. Thus we conclude that equation (35) in [1] does not hold for 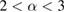 since C1 is a negative value in this case. Correspondingly, theorem 2 cannot be proved using the method in [1]. Furthermore, it is shown in figure 1 that
since C1 is a negative value in this case. Correspondingly, theorem 2 cannot be proved using the method in [1]. Furthermore, it is shown in figure 1 that 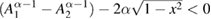 for
for  . For
. For 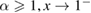 , we have
, we have
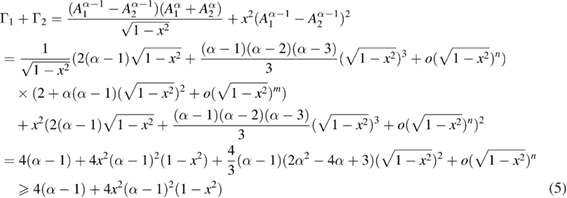
where 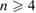 . Thus we have
. Thus we have
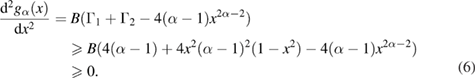
Figure 1. The plot of 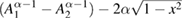 as a function of α and x for
as a function of α and x for  .
.
Download figure:
Standard image High-resolution imageBelow we present a strict proof to show that  is non-negative and we summarize our result as the following lemma.
is non-negative and we summarize our result as the following lemma.
Lemma 1. The second-order derivative of 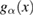 is a non-negative function for
is a non-negative function for 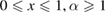 .
.
Proof. We first define a function 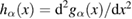 on the domain
on the domain  . For the proof of the non-negativity of
. For the proof of the non-negativity of  , it is sufficient to analyze its maximal or minimal value on the domain
, it is sufficient to analyze its maximal or minimal value on the domain  . The critical points of
. The critical points of  satisfy the condition
satisfy the condition

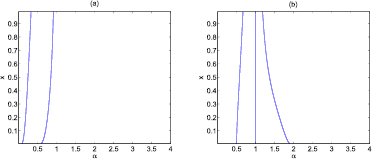
In figures 2(a) and (b) we plot the solution to equations 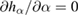 and
and 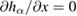 , respectively. We can see clearly from figure 2 that they have no common solutions on the domain
, respectively. We can see clearly from figure 2 that they have no common solutions on the domain 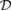 . Therefore, there are no critical points on the domain
. Therefore, there are no critical points on the domain 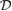 and the maximal or minimal value of
and the maximal or minimal value of 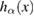 can arise only on the boundary of
can arise only on the boundary of 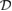 . Next, we consider the function value of
. Next, we consider the function value of 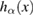 on the boundaries of
on the boundaries of 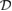 and we divide the proof into the following cases.
and we divide the proof into the following cases.
- Case 1.When x = 0, we have
 .
. - Case 2.When
 , we have
, we have  which is always a non-negative monotonically increasing function of α for
which is always a non-negative monotonically increasing function of α for  .
. - Case 3.When
 , we have
, we have  .Combining the above results, we have complete the proof of the lemma. □
.Combining the above results, we have complete the proof of the lemma. □
Figure 2. The plots of the equations (a) 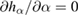 ; (b)
; (b) 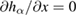 for
for  .
.
Download figure:
Standard image High-resolution imageSimilarly, the proof of theorem 3 in [1] is also incorrect because equation 49 does not hold for 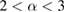 as shown in figure 1. Thus the proof of theorem 3 in [1] is incorrect for all
as shown in figure 1. Thus the proof of theorem 3 in [1] is incorrect for all 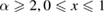 . For the proof of the non-negative of the first-order derivative of
. For the proof of the non-negative of the first-order derivative of  defined in [1], we first consider the following function in the limit of
defined in [1], we first consider the following function in the limit of 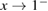 . According to equation (1) and (2), we have
. According to equation (1) and (2), we have
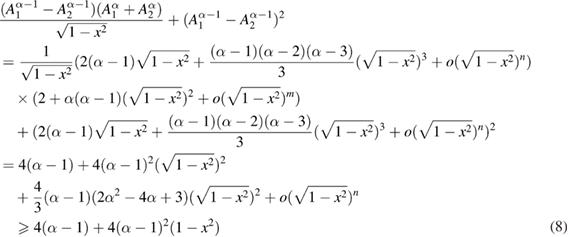
with  . Then we can prove that
. Then we can prove that
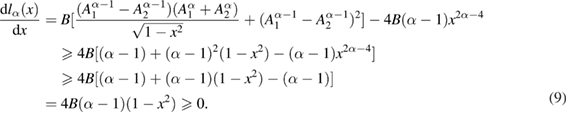
In order to prove that  for whole
for whole  , we define a two-variable function
, we define a two-variable function 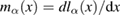 on the domain
on the domain  . The critical points of
. The critical points of 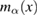 satisfy the condition
satisfy the condition  . It is shown in figures 3(a) and (b) that they have no common solutions on the domain
. It is shown in figures 3(a) and (b) that they have no common solutions on the domain  which indicate that
which indicate that 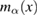 has no critical points on the domain
has no critical points on the domain 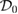 . Then we consider the value of
. Then we consider the value of 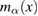 on the boundary of
on the boundary of 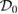 .
.
- Case 1.When x = 0, we have
 .
. - Case 2.When
 , we have
, we have  which is always a positive monotonically increasing function of α for
which is always a positive monotonically increasing function of α for  .
. - Case 3.When
 , we have
, we have  for
for  .
.
Figure 3. The plots of the equations (a) 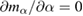 ; (b)
; (b) 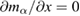 for
for 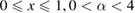 .
.
Download figure:
Standard image High-resolution imageThus we have proved that  on the domain
on the domain  , and we can complete the proof of theorem 3 with a similar procedure as Kim et al in [1].
, and we can complete the proof of theorem 3 with a similar procedure as Kim et al in [1].
We should note that the present manuscript concern different topics with [5] although their errors both come from the incorrect binomial series. [1] is mainly focused on the monogamy relation of multi-qubit systems while [4] is focused on the polygamy property. Furthermore, lemma 2 in [4] is not a generalization of theorem 3 in [1] and the details of the proofs are different. Correspondingly, their results imply different physical meanings since monogamy and polygamy properties are different kinds of entanglement constraint in multi-qubit systems.
In conclusion, we have pointed out that the proof of theorems 2 and 3 in [1] contain some errors and we also present an improved method to overcome this flaw. It should be stressed that the main conclusions of the original paper [1] remains unchanged.
Acknowledgments
This work was supported by the Anhui Provincial Natural Science Foundation under Grant Nos 1708085MA12, 1708085MA10, the Key Program of the Education Department of Anhui Province under Grant Nos KJ2016A583, KJ2017A922, the discipline top-notch talents Foundation of Anhui Provincial Universities under Grants Nos gxbjZD2017024, gxbjZD2016078, the Key Program for Excellent Young Talents in the University of Anhui Province No gxyqZD2016206.