Abstract
Akin to electron spin, the valley has become another highly valued degree of freedom in modern electronics, specifically after tremendous studies on monolayers of group-IV materials, i.e. graphene, silicene, germanene and stanene. Except for graphene, the other heavy group-IV monolayers have observable intrinsic spin–orbit interactions due to their buckled structures. Distinct from the usual electric or optical control of valley and spin, we here employ a temperature difference to drive electron motion in ferromagnetic heavy group-IV monolayers via designing a caloritronic device locally modulated by an interlayer electric (Ez) field. A unique valley–spin Seebeck (VSS) effect is discovered, with the current contributed only by one (the other) valley and one (the other) spin moving along one (the opposite) direction. This effect is suggested to be detected below the critical temperature about 18 K for silicene, 200 K for germanene and 400 K for stanene, arising from the characteristic valley–spin nondegenerate band structures tuned by the Ez field, but cannot be driven in graphene without spin–orbit interaction. Above the critical temperature, the VSS effect is broken by overlarge temperature broadening. Besides the temperature, it is also found that the Ez field can drive a transition between the VSS effect and the normal spin Seebeck effect. Further calculations indicate that the VSS effect is robust against many realistic perturbations. Our research represents a conceptually but substantially major step towards the study of the Seebeck effect. These findings provide a platform for encoding information simultaneously by the valley and spin quantum numbers of electrons in future thermal-logic circuits and energy-saving devices.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The study of Dirac electrons, as inspired by the rise of graphene since its fabrication in 2004, has made fruitful achievements in the most recent decade [1–5]. Particularly, two-dimensional (2D) heavy group-IV materials as graphene-like materials, including silicene, germanene and stanene, have attracted considerable research in the last five years owing to their controllable Dirac nature [6–14]. Distinct from graphene, electrons in the other 2D heavy group-IV monolayers have an observable intrinsic spin–orbit interaction because of their buckled structures [9–11, 15]. Significantly, the low-energy Dirac electrons in these materials can feel multiple degrees of freedom, involving charge, spin, valley and sublattice-pseudospin. Here, the 'valley' benefits from the fact that the Dirac electrons locate around two inequivalent points in the first Brillouin region. Up to now, many spin–valley related phenomena have been explored theoretically in heavy group-IV monolayers, such as the high-temperature quantum spin Hall effect [6], valley-polarized quantum anomalous Hall effect [11], topological superconducting effect [13], spin–valley filtering effect [16–18] and bipolar spin–valley diode effect [19]. Any of these predictions, if verified in experiment, can provide giant opportunities not only for the development of physics and material science but also for future technology applications.
To control the valley and spin in 2D Dirac materials, people usually adopt electric and optical methods to obtain valley-polarized or spin-polarized detectable effects [20–28], whereas only limited work has utilized the temperature difference to understand the valley Seebeck effect [29, 30] or spin Seebeck effect [31–34], which can explore the possibility of directly converting heat into electrical power. Phenomenologically, the valley (spin) Seebeck effect indicates currents from two different valleys (spins) flowing in opposite directions. Experimentally, based on the magnon-driven or phonon-dragged mechanisms [35–38], great progress has recently been made in detecting the spin Seebeck effect, in magnetic materials NiFe [39], GaMnAs [40], LaY3Fe5O12 [41] and MnF2 [42] as well as non-magnetic metal InSb [43]. With attention to the recent valley–spin related experiments in graphene [44–47], there is reason to believe that the valley Seebeck effect or spin Seebeck effect should also be observed in 2D heavy group-IV materials.
In spite of many previous findings related to spin and valley, we notice that no one has ever proved whether the spin Seebeck effect and valley Seebeck effect could coexist in a real condensed-matter system. By studying the temperature-driven valley–spin transport in a designed ferromagnetic device locally modulated by an interlayer electric (Ez) field, we here discover a unique phenomenon we call the valley–spin Seebeck (VSS) effect, for which the current is contributed only by one (the other) valley and one (the other) spin moving along one (the opposite) direction. This effect surely reflects the coexistence of the spin Seebeck effect and valley Seebeck effect, and is suggested to be detected below the critical temperature 18 K for silicene, 200 K for germanene and 400 K for stanene, attributed to the specific valley–spin nondegenerate band structures, but cannot be driven in graphene without spin–orbit interaction. Above the critical temperature, the VSS effect disappears because of overlarge source-temperature broadening, independent of temperature difference. Besides the temperature, the VSS effect can also be turned on and off by the Ez field. It is further demonstrated that the VSS effect is robust against many realistic perturbations. Our findings pave the way for 2D heavy group-IV materials applied in future thermal-logic circuits and energy-saving devices.
2. Design principle for the valley–spin Seebeck effect
For any temperature-driven caloritronic device, two heat reservoirs are requisite: one is a high-temperature source (S), the other is a low-temperature drain (D). We here use  to describe the temperature of S (D). We define the direction of the current from S to D as positive. Because electrons in heavy group-IV monolayers have valley and spin degrees of freedom, the current should be valley–spin dependent. Below we use
to describe the temperature of S (D). We define the direction of the current from S to D as positive. Because electrons in heavy group-IV monolayers have valley and spin degrees of freedom, the current should be valley–spin dependent. Below we use  to denote the valley (spin) index. According to the generalized Laudauer–Büttiker approach [18, 29–32], the current driven by temperature difference
to denote the valley (spin) index. According to the generalized Laudauer–Büttiker approach [18, 29–32], the current driven by temperature difference  can be expressed as
can be expressed as

where  C is the electron charge, h is Planck's constant,
C is the electron charge, h is Planck's constant,  denotes the Fermi–Dirac distribution function and satisfies
denotes the Fermi–Dirac distribution function and satisfies ![${f}_{{\rm{S}}({\rm{D}})}(\varepsilon ,{T}_{{\rm{S}}({\rm{D}})})=1/[\exp (\varepsilon -{\varepsilon }_{{\rm{F}}})/{k}_{B}{T}_{{\rm{S}}({\rm{D}})}+1]$](https://content.cld.iop.org/journals/1367-2630/19/6/063007/revision2/njpaa6d37ieqn6.gif) .
.  represents the number of valley–spin dependent transmission modes, depending on the detailed device structure. Because silicene, germanene and stanene are semiconductors with small spin–orbit band gaps less than 0.2 eV, the temperature primarily plays the role of exciting thermoelectrons here [31–33], different from that of exciting magnons in ferromagnetic insulators [41]. From the distribution difference
represents the number of valley–spin dependent transmission modes, depending on the detailed device structure. Because silicene, germanene and stanene are semiconductors with small spin–orbit band gaps less than 0.2 eV, the temperature primarily plays the role of exciting thermoelectrons here [31–33], different from that of exciting magnons in ferromagnetic insulators [41]. From the distribution difference  in equation (1), we judge that electrons with energy higher than the Fermi energy
in equation (1), we judge that electrons with energy higher than the Fermi energy  flow from S to D on account of
flow from S to D on account of  , resulting in electron current
, resulting in electron current  . Conversely, electrons with energy lower than
. Conversely, electrons with energy lower than  flow from D to S as a result of
flow from D to S as a result of  , leading to hole current
, leading to hole current  . A specific case is that, if
. A specific case is that, if  is symmetric about the Fermi energy, the electron current and the hole current will cancel out each other, leading to no net current, i.e.
is symmetric about the Fermi energy, the electron current and the hole current will cancel out each other, leading to no net current, i.e.  . This happens in undoped pristine graphene and its derivatives with electron–hole symmetry.
. This happens in undoped pristine graphene and its derivatives with electron–hole symmetry.
To create electron–hole asymmetry near the Fermi energy it is a necessary condition to generate nonzero current, but needs to far from enough to effectively drive the VSS effect in heavy group-IV monolayers. Based on band theory, we conclude that the detailed form of  in equation (1) depends on the band-to-band tunneling mechanism, and dictates whether the valley or spin Seebeck effect happens. On the one hand, to drive the normal spin Seebeck (NSS) effect, the transmission should be electron-dominated for one spin but hole-dominated for the other spin. This requires that the band structure near the Fermi energy must be nondegenerate for two spins besides electron–hole asymmetry. This is relatively easy to realize in the ferromagnetic state of semiconductors [10, 19, 31]. On the other hand, to generate the valley Seebeck effect, one must ensure that the transmission near the Fermi energy is electron-dominated for one valley but hole-dominated for the other valley [29, 30]. This condition cannot be satisfied in a sample of silicene, germanene or stanene only in the presence of the Ez field, although the band structure is both valley-polarized and spin-polarized [10]. Conceivably, to realize the VSS effect, the transmission should be electron-dominated for one spin in one valley but hole-dominated for the other spin in the other valley. In this case, there might exist a particular energy region, inside which one valley is insulating for two spins but the other valley is conductive for only one spin. Luckily, we notice that, for heavy group-IV monolayers, the coexistence of ferromagnetic field and Ez field could satisfy this criterion [29]. Additionally, to observe the VSS effect, the energy broadening induced by the source temperature cannot exceed the particular insulating region for two spins, or otherwise the deep-energy bands outside the band gap can break the transport feature of the VSS effect.
in equation (1) depends on the band-to-band tunneling mechanism, and dictates whether the valley or spin Seebeck effect happens. On the one hand, to drive the normal spin Seebeck (NSS) effect, the transmission should be electron-dominated for one spin but hole-dominated for the other spin. This requires that the band structure near the Fermi energy must be nondegenerate for two spins besides electron–hole asymmetry. This is relatively easy to realize in the ferromagnetic state of semiconductors [10, 19, 31]. On the other hand, to generate the valley Seebeck effect, one must ensure that the transmission near the Fermi energy is electron-dominated for one valley but hole-dominated for the other valley [29, 30]. This condition cannot be satisfied in a sample of silicene, germanene or stanene only in the presence of the Ez field, although the band structure is both valley-polarized and spin-polarized [10]. Conceivably, to realize the VSS effect, the transmission should be electron-dominated for one spin in one valley but hole-dominated for the other spin in the other valley. In this case, there might exist a particular energy region, inside which one valley is insulating for two spins but the other valley is conductive for only one spin. Luckily, we notice that, for heavy group-IV monolayers, the coexistence of ferromagnetic field and Ez field could satisfy this criterion [29]. Additionally, to observe the VSS effect, the energy broadening induced by the source temperature cannot exceed the particular insulating region for two spins, or otherwise the deep-energy bands outside the band gap can break the transport feature of the VSS effect.
Here, we need to make clear how to obtain the transmission modes  in equation (1). For simplicity, the reduced Planck constant ℏ is set as 1, and the Fermi velocity
in equation (1). For simplicity, the reduced Planck constant ℏ is set as 1, and the Fermi velocity  (
( m s−1 for silicene,
m s−1 for silicene,  m s−1 for germanene,
m s−1 for germanene,  m s−1 for stanene [10, 15]) is set as 1. For a sample of width W, the total transmission modes are generally obtained by [19, 29]
m s−1 for stanene [10, 15]) is set as 1. For a sample of width W, the total transmission modes are generally obtained by [19, 29]
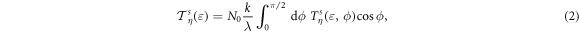
where k, ϕ are the modulus and angle of the wave-vector,  represents the reduced constant with the dimension of density of states, and
represents the reduced constant with the dimension of density of states, and  describes the angle-dependent transmission for each mode. Then the spin–valley dependent current is calculated from equation (1) as
describes the angle-dependent transmission for each mode. Then the spin–valley dependent current is calculated from equation (1) as
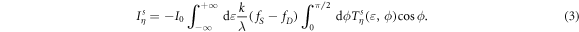
where the constant  is used as the reduced value of
is used as the reduced value of  .
.
3. Realization of the valley–spin Seebeck effect
At the top of figure 1(a), we show our proposed caloritronic field effect transistor device, including S, D and G (the central gate region controlled by an Ez field). A ferromagnetic field with strength M is uniformly applied in the whole sample. From previous first-principles calculations, it is known that the low-energy electrons in heavy group-IV monolayers can be described by an effective Hamiltonian which reads 
 [20–23], where λ (3.9 meV for silicene, 43 meV for germanene, 100 meV for stanene) represents the spin–orbit coupling,
[20–23], where λ (3.9 meV for silicene, 43 meV for germanene, 100 meV for stanene) represents the spin–orbit coupling,  labels valley
labels valley  , and
, and  ,
,  (
( ) describe the Pauli matrices of sublattice pseudospin and electron real-spin respectively. Although Rashba-type spin–orbit couplings as perturbations in these heavy group-IV monolayers exist in principle, they play little role even under external fields in studying the band structures and transport properties [6, 10]. Thus the low-energy effective Hamiltonian here can be expressed as
) describe the Pauli matrices of sublattice pseudospin and electron real-spin respectively. Although Rashba-type spin–orbit couplings as perturbations in these heavy group-IV monolayers exist in principle, they play little role even under external fields in studying the band structures and transport properties [6, 10]. Thus the low-energy effective Hamiltonian here can be expressed as
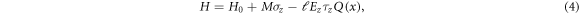
where the second term indicates the ferromagnetic field, the third term represents the Ez field with  . Herein,
. Herein,  is the Heaviside function, and ℓ denotes the interlayer distance. After matrix diagonalization, the energy bands are solved as
is the Heaviside function, and ℓ denotes the interlayer distance. After matrix diagonalization, the energy bands are solved as
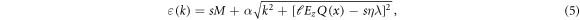
The energies at valleys  (k = 0) read
(k = 0) read  . In regions S and D, it is found that the transport-forbidden regions for spin-up and spin-down electronic states read, respectively,
. In regions S and D, it is found that the transport-forbidden regions for spin-up and spin-down electronic states read, respectively,  and
and  , identical for two different valleys. In region G, the valley degeneracy is destroyed by locally applying
, identical for two different valleys. In region G, the valley degeneracy is destroyed by locally applying  , and the band gap regions for spin-up and spin-down bands are obtained, respectively, as
, and the band gap regions for spin-up and spin-down bands are obtained, respectively, as  and
and  . The mutual insulating region for two spins is
. The mutual insulating region for two spins is  if it exists. The energy bands for S, D and G, at
if it exists. The energy bands for S, D and G, at  and
and  , are shown at the bottom of figure 1(a). There are two factors that lead to the forbidden transmission: (i) spin–valley dependent band gaps provided by S, D and G, (ii) spin mismatch between S, D and G. The shaded regions
, are shown at the bottom of figure 1(a). There are two factors that lead to the forbidden transmission: (i) spin–valley dependent band gaps provided by S, D and G, (ii) spin mismatch between S, D and G. The shaded regions  are just the mutual insulating regions for two spins to drive the VSS effect, and the bands in region G are electron-dominated for one spin in one valley but hole-dominated for the other spin in the other valley.
are just the mutual insulating regions for two spins to drive the VSS effect, and the bands in region G are electron-dominated for one spin in one valley but hole-dominated for the other spin in the other valley.
Figure 1. (a) Top: overhead view of our proposed caloritronic FET device, where the valley–spin Seebeck (VSS) effect is illustrated. The device is constructed from the left source (S) with higher temperature  , the right drain (D) with lower temperature
, the right drain (D) with lower temperature  , and the central gate region (G) where the Ez field can be tuned by dual gates. Bottom: band-matching mechanism for the VSS effect at
, and the central gate region (G) where the Ez field can be tuned by dual gates. Bottom: band-matching mechanism for the VSS effect at  . The shaded regions indicate the mutual transport gaps for two spins. (b)–(d) Current
. The shaded regions indicate the mutual transport gaps for two spins. (b)–(d) Current  versus
versus  for silicene, germanene and stanene, respectively, at
for silicene, germanene and stanene, respectively, at  . Two different phases are denoted, including phase I-VSS and phase II-NSS (normal spin Seebeck effect). The temperature difference is fixed at
. Two different phases are denoted, including phase I-VSS and phase II-NSS (normal spin Seebeck effect). The temperature difference is fixed at  K, except for the inset in figure (b) where
K, except for the inset in figure (b) where  K.
K.
Download figure:
Standard image High-resolution imageTo obtain information on  , it is still needed to solve
, it is still needed to solve  in equation (3). Based on quantum mechanics, we derive the transmission amplitude by matching the wave functions at the interfaces
in equation (3). Based on quantum mechanics, we derive the transmission amplitude by matching the wave functions at the interfaces  as
as
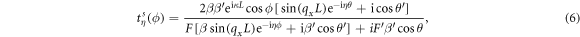
where  ,
,  ,
,  ,
,  . The wave-vector modulus in regions S, D and G are obtained respectively as
. The wave-vector modulus in regions S, D and G are obtained respectively as  ,
,  . The angular dependent functions F,
. The angular dependent functions F,  are obtained as
are obtained as  where
where  and
and  . The transmission coefficient in equation (1) is then given by
. The transmission coefficient in equation (1) is then given by
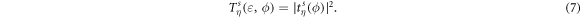
Note that, for uniformity, the parameters  and L = 50 nm are used below to carry out the calculations and plot figures without special instructions.
and L = 50 nm are used below to carry out the calculations and plot figures without special instructions.
In figures 1(b)–(d), we plot the current  versus the source temperature
versus the source temperature  for silicene, germanene and stanene, respectively, at
for silicene, germanene and stanene, respectively, at  . The temperature difference is fixed at
. The temperature difference is fixed at  K, except for the inset in figure 1(b) where
K, except for the inset in figure 1(b) where  K. Two different phases are found, one is marked as I-VSS and the other is marked as II-NSS. It can be seen that the VSS effect can be observed below the critical temperature 18 K for silicene, 200 K for germanene and 400 K for stanene. The increasing critical temperature from silicene to stanene is consistent with the increasing spin–orbit interaction. The critical temperature Tc could be approximately determined by
K. Two different phases are found, one is marked as I-VSS and the other is marked as II-NSS. It can be seen that the VSS effect can be observed below the critical temperature 18 K for silicene, 200 K for germanene and 400 K for stanene. The increasing critical temperature from silicene to stanene is consistent with the increasing spin–orbit interaction. The critical temperature Tc could be approximately determined by  , where
, where  is the Boltzmann constant. Above the critical temperature, the NSS effect is detectable. As is known, the index-change relationship of the Fermi–Dirac distribution function determines that only electronic states near the Fermi energy could contribute to the current. Consequently, the thermodynamical transition from VSS phase to NSS phase is attributed to the fact that, only if the energy broadening
is the Boltzmann constant. Above the critical temperature, the NSS effect is detectable. As is known, the index-change relationship of the Fermi–Dirac distribution function determines that only electronic states near the Fermi energy could contribute to the current. Consequently, the thermodynamical transition from VSS phase to NSS phase is attributed to the fact that, only if the energy broadening  induced by the source temperature does not exceed the gap size
induced by the source temperature does not exceed the gap size  , high-energy subbands cannot break the transport feature of the VSS effect. For the phase I-VSS, it is seen that only spin-up (down) states from valley
, high-energy subbands cannot break the transport feature of the VSS effect. For the phase I-VSS, it is seen that only spin-up (down) states from valley  contribute to the positive (negative) current, in agreement with the band structures in figure 1(a), where hole (electron) states contribute most to
contribute to the positive (negative) current, in agreement with the band structures in figure 1(a), where hole (electron) states contribute most to  . As
. As  increases, the hole-dominated current
increases, the hole-dominated current  and the electron-dominated current
and the electron-dominated current  become nonzero due to enhanced temperature broadening. As
become nonzero due to enhanced temperature broadening. As  becomes much larger than 400 K, all the values of
becomes much larger than 400 K, all the values of  in figures 1(c) and (d) tend to stabilize due to convergence of the integral in equation (3), just as calculated in figure 1(b).
in figures 1(c) and (d) tend to stabilize due to convergence of the integral in equation (3), just as calculated in figure 1(b).
In figure 2, we plot the curves of the current  versus the temperature difference
versus the temperature difference  for silicene (left), germanene (middle) and stanene (right), respectively, at
for silicene (left), germanene (middle) and stanene (right), respectively, at  . The source temperature is fixed at
. The source temperature is fixed at  K, except for the inset in silicene where
K, except for the inset in silicene where  K. It is easy to understand that, under the condition of
K. It is easy to understand that, under the condition of  , the driving force tends to zero and thus all the currents
, the driving force tends to zero and thus all the currents  tend to zero. Owing to
tend to zero. Owing to  , except for the inset in figure 2(a), the nonzero
, except for the inset in figure 2(a), the nonzero  curves basically increase linearly as
curves basically increase linearly as  increases. Also, such linear relationships can be judged from equation (3), where
increases. Also, such linear relationships can be judged from equation (3), where  under
under  could be expressed as
could be expressed as
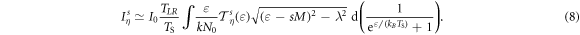
In the low- case, the linear relationships disappear although the curves
case, the linear relationships disappear although the curves  vary monotonically, as seen from the inset in figure 2(a). In comparison with figures 1(b)–(d), TS and
vary monotonically, as seen from the inset in figure 2(a). In comparison with figures 1(b)–(d), TS and  here do not change, and hence we have reason to conclude that the presence of the VSS effect is basically independent of
here do not change, and hence we have reason to conclude that the presence of the VSS effect is basically independent of  , because no new phase is induced by increasing
, because no new phase is induced by increasing  . For germanene, the VSS effect could also be detected if
. For germanene, the VSS effect could also be detected if  is fixed at a small value less than the critical temperature 200 K, just as shown by the inset in figure 2(a).
is fixed at a small value less than the critical temperature 200 K, just as shown by the inset in figure 2(a).
Figure 2. Reduced current  versus temperature difference TSD for silicene (left), germanene (middle) and stanene (right). The parameters are fixed at
versus temperature difference TSD for silicene (left), germanene (middle) and stanene (right). The parameters are fixed at  K,
K,  , while
, while  is fixed at 15 K in the left-panel inset.
is fixed at 15 K in the left-panel inset.
Download figure:
Standard image High-resolution imageIn figure 3, we further show the reduced current  as a function of the electric field
as a function of the electric field  for silicene (top), germanene (middle) and stanene (bottom). The temperature conditions read
for silicene (top), germanene (middle) and stanene (bottom). The temperature conditions read  K,
K,  K, except for the left-panel inset where
K, except for the left-panel inset where  K,
K,  K. The main result here is that the VSS and NSS effects could be switched to each other by tuning the Ez field. To understand this phenomenon, we need to analyze the variation of band structures in region G induced by the Ez field. As
K. The main result here is that the VSS and NSS effects could be switched to each other by tuning the Ez field. To understand this phenomenon, we need to analyze the variation of band structures in region G induced by the Ez field. As  varies, the mutual insulating region for two spins
varies, the mutual insulating region for two spins  changes. The energy scale of this region is
changes. The energy scale of this region is  . We find the VSS effect can happen only when
. We find the VSS effect can happen only when  is approximately satisfied. It can be checked that the critical
is approximately satisfied. It can be checked that the critical  -values, determined by
-values, determined by  , are approximately
, are approximately  meV for germanene and
meV for germanene and  meV for stanene at
meV for stanene at  K, and
K, and  meV for silienece at
meV for silienece at  K. If the Ez field becomes large enough, all the currents of
K. If the Ez field becomes large enough, all the currents of  are turned 'off' because no electronic states near the Fermi energy can be excited due to the large band gap. Thus, to realize the VSS effect,
are turned 'off' because no electronic states near the Fermi energy can be excited due to the large band gap. Thus, to realize the VSS effect,  should be neither too small nor too large. All these analyses agree well with the numerical curves, where the VSS effect is valid under
should be neither too small nor too large. All these analyses agree well with the numerical curves, where the VSS effect is valid under  for germanene and
for germanene and  for stanene at
for stanene at  K, but
K, but  for silicene at
for silicene at  K. In addition, the symmetry of the system decides the relation
K. In addition, the symmetry of the system decides the relation  . Physically, by changing the sign of
. Physically, by changing the sign of  (inverse electric field), the band structures between valley K and
(inverse electric field), the band structures between valley K and  can be exchanged. Specifically at
can be exchanged. Specifically at  ,
,  and
and  cross due to the valley degeneracy.
cross due to the valley degeneracy.
Figure 3. Reduced current  versus the electric-field parameter
versus the electric-field parameter  for silicene (top), germanene (middle) and stanene (bottom). The parameters are chosen at
for silicene (top), germanene (middle) and stanene (bottom). The parameters are chosen at  K,
K,  K except for the silicene inset, where
K except for the silicene inset, where  K,
K,  K.
K.
Download figure:
Standard image High-resolution imageNow one may wonder whether inelastic scattering at higher temperatures affects our ballistic results in figures 1–3. It is true that electron–phonon interactions should be enhanced as temperature increases due to more excited phonon modes, and thus electron mobility naturally decreases. For electron–phonon scattering, we divide it into two types: intravalley scattering and intervalley scattering. For intravalley scattering, increasing temperature cannot drive the jump between different states labeled by different valley–spin indexes due to the absence of the spin–valley flipping mechanism, but only reduces the magnitude of  . This indicates that the qualitative conclusions in the ballistic regime remain the same. For intervalley scattering, recent first-principles calculations have demonstrated that only electrons with energy more than several tens of meV or larger in silicene and germanene could feel this scattering induced by the stronger electron–phonon coupling [48], even near room temperature. Consequently, it is reasonable to believe that inelastic scattering has little effect on the detectable properties of the VSS effect in our considered range of temperatures.
. This indicates that the qualitative conclusions in the ballistic regime remain the same. For intervalley scattering, recent first-principles calculations have demonstrated that only electrons with energy more than several tens of meV or larger in silicene and germanene could feel this scattering induced by the stronger electron–phonon coupling [48], even near room temperature. Consequently, it is reasonable to believe that inelastic scattering has little effect on the detectable properties of the VSS effect in our considered range of temperatures.
Additionally, note that the net current contributed by spin-up and spin-down electrons always flows in opposite directions (pure spin current) in figures 1–3 and indeed the spin polarizability is 100%, benefiting from the completely spin-polarized subbands near the Fermi energy (see figure 1(a)). Thus it is not necessary to define the degree of spin polarization here. Nevertheless, one can notice that the NSS in figure 2(b) for gemanene is different from that in figure 2(a) for silicene, resulting from different degrees of valley polarization  . Further considering that the total current contributed by two opposite directions is always zero in figures 1–3 due to symmetry, it is difficult to define an overall effective
. Further considering that the total current contributed by two opposite directions is always zero in figures 1–3 due to symmetry, it is difficult to define an overall effective  for bidirectional transport, but one can still treat
for bidirectional transport, but one can still treat  separately for positive and negative currents via a definition
separately for positive and negative currents via a definition  , where all the possible currents
, where all the possible currents  are either nonnegative (positive transport) or nonpositive (negative transport). For II-NSS in figure 2(a),
are either nonnegative (positive transport) or nonpositive (negative transport). For II-NSS in figure 2(a),  for both positive and negative currents, while
for both positive and negative currents, while  for II-NSS in figure 2(b). Distinct from II-NSS, it must satisfy
for II-NSS in figure 2(b). Distinct from II-NSS, it must satisfy  in both directions for I-VSS. To distinguish the boundary between I-VSS and II-NSS in figures 1–3 more strictly, we here use a relatively accurate approximation that if the current component
in both directions for I-VSS. To distinguish the boundary between I-VSS and II-NSS in figures 1–3 more strictly, we here use a relatively accurate approximation that if the current component  is less than 5% of the total current, one can ignore this component.
is less than 5% of the total current, one can ignore this component.
4. Robustness of the valley–spin Seebeck effect
Since we have obtained information for how to realize the VSS effect in silicene, germanene and stanene, it is still necessary to discuss the robustness of the VSS effect in some real complex experimental conditions. Below, we take stanene for instance and study the influence of the ferromagnetic field and the Fermi energy on the VSS effect near room temperature. The fixed parameters read  K,
K,  K,
K,  . Note that the conclusions for stanene here are universally valid for germanene and silicene under lower
. Note that the conclusions for stanene here are universally valid for germanene and silicene under lower  .
.
Firstly, we show the influence of ferromagnetic field M on the VSS effect in figure 4(a). Our results indicate that the VSS effect is always robust at  . This result depends on such a fact that the ferromagnetic field does not essentially change the electron–hole asymmetry in figure 1(a) in spite of band variations. Further considering that the ferromagnetic field has been successfully introduced in graphene by the proximity effect of the ferromagnetic insulating substrate [49], it is reasonable to believe that the ferromagnetic field could also be applied in silicene, germanene and stanene. In this sense, one can easily observe the VSS effect in a large range of M-strength. In addition, provably, the length L of region G does also not change the realization of the VSS effect.
. This result depends on such a fact that the ferromagnetic field does not essentially change the electron–hole asymmetry in figure 1(a) in spite of band variations. Further considering that the ferromagnetic field has been successfully introduced in graphene by the proximity effect of the ferromagnetic insulating substrate [49], it is reasonable to believe that the ferromagnetic field could also be applied in silicene, germanene and stanene. In this sense, one can easily observe the VSS effect in a large range of M-strength. In addition, provably, the length L of region G does also not change the realization of the VSS effect.
Figure 4. Robustness of the VSS effect in realistic conditions for stanene at  K,
K,  K,
K,  . (a) Reduced current
. (a) Reduced current  versus the ferromagnetic field M. (b) Reduced current
versus the ferromagnetic field M. (b) Reduced current  versus the Fermi energy
versus the Fermi energy  , which is uniform for the whole silicene sample. NSP denotes the normal spin polarized phase III. (c) Reduced current
, which is uniform for the whole silicene sample. NSP denotes the normal spin polarized phase III. (c) Reduced current  versus the Fermi energy
versus the Fermi energy  in region G while the Fermi energy in regions S and D reads
in region G while the Fermi energy in regions S and D reads  . NSF denotes the normal spin filtering phase IV.
. NSF denotes the normal spin filtering phase IV.
Download figure:
Standard image High-resolution imageSecondly, we consider a stanene sample that is uniformly doped  for both S, D and G. It is verified that the VSS effect is robust under
for both S, D and G. It is verified that the VSS effect is robust under  , beyond which phase III-NSP (normal spin polarized current) with weak spin–valley polarizaton works. Due to the specific valley–spin symmetry for the band structures in figure 1(a),
, beyond which phase III-NSP (normal spin polarized current) with weak spin–valley polarizaton works. Due to the specific valley–spin symmetry for the band structures in figure 1(a),  is always valid here. This means we only need to analyze the curves when
is always valid here. This means we only need to analyze the curves when  has positive values. By changing
has positive values. By changing  , the band structures remain the same while the electron–hole asymmetry varies. The magnitude of
, the band structures remain the same while the electron–hole asymmetry varies. The magnitude of  is determined by the degree of asymmetry: the stronger the electron–hole asymmetry, the larger the current is. As
is determined by the degree of asymmetry: the stronger the electron–hole asymmetry, the larger the current is. As  increases from 0 to
increases from 0 to  , the current
, the current  first decreases to zero then changes its sign because the electron–hole asymmetry about
first decreases to zero then changes its sign because the electron–hole asymmetry about  first decreases (hole-dominated,
first decreases (hole-dominated,  ) then increases (electron-dominated,
) then increases (electron-dominated,  ), as expected from figure 1(a);
), as expected from figure 1(a);  can also be turned on as the temperature broadening exceeds the corresponding valley–spin conduction band (electron-dominated,
can also be turned on as the temperature broadening exceeds the corresponding valley–spin conduction band (electron-dominated,  );
);  (electron-dominated,
(electron-dominated,  ) is turned on when the temperature broadening is larger than the corresponding transport gap; the current
) is turned on when the temperature broadening is larger than the corresponding transport gap; the current  is always electron-dominated (see figure 1(a)), and thus
is always electron-dominated (see figure 1(a)), and thus  . As a result, the NSP phase happens as
. As a result, the NSP phase happens as  increases.
increases.
Thirdly, we further consider the robustness of the VSS effect on the Fermi energy  in region G for a sample that is undoped
in region G for a sample that is undoped  in regions S and D in figure 4(c). It is found that the VSS effect is robust at
in regions S and D in figure 4(c). It is found that the VSS effect is robust at  , beyond which phases II-NSS and IV-NSF (normal spin-filtering phase) can be gradually observed as
, beyond which phases II-NSS and IV-NSF (normal spin-filtering phase) can be gradually observed as  increases. Different from bidirectional current in the Seebeck effect, the NSF phase only supports unidirectional current. Depending on the system symmetry,
increases. Different from bidirectional current in the Seebeck effect, the NSF phase only supports unidirectional current. Depending on the system symmetry,  always holds, and thus we only need to analyze the curves when
always holds, and thus we only need to analyze the curves when  has positive values. By changing
has positive values. By changing  , the band structures in region G do not change while the electron–hole asymmetry varies, just as demonstrated in figure 4(b). As
, the band structures in region G do not change while the electron–hole asymmetry varies, just as demonstrated in figure 4(b). As  increases from 0 to
increases from 0 to  ,
,  (hole-dominated,
(hole-dominated,  ) gradually tends to zero because the corresponding transport gap increases; when
) gradually tends to zero because the corresponding transport gap increases; when  ,
,  (electron-dominated,
(electron-dominated,  , as seen from figure 1(a)) could be turned on;
, as seen from figure 1(a)) could be turned on;  is always turned off because
is always turned off because  cannot overreach the corresponding transport-gap region;
cannot overreach the corresponding transport-gap region;  (electron-dominated,
(electron-dominated,  ) decreases because the transport gap keeps away from the Fermi energy. No surprise is that the NSS phase can occur. At
) decreases because the transport gap keeps away from the Fermi energy. No surprise is that the NSS phase can occur. At  , only spin-up states dominated by electrons from two valleys contribute to the current
, only spin-up states dominated by electrons from two valleys contribute to the current  , and thus the NSF effect is observed.
, and thus the NSF effect is observed.
Lastly, we discuss the influence of some complex conditions on the VSS effect. Firstly, in terms of band changes, the Rashba interactions do not change the valley–spin dependent band gap although there is spin splitting outside the valley points [13–17]. Actually, for silicene, germanene and stanene, the spin splitting induced by Rashba perturbations plays little role in affecting the spin–valley transport, as proved by previous first-principles calculations [10]. Secondly, note that our concerned VSS effect is based on bulk states of the materials but not edge states [47] and thus could be detected in experiments more easily due to the stronger signal, although this VSS effect has some common transport features to valley-polarized quantum spin Hall edge states [28]. Thirdly, a real sample of heavy group-IV monolayers also inevitably contains atomic defects in the bulk, such as bits of vacancies [12, 49], which induce variations of supercell bands. To realize the VSS effect, the defect ratio cannot exceed 8%, otherwise the VSS effect is broken by defect states that contribute to the current [50]. Fourthly, to avoid intervalley scattering, local gates are suggested to deplete edge carriers and form gate-defined sample edges, near which the variations of edge potential do not change the delectability of the VSS effect owing to the negligible proportion of edge atoms [19]. In short, although there has been little experimental study about the temperature-driven electron motion in heavy group-IV monolayers so far, we still have sufficient reason to believe that the VSS effect discussed here is detectable by developing the latest experimental detection techniques on valley or spin in graphene [44–47]. To be sure, our results here advance our previous work about the realization of NSS or valley Seebeck effects as well as confirm the rough prediction of the coexistence of these two effects [51].
5. Conclusion
In summary, based on monolayers of heavy group-IV materials, we have designed a caloritronic device locally modulated by an interlayer electric field to realize a unique valley–spin Seebeck (VSS) effect, which supports bidirectional transport with each net current direction locked by both valley and spin. Associated with the strength of the spin–orbit band gap, such a VSS effect is suggested to be detectable using current experimental technology below the critical temperature 18 K for silicene, 200 K for germanene and 400 K for stanene, arising from the specific valley–spin band structures. We have also found that above the critical temperature, the VSS effect may be broken by overlarge temperature broadening, basically independent of temperature difference. Besides the temperature, the local electric field can also drive a transition between the VSS and normal spin Seepbeck effects by tuning the band structures. Furthermore, we have proved that the VSS effect found here is robust against many realistic perturbations. These findings provide new insights to apply two-dimensional heavy group-IV materials in future information procession (encoding information simultaneously by valley and spin) in thermal logic circuits and low-dissipation devices.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 11504179), the Natural Science Foundation of Jiangsu Province (Grant No. BK20150830), NUPTSF (Grant No. NY214193), and the State Key Program for Basic Research of China (Grant No. 2015CB921202).







