Abstract
Wavefront engineering is an important quantum technology, often applied to the production of states carrying orbital angular momentum (OAM). Here, we demonstrate the design and production of robust C-shaped beam states carrying OAM, in which the usual doughnut-shaped transverse intensity structure of the vortex beam contains an adjustable gap. We find that the presence of the vortex lines in the core of the beam is crucial for maintaining the stability of the C-shape structure during beam propagation. The topological charge of the vortex core controls mainly the size of the C-shape, while its opening angle is related to the presence of vortex–anti-vortex loops. We demonstrate the generation and characterisation of C-shaped electron vortex beams, although the result is equally applicable to other quantum waves. C-shaped electron vortex beams have potential applications in nanoscale fabrication of planar split-ring structures and three-dimensional chiral structures as well as depth sensing and magnetic field determination through rotation of the gap in the C-shape.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Structured quantum waves with a patterned phase or intensity distribution are of theoretical and practical interest in emerging quantum technologies. An important subset of structured waves is vortex beams. These are waves endowed with a phase singularity around which there is a linear azimuthal phase ramp. The phase singularity is known to be associated with the property of orbital angular momentum (OAM) carried by the beam [1, 2], which has given rise to prominent applications including nano-manipulation of particles [3], OAM entanglement [4], and multiplexed data transfer [5]. Vortex beam states were initially discovered as dislocations in ultrasonic acoustic waves reflected from a rough surface [6]. Later the same physical concept was transferred from classical wave phenomena to photon waves by Allen et al [1]. Recently, electron matter waves have been shown to also support vortex states [2]. These are currently produced inside transmission electron microscopes using various methods including amplitude diffraction masks [7–9], phase masks [10, 11] and magnetic needles [12]. Most recent research has focused on electron and optical beams; however there has also been investigation of other types of beams with phase vortices such as x-ray vortices [13] and atom vortex beams [14] . Research on vortex beams has also stimulated interest in other types of structured quantum waves such as Airy beams which have an interesting 'self-accelerating' property [15]. It is clear that there is an opportunity to explore more variations of shaped beams. The characterisation of these beams as well as their interactions with matter would greatly enrich our understanding of the nature of quantum physics, with potential for practical applications.
Here we focus on the controlled formation of C-shaped vortex beams which have many useful characteristics and applications distinct from those in the case of beams with a circularly symmetric intensity distribution [9, 16]. For example, non-zero OAM in a beam devoid of cylindrical symmetry is itself of fundamental interest. In addition, a C-shaped beam can be directly used in lithography to produce shaped nanostructures, such as split-ring structures used in metamaterials research [17], without the need to scan the beam. Successfully producing a split-ring structure with a well defined and controllable gap is crucial for investigations of split-ring resonator metamaterials where the local field enhancement could be the largest in the gap (for example [18]). We point out that our C-shaped vortex beam could be applied to the fabrication of three-dimensional chiral structures [19]. C-shaped beams also have applications in atomtronic quantum interference devices [20] and, for the electron vortex version, in the sensing of the Gouy phase and applied magnetic fields [21–24].
We begin by introducing an analytically defined phase mask function used to generate C-shaped vortex beams whose opening gaps can be continuously tuned from zero. We attribute this to the presence of vortex lines threading its core, which also enhances the robustness of the C-shaped beam against the break-up of the intensity pattern during propagation in free space. We show here that it carries a well defined OAM despite not having a circularly symmetric cross section. Finally, we discuss the application of such C-shaped electron vortex beams in nanostructure fabrication.
The phase structure which needs to be imprinted onto an incoming plane wave, such that a C-shaped vortex beam can be produced by a focusing lens, has a very simple form:
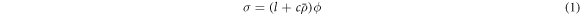
where l and c are adjustable constant parameters, ϕ (= 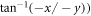 is the azimuthal angular variable in cylindrical polar coordinates and
is the azimuthal angular variable in cylindrical polar coordinates and 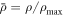 where ρ is the radial variable and
where ρ is the radial variable and 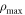 is a scaling parameter. Experimentally an aperture is required, defining a cut-off radius for the function; in this paper we choose
is a scaling parameter. Experimentally an aperture is required, defining a cut-off radius for the function; in this paper we choose 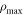 to be equal to the aperture radius. The produced wavefunction after phase manipulation is then described by
to be equal to the aperture radius. The produced wavefunction after phase manipulation is then described by
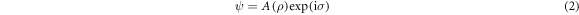
where A is an aperture function which only depends on radial distance, chosen to be a binary top-hat function such that 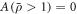 ,
, 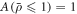 .
.
The C-shaped vortex beam is produced at the focal plane of a lens, for example as shown in a practical example in figure 3 below. In this paper the plane where the wavefunction of the incident beam is modified by the phase mask described by equation (2) will be referred to as the 'mask plane' and the focal plane of the lens will be referred to as the 'Fourier plane' as the effect of the lens is to produce a far-field diffraction pattern of the mask-modulated incident beam. An example, with l = 6.1 and c = 3.9 in the circular top-hat limited function of equation (2) is shown in figure 1. The phase is evaluated within the range 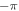 to π, so that the phase discontinuity line coincides with the positive y-axis, forming the gap of the C-shaped beam along the positive x-axis in the far-field diffraction plane (figure 1(viii)).
to π, so that the phase discontinuity line coincides with the positive y-axis, forming the gap of the C-shaped beam along the positive x-axis in the far-field diffraction plane (figure 1(viii)).
Figure 1. (i), (iv), (vii) Examples of the phase function of equation (1) wrapped in units of 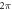 (black =
(black = 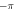 and white = π). (ii), (v), (viii) Fourier transform intensity distributions (white is high intensity), with constant phase contours shown in green. (iii), (vi), (ix) Phase of the Fourier transform (black =
and white = π). (ii), (v), (viii) Fourier transform intensity distributions (white is high intensity), with constant phase contours shown in green. (iii), (vi), (ix) Phase of the Fourier transform (black = 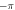 and white = π). The inset in the bottom left of (ix) shows vortices and anti-vortices (blue and green arrows) found in the green rectangle in (ix). The l and c values for each row are shown on the left-hand side. (The scale bar on (ii) is
and white = π). The inset in the bottom left of (ix) shows vortices and anti-vortices (blue and green arrows) found in the green rectangle in (ix). The l and c values for each row are shown on the left-hand side. (The scale bar on (ii) is 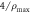 and applies to all images in the second and third columns).
and applies to all images in the second and third columns).
Download figure:
Standard image High-resolution imageThe phase function can be understood by examining the two contributions to the phase in equation (1) separately. The first contribution, controlled by the parameter l, has only an azimuthal dependence. If the parameter l is an integer, this term gives rise to an azimuthal phase step increase of 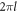 expected in vortex beams whose far-field diffraction consists of a doughnut intensity ring with a topological vortex charge, or winding number, l at its core. When l is a fractional number, the phase difference between the start and end of a
expected in vortex beams whose far-field diffraction consists of a doughnut intensity ring with a topological vortex charge, or winding number, l at its core. When l is a fractional number, the phase difference between the start and end of a  rotation is no longer an integer multiple of
rotation is no longer an integer multiple of 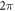 . The far-field diffraction of the wavefunction with such a phase discontinuity creates a beam with a localised defect in the doughnut-like intensity structure. Figures 1(i)–(iii) show the mask phase as well as the intensity and phase of the focused beam of such an example for l = 6.5 (c = 0); the last two are calculated by Fourier transform. These results can be understood in terms of a geometric ray model in which the local phase gradients of the incident wave after phase modification can be considered as wavevectors of the rays contributing to the intensity of the diffraction pattern. In the case of an integer l vortex beam the uniform azimuthal phase gradient gives rises to rays whose transverse wavevector components are uniformly distributed azimuthally. Alternatively an azimuthal phase discontinuity, different from
. The far-field diffraction of the wavefunction with such a phase discontinuity creates a beam with a localised defect in the doughnut-like intensity structure. Figures 1(i)–(iii) show the mask phase as well as the intensity and phase of the focused beam of such an example for l = 6.5 (c = 0); the last two are calculated by Fourier transform. These results can be understood in terms of a geometric ray model in which the local phase gradients of the incident wave after phase modification can be considered as wavevectors of the rays contributing to the intensity of the diffraction pattern. In the case of an integer l vortex beam the uniform azimuthal phase gradient gives rises to rays whose transverse wavevector components are uniformly distributed azimuthally. Alternatively an azimuthal phase discontinuity, different from 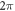 , corresponds to reduced Fourier plane intensity for wavevectors within certain azimuthal directions.
, corresponds to reduced Fourier plane intensity for wavevectors within certain azimuthal directions.
A C-approximate beam can be realized when using a fractional l which is half-way between integers [25–28]. However, even in that case there is still significant intensity in the opening, making the fractional vortex beam not an ideal C-shaped beam (for example, see figure 1(ii)).
Here we demonstrate that the fractional OAM beam states can be improved on to generate a well defined C-shaped beam by introducing a spiral phase function term that depends on both the radial and azimuthal coordinates, as shown in figure 1(iv)–(vi). The spiral phase function is controlled by the parameter c and involves a mixture of radial and azimuthal phase gradients. A similar phase function, when defined over the azimuthal interval between 0 and 2π, has previously been shown to produce a spiralling intensity pattern [29–31]. By defining the phase function over the azimuthal interval between −π to π we produce a beam with a symmetric opening in the far-field diffraction pattern. The size of the phase jump at the azimuthal phase discontinuity is now also a linear function of the radial coordinate (see figure 1). The opening due to the phase discontinuity is now much more clearly defined when compared with the results produced by the fractional vortex beams. This is associated with a high-density packing of local vortex and anti-vortex components in the phase pattern of the far-field diffraction as shown in figure 1(vi). As the singularities in phase vortices are associated with regions of darkness, a high-density packing of phase vortices is required for an extended dark region, an essential requirement for a C-shaped beam with a large opening.
Control over the characteristics of the C-shaped beam is realized by varying the ratio 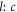 , i.e., by changing the relative importance of the term involving fractional topological charge (proportional to l) [25, 26, 32] with respect to the term involving radially dependent phase gradients of σ (proportional to c, as seen in optical twists [33]). An analysis of the computed phase distributions of the resultant C-shaped beam (figure 1(vii)–(ix)) shows that it retains an overall topological charge at the centre, as one would expect from a regular vortex beam. In addition, the beam also possesses other phase vortices of both signs distributed over a finite area along the line bisecting the gap region. The density of vortex and anti-vortex pairs is higher than that in the case of the fractional vortex beams and this density is adjustable. As the value of c increases, the phase distribution at the focal plane shows a gradual stacking of vortex–anti-vortex pairs into a grid-like collection (similar to those shown in figure 1(vi) and (ix)), producing a clear opening of increasing size. This occurs through the displacement of the isophase lines (figure 1(ii), (v), (viii)) for larger c where similar phase lines are seen to occur at larger angles to the negative x-axis (upper isophase lines moving 'clockwise' and lower isophase lines moving 'anticlockwise') (see supplementary material, animation available online at stacks.iop.org/NJP/19/063008/mmedia).
, i.e., by changing the relative importance of the term involving fractional topological charge (proportional to l) [25, 26, 32] with respect to the term involving radially dependent phase gradients of σ (proportional to c, as seen in optical twists [33]). An analysis of the computed phase distributions of the resultant C-shaped beam (figure 1(vii)–(ix)) shows that it retains an overall topological charge at the centre, as one would expect from a regular vortex beam. In addition, the beam also possesses other phase vortices of both signs distributed over a finite area along the line bisecting the gap region. The density of vortex and anti-vortex pairs is higher than that in the case of the fractional vortex beams and this density is adjustable. As the value of c increases, the phase distribution at the focal plane shows a gradual stacking of vortex–anti-vortex pairs into a grid-like collection (similar to those shown in figure 1(vi) and (ix)), producing a clear opening of increasing size. This occurs through the displacement of the isophase lines (figure 1(ii), (v), (viii)) for larger c where similar phase lines are seen to occur at larger angles to the negative x-axis (upper isophase lines moving 'clockwise' and lower isophase lines moving 'anticlockwise') (see supplementary material, animation available online at stacks.iop.org/NJP/19/063008/mmedia).
By controlling both parameters, namely l and c, for a given 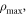 one can alter independently both the size (D) and the opening angle (
one can alter independently both the size (D) and the opening angle (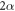 ), of the C-shape. D is defined as the intersection of the peak intensity of the C-shape arc with the negative x-axis in reciprocal space and α is the angle between the reciprocal space x-axis and the line linking the reciprocal space origin to the ends of the C [34].
), of the C-shape. D is defined as the intersection of the peak intensity of the C-shape arc with the negative x-axis in reciprocal space and α is the angle between the reciprocal space x-axis and the line linking the reciprocal space origin to the ends of the C [34].
To characterise the vortex beams produced by our analytical phase function (1) we can look at the C-shape produced with parameters l = 7.91 and c = 2.09. These values were chosen as a compromise between producing a large enough D and α to have a well defined arc and an experimentally visible opening whilst requiring a hologram mask which can be feasibly milled with a focused ion beam (FIB). The simulated results with these parameters can be compared with another beam also with a C-shaped intensity distribution. Following [11, 35], we use an iterative Fourier Transform algorithm (IFTA) to find a suitable mask for the latter C-shaped beam. We have carried out an IFTA calculation involving 2000 iterations with a C-shaped target intensity distribution and the results are shown in figure 2.
Figure 2. (i), (ii) Phase at focus (left, black = −π to white = 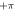 ) and intensity at focus (right, black = low intensity to white = high intensity) plots for the C-shaped beam shown in (iii) and (iv) respectively. (iii) A simulated electron C-shaped beam using the analytical phase function with l = 7.91 and c = 2.09. The blue lines show the central collection of vortex lines responsible for the OAM and robustness of the C-shaped beam. Other vortex lines are shown in red and the high-intensity volume is shown in green. (iv) As for C but using the non-vortex phase function from the IFTA result. The simulated propagation is between −13.6 μm and +13.6 μm relative to the focal plane along the z-axis, for an electron beam with
) and intensity at focus (right, black = low intensity to white = high intensity) plots for the C-shaped beam shown in (iii) and (iv) respectively. (iii) A simulated electron C-shaped beam using the analytical phase function with l = 7.91 and c = 2.09. The blue lines show the central collection of vortex lines responsible for the OAM and robustness of the C-shaped beam. Other vortex lines are shown in red and the high-intensity volume is shown in green. (iv) As for C but using the non-vortex phase function from the IFTA result. The simulated propagation is between −13.6 μm and +13.6 μm relative to the focal plane along the z-axis, for an electron beam with 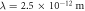 in an optical system with a camera length of 0.016 m and a mask diameter of 30 micron. The insets in the lower right of (iii) and (iv) show the phase required in the mask plane as in column 3 of figure 1. (v), (vi) OAM mode decompositions for the corresponding wavefunctions of the C-shaped beams in the focal plane respectively.
in an optical system with a camera length of 0.016 m and a mask diameter of 30 micron. The insets in the lower right of (iii) and (iv) show the phase required in the mask plane as in column 3 of figure 1. (v), (vi) OAM mode decompositions for the corresponding wavefunctions of the C-shaped beams in the focal plane respectively.
Download figure:
Standard image High-resolution imageAlthough the intensity distributions of both beams have the overall C-like shape as required, there are some significant differences in the finer details. These can be traced to even bigger differences in the phase structures, as our C-shaped beam contains a well defined vortex structure at the beam center while the phase structure of the IFTA-generated beam contains far more numerous off-axis vortex lines (as shown by the red lines in figure 2(ii)); but also, many of these vortex lines are loops, a feature characteristic of the speckle pattern seen in figure 2(iv). For clarity we shall refer to our C-shaped beam as the 'vortex C-beam' and the focused beam generated by the phase mask found via the IFTA as the 'non-vortex C-beam'. It is important to keep in mind that, in this case, the IFTA is only tasked to design a structured beam intensity in the focal plane.
The importance of a well-defined vortex structure at the beam centre can be highlighted by comparing the propagation of our vortex C-beam with that of the non-vortex C-beam. This is studied numerically by applying a Fresnel propagator analysis [36] to the wavefunctions of the focused beams. We can see that a collection of simple phase singularities propagates along the axis of the C-shaped vortex beam (blue lines in figure 2(iii)). The combined effect of this and nodal line loops at larger radii creates the C-shaped illumination with the opening seen in the green volume of figure 2. Correspondingly away from focus the C-shaped intensity gradually becomes more spiral like; however, it maintains a high-intensity arc with a gap. Thus the C-shaped intensity distribution of the vortex C-beam is quite robust against beam propagation around the focal plane. By contrast, the C-shaped intensity of the non-vortex C-beam breaks apart very quickly from the focal plane. This is shown in figure 2(iv) where the green volume encloses regions of high intensity. The slow rotation of the gap direction in the vortex C-beam as a function of beam propagation distance away from the focal plane can be attributed to the Gouy phase change at the beam waist [24]. These results agree with previous findings that vortices of the fractional OAM are split into multiple  phase singularities and show intensities which distort and rotate as a function of distance [27] . It has been previously shown that fractional vortex beams can be synthesized to only show rotation but maintain the shape of the intensity as the beam propagates. This was achieved by the use of a radial quantum number such that the Gouy phases of individual contributions compensate to produce a uniform Gouy phase [27, 37]. There is the potential that application of such an approach could provide additional stability to the C-shaped beam structure, beyond that bestowed by the threading vortex lines; however, this is beyond the scope of the current paper.
phase singularities and show intensities which distort and rotate as a function of distance [27] . It has been previously shown that fractional vortex beams can be synthesized to only show rotation but maintain the shape of the intensity as the beam propagates. This was achieved by the use of a radial quantum number such that the Gouy phases of individual contributions compensate to produce a uniform Gouy phase [27, 37]. There is the potential that application of such an approach could provide additional stability to the C-shaped beam structure, beyond that bestowed by the threading vortex lines; however, this is beyond the scope of the current paper.
Another important characteristic of our C-shaped vortex beams is the non-zero OAM content. The net OAM content can be calculated from the beam wavefunctions by 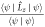 . At the mask plane, it can be evaluated analytically using the wavefunction given in equation (2) to give
. At the mask plane, it can be evaluated analytically using the wavefunction given in equation (2) to give ![$(l+[2c/3]){\hslash }$](https://content.cld.iop.org/journals/1367-2630/19/6/063008/revision2/njpaa6e3cieqn23.gif) or a value of
or a value of 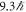 with l = 7.91 and c = 2.09. The contribution from the mixed-phase term (proportional to c) is to cause a shift of the barycenter of the beam away from the beam axis. The mask plane OAM content is equal to that of the C-shaped beam which is the result of performing the expectation value integration numerically in the Fourier plane, indicating the conservation of OAM content in a Fourier-transforming lens system. This conservation is also shown when comparing the Fourier plane numerical and mask plane analytical OAM expectation values for C-shapes with different opening angles. A plot of the predicted OAM for different opening angles is shown in figure S2 in the supplementary material. The OAM content of the non-vortex beam is negligible by comparison, as expected.
with l = 7.91 and c = 2.09. The contribution from the mixed-phase term (proportional to c) is to cause a shift of the barycenter of the beam away from the beam axis. The mask plane OAM content is equal to that of the C-shaped beam which is the result of performing the expectation value integration numerically in the Fourier plane, indicating the conservation of OAM content in a Fourier-transforming lens system. This conservation is also shown when comparing the Fourier plane numerical and mask plane analytical OAM expectation values for C-shapes with different opening angles. A plot of the predicted OAM for different opening angles is shown in figure S2 in the supplementary material. The OAM content of the non-vortex beam is negligible by comparison, as expected.
To further investigate the nature of the OAM content of the vortex and non-vortex C-shaped beams, an OAM mode decomposition procedure has been performed on the wavefunctions of these types of beams when considered at the focal plane (as shown in figure 2(v) and (vi)), in terms of the spiral harmonic basis. The procedure follows the method put forward by Molina-Terriza et al [38]. With its simple vortex structure at the beam axis, the vortex C-beam has a chiral phase structure and a narrow OAM mode distribution centred around l = 9 as shown in figure 2(v). We expect very negligible contributions to the OAM measured on the beam axis from the off-centred vortices as the wavefunction has negligible amplitude there.
The non-vortex C-beam, however, shows an OAM distribution with a much wider range and a much smaller net OAM of 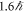 . This shows that the vortex C-beam has clear advantages in applications where OAM is desired, such as in particle manipulation experiments [39–41]. In pure vortex beams, the OAM of the beam is associated with probability current density which circulates the propagation axis and is connected with the cylindrical symmetry of the transverse structure. The existence of a net OAM content in a non-symmetric intensity distribution is non-trivial, but can be understood as a quantum mechanical effect due to the coherent superposition of several OAM beam states such that the local intensity minimum is the result of destructive interference between different OAM modes.
. This shows that the vortex C-beam has clear advantages in applications where OAM is desired, such as in particle manipulation experiments [39–41]. In pure vortex beams, the OAM of the beam is associated with probability current density which circulates the propagation axis and is connected with the cylindrical symmetry of the transverse structure. The existence of a net OAM content in a non-symmetric intensity distribution is non-trivial, but can be understood as a quantum mechanical effect due to the coherent superposition of several OAM beam states such that the local intensity minimum is the result of destructive interference between different OAM modes.
Our results are applicable to all beams that can be described by scalar quantum waves. In our analytical approach, we have neglected electron spin and spin–orbit coupling, which will be significant at relativistic energies and for electron lenses of high numerical aperture. These assumptions are justified by our experimental conditions used to study C-shaped beams. In the following, we present an experimental demonstration of a C-shaped beam inside a transmission electron microscope. Whilst in this case electrons were used, the results are equally valid for the shaping of wavefronts of different quantum waves such as electromagnetic and other matter waves, under paraxial conditions.
We chose to encode our desired phase structure to an incoming plane wave by passing the latter through a binary computer-generated hologram mask. The hologram (see figure 3(iii)) is generated by the well known method of interfering the quantum wave defined in equation (2) with a reference plane wave [7, 9]. The hologram was designed to produce a vortex C-beam with an opening angle 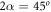 , by setting
, by setting 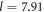 ,
, 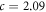 . The size of the focused vortex beam is given by
. The size of the focused vortex beam is given by 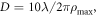 where λ is the wavelength of the electron beam. The binary hologram pattern is then transferred as a thickness profile using FIB milling, onto a silicon nitride membrane of 200 nm thickness, covered with a 50 nm thick Pt/Pd alloyed layer. A part of the Pt/Pd layer is removed to define a circular aperture of radius
where λ is the wavelength of the electron beam. The binary hologram pattern is then transferred as a thickness profile using FIB milling, onto a silicon nitride membrane of 200 nm thickness, covered with a 50 nm thick Pt/Pd alloyed layer. A part of the Pt/Pd layer is removed to define a circular aperture of radius 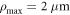 and the mask pattern is employed to direct the FIB milling to create the desired thickness variation of the remaining silicon nitride films inside the defined aperture. Energy-filtered transmission electron microscopy analysis provides the maximum and minimum bar thickness as roughly 1.6 and 0.8 mean free paths. Using an approximate mean free path of
and the mask pattern is employed to direct the FIB milling to create the desired thickness variation of the remaining silicon nitride films inside the defined aperture. Energy-filtered transmission electron microscopy analysis provides the maximum and minimum bar thickness as roughly 1.6 and 0.8 mean free paths. Using an approximate mean free path of 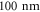 [42] this gives 80 nm to 160 nm and so 40 nm was removed when milling the circular aperture and the mask had a groove depth of around 80 nm. This agrees well with AFM measurements done on similar samples which showed approximately 45 nm of silicon nitride removed when milling the aperture circle and groove depths of 50 nm to 70 nm. As the total sample thickness of the mask is less than 200 nm , it is reasonable to neglect absorption as a first approximation and the resulting structure, when illuminated by a coherent electron wave, acts as an apertured binary phase mask due to interactions with the mean inner potential of the film [11, 43].
[42] this gives 80 nm to 160 nm and so 40 nm was removed when milling the circular aperture and the mask had a groove depth of around 80 nm. This agrees well with AFM measurements done on similar samples which showed approximately 45 nm of silicon nitride removed when milling the aperture circle and groove depths of 50 nm to 70 nm. As the total sample thickness of the mask is less than 200 nm , it is reasonable to neglect absorption as a first approximation and the resulting structure, when illuminated by a coherent electron wave, acts as an apertured binary phase mask due to interactions with the mean inner potential of the film [11, 43].
Figure 3. (i) A scanning electron microscopy image of the produced mask; (ii) the focal plane experimental intensity distribution of the first diffraction order; white regions are areas of higher charge coupled detector (CCD) counts, with the green lines highlighting a 45o angle; (iii) the calculated hologram design used to create the mask; (iv) the simulated intensity distribution of the target C-shape; (v) experimental intensity distributions at different z-planes, with the green volume being the volume of high intensity. The experimental set-up is also shown with the intermediate lenses and projector lenses focusing different propagation distances onto the CCD. The intermediate lens voltages for IL1 were varied between 3.5 V and 2.5 V in steps of approximately 0.017 V (scale bars: (i) 1 μm (also applies to (iii)), (ii) 500 μm on the CCD, (iv) 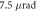 for a mask diamete of 4 micron).
for a mask diamete of 4 micron).
Download figure:
Standard image High-resolution imageThe mask is placed in the sample plane of a JEOL 2200FS transmission electron microscope and the Fourier transform of the beam wavefunction (2) is observed as the diffraction pattern of the computer-generated binary mask using the intermediate lens of the microscope as the focusing element. Figure 3(ii) displays one of the first-order far-field Fraunhofer diffraction patterns of the mask (figure 3(i)) using an operating voltage of 200 kV (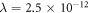 m). The 'free lens control' of the JEOL 2200FS was used to collect a series of images of the focused probe, by varying the voltage on the current driver of the first intermediate lens (IL1) between 2.5 V and 3.5 V. This moves the crossover point (focal plane) before or after the imaging plane (see the dot-dashed and dashed orange lines in 3(v) respectively) of the projector lens of the microscope. In this way the beam intensity pattern at different defocus distances are recorded using a charge coupled detector (CCD) camera.
m). The 'free lens control' of the JEOL 2200FS was used to collect a series of images of the focused probe, by varying the voltage on the current driver of the first intermediate lens (IL1) between 2.5 V and 3.5 V. This moves the crossover point (focal plane) before or after the imaging plane (see the dot-dashed and dashed orange lines in 3(v) respectively) of the projector lens of the microscope. In this way the beam intensity pattern at different defocus distances are recorded using a charge coupled detector (CCD) camera.
The experimental intensity in figure 3(ii) shows a strong match with the corresponding simulation shown in figure 3(iv), demonstrating a successful realization of the controlled generation of the C-shape structured illumination with an opening angle 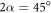 .
.
We found that the intensity of the lower section of the illumination from the phase mask is less than expected. This is most likely due to limitations of the FIB process which cannot completely reproduce the fine detail in the central region of the hologram mask. The inherent stochastic nature of the milling process also limits reproduction, causing random imperfections in the mask. A volumetric reconstruction of the through focus data set collected is shown in figure 3(v). Whilst varying the IL1 voltage slightly alters the overall magnification, the experimental intensity clearly shows a well defined low-intensity opening, which rotates as expected.
The robustness of the C-shaped intensity pattern against beam propagation is evident in the preservation of the pattern as a function of defocus (figure 3(v)). This is similar to the result of the simulation shown in figure 2, apart from an artefact due to overlapping with the tail of the zero-order beam at large defocus.
Such a C-shaped electron vortex beam can be directly used in coherent electron beam lithography, for example, producing nanostructures by exposing direct writing electron beam resists to such beams [34]. When inorganic resists used in direct writing lithography, such as AlF3, are exposed to a focused electron beam, aluminium metal particles are produced in the area surrounding the interaction volume [44], making the surrounding area much less sensitive to further electron beam illumination. Due to this proximity effect, subsequent pixels must be placed away from the initial interaction spot and this could hinder the faithful reproduction of intricate or curved designs. The advantage of using beams with a predefined electron intensity structure is that no scanning is required; as such all the electrons interact only with the 'virgin' resist at the same time and the patterning is not affected by any previous exposures of the inorganic resist. In the preliminary test, we demonstrated beam-induced etching of C-shaped holes with an overall dimension as small as 10 nm also in AlF3 resist (see figure S3 of the supplementary information and [34]).
Currently methods are being developed to utilise the electron probe in a scanning transmission electron microscope to construct materials by moving individual atoms or causing structural changes at the nanoscale [19, 45]. This has mostly been limited to two-dimensional patterning; however, experimental methods such as focused electron beam-induced deposition have been shown to produce three-dimensional spirals [46]. In this emerging field, electron intensity shaped in three dimensions will be extremely useful as it allows intensity to be defined in all three dimensions simultaneously, potentially speeding up the writing process by removing the need for separate probe-positioning steps. The central left inset in figure 2(iii) shows the regions of high intensity which form a spiral close to the focal region. This high-intensity spiral could be used to produce chiral spiral structures or spiral crystalline volumes where scanning a focused probe may otherwise be time consuming or alter the resist through its entire thickness.
In addition, the rotation of the C-shaped beams can be used for depth sensing and in magnetic field determination. Greengard et al [47] have shown (in the case of optics) that Gouy phase-induced rotation of the point-spread function can be used to determine the vertical position of the imaged feature more sensitively than the depth of focus method because of the linear dependence of rotation on the defocus distance. A similar linear dependence can also be seen, for our electron C-shaped beam, in figures 2(iii) and 3(v). This then gives rise to the possibility of depth determination from atoms to nanoparticles by electron microscopy by placing our phase mask at the imaging lens aperture plane. The determination of the spatial distribution of the strength of the longitudinal magnetic field component using Larmor rotation [24] is another possible area of application using our C-shaped focused beam. Although the general principle has been demonstrated using C-shaped beams created by inserting a beam-blocking knife edge into the path of a pure vortex beam, our beam does not need such additional mechanical intervention, hence can be more flexibly applied. For example, when used in a scanning transmission electron microscopy setting, it can map out the spatial variation of the magnetic field components.
In summary, we have shown how a simple analytical phase mask function can be used to produce a C-shaped beam embedded with a vortex structure at its centre. Such a shaped quantum wave has an adjustable opening angle due to the high density of vortex–anti-vortex pairs because of a radially dependent non-integer 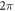 phase discontinuity. We have demonstrated that the structure of the intensity distribution of the generated C-shaped vortex beam is more stable as the beam propagates than that of a non-vortex beam found by the simple application of an iterative method. Analysis shows that this robustness stems from the presence of the threading topological structure at the core of our C-shape. This stability upon propagation of an intensity distribution other than a ring highlights the potential for future research on the stabilisation of other intensity distributions by an arrangement of phase vortices.
phase discontinuity. We have demonstrated that the structure of the intensity distribution of the generated C-shaped vortex beam is more stable as the beam propagates than that of a non-vortex beam found by the simple application of an iterative method. Analysis shows that this robustness stems from the presence of the threading topological structure at the core of our C-shape. This stability upon propagation of an intensity distribution other than a ring highlights the potential for future research on the stabilisation of other intensity distributions by an arrangement of phase vortices.
There are many possible applications of such C-shaped electron vortex beams. For example in holographic lithography, it can lead to complex two-dimensional patterning and three-dimensional nanostructure fabrication. Applications also include the creation of split-ring nano-structures used in metamaterials or three-dimensional chiral metallic plasmonic structures. Potentially, the C-shaped beam can also be used for depth sensing and magnetic field measurement through rotation of the gap in the C-shape.
Acknowledgments
This work was carried out with funding from the EPSRC under the grant EP/J022098/1. We would like to thank Dr Michael Ward at the University of Leeds for help with the fabrication of the mask. Finally we would like to express our thanks to the Royal Society Laboratory Refurbishment Fund.







