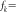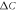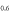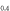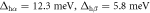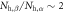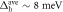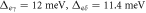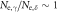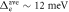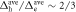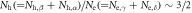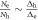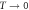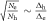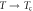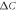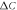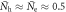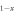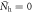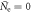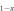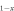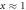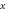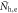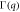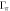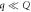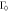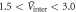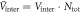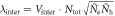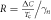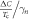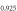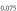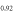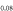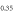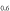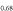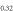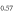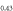Abstract
The strong power law behavior of the specific heat jump 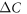 versus Tc
versus Tc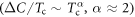 , first observed by Bud'ko et al (2009 Phys. Rev. B 79 220516), has been confirmed with several families of the Fe-based superconducting compounds with various dopings. We have tested a minimal two band BCS model to understand this anomalous behavior and showed that this non-BCS relation between
, first observed by Bud'ko et al (2009 Phys. Rev. B 79 220516), has been confirmed with several families of the Fe-based superconducting compounds with various dopings. We have tested a minimal two band BCS model to understand this anomalous behavior and showed that this non-BCS relation between 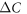 versus Tc is a generic property of the multiband superconducting state paired by a dominant interband interaction (
versus Tc is a generic property of the multiband superconducting state paired by a dominant interband interaction (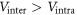 ) reflecting the relation
) reflecting the relation 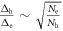 near Tc, as in the
near Tc, as in the 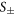 -wave pairing state. We also found that this
-wave pairing state. We also found that this 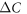 versus Tc power law can continuously change from the ideal BNC scaling to a considerable deviation by a moderate variation of the impurity scattering rate
versus Tc power law can continuously change from the ideal BNC scaling to a considerable deviation by a moderate variation of the impurity scattering rate 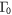 (non-pair-breaking). As a result, our model provides a consistent explanation why the electron-doped Fe-based superconductors follow the ideal BNC scaling very well while the hole-doped systems often show varying degree of deviations.
(non-pair-breaking). As a result, our model provides a consistent explanation why the electron-doped Fe-based superconductors follow the ideal BNC scaling very well while the hole-doped systems often show varying degree of deviations.
Export citation and abstract BibTeX RIS
1. Introduction
The specific heat (SH) jump  is the most well known thermodynamic signature of the second order phase transition and hence contains the generic information of the transition as well as the material specific information. For example, the BCS theory of superconductivity predicts the universal ratio
is the most well known thermodynamic signature of the second order phase transition and hence contains the generic information of the transition as well as the material specific information. For example, the BCS theory of superconductivity predicts the universal ratio 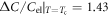 , hence
, hence 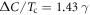 is a temperature independent constant and tells us the material specific quantity γ, the Sommerfeld coefficient of the normal state
is a temperature independent constant and tells us the material specific quantity γ, the Sommerfeld coefficient of the normal state 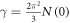 (N(0) density of states (DOSs) at Fermi level). In view of this BCS prediction of
(N(0) density of states (DOSs) at Fermi level). In view of this BCS prediction of 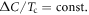 , the experimental observation by Bud'ko, Ni, and Canfield (BNC) [1],
, the experimental observation by Bud'ko, Ni, and Canfield (BNC) [1], 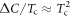 for a family of doped Ba(Fe
for a family of doped Ba(Fe TMx)2As2 compounds with TM = Co, Ni is a very intriguing behavior and stimulated active investigations both experimentally and theoretically. After the work of [1], this so-called BNC scaling relation was expanded with an increasing list of the iron pnictide and iron chalcogenide (FePn/Ch) superconducting (SC) compounds [2–9], hence strengthens the speculation that some generic mechanism must exist behind this unusual scaling behavior.
TMx)2As2 compounds with TM = Co, Ni is a very intriguing behavior and stimulated active investigations both experimentally and theoretically. After the work of [1], this so-called BNC scaling relation was expanded with an increasing list of the iron pnictide and iron chalcogenide (FePn/Ch) superconducting (SC) compounds [2–9], hence strengthens the speculation that some generic mechanism must exist behind this unusual scaling behavior.
However, recently a few cases—all hole-doped systems—were also reported that they do not follow the ideal BNC scaling behavior. For example, the observation of a strong deviation from the BNC scaling in the K-doped Ba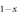 KxFe2As2 for
KxFe2As2 for 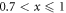 [10] is contrasted to the Na-doped Ba
[10] is contrasted to the Na-doped Ba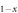 NaxFe2As2 (
NaxFe2As2 (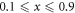 ) [8] which displays an excellent BNC scaling. Furthermore, in a more recent measurement [11] on Na-doped
) [8] which displays an excellent BNC scaling. Furthermore, in a more recent measurement [11] on Na-doped 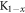 NaxFe2As2 the authors claimed that
NaxFe2As2 the authors claimed that 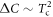 fits the data instead of
fits the data instead of 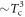 although data of this compound is limited to a very narrow range of Tc variation. Summarizing the experimental situation, it is fair to say that the large majority of Fe-pnictide superconductors fits the BNC scaling
although data of this compound is limited to a very narrow range of Tc variation. Summarizing the experimental situation, it is fair to say that the large majority of Fe-pnictide superconductors fits the BNC scaling 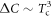 but there exists a small subset of Fe-pnictide systems showing some deviation of varying degrees. In any case, all reported data of the Fe-pnictide superconductors up to now universally exhibit anomalously strong non-BCS dependence4
between
but there exists a small subset of Fe-pnictide systems showing some deviation of varying degrees. In any case, all reported data of the Fe-pnictide superconductors up to now universally exhibit anomalously strong non-BCS dependence4
between 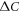 versus Tc and it deserves a theoretical understanding.
versus Tc and it deserves a theoretical understanding.
For the theoretical investigations, there are three attempted explanations. Kogan [13] argued that strong pair-breaking can cause 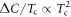 . The essence of this theory is a dimensional counting. The free energy difference near Tc,
. The essence of this theory is a dimensional counting. The free energy difference near Tc, 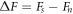 , can be expanded in powers of
, can be expanded in powers of 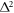 (Δ: the SC order parameter (OP)). In the BCS theory,
(Δ: the SC order parameter (OP)). In the BCS theory, 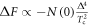 [14]. Using the BCS result of
[14]. Using the BCS result of 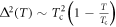 , we get
, we get  , the well known BCS prediction. In the case of the strong pair-breaking limit,
, the well known BCS prediction. In the case of the strong pair-breaking limit, 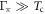 (
(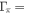 pair-breaking rate), considered by Kogan,
pair-breaking rate), considered by Kogan, 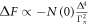 by a dimensional counting. Substituting the same BCS behavior of
by a dimensional counting. Substituting the same BCS behavior of 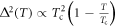 , we immediately recover Kogan's result
, we immediately recover Kogan's result 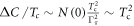 . However, we believe that this result is the consequence of an inconsistent approximation5
. The theory of Vavilov et al [15] mainly studied the coexistence region with magnetic order M and SC order Δ. It is a plausible theory that the coexisting magnetic order over the SC order can substantially reduce
. However, we believe that this result is the consequence of an inconsistent approximation5
. The theory of Vavilov et al [15] mainly studied the coexistence region with magnetic order M and SC order Δ. It is a plausible theory that the coexisting magnetic order over the SC order can substantially reduce 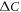 , hence develops a steep variation of
, hence develops a steep variation of 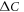 versus Tc. However this theory did not reveal any generic mechanism as to why
versus Tc. However this theory did not reveal any generic mechanism as to why 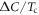 follows the BNC scaling
follows the BNC scaling 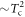 . Finally, Zannen [16] attributed the origin of
. Finally, Zannen [16] attributed the origin of 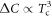 to the anomalous temperature dependence of the normal state electronic SH with the scaling form
to the anomalous temperature dependence of the normal state electronic SH with the scaling form 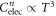 due to the critical fluctuations near the quantum critical point (QCP). A problem of this theory is that there is no evidence of
due to the critical fluctuations near the quantum critical point (QCP). A problem of this theory is that there is no evidence of 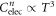 for a wide doping range of the FePn/Ch superconductors. Moreover all three theories mentioned above are single band theories and do not particularly utilize the unique properties of the FePn/Ch superconductors. In this paper, we propose a theory in which the multi-band nature of the FePn/Ch superconductors is the root cause for producing the BNC scaling behavior.
for a wide doping range of the FePn/Ch superconductors. Moreover all three theories mentioned above are single band theories and do not particularly utilize the unique properties of the FePn/Ch superconductors. In this paper, we propose a theory in which the multi-band nature of the FePn/Ch superconductors is the root cause for producing the BNC scaling behavior.
2. Minimal two band model for the SH jump 
The SH jump 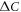 in any 2nd order phase transition is an indication of the entropy change through the phase transition at Tc. For SC transition, regardless of pairing mechanism,
in any 2nd order phase transition is an indication of the entropy change through the phase transition at Tc. For SC transition, regardless of pairing mechanism, 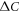 is due to the opening of the SC gap on Fermi surface and its magnitude is proportional to how rapidly the gap opens6
. We also note that the Fe-based superconductors are multi-band superconductors, hence the total SH jump
is due to the opening of the SC gap on Fermi surface and its magnitude is proportional to how rapidly the gap opens6
. We also note that the Fe-based superconductors are multi-band superconductors, hence the total SH jump  should be a summation of the SH jump contribution of each band. Therefore, the standard single band formula [17] should be generalized for many bands as
should be a summation of the SH jump contribution of each band. Therefore, the standard single band formula [17] should be generalized for many bands as
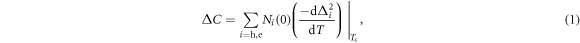
where the band index 'i' counts the different bands, and Ni are the DOSs and 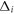 are the SC OPs of each band. For the minimal two band model, which will be used in this paper, 'i' counts the hole and electron bands typical in the Fe-based superconductors.
are the SC OPs of each band. For the minimal two band model, which will be used in this paper, 'i' counts the hole and electron bands typical in the Fe-based superconductors.
In the one band BCS superconductor, using 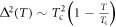 , the above equation yields the BCS result
, the above equation yields the BCS result 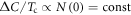 . However, in the case of a multiband superconductor, with the same BCS pairing mechanism but generalized to multiband, the standard single band BCS result can strongly deviate for the following reasons. First, each
. However, in the case of a multiband superconductor, with the same BCS pairing mechanism but generalized to multiband, the standard single band BCS result can strongly deviate for the following reasons. First, each 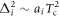 has non-universal and strongly band dependent coefficient ai because ai is determined by the combination of Ni of several bands and the inter- and intra-band pairing interactions Vij among them. Second, the size of
has non-universal and strongly band dependent coefficient ai because ai is determined by the combination of Ni of several bands and the inter- and intra-band pairing interactions Vij among them. Second, the size of 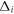 and Ni is inversely correlated when the interband pairing is dominant [18], hence equation (1) is not a simple summation of the BCS behavior of many bands. Therefore, the behavior of equation (1) for the multi-band superconductors can reveal more information about the pairing interactions as well as the pairing state.
and Ni is inversely correlated when the interband pairing is dominant [18], hence equation (1) is not a simple summation of the BCS behavior of many bands. Therefore, the behavior of equation (1) for the multi-band superconductors can reveal more information about the pairing interactions as well as the pairing state.
At present the most widely accepted pairing state in the Fe-based superconductors is the sign-changing S-wave state (S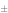 -wave) mediated by a dominant interband repulsive interaction (
-wave) mediated by a dominant interband repulsive interaction (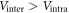 ) between the hole band(s) around Γ point and the electron band(s) around M point [19]. In real compounds, there exist multiple hole and multiple electron bands with their corresponding SC OPs
) between the hole band(s) around Γ point and the electron band(s) around M point [19]. In real compounds, there exist multiple hole and multiple electron bands with their corresponding SC OPs 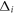 [20] and there should exist a multitude of inter- and intra-band pairing interactions Vij among them. However, we notice that the SH and Tc, studied in this paper, are the thermodynamically averaged quantities and these two quantities do not sensitively depend on the details of the multiple hole bands and multiple electron bands. Instead, the total SH and Tc are determined by the interaction between the averaged hole bands and the averaged electron bands in the following way:
[20] and there should exist a multitude of inter- and intra-band pairing interactions Vij among them. However, we notice that the SH and Tc, studied in this paper, are the thermodynamically averaged quantities and these two quantities do not sensitively depend on the details of the multiple hole bands and multiple electron bands. Instead, the total SH and Tc are determined by the interaction between the averaged hole bands and the averaged electron bands in the following way: 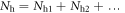 and
and ![${{\rm{\Delta }}}_{{\rm{h}}}^{2}=[{N}_{{\rm{h}}1}{{\rm{\Delta }}}_{{\rm{h}}1}^{2}+{N}_{{\rm{h}}2}{{\rm{\Delta }}}_{{\rm{h}}2}^{2}+\ldots ]/{N}_{{\rm{h}}}$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn71.gif) (when
(when 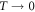 ) and a similar definition for the electron bands. Therefore, as far as we are interested in the relation between the total SH jump
) and a similar definition for the electron bands. Therefore, as far as we are interested in the relation between the total SH jump 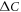 and Tc, the minimal two band model is sufficient and the values of
and Tc, the minimal two band model is sufficient and the values of 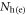 and
and  in our two band model should be understood as the thermodynamically averaged quantities as above7
.
in our two band model should be understood as the thermodynamically averaged quantities as above7
.
Having justified the two band model for the study of the SH jump 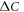 versus Tc, we again emphasize that our purpose of this paper is not to prove any pairing mechanism or model for the Fe-based superconductors but to test a minimal model to see how much we can understand the BNC scaling with it. The essential physics of the two band
versus Tc, we again emphasize that our purpose of this paper is not to prove any pairing mechanism or model for the Fe-based superconductors but to test a minimal model to see how much we can understand the BNC scaling with it. The essential physics of the two band 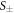 -wave state can be studied with the two coupled gap equations [21]
-wave state can be studied with the two coupled gap equations [21]
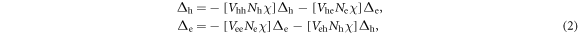
where the pair susceptibility χ at Tc is defined as
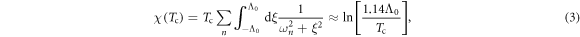
where 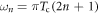 and
and 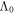 is a pairing energy cut-off. The pairing potentials Vab (
is a pairing energy cut-off. The pairing potentials Vab ( ) are all positive and further simplified in this paper as
) are all positive and further simplified in this paper as 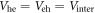 and
and 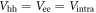 without loss of generality.
without loss of generality.
In the limit 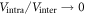 , equation (2) can be analytically solved and provides the interesting kinematic constraint relation [18]
, equation (2) can be analytically solved and provides the interesting kinematic constraint relation [18]
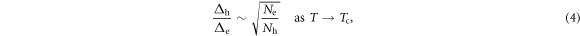
and the critical temperature is given by
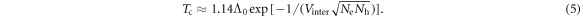
To calculate the experimental data of 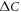 versus Tc for a Fe-122 compound with a series of doping, we need a modeling of doping. First, we notice that the undoped parent compound such as BaFe2As2 is a compensated metal, hence has the same number of electrons and holes, i.e. nh = ne. Therefore it is a reasonable approximation to take Nh = Ne at no doping and then the doping of holes (K, Na, etc) or electrons (Co, Ni, etc) is simulated by varying Nh and Ne while keeping
versus Tc for a Fe-122 compound with a series of doping, we need a modeling of doping. First, we notice that the undoped parent compound such as BaFe2As2 is a compensated metal, hence has the same number of electrons and holes, i.e. nh = ne. Therefore it is a reasonable approximation to take Nh = Ne at no doping and then the doping of holes (K, Na, etc) or electrons (Co, Ni, etc) is simulated by varying Nh and Ne while keeping 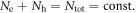 We have several remarks on this modeling of doping: (1) the assumption
We have several remarks on this modeling of doping: (1) the assumption 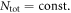 is only for convenience. The sensitive parameters of our model are the relative values between Ne and Nh but not the total DOS Ntot8
. Therefore, we use normalized parameters such as
is only for convenience. The sensitive parameters of our model are the relative values between Ne and Nh but not the total DOS Ntot8
. Therefore, we use normalized parameters such as 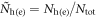 and dimensionless coupling constants
and dimensionless coupling constants 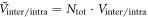 in our calculations. (2) We do not literally mean
in our calculations. (2) We do not literally mean  . The actual change of DOS
. The actual change of DOS 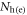 with doping '
with doping '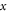 ' (holes or electrons) should be complicated and also nonlinear. What our model assumes is:
' (holes or electrons) should be complicated and also nonlinear. What our model assumes is: 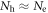 at no doping and the difference of DOSs
at no doping and the difference of DOSs  increases with doping9
. This assumption is consistent with the angle-resolved-photo-emission-spectroscopy measurements of (Ba
increases with doping9
. This assumption is consistent with the angle-resolved-photo-emission-spectroscopy measurements of (Ba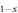 Kx)Fe2As2[22] and Ba(Fe
Kx)Fe2As2[22] and Ba(Fe Cox)2As2 [23] which show the systematic changes of hole (electron) FS sizes with dopings. For the rest of this paper, it is convenient to use the normalized DOSs as
Cox)2As2 [23] which show the systematic changes of hole (electron) FS sizes with dopings. For the rest of this paper, it is convenient to use the normalized DOSs as 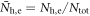 and define the dimensionless coupling constants as
and define the dimensionless coupling constants as 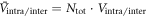 .
.
Expanding the gap equation (2) near Tc and using equation (4), we obtain 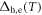 near Tc as
near Tc as
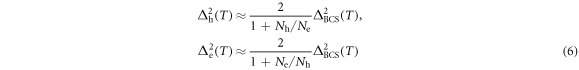
with 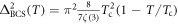 . Combining the results of equations (4) and (6), equation (1) provides
. Combining the results of equations (4) and (6), equation (1) provides
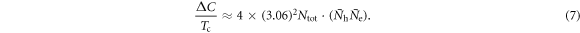
This is our key result of this paper. In contrast to the one band BCS superconductor, equation (7) clearly shows that 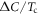 can have a strong Tc dependence through
can have a strong Tc dependence through  even with a constant Ntot (see equation (5)). With doping in a given FePn/Ch compound,
even with a constant Ntot (see equation (5)). With doping in a given FePn/Ch compound, 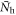 and
and 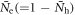 varies over the range of
varies over the range of ![$[0,1]$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn132.gif) (see footnote 8). As such if
(see footnote 8). As such if 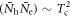 at least for some region of
at least for some region of 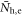 , we would obtain the BNC scaling for that region.
, we would obtain the BNC scaling for that region.
Having analyzed the simple case (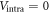 ), in the next section we numerically study more realistic cases with
), in the next section we numerically study more realistic cases with 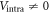 and including the impurity scatterings. We solve the coupled gap equation (2) for
and including the impurity scatterings. We solve the coupled gap equation (2) for 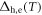 near Tc and directly calculate
near Tc and directly calculate 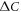 using equation (1). We find that the non-pair-breaking impurity scattering plays a crucial role in order to explain the ideal BNC scaling
using equation (1). We find that the non-pair-breaking impurity scattering plays a crucial role in order to explain the ideal BNC scaling 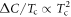 in Ba(Fe
in Ba(Fe TMx)2As2 (TM = Co, Ni) as well as a strong deviation in Ba
TMx)2As2 (TM = Co, Ni) as well as a strong deviation in Ba KxFe2As2[10].
KxFe2As2[10].
3. Numerical results
In figure 1(A), we calculated Tc versus 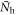 of the two band model equation (2) for
of the two band model equation (2) for 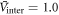 and 2.0, respectively, with
and 2.0, respectively, with 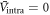 for both cases. Indeed, the calculated Tc shows a strong dependence on
for both cases. Indeed, the calculated Tc shows a strong dependence on 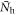 , symmetric with respect to
, symmetric with respect to  . We plot the same data as
. We plot the same data as  versus Tc in figure 1(B). In the case of
versus Tc in figure 1(B). In the case of 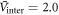 , we find
, we find 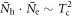 near the maximum Tc region which is the necessary condition for the BNC scaling from equation (7). It also shows that the overall power of the relation
near the maximum Tc region which is the necessary condition for the BNC scaling from equation (7). It also shows that the overall power of the relation 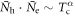 becomes weaker with the weaker pairing potential
becomes weaker with the weaker pairing potential 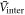 . Now we calculate
. Now we calculate 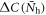 and
and 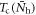 from equations (1) and (2).
from equations (1) and (2). 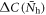 and
and 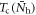 are implicitly related through
are implicitly related through ![${\bar{N}}_{{\rm{h}}}\in [0,1]$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn156.gif) . In figure 1(C), we plot
. In figure 1(C), we plot 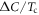 versus Tc in log–log scale, for different pairing potentials
versus Tc in log–log scale, for different pairing potentials 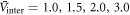 and 5.0, respectively, with
and 5.0, respectively, with  for all cases. First, as seen in figure 1(C), we can see the general trend that the region where the BNC scaling
for all cases. First, as seen in figure 1(C), we can see the general trend that the region where the BNC scaling 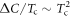 holds becomes widened near the maximum Tc region with increasing the pairing potential strength
holds becomes widened near the maximum Tc region with increasing the pairing potential strength 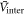 . With extensive numerical experiments, we found: (1)
. With extensive numerical experiments, we found: (1) 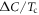 becomes
becomes 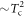 for the whole region if
for the whole region if  , however, this strength of pairing potential might be unrealistically strong. (2) Including
, however, this strength of pairing potential might be unrealistically strong. (2) Including 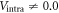 does not change the general behavior shown in figure 1(C) as long as
does not change the general behavior shown in figure 1(C) as long as 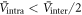 . (3) Finally, as Tc approaches its maximum value (as
. (3) Finally, as Tc approaches its maximum value (as 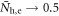 ),
),  approaches the BCS limit (
approaches the BCS limit ( ) for weak coupling (
) for weak coupling (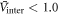 ) and exceeds it for strong coupling (
) and exceeds it for strong coupling (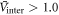 ). This shows that our results—although our model is a mean field theory—partially capture a strong coupling effect by full numerical calculations of
). This shows that our results—although our model is a mean field theory—partially capture a strong coupling effect by full numerical calculations of 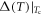 .
.
Figure 1. (A) Numerical calculations of Tc versus 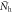 of the two band model for
of the two band model for 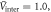 and 2.0, respectively, with
and 2.0, respectively, with 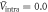 for both cases. (B) Plots of
for both cases. (B) Plots of 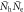 versus Tc with the same data of (A). Solid lines are of
versus Tc with the same data of (A). Solid lines are of 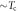 and
and 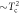 , respectively. (C) Numerical calculations of
, respectively. (C) Numerical calculations of 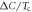 versus Tc for
versus Tc for 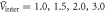 and 5.0, respectively, with
and 5.0, respectively, with  for all cases. Horizontal dashed line is the BCS limit of
for all cases. Horizontal dashed line is the BCS limit of 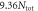 and the dotted lines of
and the dotted lines of 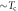 and
and 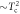 (BNC scaling) are guides for the eyes.
(BNC scaling) are guides for the eyes.
Download figure:
Standard image High-resolution imageAlthough it is not completely successful to produce the ideal BNC scaling behavior, the results of the generic two band model in figure 1(C) is remarkably non-BCS and very encouraging in that it shows that 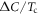 has changed more than one order of magnitude with
has changed more than one order of magnitude with 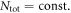 for all calculations. However, the BNC scaling behavior is still limited in a region near the higher Tc region (where
for all calculations. However, the BNC scaling behavior is still limited in a region near the higher Tc region (where 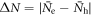 is small) and we need an extra mechanism to extend the power law scaling behavior at lower temperatures. We remind the fact that the jump
is small) and we need an extra mechanism to extend the power law scaling behavior at lower temperatures. We remind the fact that the jump 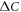 occurs at Tc (a finite temperature) and the impurity scattering effect will be increasingly effective at lower temperatures. In particular, if the impurity scattering should efficiently reduce
occurs at Tc (a finite temperature) and the impurity scattering effect will be increasingly effective at lower temperatures. In particular, if the impurity scattering should efficiently reduce  but not so much affect Tc, then the slope of
but not so much affect Tc, then the slope of 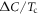 versus Tc would become steeper in this region and the region of the BNC scaling would be widened even with a moderate strength of
versus Tc would become steeper in this region and the region of the BNC scaling would be widened even with a moderate strength of 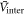 .
.
Phenomenologically we can consider two kind of impurity scattering in the two band model: 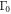 (intra-band scattering) and
(intra-band scattering) and 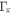 (inter-band scattering)10
. As we assumed the S± -wave state,
(inter-band scattering)10
. As we assumed the S± -wave state, 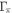 causes strong pair-breaking effect (e.g. suppression of Tc and reduction of
causes strong pair-breaking effect (e.g. suppression of Tc and reduction of 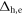 ), while
), while 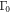 does not affect the superconductivity itself [24]. For example, the pair-breaking scattering
does not affect the superconductivity itself [24]. For example, the pair-breaking scattering 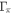 enters the pair-susceptibility
enters the pair-susceptibility 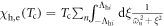 of equation (3) replacing as
of equation (3) replacing as 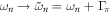 . As a result,
. As a result, 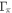 directly affects both Tc and
directly affects both Tc and 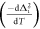 . However, we have already discussed in the Introduction that increasing
. However, we have already discussed in the Introduction that increasing 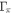 does not help to produce the BNC scaling (see footnote 4). On the other hand, there is another effect of the impurity scattering which does not directly affect the superconductivity, namely the quasiparticle broadening. This quasiparticle broadening is determined by the total scattering rate
does not help to produce the BNC scaling (see footnote 4). On the other hand, there is another effect of the impurity scattering which does not directly affect the superconductivity, namely the quasiparticle broadening. This quasiparticle broadening is determined by the total scattering rate  and the SH jump of
and the SH jump of 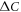 of equation (1) should take into account of this quasiparticle broadening as follows [25],
of equation (1) should take into account of this quasiparticle broadening as follows [25],
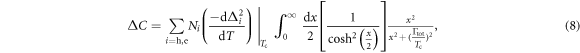
where 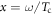 . Compared to equation (1), the additional integration part in the above equation contains the thermal average effect including the quasiparticle broadening
. Compared to equation (1), the additional integration part in the above equation contains the thermal average effect including the quasiparticle broadening  . And it shows that the non-pair-breaking scattering rate
. And it shows that the non-pair-breaking scattering rate 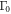 entering the thermal average part can strongly reduce
entering the thermal average part can strongly reduce 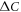 without affecting Tc.
without affecting Tc.
In figure 2, we show the numerical results of 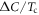 versus Tc in log–log scale with a choice of a moderate strength of the pairing potentials,
versus Tc in log–log scale with a choice of a moderate strength of the pairing potentials, 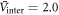 and
and 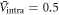 11
and varied the impurity scattering rates
11
and varied the impurity scattering rates 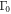 , and
, and 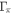 . First, all cases, with and without impurity scattering, show a strong deviation from the standard BCS limit (the horizontal dashed line). This behavior is the generic feature of the multiband superconductors as we explained in the previous section. The case without impurity scattering (red '
. First, all cases, with and without impurity scattering, show a strong deviation from the standard BCS limit (the horizontal dashed line). This behavior is the generic feature of the multiband superconductors as we explained in the previous section. The case without impurity scattering (red ' ' symbols,
' symbols, 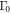 =
= 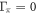 ),
), 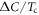 shows the Tc2 scaling only for the limited region near the maximum Tc and it quickly becomes flattened and slower than
shows the Tc2 scaling only for the limited region near the maximum Tc and it quickly becomes flattened and slower than  . Interestingly, this behavior looks very similar to the experimental data of Ba
. Interestingly, this behavior looks very similar to the experimental data of Ba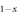 KxFe2As2[10]. Therefore, we speculate that Ba
KxFe2As2[10]. Therefore, we speculate that Ba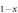 KxFe2As2 system belongs to the clean limit superconductor. This is understandable since K and Ba ions are out of the Fe–As planes and hence the doped K ions would introduce much weaker impurity potentials for the superconductivity. Next, only a small increase of impurity scattering (green '
KxFe2As2 system belongs to the clean limit superconductor. This is understandable since K and Ba ions are out of the Fe–As planes and hence the doped K ions would introduce much weaker impurity potentials for the superconductivity. Next, only a small increase of impurity scattering (green ' ' symbols,
' symbols, 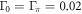 in unit of
in unit of  ) immediately changes
) immediately changes  versus Tc steeper such as
versus Tc steeper such as 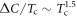 over the whole Tc range. Further increasing the impurity scattering rate the case with
over the whole Tc range. Further increasing the impurity scattering rate the case with 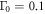 and
and 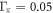 (pink '
(pink '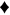 ' symbols) displays an ideal BNC scaling
' symbols) displays an ideal BNC scaling 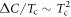 for the entire range of Tc. For the demonstration purposes, we also calculated the case with unrealistically large impurity scattering rates,
for the entire range of Tc. For the demonstration purposes, we also calculated the case with unrealistically large impurity scattering rates, 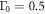 and
and 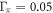 (dark yellow '
(dark yellow '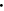 ' symbols), which displays
' symbols), which displays 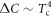 , a super-strong scaling.
, a super-strong scaling.
Figure 2. Numerical calculations of 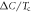 versus Tc with
versus Tc with 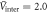 and
and 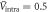 , for different impurity scattering strengths of
, for different impurity scattering strengths of 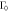 and
and 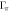 (in unit of
(in unit of 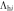 ). Horizontal dashed line is the BCS limit of
). Horizontal dashed line is the BCS limit of 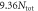 and the dotted lines of
and the dotted lines of 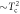 (BNC scaling) and
(BNC scaling) and 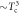 (super-strong scaling) are guides for the eyes.
(super-strong scaling) are guides for the eyes.
Download figure:
Standard image High-resolution imageAlthough it is not our main interest in this paper, we have a remark on the absolute magnitude of 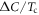 which is traditionally compared to the Sommerfeld coefficient
which is traditionally compared to the Sommerfeld coefficient 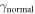 (
(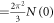 ). The BCS value
). The BCS value 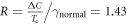 is a common criterion to indicate the strong coupling superconductors (if
is a common criterion to indicate the strong coupling superconductors (if 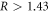 ). However, reliable measurement of
). However, reliable measurement of 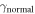 is difficult in most of cases and that was the original reason why Canfield and coworkers [1] plotted
is difficult in most of cases and that was the original reason why Canfield and coworkers [1] plotted 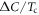 versus Tc instead of the conventional plotting of
versus Tc instead of the conventional plotting of 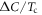 versus
versus  . In figure 2, the values of
. In figure 2, the values of 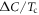 in clean limit (
in clean limit (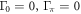 ) have a maximum value slightly above the BCS limit (
) have a maximum value slightly above the BCS limit (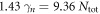 ) and other cases with finite impurity scatterings have the reduced values of
) and other cases with finite impurity scatterings have the reduced values of 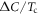 because the SH jump becomes broadened by the impurity scatterings—both by
because the SH jump becomes broadened by the impurity scatterings—both by 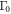 and
and 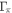 . These values and the trend are not inconsistent with most of experiments. Among the data collected in12
, it is notable that the Co-doped Ba(Fe
. These values and the trend are not inconsistent with most of experiments. Among the data collected in12
, it is notable that the Co-doped Ba(Fe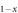 Cox)2As2 compounds have uniformly smaller value of
Cox)2As2 compounds have uniformly smaller value of 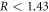 while the K-doped Ba
while the K-doped Ba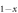 KxFe2As2 compounds have values R from slightly to moderately larger than
KxFe2As2 compounds have values R from slightly to moderately larger than 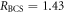 . As discussed in the next section, this different trend can be understood from the fact that the the K-doping in Ba
. As discussed in the next section, this different trend can be understood from the fact that the the K-doping in Ba KxFe2As2 does not introduce strong impurity scattering while the Co-doping in Ba(Fe
KxFe2As2 does not introduce strong impurity scattering while the Co-doping in Ba(Fe Cox)2As2 does introduce strong impurity scattering. And in general the magnitude of
Cox)2As2 does introduce strong impurity scattering. And in general the magnitude of 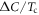 increases with increasing the strength of the pairing interaction (Vinter) due to a strong coupling effect as shown in figure 1(C).
increases with increasing the strength of the pairing interaction (Vinter) due to a strong coupling effect as shown in figure 1(C).
4. BNC scaling and its deviation
The main message of the numerical calculations in figures 1 and 2 is: (1) the strong non-BCS relation (see footnote 3) of 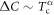 with a power α larger than
with a power α larger than 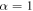 (BCS limit) is a generic feature of the multiband superconductors, and this is due to a pure kinematic constraint of equation (4); (2) however, the system needs some amount of impurity scattering (for example,
(BCS limit) is a generic feature of the multiband superconductors, and this is due to a pure kinematic constraint of equation (4); (2) however, the system needs some amount of impurity scattering (for example, 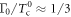 , the pink '
, the pink ' ' symbols in figure 2) to have the observed BNC scaling. If the impurity scattering strength is weaker, a deviation from the BNC scaling becomes stronger, in particular in the low Tc region. These theoretical features can consistently explain why a majority of the Fe-pnictide systems [1–9] follow the BNC scaling but some systems [10, 11] show a deviation from it.
' symbols in figure 2) to have the observed BNC scaling. If the impurity scattering strength is weaker, a deviation from the BNC scaling becomes stronger, in particular in the low Tc region. These theoretical features can consistently explain why a majority of the Fe-pnictide systems [1–9] follow the BNC scaling but some systems [10, 11] show a deviation from it.
We note that most of data which best fit the BNC scaling are from the electron doped compounds Ba(Fe TMx)2As2 (TM transition metals such as Co, Ni). Electron doping ions, replacing Fe sites, directly enters onto the Fe–As plane so that they introduce more efficient scattering centers (pair-breaking and non-pair-breaking (see footnote 9)). Therefore, the electron doped systems will have a sufficient strength of impurity scattering to produce an ideal BNC scaling as shown in figure 2. On the other hand, in the case of the hole doped systems such as (Ba
TMx)2As2 (TM transition metals such as Co, Ni). Electron doping ions, replacing Fe sites, directly enters onto the Fe–As plane so that they introduce more efficient scattering centers (pair-breaking and non-pair-breaking (see footnote 9)). Therefore, the electron doped systems will have a sufficient strength of impurity scattering to produce an ideal BNC scaling as shown in figure 2. On the other hand, in the case of the hole doped systems such as (Ba Kx)Fe2As2[10], (K
Kx)Fe2As2[10], (K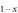 Nax)Fe2As2[8, 11], and (Ba
Nax)Fe2As2[8, 11], and (Ba Nax)Fe2As2[8], etc the doped ions enters in between the Fe–As planes so that they will introduce relatively weak scattering centers. Therefore, the hole doped systems would have more chance to be in the weak impurity scattering limit, hence would have more chance to deviate from the ideal BNC scaling. In fact, the case of (Ba
Nax)Fe2As2[8], etc the doped ions enters in between the Fe–As planes so that they will introduce relatively weak scattering centers. Therefore, the hole doped systems would have more chance to be in the weak impurity scattering limit, hence would have more chance to deviate from the ideal BNC scaling. In fact, the case of (Ba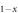 Kx)Fe2As2[10] shows a very strong deviation from the BNC scaling and the case of (K
Kx)Fe2As2[10] shows a very strong deviation from the BNC scaling and the case of (K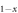 Nax)Fe2As2[8, 11] shows a moderate deviation as
Nax)Fe2As2[8, 11] shows a moderate deviation as 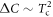 (although this power law has a large uncertainty because it has a very limited data distribution). On the other hand, another hole doped system (Ba
(although this power law has a large uncertainty because it has a very limited data distribution). On the other hand, another hole doped system (Ba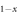 Nax)Fe2As2 [8] displays a perfect BNC scaling. According to our theory, we should conclude that Na ions substituting Ba ions should create relatively strong scattering centers although they enter in between the Fe–As planes. This speculation is quite reasonable because the difference of the ion sizes between Na1+ (period 3) and Ba2+ (period 6) is the largest compared to the other cases where the combinations are between
Nax)Fe2As2 [8] displays a perfect BNC scaling. According to our theory, we should conclude that Na ions substituting Ba ions should create relatively strong scattering centers although they enter in between the Fe–As planes. This speculation is quite reasonable because the difference of the ion sizes between Na1+ (period 3) and Ba2+ (period 6) is the largest compared to the other cases where the combinations are between 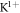 (period 4) and Ba2+ (period 6), and between Na1+ (period 3) and K1+ (period 4).
(period 4) and Ba2+ (period 6), and between Na1+ (period 3) and K1+ (period 4).
All these behaviors tell us that the BNC scaling is indeed a reflection of the specific features of the Fe-based superconductors. Namely, the slope of 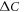 versus Tc in the Fe-based superconductors is universally much steeper than the BCS limit due to the generic feature of the multiband superconductors. Then doping inevitably provides a sufficient strength of impurity scattering (in particular, the electron doped cases) which makes the already steep slope of
versus Tc in the Fe-based superconductors is universally much steeper than the BCS limit due to the generic feature of the multiband superconductors. Then doping inevitably provides a sufficient strength of impurity scattering (in particular, the electron doped cases) which makes the already steep slope of 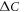 versus Tc into a BNC power law
versus Tc into a BNC power law 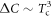 . When the impurity scattering is not sufficiently strong (mostly, hole doped systems), a varying degrees of deviation from the ideal BNC scaling would occur.
. When the impurity scattering is not sufficiently strong (mostly, hole doped systems), a varying degrees of deviation from the ideal BNC scaling would occur.
5. Coexistence region with the magnetic and SC orders
Experiments showed that the BNC scaling continues to be valid even when the spin density wave (SDW) order coexists with the SC order in the underdoped regime [5]. Therefore we would like to extend our model including the magnetic order in the underdoped regime. We consider only the hole doped region ![${\bar{N}}_{{\rm{h}}}\in [0.5,1]$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn305.gif) , because our model is symmetric with respect to the hole or electron dopings. We took a simple phenomenological approach ignoring the self-consistent calculation of the magnetic and the SC orders. We arbitrarily chose the coexistence region for
, because our model is symmetric with respect to the hole or electron dopings. We took a simple phenomenological approach ignoring the self-consistent calculation of the magnetic and the SC orders. We arbitrarily chose the coexistence region for 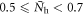 (this is the underdoped regime;
(this is the underdoped regime;  means no doping in our model), just for the sake of demonstration, and introduced the magnetic order
means no doping in our model), just for the sake of demonstration, and introduced the magnetic order 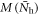 for this region by hand. This negligence of the self-consistency is a posteriori well justified by the result we found that the BNC scaling relation
for this region by hand. This negligence of the self-consistency is a posteriori well justified by the result we found that the BNC scaling relation 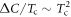 is insensitive to the details of
is insensitive to the details of 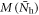 .
.
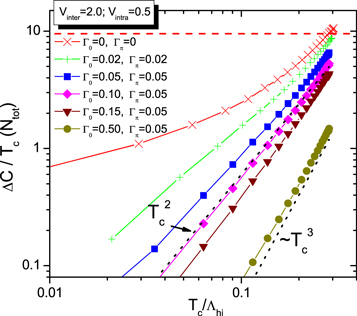
We assumed that the magnetic OP 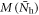 linearly grows from zero at
linearly grows from zero at  to a maximum value Mmax at
to a maximum value Mmax at  as shown in figure 3(A). When a finite M exists, it affects the superconductivity in two important ways: (1) it weakens the SC pair susceptibility and we take the simplest approximation as
as shown in figure 3(A). When a finite M exists, it affects the superconductivity in two important ways: (1) it weakens the SC pair susceptibility and we take the simplest approximation as 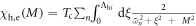 [15]; (2) the presence of SDW order M also removes a part of the FSs. Phenomenologically, we take this effect into account by linearly reducing the total DOS Ntot starting from
[15]; (2) the presence of SDW order M also removes a part of the FSs. Phenomenologically, we take this effect into account by linearly reducing the total DOS Ntot starting from  to a maximum reduction at
to a maximum reduction at  as
as ![${N}_{\mathrm{tot}}({\bar{N}}_{{\rm{h}}})={N}_{\mathrm{tot}}^{0}\left[1-a\frac{M({\bar{N}}_{{\rm{h}}})}{{{\rm{\Lambda }}}_{{\rm{h}}i}}\right]$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn317.gif) (a = 0.5 was chosen for calculations in figure 3; for example, Ntot reduced to
(a = 0.5 was chosen for calculations in figure 3; for example, Ntot reduced to 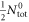 at
at  with
with 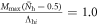 ). With these phenomenological ansätze, we solved the Tc-equations from equation (2) with fixed pairing interactions and impurity scattering rates (
). With these phenomenological ansätze, we solved the Tc-equations from equation (2) with fixed pairing interactions and impurity scattering rates (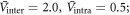 and
and 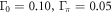 ) for three different strengths of
) for three different strengths of 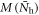 in figure 3(A). The results qualitatively simulate the experimental phase diagram: Tc starts decreasing when
in figure 3(A). The results qualitatively simulate the experimental phase diagram: Tc starts decreasing when  starts growing from
starts growing from  to a maximum value Mmax at
to a maximum value Mmax at  and the reduction of Tc is faster with a stronger magnetic order. For the region where M = 0 for
and the reduction of Tc is faster with a stronger magnetic order. For the region where M = 0 for 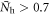 , the calculations of Tc and
, the calculations of Tc and 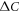 are the same as the results in figure 2.
are the same as the results in figure 2.
Figure 3. (A) Numerical calculations of Tc (solid symbols) versus 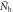 with coexisting magnetic order
with coexisting magnetic order  of three different strengths of
of three different strengths of 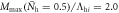
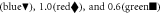 (in unit of
(in unit of 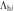 ). For the region
). For the region ![${\bar{N}}_{{\rm{h}}}\in [0.7,1]$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn334.gif) where
where 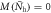 , Tc are all the same for three cases. Open symbols are the magnitudes of the corresponding magnetic order
, Tc are all the same for three cases. Open symbols are the magnitudes of the corresponding magnetic order 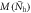 . The pairing interactions and the impurity scattering rates are chosen
. The pairing interactions and the impurity scattering rates are chosen 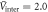 ,
, 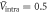 , and
, and 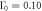 ,
, 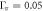 , respectively. (B) Calculated
, respectively. (B) Calculated 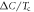 versus Tc for the corresponding three cases of (A). The results for the region
versus Tc for the corresponding three cases of (A). The results for the region ![${\bar{N}}_{{\rm{h}}}\in [0.7,1]$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn342.gif) where
where 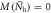 are the same for all three cases and displayed with dark yellow '
are the same for all three cases and displayed with dark yellow ' ' symbols.
' symbols.
Download figure:
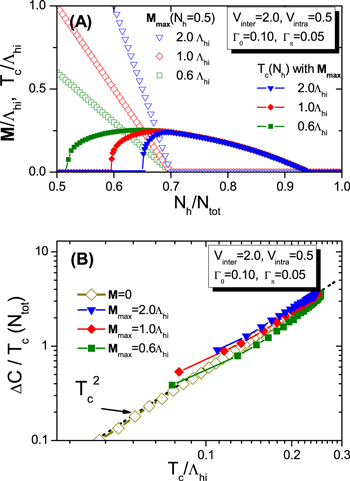
Standard image High-resolution imageIn figure 3(B), 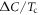 versus Tc is calculated for the corresponding three cases of figure 3(A). The data with dark yellow '
versus Tc is calculated for the corresponding three cases of figure 3(A). The data with dark yellow '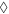 ' symbols, displaying the
' symbols, displaying the 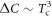 BNC scaling, is the same calculation as in figure 2 with
BNC scaling, is the same calculation as in figure 2 with 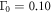 and
and 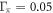 but only over the region
but only over the region ![${\bar{N}}_{{\rm{h}}}\in [0.7,1]$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn350.gif) where M = 0. Then the three solid symbols are the calculation results for the region of
where M = 0. Then the three solid symbols are the calculation results for the region of ![${\bar{N}}_{{\rm{h}}}\in [0.5,0.7]$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn351.gif) with three different strengths of magnetic order
with three different strengths of magnetic order 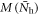 of figure 3(A). The results of figure 3(B) reveal an interesting behavior. Namely, while it is more natural to expect that the relation between
of figure 3(A). The results of figure 3(B) reveal an interesting behavior. Namely, while it is more natural to expect that the relation between 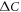 and Tc should dramatically change with and without a magnetic order [15], the calculations of figure 3(B) with the coexisting magnetic and SC orders show that the BNC scaling is robustly obeyed even with widely different strengths of M. We trace the origin of this surprising result to the fact that the underdoped region (i.e. where
and Tc should dramatically change with and without a magnetic order [15], the calculations of figure 3(B) with the coexisting magnetic and SC orders show that the BNC scaling is robustly obeyed even with widely different strengths of M. We trace the origin of this surprising result to the fact that the underdoped region (i.e. where 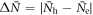 is small and Tc is maximum) is the region where the BNC scaling is best obeyed due to the kinematic constraint of the multiband superconductor when the magnetic order was not considered (see figures 1(c) and 2). Therefore, even if the magnetic order modifies the pair susceptibility
is small and Tc is maximum) is the region where the BNC scaling is best obeyed due to the kinematic constraint of the multiband superconductor when the magnetic order was not considered (see figures 1(c) and 2). Therefore, even if the magnetic order modifies the pair susceptibility  and cuts out some part of DOS from Ntot0, the generic kinematic constraint (equation (4)) of the multiband superconductor is still operative to enforce the BNC scaling relation.
and cuts out some part of DOS from Ntot0, the generic kinematic constraint (equation (4)) of the multiband superconductor is still operative to enforce the BNC scaling relation.
Finally, we emphasize that our approach here is only a mean field theory and did not include the fluctuation effect of the SDW order which would enhance the SH jump [36]. However, this fluctuations would also affect Tc and fully self-consistent calculations of the scaling relation of 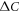 versus Tc including the fluctuation effects is beyond the scope of our theory.
versus Tc including the fluctuation effects is beyond the scope of our theory.
6. Summary and conclusions
We have shown that the puzzling BNC scaling relation 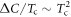 observed in a wide range of the FePn/Ch SC compounds [1–9] is a manifestation of the generic property of the multiband superconductor paired by a dominant inter-band pairing potential
observed in a wide range of the FePn/Ch SC compounds [1–9] is a manifestation of the generic property of the multiband superconductor paired by a dominant inter-band pairing potential 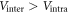 . While each of
. While each of 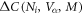 and
and 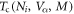 have non-trivial and non-universal dependencies on the material specific parameters such as the DOSs (Ni), pairing potentials (
have non-trivial and non-universal dependencies on the material specific parameters such as the DOSs (Ni), pairing potentials (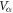 ), competition with SDW (M), etc, these non-universal dependencies are largely cancelled in the plot of
), competition with SDW (M), etc, these non-universal dependencies are largely cancelled in the plot of  versus Tc because
versus Tc because 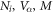 , etc are implicit variables in this plot. As such, the
, etc are implicit variables in this plot. As such, the 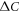 versus Tc plot filters out these material specific details and only reveals the universal and generic features of the Fe-based superconductors.
versus Tc plot filters out these material specific details and only reveals the universal and generic features of the Fe-based superconductors.
In this sense, the BNC plotting of 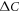 versus Tc was an ingenious idea—although it was originally done reluctantly in that way instead of the standard plotting of
versus Tc was an ingenious idea—although it was originally done reluctantly in that way instead of the standard plotting of 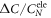 versus
versus 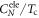 because of the lack of the reliable data of CeleN (the normal state electronic SH). In a similar sprit, but in theory, our minimal two band model is a maximally simplified model only to capture the origin of this universal behavior by filtering out (in fact ignoring) the numerous details of the real materials. Using this minimal model, we were able to identify the origin of this universal behavior: the presence of one single parameter
because of the lack of the reliable data of CeleN (the normal state electronic SH). In a similar sprit, but in theory, our minimal two band model is a maximally simplified model only to capture the origin of this universal behavior by filtering out (in fact ignoring) the numerous details of the real materials. Using this minimal model, we were able to identify the origin of this universal behavior: the presence of one single parameter 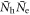 which governs both
which governs both 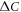 and Tc (see equations (5) and (7)) and the kinematic constraint
and Tc (see equations (5) and (7)) and the kinematic constraint 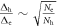 near Tc. Then a consideration of the non-pair-breaking impurity effect which broadens the quasiparticle spectra near Tc explains the systematic evolution from the ideal BNC scaling [1–9] to its deviations as found in Ba
near Tc. Then a consideration of the non-pair-breaking impurity effect which broadens the quasiparticle spectra near Tc explains the systematic evolution from the ideal BNC scaling [1–9] to its deviations as found in Ba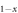 KxFe2As2[10] and K
KxFe2As2[10] and K NaxFe2As2[11]. In essence, the BNC scaling and its varying degree of deviations reconfirm the fact that the Fe-based superconductors are the multiband superconductors paired by a dominant interband interaction.
NaxFe2As2[11]. In essence, the BNC scaling and its varying degree of deviations reconfirm the fact that the Fe-based superconductors are the multiband superconductors paired by a dominant interband interaction.
Acknowledgments
YB was supported by Chonnam National University Grant 2014 and Grant No. 2013-R1A1A2-057535 of the National Research Foundation of Korea. GRS was supported by the US Department of Energy, Office of Basic Energy Sciences, Contract No. DE-FG02-86ER45268.
Footnotes
- 4
According to the standard single band BCS theory,
 . If we adopt this single band BCS formula to understand the typical BNC scaling data, it would require that the total DOS
. If we adopt this single band BCS formula to understand the typical BNC scaling data, it would require that the total DOS  of Fe-pnictides should change by two orders of magnitude by doping. Although there is a large uncertainty in the experimental data, the variation of
of Fe-pnictides should change by two orders of magnitude by doping. Although there is a large uncertainty in the experimental data, the variation of  by doping is less than a factor 3 (within the hole and electron doping regions, respectively) [12].
by doping is less than a factor 3 (within the hole and electron doping regions, respectively) [12]. - 5
In the strong pair-breaking limit (
 ) where
) where  is valid, the behavior of
is valid, the behavior of  should also change to
should also change to  instead of the BCS behavior
instead of the BCS behavior  . Then the SH jump in this limit becomes
. Then the SH jump in this limit becomes  , quite opposite to the BNC scaling.
, quite opposite to the BNC scaling. - 6
One assumption for this statement is that fermionic quasiparticles are defined as low energy excitations both at normal state and superconducting state, of course, with different contents for each phase. Then, the general form of entropy can always be written as
![${S}_{{\rm{e}}}=-2{k}_{B}{\sum }_{k}[(1-{f}_{k})\mathrm{ln}(1-{f}_{k})+{f}_{k}\mathrm{ln}{f}_{k}]$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=) (
( Fermi–Dirac distribution function). This statement is more general than the BCS theory and holds regardless of pairing mechanism. The SH jump
Fermi–Dirac distribution function). This statement is more general than the BCS theory and holds regardless of pairing mechanism. The SH jump  is derived by taking a differentiation as
is derived by taking a differentiation as  .
. - 7
This thermodynamic average formula is consistent with the experimental gap values. For example, in the optimal doped Ba
 K
K Fe2As2[30], the gap values
Fe2As2[30], the gap values  for the hole bands, combined with a estimate of the relative DOSs from the sizes of the FSs
for the hole bands, combined with a estimate of the relative DOSs from the sizes of the FSs  gives
gives  , and for the electron band gaps
, and for the electron band gaps  with
with  gives
gives  . The obtained values
. The obtained values  and
and  are then consistent with the inverse relation of our two band model (
are then consistent with the inverse relation of our two band model ( as
as  , and
, and  as
as  ).
). - 8
As we mentioned in footnote 4, Ntot can change by a factor 3 with dopings in real compounds. In our two band model, changing the value Ntot would change the results of
 and Tc. However, when we plot
and Tc. However, when we plot  versus Tc, the effect of varying Ntot is mostly cancelled in the relation of
versus Tc, the effect of varying Ntot is mostly cancelled in the relation of  versus Tc.
versus Tc. - 9
For the undoped parent compound BaFe2As2, our model assumes
 . For electron doping in Ba(Fe
. For electron doping in Ba(Fe Cox)2As2, hole pocket(s) disappears (
Cox)2As2, hole pocket(s) disappears ( ) around
) around  . For the hole doping cases, electron pockets(s) disappears (
. For the hole doping cases, electron pockets(s) disappears ( ) in (Ba
) in (Ba Kx)Fe2As2 when
Kx)Fe2As2 when  but in (Ba
but in (Ba Nax)Fe2As2 the electron pocket still remains when
Nax)Fe2As2 the electron pocket still remains when  . Therefore, the actual doping '
. Therefore, the actual doping ' ' and our model doping parameter
' and our model doping parameter  should be properly rescaled according to the Tc variation versus doping.
should be properly rescaled according to the Tc variation versus doping. - 10
In general, the impurity potential is a momentum dependent function
 . For the
. For the  -wave pairing state, a large momentum (
-wave pairing state, a large momentum ( ) scattering part acts as a pair-breaking component
) scattering part acts as a pair-breaking component  and the small momentum (
and the small momentum ( ) scattering part acts as a non-pair-breaking component
) scattering part acts as a non-pair-breaking component  .
. - 11
As can be seen in figure 1(c), any choice of values in between
 would yield qualitatively similar results. Also the dimensionless interaction
would yield qualitatively similar results. Also the dimensionless interaction  defined in our paper should be compared to a more conventional dimensionless interaction, defined in the Tc-equation (see equation (5)),
defined in our paper should be compared to a more conventional dimensionless interaction, defined in the Tc-equation (see equation (5)),  . This means that the typical dimensionless coupling strength can be
. This means that the typical dimensionless coupling strength can be  .
. - 12






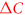

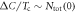
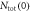
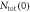
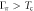
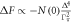
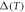
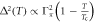
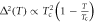
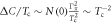
![${S}_{{\rm{e}}}=-2{k}_{B}{\sum }_{k}[(1-{f}_{k})\mathrm{ln}(1-{f}_{k})+{f}_{k}\mathrm{ln}{f}_{k}]$](https://content.cld.iop.org/journals/1367-2630/18/2/023017/revision1/njpaa11a0ieqn57.gif)