Abstract
We suggest that the force F exerted upon a chiral molecule by light assumes the form 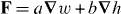 under appropriate circumstances, where a and b pertain to the molecule whilst w and h are the local densities of electric energy and helicity in the optical field; the gradients
under appropriate circumstances, where a and b pertain to the molecule whilst w and h are the local densities of electric energy and helicity in the optical field; the gradients  of these quantities thus governing the molecule's centre-of-mass motion. Whereas a is identical for the mirror-image forms or enantiomers of the molecule, b has opposite signs; the associated contribution to F therefore pointing in opposite directions. A simple optical field is presented for which
of these quantities thus governing the molecule's centre-of-mass motion. Whereas a is identical for the mirror-image forms or enantiomers of the molecule, b has opposite signs; the associated contribution to F therefore pointing in opposite directions. A simple optical field is presented for which 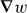 vanishes but
vanishes but 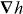 does not, so that F is absolutely discriminatory. We then present two potential applications: a Stern–Gerlach-type deflector capable of spatially separating the enantiomers of a chiral molecule and a diffraction grating to which chiral molecules alone are sensitive; the resulting diffraction patterns thus encoding information about their chiral geometry.
does not, so that F is absolutely discriminatory. We then present two potential applications: a Stern–Gerlach-type deflector capable of spatially separating the enantiomers of a chiral molecule and a diffraction grating to which chiral molecules alone are sensitive; the resulting diffraction patterns thus encoding information about their chiral geometry.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
It was Kelvin who introduced the word chiral [1, 2] to refer to any geometrical figure or group of points that cannot be brought into coincidence with its image as seen in a plane mirror, thus possessing a sense of handedness. Chirality pervades the natural world [3], from the enigmatic preferences of the weak interaction [4, 5] to the helices traced out by the arms of spiral galaxies [6].
Under 'normal' circumstances, an atom is essentially achiral as it possesses the high degree of symmetry associated with a sphere [7]. In contrast, many types of molecule are chiral owing to the nature and arrangement in space of their constituent atoms [3]. The separate and seemingly stable existence of mirror-image forms, or enantiomers, of certain chiral molecules is a remarkable example of symmetry breaking [7]: see figure 1. Whilst they are similar in many respects, the enantiomers of a chiral molecule can, for example, exert drastically different influences upon living things, the inner workings of which are themselves invariably chiral [3, 10]. The development of means to detect and discriminate between the enantiomers of a chiral molecule is a task of utmost importance and, indeed, constitutes a vibrant field of modern research [11, 12].
Figure 1. The left-handed (a) and right-handed (b) enantiomers of hexahelicene, a chiral molecule with a shape resembling that of a finite cylindrical helix. The normalized pitch γ of hexahelicene is a pseudoscalar: it assumes opposite signs for the molecule's enantiomers [7–9].
Download figure:
Standard image High-resolution imageIt is well established that chiral molecules can exert discriminatory mechanical forces upon each other [13–15]. In recent years, interest has been expressed regarding the possibility of using light, such as that produced by a laser, to exert a mechanical force of discriminatory character upon a single chiral molecule [16–21]. The present paper is concerned with this possibility. Specifically, we suggest that the centre-of-mass motion of a chiral molecule is, under appropriate circumstances, sensitive to gradients in the helicity of an optical field and observe that the force associated with these gradients points in opposite directions for the molecule's enantiomers (section 2). We present a simple optical field for which this phenomenon is brought to prominence (section 3) and propose two potential applications, namely a Stern–Gerlach-type deflector capable of spatially separating the enantiomers of a chiral molecule (section 4) and a diffraction grating to which chiral molecules alone are sensitive, the resulting diffraction patterns thus encoding information about their chiral geometry (section 5). Our approach differs, it seems, from others that have been presented in the literature [16–20] in that we make no critical assumptions regarding the energy-level structure of our molecule but rather, rely upon the sign of a certain polarizability. Whilst drafting the present paper for submission, however, another paper of closely related content was published, independently, on the arXiv [21]. We believe that our contributions are complementary.
In what follows, we consider ourselves to be in an inertial frame of reference and adopt a right-handed Cartesian coordinate system (x,y and z), employing SI units.
2. Force exerted by light upon a chiral molecule
Consider a 'small', neutral, non-polar, non-magnetic, chiral molecule irradiated by monochromatic light of angular frequency ω that is (otherwise) freely propagating. We shall presume that the Coulomb field binding the molecule together is 'sufficiently' stronger than the optical field [13], that the molecule is 'essentially' transparent at ω, which we take to be far off-resonance (in the near infrared, perhaps), and that the molecule has come into contact with the optical field in an adiabatic manner [22]. A simple, classical picture then emerges in which the optical field drives steady oscillations of the molecule's charge and current distributions, also at angular frequency ω, the radiation attributable to these oscillations constituting Rayleigh scattered light [7, 13]. During the course of their interactions, the optical field will, in general, exchange linear momentum with the molecule, giving rise to a force which governs the molecule's centre-of-mass motion.
We derive an expression for the force using only classical electromagnetism. The electric field E = E(r,t) and magnetic flux density B = B(r,t) that comprise the light, which we treat as an externally imposed influence acting upon the molecule, evolve as functions of space r and time t in accord with the charge-free Maxwell equations:




Here 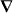 is the gradient operator with respect to r, an overdot is used to indicate (partial) differentiation with respect to t,
is the gradient operator with respect to r, an overdot is used to indicate (partial) differentiation with respect to t,  0 and μ0 are the electric and magnetic constants and
0 and μ0 are the electric and magnetic constants and  is the speed of light [23–25]. As the optical field is presumed monochromatic, it is convenient to introduce complex (denoted by a tilde) quantities
is the speed of light [23–25]. As the optical field is presumed monochromatic, it is convenient to introduce complex (denoted by a tilde) quantities 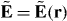 and
and 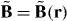 defined such that
defined such that


where the function ℜ yields the real part of its argument [24, 25]. It should be noted that we are not restricting ourselves to the consideration of a single plane wave or even a single beam of light. Instead, we work with the presumed forms (2.5) and (2.6) in direct accord with the charge-free Maxwell equations (2.1)–(2.4), which are general and exact. We are thus free in what follows to consider, in particular, any suitable superposition of plane electromagnetic waves of angular frequency ω. This freedom allows us to construct rather exotic optical fields [26], the unusual properties of which open the door to novel possibilities, as we shall see. We consider the molecule to consist of a collection of non-relativistic point particles (labelled n = 1,2,...) of charge qn, mass mn and position rn = rn(t). Some of these particles are electrons, the remainder are nuclei. It is convenient, albeit artificial, to suppose, at present, that the centre of mass 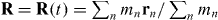 of the molecule is fixed at some position
of the molecule is fixed at some position 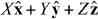 in the optical field, where
in the optical field, where  ,
,  and
and 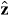 are unit vectors for the x, y and z axes. We neglect the forces experienced by the particles due to their own electromagnetic fields, which give rise, in particular, to radiation reaction effects [23–25]. Moreover, we approximate the true electromagnetic interactions between the particles by non-retarded Coulomb interactions [23], the forces associated with which cancel for any given pair of particles. Thus, the net electromagnetic force
are unit vectors for the x, y and z axes. We neglect the forces experienced by the particles due to their own electromagnetic fields, which give rise, in particular, to radiation reaction effects [23–25]. Moreover, we approximate the true electromagnetic interactions between the particles by non-retarded Coulomb interactions [23], the forces associated with which cancel for any given pair of particles. Thus, the net electromagnetic force 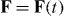 experienced by the molecule derives solely from the Lorentz forces [23–25] exerted upon the individual particles by the optical field
experienced by the molecule derives solely from the Lorentz forces [23–25] exerted upon the individual particles by the optical field
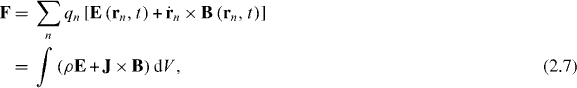
where ρ = ρ(r,t) and J = J(r,t) are the charge and current densities attributable to the molecule


with δ(r) the three-dimensional Dirac delta function. Introducing the associated electric polarization P = P(r,t) and magnetization M = M(r,t) fields4
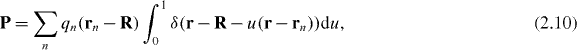
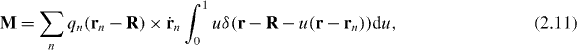
through the relations 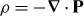 and
and 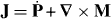 [13, 23], we find that
[13, 23], we find that
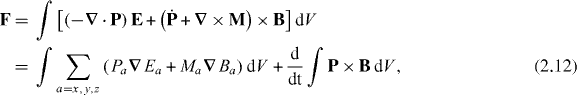
where we have performed integrations by parts and have made use of the Faraday–Lenz law (2.3) [27]. Being a total derivative with respect to t, the third term here contributes nothing when averaged in time over an optical period 2π/ω.5 Expanding δ(r − R − u(rn − R)) about r − R in P and M on the second line of (2.12) yields a multipole expansion of F: a sum of terms in which the electric-multipole moments (from P) and mechanical magnetic-multipole moments (from M) [7, 13, 23] of the molecule's charge and current distributions couple to various spatial derivatives of the components of E and B. The contributions to these multipole moments that are induced by the optical field can be related to the latter through the use of appropriate polarizabilty tensors and pseudotensors [7, 31].
We imagine that the molecule is 'tumbling' freely in the optical field6 and content ourselves accordingly with an examination of the cycle-averaged (denoted by an overbar), rotationally averaged (denoted by angular brackets) form 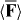 of the multipolar expansion of F, restricting our attention to those terms that are of leading order under 'typical' circumstances. To arrive at our desired result, we consider the molecule's electric-dipole moment μ = μ(t), its symmetric and traceless electric-quadrupole moment Θ = Θ(t) and its mechanical magnetic-dipole moment7 m' = m'(t). The rotationally averaged forms 〈μ〉 = 〈μ〉(t), 〈Θ〉 = 〈Θ〉(t) and 〈m'〉 = 〈m'〉(t) are, to the order of present interest, expressible as
of the multipolar expansion of F, restricting our attention to those terms that are of leading order under 'typical' circumstances. To arrive at our desired result, we consider the molecule's electric-dipole moment μ = μ(t), its symmetric and traceless electric-quadrupole moment Θ = Θ(t) and its mechanical magnetic-dipole moment7 m' = m'(t). The rotationally averaged forms 〈μ〉 = 〈μ〉(t), 〈Θ〉 = 〈Θ〉(t) and 〈m'〉 = 〈m'〉(t) are, to the order of present interest, expressible as



with the complex quantities  and
and 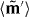 related to the optical field via
related to the optical field via


The vanishing of 〈Θ〉 seen in (2.14) is a direct consequence of the rotational averaging procedure8 [7, 13]. A subscripted zero accompanying a pair of brackets indicates evaluation at R whilst 3α = αxx(fω) + αyy(fω) + αzz(fω) and 3G' = G'xx(fω) + G'yy(fω) + G'zz(fω) are the traces of the dispersive pieces of the molecule's unprimed electric-dipole/electric-dipole polarizability tensor αab(fω) and primed electric-dipole/magnetic-dipole polarizability pseudotensor G'ab(fω), where fω is the molecule's dispersion lineshape evaluated at ω [7]. The forms seen in (2.13)–(2.17) may be justified through appropriate semi-classical calculations, for example: see [7], where explicit quantum-mechanical expressions for 3α and 3G' are presented. In adopting the forms seen in (2.16) and (2.17), we have presumed the relevant unperturbed energy eigenstate wavefunctions of the molecule to be real, as may be done in the absence of externally imposed time-odd influences such as a static magnetic flux density, provided these eigenstates are non-degenerate [7, 22]. Taking the rotationally averaged electric polarization 〈P〉 = 〈P〉(r,t) and magnetization 〈M〉 = 〈M〉(r,t) fields to be


we find that 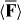 is conservative and is comprised of two distinct pieces
is conservative and is comprised of two distinct pieces

where the potential energies Uw = Uw(r) and Uh = Uh(r) are introduced below.
Note that in obtaining the result seen in (2.20) we supposed R to be fixed. In what follows, however, we employ this result to describe scenarios in which R may be changing with time. In doing so, we neglect certain phenomena that are attributable directly to the centre-of-mass motion of the molecule (Röntgen current, Doppler shifts, etc [13, 32]), the effects of which will be 'small' for realistic molecular speeds.
The potential energy Uw seen in the first term of (2.20) is the familiar 'dipole' potential energy [31, 32]:

where wE = wE(r,t) is an electric energy density of the optical field [24, 25]:

Except for a factor of twice the speed of light c, 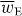 is often referred to loosely as the 'intensity' of an optical field, although this nomenclature is not appropriate in general. It seems natural that 3α should appear in connection with wE. The former is a time-even scalar associated with the interference of electric-dipole transition moments within a molecule [7] whilst the latter is a time-even scalar field that is also of apparent electric character [24]. For ω far off-resonance, 3α may be well-approximated by its static value, which is usually positive [7, 33]. In general, wE is also positive although it may, of course, vanish at certain points in space at certain times [26]. Uw thus attracts the molecule towards those regions in the optical field where
is often referred to loosely as the 'intensity' of an optical field, although this nomenclature is not appropriate in general. It seems natural that 3α should appear in connection with wE. The former is a time-even scalar associated with the interference of electric-dipole transition moments within a molecule [7] whilst the latter is a time-even scalar field that is also of apparent electric character [24]. For ω far off-resonance, 3α may be well-approximated by its static value, which is usually positive [7, 33]. In general, wE is also positive although it may, of course, vanish at certain points in space at certain times [26]. Uw thus attracts the molecule towards those regions in the optical field where 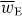 is maximum. The employment of the dipole potential energy to manipulate molecules has been pursued in a wealth of theoretical [33–49] and experimental [50–67] contexts.
is maximum. The employment of the dipole potential energy to manipulate molecules has been pursued in a wealth of theoretical [33–49] and experimental [50–67] contexts.
The potential energy Uh seen in the second term of (2.20) is

where h = h(r,t) is a helicity density of the optical field [26, 70–73]

with A⊥ = A⊥(r,t) and C⊥ = C⊥(r,t) the transverse, gauge-invariant pieces [23] of the familiar magnetic vector potential [24, 25] and an analogous electric pseudovector potential [68, 69] defined here such that 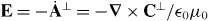 and
and 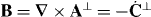 . Helicity is a property of light that is familiar from particle physics, where it is recognized as being the value taken by the component of a photon's spin angular momentum in the direction of propagation: the helicity
. Helicity is a property of light that is familiar from particle physics, where it is recognized as being the value taken by the component of a photon's spin angular momentum in the direction of propagation: the helicity  of an optical field assumes a value equivalent to ±ℏ per circularly polarized plane-wave-mode photon, in particular [26, 70–73]. Locally, h is found to be time independent for a strictly monochromatic optical field and may exhibit other interesting characteristics besides [26]. It seems natural that 3G' should appear in connection with h. The former is a time-even pseudoscalar associated with the mutual interference of electric-dipole and magnetic-dipole transition moments within a molecule [7] whilst the latter is a time-even pseudoscalar field that embodies the electric-magnetic symmetry inherent to freely propagating light [73–77]. Moreover, such transformation properties are the hallmarks of true chirality [7, 78–81] and indeed, 3G' possesses equal magnitudes but opposite signs for the enantiomers of a chiral molecule [13, 15, 22] whilst
of an optical field assumes a value equivalent to ±ℏ per circularly polarized plane-wave-mode photon, in particular [26, 70–73]. Locally, h is found to be time independent for a strictly monochromatic optical field and may exhibit other interesting characteristics besides [26]. It seems natural that 3G' should appear in connection with h. The former is a time-even pseudoscalar associated with the mutual interference of electric-dipole and magnetic-dipole transition moments within a molecule [7] whilst the latter is a time-even pseudoscalar field that embodies the electric-magnetic symmetry inherent to freely propagating light [73–77]. Moreover, such transformation properties are the hallmarks of true chirality [7, 78–81] and indeed, 3G' possesses equal magnitudes but opposite signs for the enantiomers of a chiral molecule [13, 15, 22] whilst 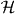 itself possesses equal magnitudes but opposite signs for the enantiomorphs of an optical field [26, 71–73]. Thus, the force associated with Uh is entirely discriminatory, pointing in opposite directions for the enantiomers of the molecule: Uh attracts the enantiomer for which 3G' > 0 towards those regions in the optical field where
itself possesses equal magnitudes but opposite signs for the enantiomorphs of an optical field [26, 71–73]. Thus, the force associated with Uh is entirely discriminatory, pointing in opposite directions for the enantiomers of the molecule: Uh attracts the enantiomer for which 3G' > 0 towards those regions in the optical field where 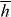 is minimum whilst the opposite enantiomer, with 3G' < 0, is instead attracted to those regions in the optical field where
is minimum whilst the opposite enantiomer, with 3G' < 0, is instead attracted to those regions in the optical field where 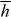 is maximum. We suggest, therefore, that Uh represents something of a marriage between the chirality of the molecule and the chirality of the optical field. This, in essence, is our main result.
is maximum. We suggest, therefore, that Uh represents something of a marriage between the chirality of the molecule and the chirality of the optical field. This, in essence, is our main result.
It seems that the explicit identification of 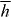 in Uh is only possible because we are restricting our attention to a monochromatic, optical field. In this context, it appears, in fact, that we could equally well have identified any one of an infinite number of lower- and higher-order extensions of h [71, 73, 82], amongst them, the 00-zilch density Z000 [83, 84], which was re-introduced into the literature recently in connection with fluorescence-detected circular dichroism [85] and has since been considered in a sizeable body of research [21, 86–97]. A similar ambiguity prevails when considering the explicit identification of
in Uh is only possible because we are restricting our attention to a monochromatic, optical field. In this context, it appears, in fact, that we could equally well have identified any one of an infinite number of lower- and higher-order extensions of h [71, 73, 82], amongst them, the 00-zilch density Z000 [83, 84], which was re-introduced into the literature recently in connection with fluorescence-detected circular dichroism [85] and has since been considered in a sizeable body of research [21, 86–97]. A similar ambiguity prevails when considering the explicit identification of 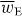 in Uw and we observe more generally that it does not appear possible to identify every term in the complete form of
in Uw and we observe more generally that it does not appear possible to identify every term in the complete form of 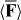 with the density of a familiar quantity in a convincing manner. This fact becomes clear, perhaps, when one considers those contributions to our molecule's response that are nonlinear in our optical field. Thus, such identifications can hardly be said to be of any fundamental significance. They do, however, provide us with useful pictures.
with the density of a familiar quantity in a convincing manner. This fact becomes clear, perhaps, when one considers those contributions to our molecule's response that are nonlinear in our optical field. Thus, such identifications can hardly be said to be of any fundamental significance. They do, however, provide us with useful pictures.
Although the derivation given in the present section and indeed, the concept of a force, is classical in nature, we note that the forms of Uw and Uh can also be justified by an appropriate calculation in the quantum domain.
3. Bringing the discriminatory optical force to prominence
In section 2, we found that the cycle-averaged, rotationally averaged force 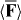 exerted upon the molecule by the optical field could be expressed as
exerted upon the molecule by the optical field could be expressed as

The first term here points in the same direction for the enantiomers of the molecule whereas the second term points in opposite direction and is, therefore, the contribution to  that we envisage using to manipulate the centre-of-mass motion of the molecule in a discriminatory manner. A simple estimate reveals that the ratio |cα/G'| is 'typically' of the order of 1 × 103 [7, 13, 14] and so it may appear that the first term dominates. However, this need not be the case: we can, in fact, eliminate the first term so that
that we envisage using to manipulate the centre-of-mass motion of the molecule in a discriminatory manner. A simple estimate reveals that the ratio |cα/G'| is 'typically' of the order of 1 × 103 [7, 13, 14] and so it may appear that the first term dominates. However, this need not be the case: we can, in fact, eliminate the first term so that 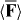 is in turn entirely discriminatory, by constructing the optical field such that the cycle-averaged electric energy density
is in turn entirely discriminatory, by constructing the optical field such that the cycle-averaged electric energy density 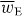 is homogeneous (and, therefore,
is homogeneous (and, therefore, 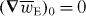 ) whilst the cycle-averaged helicity density
) whilst the cycle-averaged helicity density 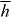 is not (and (
is not (and (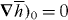 ).
).
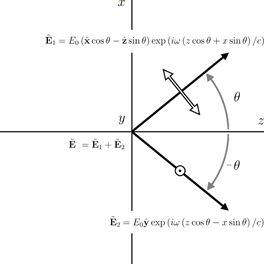
To demonstrate this, we consider one such optical field [26] which is constructed by superposing two linearly polarized plane electromagnetic waves of equal amplitude E0 > 0 and angular frequency ω, propagating such that their wavevectors lie in the x-z-plane making angles of ±θ (θ > 0) with the +z-axis. We take the electric fields of the ±θ waves to be oscillating in the x-z-plane and parallel to the y-axis, respectively: see figure 2. We suppose that θ ≪ 1 but work in an exact manner at present nonetheless, taking the complex quantity 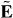 to be
to be
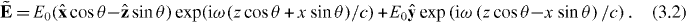
From (2.22), we find that 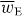 is homogeneous
is homogeneous

which is unsurprising given that the waves possess orthogonal polarizations and so do not interfere. From (2.24), we find, however, that 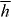 undulates in x
undulates in x

a characteristic attributable to the undulation, in x, of the relative phase of the waves, with associated wavenumber κ = 2ω sin θ/c. We refer to these undulations in h as helicity fringes [26]. Optical fields of this character have been produced experimentally in various contexts [98–100]. From (2.21), (2.23), (3.3) and (3.4) we have that Uw and Uh are


From (2.20), 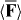 is then
is then

which is non-vanishing, in general, and points in opposite directions for the enantiomers of the molecule by virtue of the opposite signs of the trace 3G', as claimed. See figure 3.
Figure 2. The structure of the optical field presented in section 3. Wavevectors and polarizations are depicted by black arrows and white arrows.
Download figure:
Standard image High-resolution imageFigure 3. Plots pertaining to the optical field presented in section 3. We consider 2π/κ ⩾ x ⩾ − 2π/κ, the specific values of y and z being irrelevant. (a) The potential energies Uw and Uh seen in (3.5) and (3.6), the latter being depicted for positive and negative values of the trace 3G'. (b) The x-component 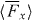 of the associated cycle-averaged, rotationally averaged force
of the associated cycle-averaged, rotationally averaged force 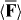 seen in (3.7), again depicted for positive and negative values of 3G'. (c) A two-dimensional section of the optical field with regions of negative helicity and positive helicity depicted in dark purple and light green. The influence of
seen in (3.7), again depicted for positive and negative values of 3G'. (c) A two-dimensional section of the optical field with regions of negative helicity and positive helicity depicted in dark purple and light green. The influence of 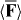 is indicated here for the enantiomers of hexahelicene (see figure 1) by black arrows. Not to scale.
is indicated here for the enantiomers of hexahelicene (see figure 1) by black arrows. Not to scale.
Download figure:
Standard image High-resolution imageIt is possible, of course, to conceive of many other optical fields for which 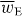 is homogeneous whilst
is homogeneous whilst  is not. We emphasize that
is not. We emphasize that 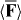 is entirely discriminatory in all such cases. The simple examples of which we are aware are obtained, as above, from various superpositions of electromagnetic waves that possess orthogonal polarizations [26, 101].
is entirely discriminatory in all such cases. The simple examples of which we are aware are obtained, as above, from various superpositions of electromagnetic waves that possess orthogonal polarizations [26, 101].
4. Newtonian molecular optics: chiral Stern–Gerlach deflector
The field of Newtonian molecular optics is concerned with the manipulation of the centre-of-mass motion of a molecule in a regime where the motion can be viewed classically [32], as we have presumed to be the case so far. The dipole potential energy Uw seen in (2.21) and its contribution to the force 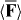 seen in (2.20) have been utilized successfully in this regime in a multitude of experiments [50, 51, 53, 55, 56, 58–61, 65–67]. It is natural, therefore, to investigate the novel possibilities offered for our molecule in the regime of Newtonian molecular optics by the discriminatory potential energy Uh seen in (2.23) and its contribution to
seen in (2.20) have been utilized successfully in this regime in a multitude of experiments [50, 51, 53, 55, 56, 58–61, 65–67]. It is natural, therefore, to investigate the novel possibilities offered for our molecule in the regime of Newtonian molecular optics by the discriminatory potential energy Uh seen in (2.23) and its contribution to  .
.
The use of an optical field akin to the one presented in section 3 to deflect the centre-of-mass trajectory of the molecule in a discriminatory manner with a single helicity fringe, say, presents itself as one possibility: see figure 4. Such a device may, for example, be employed to spatially separate the enantiomers of a chiral molecule. In apparent analogy to a traditional Stern–Gerlach deflector [102], we refer to it as a chiral Stern–Gerlach deflector. Closely related devices have been proposed theoretically elsewhere [16, 18–20], albeit making use of seemingly different mechanisms.
Figure 4. The principle of operation of our chiral Stern–Gerlach deflector, depicted here for the enantiomers of hexahelicene (see figure 1). (a) A single helicity fringe deflects the left-handed enantiomer to the left. (b) The same fringe deflects the right-handed enantiomer to the right. Not to scale.
Download figure:
Standard image High-resolution imageWe perform a simple estimate to gauge the feasibility of our chiral Stern–Gerlach deflector. We suppose that the molecule, of mass M, resides, at some initial time t = 0, at the origin of the optical field presented in section 3, moving in the +z direction with speed Vz. We suppose, moreover, that its subsequent centre-of-mass motion is governed by Newton's second law and the cycle-averaged, rotationally averaged force 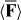 seen in (3.7). Considering an interaction time
seen in (3.7). Considering an interaction time 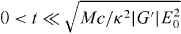 such that the molecule does not reach its nearest helicity trough or peak and |X(t)| ≪ π/2κ, we deduce that its angular deflection ϕ = ϕ(t), as measured with respect to the +z-axis, is given approximately by
such that the molecule does not reach its nearest helicity trough or peak and |X(t)| ≪ π/2κ, we deduce that its angular deflection ϕ = ϕ(t), as measured with respect to the +z-axis, is given approximately by

to first order in the angle θ here and also ϕ, as we presume that θ,ϕ ≪ 1. We consider an optical angular frequency ω that corresponds to a free-space wavelength of 2πc/ω = 1.064 × 10−6 m, which lies in the near infrared to which many molecules are indeed essentially transparent [50, 51, 53, 55, 56, 58–61, 65, 67]. We choose θ, and hence, the wavenumber κ = 2ωθ/c, to yield helicity fringes of wavelength 2π/κ = 1 × 10−5 m, which is also in line with experimental demonstrations [99, 100]. As an example, we consider hexahelicene, a chiral molecule with M = 5.45 × 10−25 kg: see figure 1 [7–9]. Using an empirical result obtained from a measurement of specific rotation [7–9], together with an appropriate theoretical angular frequency scaling [7, 103], we estimate hexahelicene's trace to be 3G' = ± 1 × 10−34 m kg−1 s3 A2; the plus and minus signs referring to the left-handed and right-handed enantiomers of the molecule. We consider an amplitude E0 that corresponds to a notional intensity of  0cE20 = 1 × 1015 kg s−3, the latter being approximately one order of magnitude smaller than that typically employed [50, 51, 53, 56, 58–61, 65, 67]. This may help to reduce the possible effects of polarization-dependent alignment [65, 66] that threaten to complicate our picture and also allows us, we assume, to consider t = 1 × 10−6 s, which is approximately two orders of magnitude larger than usual [50, 51, 53, 55, 56, 58–61, 65, 67]: the probabilities of certain processes such as multi-photon ionization that promise to damage the molecule, thus limiting the maximum interaction time, scale in a highly nonlinear fashion with intensity [50, 51]. We take Vz = 1 × 102 m s−1, as may be obtained, perhaps, with a velocity selector [104], and identify a notional width Vzt = 1 × 10−4 m of the optical field. Using these values in (4.1), we find that
0cE20 = 1 × 1015 kg s−3, the latter being approximately one order of magnitude smaller than that typically employed [50, 51, 53, 56, 58–61, 65, 67]. This may help to reduce the possible effects of polarization-dependent alignment [65, 66] that threaten to complicate our picture and also allows us, we assume, to consider t = 1 × 10−6 s, which is approximately two orders of magnitude larger than usual [50, 51, 53, 55, 56, 58–61, 65, 67]: the probabilities of certain processes such as multi-photon ionization that promise to damage the molecule, thus limiting the maximum interaction time, scale in a highly nonlinear fashion with intensity [50, 51]. We take Vz = 1 × 102 m s−1, as may be obtained, perhaps, with a velocity selector [104], and identify a notional width Vzt = 1 × 10−4 m of the optical field. Using these values in (4.1), we find that

Even for our optimistic estimate, ϕ is rather 'small'. Nevertheless, we hope that such deflections may be detectable in careful experiments.
It is possible, of course, to conceive of other novel possibilities offered for chiral molecules in the regime of Newtonian molecular optics by Uh and its contribution to 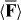 . At present, however, we turn our attention to a more delicate but sensitive regime, namely that of de Broglie molecular optics.
. At present, however, we turn our attention to a more delicate but sensitive regime, namely that of de Broglie molecular optics.
5. de Broglie molecular optics: chiral diffraction grating
In contrast to Newtonian molecular optics, de Broglie molecular optics is concerned with the manipulation of the centre-of-mass motion of a molecule in the delicate but sensitive regime where the motion cannot be viewed classically but rather should be viewed quantum mechanically [32]. The dipole potential energy Uw seen in (2.21) has also been utilized successfully in this regime in various experiments [57, 62–64, 105]. It seems natural, therefore, to enquire as to the novel possibilities offered for our molecule in the regime of de Broglie molecular optics by the discriminatory potential energy Uh seen in (2.23).
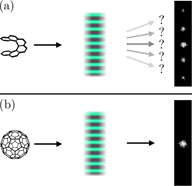
We recognize, for example, the possibility of using an optical field akin to the one presented in section 3 to diffract the molecule by virtue of its chirality. Specifically, we imagine employing a collection of helicity fringes as an optical phase grating to which the molecule is sensitive by virtue of its non-vanishing trace 3G' ≠ 0. As a similar achiral molecule can only support a vanishing trace 3G' = 0 [13, 15, 22], it will not 'sense' these helicity fringes and thus, will not exhibit such diffraction: see figure 5. A device of this nature may constitute an incisive probe for chiral molecules in that the diffraction patterns it produces encode information regarding the molecules' chiral geometry. We refer to our device simply as a chiral diffraction grating.
Figure 5. The principle of operation of our chiral diffraction grating. (a) A chiral molecule such as the right-handed enantiomer of hexahelicene (see figure 1) is diffracted by a collection of helicity fringes. (b) An achiral molecule such as buckminsterfullerene (C60) does not 'sense' these fringes and hence, is not diffracted. Not to scale.
Download figure:
Standard image High-resolution imageLet us now consider the results of some simple calculations pertaining to our chiral diffraction grating. We suppose that the molecule, of mass M, resides in the optical field presented in section 3 and describe it as a point particle behaving in accord with the Schrödinger equation under the influence of the potential energies Uw and Uh seen in (3.5) and (3.6). We suppose, moreover, that the molecule occupies, at some initial time t = 0, a linear momentum eigenstate with eigenvalue 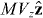 , where Vz is a speed. Considering an interaction time 0 < t ≪ 2Mc2/ℏω2 significantly shorter than the inverse of the single-photon recoil angular frequency, say, we employ the Raman–Nath approximation and find, following a slight variant of a standard calculation [106], that the molecule evolves into a superposition of linear momentum eigenstates with eigenvalues
, where Vz is a speed. Considering an interaction time 0 < t ≪ 2Mc2/ℏω2 significantly shorter than the inverse of the single-photon recoil angular frequency, say, we employ the Raman–Nath approximation and find, following a slight variant of a standard calculation [106], that the molecule evolves into a superposition of linear momentum eigenstates with eigenvalues 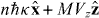 , where n∈{0,±1,...} and the probabilities pn = pn(t) associated with these eigenvalues are
, where n∈{0,±1,...} and the probabilities pn = pn(t) associated with these eigenvalues are

to first order in the angle θ ≪ 1 here, with ℏ the reduced Planck constant and Jn the Bessel function of the first kind of order n. In reality, we may associate t with a notional width d of the optical field as t = d/Vz. The Raman–Nath approximation then corresponds to a 'thin' [32, 106] chiral diffraction grating and the relative intensities of the diffraction orders observable in the far-field [57, 105], for example, are governed by the pn. It will be noticed that the pn depend upon the magnitude of 3G' but not the sign. They are, therefore, equal for the enantiomers of the molecule. Consider now, as in section 4, an optical angular frequency ω that corresponds to a free-space wavelength of 2πc/ω = 1.064 × 10−6 m and hexahelicene, for which we estimate 3G' = ± 1 × 10−34 m kg−1 s3 A2, as will be recalled. In line with an analogous experiment in which the diffraction of fullerenes due to their interaction with a traditional optical standing wave was observed, we consider Vz = 1 × 102 m s−1 and d = 5 × 10−5 m [57, 105], corresponding to t = d/Vz = 5 × 10−7 s. With 3G' and t fixed, the pn are found to depend upon the amplitude E0 and hence, the notional intensity  0cE20 in a highly sensitive manner: see figure 6.
0cE20 in a highly sensitive manner: see figure 6.
Figure 6. Plots of the probabilities pn seen in (5.1), for n = 0,±1,±2,±3,±4, an interaction time of t = 5 × 10−7 s, a trace of 3G' = ± 1 × 10−34 m kg−1 s3 A2 and various values of the notional intensity  0cE20.
0cE20.
Download figure:
Standard image High-resolution imageTo illustrate the sensitivity of the chiral diffraction grating and its associated diffraction patterns to the chiral geometry of the molecule, we employ an analytical expression for hexahelicene's trace 3G', obtained elsewhere using a dynamic coupling model [7, 107, 108]. As above, we consider 2πc/ω = 1.064 × 10−6 m and t = 5 × 10−7 s. We fix  0cE20 = 2.5 × 1013 kg s−3, however, and vary the normalized pitch −1 ⩽ γ ⩽ 1 of the molecule in a hypothetical manner, examining the corresponding changes in the pn. As the pn are identical for the enantiomers of the molecule, we need only consider the magnitude of γ. The limiting values |γ| = 1 and |γ| = 0 correspond to the usual helical shape adopted by hexahelicene, depicted in figure 1, and to a 'flattened' version of the molecule which is achiral. Thus, for |γ| = 1 our chiral diffraction grating gives rise to the diffraction pattern expected of hexahelicene in reality9 whereas for |γ| = 0, no diffraction pattern is found. Between these limiting cases, the pn vary drastically in responses to 'small' changes in |γ|: see figure 7.
0cE20 = 2.5 × 1013 kg s−3, however, and vary the normalized pitch −1 ⩽ γ ⩽ 1 of the molecule in a hypothetical manner, examining the corresponding changes in the pn. As the pn are identical for the enantiomers of the molecule, we need only consider the magnitude of γ. The limiting values |γ| = 1 and |γ| = 0 correspond to the usual helical shape adopted by hexahelicene, depicted in figure 1, and to a 'flattened' version of the molecule which is achiral. Thus, for |γ| = 1 our chiral diffraction grating gives rise to the diffraction pattern expected of hexahelicene in reality9 whereas for |γ| = 0, no diffraction pattern is found. Between these limiting cases, the pn vary drastically in responses to 'small' changes in |γ|: see figure 7.
Figure 7. Plots of the probabilities pn seen in (5.1), for n = 0,±1,±2,±3,±4, an interaction time of t = 5 × 10−7 s, a notional intensity of  0cE20 = 2.5 × 1013 kg s−3 and various hypothetical magnitudes of the normalized pitch γ of the molecule, the corresponding shapes of which are depicted in each panel. The trace 3G' has been calculated here using a dynamic coupling model [7, 107, 108]. Note: for a given magnitude of γ, either enantiomer of the molecule gives rise to the pn shown.
0cE20 = 2.5 × 1013 kg s−3 and various hypothetical magnitudes of the normalized pitch γ of the molecule, the corresponding shapes of which are depicted in each panel. The trace 3G' has been calculated here using a dynamic coupling model [7, 107, 108]. Note: for a given magnitude of γ, either enantiomer of the molecule gives rise to the pn shown.
Download figure:
Standard image High-resolution imageFor the enantiomers of the molecule, the chiral diffraction grating takes obvious advantage of the non-vanishing and equal magnitudes of 3G' but not of the opposite signs of 3G'. It should be viewed, therefore, as something of a chirality detector, rather than a chirality discriminator. We can envisage, however, employing a two-stage device comprised of a chiral Stern–Gerlach deflector followed by a chiral diffraction grating. The absolute location of the resulting diffraction pattern would then differ for the enantiomers of the molecule whilst the shape of the resulting diffraction pattern would encode information about their chiral geometry, as above.
It is possible, of course, to conceive of other novel possibilities offered for chiral molecules in the regime of de Broglie molecular optics by Uh. We will return to these ideas elsewhere.
6. Discussion
We have suggested that the centre-of-mass motion of a chiral molecule is, under appropriate circumstances, sensitive to gradients in the helicity of an optical field. As we have not made any critical assumptions regarding the energy-level structure of the molecule, our findings may be applicable to a wide range of species in a wealth of different contexts. It should be noted, however, that molecular polarizabilities, upon which our approach is based, are state dependent [7]. This may give rise to interesting subtleties and additional possibilities for manipulation. We have imagined the molecule to be tumbling freely in the optical field, thus neglecting the possibility of alignment effects and treating the molecule, heuristically, in an isotropic manner. In reality, the molecule might initially occupy a suitable thermal mixed state of 'high' temperature that spans many rotational levels, for example. At 'low' temperatures and/or 'high' optical intensities, however, polarization-dependent alignment effects in certain optical fields may be important [65, 66], giving rise to further subtleties and possibilities for manipulation.
Acknowledgments
This work was supported by the Carnegie Trust for the Universities of Scotland, the United Kingdom Engineering and Physical Sciences Research Council (EPSRC) and the Leverhulme Trust. We thank Laurence D Barron and Joshua S Robertson for their encouragement and advice.
Footnotes
- 4
We have expressed P and M with respect to R. A different position within or near to the molecule may be more convenient, however, and can be used instead.
- 5
- 6
In reality, the molecule might, for example, initially occupy a suitable thermal mixed state of 'high' temperature that spans many rotational levels.
- 7
- 8
In the present context, it is permissible to work with the rotationally averaged forms of μ, Θ and m' from the outset. There are, however, contexts in which it is not appropriate to perform a rotational averaging at this early stage: when calculating scattering intensities, for example, where electromagnetic waves attributable to different multipole moments interfere with each other [7].
- 9