Abstract
For any quantum state representing a physical system of identical particles, the density operator must satisfy the symmetrization principle (SP) and conform to super-selection rules (SSR) that prohibit coherences between differing total particle numbers. Here we consider bi-partitite states for massive bosons, where both the system and sub-systems are modes (or sets of modes) and particle numbers for quantum states are determined from the mode occupancies. Defining non-entangled or separable states as those prepared via local operations (on the sub-systems) and classical communication processes, the sub-system density operators are also required to satisfy the SP and conform to the SSR, in contrast to some other approaches. Whilst in the presence of this additional constraint the previously obtained sufficiency criteria for entanglement, such as the sum of the  and
and 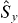 variances for the Schwinger spin components being less than half the mean boson number, and the strong correlation test of
variances for the Schwinger spin components being less than half the mean boson number, and the strong correlation test of 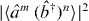 being greater than
being greater than 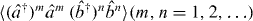 are still valid, new tests are obtained in our work. We show that the presence of spin squeezing in at least one of the spin components
are still valid, new tests are obtained in our work. We show that the presence of spin squeezing in at least one of the spin components 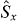 ,
, 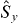 and
and 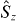 is a sufficient criterion for the presence of entanglement and a simple correlation test can be constructed of
is a sufficient criterion for the presence of entanglement and a simple correlation test can be constructed of 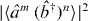 merely being greater than zero. We show that for the case of relative phase eigenstates, the new spin squeezing test for entanglement is satisfied (for the principle spin operators), whilst the test involving the sum of the
merely being greater than zero. We show that for the case of relative phase eigenstates, the new spin squeezing test for entanglement is satisfied (for the principle spin operators), whilst the test involving the sum of the 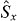 and
and 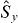 variances is not. However, another spin squeezing entanglement test for Bose–Einstein condensates involving the variance in
variances is not. However, another spin squeezing entanglement test for Bose–Einstein condensates involving the variance in 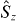 being less than the sum of the squared mean values for
being less than the sum of the squared mean values for  and
and 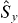 divided by the boson number was based on a concept of entanglement inconsistent with the SP, and here we present a revised treatment which again leads to spin squeezing as an entanglement test.
divided by the boson number was based on a concept of entanglement inconsistent with the SP, and here we present a revised treatment which again leads to spin squeezing as an entanglement test.
Export citation and abstract BibTeX RIS

Content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Since the work of Einstein et al [1] on local realism, the famous cat paradox of Schrodinger [2] and the derivation of inequalites by Bell [3] and others [4], entanglement has been recognized as being one of the essential features that distinguishes quantum physics from classical physics. In macroscopic systems entanglement is of particular importance as it blurs the boundary between the classical and quantum worlds. This paper considers tests that are sufficient (though not necessary) to confirm such entanglement.
One way to detect macroscopic entanglement is by applying the so called spin squeezing inequalities [5] to a large number of particles. The importance of spin squeezing in quantum metrology was emphasized by Kitagawa and Ueda [6] and it has been demonstrated that such states beat the standard quantum limit in interferometry [7]. For spin angular momentum operators 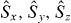 spin squeezing of
spin squeezing of 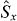 with respect to
with respect to 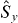 is defined as
is defined as
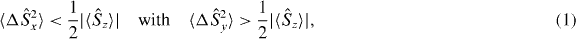
where 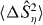 is the variance of the spin operator
is the variance of the spin operator  (η = x,y,z) Analogous definitions apply to other pairs of spin operators, or to a spin operator and any of its perpendicular components. For N spin-1/2 distinguishable particles each in the same coherent state, correlations between the spins resulted in spin squeezing in the total spin components [6], as it allows the fluctuations in one direction perpendicular to the spin component to be reduced. In such systems of distinguishable particles Sorensen et al [8, 9] showed that spin squeezing required entanglement of the N particles. Here however, we consider N identical bosons occupying two modes, where the Schwinger angular momentum operators for two modes, A and B with annihilation operators
(η = x,y,z) Analogous definitions apply to other pairs of spin operators, or to a spin operator and any of its perpendicular components. For N spin-1/2 distinguishable particles each in the same coherent state, correlations between the spins resulted in spin squeezing in the total spin components [6], as it allows the fluctuations in one direction perpendicular to the spin component to be reduced. In such systems of distinguishable particles Sorensen et al [8, 9] showed that spin squeezing required entanglement of the N particles. Here however, we consider N identical bosons occupying two modes, where the Schwinger angular momentum operators for two modes, A and B with annihilation operators 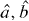 are
are  and
and  and the system behaves like a giant spin with spin quantum number S = N/2.
and the system behaves like a giant spin with spin quantum number S = N/2.
A notable area in which the detection of macroscopic entanglement can take place is that of trapped ultra-cold gases, where entanglement may be present over micron scales. Moreover, since nonlinear interactions between particles are required to generate spin squeezing [6], ultra-cold gases are an ideal test bed for witnesses based on spin-squeezing inequalities due to the tunable atom–atom interaction. In addition to achieving interferometry beyond the standard quantum limit, existing experiments have claimed to demonstrate macroscopic entanglement in ultra-cold gases via witnesses based on spin squeezing inequalities [10–12].
However, when detecting entanglement in systems of identical massive bosons with such inequalities care must be taken for two reasons. Firstly, entanglement is a relative concept that crucially depends on which sub-systems are being considered. A quantum state may be entangled for one choice of the sub-systems but may be non-entangled if another choice of sub-systems is made. For distinguishable particles, the sub-systems are usually individual particles, with internal (spin and polarization) or external (position and momentum) degrees of freedom possessing the quantum correlations. However, for identical particles the individual atoms cannot be distinguishable sub-systems, and entanglement will refer to the quantum field modes that the particles may occupy [13]. The modes are orthonormal single particle states, which may be localized in different spatial regions or may be delocalized where the opposite applies. The system and sub-systems are now modes, and cases with differing N are just different quantum states of the same system. Note however that a different concept of entanglement—particle entanglement—has also been applied to identical particle systems [14, 15]. Here we formulate spin squeezing entanglement witnesses for massive identical bosons as above in equation (1) via second quantization, so the symmetrization principle (SP) applies to all the identical bosons.
In the present paper we follow the approach of Werner [16] and define separable states as those which can be prepared via local operations (on the sub-systems) and classical communication processes (LOCC). A relevant example of such states occurs in ultra-cold atom experiments, where mesoscopic ensembles can be prepared with definite particle numbers in optical lattice sites. This means that for bipartite systems the density operator for separable states can be written in the form

where sub-systems A, B have been prepared in correlated quantum states 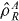 and
and 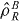 with a probability PR. Entangled states are those which are not of this form. This definition can be straightforwardly extended to multiple modes. It is important to realize that the terms in
with a probability PR. Entangled states are those which are not of this form. This definition can be straightforwardly extended to multiple modes. It is important to realize that the terms in 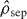 have a physical meaning—the sub-system quantum states
have a physical meaning—the sub-system quantum states 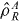 and
and  must correspond to physical states that can actually be prepared in A, B considered as stand-alone systems. The sub-system states before the preparation begins are unimportant, apart from being a separable product of sub-system states—these might be easily preparable sub-system lowest energy pure states. This point of view regarding the nature of separable states is not new, see for example [17–19]. However, other papers focus on the mathematical form for
must correspond to physical states that can actually be prepared in A, B considered as stand-alone systems. The sub-system states before the preparation begins are unimportant, apart from being a separable product of sub-system states—these might be easily preparable sub-system lowest energy pure states. This point of view regarding the nature of separable states is not new, see for example [17–19]. However, other papers focus on the mathematical form for 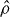 and do not require LOCC preparation for defining what they refer to as separable but non-local states [20, 21]. In the latter papers the
and do not require LOCC preparation for defining what they refer to as separable but non-local states [20, 21]. In the latter papers the 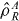 and
and  are not required to represent physical states that could be prepared in the isolated sub-systems. However, for LOCC based separable states the joint probability for measurements of physical quantities
are not required to represent physical states that could be prepared in the isolated sub-systems. However, for LOCC based separable states the joint probability for measurements of physical quantities 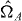 and
and 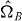 for the sub-systems resulting in eigenvalues λAi and λBj will be of the form
for the sub-systems resulting in eigenvalues λAi and λBj will be of the form 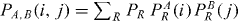 , where
, where 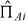 and
and  are the projectors onto sub-spaces with eigenvalues λAi, λBj and the factors
are the projectors onto sub-spaces with eigenvalues λAi, λBj and the factors 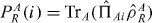 and
and 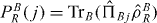 give the probabilities that the measurement results λAi and λBj occur if the sub-systems A and B are in states
give the probabilities that the measurement results λAi and λBj occur if the sub-systems A and B are in states 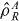 and
and 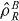 . If the
. If the 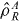 and
and 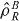 did not specify possible physical states for the sub-systems, then the probabilities PAR(i) and PBR(j) would not have a physical meaning. This property of separable states in which the joint measurement probability is determined from measurement probabilities of physically possible separate sub-system states, is the key feature whose absence in non-separable states led Schrodinger to refer to such states as entangled states. Note that after preparation, a separable state may evolve into an entangled state, such as when interactions between the sub-systems take effect.
did not specify possible physical states for the sub-systems, then the probabilities PAR(i) and PBR(j) would not have a physical meaning. This property of separable states in which the joint measurement probability is determined from measurement probabilities of physically possible separate sub-system states, is the key feature whose absence in non-separable states led Schrodinger to refer to such states as entangled states. Note that after preparation, a separable state may evolve into an entangled state, such as when interactions between the sub-systems take effect.
In addition, for systems of identical bosons we argue that to define the separable states (and hence the entangled states) one should take into account the presence of the particle-number super-selection rule (SSR) not only at the global level—as required for any quantum state but also crucially at the level of the local sub-systems in the case of separable states. Simply put, the global SSR means that for any quantum state of massive bosons, 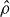 , should commute with the total particle number in the system
, should commute with the total particle number in the system ![$[\skew3\hat{\rho },\skew3\hat{N}]=0$](https://content.cld.iop.org/journals/1367-2630/16/1/013026/revision1/nj482124ieqn42.gif) , and hence no coherences exist between Fock states with differing N. For the separable states given by equation (2) for two modes, this means in addition that for physical sub-system states,
, and hence no coherences exist between Fock states with differing N. For the separable states given by equation (2) for two modes, this means in addition that for physical sub-system states, 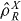 for X = A, B should also commute with the local particle numbers—thus
for X = A, B should also commute with the local particle numbers—thus 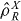 satisfy
satisfy ![$[\skew3\hat{\rho }_{R}^{X},\skew3\hat{N}_{X}]=0$](https://content.cld.iop.org/journals/1367-2630/16/1/013026/revision1/nj482124ieqn45.gif) . Note that both
. Note that both  and the
and the  may be mixed states, with statistical mixtures of particle number states. This additional local particle number SSR restriction leads to further tests of entanglement based on spin squeezing which are radically different to some of the well known entanglement witnesses. As we shall see below, a similar situation applies to other entanglement tests. In this letter, following an overview of the pertinent concepts, we will investigate how the spin squeezing and other inequalities are modified to detect entanglement when local particle number SSR are enforced for separable states.
may be mixed states, with statistical mixtures of particle number states. This additional local particle number SSR restriction leads to further tests of entanglement based on spin squeezing which are radically different to some of the well known entanglement witnesses. As we shall see below, a similar situation applies to other entanglement tests. In this letter, following an overview of the pertinent concepts, we will investigate how the spin squeezing and other inequalities are modified to detect entanglement when local particle number SSR are enforced for separable states.
2. Global and local super-selection (SSR)
The particle-number SSR is a fundamental constraint for systems of massive bosons. It occurs because physically realizable processes cannot create states which are coherent superpositions of different Fock states with differing total particle number. Thus, all global operators should commute with the total particle number operator. For states that are separable, the sub-system states are also required to be physical states, so analogous constraints must also apply to the sub-systems, and hence the sub-system states also have no coherences between Fock states with differing local particle number. This feature is required for separable states in identical particle systems if—as described above—joint measurements are to be based on physical probabilities for such measurements on the sub-systems. Indeed, the SSR also limits the allowed local operations on the modes (e.g. unitary operations of the form 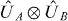 )—they too have to commute with the local particle numbers. Enforcing the local SSR leads to a more restricted set of separable states than would apply if they are ignored, which can be expected to modify an entanglement witness that was based upon the non-restricted definition of separability, in which the
)—they too have to commute with the local particle numbers. Enforcing the local SSR leads to a more restricted set of separable states than would apply if they are ignored, which can be expected to modify an entanglement witness that was based upon the non-restricted definition of separability, in which the 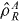 and
and 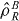 are not required to satisfy the local particle number SSR. Other authors have applied the SSR at a local level, see [17, 20, 22–26] for instance. A similar separable state was used [27] to show that the visibility of interference fringes between two spatial modes is an entanglement witness for modes of massive particles. Non-local SSR conforming coherent superpositions of number states (such as Glauber coherent states) were once thought necessary for describing interferometry and coherence effects in Bose–Einstein condensates (BEC), but it is now recognized [28, 29] that valid descriptions of these effects can be based on Fock states.
are not required to satisfy the local particle number SSR. Other authors have applied the SSR at a local level, see [17, 20, 22–26] for instance. A similar separable state was used [27] to show that the visibility of interference fringes between two spatial modes is an entanglement witness for modes of massive particles. Non-local SSR conforming coherent superpositions of number states (such as Glauber coherent states) were once thought necessary for describing interferometry and coherence effects in Bose–Einstein condensates (BEC), but it is now recognized [28, 29] that valid descriptions of these effects can be based on Fock states.
We will now make a brief comment about the connection between reference systems and SSR. It has long been known [30] that by using a suitable reference system one can, at least in principle, perform protocols (e.g. Ramsay interferometry, dense coding and Bell inequalities) whose description involves coherences between different particle numbers [24, 31, 32]. However, this apparent inconsistency can be resolved [33]. The key point is that the system states involved in a process are described differently by observers possessing different phase reference systems. If one observer describes the state as in equation (2) in terms of a reference system where the sub-system density operators 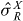 do not conform to the local particle number SSR, then a second observer without access to this reference system would also describe a separable state, but now with the transformed sub-system density operators
do not conform to the local particle number SSR, then a second observer without access to this reference system would also describe a separable state, but now with the transformed sub-system density operators 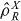 compatible with the local sub-system SSR. A more detailed discussion in terms of the U(1) symmetry group is presented in [22] (see also [34, appendix 4]). In this paper, we work from the viewpoint of the second observer. Phase reference systems such as BEC with large boson numbers—described by the second observer as being in statistical mixtures of Glauber coherent states with large fixed amplitudes and all phases having equal weight, and which satisfies the SSR for the BEC mode—are often involved in protocols such as Ramsay interferometry, dense coding, Bell inequalities. Bosons from the BEC reference interact and exchange with the primary system that is involved, for example two mode [31, 32] or four mode systems [24]. From the point of view of the first observer, the evolution from each large amplitude Glauber coherent state of the BEC times the initital state of the primary system can create states of the primary system that violate the SSR. However, from the point of view of the second observer, the evolved state of the primary system conforms to the SSR following averaging over the BEC phases. In our approach, separable states are described by an observer with different phase reference systems with unknown phases for the different sub-systems—as is appropriate for sub-systems that are separate. On the other hand, entangled states are described by an observer with a single phase reference system (albeit one where the phase is unknown), so that entangled states are global particle number SSR compliant. This is appropriate for composite systems where the sub-systems are combined into an entangled state on which measurements for overall system operators can also be performed. In the present paper the protocol is spin squeezing and we will describe this in terms of reference systems so that the state equation (2) satisfies
compatible with the local sub-system SSR. A more detailed discussion in terms of the U(1) symmetry group is presented in [22] (see also [34, appendix 4]). In this paper, we work from the viewpoint of the second observer. Phase reference systems such as BEC with large boson numbers—described by the second observer as being in statistical mixtures of Glauber coherent states with large fixed amplitudes and all phases having equal weight, and which satisfies the SSR for the BEC mode—are often involved in protocols such as Ramsay interferometry, dense coding, Bell inequalities. Bosons from the BEC reference interact and exchange with the primary system that is involved, for example two mode [31, 32] or four mode systems [24]. From the point of view of the first observer, the evolution from each large amplitude Glauber coherent state of the BEC times the initital state of the primary system can create states of the primary system that violate the SSR. However, from the point of view of the second observer, the evolved state of the primary system conforms to the SSR following averaging over the BEC phases. In our approach, separable states are described by an observer with different phase reference systems with unknown phases for the different sub-systems—as is appropriate for sub-systems that are separate. On the other hand, entangled states are described by an observer with a single phase reference system (albeit one where the phase is unknown), so that entangled states are global particle number SSR compliant. This is appropriate for composite systems where the sub-systems are combined into an entangled state on which measurements for overall system operators can also be performed. In the present paper the protocol is spin squeezing and we will describe this in terms of reference systems so that the state equation (2) satisfies ![$[\skew3\hat{\rho }_{R}^{X},\skew3\hat{N}_{X}]=0$](https://content.cld.iop.org/journals/1367-2630/16/1/013026/revision1/nj482124ieqn53.gif) for X = A, B, which can be achieved in ultra-cold gas experiments.
for X = A, B, which can be achieved in ultra-cold gas experiments.
3. Spin squeezing requires entanglement
Under the global and local particle-number SSR requirements for physical states of indistinguishable particles, the spin squeezing inequalities equation (1) are satisfied only if entanglement is present between the modes A and B. The proof is as follows. Using realization, 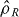 , of the separable state equation (2), the operators in the variance are
, of the separable state equation (2), the operators in the variance are 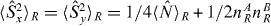 and
and 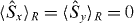 , with
, with 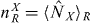 . Then, since for any operator
. Then, since for any operator  the inequality
the inequality 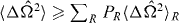 applies [35], the inequality
applies [35], the inequality 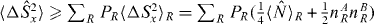 holds and likewise for
holds and likewise for 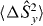 . For SSR-restricted separable states, equation (2), the expectation values of the z spin component
. For SSR-restricted separable states, equation (2), the expectation values of the z spin component 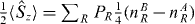 can be bounded from above as
can be bounded from above as 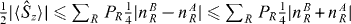 . Thus,
. Thus, 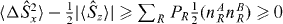 and likewise
and likewise 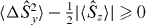 . This shows for general separable states in equation (2) over two modes, A and B in which the local mode SSR applies, the spin variances in both the x and y directions satisfy
. This shows for general separable states in equation (2) over two modes, A and B in which the local mode SSR applies, the spin variances in both the x and y directions satisfy

and hence there is no spin squeezing of 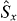 with respect to
with respect to  or vice versa It is straightforward to show that analogous results apply to the other pairs of spin components
or vice versa It is straightforward to show that analogous results apply to the other pairs of spin components 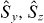 and
and 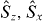 or to each spin component and any perpendicular spin component. Thus we have now shown that spin squeezing in any spin component is a test of entanglement—entanglement being defined here in terms of separable states satisfying the local particle number SSR. There are, of course, entangled states which do not show spin squeezing. One example is the famous Schrodinger cat like NOON state,
or to each spin component and any perpendicular spin component. Thus we have now shown that spin squeezing in any spin component is a test of entanglement—entanglement being defined here in terms of separable states satisfying the local particle number SSR. There are, of course, entangled states which do not show spin squeezing. One example is the famous Schrodinger cat like NOON state, 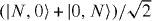 , which describes all the particles in mode A and none in mode B superposed with no particles in mode A and all particles in mode B. For large N such states are however notoriously difficult to create in experiments. The NOON state is global particle number SSR compliant, and its density operator is the same for any observer with a different overall phase reference system. Note that for an observer with separate unrelated phase reference systems for the two modes, the state is seen as a separable state, whose density operator is a 50:50 mixture with one state having N bosons in mode A and none in mode B, the other having no bosons in mode A and N in mode B.
, which describes all the particles in mode A and none in mode B superposed with no particles in mode A and all particles in mode B. For large N such states are however notoriously difficult to create in experiments. The NOON state is global particle number SSR compliant, and its density operator is the same for any observer with a different overall phase reference system. Note that for an observer with separate unrelated phase reference systems for the two modes, the state is seen as a separable state, whose density operator is a 50:50 mixture with one state having N bosons in mode A and none in mode B, the other having no bosons in mode A and N in mode B.
4. Other spin squeezing tests and local SSR separable states
There are several entanglement tests, based both on spin squeezing and other protocols that can be used to detect entanglement in systems, where the definition of entanglement is based on separable states which do not satisfy the physically based particle-number SSR. Of course any test that is derived for arbitrary 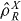 must also demonstrate the present entanglement based on
must also demonstrate the present entanglement based on ![$[\skew3\hat{\rho }_{R}^{X},\skew3\hat{N}_{X}]=0$](https://content.cld.iop.org/journals/1367-2630/16/1/013026/revision1/nj482124ieqn72.gif) . Several such tests are discussed elsewhere [34]. However, it is interesting and necessary for experiments to consider whether additional tests arise when they are re-derived for systems of identical massive bosons based on the physical definition of a separable state (2), where the local SSR is satisfied. We will focus on certain commonly used inequalities in this paper, although other tests also exist (see [36, 37]).
. Several such tests are discussed elsewhere [34]. However, it is interesting and necessary for experiments to consider whether additional tests arise when they are re-derived for systems of identical massive bosons based on the physical definition of a separable state (2), where the local SSR is satisfied. We will focus on certain commonly used inequalities in this paper, although other tests also exist (see [36, 37]).
4.1. Hillery et al 2006 spin squeezing test
A paper by Hillery and co-workers [38] derives an entanglement witness (equation (4)) based upon spin squeezing, based on general (non-SSR-restricted) separable states of the electromagnetic field. It has been used to detect entanglement in e.g. the following proposals for trapped ultra-cold gases [39, 40]. We confirm that the main result of [38] is still valid for the SSR restricted state (2), but provide an example where the Hillery test based on the sum of  and
and 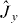 variances for rotated spin components fails to detect entanglement in the relevant modes, whereas a simple spin squeezing test (as in equation (3)) involving a rotated component
variances for rotated spin components fails to detect entanglement in the relevant modes, whereas a simple spin squeezing test (as in equation (3)) involving a rotated component 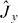 is satisfied.
is satisfied.
Hillery et al [38] show that for general separable states

To obtain this result it is found that for a product state 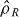 that
that 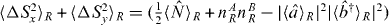 , where for non-SSR compliant
, where for non-SSR compliant 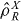 the terms
the terms 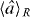 and
and 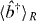 are not necessarily zero. Noting that
are not necessarily zero. Noting that  and likewise for mode b, it follows that
and likewise for mode b, it follows that  . From
. From 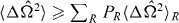 the result in equation (4) then follows. For SSR-restricted separable states however, the result
the result in equation (4) then follows. For SSR-restricted separable states however, the result 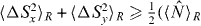 still holds because nARnBR ⩾ 0 alone is needed. The Hillery et al spin squeezing test for entanglement then is
still holds because nARnBR ⩾ 0 alone is needed. The Hillery et al spin squeezing test for entanglement then is 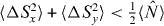 . If this applies the state cannot be separable.
. If this applies the state cannot be separable.
Note that we have previously shown that for local SSR compliant separable states that 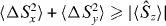 . The quantity
. The quantity 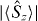 is smaller than
is smaller than  since
since 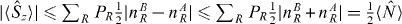 . However,
. However, 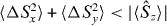 is not a valid entanglement test because there are no quantum states where this is true, as noted in [38].
is not a valid entanglement test because there are no quantum states where this is true, as noted in [38].
Although it may be thought that because 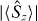 is smaller than
is smaller than 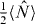 the Hillery test involving 〈ΔS2x〉 + 〈ΔS2y〉 <
the Hillery test involving 〈ΔS2x〉 + 〈ΔS2y〉 < 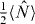 would be more likely to demonstrate entanglement in the modes A, B than the tests obtained in this paper such as showing
would be more likely to demonstrate entanglement in the modes A, B than the tests obtained in this paper such as showing 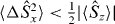 or
or 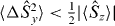 , this is not always the case. The relative phase eigenstate [41, 42] is an entangled pure state for N bosons defined by
, this is not always the case. The relative phase eigenstate [41, 42] is an entangled pure state for N bosons defined by 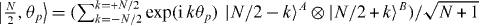 , where θp = p(2π/(N + 1)) with p = −N/2,−N/2 + 1,..,+N/2 specifies the relative phase. In terms of spin components
, where θp = p(2π/(N + 1)) with p = −N/2,−N/2 + 1,..,+N/2 specifies the relative phase. In terms of spin components  and
and  the covariance matrix [43] for spin fluctuations is non-diagonal and spin squeezing does not occur. As the variances are such that
the covariance matrix [43] for spin fluctuations is non-diagonal and spin squeezing does not occur. As the variances are such that 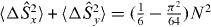 and which exceeds
and which exceeds 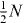 , the Hillery test for entanglement also fails even though the state is entangled for modes A, B. Principal spin components
, the Hillery test for entanglement also fails even though the state is entangled for modes A, B. Principal spin components  are obtained by a rotation, and for these the covariance matrix is diagonal with
are obtained by a rotation, and for these the covariance matrix is diagonal with  and
and 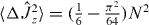 for large N. The mean values are
for large N. The mean values are  (see [42] for details). The principal spin components are related to annihilation operators
(see [42] for details). The principal spin components are related to annihilation operators 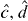 for new modes C,D via expressions of the form
for new modes C,D via expressions of the form 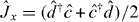 , etc, where
, etc, where 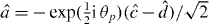 and
and  , and the relative phase state can be rewritten as a linear combination of Fock states for the new modes
, and the relative phase state can be rewritten as a linear combination of Fock states for the new modes 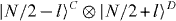 with l = −N/2,··· , + N/2. Note that there must be terms with differing l since
with l = −N/2,··· , + N/2. Note that there must be terms with differing l since 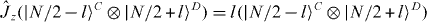 and
and 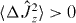 . The relative phase state is therefore an entangled state for the modes C,D. In the relative phase state
. The relative phase state is therefore an entangled state for the modes C,D. In the relative phase state 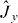 is squeezed with respect to
is squeezed with respect to 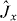 so the spin squeezing test for entanglement of modes C,D based on separable states consistent with the local particle number SSR is satisfied. However, for the Hillery test
so the spin squeezing test for entanglement of modes C,D based on separable states consistent with the local particle number SSR is satisfied. However, for the Hillery test 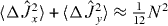 , which considerably exceeds
, which considerably exceeds 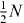 . Thus the Hillery test for entanglement fails.
. Thus the Hillery test for entanglement fails.
4.2. Sorensen et al 2001 spin squeezing test
Care must be taken when applying a spin squeezing entanglement based witness derived in an early paper by Sorensen et al [8] for systems of N distinguishable two-level particles to the situation when the particles are identical [15]. The witness shows that entanglement exists when the state satisfies the following spin squeezing inequality

The proof is based on writing the separable state density operator in the form 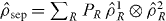
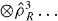 where
where 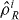 is the density operator for the ith distinguishable particle, whose internal states are
is the density operator for the ith distinguishable particle, whose internal states are 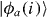 and
and 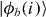 . The density matrix for
. The density matrix for 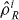 is a 2 × 2 matrix and the spin operators are defined by expressions such as
is a 2 × 2 matrix and the spin operators are defined by expressions such as 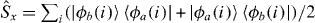 , etc, which are sums over the particles. The hermiticity, positiveness, unit trace for all the density matrices lead to ξ2 ⩾ 1 for these separable states of two level distinguishable particles. This result cannot just be applied to identical bosonic particles without further development, since the Sorensen separable state density operator does not satisfy the SP. Also Benatti et al [44] have shown that this inequality diverges for two mode states where the local particle-number SSR is enforced, as is easily seen by noting that
, etc, which are sums over the particles. The hermiticity, positiveness, unit trace for all the density matrices lead to ξ2 ⩾ 1 for these separable states of two level distinguishable particles. This result cannot just be applied to identical bosonic particles without further development, since the Sorensen separable state density operator does not satisfy the SP. Also Benatti et al [44] have shown that this inequality diverges for two mode states where the local particle-number SSR is enforced, as is easily seen by noting that 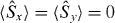 for a physical separable state, equation (2) involving single modes as sub-systems. Just considering N boson states for a total of two modes is not adequate. One way to revise the Sorensen et al result to an equivalent theory now based on mode entanglement involves sub-systems each consisting of two modes, which we may list as αk, where α = a,b and k lists modes with the same α. The k may correspond to spatial modes localized on different lattice sites. For identical particles occupying these modes the spin operators
for a physical separable state, equation (2) involving single modes as sub-systems. Just considering N boson states for a total of two modes is not adequate. One way to revise the Sorensen et al result to an equivalent theory now based on mode entanglement involves sub-systems each consisting of two modes, which we may list as αk, where α = a,b and k lists modes with the same α. The k may correspond to spatial modes localized on different lattice sites. For identical particles occupying these modes the spin operators 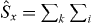
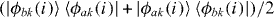 , etc, become Schwinger spin operators
, etc, become Schwinger spin operators 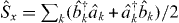
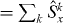 , etc, where the
, etc, where the 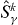 and
and  satisfy the usual commutation rules. The sub-system density operators
satisfy the usual commutation rules. The sub-system density operators 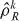 now refer to two mode sub-systems and can be made consistent with the local particle number SSR by requiring that
now refer to two mode sub-systems and can be made consistent with the local particle number SSR by requiring that ![$[\skew3\hat{\rho }_{R}^{k},\skew3\hat{N}_{a}^{k}+\skew3\hat{N}_{b}^{k}]=0$](https://content.cld.iop.org/journals/1367-2630/16/1/013026/revision1/nj482124ieqn131.gif) . The SP automatically applies for
. The SP automatically applies for  in this second quantization treatment. If in addition, we require that the
in this second quantization treatment. If in addition, we require that the  are density operators for a single boson, then the bosons in different k modes are effectively distinguishable. The proof in Sorensen et al [8] then applies, noting that for two mode sub-systems
are density operators for a single boson, then the bosons in different k modes are effectively distinguishable. The proof in Sorensen et al [8] then applies, noting that for two mode sub-systems 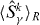 and hence
and hence 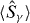 (γ = x,y,z) are not necessarily zero. States of this type are routinely created in experiments, for instance in [45], where the gas is frozen deep in the Mott regime with unity filling and each atom has two accessible internal states. The sites then act like distinguishable qubits. The physicality of a separable state is thus guaranteed and there may be entanglement between the modes within each sub-system. A similar proof extending the test of Sorensen et al to identical two level systems is given by Hyllus et al [15] based on a particle entanglement approach. In their approach bosons in different external modes (such as the different k) are treated as distinguishable and the SP is ignored for such bosons.
(γ = x,y,z) are not necessarily zero. States of this type are routinely created in experiments, for instance in [45], where the gas is frozen deep in the Mott regime with unity filling and each atom has two accessible internal states. The sites then act like distinguishable qubits. The physicality of a separable state is thus guaranteed and there may be entanglement between the modes within each sub-system. A similar proof extending the test of Sorensen et al to identical two level systems is given by Hyllus et al [15] based on a particle entanglement approach. In their approach bosons in different external modes (such as the different k) are treated as distinguishable and the SP is ignored for such bosons.
It should be noted that for separable states where the 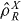 are required to satisfy further conditions in addition to the local particle number SSR, the entanglement tests will differ from those where the additional conditions are absent. The requirement that the sub-system density operators
are required to satisfy further conditions in addition to the local particle number SSR, the entanglement tests will differ from those where the additional conditions are absent. The requirement that the sub-system density operators 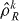 are restricted to one boson states is an example of such an additional condition.
are restricted to one boson states is an example of such an additional condition.
5. Non-spin squeezing tests and local SSR separable states
In [38, 46] it was found that for separable states based on arbitrary sub-system density operators 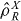

for m,n = 0,1,... so that 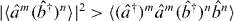 is a test for entanglement. This test must also apply for separable states where the local SSR is satisfied. A particular case of the test is
is a test for entanglement. This test must also apply for separable states where the local SSR is satisfied. A particular case of the test is 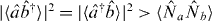 .
.
However, for separable states satisfying the local particle number SSR we can easily show that

Hence  is a test for entanglement based on local SSR compliant separable states. Since
is a test for entanglement based on local SSR compliant separable states. Since  is merely required to be non-zero this test is easier to satisfy than the Hillery one based on equation (6). A particular case of the test is
is merely required to be non-zero this test is easier to satisfy than the Hillery one based on equation (6). A particular case of the test is 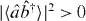 . The last result also follows from
. The last result also follows from 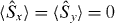 for SSR compatible states. Hence this is a simpler test for entanglement than
for SSR compatible states. Hence this is a simpler test for entanglement than  and has been used instead to detect entanglement [27].
and has been used instead to detect entanglement [27].
6. Experimental considerations
A recent experiment [12], uses the inequality (5) to detect the entanglement in an ultra-cold gas. Here, despite their indistinguishability, they consider the particles themselves as the sub-systems and generate 'entanglement' via their internal degrees of freedom. Due to this, the inequality (5) would be valid as described above if distinguishability could be recovered. This while technically very difficult, can in principle be achieved. For instance, the gas could be frozen (without disturbing the internal states of the particles—into the Mott phase of an optical lattice so that the system behaves as a set of distinguishable qubits. Such a scheme has been considered above.
On the other hand, an earlier experiment [10] considers the entanglement of two spatial field modes. Here the application of inequality (5) should be reconsidered due to the fact that the sub-systems are single modes (with no internal structure).
The experiments only involve a single test for entanglement, and it would be desirable to confirm entanglement via an independent test.
7. Conclusions
Only three ground breaking experiments [10–12] have shown spin squeezing in cold atom systems, from which the presence of entanglement is inferred. As such the field is still very much in its infancy. Our results will advance the field by allowing a greater understanding of the role of indistinguishability when detecting entanglement. A more extensive presentation of the work in this paper is in preparation [34].
Acknowledgments
The authors thank S M Barnett, J F Corney, P D Drummond, J Jeffers, K Molmer, D Oi, M D Reid, K Rzazewski, T Rudolph, J A Vaccaro and V Vedral for helpful discussions. BJD thanks the Science Foundation of Ireland for funding this research via an E T S Walton Visiting Fellowship.


