Topological phase transitions with and without energy gap closing

The quantum Hall (QH) effect [1, 2] in a two-dimensional (2D) electron gas under a strong magnetic field provided the first example of a topological state of matter in condensed matter physics, which cannot be described by the Landau theory of symmetry breaking. Thouless, Kohmoto, Nightingale and Nijs (TKNN) revealed that the essential character of a QH insulator, different from an ordinary insulator, is a topological invariant of occupied electron states [3] or many-body wavefunctions [4]. They related the Hall conductivity of the system to the first Chern number (or TKNN number), which is quantized when the Fermi level lies in an energy gap between Landau levels. In such systems, topological phase transitions can happen only by closing the energy gap. Gapless edge states must appear on the boundary between a QH insulator and an ordinary insulator, which is ensured by the topological invariant. Interestingly, Haldane [5] proposed a spinless electron model on a 2D honeycomb lattice with staggered magnetic fluxes to realize the topological QH effect without Landau levels.

The quantum spin Hall (QSH) effect was first theoretically predicted by Kane and Mele [6] and by Bernevig and Zhang [7], and then experimentally observed in HgTe quantum wells [8, 9]. Unlike the QH systems, where time reversal (TR) symmetry must be broken, the QSH systems preserve the TR symmetry. The main ingredient is the existence of strong spin–orbital coupling, which acts as spin-dependent magnetic fluxes coupled to the electron momentum. The QSH state is characterized by a bulk band gap and gapless helical edge states on the sample boundary [6–11]. The existence of the edge states is due to nontrivial topological properties of bulk energy bands. However, the bulk band topology of the QSH systems cannot be classified by the first Chern number, which always vanishes. Instead, it is classified by new topological invariants, namely, the Z₂ index [12] or the spin Chern numbers [13–15]. For TR-invariant systems, both Z₂ and spin Chern numbers were found to give an equivalent description [14, 15]. The robustness of the Z₂ index relies on the presence of the TR symmetry. In contrast, the spin Chern numbers remain to be integer-quantized, independent of any symmetry, as long as both the band gap and spin spectrum gap stay open [14]. They are also different from the first Chern number for the QH state, which is protected by the bulk energy gap alone. The spin Chern numbers have been employed to study the TR-symmetry-broken QSH effect [16].

The QSH system is an example of the 2D topological insulators (TIs). Its generalization to higher dimension led to the birth of three-dimensional (3D) TIs [17–21]. A 3D TI has a bulk band gap and surface states on the sample boundary. The metallic surface states provide a unique platform for realizing some exotic physical phenomena, such as Majorana fermions [22] and topological magnetoelectric effect [23, 24]. The 3D TIs have been experimentally observed in Bi_1−xSb_x, Bi₂Te₃ and Bi₂Se₃ materials [25–29], which greatly stimulates the research in this field. The 3D TIs with TR symmetry are usually classified by four Z₂ indices [17, 18, 30], and are divided into two general classes: strong and weak TIs, depending on the sum of the four Z₂ indices. In the presence of disorder, while the weak TIs are unstable, the strong TIs remain to be robust. The Z₂ indices are essentially defined only on the TR-symmetric planes in the Brillouin zone [17, 18, 30], and do not provide information about the distribution of surface states in the full momentum space. When the TR symmetry is broken, the Z₂ indices become invalid. Therefore, a more general characterization scheme for the bulk band topology, which does not rely on any symmetry and can provide more information about the distribution of surface states, is highly desirable.

In this work, for a 3D TI with an exchange field of strength g, we consider a momentum component, e.g. k_z as a parameter, and analytically calculate spin Chern numbers C^±(k_z) for the effective 2D system. The phase diagram for C^±(k_z) obtained describes the systematic evolution of the bulk band topology. For small g, an unconventional topological phase transition is discovered, which controls the basic properties of surface states. C^±(k_z) undergo a transition from ±1 to 0 with increasing |k_z| to a critical value k^C_z. Correspondingly, on a sample surface parallel to the z-axis, helical surface states are found to exist in the region |k_z| < k^C_z, and disappear for |k_z| ⩾ k^C_z. At |k_z| = k^C_z, the bulk spin spectrum gap closes, but the energy gap remains open. When |g| is greater than a critical value g_C, a transition of the 3D TI into a Weyl semimetal occurs. Two Weyl points appear as critical points separating a QH phase of the effective 2D system for |k_z| < k^W_z from an ordinary insulator for |k_z| > k^W_z, indicating that their appearance is topological rather than accidental. Chiral surface states existing in the region |k_z| < k^W_z give rise to the Fermi arcs.

Let us start from the effective Hamiltonian proposed in [19]: H = A₂τ_x(k_xσ_x + k_yσ_y) + M( k)τ_z + A₁k_zτ_xσ_z + gσ_z, which was used to describe the strong TI of Bi₂Se₃. Here, σ_m and τ_m (m = x,y or z) denote the Pauli matrices in spin and orbital spaces, and M(k) = M₀ − B₁k²_z − B₂k²_⊥ with k²_⊥ = k²_x + k²_y is the mass term expanded to the second order. In the last term, we include an exchange field of strength g, in order to study the TR-symmetry-broken effect on topological properties of the TI. For convenience, the momentum is set to be dimensionless, by properly choosing the units of parameters in the model, namely, M₀, A₁, A₂, B₁ and B₂.

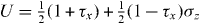Making a unitary transformation ${\cal H}=U^\dagger HU$ with $U=\frac {1}{2}(1+\tau _x)+\frac {1}{2} (1-\tau _x)\sigma _z$, we obtain

$$\begin{equation} {\cal H}={A_2}({k_x}{\sigma _x} + {k_y}{\sigma _y})+[M({\bf k}){\tau _z} + {A_1}{k_z}{\tau _x}+g]{\sigma _z} . \end{equation} \tag{ 1 }$$

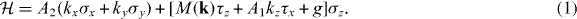
The eigenstates of Hamiltonian (1) can be easily solved by first diagonalizing the operator in the square bracket. The four eigenenergies are obtained as

$$\begin{equation} E^{v(c)}_{\pm}({\bf k})=-(+)\sqrt{A_2^2k_{\perp}^2+[g\pm\lambda({\bf k})]^2} , \end{equation} \tag{ 2 }$$

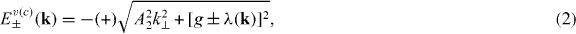
where 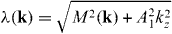$\lambda ({\bf{ k}})=\sqrt {M^2({\bf{ k}})+A^2_{1}k_z^2}$, and subscripts ± indicate two valence (conduction) bands with superscript v (c). The electron wavefunctions in the valence bands are given by

$$\begin{equation} \varphi_\pm({\bf k})=\phi_\pm({\bf k})\otimes \chi_\pm({\bf k})\ . \end{equation} \tag{ 3 }$$

Here, ϕ₊( k) = [sgn(A₁k_z) cos α_k, sin α_k]^T and ϕ₋(k) = [sgn(A₁k_z)sin α_k, −cos α_k]^T are wavefunctions in the τ_z space, and $\chi _{\pm }=(\frac {k_x -{\mathrm { i}}k_y}{k_{\perp }}\sin {\theta _{k}^{\pm }}$, −cos θ^±_k)^T are wavefunctions in the σ_z space, with 2α_k = arcctg[M( k)/|A₁k_z|] and 2θ^±_k = arcctg[(g ± λ( k))/|A₂k_⊥|].

The basic idea of our theoretical calculation is explained as follows. We consider one of the momentum components, e.g. k_z as a parameter. For a given k_z, equation (1) is equivalent to a 2D system, for which spin Chern numbers C^±(k_z) can be defined. For a semi-infinite sample of the 3D TI with its surface parallel to the z-axis, k_z remains to be a good quantum number. Correspondingly, nonzero C^±(k_z) indicate that edge states with the given k_z must appear on the edge of the effective 2D system. The edge states at various k_z essentially form surface states of the 3D sample. Therefore, the characteristics of the surface states can be determined from the calculation of the k_z-dependent spin Chern numbers C^±(k_z).

The spin Chern numbers for the effective 2D system are calculated in a standard way, which has been described in detail in previous works [15, 16]. By studying a special case of k_z = 0, we find that the topological properties of equation (1) can be described by the spin Chern numbers C^±(k_z) associated with τ_z. Here, τ_z corresponds to Uτ_zU^† = τ_zσ_z in the original Hamiltonian H, and so can be considered as a spin operator, measuring the difference of spin polarization between the two orbitals. The eigenstates of projected spin operator Pτ_zP need to be calculated first, where P is the projection operator into the valence bands. Since Pτ_zP commutes with momentum operator, its eigenstates can be obtained at each momentum k separately. The eigenvalues of Pτ_zP are given by

$$\begin{equation} \xi^{\pm}({\bf k})=\pm\sqrt{\cos^2 2\alpha_k+\cos^2 (\theta_{k}^{+}-\theta_{k}^{-})\sin^2 2\alpha_{k}} . \end{equation} \tag{ 4 }$$

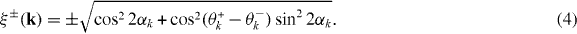
The corresponding eigenfunctions are denoted by Ψ^±(k), whose expressions are lengthy and will not be written out here. The spin Chern numbers are just the Chern numbers of the two spin sectors formed by Ψ^±( k), i.e. $C^{\pm }(k_z)=\frac {\mathrm { i}}{2\pi }\int \,{\mathrm { d}}k_x\,{\mathrm { d}}k_y\hat {\bf e }_z\cdot \bigl [\nabla _2\times \langle \Psi ^{\pm }({\bf k})\vert \nabla _{2}\vert \Psi ^{\pm }({\bf{ k}}\rangle \bigr ]$, where ∇₂ is the 2D gradient operator acting on (k_x, k_y). By some algebra, C^±(k_z) are derived to be

$$\begin{equation} C^\pm(k_z)=\pm\frac{1}{2}[{\rm sgn}(B_2)+{\rm sgn}(Q(k_z){\rm sgn} [P(k_z)]\pm g)] \end{equation} \tag{ 5 }$$

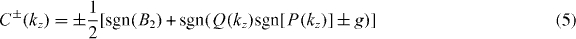
with P(k_z) = M₀ − B₁k²_z and 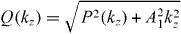$Q(k_z)=\sqrt {P^2(k_z)+A_1^2k_z^2}$.

Equations (2), (4) and (5) are the main analytical results of this work. For g = 0, the spin Chern numbers at k_z = 0 reduces to $C^{\pm }(0)=\pm \frac {1}{2}[{\mathrm { sgn}}(B_2)+{\mathrm { sgn}}(M_0)]$. C^±(0) are nonzero when B₂ and M₀ have the same sign, and vanish otherwise. C^±(0) play a role similar to the Z₂ index. Nonzero C^±(0) ensure that surface states exist in the vicinity of k_z = 0 on a surface parallel to the z-axis. Without loss of generality, we will focus on the parameter region of B₂ > 0 and M₀ > 0, to which Bi₂Se₃ belongs. We wish to emphasize here that when k_z is considered as a parameter, the effective 2D Hamiltonian (1) breaks the TR symmetry for any k_z ≠ 0, even if g = 0, as its TR counterpart is at −k_z. Therefore, while the k_z-dependent spin Chern numbers given by equation (5) remain to be valid at any k_z, a Z₂ index cannot be defined for any k_z ≠ 0. Equation (5) allows us to extract more information about the basic characteristics of the surface states.

A typical phase diagram for the spin Chern numbers in the k_z versus g plane, as determined by equation (5), is plotted in figure 1. For simplicity, A₂ is taken to be the unit of energy. For small |g|, C^±(k_z) = ± 1 at small |k_z|, corresponding to a QSH phase of the effective 2D system, and drop to 0 with increasing |k_z| to a critical value 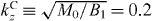$k_{z}^{\mathrm { C}}\equiv \sqrt {M_0/B_1}=0.2$, as indicated by the dotted lines. The system becomes an ordinary insulator for |k_z| > k^C_z. When |g| is greater than a critical value g_C, the effective 2D system enters a QH phase with a nonzero total (first) Chern number C(k_z) ≡ C⁺(k_z) + C⁻(k_z) = 1 if g > 0, and −1 if g < 0. The boundary enclosing this phase, as indicated by the solid curves in figure 1, is determined by equation g = ± Q(k_z), with the analytical expression for Q(k_z) being given below equation (5). The critical exchange field is given by g_C = min[Q(k_z)], and g_C ≃ 0.1 in figure 1.

Zoom In Zoom Out Reset image size

It is interesting to see how the energy gap Δ_E(k_z) = min[E^c_±( k) − E^v_±(k)]|_kz and the spin spectrum gap Δ_τ(k_z) = min[ξ⁺( k) − ξ⁻(k)]|_kz behave on the boundary (solid and dashed lines) between different phases. From equations (2) and (4), we find that on the dotted lines in figure 1, the spin spectrum gap closes at k_x = k_y = 0, but the energy gap remains open. On the contrary, on the solid boundary lines, the energy gap closes at k_x = k_y = 0, but the spin spectrum gap remains open. Δ_E and Δ_τ as functions of k_z for several values of g are plotted in figures 2(a) and (b), respectively. We notice that at g = 0.14 and k_z = k^C_z = 0.2, the energy gap and spin spectrum gap vanish simultaneously. This is because the dotted and solid boundary lines in figure 1 intersect just at that point.

Zoom In Zoom Out Reset image size

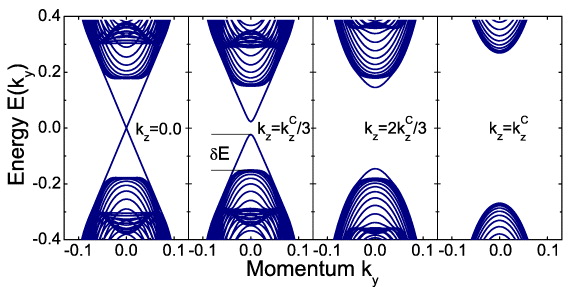
To study the surface states directly, we construct a tight binding model on a cubic lattice with two spins and two orbitals on each site, which recovers the Hamiltonian equation (1) in the continuum limit. A semi-infinite sample with its surface parallel to the y–z plane is considered, where k_y and k_z remain as good quantum numbers.

The calculated energy spectrum for g = 0.05 is plotted as a function of k_y for four different values of k_z in figure 3. Although g ≠ 0 breaks the TR symmetry, the surface states remain gapless at k_z = 0, because τ_z in equation (1) is conserved at k_z = 0. From figure 3, it is found that for k_z = 0, k^C_z/3 and 2k^C_z/3, surface states always exist in the bulk energy gap, but no surface states appear at k_z = k^C_z. To see the evolution of surface states with k_z more clearly, we define a maximum level spacing δE between the surface states and bulk states, as illustrated in figure 3. In figure 4(a), δE is plotted as a function of k_z. One can see that δE decreases with increasing k_z, and drops to nearly 0 at k_z ⩾ k^C_z. Therefore, we conclude that surface states exist only in the region |k_z| < k^C_z, and vanish for |k_z| ⩾ k^C_z, which is well consistent with the phase diagram of figure 1.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The critical momentum k^C_z marks a topological phase transition, characterized by the change in the spin Chern numbers, with disappearance of surface states as an observable consequence. This topological phase transition is accompanied by closing the spin spectrum gap rather than the energy gap. It is worth mentioning that topological phase transitions without closing the single-particle energy gap have previously been observed in some interactive electron systems. For example, in the Kane–Mele–Hubbard model, the spin excitation gap closes across the transition from the TI to the anti-ferromagnetic Mott insulator [31]. Similarly, in the Haldane–Fermi–Hubbard model, a generic excitation gap closes at the topological phase transition, while the single-particle gap remains intact [32]. Our work demonstrates that such unconventional topological phase transitions can happen in noninteracting electron systems as well. While the closing of the spin spectrum gap may not be observed directly, we find that the average of operator τ_z in H, namely, $\sum _{\beta =\pm }\langle \varphi _{\beta }({\bf k})\vert \ U^\dagger \tau _zU\vert \varphi _{\beta }({\bf k})\rangle \propto \cos (2\alpha _{k})$, changes its sign at k = (0,0,±k^C_z), which indicates a reversal of the orbital polarization, leading to a bulk physical observable at the transition. For the strong TI under consideration, the nontrivial bulk band topology can be examined in any direction. For example, by considering k_y as a parameter, we can calculate the spin Chern numbers in the effective 2D space of (k_x,k_z), and obtain a critical $k_y^{\mathrm { C}}=\sqrt {(M_0+\vert g\vert )/B_2}$. Combining k^C_y and k^C_z together, we can depict the region in the k_y–k_z plane, where topological surface states exist on a surface parallel to the y–z plane, as shown in figure 4(b).

For |g| > g_C, the 3D system enters another topological phase characterized by a nonzero total Chern number C(k_z) for small |k_z|, which is essentially a Weyl semimetal phase [33–36]. The quantum phase transition from the 3D TI to the Weyl semimetal with tuning g can be understood as a topological transition, at which the energy gap closing causes one of spin Chern numbers C^±(k_z) to vanish, while the other remains to be quantized.

At a given g, from equation g = ± Q(k_z) for the solid boundary lines in figure 1, one can obtain two critical values of k_z, namely, ±k^W_z, as indicated in figure 1. k = (0,0,±k^W_z) are a pair of Weyl points, or 3D Dirac points, at which the conduction and valence bands touch. The appearance of Weyl points is usually attributed to accidental degeneracy or symmetry [33–36]. The obtained phase diagram in figure 1 sheds more light on its topological origin. At a given g, the Weyl points appear as two critical points separating a QH state of the effective 2D system for |k_z| < k^W_z from an ordinary insulator state for |k_z| > k^W_z, at which the energy gap must vanish. Changing parameters cannot open energy gaps at the two Weyl points, unless they come together, so that the QH state in between is destroyed.

At g = 0.2, the calculated energy spectrum as a function of k_y for four different k_z is plotted in figure 5, for a semi-infinite sample with its surface parallel to the y–z plane. It is found that for k_z < k^W_z, chiral surface states appear in the energy gap; the conduction and valence bands touch at k_z = k^W_z; and for k_z > k^W_z, the energy gap reopens, but surface states no longer exist. These results are in good agreement with the phase diagram in figure 1. The chiral surface states appearing in the region of |k_z| < k^W_z give rise to the Fermi arcs [33–36].

Zoom In Zoom Out Reset image size

We have studied topological phase transitions in a 3D TI with an exchange field of strength g by calculating spin Chern numbers C^±(k_z) with a momentum k_z considered as a parameter. The phase diagram for C^±(k_z) obtained can describe the systematic evolution of the bulk band topology, and provide more information about the surface states. We predicted that there exists a critical value g_c, for |g| < g_c, C^±(k_z) undergo a transition from ±1 to 0 with increasing k_z to a critical value k^C_z. Correspondingly, surface states are found to exist for |k_z| < k^C_z, and vanish for |k_z| < k^C_z. The transition at |k_z| < k^C_z is accompanied by closing of spin spectrum gap without energy gap closing, in contrast to a usual topological phase transition, where the energy gap always collapses. It is also shown that when |g| exceeds the critical value g_c, a transition of the 3D TI into a Weyl semimetal occurs, with surface states forming the Fermi arcs. Our work suggests a possible way to realize this interesting topological state of matter via magnetic doping in 3D TIs.

This work was supported by the State Key Program for Basic Researches of China under grants numbers 2014CB921103 (LS), 2011CB922103 and 2010CB923400 (DYX), the National Natural Science Foundation of China under grant numbers 11225420, 11074110 (LS), 11174125, 11074109, 91021003 (DYX) and a project funded by the PAPD of Jiangsu Higher Education Institutions. We also thank the US NSF grants numbers DMR-0906816 and DMR-1205734, and Princeton MRSEC grant number DMR-0819860 (DNS).