Work done on a bouncing ball

Work and energy are closely related in physics, and are usually related by the work-energy principle in introductory mechanics. That is, the work done by a force on an object is equal to the change in kinetic energy of the object. If the force remains constant and acts in the same direction as the displacement of the object then the work done is defined as the product of the force multiplied by the displacement of the point at which the force is applied. Despite the relative simplicity of the work-energy principle, there are some situations where the principle is not easy to apply. For example, the force might vary with time or it might act to change both the translational and rotational kinetic of the object or both the kinetic and potential energy of the object. In addition, there might be a change in the kinetic energy of the object even when the displacement of the point of application of the force is zero.

An example of the latter problem involves the bounce of a ball incident vertically on a rigid, horizontal surface. During the collision, the ball comes to a temporary stop and then bounces vertically upwards. If the ball is perfectly elastic then the rebound speed is the same as the incident speed and energy is conserved. There are two stages involved. While the ball is slowing down to a stop, the kinetic energy of the ball decreases and is converted to elastic energy due to compression of the ball. During the second stage, the ball expands back to its initial shape and the stored elastic energy is converted back to kinetic energy.

An interesting question concerns the work done by the vertical force acting at the bottom of the ball. There is no displacement of the point of application of the force, so the work done by that force is zero. Nevertheless, there is a decrease in kinetic energy during the collision and an equal and opposite increase in the stored elastic potential energy. Since negative work is done to decrease the kinetic energy and positive work is done to increase the potential energy, it is the total work done by the force at the bottom of the ball that is zero.

If the ball has a mass m and the external force acting on the bottom of the ball is F, then the acceleration, a, of the ball is given by $a = F/m$, where a refers to the acceleration of the centre of mass rather than the acceleration of the bottom of the ball. The gravitational force on the ball can usually be neglected since it is typically much smaller than the impact force at the bottom of the ball.

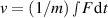The velocity, v, of the ball is therefore given by $a = \textrm{d}v/\textrm{d}t = F/m$ so $v = (1/m) \smallint F \, \textrm{d}t$. The work, W, done by F to change the kinetic energy of the ball is then given by

$$\begin{align} W & = \int F \, \textrm{d}y = \int m \frac{\textrm{d}v}{\textrm{d}t} \textrm{d}y \nonumber\\ & = \int m v \, \textrm{d}v = \Delta \left(\frac{1}{2}mv^{2} \right) \end{align} \tag{ 1 }$$

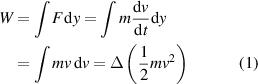
where 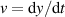$v = \textrm{d}y/\textrm{d}t$ and y is the vertical displacement of the centre of mass due to compression or expansion of the ball. The bottom of the ball remains at rest.

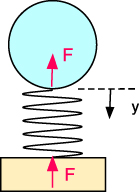
In order to calculate F, an estimate is needed for the ball stiffness. A simple model for the bounce of a ball is shown in figure 1, consisting of a mass m connected to a massless spring with spring constant k. The spring represents the bottom part of the ball that compresses and expands during the impact, just like a spring. If the ball impacts a rigid floor, then the bottom of the spring exerts a force, F, on the floor and the floor exerts an equal and opposite force on the bottom of the spring. The force of the spring on the floor does not remain constant but increases to a maximum when the ball comes to a stop, since the compression of the spring is a maximum at that time. The force decreases back to zero when the ball bounces off the floor.

Zoom In Zoom Out Reset image size

The force on the bottom end of the spring is transmitted to the top end of the spring, so the top end of the spring exerts a vertical force, F, on the mass m. If the ball is incident at speed v₀ then its kinetic energy is 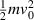$\frac{1}{2}mv_{0}^{2}$ so the decrease in kinetic energy when it comes to a stop is $\int F \, \textrm{d}y = \frac{1}{2}mv_{0}^{2}$ where y is the displacement of the centre of mass of m during the collision with the floor.

Some authors claim that $\smallint F \, \textrm{d}y$ is not 'real' work, since y is not the displacement of the point of application of F at the bottom of the spring, and classify it as 'pseudowork' or 'centre of mass work' [1–3]. That problem arises only if the spring is omitted from the bounce model, in which case the displacement of the bottom of the ball is not the same as the displacement of its centre of mass. In figure 1, the displacement of the centre of mass is the same as the displacement, y, of the top end of the spring. 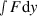The fact remains that $\smallint F\, \textrm{d}y$ is equal to the change in the translational kinetic energy of m, even if the spring is omitted in the model.

Since the top end of the spring exerts a force F on the bottom of m, there is an equal and opposite force F exerted by m on the top end of the spring. If the spring compresses by a distance y then F = ky and the work done on the spring is given by

$$\begin{equation} \int F \, \textrm{d}y = \int ky \, \textrm{d}y = \frac{1}{2}ky^{2} \end{equation} \tag{ 2 }$$

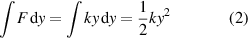
assuming that the spring is linear with a constant stiffness k. The potential energy stored in the spring is therefore $\frac{1}{2}ky^{2}$ and it increases with time until the mass m comes to a stop. If energy is conserved then at maximum compression, where $y = y_{0}$,

$$\begin{equation} \frac{1}{2}ky_{0}^{2} = \frac{1}{2} mv_{0}^{2} \end{equation} \tag{ 3 }$$

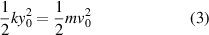
which means that the work done to decrease the kinetic energy of m is equal to the work done to increase the potential energy in the spring, and that

$$\begin{equation} y_{0} = v_{0} \sqrt{m/k} \, . \end{equation} \tag{ 4 }$$

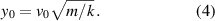
The maximum force on the spring and on m is given by

$$\begin{equation} F_\textrm{max} = ky_{0} = v_{0} \sqrt{mk} \, . \end{equation} \tag{ 5 }$$

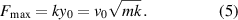
After m comes to a stop, the spring starts to expand and the ball starts rising vertically upwards. In that case, the work done to increase the kinetic energy of m is equal to the negative work done to decrease the potential energy in the spring. The total work done by F at the bottom end of the spring remains zero during the whole collision.

A similar model can be used to account for work done when a person jumps vertically off a rigid floor [1]. In that case, the energy stored in the legs can be represented in a simplified manner by a spring. The total work done by the floor is zero but work done by the gravitational force also needs to be considered when calculating the jump height.

If the ball is not perfectly elastic then a different model is needed to describe energy losses in the ball. An alternative version of figure 1 is described in [4] using a dashpot or shock absorber in parallel with a lossless spring. Calculated results are given in [4], and are compared with results measured for a happy ball and an unhappy ball.

All data that support the findings of this study are included within the article (and any supplementary files).