Work done by static friction on a bouncing ball

When a ball is incident obliquely on a horizontal surface, the friction force acting backwards at the bottom of the ball results in a decrease in the horizontal speed of the ball and it also results in an increase in the angular velocity of the ball. If the ball is incident at a glancing angle then it slides on the horizontal surface during the whole impact. At incident angles close to the normal, the bottom of the ball slides to a stop very quickly since the normal force on the ball is relatively large and the incident horizontal speed is relatively small. When the bottom of the ball stops sliding it grips the surface and remains at rest until the ball bounces off the surface. The friction force in that case is due primarily to static friction [1].

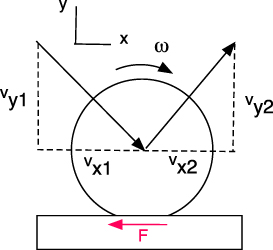
The change in horizontal speed and the change in spin is easy to calculate for a perfectly elastic ball, as indicated in figure 1. It is assumed that the ball is incident without spin and the friction force is due to static friction only. The bottom part of the ball stores elastic energy since it squashes in the vertical direction and stretches in the horizontal direction during the impact.

Zoom In Zoom Out Reset image size

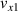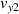The horizontal and vertical components of the ball speed at its centre of mass are $v_{x1}$ and $v_{y1}$ before the ball bounces, and $v_{x2}$ and $v_{y2}$ after the ball bounces. If the ball is perfectly elastic then $v_{y2} = - v_{y1}$. If the ball rotates clockwise at angular velocity ω₂ after the bounce, then the horizontal speed of a point at the bottom of the ball, after the bounce, is $v_{x2} - R\omega_{2}$ where R is the ball radius. 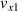The horizontal speed of a point at the bottom of the ball, before the ball bounces, is $v_{x1}$ since the ball is incident without spin. If the ball is perfectly elastic then

$$\begin{equation} R\omega_{2} - v_{x2} = v_{x1} \end{equation} \tag{ 1 }$$

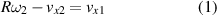
which means that there is no change in the horizontal speed of the contact point at the bottom of the ball but the direction of motion is reversed, in the same way that it is reversed in the vertical direction. The effect can be observed using a highly elastic superball [2]. For a perfectly elastic ball, elastic energy stored in the ball during the impact is completely recovered, in both the vertical and horizontal directions.

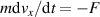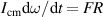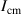During the impact, the horizontal speed changes according to the relation $m \textrm{d}v_{x}/\textrm{d}t = -F$ where m is the mass of the ball and F is the friction force. The angular velocity of the ball changes according to the relation $I_\textrm{cm} \textrm{d}\omega/\textrm{d}t = FR$ where $I_\textrm{cm}$ is the moment of inertia of the ball. For a uniform, solid ball, 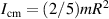$I_\textrm{cm} = (2/5)mR^{2}$. If these relations are integrated over the duration of the impact, and if the change in R during the impact is negligible, then

$$\begin{equation} \int F \, \textrm{d}t = m\left(v_{x1} - v_{x2}\right) = \frac{2}{5} mR \omega_{2} \, . \end{equation} \tag{ 2 }$$

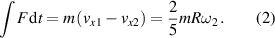
By combining equations (1) and (2), it is easy to show that

$$\begin{equation} v_{x2} = \frac{3}{7} v_{x1} \end{equation} \tag{ 3 }$$

and

$$\begin{equation} R\omega_{2} = \frac{10}{7} v_{x1} = \frac{10}{3} v_{x2} \, . \end{equation} \tag{ 4 }$$

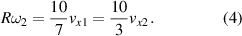
The bottom of the ball therefore rotates backwards after the ball bounces since 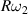$R\omega_{2}$ is 3.33 times larger than 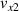$v_{x2}$. The increase in the rotational kinetic energy is

$$\begin{equation} \frac{1}{2}I_{cm} \, \omega_{2}^{2} = \frac {mR^{2}\omega_{2}^{2}}{5} = \frac{20 m v_{x1}^{2}}{49} \end{equation} \tag{ 5 }$$

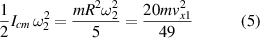
and the decrease in the translation kinetic energy is

$$\begin{equation} \frac{1}{2}m\left(v_{x1}^{2} - v_{x2}^{2}\right) = \frac{1}{2}mv_{x1}^{2} \left(1- \frac{9}{49} \right) = \frac{20 m v_{x1}^{2}}{49} \, . \end{equation} \tag{ 6 }$$

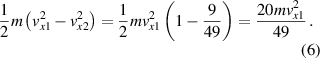
The work done by F to increase the rotational kinetic energy is therefore equal and opposite the work done to change the translational kinetic energy, so the total work done by F is zero. The static friction force acts to convert some of the translational kinetic energy of the ball into rotational kinetic energy, without adding to or subtracting from the total kinetic energy of the ball. A similar result is found when a ball rolls without sliding down an inclined plane. The friction force is then due to static friction which acts to increase the rotational kinetic energy of the ball and to decrease its translational kinetic energy by the same amount [3].

All data that support the findings of this study are included within the article (and any supplementary files).

The author has no conflicts to disclose.