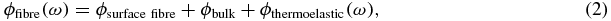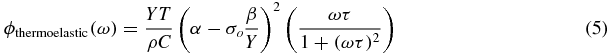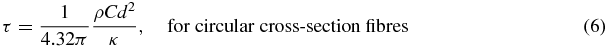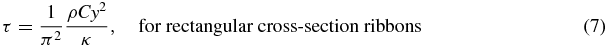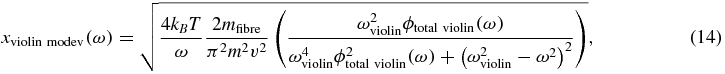Silicon mirror suspensions for gravitational wave detectors

Future upgrades to advanced detectors, together with third generation detectors such as the Einstein Telescope (ET) [19] may look to directly address thermal noise via implementation of cryogenic cooling of the test mass mirror suspensions. This would reduce further the thermal noise of the mirrors, their suspensions and their coatings [19]. For this, fused silica is not an ideal material for the test mass or suspension, since it is known to have a wide mechanical dissipation peak centred around 40 K [10], and also has low thermal conductivity [20] which makes extraction of heat from the incident interferometer laser beam potentially challenging. However, crystalline materials such as sapphire (currently proposed for use in the Japanese cryogenic detector KAGRA [21]) or silicon (the baseline choice for ET) [19] have more attractive low temperature properties and are therefore promising future candidate suspension materials. In particular, at temperatures around 18 K and around 125 K the thermal expansion coefficient of silicon goes through zero [22], and hence the dissipation due to thermoelastic damping is essentially negligible around these temperatures [23]. Our studies [24] have also indicated that the surface loss of silicon in the form of flexures at low temperature may be at least an order of magnitude lower than that of fused silica. Initial studies in [25, 26] have shown the feasibility of pulling crystalline fibres by the pedestal growth technique.

Two fibre geometries are of particular interest for use in detector suspensions—rectangular cross section suspension 'ribbons', or circular cross section 'fibres' [2]. The mechanical loss of these suspension elements can be calculated from the individual loss components—a loss ϕ_bulk associated with the bulk material making up the fibre, a frequency independent component from loss arising at the fibre surface, ϕ_{surface fibre}, and a frequency dependent thermoelastic loss component, ϕ_{thermoelastic}(ω):

$$\begin{equation} \phi _{{\rm fibre}} ( \omega ) = \phi _{{\rm surface\ fibre}} + \phi _{{\rm bulk}} + \phi _{{\rm thermoelastic}} (\omega), \end{equation} \tag{ 2 }$$

with the surface loss given by:

$$\begin{equation} \phi _{{\rm surface}\ {\rm fibre}} \approx \frac{{8h\phi _s }}{d}, \end{equation} \tag{ 3 }$$

where hϕ_s is the product of the mechanical loss of the material surface, ϕ_s, and the depth, h, over which surface loss mechanisms are believed to occur. From [24] we take the value of 5 × 10⁻¹³ as hϕ_s. For rectangular cross section ribbons, the surface loss takes the form [27]:

$$\begin{equation} \phi _{{\rm surface\ ribbon}} = \frac{3+\frac{x }{y}} {1+ \frac{x }{y}} h\phi _s \frac{{2( {x + y} )}}{{xy}}, \end{equation} \tag{ 4 }$$

where x is the width of the ribbon, and y is the thickness (in the direction of bending).

Thermoelastic loss for a suspension fibre, which generates motion via the thermal expansion of the material due to localized variations in temperature [28–30] is given by:

$$\begin{equation} \phi _{{\rm thermoelastic}} (\omega ) = \frac{{YT}}{{\rho C}}\left( {\alpha - \sigma _o \frac{\beta }{Y}} \right)^2 \left( {\frac{{\omega \tau }}{{1 + ( {\omega \tau } )^2 }}} \right) \end{equation} \tag{ 5 }$$

with

$$\begin{equation} \tau = \frac{1}{{4.32\pi }}\frac{{\rho Cd^2 }}{\kappa },\quad {\rm for}\;{\rm circular}\;{\rm cross} \hbox{-} {\rm section\ fibres} \end{equation} \tag{ 6 }$$

$$\begin{equation} \tau = \frac{1}{{\pi ^2 }}\frac{{\rho Cy^2 }}{\kappa },\quad {\rm for\ rectangular\ cross} \hbox{-} {\rm section\ ribbons} \end{equation} \tag{ 7 }$$

where Y is the Young's modulus of the fibre, C is the specific heat capacity, κ is its thermal conductivity, ρ is the density, α is the coefficient of linear thermal expansion, σ_o is the static stress in the fibre due to the suspended load, $\beta = {\textstyle{1 \over Y}}{\textstyle{{{\rm d}Y} \over {{\rm d}T}}}$ is the thermal elastic coefficient, d is the diameter of the fibre in the circular cross-section case, and y is the thickness of the ribbon in the rectangular cross-section case.

The total mechanical loss of the system for the pendulum suspension is less than that of the material as often a significant amount of energy is stored in the lossless gravitational field. This is dissipation dilution, D:

$$\begin{equation} \phi _{{\rm total\ pendulum}} (\omega) = \frac{{\phi _{{\rm fibre}} ( \omega)}}{D}, \end{equation} \tag{ 8 }$$

where D is evaluated for each resonant mode [29, 31]:

$$\begin{equation} D = \frac{{2mgL}}{{\gamma n\sqrt {FYI} }}, \end{equation} \tag{ 9 }$$

with L the length of the suspension, F is the tension in each fibre, I is the second area moment of the fibres, n is the number of fibres and γ takes the value of unity if the wires bend only at the top, and the value 2 if they bend both top and bottom [2].

It is clear that surface loss, thermoelastic loss and dissipation dilution of suspension elements are dependent on the cross-sectional dimensions of the suspension fibres. For fused silica suspensions these values were chosen carefully to minimise the mechanical loss and provide appropriate resonant modes of the suspension [32]. However, for low temperature detectors using silicon suspensions, additional constraints are present. This paper presents analysis of silicon suspension performance focusing on two of these additional factors that will have a significant bearing on the fibre dimensions—namely extraction of heat injected by the main interferometer laser beam; and the tensile strength of silicon.

Cryogenic mirrors will experience heating from absorption of a fraction the laser light incident on the mirror surface. Radiative cooling may be possible at higher temperatures (>∼120 K) [33], but at lower temperatures conduction of the heat along the suspension fibres will be the primary mechanism for extracting the heat deposited in the test mass [34].

This therefore places a limit on their cross sectional area—if the fibres are too thin then this will inhibit heat extraction. This limit on minimizing fibre cross-section directly affects the resulting thermal noise performance of the suspension via the achievable dissipation dilution and the surface loss.

The minimum radius of circular fibre required can be estimated using the conduction equation [35]:

$$\begin{equation} \frac{{{\rm d}T}}{{{\rm d}y}} = \frac{H}{{4Ak (T)}}, \end{equation} \tag{ 10 }$$

where H is the heat flow along the fibres, A is the cross sectional area of an individual fibre (with 4A being the total cross sectional area of the 4 suspension fibres available for heat conduction), and k(T) is the temperature dependent thermal conductivity. For a fibre length L, the required area, A, to precisely extract the deposited heat is then:

$$\begin{equation} A = \frac{{HL}}{{4\int_{T_1 }^{T_2 } {k( T )}\, {\rm d}T}}, \end{equation} \tag{ 11 }$$

where T₁ and T₂ are the lower and upper mass temperatures respectively. Values for the temperature dependent thermal conductivity over much of the temperature range were taken from [22].

The thermal conductivity of a material is limited by phonon scattering, and at low temperatures (<40 K), will eventually be limited by the sample's smallest dimension, due to scattering at the material surface boundaries [36]. In this case, the thermal conductivity values used were set by the smallest dimension of the samples:

$$\begin{equation} A_{{\rm Low\ temp}} = \frac{{t_{{\rm meas}} }}{t}\frac{{HL}}{{4\int_{T_1 }^{T_2 } {k( T )}\, {\rm d}T}}, \end{equation} \tag{ 12 }$$

where t_meas is the minimum dimension of the relevant sample in [22], and t is the minimum dimension of the suspension ribbon/fibre.

For future detectors such as the ET, the circulating laser powers in the interferometer may be of the order of 18 kW, with an anticipated worst case mirror absorption of 1 part per million [19], meaning 18 mW will be required to be extracted from the test mass. To set the framework for the physical demands on suspension performance we make the simplified assumption that the tops of the fibres are held at liquid helium temperature of 4 K, and we then vary the desired temperature of the test mass. Several lengths of suspension were also analysed: 60 cm (as in aLIGO) and two larger suspensions at 100 cm and 140 cm respectively. Considering effects of suspension length on performance is important, as longer fibres give greater dilution through equation (9). However the longer the fibre, the larger its dimensions need to be to extract the heat (see equation (12)). The minimum radius of circular fibre required to extract the 18 mW absorbed power is shown in figure 1(a), and the minimum thickness of a ribbon with 5:1 width:thickness aspect ratio is shown in figure 1(b).

Zoom In Zoom Out Reset image size

It can be seen in figure 1 that the required fibre diameter rapidly increases as temperatures decrease below 40 K, as thermal conductivity drops significantly at these temperatures. This means a significantly thicker fibre is required to extract the deposited energy as the desired test mass temperature decreases. This in turn influences the observed dissipation dilution of a suspension through equation (9), as shown in figure 2.

Zoom In Zoom Out Reset image size

Dissipation dilution is seen to be greater by a factor of ∼2 for rectangular ribbons as compared to the circular fibres at equivalent temperatures—this is because the required ribbon thickness in the direction of bending is smaller than the equivalent fibre radius, as was shown in figure 1.

Figure 3 shows the surface, bulk and thermoelastic loss components of these ribbons and fibres at 10 Hz, where we assume a worst case where the fibre is at the same temperature as the test mass along its length⁵. For temperatures below ∼40 K, thermoelastic loss drops away and is no longer a dominant or significant loss term for circular fibres. For the rectangular ribbons surface loss is dominant over most of the temperature range. However, as fibre length (and therefore thickness) increases the thermoelastic loss rises, to be about equal to surface loss at temperatures of ∼70–90 K for the 140 cm long suspension. Longer suspensions than this would see the thermoelastic loss start to rise above surface loss at these temperatures.

Zoom In Zoom Out Reset image size

In both cases, the significant fall off of thermoelastic loss at low temperatures is due to both the approach of the null in thermal expansion coefficient of the silicon at ∼18 K, and also because thermoelastic loss is directly proportional to temperature, as displayed by equation (5).

Bulk loss is taken from measurements by McGuigan [38]. These show a peak at ∼13 K, with the bulk dropping away to leave the other loss components dominating in the region from ∼17 K upwards. The loss peak at 13 K has not been observed in [39], however we include here as a worst case.

The displacement thermal noise for a single suspension, calculated at 10 Hz via equation (1) is shown in figure 4(a) for circular fibres and figure 4(b) for ribbons for a 200 kg test mass (the current design choice for the ET [40]). Ribbons are seen to have better thermal noise performance—this is due to their higher dissipation dilution. In both ribbon and fibre cases, only very small gains in noise performance are seen for temperatures less than ∼40 K. Indeed, at temperatures between 20 and 40 K the observed thermal noise begins to level off—this is due to the much lower dissipation dilution experienced at these temperatures—this being a result of a much larger radius fibre/thickness of ribbon that is needed to maintain the low test mass temperature. At lower temperatures than this the peak in bulk loss causes a low temperature peak in noise.

Zoom In Zoom Out Reset image size

The flattening off of the noise in 20–40 K temperature gives the opportunity to broaden the range of potential operating temperatures in the low temperature regime, without significant impact on performance. Due to the technical challenge of ensuring no external heat leaks into the system, temperatures at the higher end of this range will potentially be an easier goal to meet, so for the remainder of this paper we will analyse for suspensions running at 40 K.

It is of note that the suspension thermal noise at 40 K is between a factor of 40–76 times lower (depending on the suspension length) than that of the current room temperature silica suspensions in aLIGO for circular fibres, whose thermal noise at 10 Hz is ∼1 × 10⁻¹⁹m Hz^−1/2 [41, 42]. For rectangular cross-section ribbons the noise is a factor of 58–113 lower depending on the suspension length. However, the calculations above are based solely on the minimum fibre dimension required for desired heat extraction from a test mass. Another key parameter needed to practically fabricate a cryogenic mirror suspension is an appropriate level of tensile strength in the silicon suspension fibres.

2.2.1. Previous studies

2.2.2. Measurement of tensile strength of silicon

An initial experimental study of tensile strength at room temperature has been undertaken. In this study a total of 93 silicon samples of 9 different varieties were tested, with 5 different variations of standard surface treatments undertaken, to give an indication of their effects. Two crystal axis orientations of silicon wafer, 〈1 0 0〉, 〈1 1 0〉, were available for test. Sample details are given in table 1.

Table 1. Details of silicon suspension samples used in tensile strength tests.

Sample set	Silicon orientation	Sample dimensions (mm)	Edge quality	Surface treatment
1	〈1 1 0〉	45 × 2.2 × 0.5	Mechanically	None
			polished
2	〈1 0 0〉	45 × 2.2 × 0.5	Mechanically	None
			polished
3	〈1 0 0〉	45 × 3.5 × 0.5	Etched	None
4	〈1 1 0〉	45 × 2.2 × 0.5	Mechanically	Front and back surfaces
			polished	coated with Si3N4
5	〈1 0 0〉	45 × 2.2 × 0.5	Mechanically	Front and back surfaces
			polished	coated with Si3N4
6	〈1 0 0〉	45 × 2.2 × 0.5	Mechanically	Entire sample
			polished	wet oxidized
7	〈1 1 0〉	45 × 2.2 × 0.5	Mechanically	Entire sample
			polished	wet oxidized
8	〈1 1 0〉	45 × 2.2 × 0.5	Mechanically	Front and back surfaces
			polished	coated with Si3N4,
				edges wet oxidized
9	〈1 0 0〉	45 × 2.2 × 0.5	Mechanically	Front and back surfaces
			polished	coated with Si3N4,
				edges wet oxidized

The samples were rectangular cross section, with all apart from sample set 3 mechanically cut out of standard 0.5 mm thick silicon wafers, with the edges then mechanically polished. Sample set 3 was chemically etched from wafers to provided a comparison with etched samples.

Sample sets 4, 5, 8 and 9 were wet oxidized in a saturated atmosphere at 1000 °C for 1 h, with a range of oxide thicknesses from 100–300 nm measured after oxidation, this being done using a Sentech SE850 spectroscopic ellipsometer [49] prior to breaking the samples.

Since clamping the samples mechanically could cause surface damage, or be prone to slippage during testing, the samples were bonded between two metal attachment pieces using Aradite 2012 epoxy adhesive as shown in figure 5(a). Prior to curing of the bonding adhesive, the sample was set in an alignment jig to ensure the samples were aligned consistently and parallel to the attachment pieces, as in figure 5(b). Once cured, the samples were mounted on an adaptable tensile strength testing apparatus [50] as shown in figure 5(c). Universal joints were installed above and below the sample to ensure that minimal bending or torsional forces would be experienced by the samples.

Zoom In Zoom Out Reset image size

2.2.3. Strength results

The tensile strength test results for the nine sample sets are shown in figure 6.

Zoom In Zoom Out Reset image size

It appears that the samples with etched edges (set 3) are stronger by on average ∼50% with an average strength of (210±17) MPa compared to the equivalent unetched samples in sets 1 and 2 which had average strengths of (147±13) MPa, (133±13) MPa respectively. Sets 1 and 2 are also within error indicating that the orientation of the silicon sample is not a dominant influence on strength. The results for the etched samples are consistent with the maximum strength of ∼200 MPa reported in [45] at room temperature, which had a similar etched surface treatment. Indeed a significant number of the datapoints presented here show higher strength than 200 MPa – higher than those of [45]. The lower values of strength seen for sample sets 1 and 2 imply that the surface edge quality is a limiting factor on strength, as could be expected. Figure 7 shows an SEM image of typical sample edges showing damage as could be expected from mechanical polishing, with chips of order of 10–20 µm in size visible.

Zoom In Zoom Out Reset image size

The samples with Si₃N₄ on their front and back surfaces (sets 4 and 5) were seen to be no stronger than their untreated equivalents in sets 1 and 2. This implies again that the surface quality of the untreated edges is limiting the strength. Samples which had these edges oxidized (sets 8 and 9) were seen to have a notably increased strength, as were those with all surfaces oxidized. This supports the postulation that surface quality is limiting strength, and it is clear from these results that suitable surface treatment can enhance the strength of silicon suspension elements.

2.2.4. The effect of strength on suspension thermal noise performance

Mechanical loss was again modelled as in section 1.2 but in this case the dimensions of the fibres/ribbons were chosen from strength values. The thermal noise performance was then calculated for the pendulum (using equation (1)), vertical bounce and first two violin modes of the suspension, as below. A 200 kg test mass is assumed, this being the current design choice for the ET [40].

Vertical mode.

This resonance experiences no dissipation dilution [2] so the value of D was taken as 1 in the calculations. Vertical motion couples weakly into horizontal motion if the interferometer arms are long enough such that the test masses at the arm ends do not hang parallel, due to the curvature of the earth. If we assume similar cross coupling from vertical to horizontal motion as in current advanced detectors, a value of 0.1% is taken [51, 52]. Therefore, the contribution to horizontal thermal noise rms displacement from the vertical mode is then:

$$\begin{equation} x_{{\rm vertical}} ( \omega ) = 0.001\sqrt {\frac{{4k_B T}}{{m\omega }}\left( {\frac{{\omega _{{\rm vertical}} ^{2} \phi _{{\rm total}\ {\rm vertical}} ( \omega )}}{{\omega _{{\rm vertical}} ^4 \phi _{{\rm total\ vertical}} ^2 ( \omega ) + \big( {\omega _{{\rm vertical}} ^2 - \omega ^2 } \big)^2 }}} \right)} \end{equation} \tag{ 13 }$$

where ϕ_{total vertical} (ω) is the total loss for the vertical mode, and ω_vertical is the vertical resonant mode frequency.

Violin modes.

The violin mode thermal noise spectrum for the first two violin modes was calculated using [53]:

$$\begin{equation} \fl x_{{\rm violin\ mode}{\rm v}} (\omega ) = \sqrt {\frac{{4k_B T}}{\omega }\frac{{2m_{{\rm fibre}} }}{{\pi ^2 m^2 v^2 }}\left( {\frac{{\omega _{{\rm violin}} ^2 \phi _{{\rm total\ violin}} ( \omega )}}{{\omega _{{\rm violin}} ^4 \phi _{{\rm total\ violin}} ^2 ( \omega ) + \big( {\omega _{{\rm violin}} ^2 - \omega ^2 } \big)^2 }}} \right)} , \end{equation} \tag{ 14 }$$

where, m_fibre is the mass of each fibre, ω_violin is the respective violin resonant mode frequency, v is the respective violin mode number and ϕ_{total violin}(ω) is the total loss for the violin mode, calculated using [54]:

$$\begin{equation} \phi _{{\rm total\ violin}} ( \omega ) = 2\phi _{{\rm total\ pendulum}} ( \omega ). \end{equation} \tag{ 15 }$$

Noise spectra.

Figure 8 shows the noise spectra at 40 K for the cases of fibres with a stress of 133 MPa (equivalent to the average 〈1 0 0〉 strength test undertaken in section 2.2.3, figure 6), 40 MPa (equivalent to the average 〈1 0 0〉 strength test undertaken in section 2.2.3, but including a factor of ∼3 safety), 300 MPa wet oxidized fibres (this stress is taken from the average value seen from the oxidized sample set 7 in section 2.2.3, figure 6), and 573 MPa case, which is equivalent to the fibre diameter required to extract the deposited detector laser energy (taken from section 2.1). Figure 9 shows the equivalent for rectangular cross section ribbons. All suspensions are 1 m in length. In both figures 8, 9 the design sensitivity of ET (referred as ET-D [40]) is shown for comparison.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

It can be seen from figures 8, 9 that both silicon ribbons and fibres show a significant potential gain in performance over the current aLIGO room temperature suspensions. For the 40 MPa strength limited case a factor of improvement in displacement noise of 18 times is seen at 10 Hz for circular fibres. This is limited by thermoelastic loss. If fibre strength is improved, the gain in performance also increases with a factor of 39 improvement seen at 133 MPa, increasing to a factor of 57 at the heat extraction limited case of fibres where the stress in the fibres would be 573 MPa. As the strength increases and the fibre gets thinner, the thermoelastic peak frequency increases, meaning less thermoelastic loss is seen at low temperature. Equivalent rectangular cross section ribbons show slightly greater performance gains, with a gain of ∼100 at the heat extraction limited case with ribbons having a stress of 573 MPa. One potential advantage of the rectangular geometry is that the violin modes are at higher frequencies than those in the equivalently stressed circular fibre suspensions. Depending on the frequency of gravitational wave source that may be of interest, this may prove desirable. In both cases careful choices may need to be made in fibre design to place the vertical bounce mode resonance at a frequency that does not impinge too far into the detection band—as can be seen from figures 8, 9 the vertical mode comes down in frequency as strength increases (and therefore fibre cross section decreases).

Gains beyond the heat extraction limiting cases would require fibres/ribbons to be thinner still, and therefore methods of extracting the deposited detector laser energy that do not rely on conduction up the suspension fibres would need to be implemented.

These results show that improving strength via surface treatments that have low or negligible effect on the surface loss value is key in improving the thermal noise performance of future silicon suspensions—it would be required for this suspension to meet the noise requirement for ET, for example. A limit is placed on the ultimate noise performance of any given suspension by the minimum thickness of fibre required to extract the deposited heat. Improving this requires both an increase in the strength of silicon, and additional methods of cooling the test mass other than extracting heat only via conduction up the suspension fibres. The oxidized fibres have significantly greater surface loss hϕ_s value of 1 × 10⁻¹⁰ [55] as compared un-oxidized silicon (hϕ_s value of 5 × 10⁻¹³ [24]), explaining their higher thermal noise as shown in figures 8, 9. This highlights that while the surface treatment undertaken successfully increases the fibre strength (and therefore reduces the required cross sectional area and increases dissipation dilution) it does significantly increase the material's surface loss, affecting the ultimate performance. Therefore future surface treatments need to be shown to have low mechanical loss as well as increasing the strength of the silicon.