Optimizing dynamics of integrated food–energy–water systems under the risk of climate change

Milad Memarzadeh; Scott Moura; Arpad Horvath

doi:10.1088/1748-9326/ab2104

1. Introduction

In recent years, there has been significant research interest in realizing sustainable infrastructure through integrated operation of food, energy, and water systems (FEWS) (Al-Saidi and Elagib 2017, Veldhuis and Yang 2017, Helmstedt et al 2018, Liu et al 2018). Fundamental elements of integrated FEWS include uncertainty, the interdependence between sectors, risk and impact of climate change, and a generalized framework that enables scalability to a multitude of applications (Howarth and Monasterolo 2016, Cai et al 2018). A recent review paper by Albercht, Crootof, and Scott (2018) identifies two fundamental gaps in FEWS analysis: (1) the methods are generally not reproducible and are problem-specific; (2) they usually fall short of incorporating the interdependence across sectors as well as resource interdependence. More specifically, recent literature in FEWS management either focus on optimizing the food process and identifying optimal strategies for such management, or focus on the flow of information and resources among the different sectors involved in the operations, ignoring the optimization of the process due to computational complexity.

Optimizing the operations of FEWS requires identifying the management objective, constraints to the manager, strategies available to her, utilities corresponding to the operational costs, revenue, as well as the effect of exogenous (or uncontrolled) variables such as environmental variations. Once these are quantified, several approaches can be used to identify the management strategies and outcomes of such implementations on the FEWS operations in long-term, including mathematical programming (Rong et al 2012, Yu and Nagurney 2013, Zhang et al 2018, Bieber et al 2018), life-cycle assessment (Sherwood et al 2017, Wang et al 2017, Bell et al 2018), and scenario planning (Ramaswami et al 2017, Chaudhary et al 2018, Karan et al 2018). Although most of these studies focus on optimizing the crop production or food process life cycle, recent studies have focused on utilizing similar approaches to model and optimize the inter-connected sectors. Examples are modeling inter-connection of energy and food sectors towards utilization of food bi-products for energy purposes (Cuellar and Webber 2010, Boyer and Ramaswami 2017, Breunig et al 2017, Wang et al 2018), flow of energy and water within a FEWS network, as well as design of network topology itself (Kurian et al 2018, Tsolas et al 2018, Daher et al 2019, Liang et al 2019), and the interdependence with social aspects of FEWS (Givens et al 2018). Another important factor in integrated FEWS analysis is risk imbued by climate change. A few recent studies have evaluated the effect of climate change on crop production and operation within an integrated FEWS using dynamic forward simulation (Conway et al 2015, Berardy and Chester 2017, Baker et al 2018, Bieber et al 2018). Nevertheless, current efforts that incorporate climate change effects in FEWS analysis mostly rely on management strategy evaluation (Smith 1994), which is also known as scenario planning. Although management strategy evaluation can evaluate the effect of fixed management strategies on long-term FEWS operations under pre-defined realizations of random events, they cannot generate the optimal solution in a stochastic sense.

FEWS integrated management requires a combination of economic-based management strategy evaluation, with optimization that incorporates environmental impacts and risk of climate change. Decision theory and reinforcement learning make this integration possible; recent advancements in these fields have shown great promise in modeling complex dynamics of interdependent systems (Littman 2015) in many real-world applications such as human-level control in gaming (Mnih et al 2015, Silver et al 2017), natural resource management (Memarzadeh and Boettiger 2018, 2019), and robotics (Porta et al 2005, Francois-Lavet et al 2018). In this article we develop a dynamic optimization approach basing upon fundamentals of decision theory and model-based reinforcement learning, to adaptively control and optimize operation of integrated FEWS. The novelties of the proposed approach are the ability to (1) quantify and propagate uncertainty and stochasticity in the dynamics of each sector, (2) incorporate resource interdependence, (3) include the impact of the uncontrolled variables such as climate variations, and (4) adaptively optimize the management decisions to minimize the costs and environmental impacts of the agricultural production. Moreover, the proposed method is robust to problem-specific complexities and is easily reproducible. We evaluate its performance with a real-world case study of a FEWS in Ventura County, California.

2. Methods

In order to fill the gaps mentioned above, we develop a dynamic Bayesian network (Barber 2012) to optimize the management of FEWS under the effect of climate variability. Dynamic Bayesian network is a specific family of model-based reinforcement learning. When modeling a problem using this approach, one needs to define the state space, actions available to the manager, the dynamics of the system, and the utility function. We define each next (for detailed definitions refer to table A4).

The state space represents the time-varying condition (or status) of the FEWS. We factorize the state space into two sets of variables. (1) Let x ∈ X represent the status of the water and energy resources, as well as the food (i.e. crop production) state (it should be noted that food state in this article solely correspond to the agricultural production and not the state of food processes in the entire life cycle). These are controlled states, where X is the entire domain of the state space, which is a Cartesian product of the water and energy states with crop production state, i.e. X = F × E × W. (2) Let s ∈ S represent the climate and seasonal variations, defined as an exogenous variable (sometimes also called uncontrolled variable). For example, s could represent different seasons, annual changes in the temperature, or seasonal and annual changes in precipitation. Similarly, S represents the entire domain of the exogenous variables. Consequently, the entire state space is defined in a factorized space of controlled and uncontrolled variables: $\left({\bf{X}},{\bf{S}}\right)$ . The manager (also sometimes referred to as the decision-maker or the agent) of the system may select different actions corresponding to different sources of water and energy, a ∈ A, where A represents the entire domain of actions available to the manager.

The dynamics of the crop, energy, and water variables are modeled as a stochastic process, i.e. ${x}_{t+1}\,={f}_{x}\left({x}_{t},{a}_{t},{s}_{t+1}\right)+{\zeta }_{t}^{x}$ , where t denotes the time index, and ζ_t^x is a random variable representing the stochasticity in the dynamics. It should be noted that the dynamics of the FEWS variables depend on actions taken by manager, as well as exogenous state variables (e.g. temperature, precipitation, season) s_t+1. The state of the uncontrolled variable s_t also evolves stochastically, ${s}_{t+1}={f}_{s}\left({s}_{t}\right)+{\zeta }_{t}^{s}$ . We assume that the uncontrolled variables affect the dynamics of the crop production, energy and water variables, but the manager has no control over their dynamics and as a result, the manager just observes their changes.

The quality of the strategies that the manager takes is quantified by a pre-specified utility function that maps state and action spaces to real-value numbers: $u({x}_{t},{s}_{t},{a}_{t}):\left({\bf{X}},{\bf{S}}\right)\times {\bf{A}}\to {\mathbb{R}}$ . Specifically, we define utility as follow

$\begin{eqnarray}&&u({x}_{t},{s}_{t},{a}_{t})=\mathrm{Rev}-C({a}_{t})-P({x}_{t},{s}_{t}),\end{eqnarray} \tag{ 1 }$

where we assume that Rev is the constant revenue achieved from agricultural productions, C(a_t) is the costs of actions taken by the manager (which is comprised of energy cost (MJ/kg of the crops produced), GHG emissions (kgCO2/kg of the crops produced), and operational costs ($/kg of the crops produced)), and P(x_t, s_t) is the loss of revenue (i.e. penalty) due to failure of the agricultural production and not yielding the crops. Since the revenue is assumed to be constant, the optimal management strategy that maximizes the profit in agricultural production, i.e. the utility function defined above, is equivalent to the management strategy that minimizes the operational costs of the production. As a result, we define the objective of the optimization problem by minimization of the costs.

Since actions taken by a manager have both immediate and long-term effects on the system dynamics, the optimization objective need to be sensitive to both immediate and long-term outcomes. As a result, the goal of the optimization process is to minimize operational costs and environmental impacts, in some sense, over the entire FEWS network life-span. This is mathematically given by the weighted sum of costs over each time step: ${\sum }_{t=0}^{T}{\gamma }^{t}\left(C({a}_{t})+P({x}_{t},{s}_{t})\right)$ , where T is the life-span of the system (or management time horizon). Symbol $\gamma \in \left[0,1\right)$ is the discount factor, relating future costs to their net present value. We usually set T to infinity to model long-term management problems. The management strategy (sometime also referred to as policy) can then be defined as a mapping from the state space to the action space, $\pi :\left({\bf{X}},{\bf{S}}\right)\to {\bf{A}}$ . For an arbitrary strategy, π, one can calculate the long-term expected cost over the network's life-span, which we denote by V^π, and it is calculated recursively as:

$\begin{eqnarray}&&\begin{array}{c}\begin{array}{l}{V}^{\pi }\left({x}_{t},{s}_{t}\right)=C\left(\pi ({x}_{t},{s}_{t})\right)+P\left({x}_{t},{s}_{t}\right)\\ \,+\,\gamma \displaystyle \sum _{{s}_{t+1}\in {\bf{S}}}p({s}_{t+1}| {s}_{t})\left[\displaystyle \sum _{{x}_{t+1}\in {\bf{X}}}p\left({x}_{t+1}| \right.\right.\\ \,\left.\left.\,{x}_{t},\pi \left({x}_{t},{s}_{t}\right),{s}_{t+1}\right){V}^{\pi }\left({x}_{t+1},{s}_{t+1}\right)\Space{0ex}{3.7ex}{0ex}\right],\end{array}\end{array}\end{eqnarray} \tag{ 2 }$

where $C\left(\pi ({x}_{t},{s}_{t})\right)$ is the immediate costs associated with the strategy π, $P\left({x}_{t},{s}_{t}\right)$ loss in revenue (if incurred), and p(x∣y) is the probability of event x conditioned on event y. The conditional probabilities p(s_t+1 ∣ s_t) and $p\left({x}_{t+1}| {x}_{t},\pi \left({x}_{t},{s}_{t}\right),{s}_{t+1}\right)$ correspond to the respective dynamics ${f}_{s}\left({s}_{t}\right)+{\zeta }_{t}^{s}$ and ${f}_{x}\left({x}_{t},{a}_{t},{s}_{t+1}\right)+{\zeta }_{t}^{x}$ , respectively. Figure 1 visualizes the probabilistic graphical model of the factorized dynamic Bayesian network.

Figure 1. Refer to the following caption and surrounding text. — **Figure 1.** The probabilistic graphical model of a food–energy–water system. Circles represent random variables, squares represent decision variables, and diamonds represent the utility variables. As can be seen, the state space is factorized into two sets: crop production, energy, and water states, X, and the uncontrolled state, S, comprised of seasonal changes, λ, changes in temperature, ΔT, and precipitation, r. The expressions on the edges correspond to the dynamics of the uncontrolled variable, p(s_t+1 ∣ s_t), dynamics of the controlled state variables, $p\left({x}_{t+1}| {x}_{t},\pi \left({x}_{t},{s}_{t}\right),{s}_{t+1}\right)$ , utility variables, $u\left({x}_{t},{s}_{t},{a}_{t}\right)$ (as defined in equation (1)), and action selection according to a management strategy, π*. For example, the action at time step t is denoted as ${a}_{t}={\pi }^{* }\left({x}_{t},{s}_{t}\right)$ .
Download figure:
Standard image High-resolution image

**Figure 1.** The probabilistic graphical model of a food–energy–water system. Circles represent random variables, squares represent decision variables, and diamonds represent the utility variables. As can be seen, the state space is factorized into two sets: crop production, energy, and water states, X, and the uncontrolled state, S, comprised of seasonal changes, λ, changes in temperature, ΔT, and precipitation, r. The expressions on the edges correspond to the dynamics of the uncontrolled variable, p(s_t+1 ∣ s_t), dynamics of the controlled state variables, $p\left({x}_{t+1}| {x}_{t},\pi \left({x}_{t},{s}_{t}\right),{s}_{t+1}\right)$ , utility variables, $u\left({x}_{t},{s}_{t},{a}_{t}\right)$ (as defined in equation (1)), and action selection according to a management strategy, π*. For example, the action at time step t is denoted as ${a}_{t}={\pi }^{* }\left({x}_{t},{s}_{t}\right)$ .
Download figure:
Standard image High-resolution image

The difference between the method proposed here and previous attempts based on scenario planning are two-fold: (1) we seek to optimize the management objective and find the optimal management strategy, and not just evaluate a set of pre-determined strategies, and (2) uncertainty is elegantly handled by directly incorporating statistics into the strategy design, instead of evaluating strategies on a finite set of randomly generated scenarios. The optimal strategy can be found by minimizing the long-term expected costs and environmental impacts of operating the system over its entire life-span (defined in equation (2)) as follows

$\begin{eqnarray}&&\begin{array}{l}{\pi }^{* }\left(x,s\right)={{\rm{argmin}}}_{a\in {\bf{A}}}\left[\Space{0ex}{3.50ex}{0ex}C\left(a\right)\right.\ +\,P\left(x,s\right)\\ \,+\,\gamma \displaystyle \sum _{s^{\prime} \in {\bf{S}}}p\left(s^{\prime} | s\right)\ \left.\left[\displaystyle \sum _{x^{\prime} \in {\bf{X}}}p\left(x^{\prime} | x,a,s^{\prime} \right){V}^{* }\left(x^{\prime} ,s^{\prime} \right)\right]\right].\end{array}\end{eqnarray} \tag{ 3 }$

Equation (3) is the well-known Bellman equation (Bellman 1957), and we use dynamic programming (Sutton and Barto 1998) to find the optimal solution. The algorithm is reported in figure 2.

Figure 2. Refer to the following caption and surrounding text. — **Figure 2.** The value iteration algorithm for solving the optimization problem in equation (3). It should be noted that this algorithm is a variation of the original value iteration algorithm (Sutton and Barto 1998), as the changes of the state variables from time step t to t + 1, depends on the observed uncontrolled variables at time step t + 1, i.e. s_t+1.
Download figure:
Standard image High-resolution image

3. Results and discussion

We first explain the real-world case study—a FEWS in Ventura County that is used for illustrating the proposed method. Then we will discuss the main findings.

3.1. Ventura county FEWS

We focus on four crops in Ventura County, California—strawberry, lemon, avocado, and celery, which on average account for 33% of California's total production of these crops and 30% of total US production for these crops, with a gross value of $1.18 billion (Ross 2015) (for details refer to table A1). We denote the water level available for irrigation at each time step t by ${w}_{t}\in \left[0,1\right]$ , normalized to the maximum capacity so it takes values between 0 and 1. Similarly, the available energy amount is denoted by ${e}_{t}\in \left[0,1\right]$ . The seasonal water demand d_w,t and energy demand d_e,t for each of the four crops are obtained from the work of Bell et al (2018). The data of seasonal precipitation, r_t, is obtained from the Western Regional Climate Center (https://wrcc.dri.edu) for Ventura County. In the first analysis we only focus on quantifying the effect of seasonal changes on the optimal management strategy of FEWS operations. Later on, we extend the formulations to incorporate the effect of climate change, specifically the changes in temperature and precipitation, on the optimal management strategy as well.

The crop production state, which corresponds to the status of agricultural production, is given by f_t ∈ {0, 1}. We assume production takes place only if the level of water and energy available are above the demands⁴ , i.e.

$\begin{eqnarray}{f}_{t}=\left\{\begin{array}{cl}0 & {\rm{if}}\ {w}_{t}\lt {d}_{w,t}\ {\rm{or}}\ {e}_{t}\lt {d}_{e,t}\\ 1 & {\rm{if}}\ {w}_{t}\geqslant {d}_{w,t}\ {\rm{and}}\ {e}_{t}\geqslant {d}_{e,t}\end{array}\right..\end{eqnarray} \tag{ 4 }$

Manager has four actions available corresponding to utilizing the conventional or recycled water resources, ${a}_{w,t}\in {{\bf{A}}}_{w}=\left\{{{\rm{Conv}}}_{w},{{\rm{Rec}}}_{w}\right\}$ , and utilizing the conventional or renewable wind energy resources, ${a}_{e,t}\in {{\bf{A}}}_{e}=\left\{{{\rm{Conv}}}_{e},{{\rm{Ren}}}_{e}\right\}$ . We assume that the conventional water source in the region is coming from runoffs in the nearby river as well as local wells, and the conventional energy source is mostly natural gas (Bell et al 2018). It should be noted that we aggregate the two sources of water available for irrigation (water from runoffs in the nearby river and groundwater resource) in this case study for simplicity. However, as illustrated by Marston and Konar (2017), farmers tend to switch between these two resources according to seasonal changes and specially in drought conditions. This effect is currently ignored in this case study due to lack of data. Consequently, the action vector a_t is given by a_t = (a_w,t, a_e,t) ∈ A_w × A_e. The current capacity of recycled water in the region is estimated to be only sufficient to provide water for 25% of the agricultural productions for these four crops (Bell et al 2018). Similarly, we have assumed that the hypothetical wind power capacity is sufficient for 25% of the total agricultural production. This means that, for example, action (Rec_w, Ren_e) corresponds to combining maximum amount of recycled water and renewable energy available (i.e. 25%) with conventional resources (75%). Of course, the projections indicate that we will have (or should invest on) more renewable sources of water and energy available in the future and we quantify the economic benefits of increasing capacity of such renewable resources later on.

As mentioned before, the quality of the strategies that the manager takes is quantified by a pre-specified utility function, defined in equation (1). The costs associated with management actions, i.e. C(a_t), is comprised of energy cost (MJ/kg of the crops produced), green house gas (GHG) emissions (kgCO2/kg of the crops produced), and operational costs ($/kg of the crops produced). We characterize costs associated with four actions in a normalized unit-less manner. This means that the cost associated to using conventional water is assumed to be 1, and the additional costs associated to using the recycled water is reported in table A2. Similarly, costs associated with the energy resource choices is comprised of environmental GHG emissions and operational cost. Values are reported in table A3. The penalty for not yielding the crops and loss in revenue, i.e. P(x_t, s_t) in equation (1), due to lack of water or energy resources is set to a very large number. This generates management strategies that meet both water and energy demands at all times, and thus ensures sustainable agricultural production, i.e. f_t = 1 for all t. The value of the penalty is an arbitrarily large number, and the results are not sensitive to the choice of penalty, as long as it is sufficiently large with respect to the costs.

The interdependence of the water and energy states is characterized by the strategy that the manager chooses. Recycling water is assumed to consume more energy, and similarly conventional energy is assumed to consume more water than wind energy. The exact interdependence is quantified later on in equations (5)–(6). It should be noted that in this article we only model resource interdependence among the water, energy, and agricultural production and do not incorporate the comprehensive sectoral interdependence.

In the next sections, we first discuss the findings at a seasonal level, where each time step of the process is assumed to be one day to consider the effect of seasonality on the optimal FEWS operations, ignoring the long-term effects of climate change. Next, we extend the formulations to incorporate the effect of climate change, specifically the changes in temperature and precipitation, on the optimal management strategy, where FEWS operation is projected to the year 2050 and each time step is assumed to be one season.

3.2. Seasonal changes

In the dynamic Bayesian network formulation depicted before, we define two sets of state spaces as follows: (1) season is an uncontrolled variable, λ ∈ {Spring, Summer, Fall, Winter}, and (2) water, energy, and crop production states are controlled variables, X = F × E × W. The water level is discretized into 51 values, ${w}_{t}\in \left[0,1\right]$ with step 0.02. The dynamics of the water state for each crop i and season λ is formulated as follows

$\begin{eqnarray}\begin{array}{rcl}{w}_{t+1}^{(i)} & = & {w}_{t}^{(i)}-{d}_{w,t}^{(i,\lambda )}+{r}_{t}^{\lambda }-{w}_{e}\cdot {{\mathbb{1}}}_{{{\rm{Conv}}}_{e}}({a}_{e,t})\\ & & +{w}_{w}\cdot {{\mathbb{1}}}_{{{\rm{Rec}}}_{w}}({a}_{w,t})+{\zeta }_{t},\end{array}\end{eqnarray} \tag{ 5 }$

where ${w}_{t}^{(i)}$ is the water level for crop i at time step t, ${d}_{w,t}^{(i,\lambda )}$ is the water demand at time t for crop i in season λ, ${r}_{t}^{(\lambda )}$ is the seasonal precipitation, w_e is water consumed when using conventional energy (which is fixed to 10%), ${{\mathbb{1}}}_{{{\rm{Conv}}}_{e}}({a}_{e,t})$ is the indicator function which returns 1 if a_e,t = Conv_e, and 0 otherwise, w_w is the boost in the water state due to using a recycled water resource (which is maximum of 25% in Ventura County (Bell et al 2018)), ${{\mathbb{1}}}_{{{\rm{Rec}}}_{w}}({a}_{w,t})$ is the indicator function which returns 1 if recycled water is used. Finally, ζ_t is the stochasticity in the dynamics, which is assumed to be normal distribution with a known standard deviation, truncated at zero to avoid negative state values, i.e. ${\zeta }_{t}\sim {N}_{[0,+\infty ]}\left(0,\sigma =5 \% \right)$ . It should be noted that although the parameters w_w and w_e are being fixed here based on the data obtained for Ventura County, including uncertainty in these parameters is straight-forward and one can treat them as random variables with a known prior probability distribution. For example, in the next section we incorporate the uncertainty and variability in the precipitation variable due to changes in climate.

The energy level is discretized into 51 values, ${e}_{t}\in \left[0,1\right]$ with step 0.02. The dynamics of energy state for each crop i is formulated as follows

$\begin{eqnarray}\begin{array}{rcl}{e}_{t+1}^{(i)} & = & {e}_{t}^{(i)}-{d}_{e,t}^{(i)}-{e}_{w}\cdot {{\mathbb{1}}}_{{{\rm{Rec}}}_{w}}({a}_{w,t})\\ & & +{e}_{e}\cdot {{\mathbb{1}}}_{{{\rm{Ren}}}_{e}}({a}_{e,t})+{\zeta }_{t},\end{array}\end{eqnarray} \tag{ 6 }$

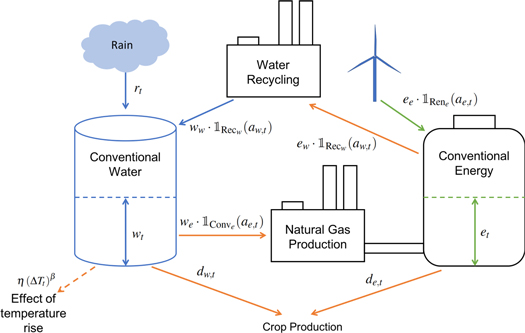
where ${e}_{t+1}^{(i)}$ is the energy level for crop i at time step t, ${d}_{e,t}^{(i)}$ is the energy demand at time t for crop i, e_w is consumed energy for using recycled water (which is fixed to 10%), and e_e is the boost of energy due to using wind energy (which is assumed to be a maximum of 25%). It should be noted that the energy dynamics do not depend on seasonal variations in this case study due to lack of data, however extension to include such seasonal dependence is straight-forward. Figure 3 provides a schematic visualization of Ventura Country's FEWS (It should be noted that, in this case study where the crop production state is binary, the state space can be implemented as the Cartesian product of only water and energy states, and as a result we have not included the crop production state in the figure).

Figure 3. Refer to the following caption and surrounding text. — **Figure 3.** This figure provides a schematic visualization of the dynamics of Ventura County's FEWS operations. The controllable states include available water w_t and energy e_t. The actions include which water resource to use (conventional or recycled) a_w,t and which energy resource to use (conventional, i.e. natural gas, or renewable, i.e. wind) a_e,t. The water and energy demand to produce each crop is denoted by d_w,t and d_e,t, respectively.
Download figure:
Standard image High-resolution image

Figure 4 visualizes the optimal management strategy for each crop in each season. Management strategies are calculated by minimizing the objective function in equation (3) using the algorithm in figure 2. Axes correspond to the energy and water states, and different shapes denote different management actions. The general trend is that managers tend to utilize recycled water (green triangle and magenta cross) more aggressively in the high water-demand seasons compared to low water-demand seasons (For example, in the case of strawberry, the manager uses the renewable water source 100% more in high water-demand seasons compared to low water-demand seasons. These differences are 134% for lemon, 85% for avocado, and 51% for celery).

Figure 4. Refer to the following caption and surrounding text. — **Figure 4.** Visualization of the optimal management strategies as a function of the water and energy states, for each crop across four seasons. Red dots represent conventional water and energy, green triangle represents recycled water and conventional energy, cyan square represents conventional water and renewable energy, and magenta cross represents recycled water and renewable energy.
Download figure:
Standard image High-resolution image

In the previous section, we mentioned that the current recycling water unit in Ventura County can output up to 25% of the total agricultural production. Similarly, we also assumed that wind energy can provide up to 25% of total energy need. Figure 5 quantifies the expected economic value (EV) of doubling the size of both the water recycling facility as well as the wind energy capacity to allow coverage for up to 50% of the total agricultural production in the region. The EV is calculated as follows

$\begin{eqnarray}&&{\rm{EV}}={{\mathbb{E}}}_{\left(\bar{{\bf{x}}},\bar{{\bf{s}}}\right)}\left[{V}_{I}^{* }\left(\bar{{\bf{x}}},\bar{{\bf{s}}}\right)-{V}_{{II}}^{* }\left(\bar{{\bf{x}}},\bar{{\bf{s}}}\right)\right],\end{eqnarray} \tag{ 7 }$

where, ${{\mathbb{E}}}_{\left(\bar{{\bf{x}}},\bar{{\bf{s}}}\right)}$ is the sample mean over N = 100 sampled trajectories of uncontrolled and controlled state variables $\left(\bar{{\bf{x}}},\bar{{\bf{s}}}\right)=\{\left({x}_{0},{s}_{0}\right),\left({x}_{1},{s}_{1}\right),\ldots ,\left({x}_{T},{s}_{T}\right)\}$ . The time span T is set to arbitrary large number for the value to converge (due to discounting future costs), ${V}_{I}^{* }$ is the optimal value for the 25% capacity case, and ${V}_{{II}}^{* }$ is the optimal value for the 50% capacity case. As it can be seen the EV is significantly higher (118%) for high energy-demand crops (i.e. strawberry and avocado) compared to low energy-demand crops (i.e. lemon and celery).

Figure 5. Refer to the following caption and surrounding text. — **Figure 5.** Economic value (EV) for doubling the size of the recycling water and renewable energy units on the operation cost of the Ventura County FEWS. The bars show average economic value based on 100 independent simulations. Top of the bars show the mean, the black line shows the median, the bottom and top of the boxes show 25% and 75% percentiles, and whiskers correspond to highest and lowest values excluding the outliers.
Download figure:
Standard image High-resolution image

3.3. Management under the risk of climate change

In this section, we incorporate the effect of climate change (i.e. variations in temperature and precipitation) on the management strategies for operating the integrated FEWS in Ventura County. We define two climate change scenarios: (1) the Low climate change which models the changes in temperature according to RCP2.6 (data obtained from IPCC (2014), figure 6(A)), and changes in precipitation according to RCP4.5 (data obtained from Pierce et al (2018), figure 6(B)); and (2) the High climate change which models the changes in temperature and precipitation both according to RCP8.5.

Figure 6. Refer to the following caption and surrounding text. — **Figure 6.** This figure shows the projection of the changes in (A) temperature and (B) precipitation by year 2050. The data are obtained from IPCC (2014) for temperature and Pierce *et al* (2018) for precipitation. It should be noted that the temporal resolution of the temperature figure (A) is seasonal. The annual variations in the precipitation are estimated according to the projections based on three different climate models of HadGEM2-ES, CNRM-CM5, and CanESM2 (refer to figure A1). After estimating the annual variations, it is translated into the standard deviation of the seasonal variations with a known mean fixed at the expected seasonal precipitation: $r(\lambda ,t)\sim {N}_{[0,+\infty ]}\left(\mu ={\bar{r}}_{\lambda },\sigma ={\sigma }_{M,t}\right)$ , where M = {RCP 4.5, RCP 8.5} and ${\bar{r}}_{\lambda }$ is obtained from Western Regional Climate Center, (https://wrcc.dri.edu).
Download figure:
Standard image High-resolution image

**Figure 6.** This figure shows the projection of the changes in (A) temperature and (B) precipitation by year 2050. The data are obtained from IPCC (2014) for temperature and Pierce *et al* (2018) for precipitation. It should be noted that the temporal resolution of the temperature figure (A) is seasonal. The annual variations in the precipitation are estimated according to the projections based on three different climate models of HadGEM2-ES, CNRM-CM5, and CanESM2 (refer to figure A1). After estimating the annual variations, it is translated into the standard deviation of the seasonal variations with a known mean fixed at the expected seasonal precipitation: $r(\lambda ,t)\sim {N}_{[0,+\infty ]}\left(\mu ={\bar{r}}_{\lambda },\sigma ={\sigma }_{M,t}\right)$ , where M = {RCP 4.5, RCP 8.5} and ${\bar{r}}_{\lambda }$ is obtained from Western Regional Climate Center, (https://wrcc.dri.edu).
Download figure:
Standard image High-resolution image

In order to incorporate the changes in these climate variables, the uncontrolled variable is defined as the Cartesian product of temperature changes, precipitation, and seasons S = ΔT × r × λ, where λ ∈ {Spring, Summer, Fall, Winter} is the variable indicating the season changes. As it can be seen in figure 6(B), the projections of the precipitation under the climate change only affects the variability of the rainfall amount and not its expected value (the data is for Ventura County and this trend is not general to other locations). As a result we model the effect of climate change on the precipitation amount in each season, λ, as: $r(\lambda ,t)\sim {N}_{[0,+\infty ]}\left(\mu ={\bar{r}}_{\lambda },\sigma ={\sigma }_{M,t}\right)$ , where ${\bar{r}}_{\lambda }$ is the average seasonal precipitation amount currently (obtained from Western Regional Climate Center, https://wrcc.dri.edu), and ${\sigma }_{{\rm{ \mathcal M }}{\rm{M}},t}$ is the standard deviation in the precipitation projected up to 2050, t ∈ [2018, 2050], according to each model, ${M}\in \{{\rm{R}}{\rm{C}}{\rm{P}}4.5,{\rm{R}}{\rm{C}}{\rm{P}}8.5\}$ . The values of these variations is estimated according to the projections based on three different climate models of HadGEM2-ES, CNRM-CM5, and CanESM2 (Pierce et al 2018) (figure A1). The controlled state variables are modeled as before: X = F × E × W, as well as the actions.

The water dynamics in equation (4) are re-formulated to account for trans-evaporation and other losses due to temperature rise, as well as changes in the precipitation variations

$\begin{eqnarray}\begin{array}{rcl}{w}_{t+1}^{(i)} & = & {w}_{t}^{(i)}-{d}_{w,t}^{(i,\lambda )}+r(\lambda ,t)\\ & & -{w}_{e}\cdot {{\mathbb{1}}}_{{{\rm{Conv}}}_{e}}({a}_{e,t})\\ & & +{w}_{w}\cdot {{\mathbb{1}}}_{{{\rm{Rec}}}_{w}}({a}_{w,t})-\eta {\left({\rm{\Delta }}{T}_{t}\right)}^{\beta }+{\zeta }_{t},\end{array}\end{eqnarray} \tag{ 8 }$

where, symbol ${d}_{w,t}^{(i,\lambda )}$ is the seasonal water demand for crop i in season λ, r(λ, t) is the precipitation at time step t and season λ defined as above, w_e is consumed water for using conventional energy (which is fixed to 10%), and $\eta {\left({\rm{\Delta }}{T}_{t}\right)}^{\beta }$ is the nonlinear effect of temperature change on water losses at time t, with constant parameters η and β fixed at 0.1 and 1.75, respectively. Effect of climate change can be similarly incorporated in energy dynamics as follows

$\begin{eqnarray}\begin{array}{rcl}{e}_{t+1}^{(i)} & = & {e}_{t}^{(i)}-{d}_{e,t}^{(i)}-{e}_{w}\cdot {{\mathbb{1}}}_{{{\rm{Rec}}}_{w}}({a}_{w,t})\\ & & +{e}_{e}\cdot {{\mathbb{1}}}_{{{\rm{Ren}}}_{e}}({a}_{e,t})-{\eta }^{{\prime} }{\left({\rm{\Delta }}{T}_{t}\right)}^{{\beta }^{{\prime} }}+{\zeta }_{t},\end{array}\end{eqnarray} \tag{ 9 }$

where, ${\eta }^{{\prime} }{\left({\rm{\Delta }}{T}_{t}\right)}^{{\beta }^{{\prime} }}$ models the effect of temperature rise in deterioration of energy resource due to increased energy demand for irrigation pumping and air conditioning. However, in this case study, we disregard this effect due to lack of data to adjust such effect. Once such data is available, it can be used to estimate parameters η' and β', and include the effect in energy dynamics according to equation (9). Moreover, the effect of climate change on wind energy is also ignored due to lack of data. The expectation is that the amount of available wind energy will be increasing, due to decreasing costs and increasing policy incentives, and we quantify the expected value of increasing the capacity of renewable sources later on (figure 7(B)).

Figure 7. Refer to the following caption and surrounding text. — **Figure 7.** (A) Comparison of management strategies that adapt to climate change (labeled as *Optimal*) against ignoring climate change (labeled as *Ignoring*), for each crop under both *Low* and *High* climate change scenarios, and (B) Economic value (EV) of doubling the size of the water recycling and renewable wind energy capacities on the operational costs. The bars show average economic value based on 100 independent forward simulations. Top of the bars show the mean, the black line shows the median, the bottom and top of the boxes show 25% and 75% percentiles, and whiskers correspond to highest and lowest values, excluding the outliers.
Download figure:
Standard image High-resolution image

As a result, the energy dynamics are equivalent to equation (6), assuming e_w to be 10% to represent the energy consumption for recycling water. It is worth mentioning that, in this section, we have discretized the water and energy state space into 21 values ${w}_{t},{e}_{t}\in \left[0,1\right]$ with step 0.05 for computational efficiency.

To understand the impact of different climate scenarios, we evaluate the risk of not adapting the FEWS management strategy to climate change in figure 7(A). Here, we compare the value of operating the network according to the optimal strategy that considers future projections of temperature rise and changes in precipitation (labeled as Optimal), with the strategy that assumes climate stays the same (ΔT_t = 0, r_t = r₀, $\forall t$ , labeled as Ignoring, where r₀ is the current observed precipitation). It is clear that ignoring climate change in the management strategy design results in significant increase in FEWS operational cost, on average for all crops around 24% and 115% more under Low and High climate scenarios, respectively⁵ .

We further quantify the EV of doubling the water recycling and renewable wind energy capacities so they can provide water and energy for up to 50% of the total operational needs, calculated using equation (7) (figure 7(B)). As it can be seen, in Low climate scenario, the EV is close to negligible across all crops (14 on average with low standard deviation). However, the EV is significantly higher for all crops in the case of High climate scenario (135.78 on average with a very high standard deviation. For example, in the case of strawberry the EV can be as high as 270). This is an interesting finding as current policy-makers must decide whether to invest in increasing the capacity of water recycling and renewable energy sources or not, given the uncertainty as to which one of these (and many other) climate projections will best represent the future reality.

4. Conclusions

We have developed a dynamic optimization approach, based upon the fundamentals of decision theory and model-based reinforcement learning, to adaptively control and optimize operation of integrated FEWS. Fundamental elements to integrated FEWS management are uncertainty, connectivity of the sectors and resource interdependence, risk and impacts of climate change, and generalizability of the methods. Most of existing quantitative literature fall short of one or more of these aspects. The novelty of our approach is to create a flexible and reproducible method that is able to quantify and propagate uncertainty in the dynamics of each sector, incorporate the resource interdependence, include the impact of uncontrolled variables such as climate variations, and adaptively optimize the management decisions to minimize the costs and environmental impacts of crop production.

We illustrated the method on a real-world case study in Ventura County, California, by evaluating the effects of seasonal changes and annual environmental variations (temperature rise) on the optimal management strategies. Generally, the intuitive observation is that the management tends to lean towards renewable water and energy resources more aggressively in high water-demand seasons (around 92% more on average for all crops, figure 4). Moreover, using a crude Monte Carlo scenario planning, we quantified the loss that occurs to management that deviates from the optimal strategy and ignores the future changes of the climate, e.g. rises in temperature and changes in precipitation (around 24% and 115% higher cost of management under Low and High climate scenarios, respectively, figure 7(A)). We also quantified the EV of increasing the capacity of alternative water and energy sources (figures 5 and 7(B)) and its effect on the operation cost and environmental impacts. Specifically, we show that the EV is significant (136% on average for all crops, figure 7(B)) under High climate scenario.

In practice, one can adapt the optimal management strategy by re-computing the solution to equations (2)–(6) as new information becomes available, thus enabling optimal integrated FEWS management that adapts to climate change. A logical next step is to incorporate the inherent uncertainty within climate projection models into the optimization framework. Another future direction is to further examine the functional form of the deterioration models used for water and energy state variables (equations (5)–(6)), and their dependence on climate change (equation (8)). Moreover, the effect of energy generation as a bi-product of the crop production sector (such as biofuels (Breunig et al 2017)) is ignored in this study, providing another idea for future direction.

Acknowledgments

This material is based upon work supported by the National Science Foundation under Grant No. 1739676. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.

Author contributions statement:

MM, SM and AH conceived the idea, MM conducted and implemented the experiments, and analyzed the results. MM and SM wrote the manuscript and all authors reviewed the manuscript.

: Appendix. Additional tables and figures

Figure A1. Refer to the following caption and surrounding text. — **Figure A1.** This figure shows the projections of changes in precipitation by the year 2050 according to the three different climate models of HadGEM2-ES, CNRM-CM5, and CanESM2, source: Pierce *et al* (2018).
Download figure:
Standard image High-resolution image

Table A1. Summary of Ventura County's top crops in 2014 (source: Ross 2015).

Crop	Gross value	Ventura's share of California	California's share of US
Strawberry	$628M	27%	91%
Lemon	$269M	37%	91%
Avocado	$128M	36%	95%
Celery	$152M	31%	83%

Table A2. Additional costs associated with using the recycled water resource in terms of energy cost (MJ/kg of the crops produced), GHG emissions (kgCO₂/kg of the crops produced), and operational costs ($/kg of the crops produced) (source: Bell et al 2018).

Crop	Energy	GHG	Operation
Strawberry	+10%	+14%	+7%
Lemon	+12%	+7%	+22%
Avocado	+17%	+9%	+34%
Celery	+54%	+59%	+25%

Table A3. Assumed costs associated with different choices of energy resource.

Source	GHG	Operation
Conventional	+1800%	—-
Renewable	—-	+1000%

Table A4. Variables used in this article and their definition.

Variable	Definition
x ∈ X	Entire domain of state variables in the dynamic Bayesian network
f ∈ {0,1}	Crop production state corresponding whether yield happens or not
e ∈ [0,1]	State of energy available for crop production
w ∈ [0,1]	State of water available for crop production
s ∈ S	Entire domain of exogenous variables corresponding to environmental variations
λ ∈ {Spring, Summer, Fall, Winter}	Exogenous variable defining seasonal changes.
ΔT	Exogenous variable defining changes in the temperature
r	Exogenous variable defining variations in precipitation
a ∈ A	Entire domain of actions available to manager
ζ	Variable defining stochasticity
u ∈ U	Utility variable quantifying the quality of manager's actions
C	Cost variable defining costs of manager's actions
P	Penalty due to not yielding crops (loosing crop production state, i.e. f = 0)
γ ∈ [0,1)	Discount factor, relating future costs to their net present value
T	Management time horizon, which we set to infinity in this article
V	Long-term expected cost of managing the system
π	Management strategy chosen for the system
d	Variable representing demands of water and energy imposed by the society

Dates

Peer review information

Optimizing dynamics of integrated food–energy–water systems under the risk of climate change

Author notes

Notes

Article metrics

Submit

Share this article