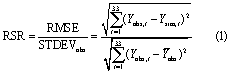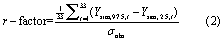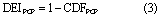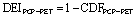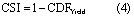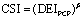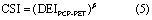Abstract
Crop yields exhibit known responses to droughts. However, quantifying crop drought vulnerability is often not straightforward, because components of vulnerability are not defined in a standardized and spatially comparable quantity in most cases and it must be defined on a fine spatial resolution. This study aims to develop a physical crop drought vulnerability index through linking the drought exposure index (DEI) with the crop sensitivity index (CSI) in sub-Saharan Africa. Two different DEIs were compared. One was derived from the cumulative distribution functions fitted to precipitation and the other from the difference between precipitation and potential evapotranspiration. DEIs were calculated for one, three, six, nine, and twelve-month time scales. Similarly, CSI was calculated by fitting a cumulative distribution function to maize yield simulated using the Environmental Policy Integrated Climate model. Using a power function, curves were fitted to CSI and DEI relations resulting in different shapes explaining the severity of vulnerability. The results indicated that the highest correlation was found between CSI and DEI obtained from the difference between precipitation and potential evapotranspiration in one, three, and six-month time scales. Our findings show that southern African countries and some regions of the Sahelian strip are highly vulnerable to drought due to experiencing more water stress, whereas vulnerability in Central African countries pertains to temperature stresses. The proposed methodology provides complementary information on quantifying different degrees of vulnerabilities and the underlying reasons. The methodology can be applied to different regions and spatial scales.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence.
Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Climate variability and mean temperatures are expected to increase across many regions of the world due to climate change (Rezaei et al 2015). The agricultural sector exhibits known responses to climate anomalies, and this has huge impacts on food security. Sub-Saharan Africa (SSA) as a home to one billion people (World Bank 2016) is also at the core of this threat. The recurrence of droughts in the past decades has triggered many famines, resulting in the deaths of millions of people. Factors such as slow progress in drought risk management, increased population, and degradation of land and environment have aggravated the situation (Masih et al 2014). The IPCC's (Intergovernmental Panel on Climate Change) assessments of climate change impacts suggest declining grain yield to be a likely future scenario. Therefore, understanding drought vulnerability is an important step to finding feasible solutions for mitigating drought impacts, overcoming food insecurity, and addressing associated drought risks.
According to the IPCC's fourth assessment report, vulnerability is defined as the interaction between three constituent components: exposure, sensitivity, and adaptive capacity (Parry et al 2007). O'Brien et al (2004) defined exposure as the degree of climate stress on a particular unit of analysis such as magnitude or frequency. Sensitivity is described as the degree of influence of a variable on a system (in this paper, crop yield) when it is stimulated by climatic factors (Parry et al 2007). Adaptive capacity has been defined as the capacity of a system to adjust to climate change effects to reduce the potential damages or to take advantage of associated opportunities. Vulnerability of a system, hence, entails both physical and socioeconomic aspects. Physical vulnerability refers to the properties of physical structures. It determines their potential damage when the system is exposed to disaster. Factors such as constructing infrastructure or irrigation systems can be used as adaptation strategies of a society to mitigate the impact of exposure. Providing a physical drought vulnerability index resulting only from intrinsic and, particularly, climatic variables would be very useful for water resources managers and policy makers to develop adaptation strategies to alleviate risks of crop failure in areas of high physical vulnerability. Therefore, the central focus of the present study is to assess the physical drought vulnerability.
Several methods are available for quantifying drought vulnerability. A large group of studies have assessed crop drought vulnerability which refers to the extent to which a drought of a given magnitude has an impact on agricultural production. Simelton et al (2009) defined drought vulnerability through relating meteorological droughts to crop harvest loss to identify regions that are resilient or vulnerable to rainfall variation in China. Wu et al (2004) established a relationship between the indicators of moisture supply and agricultural production through linking weekly-based Standardized Precipitation Index (SPI) (McKee et al 1993) and Crop Specific Drought Index with the ratio of actual to potential yield. Fraser et al (2013), Huai (2016), Simelton (2011), and Simelton et al (2012) have applied a similar approach to determine physical vulnerability of crop production in other regions. These studies have the major limitation of using a simple ratio-based definition that does not allow comparison of vulnerabilities over different areas due to the lack of a standardized scale. As the ratios can vary over a large range (0 to ∞), comparing drought vulnerability in different regions becomes very difficult. In addition, when the components of vulnerability (e.g. drought exposure or crop sensitivity) are calculated with different standards, their values vary within different ranges. Therefore, it is not possible to compare the severity of one component with the other with one base. In other words, a certain value of drought exposure or crop sensitivity might be interpreted as different levels of severity. For example, a value of −1.5 may be representative of moderate exposure in one region, but reflects a severe exposure in another region. Overall, the current studies of drought vulnerability assessment suffer from the lack of standardized procedure for defining their components.
Another approach to define crop drought vulnerability is by curve fitting to find a relationship between drought intensity and yield loss variables. Wang et al (2013) used physical vulnerability curves to define a relationship between drought intensity and yield loss. Jia et al (2012), Naumann et al (2015), and Guo et al (2016) have provided physical drought vulnerability maps by fitting assessment curves through drought intensity and yield loss variables. Drought intensities were obtained from SPI and Standardized Precipitation Evapotranspiration Index (SPEI) (Vicente-Serrano et al 2010). The drawback of studies based on fitting curve approaches is that the severity of vulnerability is not clearly explained according to the shape of the fitted curves. In other words, there is a lack of clarity on differentiating between different degrees of severity at different spatial and geographical locations.
Despite extensive studies on agricultural vulnerability assessment, most analyses have been performed at the country level (Brooks et al 2005, Naumann et al 2014, Naumann et al 2015, Shahid and Behrawan 2008). This is because crop databases are usually available at country level, which do not provide information on finer spatial coverage (Thornton et al 2009). Regional crop yield data have been sparsely collected and are available for a limited period. SSA is a case where crop data is incomplete and in most cases of poor quality (Fuglie and Nicholas 2013). Therefore, crop drought vulnerability assessment studies have been mostly done at country level (Naumann et al 2014) or limited to specific regions (Antwi-Agyei et al 2012). Application of spatially explicit crop model helps to obtain data at a fine resolution, since the model inputs are at a grid level. Such data have become more available in recent years. This has enabled the simulation of the governing physical processes of crop growth (e.g. evapotranspiration, soil moisture) at the same spatial resolution. Thus, in addition to the crop yield, the aforementioned physical variables are also obtained at a fine resolution. Several studies have attempted to select the optimal grid cell resolution (Mearns et al 2002, Orrego et al 2014). De Wit et al (2005), for example, concluded that the grid size of 50 × 50 km is an appropriate geospatial resolution. Apart from providing spatial details, crop models provide complementary concepts on identifying different stresses that a crop may experience during its growth periods. Linking a fine resolution conceptual crop model with vulnerability concepts has been less researched specially at continental scale such as SSA.
To address the mentioned gaps, we quantify the physical vulnerability of maize to drought for SSA by simulating maize yield at 0.5° resolution using the calibrated Environmental Policy Integrated Climate (EPIC) crop model. Maize was selected because it is a staple food crop covering about 20% of the calorie intake and 13% of the total cultivated land in SSA (FAO 2010). We specifically aim to address the following questions:
- 1.Which drought exposure indices can better predict grid level vulnerability in SSA as a data-scarce region and why?
- 2.How does the selection of drought exposure temporal window affect the correlation between drought exposure and crop yield sensitivity indices?
- 3.Which regions of SSA are more vulnerable and why?
We demonstrate the utility of our approach in vulnerability assessment of maize in SSA by providing a vulnerability map and discuss the implications of our method for future researches and practices.
2. Data and methods
2.1. Crop model and calibration
Maize yield was simulated using an extended version of EPIC ( EPIC+, Kamali et al (2018a)). EPIC is a field-scale crop model designed to simulate the different processes of farming systems as well as their interactions using data such as weather, soil, land use, and crop management parameters (Williams et al 1989). EPIC operates on a daily time step and can simulate crop growth under various climate and environment conditions, as well as complex management schemes. Further information on EPIC crop-related processes is given in Williams et al (1989). In order to extend the application of EPIC from field to the SSA scale, we divided the study area into 0.5° × 0.5° grids and executed EPIC on each grid cell using a framework programmed in Python (Kamali et al 2018a).
For model calibration, the developed framework was also coupled with the Sequential Uncertainty Fitting (SUFI-2) algorithm (Abbaspour et al 2007). SUFI-2 was chosen because of its flexibility and efficiency compared with other algorithms (Uniyal et al 2015, Yang et al 2008). The algorithm calculates the uncertainty of model prediction and expresses the output as the 95% prediction uncertainty (95PPU), which is obtained through propagating parameter uncertainties. We calibrated the model at national level using recorded FAO yield (Yobs) during 1980–2012 (33 years). The yields were de-trended using a linear de-trending method which appeared to be a suitable approaches in most cases to remove any influence of technology or socio-economic factors (Osborne and Wheeler 2013). We chose the standardized root mean square error (RSR) (Singh et al 2005) as the criterion to compare the performance of country-level simulated yield (Ysim) with Yobs as:
Ysim was obtained from simulating irrigated and rainfed yields in the EPIC model on n grids within a country. It was then aggregated to the country level using weighted cultivated areal averages (Kamali et al 2018a).
Two criteria in SUFI-2, r-factor and p-factor, judge the goodness-of-fit and the level of uncertainty of the model. The p-factor represents the fraction of measured data bracketed by the 95PPU uncertainty band and varies from 0 to 1, where 1 means 100% of the measured data are bracketed by the model simulation (expressed as the 95PPU). Values around 0.5 are usually acceptable for crop simulation (Abbaspour et al 2015). The r-factor is the average width of the 95PPU band divided by the standard deviation of the measured variable, which is a measure of the prediction uncertainty. The ideal value for the r-factor is 0, with an acceptable practical value of around 2 for crop yield and is defined as
where Ysim,97.5 and Ysim,2.5 are the upper and lower boundaries of 95PPU and σobs is the standard deviation of Yobs. A larger p-factor can be achieved at the expense of a larger r-factor. At acceptable values of r-factor and p-factor, the parameter ranges are taken as the calibrated parameters. More details on the parameters used for calibration are found in Kamali et al (2018a).
2.2. Model inputs
All data required for EPIC simulation were prepared at 0.5° resolution and are summarized in table 1. These include site-specific data (longitude, latitude, slope, elevation), daily climate data (precipitation, solar radiation, maximum and minimum air temperature, relative humidity, and wind speed), and soil information (organic carbon content [%], pH, Cation exchange capacity [cmol kg−1], sand [%], silt [%], bulk density [t m−3], layer depth [m], and electrical conductivity [mmho cm−1]).
Table 1. Summary of input data and their sources used for simulating maize in SSA. All data were then transformed into 0.5°× 0.5° resolution (Kamali et al 2018a).
| Input data | Description | Resolution | Year | Source |
|---|---|---|---|---|
| DEM, Slope | Digital elevation model GTOPO30 | 1 km (5'' × 5'') | Edition 2004 | US Geological Survey (2004) |
| Climate | Daily maximum and minimum temperature, precipitation, solar radiation, relative humidity, wind speed, CO2 concentration | 50 km (0.5° × 0.5°) | 1970–2012 | WFDEIb meteorological forcing data (Weedon et al 2011) |
| Soil | Soil map and database | 10 km (5' × 5') | 2006 | ISRIC-WISEc (Batjes 2006) |
| Planting and harvesting dates | Based on temperature linked to crop calendar | 50 km (0.5° × 0.5°) | 1990s to early 2000s | SAGEd (Sacks et al 2010) |
| Fertilizer | Fertilizer use | National | 2002 | FertiStat (FAO 2007) |
aMonthly irrigated and rainfed crop areas. bWATCH-forcing-data-ERA-interim. cInternational soil reference and information centre-world inventory of soil smission potentials. dCenter for sustainability and the global environment.
Agricultural operations, including tillage, fertilizer, planting, and harvest, require information such as dates of application (table 1), fertilization rate, and potential heat unit. The operations were set chronologically, by applying fertilizers 10 days before planting (Wang et al 2005) (table 1). The total number of heat units required for a plant to reach maturity was calculated for each grid based on the maximum and minimum temperatures, planting date, and length of growing seasons using the methodology proposed by the Blackland Research Center (2010).
Figure 1. Schematic representation of transforming precipitation (PCP), the difference between precipitation and potential evapotranspiration (PCP-PET), and simulated rainfed yield (Yield) into their cumulative distribution functions (CDFPCP, CDFPCP-PET, CDFYield) and then into drought exposure indices (DEIPCP, DEIPCP-PET), and Crop Sensitivity Index (CSI), respectively.
Download figure:
Standard image High-resolution image2.3. Components of crop drought vulnerability
The definition of crop drought vulnerability is based on linking the drought exposure index (DEI) to the crop sensitivity index (CSI). DEI measures the degree of stress on the system and CSI indicates the response of the system to the respective stress. Two definitions of DEI are used and compared. DEIPCP is derived from precipitation (PCP) and DEIPCP-PET is derived from the difference between precipitation and potential evapotranspiration (PCP-PET) in a similar procedure as that used for calculating SPI and SPEI. Potential evapotranspiration is calculated using the Hargreaves method (Hargreaves and Samani 1985). The SPI and SPEI are computed by first fitting a probability distribution function to precipitation and (PCP-PET), respectively. The associated cumulative distribution functions (CDF) are subsequently estimated and transformed to a normal distribution. The SPI (or SPEI) and its associated CDFPCP (or CDFPCP-PET) are transferable to each other (figure 1). In this paper, we directly use CDFPCP and CDFPCP-PET to define DEIs as:
The above definitions calculate the exceedance probability of different intensities of drought as described in table 2, which was implemented by Carrão et al (2016) for drought assessment. The DEI ranges from 0 to 1, with 1 indicating the highest exposure to drought. CDFs smaller than 0.5 are representative of drought situations, whereas values larger than 0.5 indicate non-drought conditions. Five classifications could be defined between 0 and 1: wet, near normal, mild to moderate drought, severe to extreme drought, and exceptional drought (Svoboda et al 2002) (table 2). More details on the procedure to calculate DEI are explained in Kamali et al (2018b).
Table 2. Five categories of cumulative distribution functions (CDFPCP, CDFPCP-PET, CDFYield) and equivalent drought exposure (DEI) and crop sensitivity indices (CSI).
| Category | CDFPCP, CDFPCP-PET, CDFYield | DEIPCP, DEIPCP-PET, CSI |
|---|---|---|
| Wet | 0.692 to 1.00 | 0.00 to 0.308 |
| Near normal | 0.308 to 0.692 | 0.308 to 0.692 |
| Mild to moderate | 0.115 to 0.308 | 0.692 to 0.885 |
| Severe to extreme | 0.023 to 0.115 | 0.885 to 0.997 |
| Exceptional | 0.00 to 0.0230 | 0.977 to 1.00 |
Different probability distribution functions can be fitted to P and PCP-PET. Based on the literature, we chose a two-parameter gamma distribution as the probability distribution function (Bordi et al 2001, Lloyd-Hughes and Saunders 2002). A log-logistic distribution was selected for CDFPCP-PET (Begueria et al 2014, Vicente-Serrano et al 2010) where the parameters of distribution were calculated from the unbiased probability weighted method (Begueria et al 2014). To define the most representative timescales, we also tested the suitability of five one, three, six, nine, and 12-month time scales for DEIs. A rolling metric was used to calculate each time scale. DEIPCP at the X-month time scale was obtained from total precipitation over the last X months. This means that for example DEI of three-month time scale on March 1989 was derived from precipitation summed over January, February, and March of that year. After calculating monthly DEIs, the most relevant time span of each year was selected using the planting and maturity dates (growing season) at each grid. Therefore, the average of monthly DEIs over growing season resulted in yearly DEI. From the five time scales, we selected the one with the highest correlation with CSI. The same notation is used for DEIPCP-PET.
Similarly, a suitable probability distribution function is fitted to the simulated YRF at the grid level and CSI is derived from the associated cumulative distribution function (CDFYield) as:
2.4. Crop drought vulnerability
The concept of vulnerability was adapted from the work done by Simelton et al (2009). According to their definition, if a drought with high magnitude triggers a low harvest loss, then the region is 'resilient', meaning that vulnerability is low. Conversely, if a small drought results in a high crop failure, then the case is 'sensitive' and highly vulnerable. Therefore, the level of vulnerability is determined by relating DEI to CSI.
In this paper, we translated this concept into the shape of power function obtained from fitting a curve to DEI and CSI. The different shapes of fitted curves explain how crop sensitivity increases/decreases in relation to drought exposure. Vulnerability is then defined by a power function relating DEIPCP (or DEIPCP-PET) to CSI as:
The β values were obtained by fitting the above power functions to DEIs and CSI. The values of β explain the degree of vulnerability and as elaborated in section 2.4, we defined DEI and CSI with the same base, meaning that a certain value of CSI or DEI have the same meaning in terms of severity level. This facilitates measuring the degree of vulnerability based on the shape of power function. As shown (figure 2), vulnerability becomes smaller as β increases. In the simplest form, β= 1 means that the relationship between DEI and CSI is linear. From agricultural point of view, this explains cases where a certain degree of DEI results in the same severity of CSI (medium vulnerability). The power function curves falling above the linear curve (β= 1) for β> 1 representing more vulnerable situation. This means that a certain value of DEI causes higher severity of CSI. Conversely, β> 1 means occurring droughts lead to lower CSI.
Figure 2. Schematic representation of the crop drought vulnerability index (CDVI) based on the different β values.
Download figure:
Standard image High-resolution imageTable 3. Country-level results of the EPIC calibration with the SUFI-2 algorithm based on RSR before and after calibration, p-factor and r-factor equation (3) criteria. More details are explained in Kamali et al (2018a).
| Country | RSR Before calibration | RSR After calibration | p-factor | r-factor | |
|---|---|---|---|---|---|
| Eastern Africa | Burundi | 3.94 | 1.38 | 0.55 | 1.80 |
| Comoros | 1.28 | 1.13 | 0.42 | 1.95 | |
| Eritrea | 2.32 | 1.45 | 0.58 | 1.98 | |
| Ethiopia | 1.66 | 0.91 | 0.52 | 1.81 | |
| Kenya | 6.85 | 0.86 | 0.61 | 1.74 | |
| Madagascar | 6.06 | 1.42 | 0.79 | 2.54 | |
| Malawi | 1.40 | 0.94 | 0.45 | 2.25 | |
| Mozambique | 2.79 | 1.12 | 0.61 | 1.56 | |
| Rwanda | 1.44 | 1.08 | 0.43 | 1.04 | |
| Somalia | 1.96 | 1.22 | 0.42 | 1.08 | |
| Sudan | 1.76 | 1.33 | 0.48 | 1.05 | |
| Tanzania | 1.94 | 1.20 | 0.58 | 0.94 | |
| Uganda | 1.40 | 0.85 | 0.58 | 2.48 | |
| Zambia | 1.41 | 0.89 | 0.45 | 1.31 | |
| Zimbabwe | 3.80 | 1.12 | 0.37 | 1.67 | |
| Central Africa | Angola | 6.90 | 0.99 | 0.88 | 2.38 |
| Cameroon | 1.29 | 1.00 | 0.48 | 1.38 | |
| Central African Republic | 2.49 | 1.16 | 0.49 | 0.74 | |
| Chad | 1.23 | 0.84 | 0.66 | 2.05 | |
| Democratic Republic of the Congo | 45.9 | 6.27 | 0.48 | 1.05 | |
| Gabon | 5.33 | 1.35 | 0.70 | 1.95 | |
| Republic of Congo | 19.3 | 2.16 | 0.88 | 2.39 | |
| Southern Africa | Botswana | 1.45 | 1.39 | 0.52 | 2.33 |
| Lesotho | 1.99 | 1.27 | 0.42 | 2.45 | |
| Namibia | 2.42 | 1.02 | 0.42 | 1.23 | |
| South Africa | 1.88 | 0.92 | 0.55 | 0.79 | |
| Swaziland | 3.23 | 1.06 | 0.42 | 1.49 | |
| Western Africa | Benin | 3.38 | 0.99 | 0.70 | 1.83 |
| Burkina Faso | 1.18 | 0.97 | 0.52 | 1.07 | |
| Djibouti | 4.87 | 1.20 | 0.70 | 2.73 | |
| Gambia | 1.74 | 0.93 | 0.82 | 2.97 | |
| Ghana | 5.36 | 1.07 | 0.52 | 1.14 | |
| Guinea | 8.45 | 1.96 | 0.45 | 2.02 | |
| Ivory coast | 2.40 | 1.08 | 0.48 | 1.44 | |
| Mali | 1.23 | 0.98 | 0.55 | 1.55 | |
| Mauritania | 1.98 | 1.18 | 0.61 | 2.25 | |
| Niger | 1.67 | 0.85 | 0.70 | 1.88 | |
| Nigeria | 1.16 | 0.98 | 0.70 | 1.84 | |
| Sierra Leone | 9.59 | 1.09 | 0.53 | 2.07 | |
| Senegal | 1.05 | 0.92 | 0.86 | 2.44 | |
| Togo | 4.23 | 1.26 | 0.52 | 1.18 |
After calculating CDVI, to identify the possible factors what makes a region more vulnerable to drought, we calculated the correlation coefficient between simulated yield and three types of stresses (water, nitrogen, and temperature stresses) during plant's growth period. We also explored the influence of these stresses in four stages of crop growths (emergence, heading, anthesis, and maturity).
3. Results
3.1. The performance of EPIC crop simulator
The RSR values for simulated maize before and after calibration (table 3) indicate significant improvement in model performance after calibration. The RSR values for all countries except Democratic Republic of the Congo decreased to around 1 or less. In the latter country, however, RSR decreased significantly from 45.9 to 6.27. The main reason for high RSR in this country is a reported constant yield of 0.8 t ha−1 for the entire 33 year period, which is not realistic. The p-factor with values around 0.5 or more in all countries indicates that nearly 50% of observed data are bracketed within the 95PPU band, which are satisfactory values for crop calibration during the time span of 33 years. Their values are smaller than 2.5 and in most countries even smaller than 2, which is acceptable for yield simulations as suggested by Abbaspour et al (2007).
Figure 3. The grid level annual spatial distribution of precipitation based drought exposure index (DEIPCP) at twelve-month time scale during 1981–2012.
Download figure:
Standard image High-resolution image3.2. Drought exposure indices in SSA
The monthly values of DEIPCP and DEIPCP-PET calculated at the country level for three and twelve-month time scales (figures S1 and S2 available at stacks.iop.org/ERL/13/074010/mmedia) indicated a number of dry periods with different severities during 1980–2012. DEIPCP and DEIPCP-PET at three-month time scale showed higher frequencies of dry and wet periods than DEIPCP and DEIPCP-PET at twelve-month time scale which distinguish between short- and long-term droughts. The spatial comparison of DEIPCP and DEIPCP-PET at twelve-month time scale shows a general agreement in characterizing drought periods (figures 3 and S3). Both indices indicated that SSA countries experienced more severe droughts with longer persistency during 1980–1995 than 1996–2012. The 1982–1985 and 1992–1996 periods were identified as the two most extreme drought periods in many countries. Between 1982 and 1985, all countries in western and southern Africa experienced severe to extreme droughts. Eastern Africa was mostly exposed to severe to extreme drought in 1984. During 1992–1996, many southern and Central African countries were exposed to severe to extreme droughts as identified by both indices.
After 1995, both DEIPCP and DEIPCP-PET at twelve-month time scale showed fewer droughts, but with different severities in the two indices. DEIPCP-PET at twelve-month time scale indicated more droughts, whereas based on DEIPCP at twelve-month time scale, SSA was in a near normal status. Such differences were more obvious in Central Africa in 2005 and in western Africa in 2002 and 2009, where only near normal droughts were noticeable based on DEIPCP at twelve-month time scale. The differences between drought events in the two indices arose most likely from changes in temperature rather than precipitation. The Mann–Kendall test (figure S4) also confirmed significant increases in maximum and minimum temperatures in most SSA countries, except for some regions in Somalia, Ethiopia, Burkina Faso, and Ivory Coast (figure S4). Increasing temperature resulted in more drought events than was discernable only with DEIPCP at twelve-month time scale. The precipitation trend showed insignificant increases in almost all SSA countries, resulting in less drought characterization after 1995.
Figure 4. The correlation coefficient between precipitation based drought exposure index (DEIPCP) and CSI (top row); and the DEI based on the difference between precipitation and potential evapotranspiration (DEIPCP-PET) and CSI (bottom row) at one, three, six, nine and 12-month time scales.
Download figure:
Standard image High-resolution imageFigure 5. Country-level comparison of the interaction between DEIPCP and the CSI using power curves fitted to each grid within a country. The grey band indicates 95PPU and the blue line is the average curve obtained from all fitted curves to grids of a country. The average, minimum, and maximum values of β are shown as: β= average β (minimum β, maximum β).
Download figure:
Standard image High-resolution imageFigure 6. Spatial distribution of maize drought vulnerability based on the five types of CDVI defined in figure 2.
Download figure:
Standard image High-resolution image3.3. The relation between DEI and CSI
The calculated grid-level correlation coefficient of CSI with DEIPCP and with DEIPCP-PET shows that for both indices, the correlation coefficient was larger in southern and eastern Africa and Sahelian countries where the values were mostly above 0.5. In these regions, the three and six-month time scales, with values mostly larger than 0.75, had the highest correlation. Comparison of the correlation coefficients calculated for two drought exposure indices and CSI demonstrates that DEIPCP-PET performs better than DEIPCP. This is expected as the former takes into account both temperature and precipitation, whereas the latter considers only precipitation. The advantages of DEIPCP-PET over DEIPCP is more pronounced in Central African countries such as Democratic Republic of Congo and Central African Republic where the combination of PET and precipitation has a more profound impact on crop growth than precipitation alone. The correlation coefficient values in Central African countries were generally low (values were below 0.5), however, higher values were found with DEIPCP-PET. At one, three, and six-month time scale. Overall, DEIPCP and DEIPCP-PET at twelve-month time scale were least correlated to CSI in SSA countries, especially in Central Africa (figure 4). The values were mostly below 0.5 (or even 0.1), indicating that longer time periods were not as representative for agricultural drought vulnerability assessments as shorter timescales.
3.4. Country-level and grid-level crop drought vulnerability in SSA
At each grid point and from each time scales of DEIPCP and DEIPCP-PET, we chose the one with the highest correlation with CSI for vulnerability analysis. The power function was then fitted to the relation of DEIPCP (or DEIPCP-PET) and CSI equation (5). For the country analysis, we calculated the average and 95PPU bands for all grids within a country (figures 5 and S5). The shape of average fitted curves and the β values varied from one country to another, indicating that each country has a different type of vulnerability curve described in figure 2. Using DEIPCP and based on the β values of smaller than 0.9 (figure 5), countries such as Central African Republic of Congo, Madagascar, Zimbabwe, and Mauritania were identified as high vulnerability countries. The average β for these countries are 0.88, 0.9, 0.85, and 0.88 respectively. The β< 1 value indicate that the average curves lay above the y= x line. This means that a certain intensity of DEIPCP results in a higher intensity of CSI (figure 2). In countries such as Kenya, the average β values are larger than 1 representing low vulnerability. In other words, the fitted curve falls below y = x, which is associated with lower crop sensitivity during drought.
We also found that there is a significant difference between the maximum and minimum β values obtained from grids within a country indicating that the degree of vulnerability vary significantly from one region to another (figures 5 and S5). For example, in Tanzania the β values varies between 0.4 and 1.5. To understand the spatial vulnerability, the spatial distribution of CDVIs were mapped out at each grid cell based on β. The maps indicated that most parts of SSA experienced a certain level of vulnerability as the β values are smaller than 1.05 in most regions. The CDVI map based on linking DEIPCP to CSI shows that southern Angola, Zimbabwe, and Zambia from southern Africa, Central Africa countries, and some Sahelian countries such as Sudan and Mauritania with β values smaller than 0.9 are most vulnerable (figure 6).
Comparison of CDVI maps based on DEIPCP and DEIPCP-PET shows that there is general agreement between the most vulnerable countries, however, the CDVI map based on DEIPCP-PET showed slightly higher vulnerability. As expected measuring drought exposure based on a combination of precipitation and temperature variables can better represent vulnerability as both have significant impacts on crop growth.
The correlation coefficient between simulated yield and three types of stresses (water stress, nitrogen stress, and temperature stress) shows that in southern and eastern African countries as well as in Sahelian strip countries, water stress was the limiting factor for maize growth. Within these regions, the correlation coefficient between crop yield and water stress was above 0.5. The role of water stress was more apparent during heading and anthesis stages of crop growth. In Central African countries, despite the high amount of rainfall (figure S6), higher vulnerability of maize to drought was observed. As shown, there is significant correlation between maize yield and temperature in these regions. We also noticed that CDVI map based on the relation of DEIPCP-PET and yield showed higher vulnerability. In western African countries, maize growth is more vulnerable to drought due to experiencing more nitrogen stress specially during heading and anthesis stages.
Figure 7. Correlation coefficient between simulated maize yield and different stress types (top row: water stress, middle row: nitrogen stress, and bottom row: temperature stress) at four stages of maize growth i.e. emergence, heading, anthesis, and maturity.
Download figure:
Standard image High-resolution image4. Discussion
This paper quantifies maize drought vulnerability in SSA by linking probability-based DEI with CSI using a power function. CSI was obtained from the physically based EPIC crop model at the grid level and the fitted curve explaining the interaction of these two components. Our study assesses the impacts of drought conditions on crop yield during growing season. We answer the three questions raised in the introduction in three below sub-sections.
4.1. The suitability of different drought exposure indices
Concerning the first question, the comparison of two drought exposure indices (DEIPCP and DEIPCP-PET) showed that DEIPCP-PET calculated from combining precipitation and PET outperformed DEIPCP due to considering two important hydro-climate variables including precipitation and temperature, while DEIPCP is computed based on only precipitation. The spatial comparison of the correlation coefficient between DEIs and CSI shows lower values (<0.5) in tropical forested areas of Central and Western Africa with high amount of precipitation (>2000 mm yr−1). This means that in these regions there are probably other drivers of crop failure (such as pests, disease, or flooding) that are not drought-related factors. The correlation coefficient between the simulated maize yield with different stress types confirmed that nitrogen stress has a major role in some western African countries (figure 7). In this study, PET is calculated based on the Hargreaves method. However, it is important to note that different approaches in estimating PET may produce different results, which in turn lead to large uncertainties (Liu et al 2016). Testing different PET estimation methods (e.g. Penman-Monteith, Blaney–Criddle) in EPIC+ may help reducing uncertainty. Nevertheless, this was beyond the scope of this study.
The work has built the foundation to be applied in different regions on different spatial scales. It provides a methodological template to compile a larger range of drought exposure indices to capture uncertainties associated with variables that may be incorporated to defined drought exposure. Finally, our proposed approach requires including the third dimension of vulnerability i.e. adaptive capacity defined by IPCC. With the aim of proposed standardized metrics, adaptive capacity can be calculated in similar procedure as given by DEI and CSI. This facilitates comparing the severity of different vulnerability components. The three comparable components can be integrated to build CDVI using vulnerability surface methods such as those proposed by Guo et al (2016).
4.2. The impact of different timescales of DEIPCP and DEIPCP-PET
The drought events identified based on DEIPCP and DEIPCP-PET at twelve-month time scale were consistent with actual droughts in SSA reported in recent literature (Anderson et al 2012, Masih et al 2014). For example, both indices highlighted the two extreme drought periods of 1982–1985 and 1992–1996 reported by Masih et al (2014) or the prolonged drought in Sudan after 2000 reported by Elagib and Elhag (2011). We found some differences in drought periods identified by DEIPCP and DEIPCP-PET at twelve-month time scale. For example, drought events occurring after 2006 in Central Africa and some eastern African countries such as Somalia and Djibouti (Dutra et al 2013) were better recognized by DEIPCP-PET than DEIPCP, which showed only mild droughts. DEIPCP-PET is based on both temperature and precipitation, where a combination of climate events (e.g. low precipitation and high temperature) may cause significant impact on a system, as discussed by Mazdiyasni and AghaKouchak (2015). We also found some differences in the drought events calculated at different time scales. Due to these differences and also because of the differences in the DEIPCP and DEIPCP-PET severities (in some countries), their suitability for crop vulnerability assessment should be evaluated in detail. As also mentioned by Masih et al (2014), the suitability of drought indices should be evaluated according to the sector it influences. In this study, we selected the most appropriate time scale for the agricultural sector based on their correlation with CSI.
The correlation coefficient between DEIPCP (and DEIPCP-PET) at different time scale with CSI showed overall smaller values in Central Africa and some western African countries such as Nigeria, Ghana, and Cameroon. This is related to high precipitation in these regions exceeding 1000 mm yr−1 (figure S6). In some countries such as Gabon, Liberia, and South Nigeria the yearly precipitation is above 2000 mm yr−1. Therefore, crops are less exposed to water stress. In other words, while these regions might be exposed to meteorological drought, the amount of precipitation remains sufficient for crop growth and therefore agricultural drought does not happen. In these region, the correlation of DEIPCP-PET with CSI is slightly higher than DEIPCP and CSI. This suggests that within these regions both precipitation and temperature should be considered as variable to determine drought exposure. On the other hand, in southern Africa and Sahelian countries with yearly precipitation below 660 mm yr−1, the correlation between DEIPCP (and DEIPCP-PET) with CSI is larger than 0.8 with higher values for DEIPCP compared to DEIPCP-PET, meaning that precipitation is a more limiting factor than temperature for these regions.
Concerning the second question, the comparison of different timescales of DEIPCP showed that the highest correlations of DEIPCP with CSI were for three and six-month timescales and mostly in the southern African and Sahelian countries. This corroborates the studies of Manatsa et al (2010) and Rouault and Richard (2005). Labudová et al (2016) also found that the three-month timescale correlated very well with maize yield in the Danubian Lowland and the east Slovakian Lowland. Overall, DEIPCP and DEIPCP-PET at twelve-month time scale were the least correlated with CSI compared to other timescales. This is because the twelve-month time scale is based on the accumulation of precipitation over the last 12 months. Therefore, the weight of single months becomes smaller and less significant. However, water shortage at certain phonological periods may be more important than at other phonological periods. For example, much greater losses could be expected as a result of prolonged water stress during the tasselling and ear formation stages of corn growth (Cakir (2004) than during vegetative growth.
4.3. Comparison of maize drought vulnerability in different countries
With the help of a process-based crop model, maize yields were obtained on a 0.5° grid level and vulnerability hotspots were identified with the same resolution, which is a more reasonable resolution for vulnerability assessment for sub-national studies. One advantage of our approach was that the applied crop model was coupled with SUFI-2 calibration technique which increased the reliability of simulated yields. We believe this is important, since our calibration procedure provided the possibility of taking into account the temporal variability for over three decades, which is long enough to cover various weather conditions. The evolution of drought exposure in figure 3 and S3 indicates that within this time span all grids experienced extreme wet to dry conditions. It is clear that any calibrated model does not apply to conditions beyond which it was calibrated for, but as EPIC is a physically based model, it should simulate well given a given set of condition if known.
By using EPIC, we added deeper insights on different underlying stresses making maize of one region physically vulnerable. The vulnerability maps (figure 6) showed that southern Africa and some Sahelian countries were found to be high vulnerable regions due to experiencing more periods of water stress as a result of low precipitation (figures 7 and S6). Central Africa was vulnerable due to temperature stress and for this reason we found that drought exposure based on the difference between precipitation and potential evapotranspiration (DEIPCP-PET) showed higher vulnerability compared to DEIPCP. Other studies assessed the impact of temperature on maize growth (Butler and Huybers 2015, Deryng et al 2014, Gourdji et al 2013). Gourdji et al (2013) for example found that crops are physiologically sensitive to temperatures in the reproductive stage. Here, we noticed the highest correlation to temperature during heading and anthesis. EPIC does not consider crop phenology explicitly, therefore we could not specify separate critical temperature for each growth stage of crop. Future studies can attempt to upgrade model to overcome this limitation.
5. Conclusion
The probability-based procedure use to define DEIs and CSI advances current approaches in several ways. First, the normalized metrics are more robust compared to the ratio-based definitions in current literature (Huai 2016, Simelton et al 2009). In addition, the standardized definition facilities their comparison with other most widely used drought indices such as the Palmer Drought Severity Index (Palmer 1965). Finally, defining components of vulnerability with the same base facilitates interpretation of fitted curves obtained from their aggregation in a power function.
The physical drought vulnerability maps on the fine spatial resolution provide the geographical bases for identifying vulnerable hotspots at sub-national scale. Such improved understanding is important for early warning on drought vulnerability. It also enables sub-national, national, and international policy makers to prioritize proactive and reactive agricultural adaptation strategies in response to drought. The approaches developed here can be used to project the vulnerability under future scenarios of climate change and measure the long-term impacts of droughts on food production. It is, however, important to emphasize that propose of mitigating policies for local and regional farmers, managers, and engineers by strategies such as changing the land use to grow more drought resistant crops and varieties, providing adequate water infrastructures or water use to combat water stress will need additional information and studies.
One of the limitations of this study is the lack of detailed input data such as temporal variability of cultivated area at the grid level. In addition, some FAOSTAT yield data are of poor quality in SSA. But, unfortunately, this is the only available source for the moment and is a general problem of any study in the region. However, this limitation does not significantly influence the robustness of the methodology and the general results derived because the vulnerability assessments were based on rainfed maize yield simulated on the grid level using the EPIC crop model which has a unit of t ha−1. The results can be easily validated as more regional data become available.
Acknowledgments
This study was supported by the Swiss National Science Foundation (SNF No.: CR21I3_146430. December 2013–November 2016).