For two-dimensional percolation on a domain with the topology of a disc, we introduce a nested-path (NP) operator and thus a continuous family of one-point functions 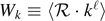 , where ℓ is the number of independent (i.e., non-overlapping) nested closed paths surrounding the center, k is a path fugacity, and
, where ℓ is the number of independent (i.e., non-overlapping) nested closed paths surrounding the center, k is a path fugacity, and  projects on configurations having a cluster connecting the center to the boundary. At criticality, we observe a power-law scaling
projects on configurations having a cluster connecting the center to the boundary. At criticality, we observe a power-law scaling 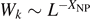 , with L the linear system size, and we determine the exponent XNP as a function of k. On the basis of our numerical results, we conjecture an analytical formula,
, with L the linear system size, and we determine the exponent XNP as a function of k. On the basis of our numerical results, we conjecture an analytical formula, 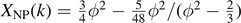 with k = 2 cos(πϕ), which reproduces the exact results for k = 0, 1 and agrees with the high-precision estimate of
with k = 2 cos(πϕ), which reproduces the exact results for k = 0, 1 and agrees with the high-precision estimate of 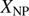 for other k values. In addition, we observe that W2(L) = 1 for site percolation on the triangular lattice with any size L, and we prove this identity for all self-matching lattices.
for other k values. In addition, we observe that W2(L) = 1 for site percolation on the triangular lattice with any size L, and we prove this identity for all self-matching lattices.
Fine Latticework: Celebrating the Craftsmanship of Robert M. Ziff in Honour of his 70th Birthday
Guest editors
Jesper Jacobsen, Laboratoire de Physique Théorique, École Normale Supérieure, FranceStephan Mertens, Otto-von-Guericke University, Germany
Christian Scullard, Lawrence Livermore National Laboratory, USA
Scope
Robert M. Ziff has had a long and fruitful career, doing path-breaking work on a wide range of problems in lattice statistical mechanics. His work on Monte Carlo methods for percolation has inspired the research of a generation of physicists. He has also made significant contributions to exact solutions in percolation, both on the lattice level and in the continuum limit. The latter regime, which is described by conformal field theory and Schramm-Loewner evolution, is a particularly fertile area of physics and mathematics. Percolation also has application in the study of networks and in particular epidemic modelling. Professor Ziff's most cited paper is on the subject of catalytic reactions and describes what has become the celebrated Ziff-Gulari-Barshad model.
This issue is intended, on the occasion of his 70th birthday, to bring together Robert M. Ziff's collaborators from his many fields of interest and to celebrate the contributions he has made.
The issue will be open to submissions until 31 December 2021 and you can submit manuscripts through ScholarOne Manuscripts
Preface
Viewpoint
Papers
The capacity to devise order metrics to characterize and classify microstructures of multiphase heterogeneous media across length scales is an outstanding but highly challenging task, given the richness of the possible geometries and topologies of the phases that can arise. This investigation initiates a program to formulate order metrics to characterize the degree of order/disorder of the microstructures of two-phase media in  -dimensional Euclidean space
-dimensional Euclidean space  across length scales. In particular, we propose the use of the local volume-fraction variance
across length scales. In particular, we propose the use of the local volume-fraction variance  associated with a spherical window of radius R as an order metric. We determine
associated with a spherical window of radius R as an order metric. We determine 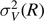 as a function of
as a function of 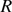 for 22 different models across the first three space dimensions, including both hyperuniform and nonhyperuniform systems with varying degrees of short- and long-range order. We find that the local volume-fraction variance as well as asymptotic coefficients and integral measures derived from it provide reasonably robust and sensitive order metrics to categorize disordered and ordered two-phase media across all length scales. Such order metrics could be employed to accelerate the discovery of novel heterogeneous materials by tailoring their degree of order/disorder.
for 22 different models across the first three space dimensions, including both hyperuniform and nonhyperuniform systems with varying degrees of short- and long-range order. We find that the local volume-fraction variance as well as asymptotic coefficients and integral measures derived from it provide reasonably robust and sensitive order metrics to categorize disordered and ordered two-phase media across all length scales. Such order metrics could be employed to accelerate the discovery of novel heterogeneous materials by tailoring their degree of order/disorder.
The cluster merging process was regarded as the central kinetics of a sol–gel transition and was solved analytically by Ziff. Since then, it has been applied to diverse phenomena, such as the evolution of social networks and spread of epidemic diseases. The sol–gel transition is applied to the robustness of complex networks with regard to the percolation transition. Percolation transition is regarded as a robust continuous transition; however, in complex systems, diseases or rumors can spread rapidly. Hence, it has been challenging to modify percolation models such that they exhibit a discontinuous transition that explains abruptly changing phenomena. Recently, researchers argued that a discontinuous percolation transition can occur when a network evolves under a rule with global information. In this study, we review earlier studies on percolation models that exhibit discontinuous transitions, focusing particularly on models with cluster-merging kinetics.
We present an algorithm to compute the exact probability Rn(p) for a site percolation cluster to span an n × n square lattice at occupancy p. The algorithm has time and space complexity O(λn) with λ ≈ 2.6. It allows us to compute Rn(p) up to n = 24. We use the data to compute estimates for the percolation threshold pc that are several orders of magnitude more precise than estimates based on Monte-Carlo simulations.
We propose a covariant definition of the fractional Klein–Gordon equation (KGE) with long-range interactions independent of the metric of the underlying manifold. As an example we consider the fractional KGE on AdS2+1, computing the explicit kernel representation of the fractional Laplace–Beltrami operator as well as the two-point propagator of the fractional KGE. Our results suggest that the propagator only exists if the mass is small compared to the inverse AdS radius, presumably because the AdS space expands faster with distance as a flat space of the same dimension. Our results are expected to be useful in particular for new applications of the AdS/CFT correspondence within statistical mechanics and quantum information.
We study transport within a spatially heterogeneous one-dimensional quantum walk with a combination of hierarchical and random barriers. Recent renormalization group calculations for a spatially disordered quantum walk with a regular hierarchy of barriers alone have shown a gradual decrease in transport but no localization for increasing (but finite) barrier sizes. In turn, it is well-known that extensive random disorder in the spatial barriers is sufficient to localize a quantum walk on the line. Here we show that adding only a sparse (sub-extensive) amount of randomness to a hierarchy of barriers is sufficient to induce localization such that transport ceases. Our numerical results suggest the existence of a localization transition for a combination of both, the strength of the regular barrier hierarchy at large enough randomness as well as the increasing randomness at sufficiently strong barriers in the hierarchy.
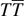 deformation
deformation
We recall the origins of the law of the distribution of areas contained within domain wall loops in critical 2D models, and its evolution under a thermal quench to the ordered phase. We conjecture that the latter is described by the so-called 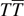 deformation of the critical model.
deformation of the critical model.
The well known problem of gradient percolation has been revisited to study the probability distribution of island sizes. It is observed that like the ordinary percolation, this distribution is also described by a power law decaying function but the associated critical exponents are found to be different. Because of the underlying gradient for the occupation probability, the average value of the island sizes also has a gradient. The variation of the average island size with the probability of occupation along the gradient has been studied together with its scaling analysis. Further, we have introduced and studied the gradient bond percolation and on studying the island size distribution statistics, we have obtained very similar results. We have also studied the characteristics of the diffusion profile of the particle system on a lattice which is initially half filled and half empty. Here also we observe the same value for the island size probability distribution exponent. Finally, the same study has been repeated for the nonlinear gradient percolation and the value of the island size distribution exponent is found to be a function of the strength of the nonlinear parameter.
Many realistic systems such as infrastructures are characterized by spatial structure and anisotropic alignment. Here we propose and study a model for dealing with such characteristics by introducing a parameter that controls the strength of the anisotropy in the spatial network. This parameter is added to an existing isotropic model used to describe networks under spatial constraints, thus generalizing the spatial model to take into account both spatial and anisotropic features. We study the resilience of such networks by using a percolation process and find that anisotropy has a negative impact on a network's robustness. In addition, our results suggest that the anisotropy in this model does not affect the critical exponent of the correlation length, ν, which remains the same as the known ν in 2D isotropic lattices.
We argue that the elastic backbone (EB) (union of shortest paths) on a cylindrical system, studied by Sampaio Filho et al [2018 Phys. Rev. Lett.120 175701], is in fact the backbone of two-dimensional directed percolation (DP). We simulate the EB on the same system as considered by these authors, and also study the DP backbone directly using an algorithm that allows backbones to be generated in a completely periodic manner. We find that both the EB in the bulk and the DP backbone have a fractal dimension of db = dB,DP = 1.681 02(15) at the identical critical point pc,DP ≈ 0.705 485 22. We also measure the fractal dimension at the edge of the EB system and for the full DP clusters, and find de = dDP = 1.840 54(4). We argue that those two fractal dimensions follow from the DP exponents as dB,DP = 2 − 2β/ν∥ = 1.681 072(12) and dDP = 2 − β/ν∥ = 1.840 536(6). Our fractal dimensions differ from the value 1.750(3) found by Sampaio Filho et al.
In previous work, two of the authors determined, completely and rigorously, a solution space  for a homogeneous system of 2N + 3 linear partial differential equations (PDEs) in 2N variables that arises in conformal field theory (CFT) and multiple Schramm–Löwner evolution (SLEκ). The system comprises 2N null-state equations and three conformal ward identities that govern CFT correlation functions of 2N one-leg boundary operators or SLEκ partition functions. M Bauer et al conjectured a formula, expressed in terms of 'pure SLEκ partition functions,' for the probability that the growing curves of a multiple-SLEκ process join in a particular connectivity. In a previous article, we rigorously define certain elements of
for a homogeneous system of 2N + 3 linear partial differential equations (PDEs) in 2N variables that arises in conformal field theory (CFT) and multiple Schramm–Löwner evolution (SLEκ). The system comprises 2N null-state equations and three conformal ward identities that govern CFT correlation functions of 2N one-leg boundary operators or SLEκ partition functions. M Bauer et al conjectured a formula, expressed in terms of 'pure SLEκ partition functions,' for the probability that the growing curves of a multiple-SLEκ process join in a particular connectivity. In a previous article, we rigorously define certain elements of  , which we call 'connectivity weights,' argue that they are in fact pure SLEκ partition functions, and show how to find explicit formulas for them in terms of Coulomb gas contour integrals. Our formal definition of the connectivity weights immediately leads to a method for finding explicit expressions for them. However, this method gives very complicated formulas where simpler versions may be available, and it is not applicable for certain values of κ ∈ (0, 8) corresponding to well-known critical lattice models in statistical mechanics. In this article, we determine expressions for all connectivity weights in
, which we call 'connectivity weights,' argue that they are in fact pure SLEκ partition functions, and show how to find explicit formulas for them in terms of Coulomb gas contour integrals. Our formal definition of the connectivity weights immediately leads to a method for finding explicit expressions for them. However, this method gives very complicated formulas where simpler versions may be available, and it is not applicable for certain values of κ ∈ (0, 8) corresponding to well-known critical lattice models in statistical mechanics. In this article, we determine expressions for all connectivity weights in 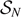 for N ∈ {1, 2, 3, 4} (those with N ∈ {3, 4} are new) and for so-called 'rainbow connectivity weights' in
for N ∈ {1, 2, 3, 4} (those with N ∈ {3, 4} are new) and for so-called 'rainbow connectivity weights' in 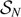 for all
for all 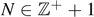 . We verify these formulas by explicitly showing that they satisfy the formal definition of a connectivity weight. In appendix B, we investigate logarithmic singularities of some of these expressions, appearing for certain values of κ predicted by logarithmic CFT.
. We verify these formulas by explicitly showing that they satisfy the formal definition of a connectivity weight. In appendix B, we investigate logarithmic singularities of some of these expressions, appearing for certain values of κ predicted by logarithmic CFT.
During the COVID pandemic, periods of exponential growth of the disease have been mitigated by containment measures that in different occasions have resulted in a power-law growth of the number of cases. The first observation of such behaviour has been obtained from 2020 late spring data coming from China by Ziff and Ziff in reference Ziff and Ziff (2020 Fractal kinetics of COVID-19 pandemic MedRxiv). After this important observation the power-law scaling (albeit with different exponents) has also been observed in other countries during periods of containment of the spread. Early interpretations of these results suggest that this phenomenon might be due to spatial effects of the spread. Here we show that temporal modulations of infectivity of individuals due to containment measures can also cause power-law growth of the number of cases over time. To this end we propose a stochastic well-mixed susceptible-infected-removed model of epidemic spreading in presence of containment measures resulting in a time dependent infectivity and we explore the statistical properties of the resulting branching process at criticality. We show that at criticality it is possible to observe power-law growth of the number of cases with exponents ranging between one and two. Our asymptotic analytical results are confirmed by extensive Monte Carlo simulations. Although these results do not exclude that spatial effects might be important in modulating the power-law growth of the number of cases at criticality, this work shows that even well-mixed populations may already feature non trivial power-law exponents at criticality.
The size and shape of the region affected by an outbreak is relevant to understand the dynamics of a disease and help to organize future actions to mitigate similar events. A simple extension of the SIR model is considered, where agents diffuse on a regular lattice and the disease may be transmitted when an infected and a susceptible agents are nearest neighbors. We study the geometric properties of both the connected cluster of sites visited by infected agents (outbreak cluster) and the set of clusters with sites that have not been visited. By changing the density of agents, our results show that there is a mixed-order (hybrid) transition separating a phase where the outbreak cluster is finite from the other one where it percolates through the system. Moreover, the outbreak cluster seems to have the same exponents of the backbone of the critical cluster of the ordinary percolation while the clusters with unvisited sites have a size distribution with a Fisher exponent τ < 2.
The site percolation threshold of the hexagonal lattice satisfies 0.656 246 < pc < 0.739 695. For comparison, the largest previous lower bound of 0.652 703... was established in 1981, and the smallest previous upper bound of 0.743 359 was derived in 2007. The bound is obtained by using the substitution method to compare the hexagonal lattice site model to an exactly-solved two-parameter site percolation model on the martini lattice. Computational reductions involving graph-welding, symmetry, non-crossing partitions, and network flow computations overcome challenges to establishing stochastic ordering between the models.
We have found analytical expressions (polynomials) of the percolation probability for site percolation on a square lattice of size L × L sites when considering a plane (the crossing probability in a given direction), a cylinder (spanning probability), and a torus (wrapping probability along one direction). Since some polynomials are extremely cumbersome, they are presented as separate files in supplemental material. The system sizes for which this was feasible varied up to L = 17 for a plane, up to L = 16 for a cylinder, and up to L = 12 for a torus. To obtain a percolation probability polynomial, all possible combinations of occupied and empty sites have to be taken into account. However, using dynamic programming along with some ideas related to the topology, we offer an algorithm which allows a significant reduction in the number of configurations requiring consideration. A rigorous formal description of the algorithm is presented. Divisibility properties of the polynomials have been rigorously proved. Reliability of the polynomials obtained have been confirmed by the divisibility tests. The wrapping probability polynomials on a torus provide a better estimate of the percolation threshold than that from the spanning probability polynomials. Surprisingly, even a naive finite size scaling analysis allows an estimate to be obtained of the percolation threshold pc = 0.592 69.
We study the competitive irreversible adsorption of a binary mixture of monomers and square-shaped particles of linear size R on the square lattice. With the random sequential adsorption model, we investigate how the jamming coverage and percolation properties depend on the size ratio R and relative flux F. We find that the onset of percolation of monomers is always lower for the binary mixture than in the case with only monomers (R = 1). Moreover, for values F below a critical value, the higher is the flux or size of the largest species, the lower is the value of the percolation threshold for monomers.
We studied random sequential adsorption (RSA) of three classes of polygons with rounded corners: rectangles, isosceles triangles, and orthogonal triangles. Using the algorithm that enables the generation of strictly saturated RSA packing, we systematically determined the mean saturated packing fraction for RSA configurations built by these shapes. The main aim was to find the figure that forms the densest random configuration. Although for rounded rectangles the packing fractions were lower than for discorectangles, the densities reached for some rounded isosceles and right triangles exceeded the highest known two-dimensional packing fraction for configurations built of unoriented monodisperse objects. The microstructural properties of several packings were discussed in terms of the two-point density autocorrelation function.
In this article, I have outlined how an accomplished researcher like Robert Ziff has influenced a new generation of researchers across the globe like gravity as an action-at-a-distance. In the 80s Ziff made significant contributions to the kinetics of fragmentation followed by the kinetics of aggregation. Here, I will discuss fractal and multifractal that emerges in fragmentation and aggregation processes where the dynamics is governed by non-trivial conservation laws. I have then discussed my recent works and results on percolation where I made extensive use of Newman–Ziff fast Monte Carlo algorithm. To this end, I have defined entropy which paved the way to define specific heat and show that the critical exponents of percolation obey Rushbrooke inequality. Besides, we discuss how entropy and order parameter together can help us to check whether the percolation is accompanied by order–disorder transition or not. The idea of entropy also help to explain why encouraging smaller cluster to grow faster than larger clusters makes the transition explosive.
In this paper, we provide a systematic way of finding explicit solutions for a class of continuous fragmentation equations with growth or decay in the state space and derive new explicit solutions in the cases of constant and linear growth/decay coefficients.
In the conventional lattice percolation models, bonds or sites are open at random, whereas in reality there is often interplay of percolation and the kinetics under consideration. An interesting and practically important example is hydrocarbon conversion occurring in a reactor containing  mm-sized porous pellets with catalytic nanoparticles deposited at walls of the nanopores. Such catalytic heterogeneous reactions are often accompanied by coke formation deactivating catalytic nanoparticles and blocking pores for reactant diffusion, so that one needs to remove coke from time to time e.g. via reaction with oxygen. Herein, I first present generic coarse-grained Monte Carlo simulations of coke formation in a single pellet with the emphasis on the reaction regime influenced by reactant diffusion in pores. Then, the obtained coke distributions are used for similar simulations of coke removal. This combination of the models has allowed me to illustrate qualitatively new spatio-temporal regimes of the processes under consideration. For example, the removal of coke can be slow in the beginning, due to blocking of oxygen diffusion near the external pellet-gas interface and preventing its penetration to the central part of a pellet, and then fast when the pathways for diffusion to the center become to be open.
mm-sized porous pellets with catalytic nanoparticles deposited at walls of the nanopores. Such catalytic heterogeneous reactions are often accompanied by coke formation deactivating catalytic nanoparticles and blocking pores for reactant diffusion, so that one needs to remove coke from time to time e.g. via reaction with oxygen. Herein, I first present generic coarse-grained Monte Carlo simulations of coke formation in a single pellet with the emphasis on the reaction regime influenced by reactant diffusion in pores. Then, the obtained coke distributions are used for similar simulations of coke removal. This combination of the models has allowed me to illustrate qualitatively new spatio-temporal regimes of the processes under consideration. For example, the removal of coke can be slow in the beginning, due to blocking of oxygen diffusion near the external pellet-gas interface and preventing its penetration to the central part of a pellet, and then fast when the pathways for diffusion to the center become to be open.
We consider a Brownian particle with diffusion coefficient D in a d-dimensional ball of radius R with reflecting boundaries. We study the maximum Mx(t) of the trajectory of the particle along the x-direction at time t. In the long time limit, the maximum converges to the radius of the ball Mx(t) → R for t → ∞. We investigate how this limit is approached and obtain an exact analytical expression for the distribution of the fluctuations Δ(t) = [R − Mx(t)]/R in the limit of large t in all dimensions. We find that the distribution of Δ(t) exhibits a rich variety of behaviors depending on the dimension d. These results are obtained by establishing a connection between this problem and the narrow escape time problem. We apply our results in d = 2 to study the convex hull of the trajectory of the particle in a disk of radius R with reflecting boundaries. We find that the mean perimeter ⟨L(t)⟩ of the convex hull exhibits a slow convergence towards the perimeter of the circle 2πR with a stretched exponential decay  . Finally, we generalise our results to other confining geometries, such as the ellipse with reflecting boundaries. Our results are corroborated by thorough numerical simulations.
. Finally, we generalise our results to other confining geometries, such as the ellipse with reflecting boundaries. Our results are corroborated by thorough numerical simulations.
We present a method for computing transition points of the random cluster model using a generalization of the Newman–Ziff algorithm, a celebrated technique in numerical percolation, to the random cluster model. The new method is straightforward to implement and works for real cluster weight q > 0. Furthermore, results for an arbitrary number of values of q can be found at once within a single simulation. Because the algorithm used to sweep through bond configurations is identical to that of Newman and Ziff, which was conceived for percolation, the method loses accuracy for large lattices when q > 1. However, by sampling the critical polynomial, accurate estimates of critical points in two dimensions can be found using relatively small lattice sizes, which we demonstrate here by computing critical points for non-integer values of q on the square lattice, to compare with the exact solution, and on the unsolved non-planar square matching lattice. The latter results would be much more difficult to obtain using other techniques.
We investigate an averaging process that describes how interacting agents approach consensus through binary interactions. In each elementary step, two agents are selected at random and they reach compromise by adopting their opinion average. We show that the fraction of agents with a monotonically decreasing opinion decays as e−αt, and that the exponent 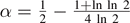 is selected as the extremum from a continuous spectrum of possible values. The opinion distribution of monotonic agents is asymmetric, and it becomes self-similar at large times. Furthermore, the tails of the opinion distribution are algebraic, and they are characterized by two distinct and nontrivial exponents. We also explore statistical properties of agents with an opinion strictly above average.
is selected as the extremum from a continuous spectrum of possible values. The opinion distribution of monotonic agents is asymmetric, and it becomes self-similar at large times. Furthermore, the tails of the opinion distribution are algebraic, and they are characterized by two distinct and nontrivial exponents. We also explore statistical properties of agents with an opinion strictly above average.